鱼雷作为潜艇进行隐蔽攻击的主要武器,实现远距攻击是大洋作战的关键。但受潜艇声呐探测能力制约,在鱼雷远距攻击中,仅仅依靠潜艇来获取目标信息较为困难,无法充分发挥鱼雷航程远的优势,必须考虑远程目标指示系统(简称目指)的信息支援。
国内对基于目指信息的鱼雷远距攻击开展了持续研究,文献[1]提出了利用目指信息实施线导+声自导鱼雷攻击的方式;文献[2]根据侦察探测兵力通报的目标位置及圆概率误差、目标运动要素及目标运动要素误差等信息,研究了基于目指信息的目标散布区域及目标散布概率密度计算公式;文献[3]通过分析目指信息引导下的鱼雷远距攻击流程,建立了采用前置点导引的线导+声自导鱼雷远距攻击数学模型。但在可查阅的文献中,缺乏对目指信息保障下线导+尾流自导和线导+尾转声制导方式的研究。本文在分析目指信息保障下线导+尾流自导鱼雷前置点推算导引法的基础上,对尾转声时机、尾转声鱼雷航向等开展研究。
1 基于目指信息的线导+尾流自导鱼雷攻击模型 1.1 目指信息传输模型目指信息传输模型主要包括目标指示时延
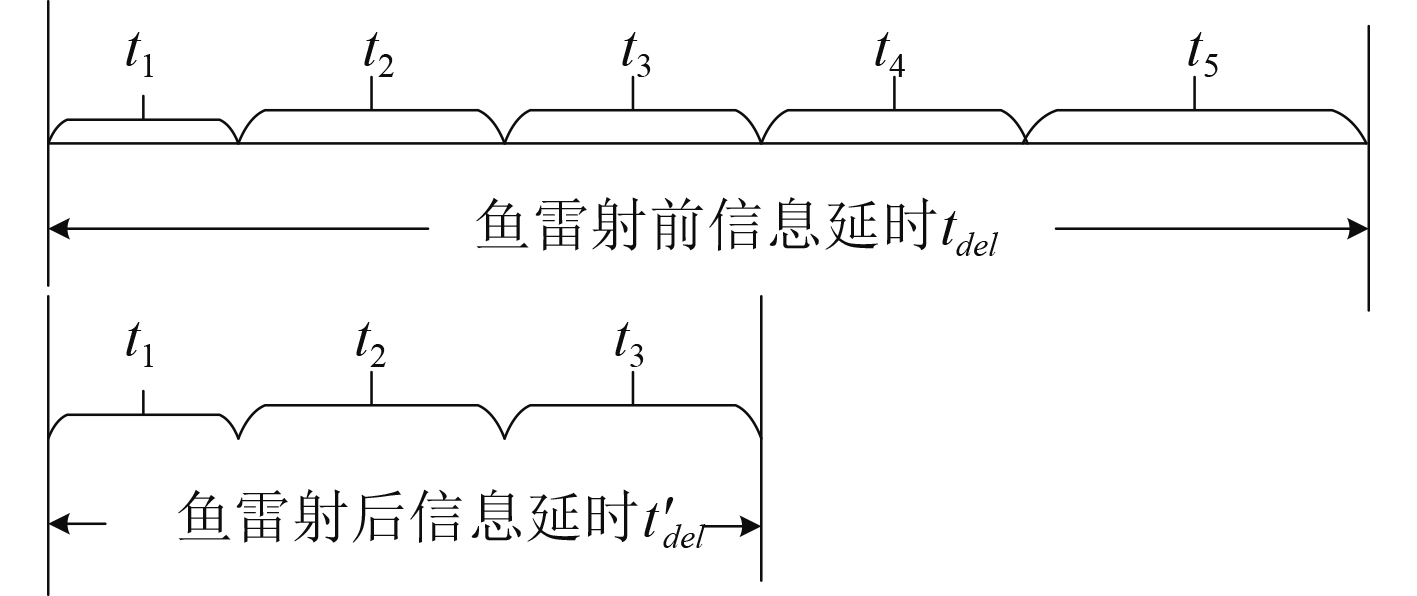
在鱼雷发射前,
|
图 1 目标指示时延示意图 Fig. 1 Target indication delay diagram |
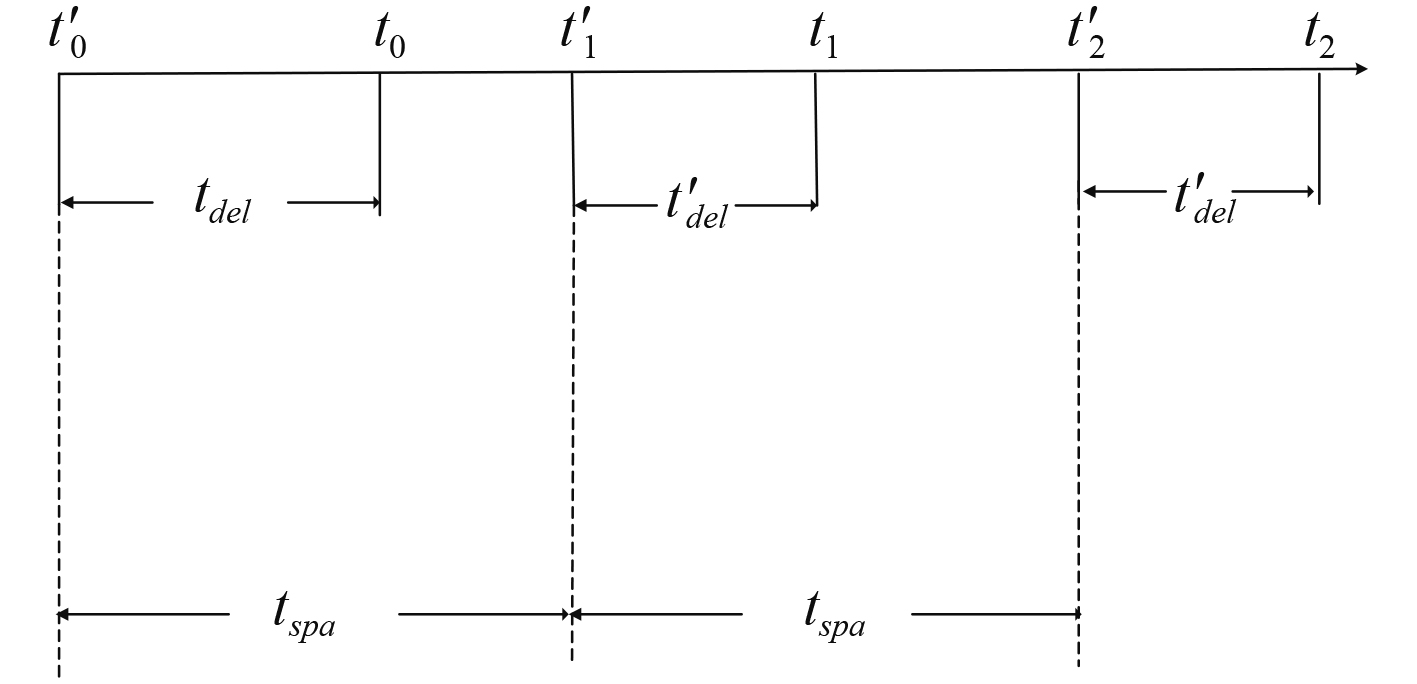
图2为目指信息传输时间轴,设引导兵力探测到目标信息的时刻为
|
图 2 目指信息传输时间轴 Fig. 2 Target indication transmission timeline |
| $ \left\{ \begin{gathered} {t_0} = t{'_0} + {t_{del}} ,\\ {t_{spa}} = t{'_1} - t{'_0} 。\\ \end{gathered} \right. $ | (1) |
式中:
以
1)
2)目标运动模型[3]
假设目标做匀速直线运动,则目标任意时刻的坐标可由下式进行推算:
| $ \left\{ \begin{gathered} {X_m}(t) = {X_m}(t - 1) + {V_m}(t - 1)\Delta t\sin {C_m}(t - 1) ,\\ {Y_m}(t) = {Y_m}(t - 1) + {V_m}(t - 1)\Delta t\cos {C_m}(t - 1) 。\\ \end{gathered} \right. $ | (2) |
式中:
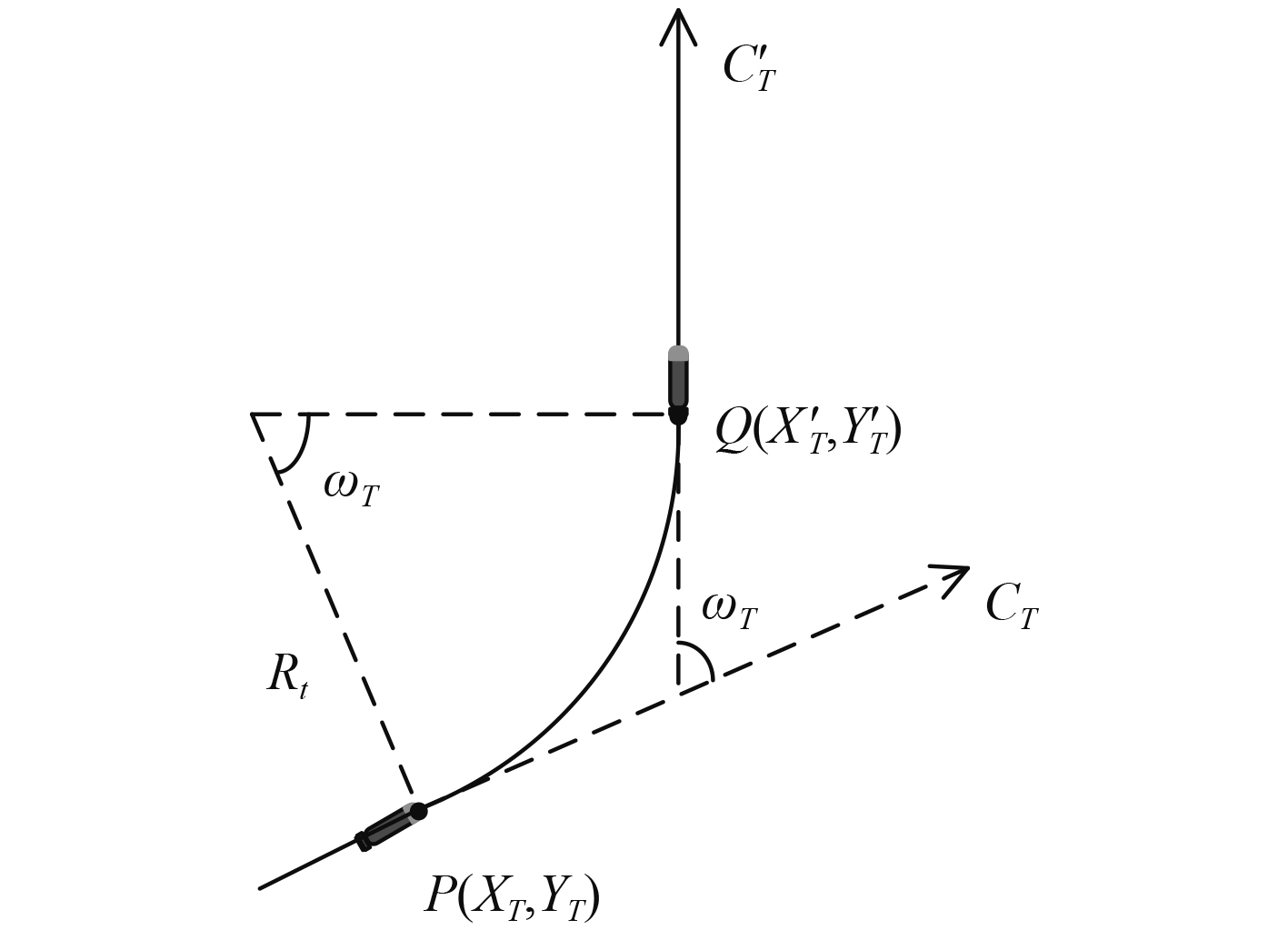
线导+声自导鱼雷导引过程中可采用折线转向替代曲线转向,以简化导引诸元解算和仿真模拟过程;线导+尾流自导鱼雷导引过程中可采用折线转向来简化导引诸元解算,但须用曲线转向模拟仿真过程[5]。当线导鱼雷转向时,可认为鱼雷做匀速圆周运动,如图3所示。设
|
图 3 鱼雷曲线转向示意图 Fig. 3 Schematic diagram of torpedo curve steering |
| $ Q = P + {R_{\text{T}}}{e^{i[{C_T} + \frac{\text{π} }{2}{{\rm{sgn}}} ({\omega _T})]}} + {R_{\text{T}}}{e^{i[{C_T} - \frac{\text{π} }{2}{{\rm{sgn}}} ({\omega _T}) + {\omega _T}{{\rm{sgn}}} ({\omega _T})]}}。$ | (3) |
式中:sgn为符号函数,其中鱼雷沿当前航向向左转时
| $ \left\{ \begin{split} X{'_T} = & {X_T} + {R_T}\cos \left[{C_T} + \frac{\text{π} }{2}{\rm sgn} ({\omega _T})\right] + \\ & {R_T}\cos \left[{C_T} - \frac{\text{π} }{2}{\rm sgn} ({\omega _T}) + {\omega _T}{\rm sgn} ({\omega _T})\right] ,\\ Y{'_T} = & {Y_T} + {R_T}\sin \left[{C_T} + \frac{\text{π} }{2}{\rm sgn} ({\omega _T})\right] + \\ & {R_T}\sin \left[{C_T} - \frac{\text{π} }{2}{\rm sgn} ({\omega _T}) + {\omega _T}{\rm sgn} ({\omega _T})\right] 。\end{split} \right. $ | (4) |
目指信息往往提供某时刻的目标位置和圆概率误差、目标速度和速度误差、目标航向和航向误差[2]。传统线导鱼雷攻击中,当可测得目标运动要素时,宜采用前置点导引法[7]。但是在目指信息保障下实施鱼雷攻击时,潜艇收到的目标位置信息并不是目标当前时刻的位置,要想将鱼雷导引到目标的前置点方位上,必须首先根据目指提供的目标运动要素推算目标当前时刻的位置,然后再根据相遇三角形原理计算出鱼雷航向,使鱼雷与目标散布中心在前置点相遇,本文将这种导引方法称之为推算前置点导引法。
尾流自导鱼雷通过检测尾流攻击目标,由于尾流较难仿造,鱼雷进入尾流后,目标难以实施有效的对抗,因此尾流自导鱼雷得到了广泛应用,是攻击敌方水上目标的重要武器[8]。与声自导鱼雷不同的是,尾流自导鱼雷是瞄准的目标有效尾流,设舰船有效尾流长度为
| $ {L_w} = {k_A} \cdot {V_m} 。$ | (5) |
式中:
设尾流宽度为
| $ \left\{ \begin{gathered} {B_{kc}} = 3 \cdot B,{V_m} \leqslant 20\;{\rm{kn}} ,\\ {B_{kc}} = 5 \cdot B,{V_m} > 20\;{\rm{kn}} 。\\ \end{gathered} \right. $ | (6) |
如图4所示,设预置尾流瞄点

|
图 4 舰船尾流进入点示意图 Fig. 4 Schematic diagram of ship wake entry point |
| $ {D_w} = k({k_A} \cdot {V_m} + A) - A。$ | (7) |
式中:
1)推算目标当前时刻位置
设
| $ \left\{ \begin{gathered} {X_m}({t_0}) = {X_m}(t{'_0}) + {V_m}(t{'_0}){t_{del}}\sin {C_m}(t{'_0}) ,\\ {Y_m}({t_0}) = {Y_m}(t{'_0}) + {V_m}(t{'_0}){t_{del}}\cos {C_m}(t{'_0}) 。\\ \end{gathered} \right. $ | (8) |
式中:
当
| $ \left\{ \begin{gathered} {X_m}({t_i}) = {X_m}(t{'_i}) + {V_m}(t{'_i})t{'_{del}}\sin {C_m}(t{'_i}) \\ {Y_m}({t_i}) = {Y_m}(t{'_i}) + {V_m}(t{'_i})t{'_{del}}\cos {C_m}(t{'_i}) \\ \end{gathered} \right.\;\;\;(i \geqslant 1) 。$ | (9) |
式中:
2)求解有利提前角
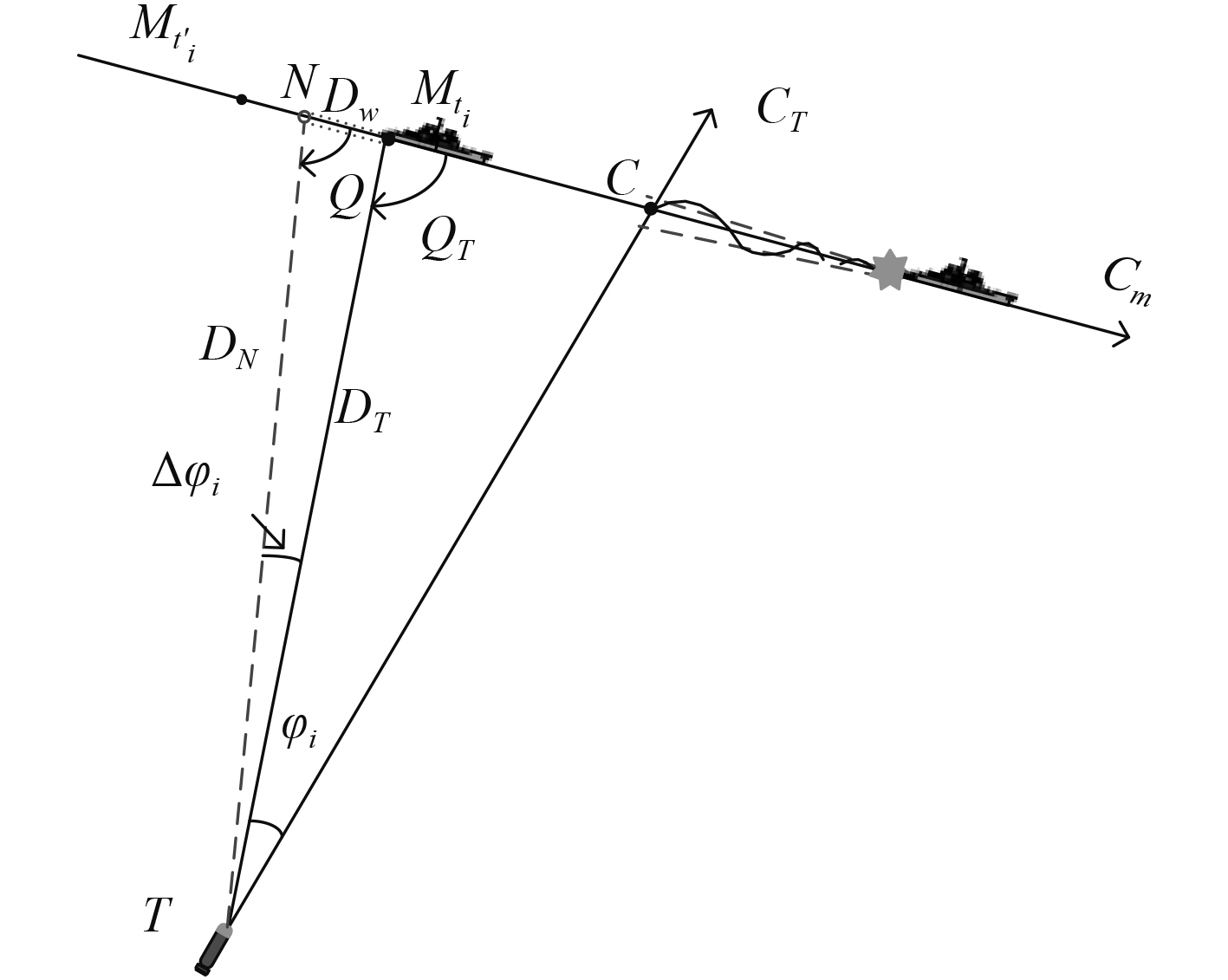
有利提前角解算模型如图5所示。
|
图 5 尾流自导鱼雷有利提前角解算模型 Fig. 5 Calculation model of wake homing torpedo's favorable advance angle |
由遥测数据可知鱼雷航向
鱼目距离为:
| $ {D_T} = \sqrt {{{({Y_m}({t_i}) - {Y_T}({t_i}))}^2} + {{({X_m}({t_i}) - {X_T}({t_i}))}^2}} ,$ | (10) |
鱼雷所处目标的舷角为:
| $ {Q_T} = \arctan \frac{{{Y_T}({t_i}) - {Y_m}({t_i})}}{{{X_T}({t_i}) - {X_m}({t_i})}} - {C_m}(t{'_i}) ,$ | (11) |
在△
| $ {D_N}{\text{ = }}\sqrt {{D^2}_{\text{T}} + {D^2}_w + 2{D_T}{D_w}\cos {Q_T}},$ | (12) |
由正弦定理得:
| $ Q = \arcsin \left(\frac{{{D_T}\sin {Q_T}}}{D}\right),$ | (13) |
从而
| $ \Delta {\varphi _i} = {Q_T} - Q ,$ | (14) |
在△
| $ \frac{{\sin (\Delta {\varphi _i} + {\varphi _i})}}{{\sin Q}} = \frac{{NC}}{{TC}} = m ,$ | (15) |
可得有利提前角为:
| $ {\varphi _i} = \arcsin (m\sin Q) - \Delta {\varphi _i} ,$ | (16) |
因此鱼雷航向为:
| $ {C_T}({t_i}) = \arctan \frac{{{Y_m}({t_i}) - {Y_T}({t_i})}}{{{X_m}({t_i}) - {X_T}({t_i})}} + {\varphi _i} ,$ | (17) |
设鱼雷初始弹道航向为
| $ \left\{ \begin{gathered} {\omega _T}({t_0}) = {C_T}({t_0}) - {C_{T0}},\\ {\omega _T}({t_i}) = {C_T}({t_i}) - {C_T}({t_{i - 1}}),\\ \end{gathered} \right.\;\;\;\;i \geqslant 1。$ | (18) |
在利用目指信息导引线导鱼雷的过程中,若尾流自导鱼雷按照相遇条件未能捕获尾流,则会越过目标航向线而逐渐远离目标,当再次收到目指信息时,虽然鱼雷可以按照新的相遇条件继续搜索目标尾流,但是再次入尾流时可能会导致目标舷别判断错误,使尾流自导鱼雷失效。如果能够在合适的时机将尾流自导转为声自导,则鱼雷可继续搜索攻击目标。针对这一目的,提出一种尾转声制导方式。
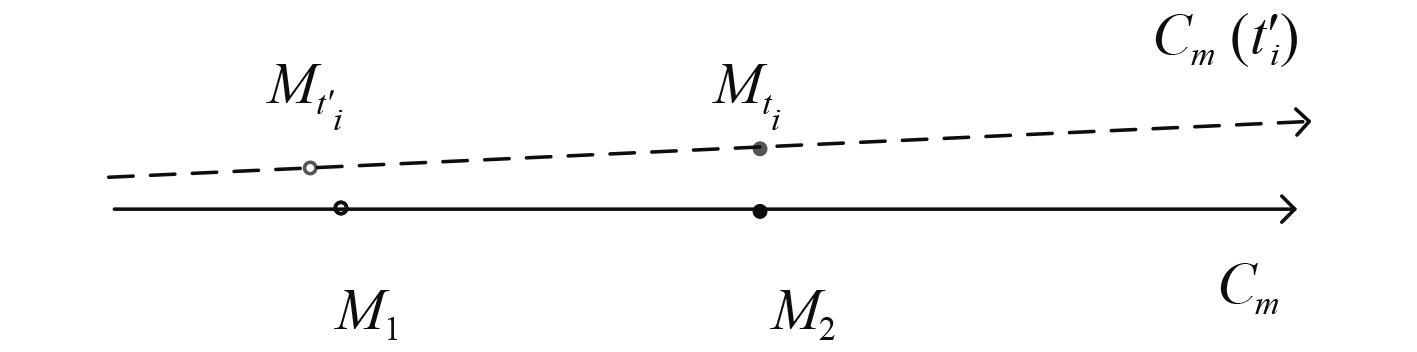
2.1 目标推算航向线目标航向线是指目标航行所形成的运动轨迹线。当潜艇在目指信息保障下实施鱼雷远距攻击时,指挥员无法得知真实的目标航向线,但可根据接收到的目标位置信息和航向信息推算其航向线,由于引导兵力存在探测误差,因此称为目标推算航向线,如图6所示。
|
图 6 目标推算航向线 Fig. 6 Target calculated course line |
图中实线所示为目标航向线、虚线所示为目标推算航向线。
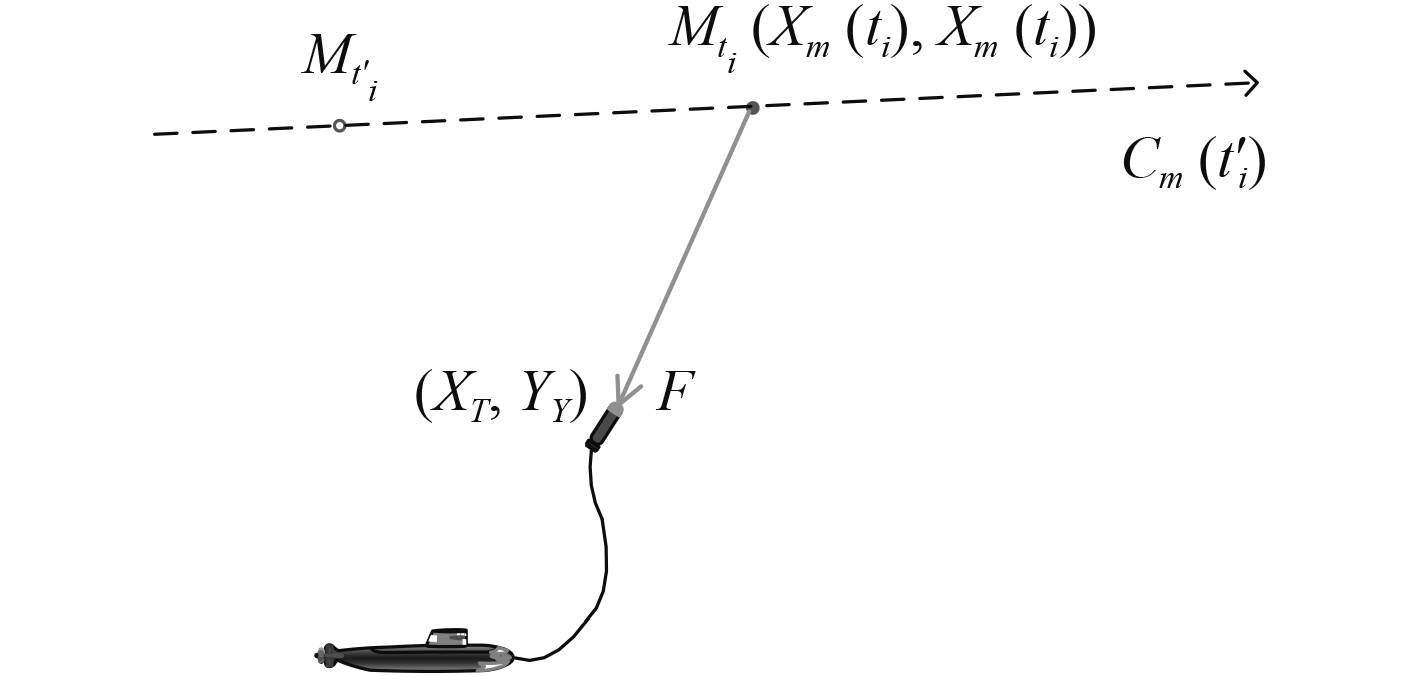
若在目指信息引导下,鱼雷成功捕获尾流,则鱼雷进入尾流后追踪目标直至完成攻击。若鱼雷越过目标推算航向线后仍未捕获尾流,则控制鱼雷制导方式由尾流自导转换为声自导。鱼雷是否越过目标推算航向线可采用目标舷别判断法,如图7所示。
|
图 7 目标舷别判断 Fig. 7 Target side judgment |
鱼雷位于目标的方位为:
| $ F = \arctan \frac{{{Y_T} - {Y_m}({t_i})}}{{{X_T} - {X_m}({t_i})}}。$ | (19) |
式中:
令
则鱼雷所处目标舷别为:
| $ S = \left\{ \begin{gathered} 1,\;\;\;\;0{\text{ < }}F' \leqslant \text{π} ,\\ - 1, - \text{π} {\text{ < }}F'{\text{ < }}0 。\\ \end{gathered} \right.\;\;\;\; $ | (20) |
式中:1和−1表示目标舷别为右舷和左舷。
当鱼雷发射时,可根据式(20)判断初始目标舷别,在鱼雷导引过程中,根据遥测数据实时判断目标舷别,在目指信息允许误差范围内,若目标舷别发生改变,则可判断鱼雷越过目标推算航向线,此时可将鱼雷制导方式由尾流自导转换为声自导。
2.3 尾转声后鱼雷航向1)推算尾转声时刻目标位置
设鱼雷尾转声的时间为
| $ \left\{ \begin{gathered} {X_m}({t_k}) = {X_m}({t_i}) + {V_m}(t{'_i}) \cdot ({t_k} - {t_i}) \cdot \sin {C_m}(t{'_i}) ,\\ {Y_m}({t_k}) = {Y_m}({t_i}) + {V_m}(t{'_i}) \cdot ({t_k} - {t_i}) \cdot \cos {C_m}(t{'_i}) 。\\ \end{gathered} \right.\;\; $ | (21) |
式中:
2)求解有利提前角
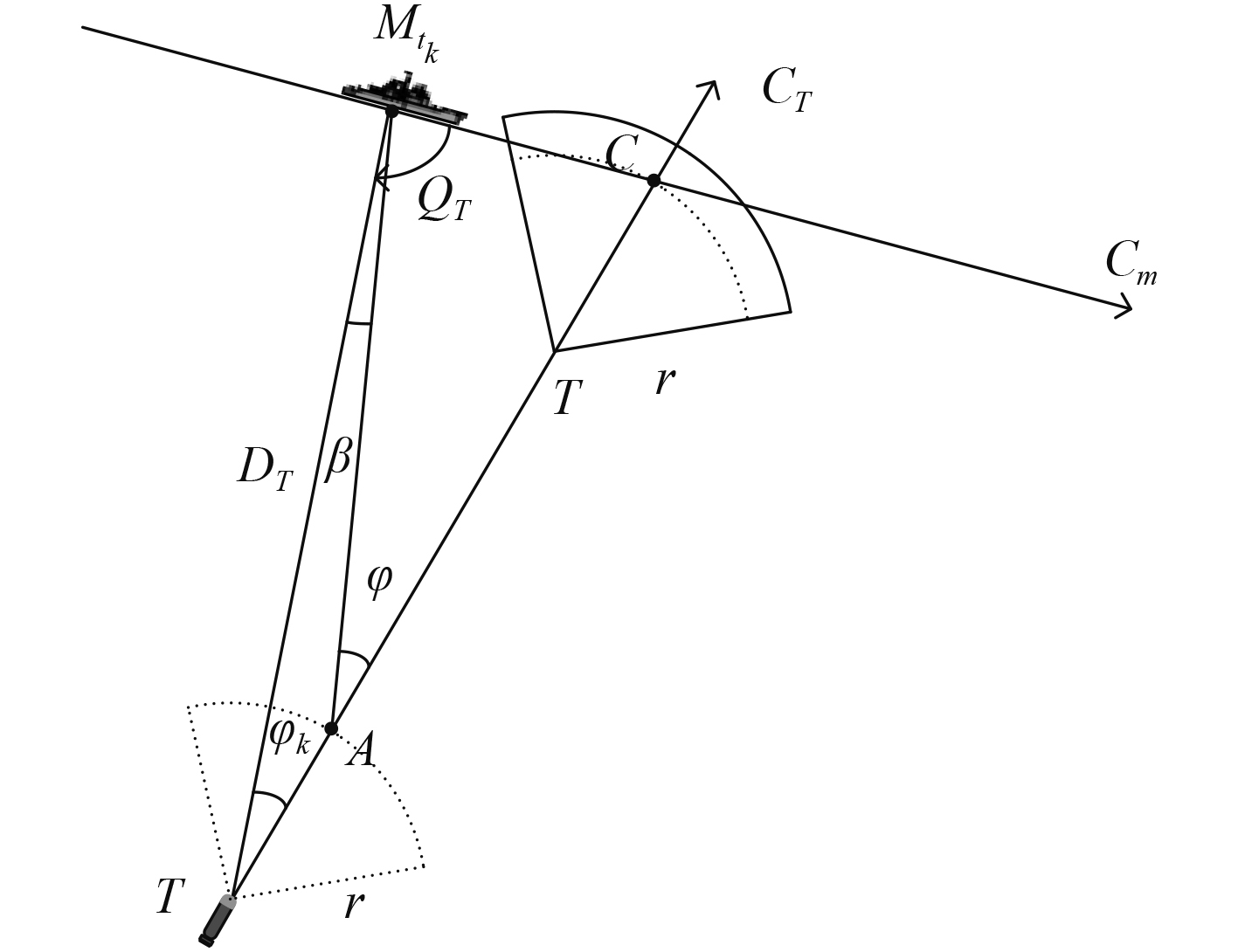
如图8所示,设装订的鱼雷自导作用距离为
|
图 8 声自导鱼雷有利提前角解算模型 Fig. 8 Calculation model of acoustic homing torpedo's favorable advance angle |
| $ {D_T} = \sqrt {{{({Y_m}({t_k}) - {Y_T}({t_k}))}^2} + {{({X_m}({t_k}) - {X_T}({t_k}))}^2}},$ | (22) |
鱼雷处于目标的舷角为:
| $ {Q_T} = \arctan \frac{{{Y_T}({t_k}) - {Y_m}({t_k})}}{{{X_T}({t_k}) - {X_m}({t_k})}} - {C_m}(t{'_i}),$ | (23) |
在△
| $ \frac{{\sin \varphi }}{{{M_{{t_k}}}C}} = \frac{{\sin ({Q_T} - \beta )}}{{AC}},$ | (24) |
其中,设
| $ \sin \varphi = m\sin ({Q_T} - \beta ) ,$ | (25) |
在△
| $ \frac{{\sin \varphi }}{{{D_T}}} = \frac{{\sin \beta }}{r} ,$ | (26) |
| $ \beta = \arctan \frac{{\sin {Q_T}}}{{\dfrac{{{D_T}}}{{mr}} + \cos {Q_T}}} ,$ | (27) |
则有利提前角为:
| $ {\varphi _i} = \varphi - \beta ,$ | (28) |
因此,鱼雷航向为:
| $ {C_T}({t_k}) = \arctan \frac{{{Y_m}({t_k}) - {Y_T}({t_k})}}{{{X_m}({t_k}) - {X_T}({t_k})}} + {\varphi _k} ,$ | (29) |
鱼雷转角为:
| $ {\omega _T}({t_k}) = {C_T}({t_k}) - {C_T}({t_i}) 。$ | (30) |
鱼雷机动搜索可在更大范围内覆盖目标位置散布,提高鱼雷捕获目标概率[10],当鱼雷到达目标散布中心后可实施扩展偏螺旋机动搜索。
扩展偏螺旋搜索是指鱼雷能够围绕具有一定速度的目标散布区域实施相对弹道为扩展螺旋的机动搜索[11]。
1)目标散布中心点
侦察兵力探测的目标位置
| $ \left\{ \begin{gathered} {X_{m0}} = {X_0} + {V_0}t\sin {C_0} ,\\ {Y_{m0}} = {Y_0} + {V_0}t\cos {C_0} 。\\ \end{gathered} \right. $ | (31) |
式中:
2)鱼雷相对弹道
相对弹道是指鱼雷绝对位置与散布中心位置的差值,即
| $ \left\{ \begin{gathered} X{'_T}(t) = {X_T}(t) - {X_{m0}}(t) ,\\ Y{'_T}(t) = {Y_T}(t) - {Y_{m0}}(t) 。\\ \end{gathered} \right. $ | (32) |
式中:
3)扩展偏螺旋搜索弹道
螺旋搜索的极坐标方程为[13]:
| $ {R_{lx}} = {R_0} + \frac{{{r_0}\sin \lambda }}{\text{π} }\left[\gamma - \left(\frac{\text{π} }{2} - {C_T}\right)\right] 。$ | (33) |
式中:
扩展偏螺旋搜索的鱼雷相对弹道与扩展螺旋搜索的鱼雷绝对弹道相同,联立式(32)和式(33)可得扩展偏螺旋搜索绝对弹道。
3 仿真实验 3.1 基本假设1)侦察兵力探测的目标位置、速度和航向均服从正态分布。
2)当满足以下条件时认为声自导鱼雷捕获目标:鱼雷发现目标且线导导引段航程+尾追航程≤鱼雷总航程。
3)当满足以下条件时认为尾流鱼雷捕获目标:①鱼雷进入尾流的角度符合进入角要求;②鱼雷进入点位于有效尾流区域内;③鱼雷进入距离
假设潜艇速度4 kn,航向090°,平台航向误差
仿真步长

|
图 9
|
|
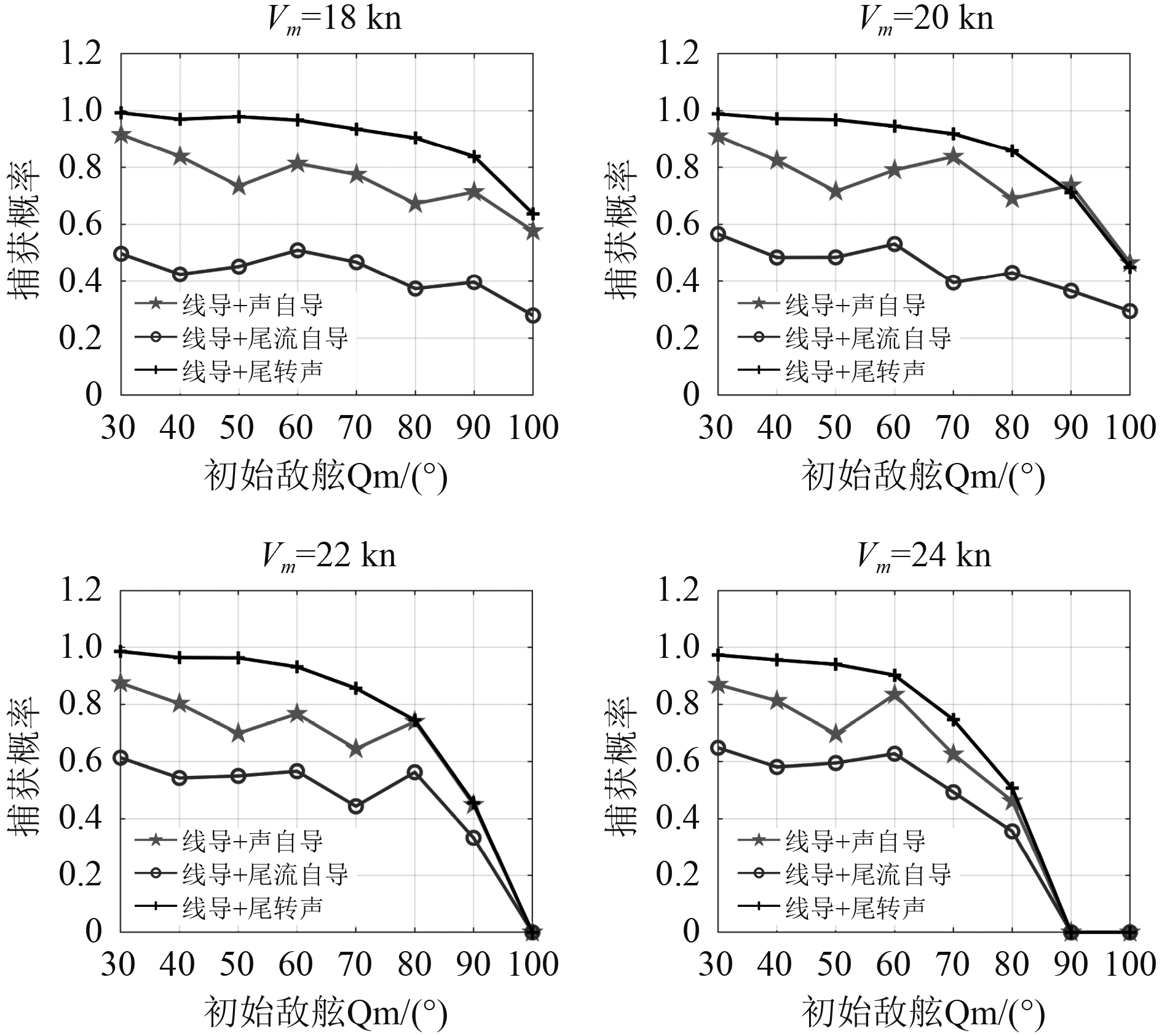
图 10
|
|
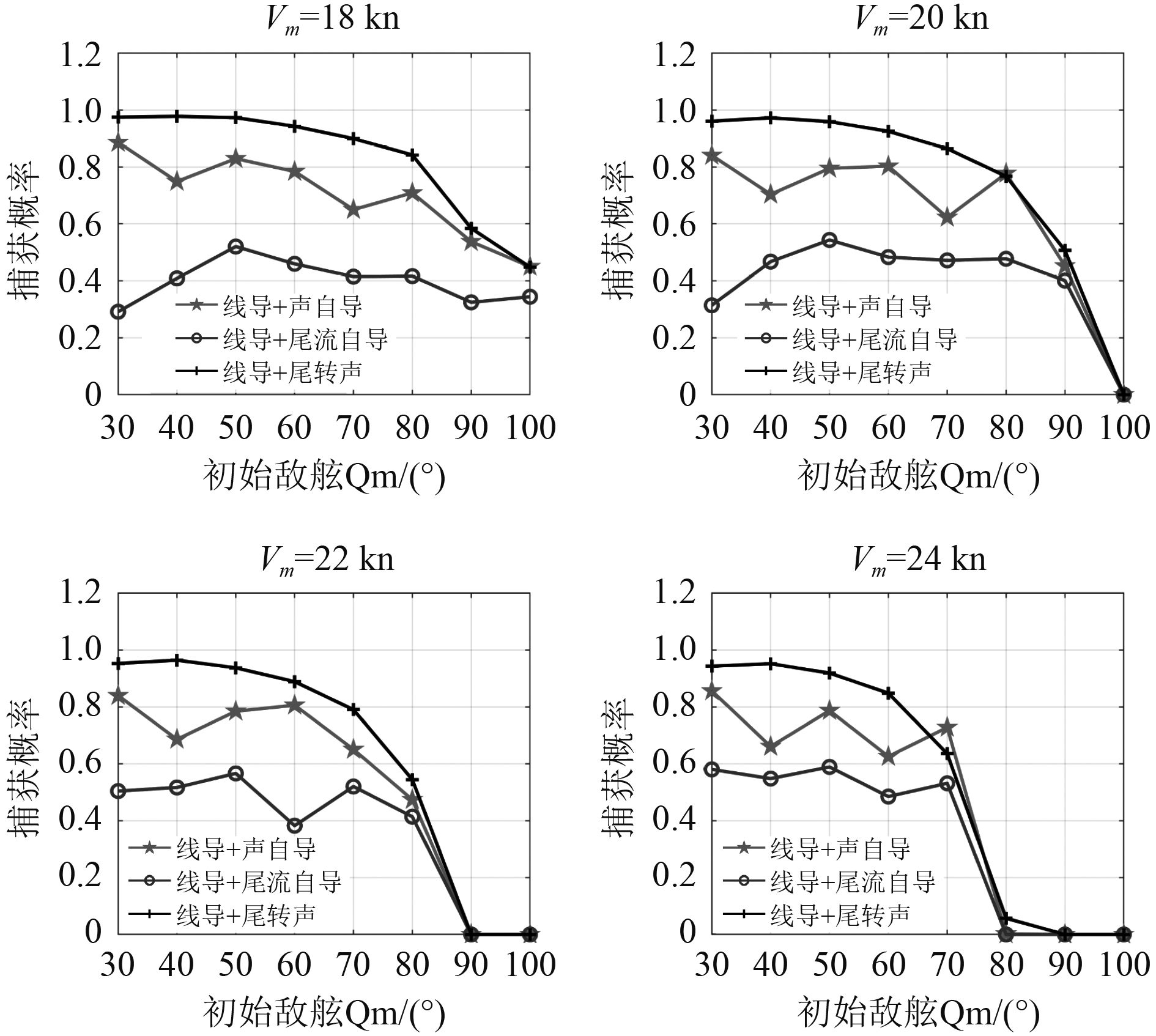
图 11
|
以初距

|
图 12 捕获次数对比图 Fig. 12 Comparison diagram of capture times |
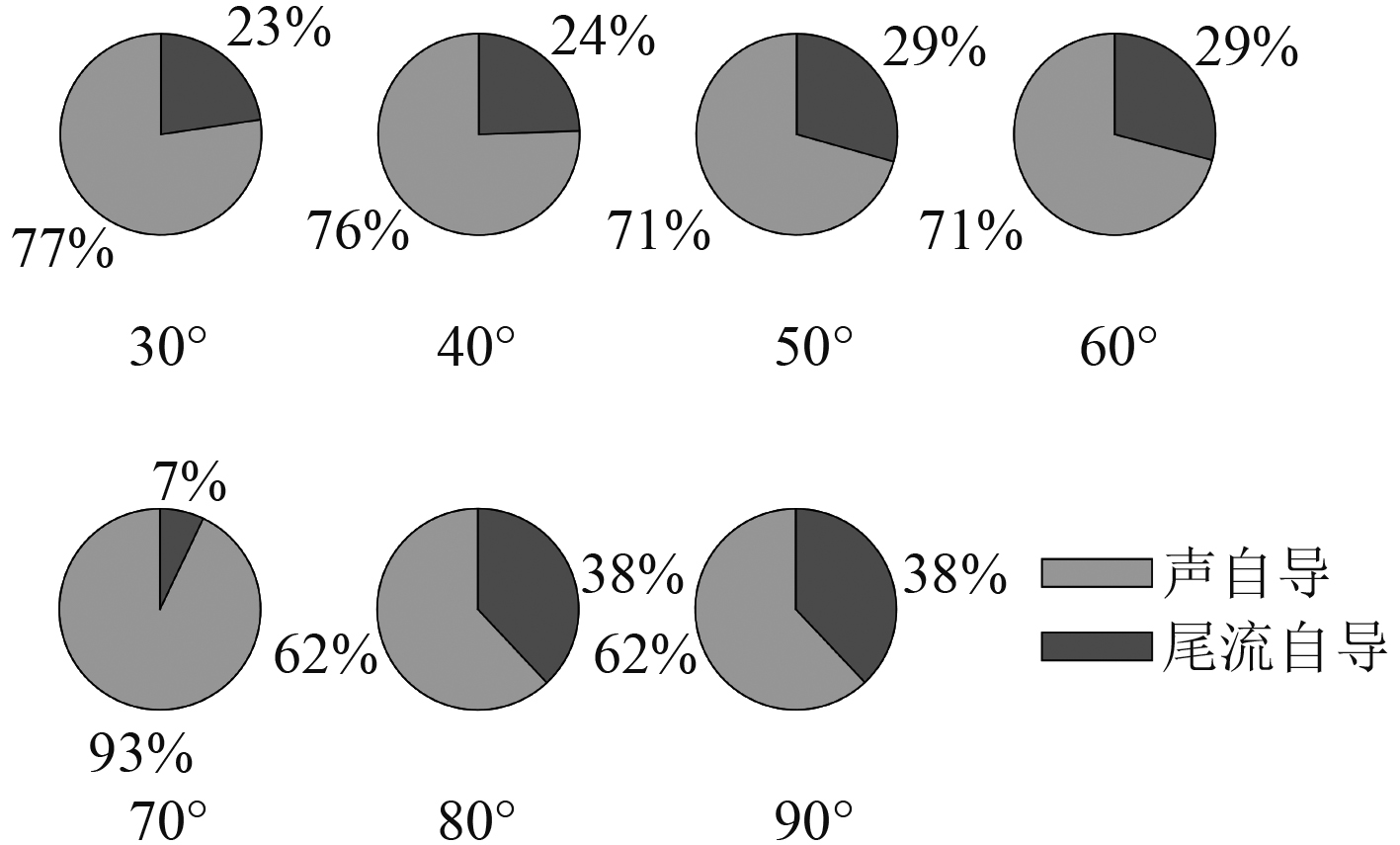
|
图 13 尾流自导和声自导鱼雷捕获目标占比图 Fig. 13 The proportion of target captured by wake homing and acoustic homing torpedoes |
由以上数据可以得出以下结论:
1)在鱼雷极限航程范围内,相同初距和敌舷角情况下,线导+尾流自导鱼雷捕获目标概率总体上随敌速的增大而增大,主要原因是在相同海况下,目标有效尾流长度与其速度呈正比,同时当目标速度超过20 kn时,尾流宽度也随之增加,速度继续增加时,尾流宽度与航速关系不大。因此,随着有效尾流长度和宽度的增加,鱼雷成功捕获尾流的可能性也逐渐增大。但是当目标速度增大到一定程度时,尾流追踪段将消耗大量鱼雷航程,受限于鱼雷极限航程的影响,线导+尾流自导鱼雷捕获概率呈断崖式下跌。
2)相同敌速和敌舷角情况下,线导+尾流自导鱼雷捕获目标概率随初距的增大而减小;相同初距和敌速情况下,随着初始敌舷角的增大,线导+尾流自导鱼雷捕获概率先增大后减小。这就要求指挥员在收到目指信息后,尽快根据目标信息确定初始态势,当处于有利态势时应尽快实施攻击,以免因敌舷角过大而贻误战机。
3)相较于单纯使用线导+尾流自导导引鱼雷实施攻击,采用线导+尾转声自导的制导方式可大幅提高鱼雷捕获目标概率。因此,尾转声制导方式为指挥员决策指挥提供了一种新的思路,当尾流自导在远距攻击中捕获目标概率较低时,可在合适的时机将尾流自导转换为声自导。
4)经统计,在设定的初始态势下,采用线导+尾转声制导方式所捕获的目标总数中,尾流自导捕获目标次数占比约25%,声自导捕获目标次数占比约75%。由此可见,线导+尾转声制导方式可以兼具尾流自导鱼雷抗干扰能力强和声自导鱼雷捕获概率高的特点。
4 结 语潜艇在目指信息引导下使用线导+尾流鱼雷实施远距攻击时,若鱼雷越过目标推算航向线后未能成功捕获尾流,通过将尾流自导转换为声自导,可有效提高鱼雷捕获目标概率。同时初始距离、初始敌舷角、目标速度等因素对鱼雷捕获目标概率也有较大影响,在复杂战场环境下,潜艇指挥员应结合具体态势,统筹各种因素的影响,灵活运用,选择合适的制导方式,保证潜射线导鱼雷的攻击效果。
| [1] |
李本昌, 唐农军, 胡定安. 重型鱼雷的机动搜索及机动搜索弹道架构[J]. 指挥控制与仿真, 2010, 32(3): 1-3. LI Ben-ching, TANG Nong-jun, HU Ding-an. Heavy torpedo’s maneuver searching and its trajectory framework[J]. Command Control & Simulation, 2010, 32(3): 1-3. DOI:10.3969/j.issn.1673-3819.2010.03.001 |
| [2] |
李长军, 杜辉, 于雪泳. 基于正态分布的水面目标位置散布分析[J]. 信息工程大学学报, 2012, 13(6): 650-653. LI Chang-jun, DU Hui, YU Xue-yong. Research on probability density of object locating based on normal distribution[J]. Journal of Information Engineering University, 2012, 13(6): 650-653. DOI:10.3969/j.issn.1671-0673.2012.06.003 |
| [3] |
杜辉, 于雪泳, 朱清浩. 潜射鱼雷在引导兵力通报下的远距攻击[J]. 火力与指挥控制, 2016, 41(3): 136-139. DOI:10.3969/j.issn.1002-0640.2016.03.033 |
| [4] |
杨晓辉, 陆铭华. 信息引导下的潜艇远程鱼雷攻击[J]. 中国科技纵横, 2009(12): 163. |
| [5] |
徐继华, 袁富宇. 基于折线简化的方位导引方法的可用性研究[J]. 指挥控制与仿真, 2017, 39(2): 3l-35. XU ji-hua, YUAN Fu-yu. Research on usability of directional guidance method based on simplification of polyline[J]. Command Control & Simulation, 2017, 39(2): 3l-35. |
| [6] |
孟庆玉, 张静远, 王鹏等. 鱼雷作战效能分析[M]. 北京: 国防工业出版社, 2020: 203-204.
|
| [7] |
杨大伟, 张培培. 线导鱼雷导引方法综述[J]. 舰船科学技术, 2010, 32(10): 140-143. YANG Da-wei, ZHANG Pei-pei. Guidance methods for the wire-guidance torpedo[J]. Ship Science and Technology, 2010, 32(10): 140-143. DOI:10.3404/j.issn.1672-7649.2010.10.034 |
| [8] |
徐海珠, 袁延艺, 余赟 等. 水面舰艇对抗尾流自导鱼雷方法研究[J]. 火力与指挥控制, 2018, 43(8): 13. XU Hai- zhu, YUAN Yan- yi, YU Yun, et al. Method study of ship countering wake homing torpedo[J]. Fire Control & Command Control, 2018, 43(8): 13. DOI:10.3969/j.issn.1002-0640.2018.08.003 |
| [9] |
曹庆刚, 毛秋丹, 房毅. 某型潜艇尾流自导鱼雷命中概率方法研究[J]. 舰船电子工程, 2015, 35(3): 132-136. DOI:10.3969/j.issn1672-9730.2015.03.037 |
| [10] |
黄文斌, 于雪泳, 李长军. 潜艇使用机动搜索鱼雷攻击水面舰艇方法[J]. 火力与指挥控制, 2020, 45(2): 71-75. HUANG Wen-bin, YU Xue-yong, LI Chang-jun. Research on method of attacking ships by thread guiding maneuver searching torpedo[J]. Fire Control & Command Control, 2020, 45(2): 71-75. DOI:10.3969/j.issn.1002-0640.2020.02.014 |
| [11] |
于雪泳, 武志东. 鱼雷扩展偏螺旋机动搜索弹道设计[J]. 火力与指挥控制, 2021, 46(4): 167-169. DOI:10.3969/j.issn.1002-0640.2021.04.031 |
| [12] |
于雪泳, 李长军, 黄文斌. 引导兵力通报情况下水面目标位置散布分析[J]. 舰船科学技术, 2013, 35(5): 119-122. YU Xue-yong, LI Chang-jun, HUANG Wen-bin. Research on probability density of object location when information is received from spy platform[J]. Ship Science and Technology, 2013, 35(5): 119-122. DOI:10.3404/j.issn.1672-7649.2013.05.028 |
| [13] |
于雪泳, 黄文斌. 鱼雷扩展螺旋机动搜索弹道设计[J]. 舰船科学技术, 2014, 36(10): 142-145. DOI:10.3404/j.issn.1672-7649.2014.10.032 |
| [14] |
YU Xue-yong, HUANG Wen-bin. Expanding spirality trajectory design of torpedo maneuver search[J]. Ship Science and Technology, 2014, 36(10): 142-145. |
 2023, Vol. 45
2023, Vol. 45
