作为一种新型发射技术,电磁弹射技术相比于蒸汽弹射、火箭弹射等传统弹射方式而言,具有可控性好、推力波动小、效率高等优点[1-2]。电磁弹射技术是利用电磁力加速携带电枢的物体,从而实现发射效果,电磁弹射对小到几千克的模型,大到导弹、航母舰载机都可以进行有效的弹射,是对传统弹射技术的重大突破,在军事、民用和工业领域具有广泛的应用前景[3-4]。
在电磁弹射系统的研制过程中,电枢及其所携带负载的速度通常用来分析弹道特性、能量控制和发射效率等[5],同时有助于分析和研究各种效应的形成机理、掌握电磁力加速的基本规律,为电磁弹射系统设计提供依据,是评估系统性能的一项重要指标[6]。在速度测量方面,常用的测量方式可大致分为接触式测速法和非接触式测速法两大类,而国内外应用于电磁弹射领域中的速度测量方法,具体包括磁探针、毫米波多普勒雷达、激光干涉测速(VISAR,PDV)、加速度计调制遥测和高速摄影等方法[7-9],但由于在电磁力加速过程中,受高压、强磁场、机械振动以及高加速度等恶劣条件的影响,完整而精确地测量内弹道速度仍然相当困难。
针对电磁弹射系统在实验室环境下负载的内弹道速度测试需求,结合系统结构特点,分别采取高速摄影、运动加速度传感器和毫米波多普勒雷达3种方案开展速度测试工作。研究结果表明:3种测试方案均能有效获取负载速度,测量结果一致性好;3种方法中,高速摄影测速结果相对较低,加速度传感器测速结果相对较高,多普勒雷达测速结果处于二者之间,多普勒雷达测速结果与速度真值更为接近,精确度更高,多普勒雷达测试方案获取了连续完整的负载速度曲线,可为电磁弹射系统的研制提供有力的数据支撑。对多普勒原始信号所采用的数据处理方法,可为其在其他领域的应用提供重要参考。
1 测试原理与方法分别采用基于区截装置法的高速摄影和基于雷达测速法的毫米波多普勒雷达,并针对实验室环境下电磁弹射系统的结构特点,在负载头部布置了运动加速度传感器测速,共3种测量方法开展负载的初速测试。
1.1 高速摄影测速高速摄影是采用最大帧频可达 104fps 量级以上的高速相机,获取高速飞行物体每一特定时刻空间图像信息的光学仪器系统,采用该仪器可实现速度的非接触式测量,与其他测速方法相比,具有试验布置方便、可靠性强、可重复使用等优点[10]。高速摄影测速采用两点法,在弹射器导向轨道一侧放置标尺,在负载头部位置做标记,当负载弹出轨道后,根据负载上标记通过标尺的帧数来计算时间,根据标尺距离和时间可计算平均速度。
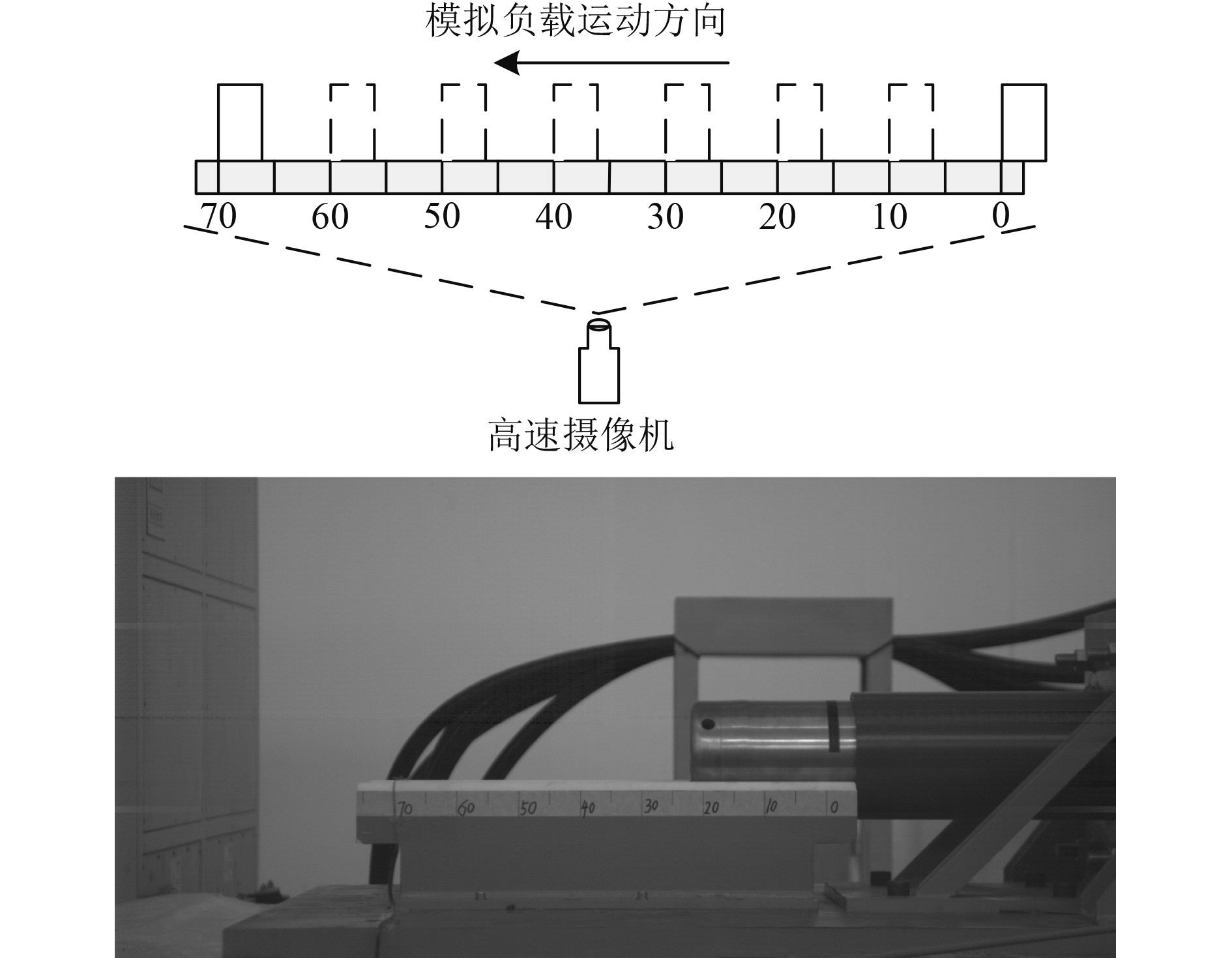
高速摄影测速系统由高速摄像机、网线和上位机组成。根据负载预示速度,设置拍摄速度为5000帧/s,将高速相机放置于弹射系统导向轨道前端,调整相机参数,使画面清晰并完全覆盖负载头部标记和标尺台,高速摄影测速原理及拍摄效果如图1所示。
|
图 1 高速摄影测速原理及实拍图 Fig. 1 The principle and real shot of high-speed photogrammetry |
速度作为物体运动信息的一个中间量,理论上可通过位移微分和加速度积分得到。而位移的测量需要有一个基准位置,且对安装布置空间有一定的要求,结合电磁弹射系统样机的结构特点,在负载头部布置一个运动加速度传感器,采用有线测量方式,获取负载运动过程中的加速度信号,再通过数据处理获取速度数据是较为可行的办法。
加速度测试系统由运动加速度传感器、测试电缆、数据采集仪和上位机组成,传感器频率范围为0~1 kHz,适用于低频的运动加速度信号的测量。将传感器粘贴在负载头部,并做好防护,同时预留足够的测试电缆,以防止负载运动过程中电缆被拉断,数据采集仪启动记录后,即可获取负载运动方向的加速度数据,再经去趋势项、数据积分等数据处理,进而得到负载速度数据。
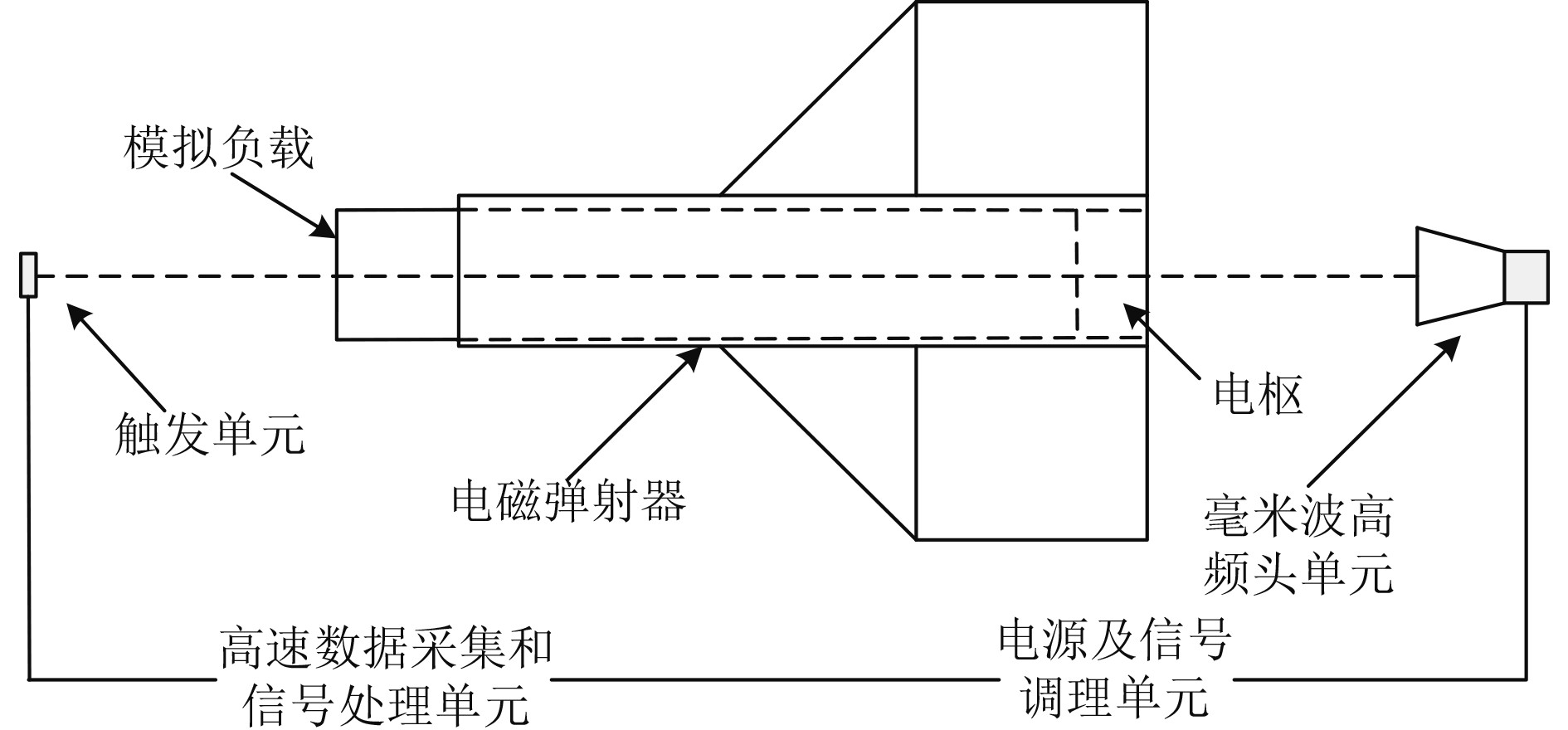
1.3 毫米波多普勒雷达测速毫米波多普勒雷达是根据多普勒原理设计出的一种速度测量仪器,测速系统主要由毫米波高频头单元、电源及信号调理单元、触发单元、高速数据采集和信号处理单元组成。其中,选用的毫米波雷达发射的电磁波频率为95 GHz,波长为3 mm,是W波段4个信号衰减相对较小的常用“窗口”之一[11-12]。测速系统工作时,毫米波高频头单元产生频率稳定的毫米电磁波信号,电磁波通过内置天线向负载飞行方向传播,在遇到负载尾部端面后反射,反射回来的电磁波经原路返回,并被天线接收,与本振混频,经高速数据采集和信号处理单元处理后输出包含有速度信息的多普勒信号,再经数据处理即可获取负载的速度数据。由于电磁发射系统的后部为敞开式,且试验过程中系统尾部不存在冲击等其他障碍干扰,负载后部的电枢为空心圆环形,因此采用将雷达放置在系统后部的方式进行测量。毫米波多普勒雷达测速的工作示意图如图2所示。
|
图 2 毫米波多普勒雷达测速工作示意图 Fig. 2 Schematic diagram of speed measurement of millimeter wave Doppler radar |
根据高速摄影测速原理,结合实拍图像中标尺的位移量和相机帧率,可获取每幅图像中包含了被测对象的时间和位移信息。如图2所示,随着负载加速运动,当负载上的黑色标志线移动至标识台0刻度线时,记录为位移起始位置,负载每向前运动0.05 m,读取期间的图像幅数ni,按照式(1)计算,即可获取负载平均速度。
| $ {\overline V _i} = \frac{{{s_i} - {s_{i - 1}}}}{{({n_i} - {n_{i - 1}})}} \cdot v 。$ | (1) |
式中:
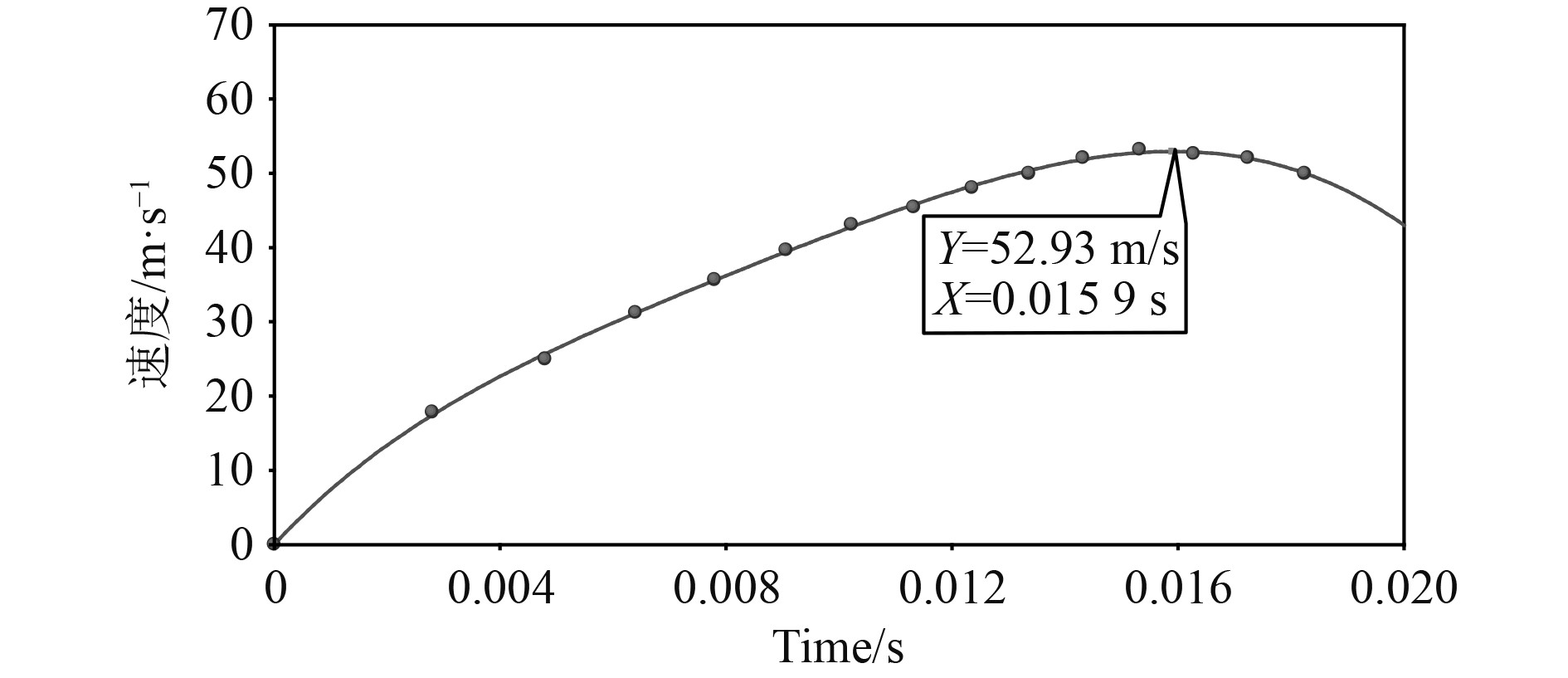
对获取的离散的速度数据,采用最小二乘法进行多项式拟合,从而获取平滑的速度曲线,如图3所示。
|
图 3 速度散点及多项式拟合曲线图 Fig. 3 Velocity scatter and polynomial fitting curve |
理论上对加速度信号直接积分即可获取速度数据。设负载运动加速度信号为a(t),则速度信号:
| $ v(t) = \int_0^t {a(t)} {\rm{d}}t = v'(t) + {v_0}。$ | (2) |
然而,实际采集获得的加速度信号包含直流分量等微小误差,即a(t)= a′(t)+ε,这将在积分过程不断累加[8],使积分结果常常出现“漂移”[9]。
| $ v(t) = \int_0^t {a(t)} {\rm{d}}t = v'(t) + (\varepsilon t + \delta ) + {v_0} 。$ | (3) |
式中:v′(t)为v(t)的原始函数;v0为初速速度;ε为直流分量;(εt+δ+v0)为一次积分后速度信号中含有的趋势项。
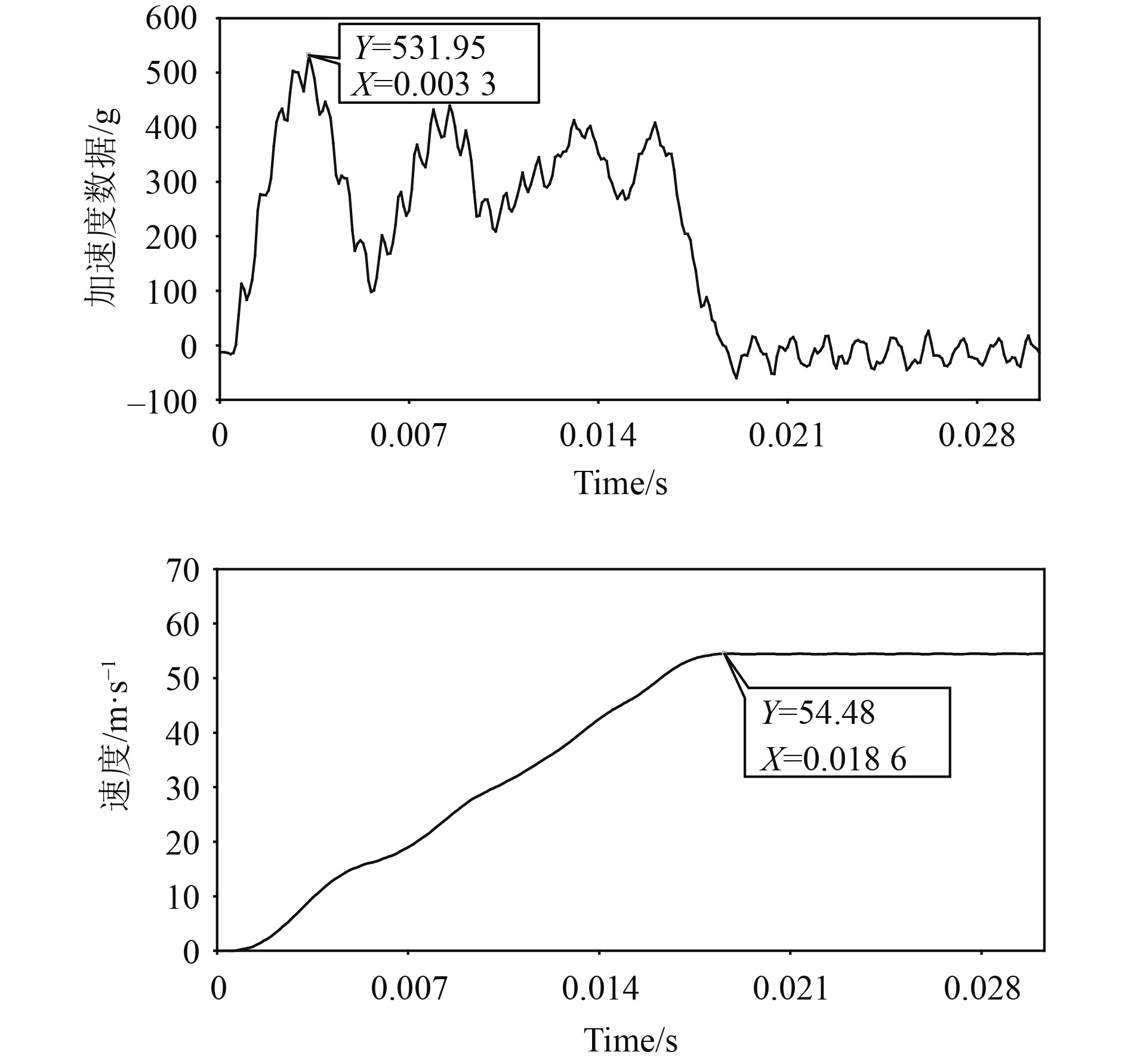
针对积分方法和去噪处理,本文在已有研究成果的基础上[13-14],首先采用10 kHz高采样频率获取原始加速度数据,以保证计算结果的精确度。同时,采用复合梯形公式算法对原始加速度数据进行积分处理,之后,采用多项式拟合的方法拟合获取趋势项,从而消除信号积分后所产生的误差, 得到更为精确的速度信号。负载加速度和处理后的速度曲线如图4所示。
|
图 4 负载加速度和处理后的速度曲线图 Fig. 4 The curve of the load acceleration and processed velocity data |
根据毫米波多普勒雷达测速原理,雷达发射天线发射的电磁波频率f0与遇到障碍物返回时,接收天线接收到的回波信号频率f1之间,有以下关系:
| $ {f_1} = {f_0} + \frac{{2{v_t}}}{c}{f_0} 。$ | (4) |
其中:vt为负载的运动速度;c为电磁波传播速度(在自由空间传播时等于光速)。
由式(4)可知,发射频率与反射频率的差值即多普勒频移为:
| $ {f_d} = {f_1} - {f_0} = \frac{{2{v_t}}}{c}{f_0} 。$ | (5) |
负载的运动速度与多普勒频移成正比,多普勒频率与负载运动速度之间的关系可表示为:
| $ {v_t} = \frac{{{f_d}\lambda }}{2} = \frac{{c{f_d}}}{{2{f_0}}} 。$ | (6) |
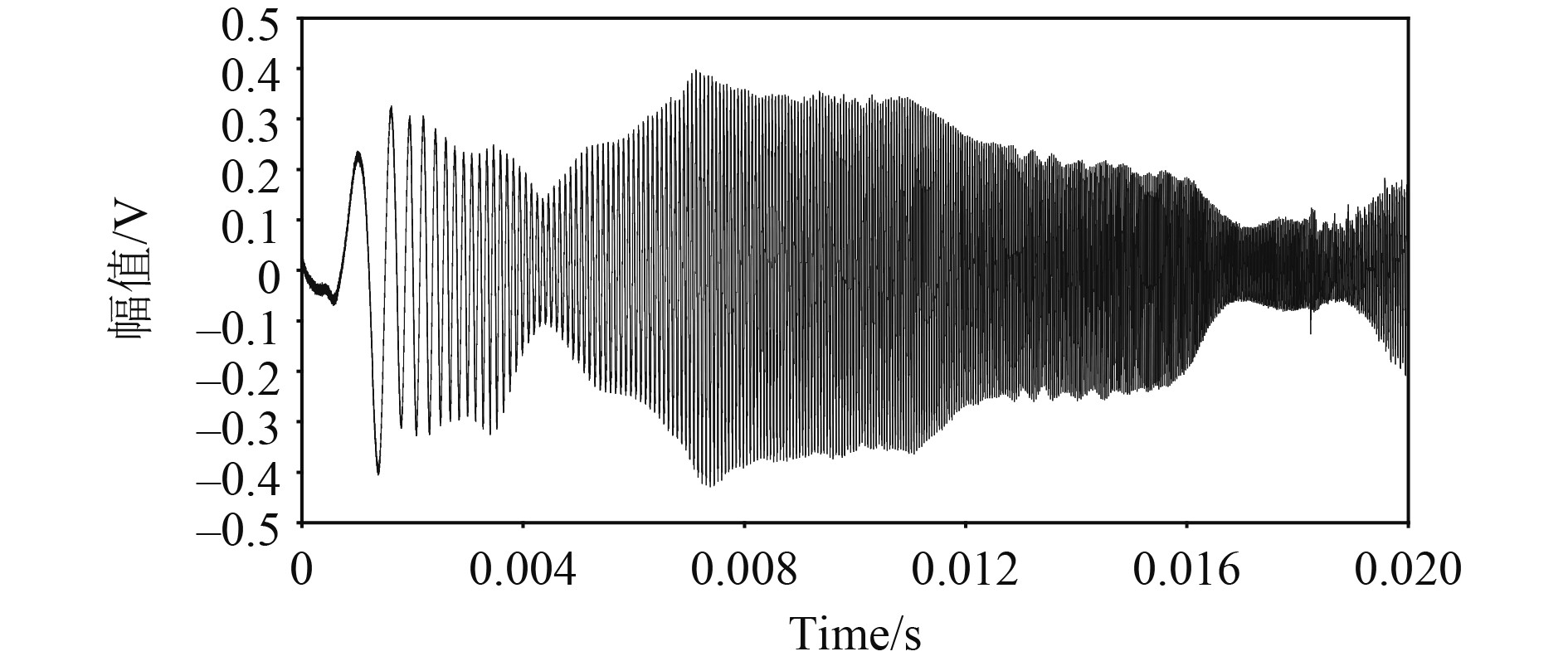
为提高测试系统信噪比,在负载的尾部反射面上粘贴反射性能好、大小合适的薄锡箔板,以增强回波信号的频率强度。同时,为消除低频干扰和趋势项信号,采用小波分析法对获得的高质量多普勒信号进行滤波预处理,再进行多普勒频率的计算,预处理后的信号如图5所示。
|
图 5 预处理后的多普勒信号图 Fig. 5 The curve of preprocessed Doppler signal |
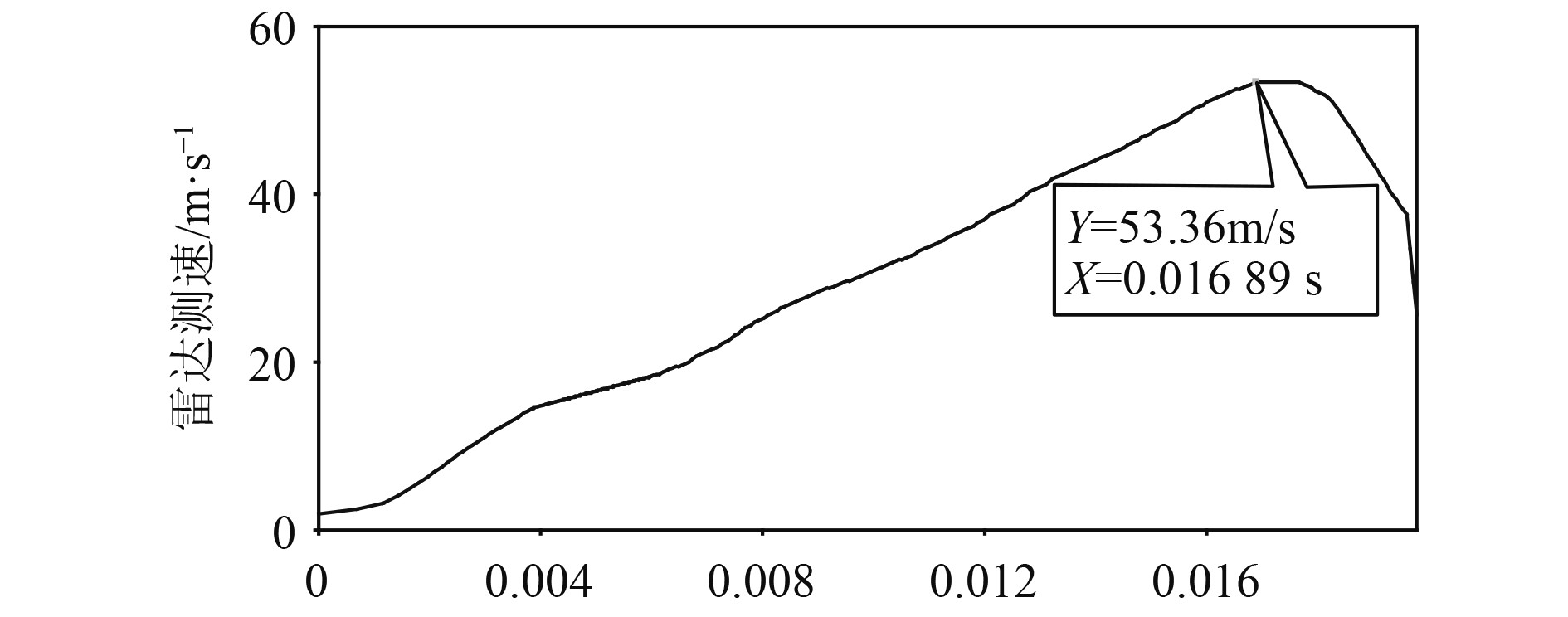
由于多普勒信号并不是单一频率,而是存在着多种频率成分,易导致速度测量模糊。特别是在目标运动起始阶段,运动速度低,多普勒频率相应较低,速度模糊问题更加突出,因此在负载运动前6ms的低速段采用极值法提取频率信息,在6 ms后的高速段用短时傅里叶变换对多普勒信号进行处理,并将2种处理方法得到的速度数据进行综合,进而得到负载在完整的运动速度数据,如图6所示。
|
图 6 多普勒雷达测速系统负载速度曲线 Fig. 6 Load velocity curve of Doppler radar velocity system |
分别采用3种测速方法对同一负载,在相同试验状态下进行3次试验。基于上述数据处理方法,3个发次的最大测速结果比对如表1所示。
|
|
表 1 三种测速方法最大测速结果对比 Tab.1 Comparison of maximum velocity measurement results of three velocity measurement methods |
由表1测试结果可知,3种测试方法均能有效获取电磁弹射系统负载的最大速度值,最大相对误差为4.6%。3种方法中,高速摄影测速结果相对较低,加速度传感器测速结果相对较高。结合测速原理,高速摄影采用的二点法测量得到的速度为2个标尺刻度点之间的平均速度,在加速运动过程中,平均速度值相较于后一刻度点时刻的速度值较低,因此在利用高速摄影离散速度值拟合得到的多项式曲线相对与速度真值同样也会较低。而加速度积分过程中,虽然对于直流分量,采用了去除趋势项的处理,但原始加速度信号中的低频噪声仍旧无法完全消除,致使在积分过程中加速度传感器测速相对速度真值较大。此外,多普勒雷达测速结果处于二者之间,理论上与速度真值更为接近,且得到了连续完整的时间速度曲线,采用的数据处理方法保证了多普勒频率的高精度计算,因此多普勒雷达速度测量的精度更高。综合以上分析,多普勒雷达测速方法是电磁弹射系统负载运动速度测量的有效手段。
3 结 语为评估电磁弹射系统样机的系统性能,针对其发射速度测试的需要,结合系统样机结构特点,采用高速摄影测速、加速度传感器测速和多普勒雷达测速3种测试方法,对负载速度开展了实测试验。综合测试结果,得到以下结论:
1)3种测试方案均可有效获取负载速度,测量方案可行;对比3种方法获取的负载最大速度值,最大相对误差为3.5%,一致性好。
2)3 种方法中,高速摄影测速结果相对较低,加速度传感器测速结果相对较高,多普勒雷达测速结果处于二者之间。结合3种方案的测速原理,测试结果与误差分析一致,多普勒雷达测速结果与速度真值更为接近,多普勒雷达测试方案获取了连续完整的负载速度曲线,可为电磁弹射系统的研制提供有力的数据支撑;
3)在采用毫米波多普勒雷达测速时,对多普勒原始信号所采用的小波分析法、在低速段采用的极值法以及在高速运动阶段采用的短时傅里叶变换等处理方法,提高了频率分辨率,实现了多普勒频率的高精度计算,可为其他领域雷达测速的数据后处理提供参考。
| [1] |
苏子舟, 张涛, 张博, 等. 导弹电磁弹射技术综述[J]. 飞航导弹, 2016, 8: 28-32. DOI:10.16338/j.issn.1009-1319.2016.08.06 |
| [2] |
马伟明, 鲁军勇. 电磁发射技术[J]. 国防科技大学学报, 2016, 38(6): 1-5. DOI:10.11887/j.cn.201606001 |
| [3] |
蔺志强, 陈桂明, 许令亮, 等. 电磁发射技术在导弹武器系统中的应用研究[J]. 飞航导弹, 2020, 7: 67-71. DOI:10.16338/j.issn.1009-1319.20190294 |
| [4] |
古刚, 向阳. 国际电磁发射技术研究现状[J]. 舰船科学技术, 2007, 29(1): 156-158. |
| [5] |
金涌, 杨春霞, 李海元, 等. 电磁发射中初速测量的初步分析[J]. 工程与试验, 2010, 50(3): 9-12. DOI:10.3969/j.issn.1674-3407.2010.03.003 |
| [6] |
郭春龙, 雷彬, 李治源, 等. 平面螺旋线圈电磁发射装置测速试验研究[J]. 火炮发射与控制学报, 2014, 35(3): 78-81. DOI:10.3969/j.issn.1673-6524.2014.03.017 |
| [7] |
周彤. 基于X射线的炮口初速测量系统研究[D]. 南京: 南京理工大学, 2016.
|
| [8] |
李笑娟, 倪晋平. 高射速火炮连发初速测试技术[J]. 兵工自动化, 2011, 30(6): 68-70. DOI:10.3969/j.issn.1006-1576.2011.06.021 |
| [9] |
马百双, 刘昌锦. 几种典型炮口初速测试方法比较[J]. 四川兵工学报, 2011, 32(11): 53-55. |
| [10] |
赖鸣, 兰山, 黄广炎, 等. 数字式高速摄像测试技术及其应用[J]. 实验技术与管理, 2012, 29(6): 51-54. DOI:10.3969/j.issn.1002-4956.2012.06.015 |
| [11] |
杨健. 毫米波干涉仪膛内信号处理研究 [D]. 南京: 南京理工大学, 2010.
|
| [12] |
杨帆. W波段连续波相参多普勒雷达前端关键技术研究 [D]. 成都: 电子科技大学, 2008.
|
| [13] |
林楠, 李东升, 李宏男. 基于零初值的测试加速度积分速度与位移的方法[J]. 中国科学, 2016, 46(6): 602-614. |
| [14] |
王建峰, 马建, 马荣贵, 等. 动位移的加速度精确测量技术研究[J]. 计算机科学, 2010, 37(12): 201-202. DOI:10.3969/j.issn.1002-137X.2010.12.046 |
 2023, Vol. 45
2023, Vol. 45

