随着大数据时代来临,信息化、智能化技术在军事领域广泛运用,战争形态发生深刻变化,数据的作用日益凸显,依托数据筹划战争、使用数据描述战争、利用数据实施战争已经成为当今军事博弈的发展趋势。装备试验数据是试验过程中获取和使用到数据的总称,是支撑装备设计、论证、鉴定、使用和改进的战略资源。如何获取高质量的装备试验数据已成为装备试验领域的研究热点[1]。
不同于一般的商业数据,装备试验数据来源广泛(包括内外部资料、光测、雷测、遥测等),类型多样(包括文档、图片、视频、结构化数据、专用数据包等),数据量大,同时数据价值不随时间推移而迅速降低[2]。传统的数据质量评价方法主要针对结构化数据,基于数据库的数据完整性约束,完成对数据的准确性、完整性和一致性评价[3-5]。随着互联网技术的发展和大数据时代的到来,数据质量评价对象逐步从单一的结构化数据拓展到半结构化和非结构化数据。程豪[6]从完整性、及时性、有效性、一致性和精度等方面提出了大数据质量评价的基本框架,但没有给出具体的评价方法。陈超[7]给出了军事数据质量评价的指标体系和基于多层次灰色评价法的军事数据质量评价建模求解方法,但在指标设置中仅考虑了数据规范性、完整性等固有指标,未将数据质量等宏观影响因素以及可用性等因素考虑在内。此外,根据静态和动态2个视角建立评估作战数据质量的指标体系[8-9]。这些指标对评价试验数据质量具有一定借鉴意义,但一些指标的获取难度大,可操作性不高。上述方法获取的指标权重都未考虑指标间的影响关系,削弱了数据质量评价结果的科学性和合理性。
本文从装备试验数据特点出发,首先建立具有3个层面、12个维度、28个指标的装备试验数据质量综合评价指标体系,综合考虑定性、定量指标,应用群体决策和模糊决策图(fuzzy decision map, FDM)的混合方法,提出一种装备试验数据质量评价的综合建模方法,提升装备试验数据质量评价模型的针对性、结果的合理性。最后,以某型舰船装备试验数据评价问题为例进行案例分析,验证所提方法的有效性。
1 装备试验数据质量综合评价指标体系装备试验数据质量评价过程复杂,具有多层次、多粒度等特点。为达到全面、准确、客观评价装备试验数据质量的目的,遵循科学性、全局性、典型性、用户优先、指标值易获取等原则,从政策环境层、固有质量层和效用质量层3个方面评价数据质量,并进一步细化制定12个维度,在每个维度中又选取定量、定性以及综合性等不同类型的指标,从而建立装备试验数据质量综合评价指标体系。
1.1 政策环境层政策环境层从外部环境角度描述数据质量,包括法规政策、标准规范、人员体制和技术手段共4个维度。
法规政策维度中包含3个指标,分别是法规政策全面性(CLR)、法规政策适用性(ALR)和法规政策执行度(ILR);标准规范维度中包含3个指标,分别是标准规范全面性(CSS)、标准规范适用性(ASS)和标准体系执行度(ISS);人员体制维度中包含2个指标,分别是专业设置(RPS)和机构设置(ROS);技术支持手段维度中包含2个指标,分别是单系统成熟度(MSS)和体系整体性(GSS)。
政策环境层指标大多是定性指标,很难用给定公式进行评价,为解决该问题,给出一种专家评价法。
1.2 固有质量层固有质量层从数据本身描述数据质量,包括规范性、完整性、一致性、安全性和及时性共5个维度。
规范性维度中包含2个指标。第1个指标是标准规范符合度(CDS),关注的是装备试验数据按照装备试验数据标准规范进行采集、处理、存储和应用的程度,可表示为:
| $ CDS = \frac{{ConNum}}{{NumT}} 。$ | (1) |
其中,ConNum表示符合装备试验数据标准规范的数据量,NumT表示数据总量。
第2个指标是数据的语义一致性(SCD),关注的是1个装备试验数据模型中不同属性间的定义,以及命名相似的属性定义的一致性,描述了相似数据对象共享一致名称与含义的程度,可表示为:
| $ SCD = 1 - \frac{{TSNum}}{{NumT}}。$ | (2) |
其中,TSNum表示名称相似的数据项个数。
完整性维度中包含2个指标。第1个指标是给定设备测试任务(CRT)的数据完成率,可表示为:
| $ CRT = \frac{{NumF}}{{NumD}}。$ | (3) |
其中,NumF为实际存在的数据量,NumD为应该存在的数据量。
第2个指标是值总体密度(VDD),反映装备试验数据的整体饱满情况,可表示为:
| $ VDD = 1 - \frac{{NumN}}{{NumT}} 。$ | (4) |
其中,NumN为空数据量。
一致性维度中包含3个指标。第1个指标是表示一致性(ECD),主要关注不同位置存储的同一类数据是否满足同一种规范;第2个指标是价值一致性(VCD),主要关注不同存储位置的同一类数据的特性是否相同;第3个指标是空值一致性(ECN),主要关注不同位置存储和使用的空数据的表示方法及含义是否相同。上述3个指标的取值可由以下方程得到:
| $ ECD = 1 - \frac{{ENum}}{{NumT}},$ | (5) |
| $ VCD = 1 - \frac{{VNum}}{{NumT}} ,$ | (6) |
| $ ECN = 1 - \frac{{NNum}}{{NumT}} 。$ | (7) |
其中:ENum,VNum,NNum分别表示各指标中对应不一致的数据项数。
安全性维度中包含2个指标。第1个指标是数据存储安全性(DSS),主要关注数据备份和灾难恢复的策略;第2个指标是加密算法安全性(EAS),主要关注装备试验数据加密算法被破解的难易程度。这2个指标都是定性指标。
及时性维度中包含2个指标。第1个指标是数据发布及时性(DPT),重点考察从装备试验数据产生到数据对外发布所花费的时间与需求紧迫度之间的关系;第2个指标是数据获取及时性(DAT),重点考察从装备试验数据最后更新到获取到所需数据所花费的时间与需求紧迫度之间的关系。
假设有n个数据集,有
| $ DPT = \frac{{\displaystyle\sum\nolimits_{i = 1}^n {\lg (T{P_i} - T{G_i})} }}{n} ,$ | (8) |
| $ DAT = \frac{{\displaystyle\sum\nolimits_{i = 1}^n {\lg (O{T_i} - U{T_i})} }}{n}。$ | (9) |
式中:TPi,TGi,OTi和UTi分别为第i个数据集的数据发布、生成、获取和更新时间。
1.3 效用质量层效用质量层从用户的角度描述数据质量,包括易用性、适用性和可信性共3个维度。
易用性维度中包括3个指标,分别是数据可获取性(AD)、数据可读性(RD)和数据可处理性(PD)。其中,数据可获取性指检查用户查找和发现数据的容易程度;数据可读性指装备试验数据的内容是否易于用户理解;数据可处理性关系到用户如何更方便地编辑和分析数据。这些指标可表示为:
| $ AD = \frac{{AN}}{n} ,$ | (10) |
| $ RD = \frac{{RN}}{n} ,$ | (11) |
| $ PD = \frac{{PN}}{n} 。$ | (12) |
其中:AN,RN,PN分别表示可读取、获取和处理的数据集数量。
适用性维度中包含2个指标,分别是数据适量性(DM)和数据内容符合度(DC)。其中,数据适量性关注的是数据量是否满足用户需求,数据内容符合度指数据的内容是否满足用户的需求。
可信性维度中包含2个指标,分别是数据源可信性(DRC)和数据流转可信性(DFC)。其中,数据源可信性一般由数据提供方的权威性决定,数据流转可信性指试验数据在传递过程中出现偏差、错误、篡改的可能性。
适用性维度和可信性维度中的4个指标难以给出有意义的公式进行准确评价,本文采用专家评价法对其进行评价。
2 方法步骤基于建立的装备试验数据质量综合评价指标体系,提出一种应用群体决策和模糊决策图法的混合方法计算数据质量整体得分,主要步骤为:
步骤1 使用群体决策方法从给出的所有指标中选取满足给定评价问题目标的核心指标;
步骤2 考虑各指标间的影响关系,使用模糊决策图法计算所选指标的优先级;
步骤3 使用2种不同的方法分别计算不同类型的指标值,再采用线性加权的方法得到数据质量整体得分。
2.1 指标选取不同情况下利益相关者关注的指标可能不同,评估目标间存在差异,提出一种群体决策方法,目的是从所有指标中选取核心指标,具体步骤为:
步骤1 假设有
步骤2 收集专家的答案,第
| $ N{D_i} = \frac{{\displaystyle\sum\limits_{j = 1}^m {Ju(i,j)} }}{m} \times 100\% 。$ | (13) |
步骤3 将
装备试验数据评价的复杂性使得所选指标间基本不具备独立性。为了合理考虑不同指标间的影响关系,本文提出使用模糊决策图法得到各指标的优先级[8-10],FDM的具体步骤如下:
假设有一个4元组
| $ f(x) = \tanh (x) = (1 - {e^{ - x}})/(1 + {e^{ - x}})。$ | (14) |
步骤1 计算指标的初始权重。比较各指标间的重要程度,使用Saaty[11]提出的两两比较矩阵法建立判断矩阵,采用1~9判断尺度导出初始权向量
步骤2 构造描述各指标间的影响权重
步骤3 根据下列方程构建稳态矩阵
| $ \left\{ \begin{gathered} C_{(t + 1)}^{} = f(C_{(t)}^{}E),\\ C_{(0)}^{} = {I_{n \times n}},\\ {C^*} = {\lim _{x \to + \infty }}\sum\nolimits_{t = 1}^x {C_{(t)}^{}} 。\\ \end{gathered} \right. $ | (15) |
其中,
步骤4 导出指标的全局权重。按下式计算归一化初始权向量
| $ \left\{ \begin{gathered} \overline z = z/\left\{ {\max (z)} \right\} ,\\ {\overline C ^*} = {C^*}/\gamma。\\ \end{gathered} \right. $ | (16) |
其中,
| $ \omega = \overline z + {\overline C ^*}\overline z ,$ | (17) |
则
装备试验数据评价过程复杂,包含多种定性、定量指标,难以通过一种方法得到所有指标值,本文提出一种混合方法用于计算数据质量得分。首先,使用专家评价法得到定性指标的值;然后,使用抽样统计方法计算得到定量指标的值。最后,使用线性加权法得到全局数据质量得分。
2.3.1 专家评价法在装备试验数据质量评价问题中存在几个定性指标,如CLR,ALR等,很难定义公式来衡量这些指标。为解决此问题,收集专家对指标的判断形成语言集,该语言集包括5个具有唯一数值的语言术语:
| $\begin{split} LS =& \{ {l_1}:{\rm{perfect}} \to 9,{l_2}:{\rm{very}}\; {\rm{good}} \to 7,\\ &{l_3}:{\rm{good}} \to 5, {l_4}:{\rm{not}}\; {\rm{ bad}} \to 3,{\kern 1pt} {\kern 1pt} {l_5}:{\rm{poor}} \to 1\}。\end{split} $ | (18) |
如果专家认为数据的值介于2个给定语言项之间,则可以选择对应2个值间的整数。在实践中,为提高评价的准确性,可邀请不同领域的多位专家对同一指标进行评价,第j个专家对第i个指标的群体判断可表示为:
| $ s{g_i} = \frac{1}{m}\sum\limits_{j = 1}^m {s_i^j}。$ | (19) |
其中,
最后,归一化判断可得:
| $ \overline {s{g_i}} = \frac{1}{9}s{g_i} 。$ | (20) |
其中,用该方法求值的指标共有16个,分别是:
| $ \begin{split}&\{ CLR,ALR,ILR,CSS,ASS,ISS,RPS,ROS,\\ &MSS,GSS,DSS,EAS,DM,DC,DRC,DFC\} 。\end{split}$ | (21) |
在装备试验数据评价问题中,除定性指标外,还有许多定量指标,如ECD及VCD等。给出所有定量指标的计算方法,但装备试验数据庞杂,为提高计算效率,提出2步采样统计方法,具体步骤为:
步骤1 在测试数据评价问题中有很多不同种类的数据集,使用系统抽样法随机选择几个数据集;
步骤2 从选择的每个数据集中选择数据项,然后根据选定的数据项,通过相应的公式直接计算出定量指标的值。
2.3.3 汇总得到全局得分通过给出的方法,可以逐个得到各指标的值,再通给出的方法得到各指标优先级,数据质量评价的最终得分可表示为:
| $ R = {\omega ^{\rm{T}}}\nu。$ | (22) |
其中,ω为指标的权重向量,v为指标的得分。
3 算 例舰船试验是舰船完工投入使用前所需的必要环节,为保障舰船试验数据质量,在进行相关数据构建过程中,必须结合具体业务要求进行数据质量评价。以某型舰船装备试验数据评价问题为例,对所提模型进行验证。
1)指标选取
为选出给定评价问题中的核心指标,邀请9位专家对所有指标进行打分,各指标的必要度可由式(13)计算得到,选取TH=0.2,得到以下8个指标:
| $ \{ CSS,MSS,GSS,CDS,VDD,DSS,EAS,PD\}。$ | (23) |
2) 指标优先级
确定各指标的权重。各指标间的影响关系如图1所示。
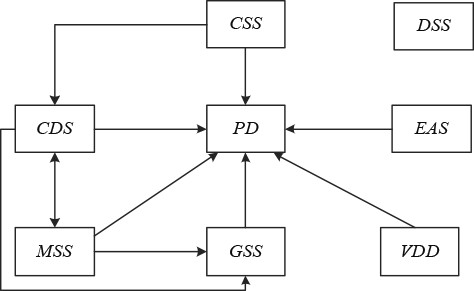
|
图 1 指标间的影响关系 Fig. 1 The influence relationship between the indicators |
利用FDM方法计算各指标权重,结果如表1所示。
|
|
表 1 指标权重 Tab.1 Weight of each index |
3)评估结果
各指标的数值如表2所示。
|
|
表 2 指标值 Tab.2 Index value |
综合以上结果,通过式(22)计算可得最终质量得分R=0.699。根据计算结果,相关人员可清楚认识到该试验数据的质量水平。
4 结 语为解决现有装备试验数据质量评价存在的诸多问题,综合考虑多项评估要素,构建装备试验数据质量综合评价指标体系,提出一种定性与定量相结合的评估数据质量水平的混合方法,并以某舰船装备试验数据评价问题为例,验证了所提方法的可行性,为大数据背景下装备试验数据质量的有效评估提供参考。
| [1] |
龚昕, 周大庆, 等. 武器装备试验数据工程理论与实践 [M]. 北京: 国防工业出版社, 2017: 5–6.
|
| [2] |
陈卫东, 张维明. 数据质量模型及选择运算中的质量传播研究[J]. 计算机工程与应用, 2007(27): 1-3. CHEN W D, ZHANG W M. Reasearch on quality propagation in data quality model and selection operation[J]. Computer engineering and applications, 2007(27): 1-3. DOI:10.3321/j.issn:1002-8331.2007.27.001 |
| [3] |
PIPINO L L, LEE Y W, WANG R Y. Data Assessment[J]. Communications of the ACM , 2002 , 45 (4): 211–218.
|
| [4] |
袁满, 张雪. 一种基于规则的数据质量评价模型[J]. 计算机技术与发展, 2013, 23(3): 81-89. YUAN M, ZHANG X. A rule-based data quality evaluation model[J]. Computer Technology and Development, 2013, 23(3): 81-89. |
| [5] |
YUAN MAN, LIU WEI. A novel data quality controling and assessing model based on rules[C]//ISECS'10 Proceedings of the 2010 Third International Symposium on Electronic Commerce and Security. Guangzhou: Academy Publisher, 2010: 29–32.
|
| [6] |
CHEN Hao, Measurement data quality for ongoing improvement[J]. China Statistics, 2016(6): 18–19.
|
| [7] |
CHEN Chao. Research for electric power big data quality evaluation model and dynamic exploration technology[J]. Modern Electronics Technique. 2014, 37 (4): 153–155.
|
| [8] |
YU R C, TZENG G H. A soft computing method for multi-criteria decision making with dependence and feedback, Applied Mathematics and Computation[J]. 2006, 180(1): 63–75
|
| [9] |
YUEFEI M A, CHEN F, YAO D, et al. Air traffic management system performance evaluation based on linguistic decision map with multi-subnets[J]. Journal of National University of Defense Technology, 2017, 39(6): 134–142.
|
| [10] |
LI C H, SUN Y H, DU Y W. An improved analytic network process based on fuzzy decision maps[C]// Control and Decision Conference, IEEE, 2008.
|
| [11] |
孙宏才, 田平等. 网络层次分析法与决策科学[M]. 北京: 国防工业出版社, 2011: 7–8.
|
| [12] |
FAN W, & GEERTS F. Foundations of data quality management[J]. Journal of Synthesis Lectures on Data Management, 2012.
|
| [13] |
马一鸣. 政府大数据质量评价体系构建研究[D]. 长春: 吉林大学, 2016
|
 2023, Vol. 45
2023, Vol. 45
