某舰用综合体武器系统兼具炮、光发射功能,2种武器通道共架安装且共随动,为保证光通道发射精度,其跟瞄系统采用了粗精复合轴结构。其中粗跟踪对目标进行捕获和跟踪,并将目标引入精跟瞄视场,精跟瞄对视场内的粗跟踪残差做进一步校正,实现光束的精确指向。粗、精2级跟踪通过光闭环和视场耦合实现级联、复合跟踪。
在精跟瞄中,通过驱动快速反射镜 (fast steering mirror,FSM)偏转控制光束指向,尽管FSM具有高带宽、高精度特性,脱靶量的延迟特性仍然对光束的指向精度有很大影响。如通过提高目标图像处理帧频,减小CCD积分时间,则易引入高频干扰,并显著增加图像处理硬件和软件上的代价和难度。
魏文军等[1]在自抗扰控制(ADRC)中采用了预报算法补偿子轴脱靶量滞后的方法。周睿等[2]采用了2级FSM分别对窄带和宽带扰动进行抑制。赵继庭等[3]采用了自适应PID的FSM控制方法。唐清等[4]在既有延迟特性的基础上,提高了FSM控制模型的型次。丁科等[5]采用了基于精跟踪误差的自适应前馈复合控制。杨东等[6]采用了基于FSM参考模型的补偿方法。上述方法均取得一定控制成效,但着重于提高FSM动态响应特性和精度方面的研究,未能有效克服精跟瞄脱靶量延迟对指向精度的影响。
粗、精跟踪具有相互独立的光电探测通道且共架安装,两者脱靶量之间有着固定的空间对应关系。本文提出利用粗跟踪脱靶量作为精跟瞄参考控制量的方法,针对粗跟踪脱靶量的高频非线性和跳变,采用LMS自适应滤波的方法进行统计学习和滤波补偿,并建立基于典型被控对象的某综合体系统模型进行仿真验证。
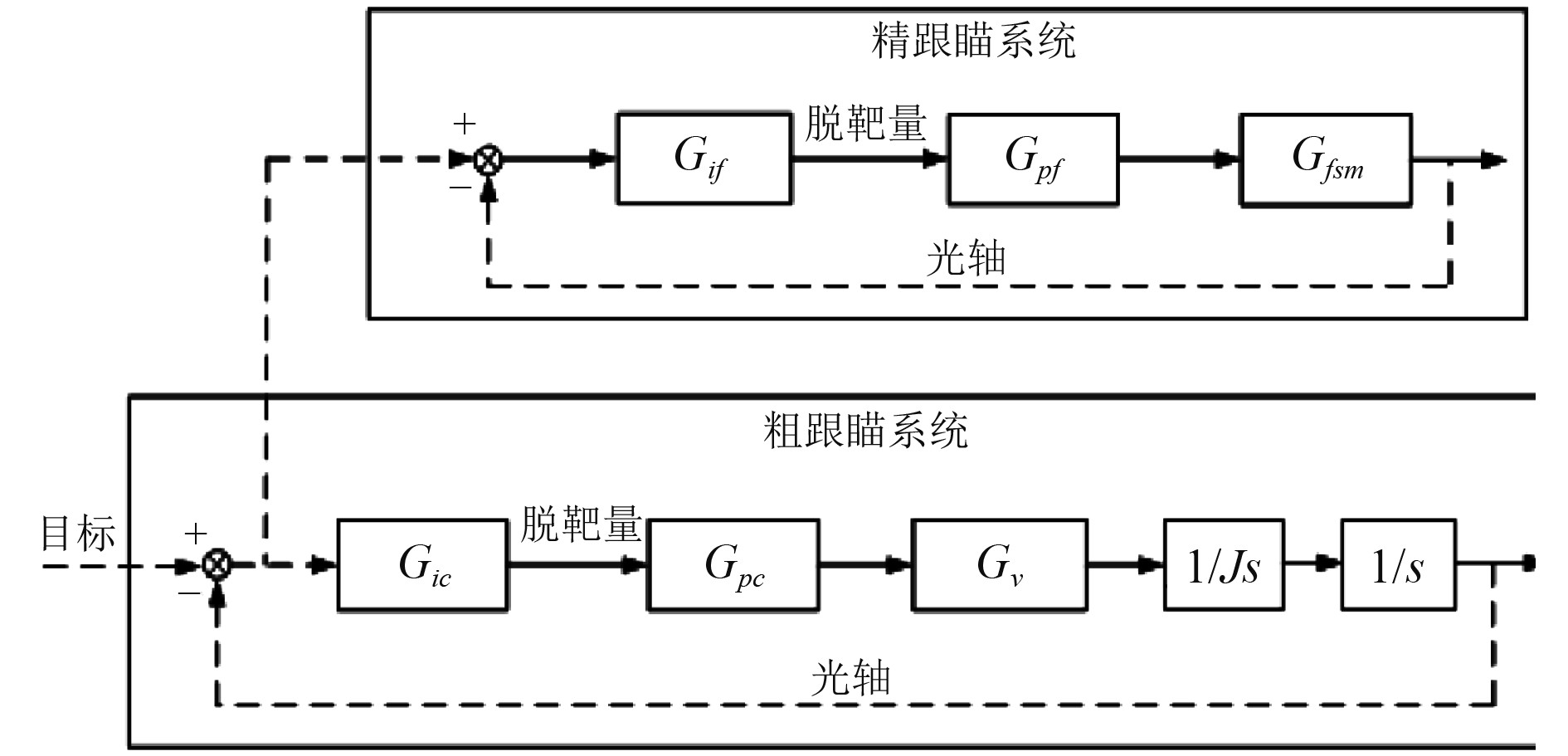
1 复合跟踪轴和典型被控对象 1.1 复合跟踪轴结构复合跟踪轴结构由粗跟踪系统、精跟瞄系统组成,如图1所示。其中粗跟踪系统主要包括粗级光电探测和图像识别单元、随动系统等,精跟瞄系统主要包括精级光电探测和图像识别单元、FSM微位移伺服系统等。
|
图 1 复合跟踪轴控制结构 Fig. 1 Control structure of combined tracking axis |
图中,Gi和Gif分别为粗跟踪、精跟瞄的光电探测和图像识别环节;Gpc和Gpf分别为粗跟踪、精跟瞄位置控制器;Gv为粗跟踪随动系统速度环传递函数;Gfsm为精跟瞄FSM传递函数。
粗跟踪在目指下进行调转,捕获目标,给出相对于其视轴的脱靶量,以光闭环的形式控制架体对目标进行稳定跟踪;目标图像进入精跟瞄视场后,精级CCD相机和图像识别单元对目标进行识别,得到相对于光轴的脱靶量,精位置控制器对脱靶量进行解算,控制FSM进行偏转,使目标趋于光轴允许偏差范围之内。
粗跟踪和精跟瞄的控制结构相互独立,通过空间光学耦合实现复合跟踪,视场取决于各自的探测精度、跟踪精度、视场匹配性、探测分辨率、光学装调等要素。目标进入粗、精视场后,粗、精光轴间基线的影响可通过射表进行主动修正或作为固有误差由FSM进行被动校正。
1.2 典型被控对象模型粗精复合跟踪系统的典型被控对象为随动系统以及FSM微位移伺服系统。为提高精度,随动系统采用力矩电机直驱形式;为提高抗射击振动和冲击性,FSM伺服系统采用音圈电机作动器驱动镜片偏转。
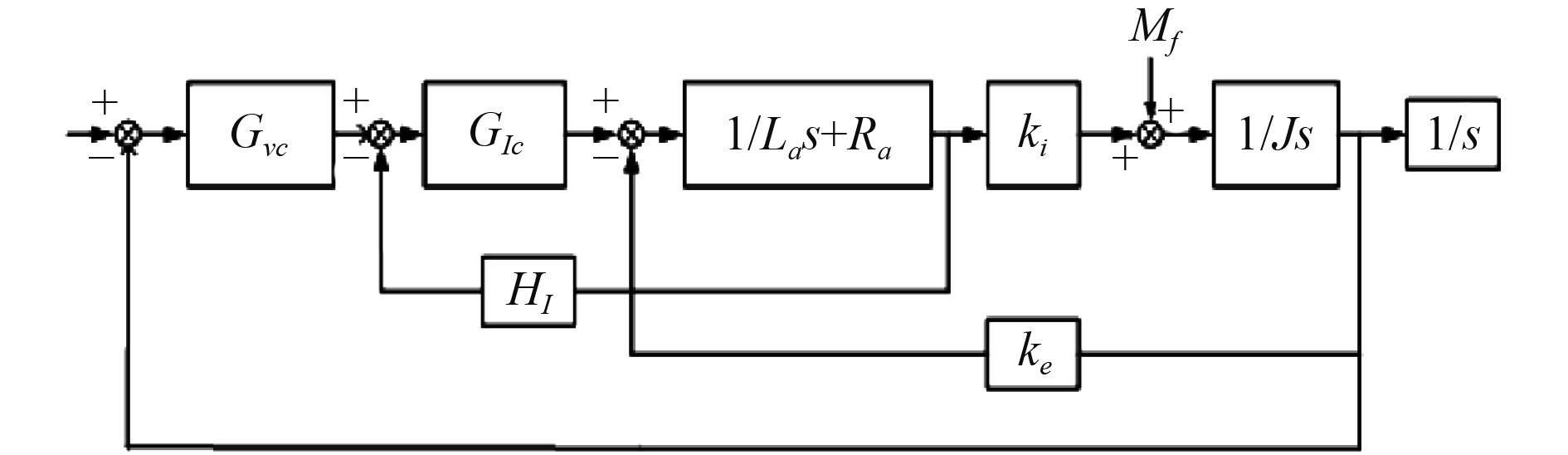
直驱随动系统采用典型的位置/速度/电流3环控制,其中速度环特性决定动态响应特性,其模型基本结构如图2所示。
|
图 2 随动系统速度环模型 Fig. 2 Velocity loop model of servo system |
图中,Gvc和GIc分别为速度环、电流环控制器;La和R分别为力矩电机电感、电阻;ki和ke分别为力矩系数、反电动势系数;J为负载转动惯量;HI为电流反馈系数。
经建模和辨识,该直驱随动系统速度环及惯性负载的等效传递函数如下式,3 dB带宽约为17 Hz。
| $ \begin{split} & {G_{vp}}(s) = \\ & {K_p} \cdot (\frac{{1 + {T_z}s}}{{{{(1 + 2 \times Zeta \cdot {T_w}s + {T_w}s)}^2}(1 + {T_p}s)}}) \cdot {e^{ - {T_d}s}}。\end{split} $ | (1) |
式中:Kp=1.0058;TW =0.0094374;Zeta=0.30303;Tp =0.15841;Td =0.037528;Tz =0.07475。
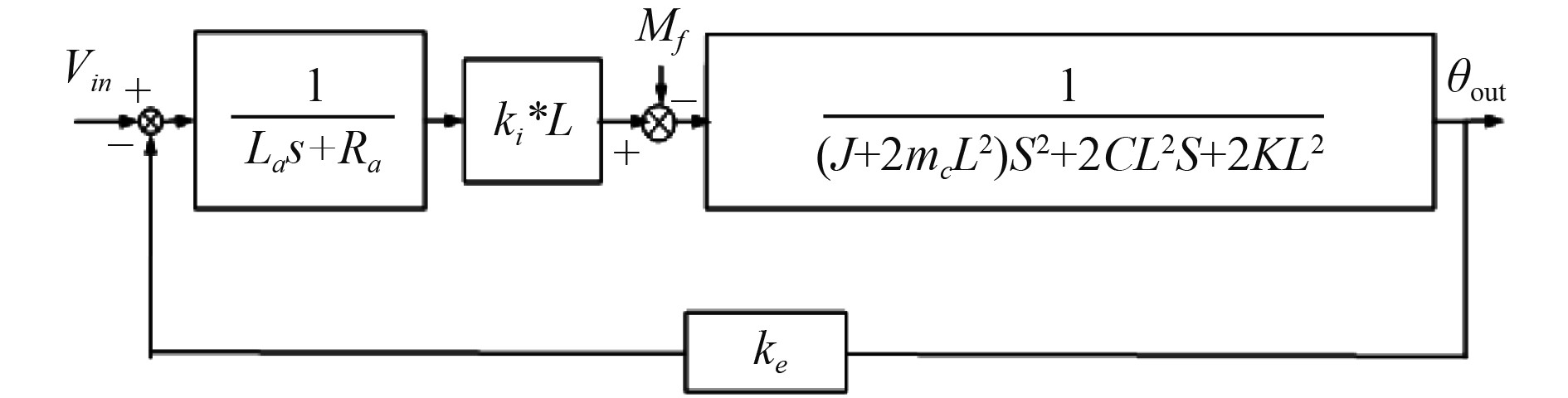
基于音圈电机驱动的FSM伺服系统单轴控制模型如图3所示。
|
图 3 FSM单轴控制模型 Fig. 3 Uniaxial control model of FSM |
图中,La和R分别为音圈电机电感、电阻;ki和ke分别为力矩系数、反电动势系数;J为镜片负载转动惯量;K为刚度系数;C为等效阻尼系数;L为作动器作用点到偏转中心的距离;mc为音圈电机动子质量。
经建模和辨识,该FSM伺服系统的单轴控制模型等效传递函数如下式,3 dB带宽约为430 Hz。
| $ \begin{split} & {W_{FSM - x}}(s) = \\ &\frac{{2.4\times 10^{10}}}{{{s^3} + 6689{s^2} + 15720000s + 2.4\times 10^{10}}}。\end{split} $ | (2) |
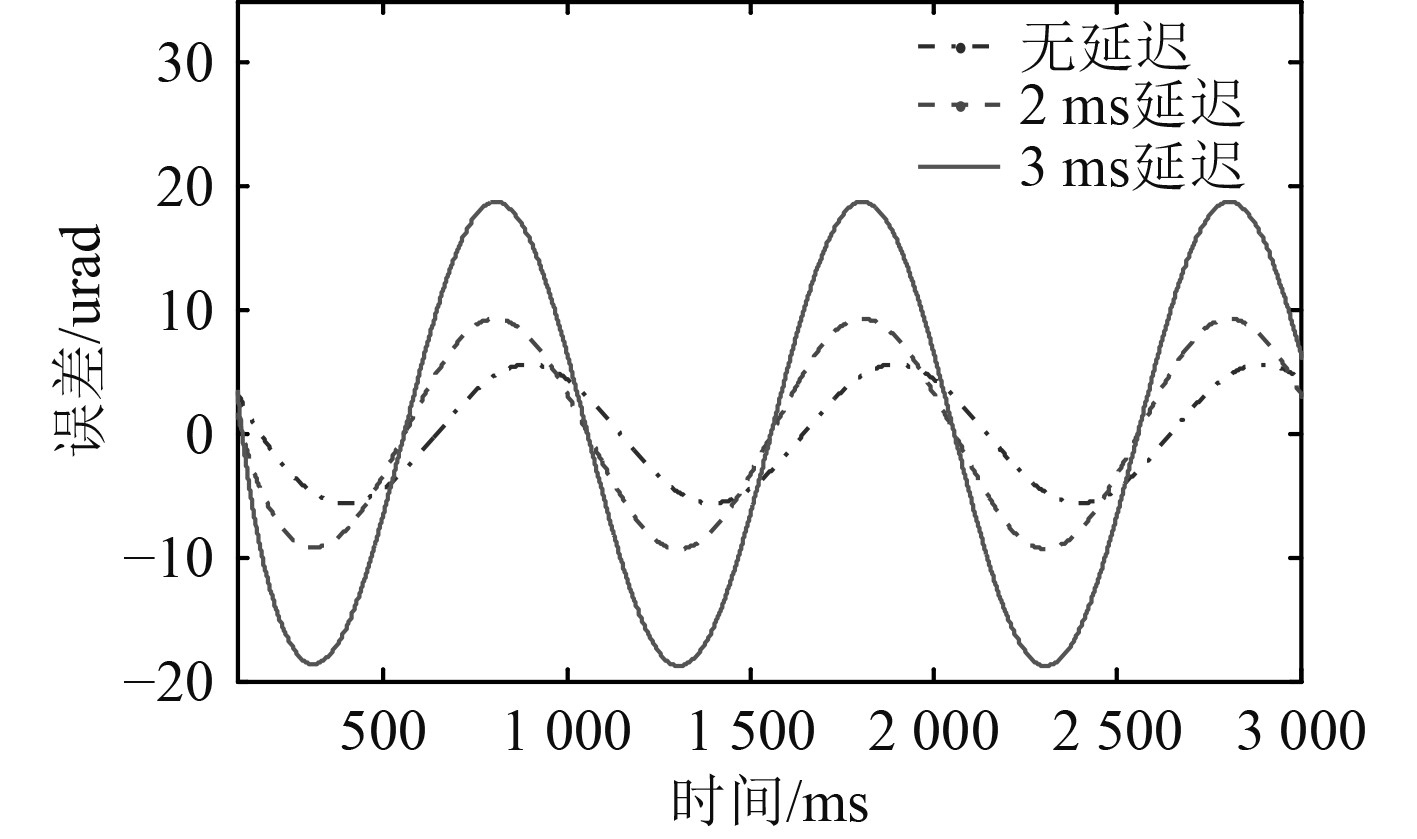
精跟瞄延迟分量主要包括CCD积分时间和脱靶量传输滞后。以式(2)所示FSM传递函数为被控对象,分别在无延迟、2 ms延迟(CCD积分时间1 ms,传输延迟1 ms)、3 ms延迟(CCD积分时间2 ms,传输延迟1 ms)下输入1000 μrad,1 Hz和130 μrad,5 Hz的正弦信号,精跟瞄精度分别如图4和图5 所示。
|
图 4 1 000 μrad,1 Hz信号控制精度 Fig. 4 Control accuracy under 1 000 μrad/1 Hz signal |

|
图 5 130 μrad、5 Hz信号控制精度 Fig. 5 Control accuracy under 130 μrad/5 Hz signal |
由图可知,图像处理帧频为500 fps(CCD积分时间2 ms)时,延迟依然对精跟瞄精度有较大影响。图像处理帧频提高到1 000 fps(CCD积分时间1 ms)时,精跟瞄精度有明显改善,但综合考虑精跟瞄视场、像元精度等因素,光电探测和图像识别单元需具备高帧频、高分辨率的图像采集、识别性能,这会急剧增加图像处理器硬件电路、识别算法的设计难度和成本,同时信号传输线路也面临衰减加剧、传输距离短的限制。
复合跟踪轴系统中,粗、精2级跟踪虽然具有相互独立的控制结构,但本质上仍是对同一目标进行识别的不同表现结果。粗跟踪脱靶量名义上可作为精跟瞄的控制量,由于粗、精采样频率和带宽区别较大,需对粗跟踪脱靶量进行滤波处理。
3 基于脱靶量的LMS滤波 3.1 滤波算法的选择对于粗跟踪,尽管目标轨迹会具有一定机动性,但在一定时间周期内目标轨迹仍可按线性建模,利用最小二乘、卡尔曼等滤波算法可以有效补偿粗跟踪脱靶量的滞后。
式(3)是基于CV模型的最小二乘滤波算法式[7]。
| $ \left\{ \begin{gathered} {{\hat x}_n} = {{\hat x}_{n - 1}} + \Delta t{{\hat {\dot x}}_n} + \frac{{2(2n - 1)}}{{n(n + 1)}}[{z_n} - ({{\hat x}_{n - 1}} + \Delta t{{\hat {\dot x}}_n})] ,\\ {{\hat {\dot x}}_n} = {{\hat {\dot x}}_{n - 1}} + \frac{6}{{n(n + 1)}}[{z_n} - ({{\hat x}_{n - 1}} + {{\hat {\dot x}}_{n - 1}}\Delta t)] 。\\ \end{gathered} \right. $ | (3) |
式中:
卡尔曼滤波主算法为下式:
| $ \left\{ \begin{gathered} {{\hat x}^ - }_n = A{{\hat x}_{n - 1}} + B{u_n} ,\\ \\ {{\hat x}^{}}_n = {{\hat x}^ - }_n + {K_k}({Z_n} - C{{\hat x}^ - }_n) 。\\ \end{gathered} \right. $ | (4) |
式中:
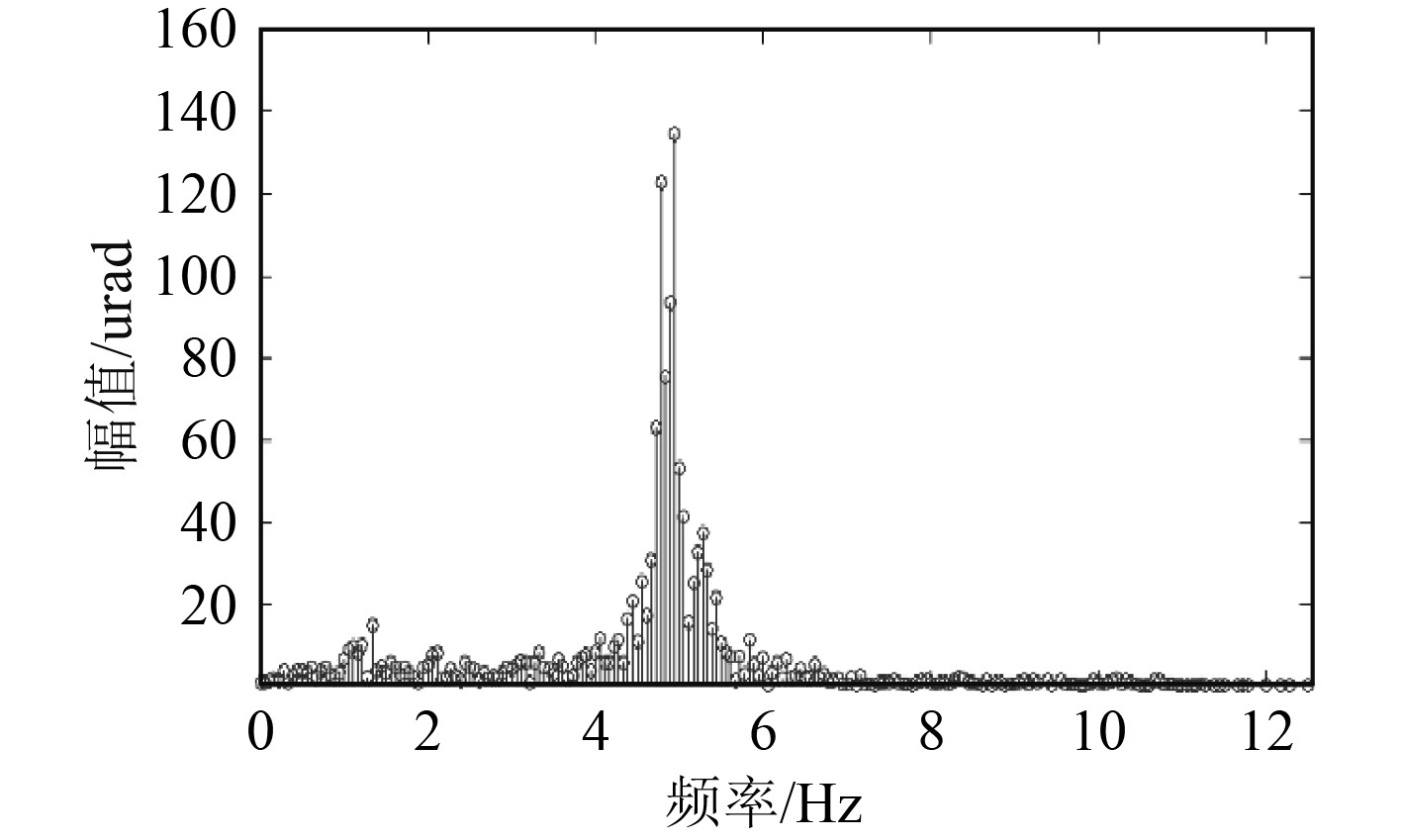
对于精跟瞄,则需对粗跟踪脱靶量进行滤波预测,图6和图7为典型粗跟踪脱靶量及其频谱。式(3)和式(4)中最小二乘滤波和卡尔曼滤波主要包含状态预计、和估计更新2部分,而粗跟踪脱靶量具有明显的高频非线性和跳变特性,其状态预计方程和更新方程难以准确建立,工程实现上,最小二乘、卡尔曼等算法难以获得理想滤波效果。

|
图 6 典型粗跟踪脱靶量 Fig. 6 Typical coarse miss error |
|
图 7 典型粗跟踪脱靶量频谱 Fig. 7 Frequency spectrum of typical coarse miss error |
鉴于此,本文采用LMS(least mean square)自适应滤波的方法对粗跟踪脱靶量进行学习和滤波,并作为精跟瞄系统的输入修正。
3.2 最小均方LMS自适应滤波LMS算法是在维纳滤波的基础上,借鉴最速下降法的思想发展而来的,其目的是使滤波器的均方误差达到最小。LMS算法具有以下特点:
1)算法简易,不需要对回归量的相关矩阵进行求逆;算法复杂度与FIR滤波器的维数呈线性关系,算法围绕此进行;
2)与维纳滤波器不同,不需要工作环境统计特性的相关知识;
3)具有一定鲁棒性。
|
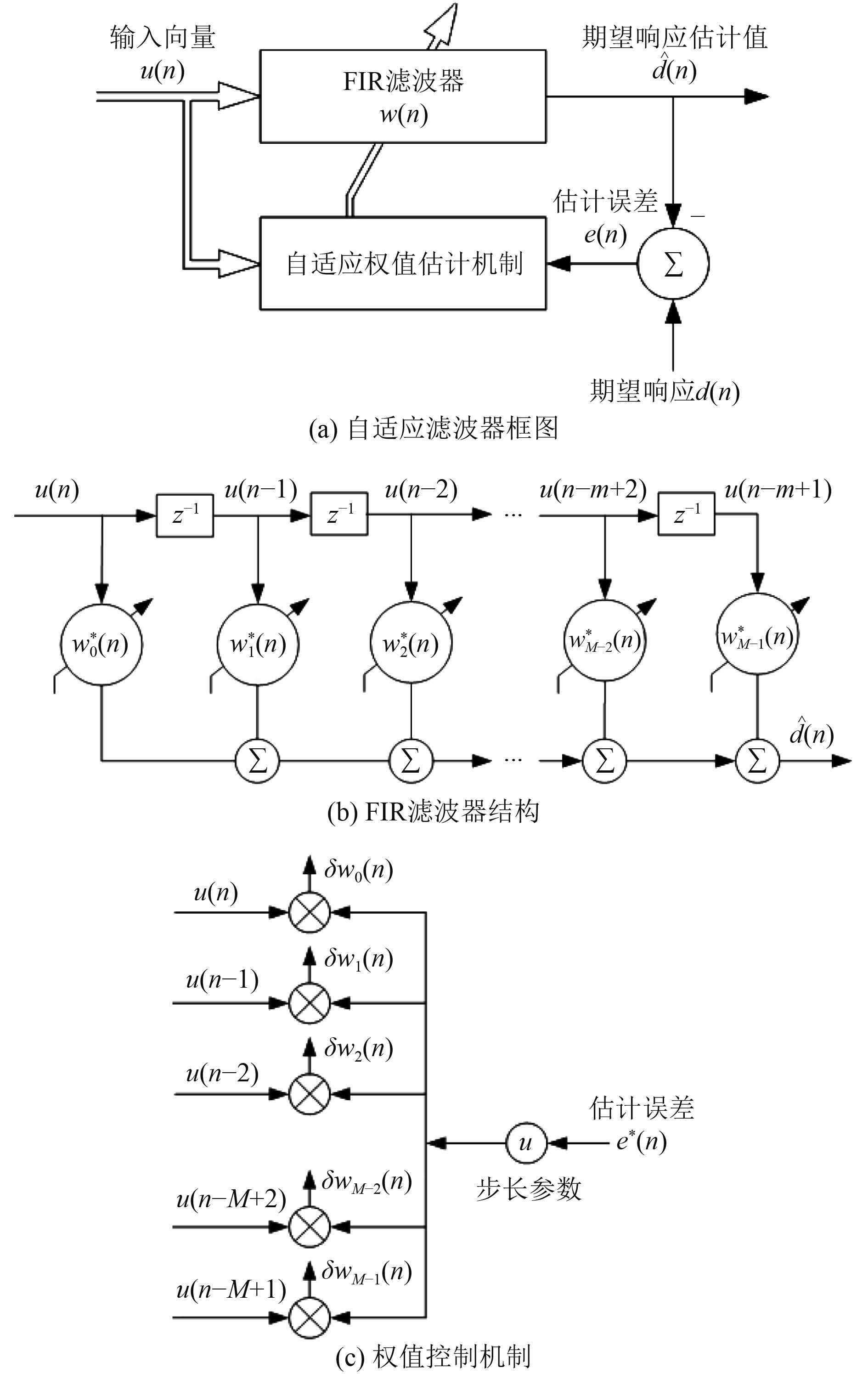
图 8 LMS算法结构 Fig. 8 Algorithm structure of LMS |
LMS算法包括3部分:
1)FIR滤波器。工作在回归量(输入向量)u(n)上,生成期望响应的估计值d(n);
2)比较器。期望响应d(n)减去估计值d(n),结果为估计误差e(n);
3)自适应权值控制机制,利用估计误差控制FIR滤波器上各抽头w(n)增量的调整。
LMS算法具体如下:
| $ y(n) = {w^{\rm{H}}}(n)u(n) ,$ | (5) |
| $ e(n) = d(n) - y(n) ,$ | (6) |
| $ w(n + 1) = w{(n)_{}} + \mu u(n){e^*}(n)。$ | (7) |
式中:y(n)为滤波器输出,u(n)为输入向量,d(n)为期望响应,w(n)抽头权向量,
为使局部扰动最小,步长参数需满足以下条件:
| $ \left|1-\mu {\Vert u(n)\Vert }^{2}\right|<1 。$ | (8) |
式中,
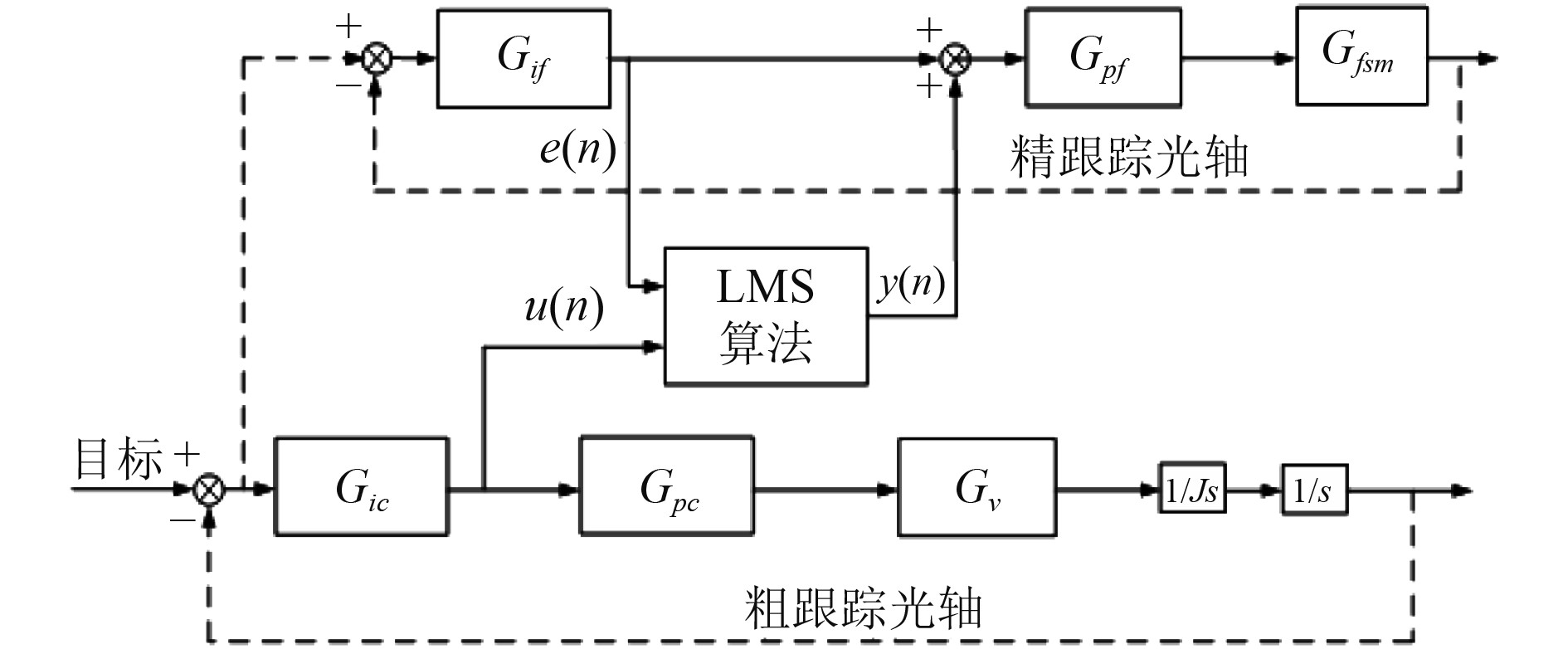
LMS算法采用最速下降法,本质上是一种局部方法,呈现局部最优,其收敛值是较之维纳解的次优解,和维纳解的差值为额外均方误差。因此,在滤波补偿的基础上仍需精跟瞄系统自身对额外的均方误差进行补偿。由此,在图1的基础上,建立如图9所示的基于粗、精脱靶量的LMS滤波控制结构。
|
图 9 基于脱靶量的LMS滤波结构 Fig. 9 LMS filtering structure based on miss error |
粗跟踪脱靶量作为LMS算法中输入向量u(n),精跟瞄脱靶量作为估计误差ef(n);LMS自适应滤波器模块同步采集n个粗跟踪脱靶量、n个精跟踪脱靶量的历史数据,并对每组粗精脱靶量进行代数加权和运算,得出滤波器输出y(n),作为精跟瞄参考控制量。
4 仿真及结果 4.1 系统仿真模型根据图9,建立如图10所示的复合跟瞄系统仿真模型。模型中,0阶保持器将粗跟踪脱靶量数据周期设定为10 ms,GV&Js为粗跟踪随动系统速度环和负载等效传递函数;精跟瞄控制周期为2 ms,图像帧频为500 fs,延迟时间为3 ms;Gfsm为FSM单轴等效传递函数;目标输入信号包括粗跟踪目标模拟信号Ct(0.0087 rad,6.28 rad/s)、精跟瞄目标模拟信号Ft(0.13 mrad、31.4 rad/s)、典型粗跟踪脱靶量At。

|
图 10 复合跟瞄系统仿真模型 Fig. 10 Simulation model of combined tracking system |
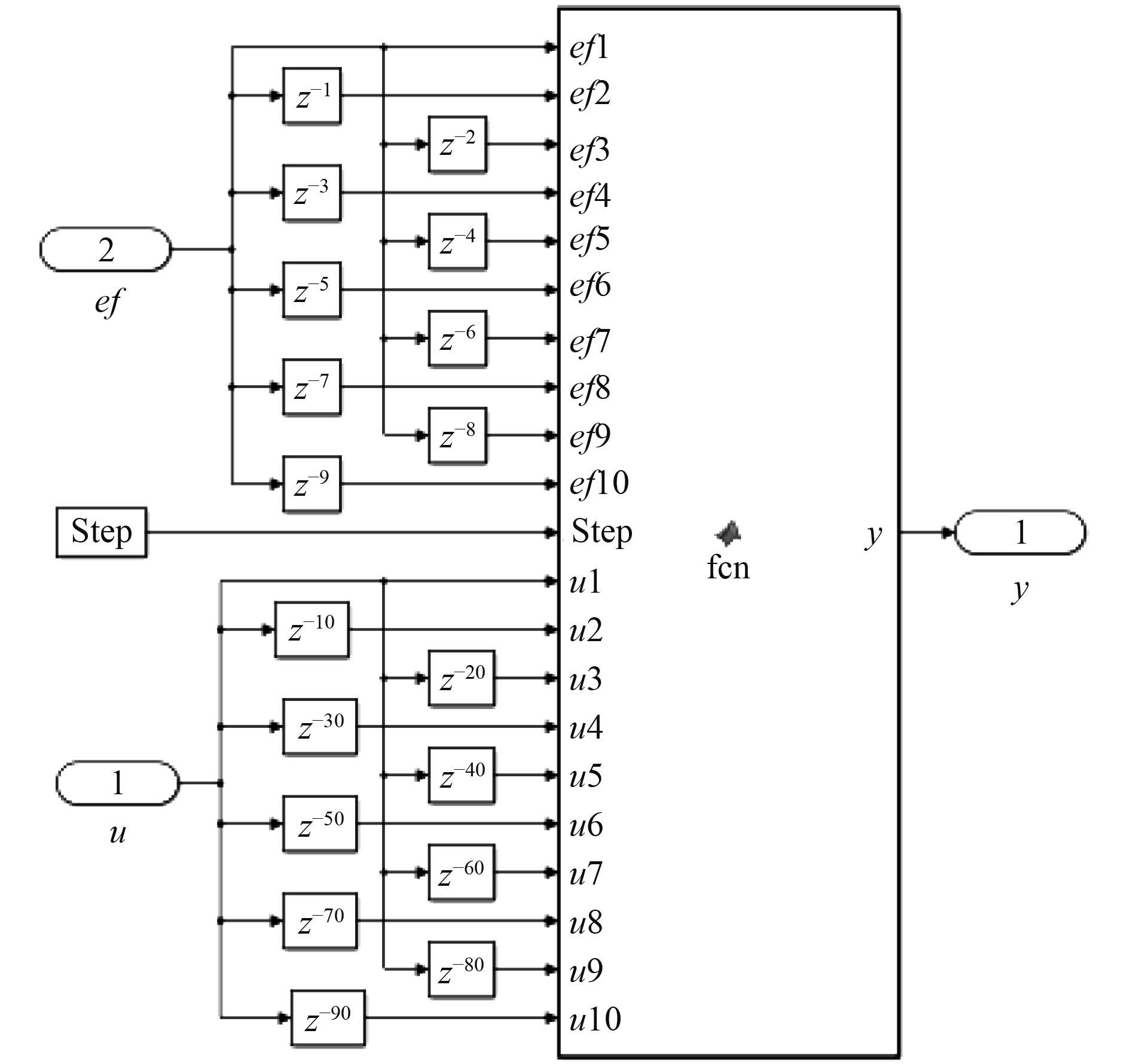
LSM滤波器如模型图11所示。u取10组历史最近粗跟踪残差数据,ef取10组历史最近精跟瞄误差数据,Step为仿真步长,w(0)~w(9)等10组抽头权值,按式(7)计算,滤波器输出y按式(5)计算。
|
图 11 LMS滤波器模型 Fig. 11 LMS filter model |
1)粗精联合仿真
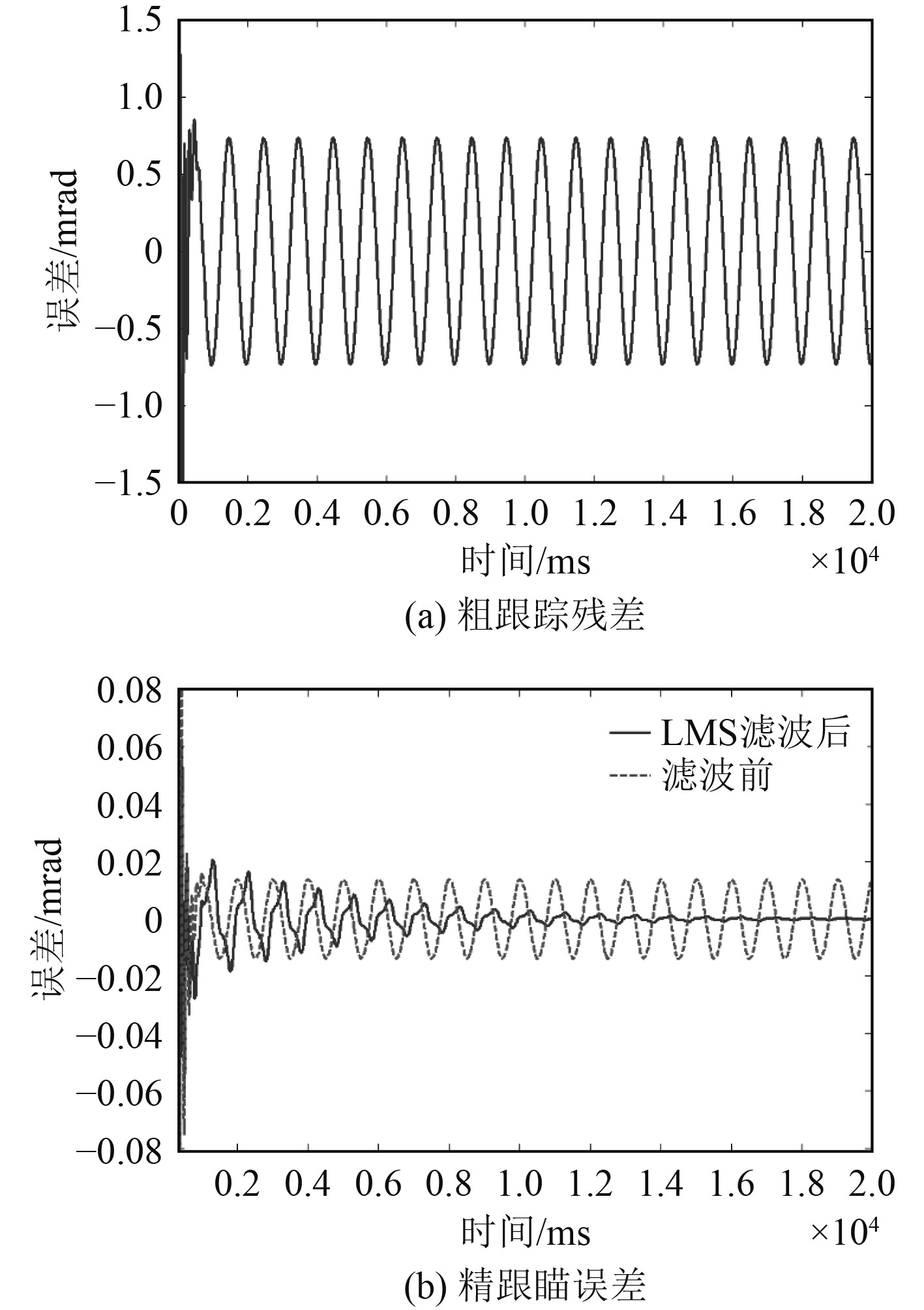
向粗跟踪系统注入Ct(0.0087 rad,6.28 rad/s)目标模拟信号,粗跟踪残差曲线如图12(a)所示,最大误差约0.8 mrad;LMS滤波前后,精跟瞄误差曲线如图12(b)所示,LMS滤波前最大误差约20 μrad,滤波后误差随时间减小至10 μrad内。
|
图 12 粗精联合仿真结果 Fig. 12 Co-simulation of coarse and fine system |
2)精跟瞄信号注入仿真
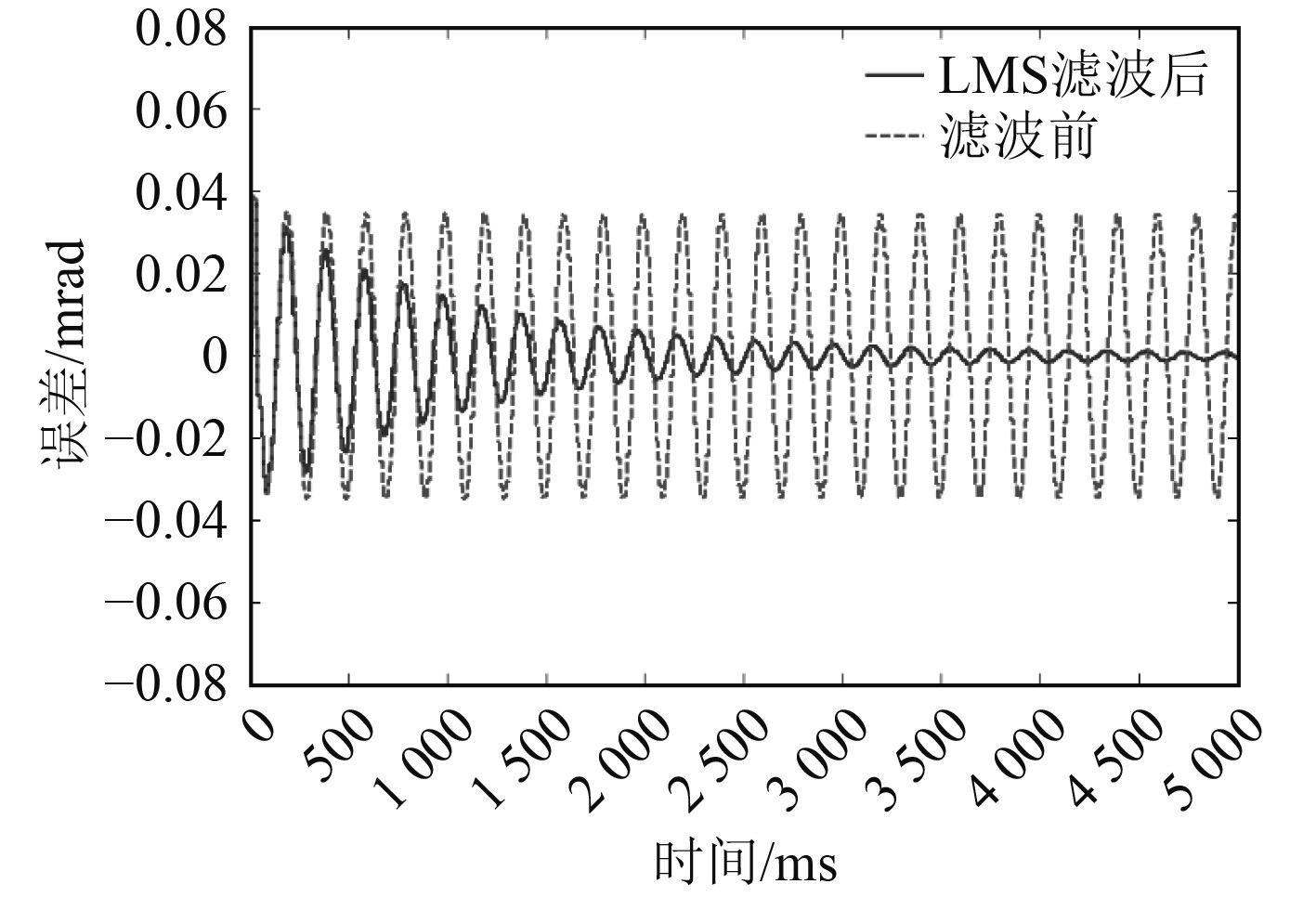
向精跟瞄系统直接注入图6频谱中最大频率分量Ft(0.13 mrad,31.4 rad/s)目标模拟信号,LMS滤波前大误差约40 μrad,滤波后误差随时间减小至最10 μrad内,如图13所示。
|
图 13 最大频率分量信号注入仿真 Fig. 13 Injection simulation of maximun frequency signal |
向精跟瞄系统直接注入图6中典型粗跟踪残差At目标模拟信号,LMS滤波前均方根误差约49 μrad,滤波后均方根误差约12 μrad,如图14所示。

|
图 14 典型粗跟踪残差注入 Fig. 14 Injection simulation of typical coarse miss error |
在仿真中,精跟瞄误差的收敛速度与步长
本文对某综合体复合跟瞄技术进行研究,针对图像延迟带来的指向精度影响,提出并采用对粗、精跟踪脱靶量进行LMS自适应滤波和预测的方法,改善了跟瞄精度,且算法结构简单,鲁棒性好,易于实现。具体工程应用时,在收敛且不失调下,可采用变步长方法改善收敛速度。
| [1] |
魏文军, 赵雪童. 基于改进自抗扰的快速反射镜控制研究[J]. 红外技术, 2018, 40(11): 1071–1076. WEI Wen-jun, ZHAO Xue-tong. Fast steering mirror control based on improved active disturbance rejection[J]. Infrared Technology. 2018, 40(11): 1071–1076. |
| [2] |
周睿, 李新阳, 沈锋, 等. 基于两级高速倾斜镜闭环控制的光束稳定技术研究[J]. 光学学报, 2016, 36(12): 1–11. ZHOU Rui, LI Xin-yang, SHEN Feng, et al. Laser beam stabilizing system based on close loop control of two fast steering mirrors in series[J]. Acta Optica Sinica. 2016, 36(12): 1–11. |
| [3] |
赵继庭, 金刚石, 高旭辉. 基于快速反射镜的模糊自适应PID 控制算法研究[J]. 激光与红外, 2018, 48(6): 756–761. ZHAO Ji-ting, JIN Gang-shi, GAO Xu-hui. Fuzzy adaptive PID control algorithm based on fast steering mirror[J]. Laser&Infrared. 2018, 48(6): 756–761. |
| [4] |
唐涛, 杨涛, 黄永梅, 等. 具有延迟特性的FSM 系统中PI-PI 控制器[J]. 光电工程, 2013, 40(5): 1–5. TANG Tao, YANG Tao, HUANG Yong-mei, et al. PI-PI Controller for the time delay control System of FSM[J]. Opto-Electronic Engineering. 2013, 40(5): 1–5. |
| [5] |
丁科, 黄咏梅, 马佳光, 等. 快速反射镜的误差自适应前馈复合控制[J]. 中国激光, 2011, 38(7): 1–6. DING Ke, HUANG Yong-mei, MA Jia-guang, et al. Error adaptive feedforward composite control of fast-steering-mirror[J]. Chinese Journal of Lasers. 2011, 38(7): 1–6. |
| [6] |
杨东, 毛耀, 丁科, 等. 模型参考算法在快速反射镜中的应用[J]. 红外与激光工程, 2013, 42(10): 2790–2795. YANG Dong, MAO Yao, DING Ke, et al. Application of model reference adaptive algorithm in fast-steering mirrors[J]. 2013, 42(10): 2790–2795. |
| [7] |
樊 鹏, 李文才, 董琦昕. 多模自适应递推最小二乘滤波在机动目标跟踪中的应用[J]. 兵工自动化, 2015, 34(8): 4–7. FAN Peng, LI Wen-cai, DONG Qi-xin. Application of multi-model adaptive recursive least square filter in maneuvering target tracking[J]. Ordnance Industry Automation. 2015, 34(8): 4–7. |
| [8] |
西蒙. 赫金. 自适应滤波器原理(第五版)[M]. 电子工业出版社, 2016, 175–177.
|
 2023, Vol. 45
2023, Vol. 45
