近年来,舰船内部安装的电子装备越来越多,为舰船航行提供便利[1],但却加大了电子装备电路维修的难度。电子电路故障区域节点跟踪定位方法可帮助维修人员快速、精准地找到故障区域节点,及时维修故障元件,为舰船安全航行提供有力保障[2]。胡创业等[3]利用辐射能谱仪模拟电子电路,采集电子电路不同状态下的电路信息,支持向量机依据不同状态下的电路信息进行故障区域节点跟踪定位。该方法的故障区域节点跟踪定位精度为76%。高校平等[4]建立存在故障距离与过渡电阻的时域方程组,同时通过最小二乘法求解该时域方程组,得到故障定位跟踪定位结果。该方法具备较高的故障跟踪定位精度。但这2种方法均受电子电路的量纲影响,并未考虑电子电路不同故障特性间的联系,无法排除故障变量间相关性的干扰。为此,以改进马氏距离为基础,研究舰船装备电子电路故障区域节点跟踪定位方法,精准跟踪定位故障区域节点。
1 电子电路故障区域节点跟踪定位利用经验模态分解(empirical mode decomposition,EMD)在舰船装备电子电路原始数据内,提取不同状态下舰船装备电子电路的故障特征,但EMD提取故障特征时,存在端点效应问题[5-6]。为此,通过最小二乘支持向量机(least square support vector machine,LSSVM),延拓处理不同状态下舰船装备电子电路的原始数据,并将延拓处理后的数据输入至EMD内,提取故障特征,解决端点效应问题[7]。采用改进马氏距离算法,计算未知故障特征与已知故障集间的马氏距离,以马氏距离为故障区域节点跟踪定位的依据,实现故障区域节点跟踪定位。
1.1 基于EMD的舰船装备电子电路故障特征提取利用EMD在舰船装备电力电路原始数据
1) 确定全部舰船装备电子电路原始数据的全部局部极值点
2) 通过三次样条线分别连接
3) 在
| $ {z_1}\left( t \right) = x\left( t \right) - {q_1}\left( t \right) 。$ | (1) |
如果
4) 若
| $ {z_{11}}\left( t \right) = {z_1}\left( t \right) - {q_{11}}\left( t \right) ,$ | (2) |
分析
| $ {z_{1k}}\left( t \right) = {z_{1\left( {k - 1} \right)}}\left( t \right) - {q_{1k}}\left( t \right)。$ | (3) |
其中:
5) 在
| $ {r_1}\left( t \right) = x\left( t \right) - {c_1}\left( t \right) 。$ | (4) |
其中,
| $ \left\{ \begin{gathered} {r_2}\left( t \right) = {r_1}\left( t \right) - {c_2}\left( t \right) ,\\ {r_3}\left( t \right) = {r_2}\left( t \right) - {c_3}\left( t \right),\\ \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \vdots \\ {r_n}\left( t \right) = {r_{n - 1}}\left( t \right) - {c_n}\left( t \right)。\\ \end{gathered} \right. $ | (5) |
在
| $ x\left( t \right) = \sum\limits_{i = 1}^n {{c_i}\left( t \right) + {r_n}\left( t \right)} ,$ | (6) |
其中:
6) 计算各IMF分量的能量
| $ {E_i} = \sum\limits_{j = 1}^{{M_i}} {{{\left| {c_i^j\left( t \right)} \right|}^2}} 。$ | (7) |
其中,
7) 以能量熵
| $ H = - \sum\limits_{i = 1}^n {\frac{{{E_i}}}{E}\ln } \frac{{{E_i}}}{E}。$ | (8) |
其中,
通过上述操作便可获取不同状态下,舰船装备电子电路故障特征
但EMD算法在提取故障特征时,存在端点效应问题。利用LSSVM算法,延拓处理
| $ f\left( x \right) = \sum\limits_{l = 1}^\eta {{\alpha _l}} K\left( {{x_l},{x_\beta }} \right) + b 。$ | (9) |
其中:
通过
| $ x_l^*\left( t \right) = f\left( {{x_{\eta - 1}},{x_{\eta - 2}}, \cdots ,{x_{\eta - \varepsilon }}} \right) 。$ | (10) |
式(10)代表通过
令舰船装备电子电路故障样本集的维度为
| $ d\left( h \right) = \sqrt {{{\left( {h - \bar Y} \right)}^{\rm{T}}}\sum _Y^{ - 1}\left( {h - \bar Y} \right)}。$ | (11) |
其中:
| $ \bar Y = \frac{{\displaystyle\sum\limits_{i' = 1}^g {{Y_{i'}}} }}{g},$ | (12) |
| $ \sum _Y^{} = \frac{{\displaystyle\sum\limits_{i' = 1}^g {{{\left( {{Y_{i'}} - \bar Y} \right)}^2}} }}{{g - 1}} 。$ | (13) |
其中,
通过在式(11)内添加权值
| $ d\left( h \right) = \sqrt {{{\left( {h - \bar Y} \right)}^{\rm{T}}}\omega \sum _Y^{ - 1}\omega \left( {h - \bar Y} \right)} ,$ | (14) |
第
| $ {\omega _{j'}} = {\left( {\frac{{{o_{j'}}}}{{\displaystyle\sum\limits_{j' = 1}^{N'} {{o_{j'}}} }}} \right)^2} 。$ | (15) |
其中:
利用改进马氏距离跟踪定位电子电路故障区域节点的具体步骤如下:
步骤1 求解各故障特征至故障样本集的马氏距离
步骤2 计算
步骤3 按照故障号,在故障样本集内搜索故障类型。
步骤4 验证
以某舰船装备的部分电子电路为实验对象,该部分电子电路内共包含5个电阻,记作
|
|
表 1 电子电路具体信息 Tab.1 Electronic circuit specific information |
利用本文方法对该舰船装备电子电路原始数据进行延拓处理,并提取故障特征,延拓处理结果以及故障特征提取结果如图1所示。根据图1(a)可知,舰船装备电子电路原始电压数据存在大量冗余数据,变化趋势并不显著,无法为后续故障区域节点跟踪定位提供较好的数据支持。根据图1(b)可知,经过本文方法延拓处理后,可剔除大量冗余数据,可明显看出电压的变化趋势。根据图1(c)可知,本文方法可有效计算各IMF分量的能量熵,即提取电子电路故障特征。实验证明:本文方法具备较优的数据延拓处理效果,并有效提取电子电路故障特征。
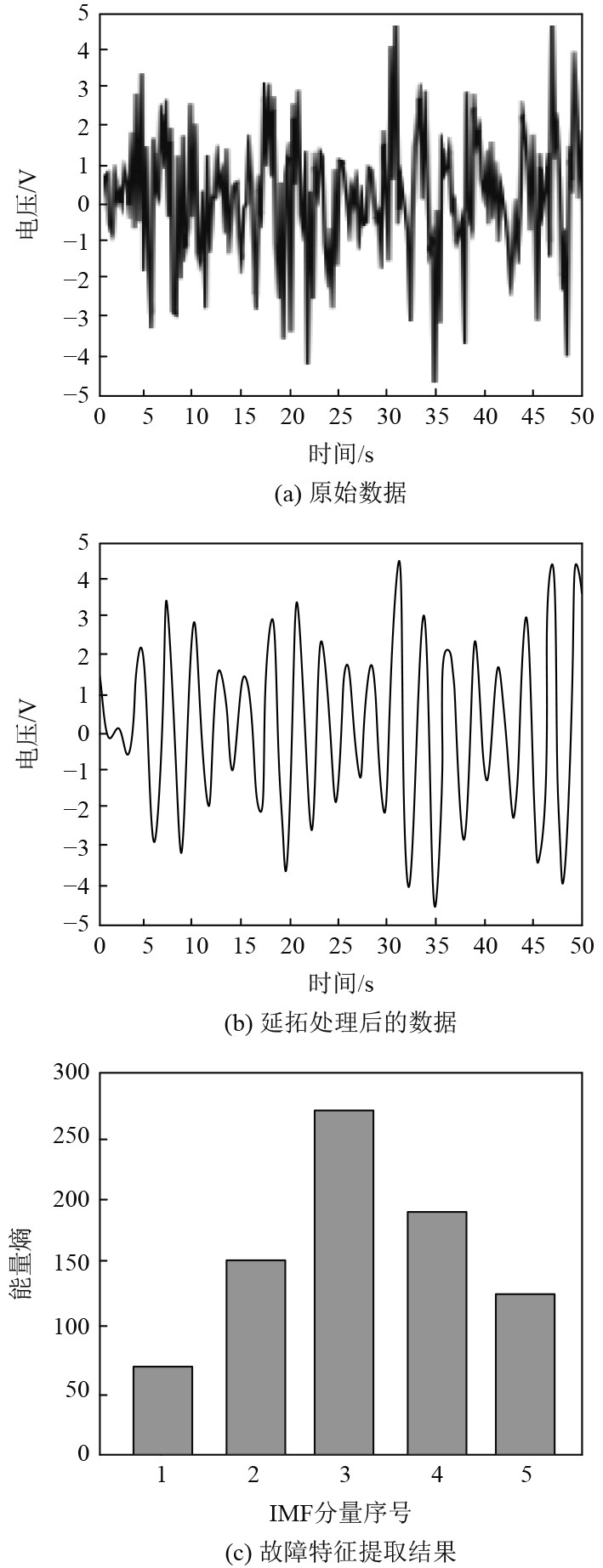
|
图 1 延拓处理结果以及故障特征提取结果 Fig. 1 Results of extension processing and fault feature extraction |
为该部分电子电路内的各节点均设置2种故障,分别是短路与短路故障,利用本文方法计算各故障特征的马氏距离,跟踪定位故障区域节点,跟踪定位结果如表2所示。可知,本文方法可有效计算各故障特征的马氏距离,且计算获取的马氏距离值,均处于马氏距离范围内,说明该故障区域节点存在故障,即本文方法可有效跟踪定位故障区域节点位置,且与实际情况一致。实验证明,本文方法可精准跟踪定位故障区域节点。
|
|
表 2 故障区域节点跟踪定位结果 Tab.2 Node tracking and locating results in the faulty area |
新型舰船内包含很多结构繁琐的电子电路,大大增加电子电路故障定位难度。为此,研究舰船装备电子电路故障区域节点跟踪定位方法,精准跟踪定位故障区域节点,为维修人员提供精准的故障位置,提升电子电路故障维修效果。
| [1] |
朱文昌, 李振璧, 姜媛媛. 联合VMD与ISSA-ELM的电力电子电路软故障诊断[J]. 电子测量与仪器学报, 2022, 36(5): 223-233. DOI:10.13382/j.jemi.B2104972 |
| [2] |
谢李为, 李勇, 罗隆福, 等. 基于极点对称分解的多分支线路故障定位方法[J]. 中国电机工程学报, 2021, 41(21): 7326-7339. DOI:10.13334/J.0258-8013.PCSEE.201320 |
| [3] |
胡创业, 张振华, 刘东昆, 等. 核辐射探测器模拟电路混合故障智能诊断与定位[J]. 核电子学与探测技术, 2020, 40(3): 417-421. HU Chuangye, ZHANG Zhenhua, LIU Dongkun, et al. Intelligent Diagnosis and Location of Hybrid Fault in Analog Circuit of Nuclear Radiation Detector[J]. Nuclear Electronics & Detection Technology, 2020, 40(3): 417-421. DOI:10.3969/j.issn.0258-0934.2020.03.008 |
| [4] |
高校平, 黄文焘, 邰能灵, 等. 基于暂态电流的MMC-LVDC双极短路故障定位方法[J]. 电力系统自动化, 2020, 44(17): 127-135. GAO Xiaoping, HUANG Wentao, TAI Nengling, et al. Transient Current Based Fault Location Method of Pole-to-pole Short-circuit for Modular Multilevel Converter Low-voltage Direct Current[J]. Automation of Electric Power Systems, 2020, 44(17): 127-135. DOI:10.7500/AEPS20200106004 |
| [5] |
赵师兵, 张志明. 基于时域信号特征和卷积神经网络的模拟电路故障诊断算法[J]. 计算机应用, 2022, 42(S2): 320-326. ZHAO Shibing, ZHANG Zhiming. Fault diagnosis algorithm of analog circuits based on time domain signal features and convolutional neural network[J]. Journal of Computer Applications, 2022, 42(S2): 320-326. |
| [6] |
马垠飞, 王力. 融合D-S证据理论的DBN电路故障诊断算法[J]. 辽宁工程技术大学学报(自然科学版), 2021, 40(5): 448-453. DOI:10.11956/j.issn.1008-0562.2021.05.011 |
| [7] |
邓勇, 胡徐松. 基于EMD和SPS的容差模拟电路故障诊断[J]. 电子测量与仪器学报, 2020, 34(2): 67-72. DENG Yong, HU Xusong. Fault diagnosis of tolerance analog circuit based on EMD and SPS method[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(2): 67-72. DOI:10.13382/j.jemi.B1902175 |
 2023, Vol. 45
2023, Vol. 45
