0 引　言

近年来，为了提高海上远距离目标的探测精度，船舶雷达系统不断进行技术迭代，分布式阵列地波雷达是一种新型雷达技术，该技术利用船舶的雷达阵列进行各个方位的目标探测，不仅能够弥补目前舰船单一雷达的探测技术局限性，还能提高雷达系统的抗干扰能力，利用多组雷达数据进行融合探测，显著提高远距离目标的探测精度。与此同时，在分布式阵列雷达系统中，数据的融合也成为一项影响系统性能的重要技术^[1]。

本文针对舰船分布式阵列雷达进行以下研究：

1）针对分布式阵列雷达与目标物体的相对运动关系，建立舰船分布式阵列雷达的方位坐标系，在坐标系的基础上进行远距离目标探测的数学建模；

2）介绍一种卡尔曼滤波算法，针对舰船阵列雷达的信号采集进行滤波和预测；

3）介绍舰船阵列雷达远距离目标探测过程的目标融合算法，通过多个雷达传感器的数据融合，提高远距离目标的探测精度。

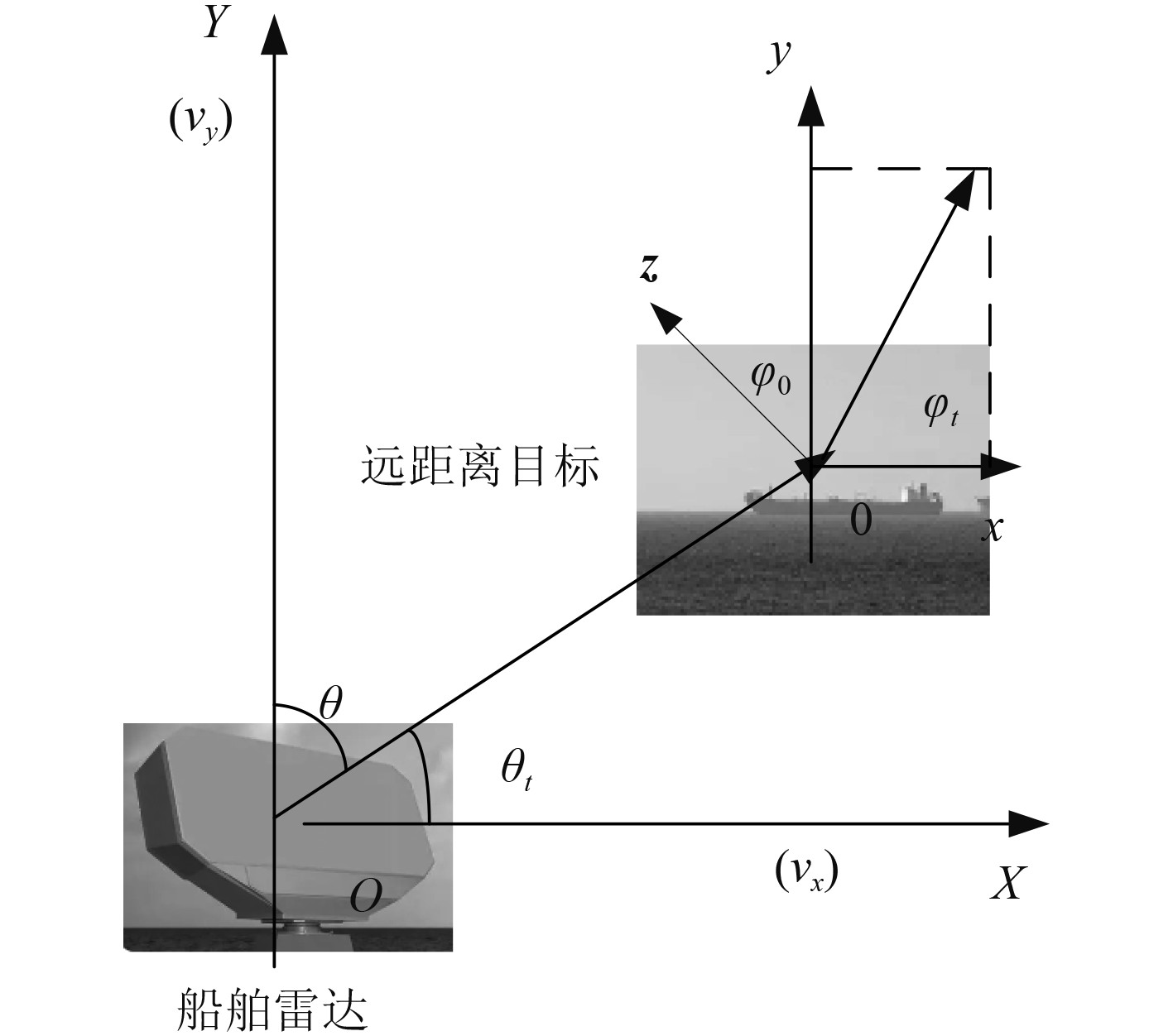
1 船舶分布式阵列雷达系统远距离目标探测的坐标系建模

在舰船分布式阵列雷达系统中，多个雷达探测器进行远距离目标探测时，往往以自身雷达探测器所在位置为坐标原点，在该原点建立坐标系表征被测目标的相对位置。这样就会导致不同雷达探测器针对同一被测目标的探测数据不一致，造成目标探测的校准出现问题。因此，对于舰船分布式阵列雷达系统，必须要建立统一的雷达坐标系，将阵列雷达系统的探测信息进行坐标系的转换。

本文建立远距离目标的阵列雷达坐标系统如图1所示。

在i时刻该坐标系统下，船舶航向角为 $\theta$ ，船舶速度为 ${v_T}$ ，远距离目标的移动速度为 $\left( {{v_x},{v_y}} \right)$ ，当前位置远距离目标相对于船舶雷达的方位角^[4]为 ${\theta _t}$ ，可得远距离目标的速度关系式：

$\left\{ {\begin{array}{*{20}{l}} {{v_x} = {v_T}\sin \left( {{\theta _t} - \theta } \right)}，\\ {{v_y} = {v_T}\cos \left( {{\theta _t} + \theta } \right)} 。\end{array}} \right.$

定义远距离目标坐标系的原点坐标在雷达坐标系O-XYZ下的坐标为 $\left( {{\lambda _0},{\varphi _0}} \right)$ ，远距离目标在自身坐标下的坐标为 $\left( {{\lambda _t},{\varphi _t}} \right)$ ，位置坐标在O-XYZ下的投影为：

$\begin{array}{*{20}{l}} {{X_t} = \left( {{\lambda _t} - {\lambda _0}} \right)\cos {\varphi _t}} ，\\ {{Y_t} = {\varphi _t} - {\varphi _0}} 。\end{array}$

远距离目标的位置极坐标形式为：

$\begin{array}{*{20}{l}} {{R_i} = \sqrt {X_t^2 + Y_t^2} }，\\ {{\alpha _i} = \arctan \frac{{{X_t}}}{{{Y_t}}} - {\varphi _0}} 。\end{array}$

在O-XYZ坐标系下观测到远距离目标的坐标为 $\left( {{x_0},{y_0},{z_0}} \right)$ ，则可以得到位置配准模型为：

${\left( {{x_0},{y_0},{z_0}} \right)^{\rm{T}}} = \left[ \begin{gathered} \cos {\theta _t} \\ 1 \\ \sin {\theta _{}} \\ \end{gathered} \right] \times {\left( {{v_x},{v_y}} \right)^{\rm{T}}} \times \left[ \begin{gathered} {R_i} \\ {\alpha _i} \\ \end{gathered} \right] 。$

2 基于卡尔曼滤波算法的船舶雷达远距离目标跟踪数据融合算法 2.1 卡尔曼滤波算法

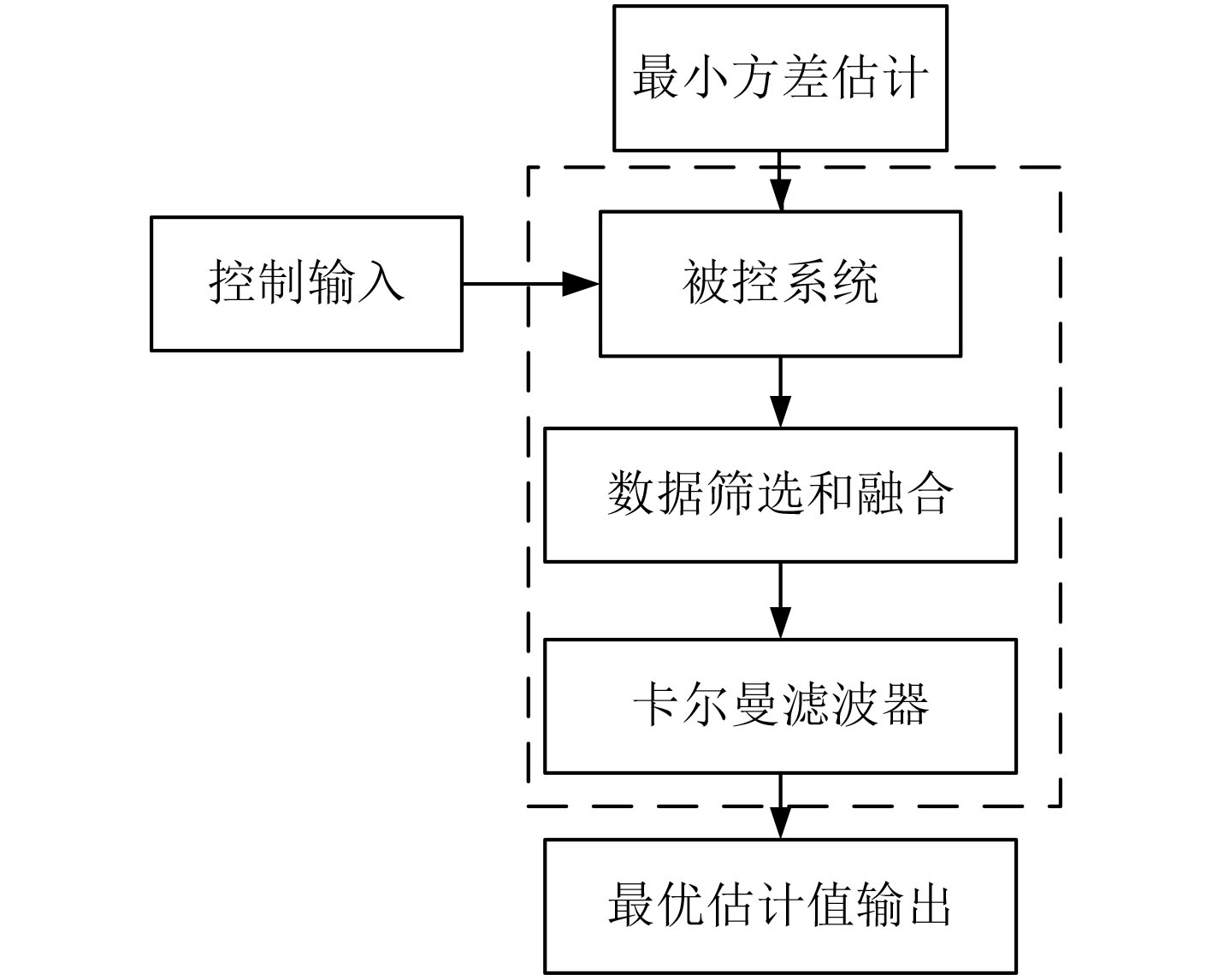
卡尔曼滤波算法是基于线性系统状态方程的输入和输出数据对比，进行系统噪声过滤，并对系统状态进行最优评估的一种算法。卡尔曼滤波算法利用系统的测量方差，可以推测动态系统的工作状态，目前，Kalman滤波算法在通信、导航等多个领域得到了较好的应用。

卡尔曼滤波方法中条件方差、最小方差估计和条件均值估计理论算法是较为常用的算法，基于最小方差理论，卡尔曼滤波算法能够对系统的数据融合、数据精度等进行较准确的预测。

卡尔曼滤波算法的应用流程如图2所示。

建立线性系统的状态方程和观测方程如下式：

$\begin{gathered} X(k + 1) = \varPhi \left( k \right)X\left( k \right) + \varGamma \left( k \right)u\left( k \right) + {\rm{G}}\left( k \right)V\left( k \right)，\\ Z\left( k \right) = {\rm{H}}\left( k \right)X\left( k \right) + W\left( k \right) 。\end{gathered}$

其中： $\varPhi \left( k \right)$ 为系统的n阶状态转移矩阵； $Z\left( k \right)$ 为m维的测量向量； $X\left( k \right)$ 为n维的系统状态向量； $\varGamma \left( k \right)$ 为n维p阶的输入矩阵； $u\left( k \right)$ 为系统的输入控制信号； $G\left( k \right)$ 为n维的噪声矩阵； $V\left( k \right)$ 为n维的过程噪声； $H\left( k \right)$ m维n阶的测量矩阵； $W\left( k \right)$ 为n维测量噪声。

线性系统的过程噪声为高斯白噪声，定义如下：

$\left\{ {\begin{aligned} & {EV(k) = 0,EV(k){V^{\rm T}}(j) = Q(k){\delta _{ij}}}，\\ & {EW(k) = 0,EW(k){W^{\rm T}}(j) = R(k){\delta _{ij}}}，\\ & {EW(k){V^{\rm T}}(k) = 0} 。\end{aligned}} \right.$

${\delta _{ij}}$ 为dirichlet函数^[2]，符合：

${\delta _{ij}} = \left\{ \begin{array}{*{20}{l}} {0,i = j} ，\\ {1,i \ne j} 。\end{array} \right.$

基于卡尔曼滤波算法，可以得到状态的预测方程为：

$\hat X(k + 1/k) = \varPhi (k)\hat X(k/k) + \varGamma (k)u(k) \text{，}$

基于卡尔曼滤波算法，可以得到测量的预测方程为：

$\hat Z(k + 1/k) = H(k + 1)\hat X(k + 1/k) \text{，}$

预测量的协方差为：

$P(k + 1/k) = \varPhi (k)P(k/k) + G(k)Q(k)G{(k)^{\rm{T}}} \text{，}$

状态量的协方差为：

$s(k + 1) = H(k + 1)P(k + 1/k){H^{\rm{T}}}(k + 1) \text{，}$

系统的滤波增益矩阵为：

$K(k + 1) = P(k + 1/k){H^{\rm{T}}}(k + 1){S^{ - 1}}(k + 1) 。$

系统的状态量更新方程为：

$v(k + 1) = Z(k + 1) - H(k + 1)\hat X(k + 1/k) \text{，}$

系统的协方差更新方程为：

$\hat X(k + 1/k + 1) = \hat X(k + 1/k) + K(k + 1)v(k + 1) 。$

2.2 船舶远距离目标探测雷达与AIS系统信号处理

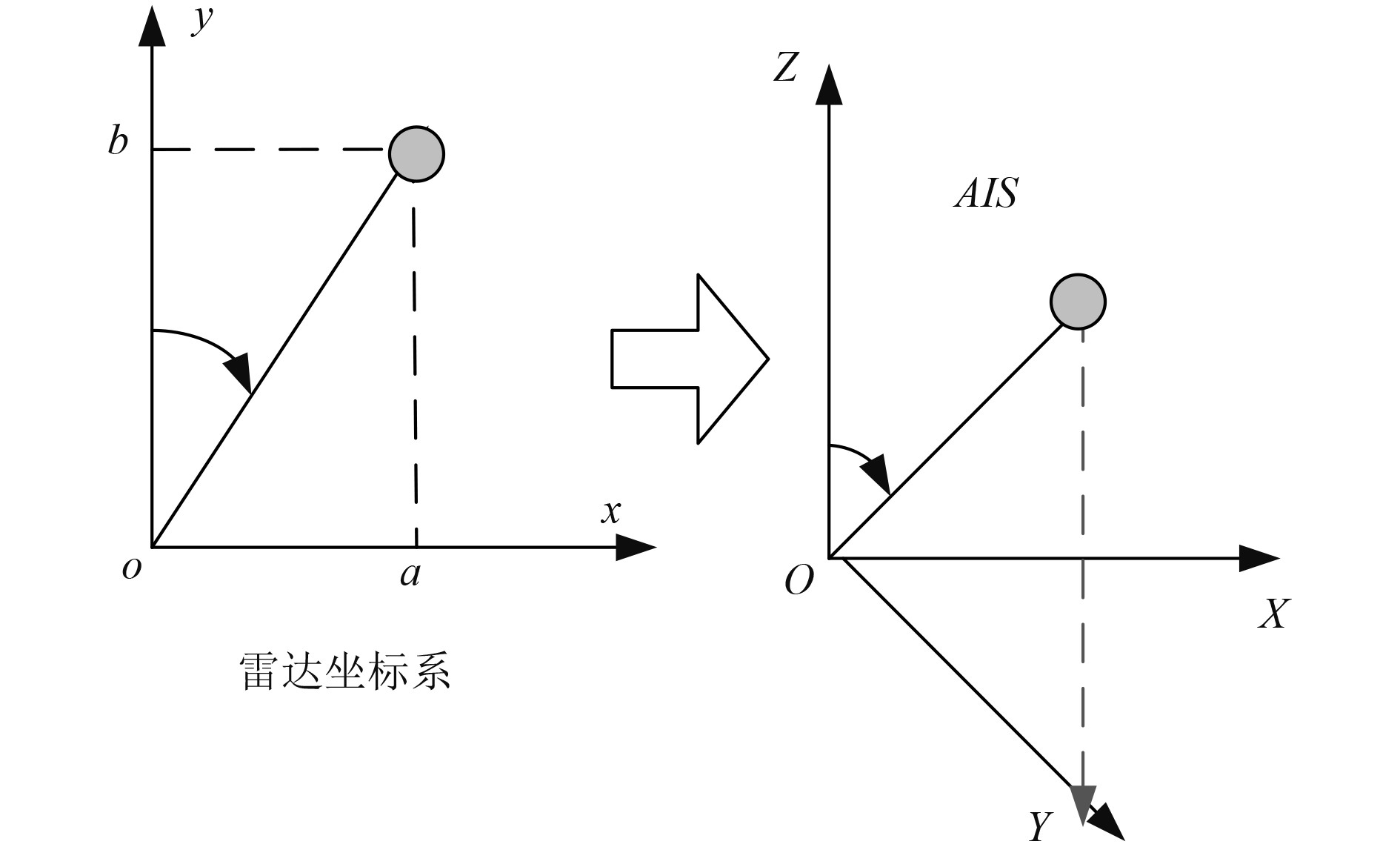
船舶自动识别AIS系统能够为船舶提供目标的方位信息，在远距离船舶目标探测过程中，可以利用AIS系统数据和雷达探测数据，提高远距离目标探测的精度。

AIS系统对船舶的定位采用地球坐标系，如图3所示。原点为地心，OZ轴指向北极，OX轴指向赤道，OY轴由地心指向赤道，雷达系统的坐标系如前文所述，可以用极坐标形式表示^[3]。

图3为雷达极坐标系和AIS系统地球坐标系的示意图。

当目标方位角为 ${\theta _t}$ ，目标在雷达坐标系中表示为：

$\left\{ \begin{gathered} x = \rho \sin {\theta _t} ，\\ y = \rho \cos {\theta _t}。\\ \end{gathered} \right.$

定义雷达探测的误差为：

$\begin{gathered} {\sigma _l} = {\sigma _0}\cos {\theta _t} + \rho \sin {\theta _t} ，\\ {\sigma _s} = {\sigma _0}\sin {\theta _t} + \rho \cos {\theta _t}。\\ \end{gathered}$

式中： ${\sigma _l}$ 为距离方差， ${\sigma _s}$ 为角度方差，目标在AIS系统的目标位置为 $\left( {{x_0},{y_0},{z_0}} \right)$ ，可得坐标转换矩阵为：

${\left( {{x_0},{y_0},{z_0}} \right)^{\rm{T}}} = \left[ \begin{gathered} \cos {\theta _t} \\ 1 \\ \sin {\theta _t} \\ \end{gathered} \right] \times {\left( {\rho ,{\theta _t}} \right)^{\rm{T}}} \times \left[ \begin{gathered} {\sigma _l} \\ {\sigma _s} \\ \end{gathered} \right] 。$

2.3 船舶远距离目标探测的雷达信号建模

船舶雷达系统的远距离目标跟踪原理图如图4所示。

假设船舶分布式阵列雷达中第i个雷达天线发射的信号为：

${s_i}(t) = {k_i}(t){e^{j2 \text{π} {f_e}t}} \text{，}$

式中： ${k_i}(t)$ 为基带信号， ${f_e}$ 为信号频率。雷达阵列之间满足：

$\int {} {k_i}(t){k_j}(t - \tau ){\rm{d}}t = 0 \text{，}$

式中：i，j为整数。

N个雷达天线的回波信号为：

$R = \left\{ {\begin{array}{*{20}{l}} {{\zeta _t}{K_t}\sqrt {\displaystyle\frac{E}{t}} {Q_r} + {n_t}}，& {{S_1}} ，\\ {{n_t}}，& {{S_0}}。\end{array}} \right.$

式中： ${\zeta _t}$ 为阵列天线回波信号的RCS系数^[4]； ${S_1}$ 为远距离目标的可被探测性； ${S_0}$ 为远距离目标的不可测性， ${K_t}$ 为阵列雷达天线的信号增益； ${n_t}$ 为空信号； $E$ 为天线功率； ${Q_r}$ 为阵列增益，。

雷达信号频率调制模型为：

$f(t) = \exp \left[ {j2\pi \left( {\frac{1}{2}\mu {t^2} + {f_0}t} \right)} \right] 。$

式中： $\mu$ 为雷达信号的波长； ${f_0}$ 为调制频率^[4]。

则远距离目标k的跟踪模型可表示为：

$H(k,t) = \sqrt {\frac{{{E^2} \cdot {\xi _t}}}{{{{(4 \text{π} )}^3} \cdot {r^4}{E_0}}}} \cdot \exp \left\{ {2 \text{π} \left[ {{f_d}t + \frac{1}{2}r{{\left( {t - {\tau _i}} \right)}^2}} \right]} \right\} 。$

式中： ${E_0}$ 为距离导致的雷达信号功率损耗； ${f_d}$ 为多普勒频率； ${\tau _i}$ 为时延。

2.4 基于卡尔曼滤波的船舶远距离目标跟踪数据融合算法设计

使用卡尔曼滤波算法对船舶分布式阵列雷达的数据进行融合处理，每个雷达对远距离目标采集的独立跟踪数据通过航迹配对、融合后，形成最终的目标跟踪数据。

图5为基于卡尔曼滤波算法的目标跟踪数据融合算法原理。

定义每个雷达的测量值为 ${X_1},{X_2}, \cdots ,{X_n}$ ，每个雷达的测量方差为 ${\sigma _i}^2$ ，基于卡尔曼的加权融合均方差为：

${\sigma ^2} = E\left[ {{{(X - \hat X)}^2}} \right] = E\left\{ {\sum\limits_{i = 1}^n {W_i^2} {{\left( {X - {X_i}} \right)}^2}} \right\} 。$

图6比较了船舶雷达常规目标观测的数据方差和基于数据融合的目标观测数据方差，可知基于数据融合算法的目标观测精度更高。

3 结　语

为了提高船舶阵列雷达对远距离目标探测和跟踪的精度，本文建立船舶雷达系统的位置模型，结合AIS系统数据和卡尔曼滤波算法，实现了船舶阵列雷达的数据融合技术。