0 引　言

针对编队作业的船舶而言，多船并行会存在行波问题，导致船舶航行时出现轨迹偏移，编队作业队形被破坏。需要使用一种精准的多船并行航行轨迹控制算法，控制多艘船舶并行的运行轨迹^[1]。

航行轨迹控制主要分为航行路径跟踪控制、轨迹跟踪控制。前者主要用于控制船舶航行轨迹，无时间约束^[2-3]。后者对船舶航行轨迹、速度都存在严格要求，比如在某时刻船舶需要在某航迹上运行至某地点。学者大多研究单艘船舶轨迹跟踪控制问题。祁林等^[4]设计自适应神经网络控制器，控制船舶航向与航线，但此方法不具备多船并行航迹控制能力。刘义等^[5]使用积分视线法，以自抗扰方式控制检查航行轨迹。此方法被证实具备较好轨迹控制效果，但仅测试其直线类轨迹控制效果，对其他线型轨迹控制效果是否满足要求，还未深入测试。

本文提出多船并行航行轨迹精准控制算法，并对此算法航行轨迹控制效果进行实验测试，测试结果验证了此算法在不同天气环境条件下，在多船并行航行轨迹控制中均存在实用价值。

1 多船并行航行轨迹控制 1.1 多船并行航行模型

水面多船并行时，设置船舶数目为 $ M $ 艘，每艘船动力学模型为：

$ \left\{\begin{aligned} & \underset{t\to \infty }{\mathrm{lim}}\Vert {\phi }_{j}\left(t\right)-{\phi }_{Z}\left(t\right)\Vert =0 ，\\ & \underset{t\to \infty }{\mathrm{lim}}\Vert {V}_{j}\left(t\right)-{V}_{Z}\left(t\right)\Vert =0,j，i\in M ，\\ & \underset{t\to \infty }{\mathrm{lim}}\Vert {Q}_{j}\left(t\right)-{Q}_{i}\left(t\right)-{s}_{ji}\Vert =0。\end{aligned}\right. $

(1)

其中： $ {\varphi _j}\left( t \right) $ ， $ {\varphi _Z}\left( t \right) $ 分别为第 $ j $ 艘船在时刻 $ t $ 航向角、领航船在时刻 $ t $ 航向角； ${V_j}\left( t \right) = {\left[ {{U_j}\left( t \right),{{\ddot v}_j}\left( t \right),{s_j}\left( t \right)} \right]^{\rm{T}}}$ 为第 $ j $ 艘跟随船在时刻 $ t $ 速度信息， $ {U_j}\left( t \right) $ ， $ {\ddot v_j}\left( t \right) $ ， $ {s_j}\left( t \right) $ 分别为纵移速度、横移速度、首摇角速度； $ {V_Z}\left( t \right) $ 为领航船在时刻 $ t $ 速度信息。 $ {Q_j}\left( t \right) $ ， $ {Q_i}\left( t \right) $ 分别为第 $ j $ 艘、第 $ i $ 艘跟随船在时刻 $ t $ 的位置信息； $ {s_{ji}} $ 为第 $ j $ 艘、第 $ i $ 艘跟随船并行时期望距离。

在轨迹控制时，船舶海面动力学方程为：

$ \left\{ \begin{aligned} & {MU = {\sigma _U}U + {\sigma _U}{U^2} + G} ，\\ & {M\left( {\ddot v + Us} \right) = {\psi _{\ddot v}} + {\psi _{U\ddot v}}U\ddot v + {\psi _{Us}}Us + }{\psi _{\ddot v\left| {\ddot v} \right|}}\ddot v\left| {\ddot v} \right|，\\ & {Ls = {\vartheta _s}s + {\vartheta _{U\ddot v}}U\ddot v + {\vartheta _{Us}}Us + {\vartheta _{\ddot v\left| {\ddot v} \right|}}\ddot v\left| {\ddot v} \right| + {{Q'}_V}} 。\end{aligned} \right.$

(2)

其中： $ M $ ， $ L $ 分别为船舶质量、转动惯量 ； $ U $ ， $ G $ 分别为船舶纵移速度、轴向推进力； $ \ddot v $ ， $ s $ 分别为横移速度、首摇角速度； $ {Q'_V} $ 为舰船垂直舵面和螺旋桨联合启动时，用于首摇转矩、螺旋桨转速控制方案； $ \sigma $ ， $ \psi $ ， $ \vartheta $ 为水动力系数。

1.2 基于位置与速度调节的多船并行航行轨迹控制

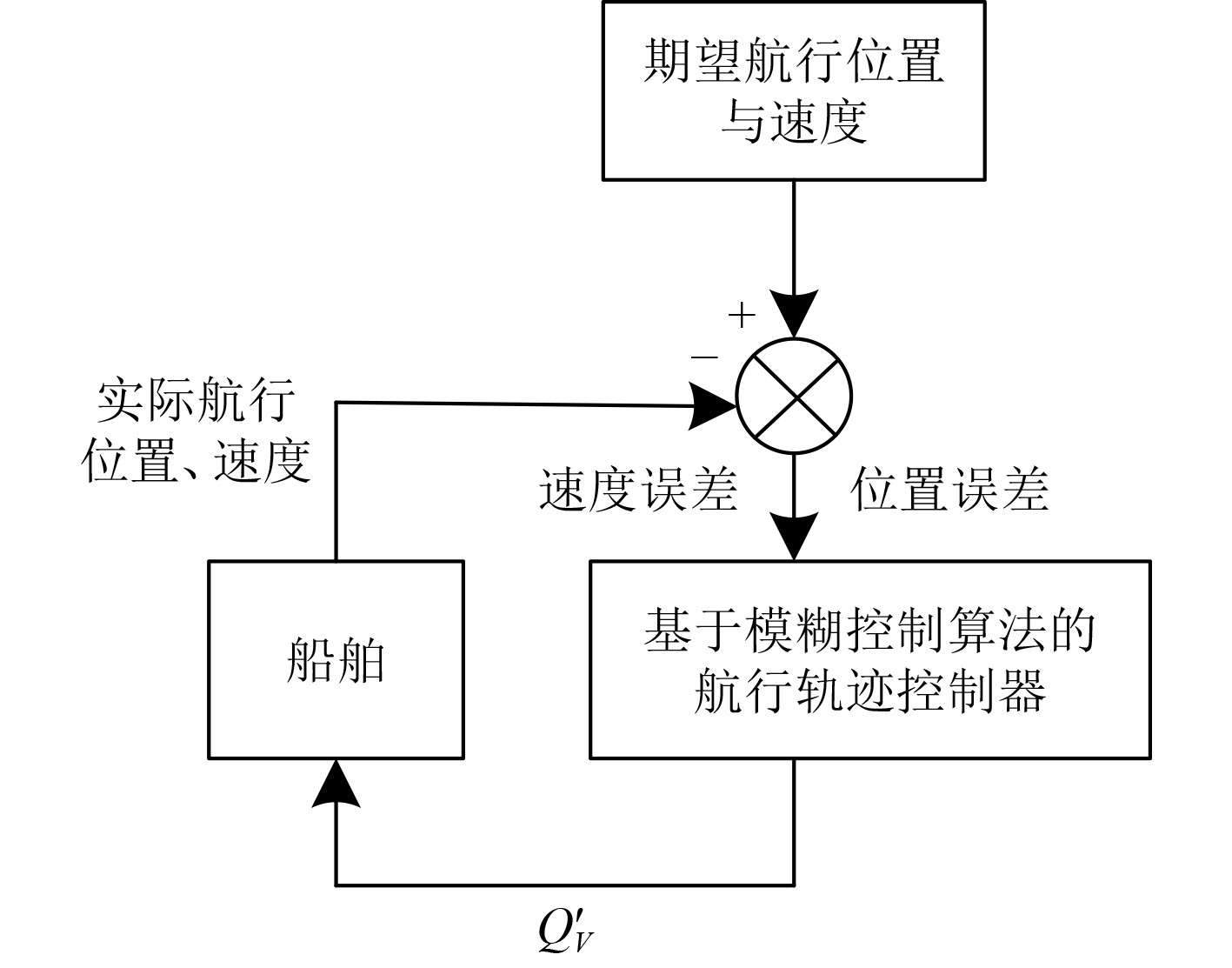
基于位置与速度调节的多船并行航行轨迹控制算法设计框图如图1所示。基于位置与速度调节的多船并行航行轨迹控制算法将模糊控制算法与PID控制器相结合，构建基于模糊控制算法的航行轨迹控制器，控制多船并行航行位置，调节多船并行时的航行速度，完成航行轨迹精准控制。

模糊控制可以在专家控制经验的协助下，有效解决非线性控制问题。为此，多船并行航行轨迹控制过程中，把多船并行之间航行位置期望状态与位置误差、期望速度状态与速度误差，作为基于模糊控制算法的航行轨迹控制器输入变量。基于模糊控制算法的航行轨迹控制器的输出量为：

$ {Q'_V} = {\dot Q_e} + {K_V}\beta + {K_Q}\dot \beta。$

(3)

其中： $ {Q'_V} $ 为控制为期望轨迹状态的控制量； $ {\dot Q_e} $ ，K_Q分别为多船并行航行的加速度矢量、航迹控制器的位置状态控制增益； $ \dot \beta $ 为位置跟踪误差矢量； $ {K_V} $ ， $ \ \beta $ 分别为多船并行航行的速度调节增益、速度误差矢量。

多船舶并行时，位置状态误差向量为：

$ \dot \beta = {Q_e} - Q 。$

(4)

其中： $ {Q_e} $ ， $ Q $ 分别为所需抵达的位置矢量、目前位置矢量。

$ \beta = {V_e} - V 。$

(5)

其中：V_e，V分别为期望速度状态、目前速度状态。

则多船并行航行位置控制表达式为：

$ {Q_e} = {K_P}\dot \beta \left( t \right) + {K_I}\sum\limits_{i = 0}^t {\dot \beta \left( t \right)\bar T + } {K_D}\frac{{\dot \beta \left( t \right) - \dot \beta \left( {t - 1} \right)}}{{\bar T}}，$

(6)

速度控制表达式为：

$ {V_e} = {K_P}\beta \left( t \right) + {K_I}\sum\limits_{i = 0}^t {\beta \left( t \right)\bar T + } {K_D}\frac{{\beta \left( t \right) - \beta \left( {t - 1} \right)}}{{\bar T}}。$

(7)

其中： $ \bar T $ ， $ t $ 分别为采样周期、时刻； $ {K_P} $ ， $ {K_I} $ ， $ {K_D} $ 分别为控制器在调节航行位置增益、速度增益时所用比例、积分、微分系数； $ \dot \beta \left( t \right) $ ， $ \dot \beta \left( {t - 1} \right) $ 分别为时刻 $ t $ ， $ t - 1 $ 的航行位置状态误差向量； $ \beta \left( t \right) $ ， $ \beta \left( {t - 1} \right) $ 分别为时刻 $ t $ 、 $ t - 1 $ 的航行速度状态误差向量。

基于模糊控制算法的航行轨迹控制器中，设置控制器的输入变量，分别为位置状态误差向量与位置误差改变量 $ \Delta \dot \beta $ 、速度状态误差向量与速度误差变化量 $ \Delta \beta $ 。因多船并行时，位置与速度矢量存在变动，需要将控制其的输入变量执行模糊化处理，将航行轨迹控制的输入变量转换为模糊子集，构建模糊规则表，如表1～表3所示。

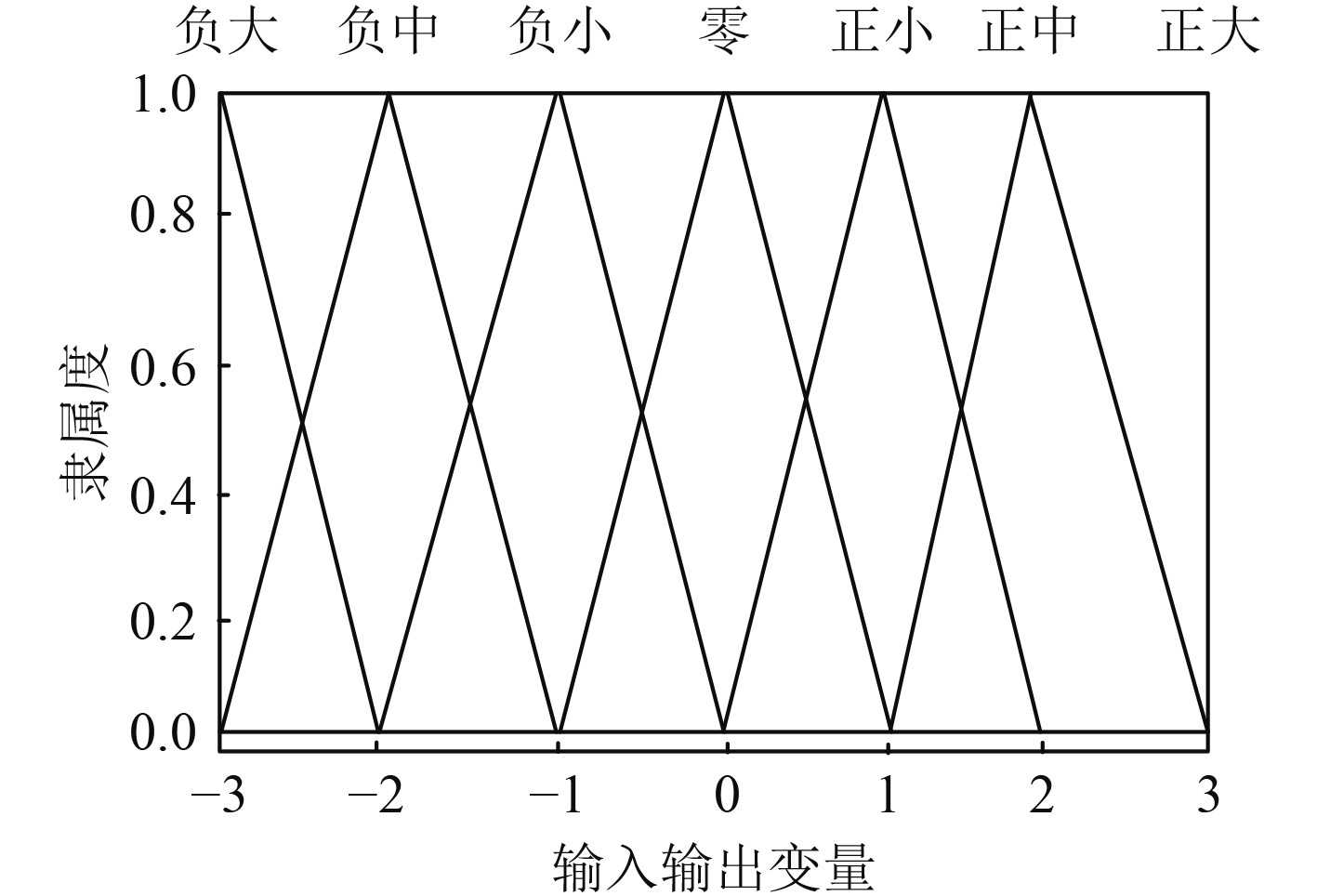
在控制过程中，使用面积中心法，执行输出控制量清晰化处理，则输入输出变量的隶属度函数如图2所示。使用模糊推理方法，便可把获取的位置、速度控制增益与K_P，K_I，K_D叠加，输出航行位置控制量、速度控制量，将2种控制量分别作为首摇转矩、螺旋桨转速控制量，便可控制跟随船并行的位置与速度处于期望状态。

2 仿真测试 2.1 相关参数设置

实验目标为编队作业的3艘船舶，其中1艘船舶为领航船，2艘为跟随船。3艘船的参数信息相同，如表4所示。2艘跟随船在领航船的带领下，处于并行状态，利用本文算法控制2艘跟随船的航行轨迹。

2.2 轨迹控制效果测试

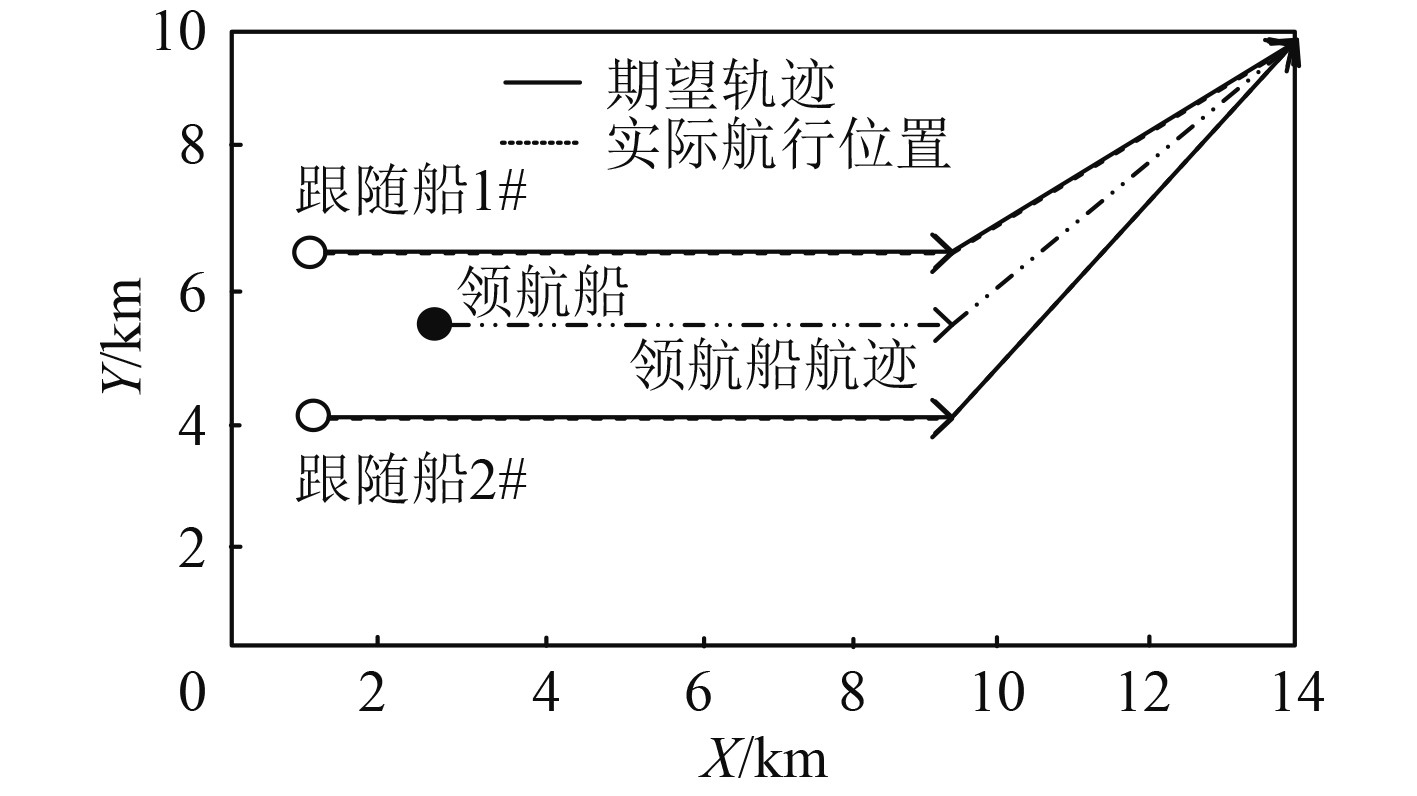
假设水面环境属于理想环境，不存在恶劣天气，2个跟随船需跟随领航船航行，则本文算法控制下，多船并行航行位置的控制效果如图3所示。可知，本文算法控制下，多船并行航行位置与期望位置重合，说明本文算法在多船并行航行轨迹控制中，具备航行轨迹位置的调控能力。

在此过程中，航行速度变化如图4所示。可知，本文算法控制下，多船并行时，跟随船1#、跟随船2#的航行速度与期望速度均一致，说明本文算法在多船并行航行轨迹控制中，能够控制多船并行航行速度，从而避免出现航行速度异常而出现偏航问题。

当航行环境因恶劣天气原因，海浪出现大幅变化时，测试本文算法使用前后，跟随船1#航行轨迹控制时，航行轨迹的X轴、Y轴位置误差值。结果如图5和图6所示。可知，在扰动环境中，本文算法控制前后，跟随船1#航行轨迹变化状态存在明显不同。本文算法使用前，跟随船1#航行轨迹的X轴、Y轴误差值均超过0.5 m，本文算法使用后，X轴、Y轴误差值均小于0.2 m。对比之下，本文算法可提高舰船航行轨迹控制精度，虽仍存在位置误差，但此误差值也有可能因船体自身器械因素所致，在允许范围内。由此证实，本文算法可实现船舶航行轨迹精准控制。

3 结　语

本文针对多船并行航行时，易受到兴波所干扰，不能保持原始编队期望轨迹、速度运行的问题，研究一种多船并行航行轨迹精准控制算法，保证多船在动态变化的航行环境中，均可按照期望轨迹，安全航行至目的地。将模糊控制算法与PID控制器相结合，设计基于位置与速度调节的多船并行航行轨迹控制算法，此算法能够通过模糊控制算法，结合船舶目前位置与速度的误差值，在线动态调节航行轨迹，以此保证多船并行航行时，轨迹不出现偏航，从而实现多船并行航行轨迹精准控制。