大型船舶改变既定航向需要一定的时间,为避免航道上船舶出现碰撞情况,对多船舶通信目标进行定位是重点关注的问题。目前有很多学者研究多船舶通信目标定位方法,简杰等[1]提出AUV协同定位方法,该方法利用阈值加权方法对船舶目标位置观测值进行粗差改善,再进行局部滤波处理后,生成位移AUV定位信息,实现多船舶通信目标定位。但该方法在处理多组船舶目标位置观测值时,受信号通信时延影响,其处理信号结果不够准确,导致其最终对船舶定位效果不佳。李宗凌等[2]提出SAR图像船舶目标定位方法,该方法通过采集船舶SAR图像,利用图像处理方式得到船舶目标位置,但该方法采集的船舶SAR图像清晰度不足,导致其定位船舶目标位置存在较大的偏差。移动互联技术是将移动通信技术和互联网技术相结合,是网络通信传输和移动应用实践活动的总称。船舶在水域上航行时,其与地面站或其他船舶联系均应用移动互联技术实现,因此本文研究移动互联技术在多船舶通信目标定位中的应用方法,为防止船舶碰撞、避障提供技术支持。
1 移动互联技术的多船舶通信目标定位方法 1.1 基于移动互联技术的相邻船舶通信节点距离计算在船舶移动互联网络内,令
| $ {P_r}(d) = {P_t} - \varOmega ({d_0}) - 10n\lg (d/{d_0}) + {N_\sigma }。$ | (1) |
式中:
| $ \varOmega ({d_0}) = - 10\lg \left[ {\frac{{{\lambda ^2}}}{{(4\text{π} )2d_0^2\eta }}} \right]。$ | (2) |
式中:
在船舶移动互联网络内[4],令
| $ {P_r}({d_0}) = {P_t} - \Omega ({d_0}) ,$ | (3) |
则船舶移动互联网络内节点和的接收信号强度可利用对数正态传输模型表达,其公式如下:
| $ {P_r}(d) = {P_r}({d_0}) - 10n\lg (d/{d_0}) + {N_\sigma },$ | (4) |
对式(4)进行简化处理,其变更如下:
| $ {P_r}(d) = \kappa - 10n\lg d 。$ | (5) |
其中:
| $ \kappa = {P_r}({d_0}) - {N_\sigma } ,$ | (6) |
将式(6)代入式(5),则
| $ 10n\lg d = \kappa - {P_r}(d) 。$ | (7) |
由于多船舶通信节点在移动互联网区域内为均匀随机分布状态,且每个多船舶通信节点的通信半径均相同,其作用范围为规则的圆[5],依据接收信号强度和节点距离之间的近似关系,则最小接收信号强度与对应最大节点距离之间的关系如下:
| $ 10n\lg {d_{\max }} = \kappa - {P_{\min }} 。$ | (8) |
式中:
信号传输路径损耗因数
| $ n = \left( {\kappa - {P_{\min }}} \right)/10n\lg {d_{\max }} ,$ | (9) |
将式(8)、式(9)代入到式(7),则多舰船通信节点距离的估算值表达式如下:
| $ d = d_{\max }^{\frac{{\kappa - {P_r}(d)}}{{\kappa - {P_{\min }}}}} \approx {r^{\frac{{\kappa - {P_r}(d)}}{{\kappa - {P_{\min }}}}}} 。$ | (10) |
利用式(10)即可得到船舶移动互联网络所有多船舶通信节点的距离。
1.2 相邻船舶通信节点距离误差补偿由于移动互联网络内通信信号内存在干扰噪声以及信号传输的衰减性,导致计算相邻船舶通信节点距离存在一定误差[6],为提升多船舶通信目标定位精度,需对相邻船舶通信节点距离误差进行补偿处理,其详细过程如下:
| $ \phi (d) = \varepsilon d + \zeta。$ | (11) |
式中:
| $ Z(\varepsilon ,\zeta ) = \sum\limits_{i = 1}^n {{{\left[ {\varepsilon {d_i} + \zeta - \phi ({d_i})} \right]}^2}} 。$ | (12) |
式中:
对式(12)结果内的误差系数进行求导,其表达式如下:
| $ \left\{ \begin{gathered} \frac{{\partial Q}}{{\partial \varepsilon }} = 2\sum\limits_{i = 1}^n {{d_i}\left[ {\varepsilon {d_i} + \zeta - \phi ({d_i})} \right] = 0},\\ \frac{{\partial Q}}{{\partial \zeta }} = 2\sum\limits_{i = 1}^n {\left[ {\varepsilon {d_i} + \zeta - \phi ({d_i})} \right] = 0}。\\ \end{gathered} \right. $ | (13) |
再利用二元一次方程对式(13)进行求解,得到一次误差系数和常误差系数数值,公式如下:
| $ \left\{ \begin{aligned} & \varepsilon = \left( {\sum\limits_{i = 1}^n {{d_i}\phi ({d_i})} - \frac{1}{n}\left[ {\sum\limits_{i = 1}^n {{d_i}} } \right]\left[ {\sum\limits_{i = 1}^n {\phi \left( {{d_i}} \right)} } \right]} \right)/\\ & \quad \left[ {\sum\limits_{i = 1}^n {d_i^2 - \frac{1}{n}{{\left[ {\sum\limits_{i = 1}^n {{d_i}} } \right]}^2}} } \right] ,\\ & \zeta = \left[ {\sum\limits_{i = 1}^n {\phi \left( {{d_i}} \right)} - \varepsilon \sum\limits_{i = 1}^n {{d_i}} } \right]/n 。\end{aligned} \right. $ | (14) |
以式(14)结果为基础,相邻船舶通信节点距离误差补偿后的修正值
| $ {\tilde d_i} = {d_i} - \phi ({d_i}) 。$ | (15) |
多船舶在航行时,其位于移动互联网络内,多船舶在移动互联网络内的移动信标会随着船舶的航行向网络内不断发送位置信息包,该位置信息包内包括信标位置和当前时间,此时未知的多船舶通信目标节点可依据概率推算其位于某个信标节点周围,从而实现多船舶通信目标的定位。以补偿后的相邻船舶通信节点距离为基础,
| $ {U_i} = \left[ {x_i^{\min },x_i^{\max }} \right] \times \left[ {y_i^{\min },y_i^{\max }} \right]。$ | (16) |
式中:
为保障多船舶通信目标定位更加准确,设置其连通性通信节点位置约束方程更新公式如下:
| $ {U_i} \to {U_i}\mathop \cap \limits_{k \in K} \left[ {x_{\min }^k - r,x_{\max }^k + r} \right] \times \left[ {y_{\min }^k - r,y_{\max }^k + r} \right] 。$ | (17) |
式中:
当一个船舶通信目标节点被检测到,则其连通性通信节点位置约束方程更新公式如下:
| $ {U_i} \to {U_i} \cap \left[ {{x_a} - s,{x_a} + s} \right] \times \left[ {{y_a} - s,{y_a} + s} \right]。$ | (18) |
式中:
当一个船舶通信目标节点没有被检测到,则其连通性通信节点位置约束方程更新公式如下:
| $ {U_i} \to {U_i} - {U_{neg}},$ | (19) |
式中,
| $ {U_{neg}} = \left[ {{x_a} - \frac{{{Q_{neg}}}}{2},{x_a} + \frac{{{Q_{neg}}}}{2}} \right] \times \left[ {{y_a} - \frac{{{Q_{neg}}}}{2},{y_a} + \frac{{{Q_{neg}}}}{2}} \right]。$ | (20) |
式中,
依据上述过程更新多船舶通信目标通信节点区域后,利用下式得到多船舶通信目标未知点的自身位置,表达式如下:
| $ O(x,y) = PD{F_{RSSI}}(({x_i},{y_i}),({x_a},{y_a})),$ | (21) |
式中:
以某港口出入港航线作为实验对象,使用本文方法对出入港航线内多船舶通信目标进行定位,其中多船舶均加入移动互联网,多船舶的信标信息发送间隔为0.1~1.0 s,其通信半径区间为10~30 m,信标节点移动速度10~50 s。
多船舶通信节点距离估算是多舰船通信目标定位的基础,在移动互联区域内选择10个多舰船通信目标节点应用本文方法估算多船舶通信节点距离。为使实验结果更加充分,同时使用文献[3]方法和文献[4]方法展开实验,实验结果如表1所示。分析表1可知,同时应用本文方法、文献[3]方法和文献[4]方法进行多船舶通信节点距离估算时,本文方法估算的结果与多船舶通信节点距离实际数值最为接近,其与多船舶通信节点距离实际数值偏差位于0.29~0.96 m之间,而文献[3]方法和文献[4]方法估算的多船舶通信节点距离实际数值偏差分别位于0.59~1.55 m和0.46~1.83 m之间。上述结果说明:本文方法估算多船舶通信节点距离与其设计距离最为接近,可有效估计多船舶通信节点距离。
|
|
表 1 多船舶通信节点距离估算结果(m) Tab.1 Distance estimation results of multiple ships communication nodes (m) |
验证本文方法对多船舶通信节点距离估算值误差补偿效果,以表1内10个多船舶通信节点作为实验对象,使用本文方法对其距离估算值误差进行补偿处理,并设置补偿后误差值不得高于0.5 m,测试结果如表2所示。可知,应用本文方法对估算的多船舶通信节点距离进行补偿后,其估算多船舶通信节点距离偏差最小为0.14 m,最大仅为0.33 m,该数值较所设的阈值低,说明本文方法可有效对多船舶通信节点距离进行补偿,补偿后的多船舶通信节点距离与其实际距离极为接近。
|
|
表 2 多船舶通信节点估算距离误差修正结果(m) Tab.2 Correction results for distance error estimation of multiple ships communication nodes (m) |
验证本文方法对多船舶通信目标的定位效果,为使实验结果更具科学性,分别在10艘和30多艘船舶环境下对其通信目标进行定位,验证本文方法实际应用效果,实验结果如图1所示。分析可知,在10艘船舶和30艘船舶的多船舶环境下,本文方法在定位船舶通信目标时的定位位置与船舶通信目标位置完全吻合。该结果说明本文方法在定位多船舶通信目标时受船舶数量影响较少,具备较强的多船舶通信目标定位方法,应用效果较好。
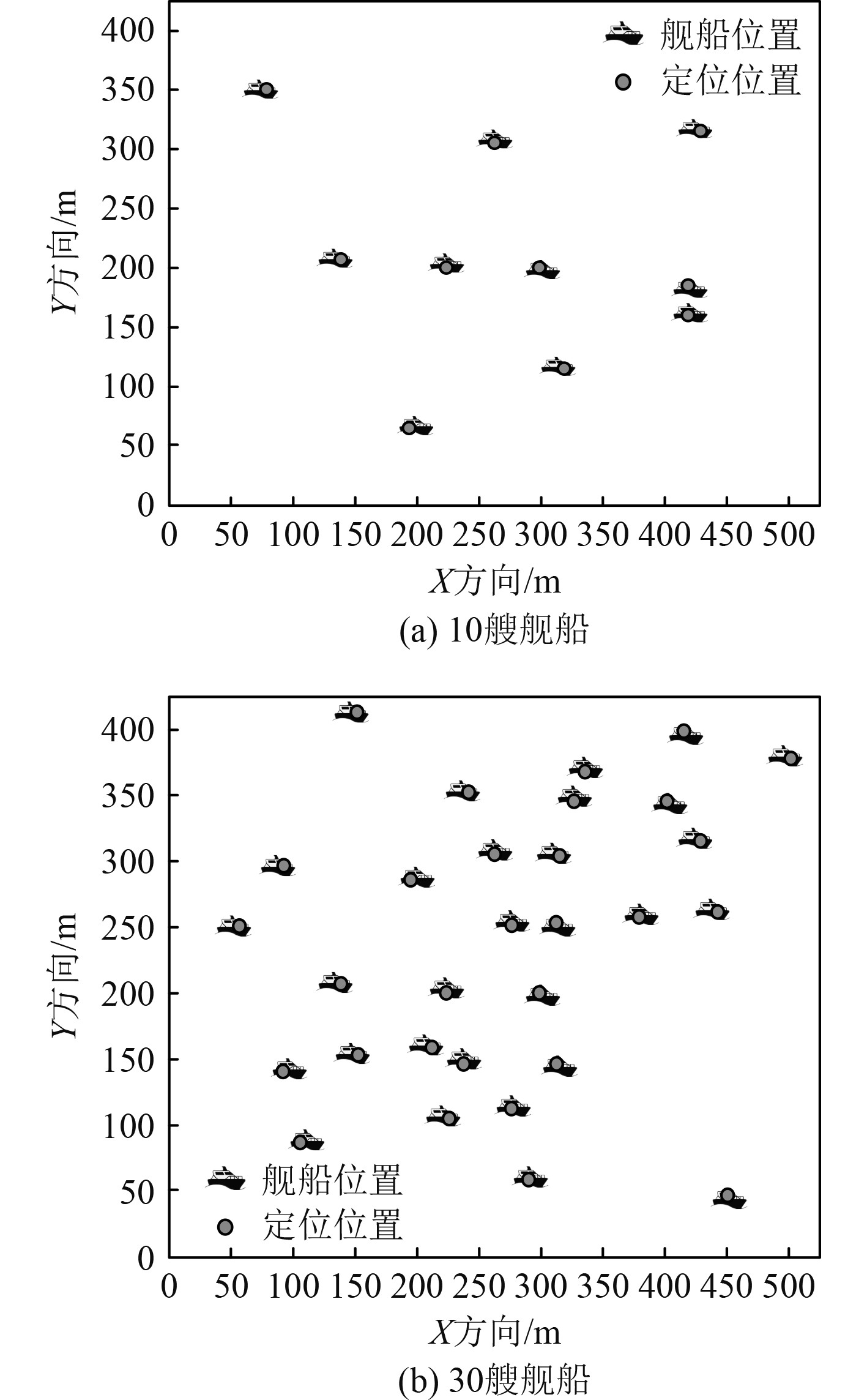
|
图 1 多船舶通信目标定位实验结果 Fig. 1 Experimental results of multiple ships communication target localization |
本文研究移动互联技术在多船舶通信目标定位中的应用方法,利用移动互联技术连接多船舶通信目标,使多船舶通信目标位于一个移动互联网络内,计算该网络内多船舶通信节点距离并对其进行补偿后,依据多船舶通信节点距离实现其通信目标定位。对本文方法进行验证表明,其具备较好的应用性,未来可为船舶导航、避障等提供有效定位信息。
| [1] |
简杰, 朱志宇. 基于加权信息增益的并行融合AUV协同定位方法[J]. 中国舰船研究, 2022, 17(4): 79-91. JIAN Jie, ZHU Zhiyu. A Parallel fusion method for AUV cooperative localization based on weighted information gain[J]. Chinese Journal of Ship Research, 2022, 17(4): 79-91. |
| [2] |
李宗凌, 汪路元, 蒋帅, 等. 超轻量网络的SAR图像舰船目标在轨提取[J]. 遥感学报, 2021, 25(3): 765-775. LI Zongling, WANG Luyuan, JIANG Shuai, et al. On orbit extraction method of ship target in SAR images based on ultra-lightweight network[J]. Journal of Remote Sensing, 2021, 25(3): 765-775. |
| [3] |
刘亚琴, 杨士莪, 张海刚, 等. 利用辐射噪声对舰船进行定位[J]. 哈尔滨工程大学学报, 2021, 42(7): 921-927. LIU Yaqin, YANG Shi'e, ZHANG Haigang, et al. Localization of ship using radiated noise[J]. Journal of Harbin Engineering University, 2021, 42(7): 921-927. DOI:10.11990/jheu.201906076 |
| [4] |
张啸尘, 赵建森, 王胜正, 等. 基于YOLOv3算法的船舶双目视觉检测与定位方法[J]. 上海海事大学学报, 2021, 42(1): 26-32. ZHANG Xiaochen, ZHAO Jiansen, WANG Shengzheng, et al. Binocular vision detection and positioning method for ships based on YOLOv3 algorithm[J]. Journal of Shanghai Maritime University, 2021, 42(1): 26-32. DOI:10.13340/j.jsmu.2021.01.005 |
| [5] |
孙忠镇, 戴牧宸, 雷禹, 等. 基于级联网络的复杂大场景SAR图像舰船目标快速检测[J]. 信号处理, 2021, 37(6): 941-951. SUN Zhongzhen, DAI Muchen, LEI Yu, et al. Fast Detection of Ship Targets for Complex Large-scene SAR Images Based on a Cascade Network[J]. Journal of Signal Processing, 2021, 37(6): 941-951. DOI:10.16798/j.issn.1003-0530.2021.06.005 |
| [6] |
马啸, 邵利民, 金鑫, 等. 基于改进Mask R-CNN的可见光图像中舰船目标检测方法[J]. 北京理工大学学报, 2021, 41(7): 734-744. MA Xiao, SHAO Limin, JIN Xin, et al. Ship Target Detection in Optical Images Based on Improved Mask R-CNN[J]. Transactions of Beijing Institute of Technology, 2021, 41(7): 734-744. |
 2023, Vol. 45
2023, Vol. 45
