2. 中国船舶集团有限公司第七〇五研究所,陕西 西安 710077
2. The 705 Research Institute of CSSC, Xi'an 710077, China
由于浅海条件下海面海底界面对于声信号传播影响显著,因此,其传播特性较深海条件恶劣,尤其是传播损失依赖于海面、海底及海水介质的多项物理参数,其中海底声学特性对声传播的影响更为显著,其不同密度、声速、海底分层结构等均对确定性信号的传播损失影响较大[1-2]。
获取海底声学特性参数的方法主要有直接测量和声学反演两类。其中直接测量法又称为原位测量法,即采用人工手段直接取得海底沉积物样品进行分析,其优点在于分析研究对象直接,但是也存在着高耗低效、结果不连续的缺点[3-5]。而声波作为可在海洋环境中远距离传播的能量形式,利用声学方法探测海底可获得大范围连续测量数据,通过对所获取声学测量数据的逆向分析得到海底沉积物特性参数的声学反演方法,因其经济易行、结果客观准确等优点而受到了越来越多的重视和研究[6-7]。
本文建立3层海底地声模型,构建浅海分层结构的海底缩比场仿真环境。基于匹配场技术,采用全局优化算法实现不同分层结构的海底地声学参数的优化反演,验证海底地声模型的正确性和可信性。
1 3层海底地声模型构建真实海底底质是河流传过暴露的陆架并携带大量的沉积物到达陆架和陆坡并沉积下来形成的,沉积物主要由固体颗粒(矿物)、孔隙流体、游离气体和有机质组成[8]。
结合对浅海海底沉积物的研究和分析,设计建立3层海底地声模型,用以表征浅海海底底质特性。定义第1层海底为黏土,第2层海底为砂,第3层海底为石。针对每层底质结合各种理论模型的特点,确定相应的建模理论:第1层建模时选择弹性理论模型,第2层和第3层选择等效密度流体近似理论[9]。
当平面波以掠射角
|
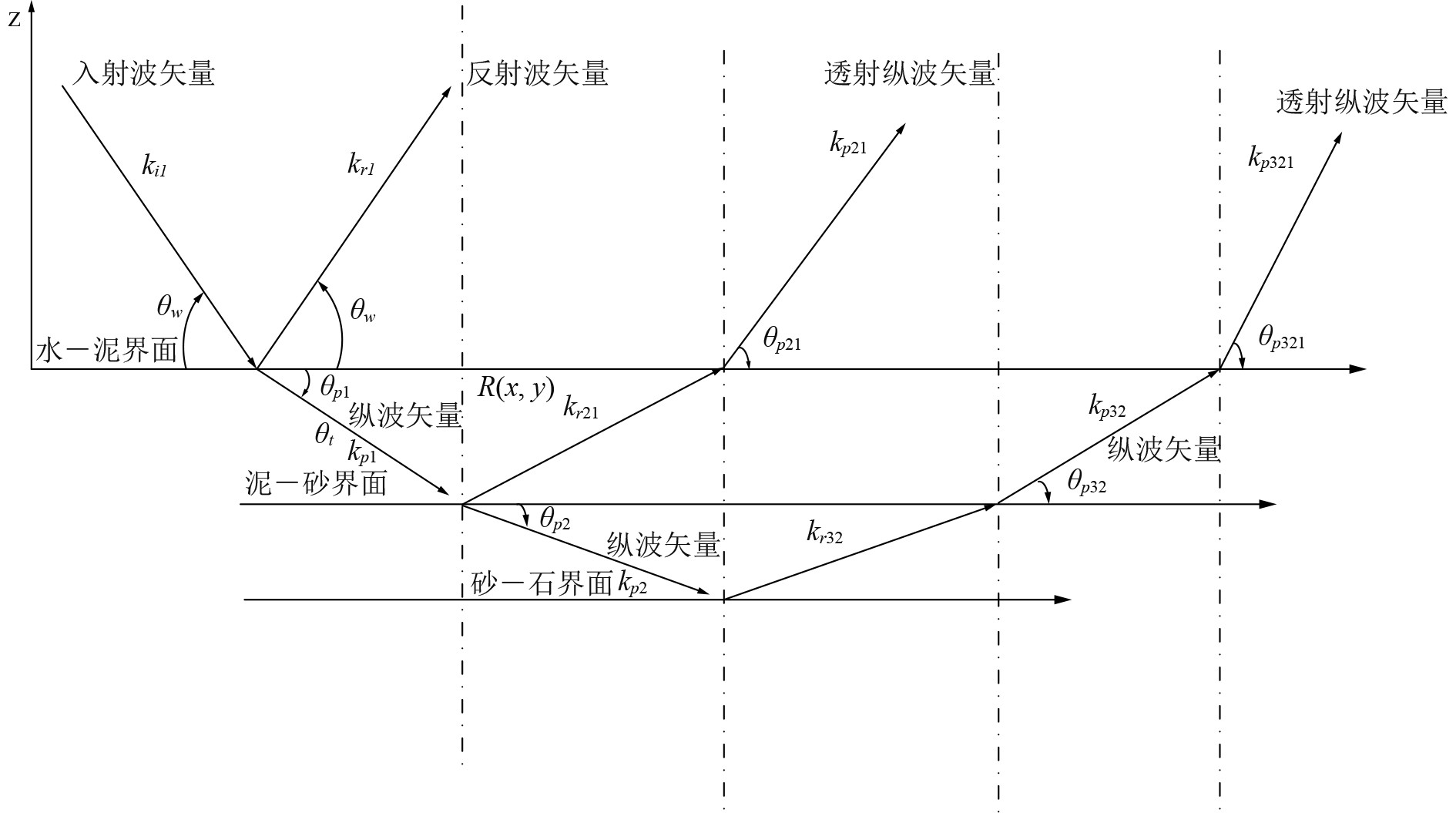
图 1 平面波入射3层海底时入射、反射、透射示意图 Fig. 1 Schematic diagram of incidence, reflection and transmission of plane wave incident on three-layer seabed |
针对鱼雷仿真应用以及缩比试验环境地声模型反演关注的重点,建立3层海底地声模型的反射和透射模型。
1)第1层反射和透射
如图1所示,第1层海底的声压反射系数和经过第1层底质透射到第2层的纵波声压透射系数可根据弹性理论计算求出。
2)第2层下行反射和透射
进入第2层后按照等效密度进行下行声波声压反射系数和声压透射系数的计算,由于第2层同样满足法向等效位移连续条件和等效压力连续条件,可采用流体理论界面反射和透射系数计算公式计算。
有耗散条件折射掠射角计算公式为:
| $ \sin \theta_{p 2}=\sqrt{1-a_{e f f 2}^{2} \cos ^{2} \theta_{w 2}} 。$ | (1) |
式中:
声压反射系数为:
| $ V_{ww 2}=V_{w p 1} \times\left(z_{w p 2}-1\right)\left(z_{w p 2}+1\right),$ | (2) |
式中:
声压透射系数为:
| $ V_{w p 2}=2 \times V_{w p l} \times z_{u p 2} \times\left(z_{w p 2}-1\right)\left(z_{w p 2}+1\right) 。$ | (3) |
3)第2层上行透射
从第2层上行经泥介质透射过程按照弹性理论进行计算。
有耗散条件折射掠射角计算公式为:
| $ \sin \theta_{p 21}=\sqrt{1-a_{p 21}^{2} \cos ^{2} \theta_{w 21}}。$ | (4) |
式中:
在上行时其反射系数不关注,仅关注透射系数,透射系数计算公式如下:
| $ \begin{split} V_{wp 21}= & -\left(V_{w w 2}-V_{ww 21}\right) \times a_{p 21} \times\\ & \cos 2 \theta_{t2 1} \times \sin \theta_{w 21} / \sin \theta_{p 21}。\end{split} $ | (5) |
4)第3层下行反射
第3层按照等效密度模型计算等效流体模量、等效密度、等效模型复声速,进而得到等效密度复速度比
假设声波到达第3层界面时是全反射的,其反射系数为:
| $ V_{w w 3}=V_{w p 2} \times\left(z_{w p 3}-1\right) /\left(z_{w p 3}+1\right)。$ | (6) |
5)第3层上行至第2层透射
第3层上行至第2层按照等效密度模型计算上行的等效流体模量、等效密度、等效模型复声速,进而得到等效密度复速度比
在第3层上行至第2层时重点考虑透射波,透射系数为:
| $ V_{w p 32}=2 \times V_{w w 3} \times z_{w p 32} /\left(z_{w p 32}+1\right) 。$ | (7) |
6)第3层上行至第2层后再上行至第1层透射
第3层上行至第2层后再上行至第1层的透射过程按照弹性计算归一化阻抗
| $ V_{w p 32}=2 \times V_{w w 3} \times z_{w p 32} /\left(z_{w p 32}+1\right)。$ | (8) |
针对浅海高频水声信号地声学传播特性,构造缩比试验环境时重点考虑多途信道的时延扩展影响和沉积层反射能量的损失因素。采用短脉冲CW作为声源信号,通过时延分离提取沉积层反射信号,同时考虑沉积层反射能力损失因素与声源掠射角、与水听器间距以及各自深度相关,在构造缩比试验环境时,设计合理、易于操作和较高精度的机械结构[10-11]。
浅海高频地声学缩比试验环境为4 m×2.4 m×0.3 m的小型水池,声源和水听器分别固定在2个滑动架上,在调整两者距离、各自深度及声源掠射角时需水面操作及标定后才能放入水中进行试验。尤其声源掠射角的调节除了将声源拿出水面进行标定放入水中外,还需保持滑动杆与水面的垂直状态。通过吊放支架的换能器基阵安装形成窄波束,从而提高声源信号能量增加反射能量的可分辨度,且吊放支架的升降连续调节、横梁沿小水池长度方向的滑动、带精细刻度的转盘连续转动均能实现不同距离、深度、掠射角等参数条件下的高频地声学特性试验。
缩比水池内表面除底面铺设泥质或砂质等沉积物外,其他内表面均覆盖高频吸声尖劈来消除小水池侧壁对反射信号的影响,提高缩比水池模拟浅海多途信道的近似度。通过发射基阵主波束角、掠射角、深度及与接收基阵之间的距离,预估直达路径与反射路径的时延分量。采用高频短脉冲作为声源信号,从接收基阵接收信号中采用时延分离方法提取反射信号[12]。
采用水平方向测量最大幅值方式测得具体偏差数据,如图2所示。通过计算可知理论波前

|
图 2 理论波前与实际波前夹角示意 Fig. 2 Angle between theoretical and actual wavefront |
从图1可以看出,当海底铺设3层底质时,入射波在泥质界面反射透射1次,在砂质界面反射透射1次,在石质界面反射1次、经砂质界面透射1次、再经过泥质界面透射1次,最终在水中接收到的回波是这些到达水中反射和透射纵波的综合反应,这些波之间存在时间差。而在试验过程中,受限于现有试验条件和采集手段,海底多次透射纵波基本捕捉不到。因此试验和反演都是针对1次反射进行的。
3.1 试验条件1)水箱底部铺设2~3 cm直径石子,厚度为6 cm,石子上铺设细泥砂厚度为10 cm,细泥砂上铺设黏土厚度为3 cm,水箱侧壁安装高频消声尖劈;
2)信号源设置信号频率为80 kHz单频,峰峰幅值为3Vpp,burst长度为3个周期,间隔为100 ms;
3)水听器供电电源为12VDC;
4)QPSO算法反演参数设置为一次反演最大迭代次数50次、最大反演参数个数4个、粒子种群最大粒子数量50个、最大可接受反演误差
1)设定发射换能器掠射角为0°,调整接收水听器角度至示波器观察幅值最大点,采集数据并记录时延信息,读取信号幅值最大值,作为直达波参考量;
2)两支架间隔120 cm,根据发射换能器掠射角度(25°、30°、35°),按试验数据记录(3层泥—砂—石)预计算结果,调整发射换能器角度及接收水听器角度,上下调整发射换能器位置,观察示波器反射波形变化(一般为紧跟直达波幅值略小的一段波形),同时满足预计算幅值条件及相对延时条件;
3)将记录的直达波及其延时乘积,以及反射波及其延时乘积代入适配度函数,反演出针对该测试结果的地声参数及掠射角,多次反演取近优解(反演掠射角近似设定掠射角,反射系数−掠射角曲线收敛)并根据所反演地声参数重绘反射系数−掠射角曲线;
4)将支架间距调整为50 cm,并进行40°,45°,50°,55°的测试;
5)将支架间距调整为35 cm,并进行60°的测试;
6)对比多次不同掠射角条件下的反演和重绘结果,给出定性结论。
上述直达波强度和延时的测量,因为最终在距离也即延时上进行归一化,所以可以取任一次结果。其中一次直达测量数据为幅值3434 mv,延时880 μs。
3.3 反演算法设计基于粒子量子行为的QPSO算法,利用种群中所有粒子的量子态出现位置建立分布概率模型,并通过随机采样操作实现对群体的更新,使得粒子能够以某一概率出现在整个可能搜索空间的任意位置,从而实现参数的全局寻优。根据理论假设前提,确定耗散系数为ϐt=0.01。根据仿真应用及实际问题需求,设定纵波速度比ap、剪切波速度比at、密度比aρ及掠射角θ为反演参数。其中掠射角θ并不是地声反演的必要参数,主要作为反演结果比对使用。
QPSO算法的总体参数设定如下:一次反演最大迭代次数Tmax= 50,最大反演参数个数N = 4,粒子种群最大粒子数量50,最大可接受反演误差10−4,最大反演次数为10。
α(t)称作伸缩因子,它的取值影响粒子的收敛效率,常用取值方法如下式:
| $ \alpha (t) = m - \frac{{(m - n)t}}{{{T_{\max }}}},$ | (9) |
其中
根据反演条件进行合理范围估计,设定待反演参数搜索区间如表1所示。
|
|
表 1 待反演参数估计区间 Tab.1 Estimated interval of parameters to be inverted |
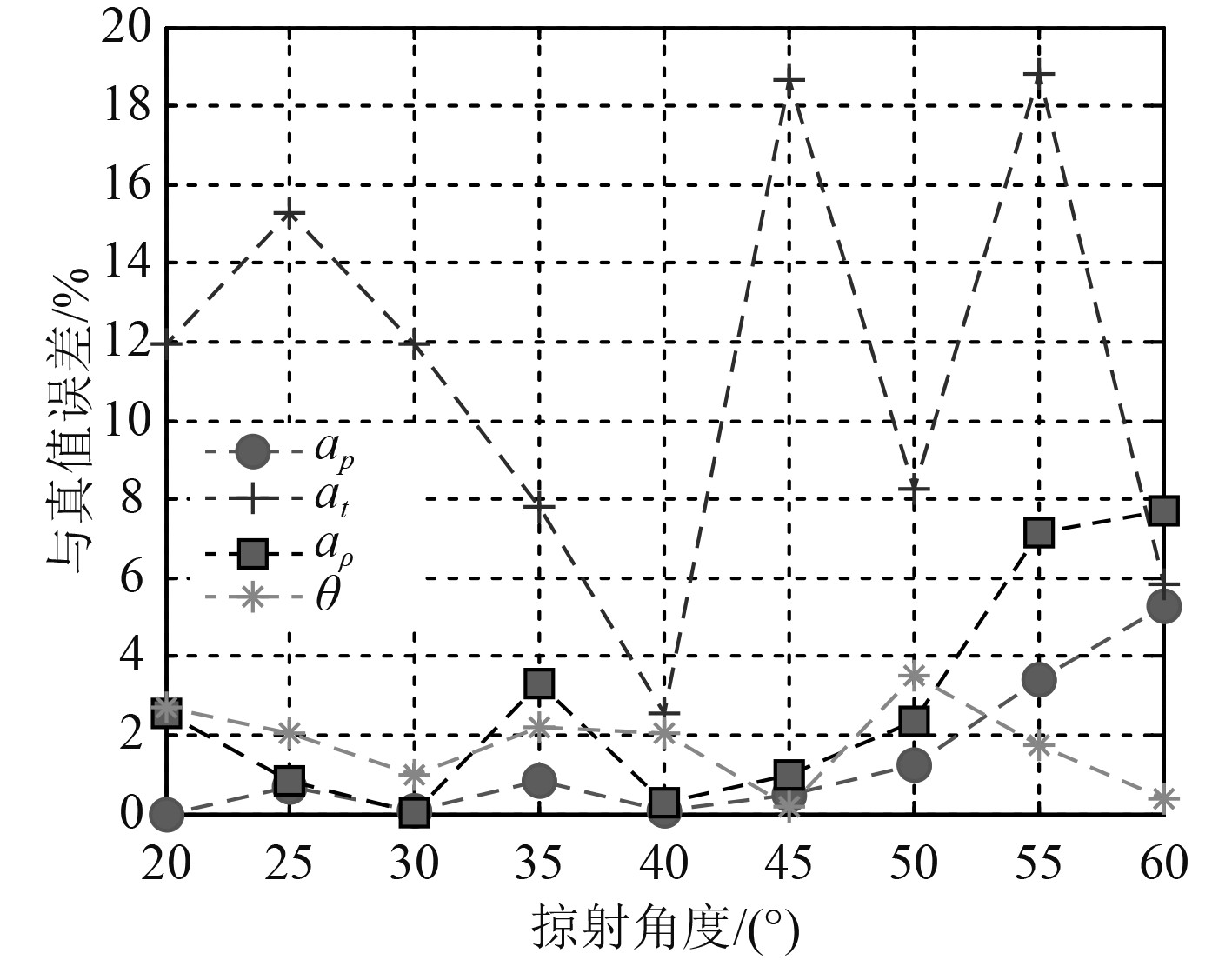
根据上述设定条件执行QPSO算法,每次反演计算所有有效结果的平均值,统计得到各掠射角下的参数反演误差结果如图3所示。
|
图 3 参数反演误差结果 Fig. 3 Error results of parameter inversion |
根据试验记录结果,参数at的反演误差较大且随机,参数ap、aρ、θ反演结果比较精确且一致性较好。弹性模型相较流体模型主要是引入了剪切波计算,而对于砂石状未固结海底,由于剪切波速度Vt相对于纵波速度Vp较小,近乎一个数量级的差别,所以对于模型的修正作用很小,属于非敏感参数,这也是参数at反演结果误差较大的原因。
反言之,在砂石或泥沙状海底条件下,即使at反演结果与真实值有较大差异(超过10%),其对海底反射系数的影响也较弱,采用45°掠射条件下的参数反演结果计算反射系数与掠射角关系,与正演模型计算结果对比如图4所示。

|
图 4 参数反演结果与正演模型计算结果对比 Fig. 4 Comparison of parameter inversion results and forward model calculation results |
根据图4显示计算结果,在小于30°掠射角的条件下,当Vt反演结果误差达到18.68%时,海底反射损失值近乎一致。随着角度的增大,反演与正演的海底反射损失仍具有较好一致性。同时从比对结果(除at采用反演结果,其他参数与正演模型一致)可以看出,大掠射角时的损失误差有相当一部分是由ap和aρ的反演误差造成的。
在接受反演结果参数的前提下,其反射系数与掠射角关系的比较如图5所示。
|
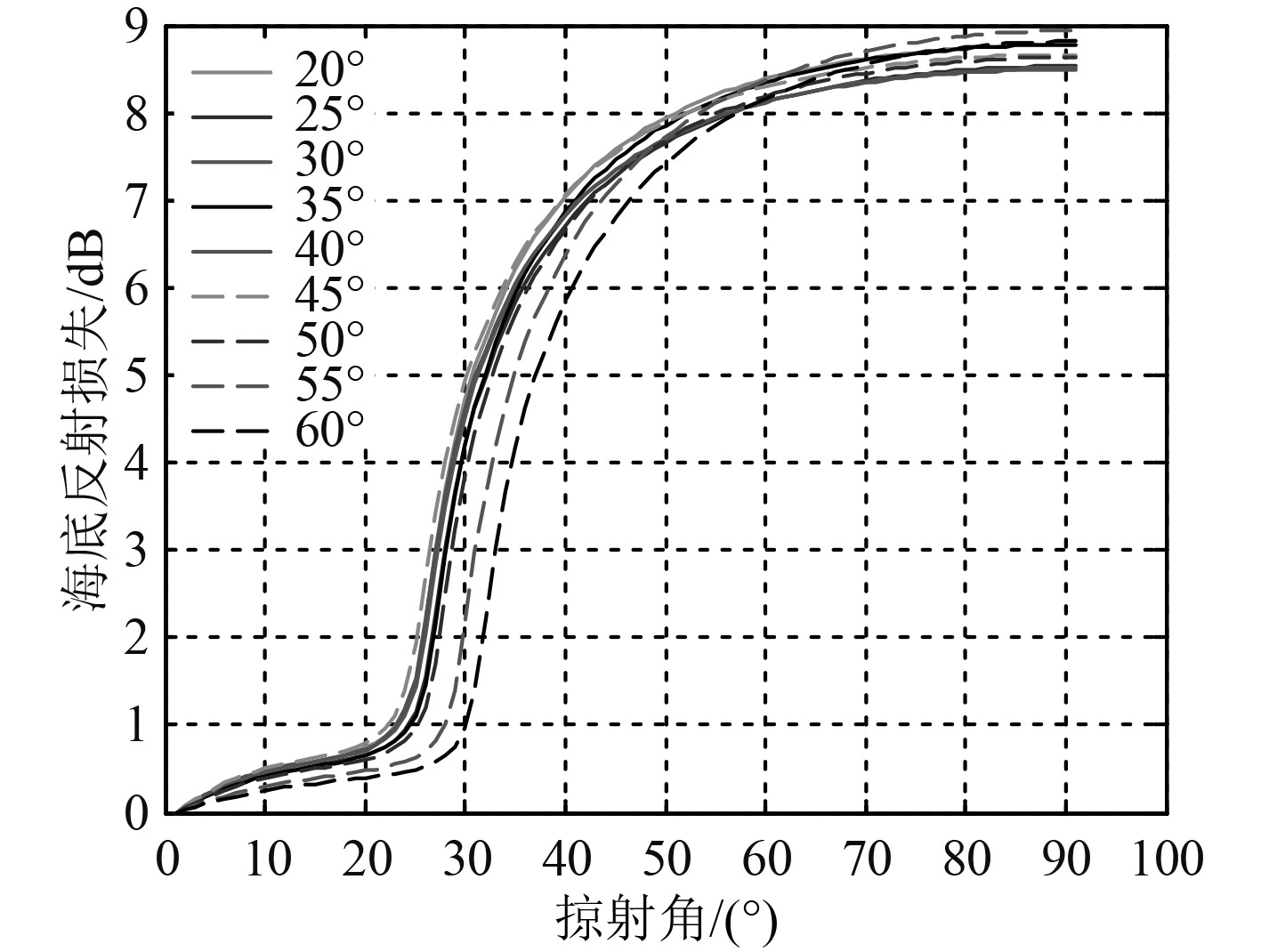
图 5 不同掠射角反演结果参数的海底损失比较 Fig. 5 Comparison of seafloor losses of inversion parameters with different grazing angles |
可以看出,基于弹性模型的QPSO算法反演结果在较小的掠射角(≤50°时)态势下的各曲线,所有角度范围的海底反射损失(海底反射系数)都收敛在一个较小的区间内。但掠射角较大时,其反演结果在反射损失变化较大区域(25°~35°掠射角时)的离散程度也比较大,最大可达到约4.5 dB。通过对不同掠射角反演参数结果进行平均计算,得到集总均值参数集Pt和小角度均值参数集Ppi,如表2所示。
|
|
表 2 集总均值参数集和小角度均值参数集 Tab.2 Lumped mean parameter set and small-angle mean parameter set |
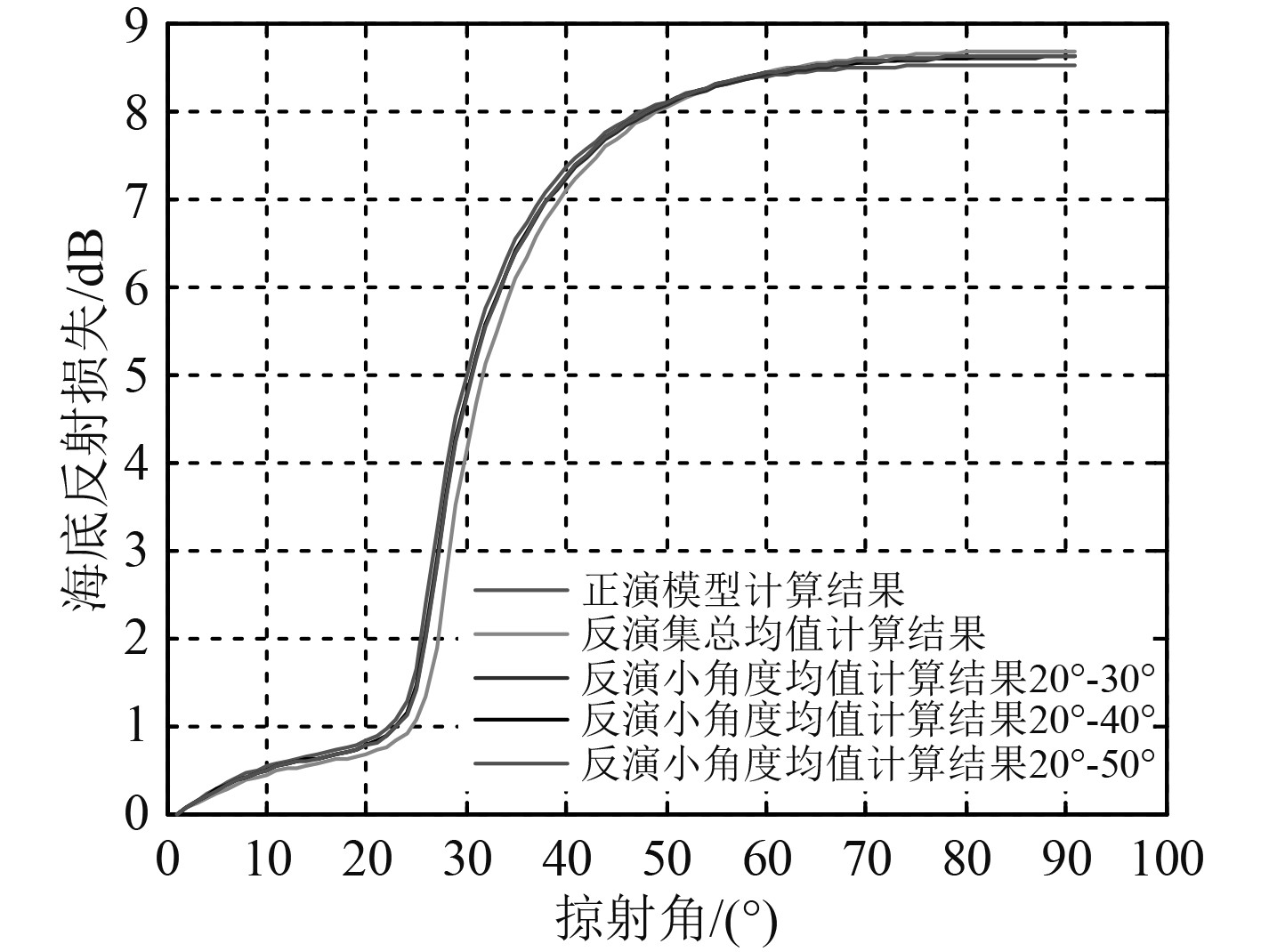
在集总均值参数及3种小角度均值参数条件下的参数反演结果与正演模型计算结果对比如图6所示。
|
图 6 不同反演结果参数均值的海底损失与掠射角关系比较 Fig. 6 Comparison of seafloor loss and grazing Angle between parameter mean values of different inversion results |
可知,小角度均值参数条件比集总均值参数有更小的估算误差。这是因为在剪切波速度Vt不敏感的情况下,at很难取得精确的反演结果从而在大角度区间代入较大的模型计算误差。为了得到该掠射角下模型大角度条件反射系数计算结果符合误差要求的参数估计,对纵波速度比ap和密度比aρ的寻优结果会一定程度偏离最优解,但其在反射损失变化较大区域(25°~35°掠射角)则会引起较大的离散。而小角度区间以反射损失变化较大区域为匹配对象,则其在其他区间的误差相对更小。
据此,选择20°~40°掠射角区间的小角度均值参数作为反演最终结果,其与各角度计算结果的对比关系如图7所示。
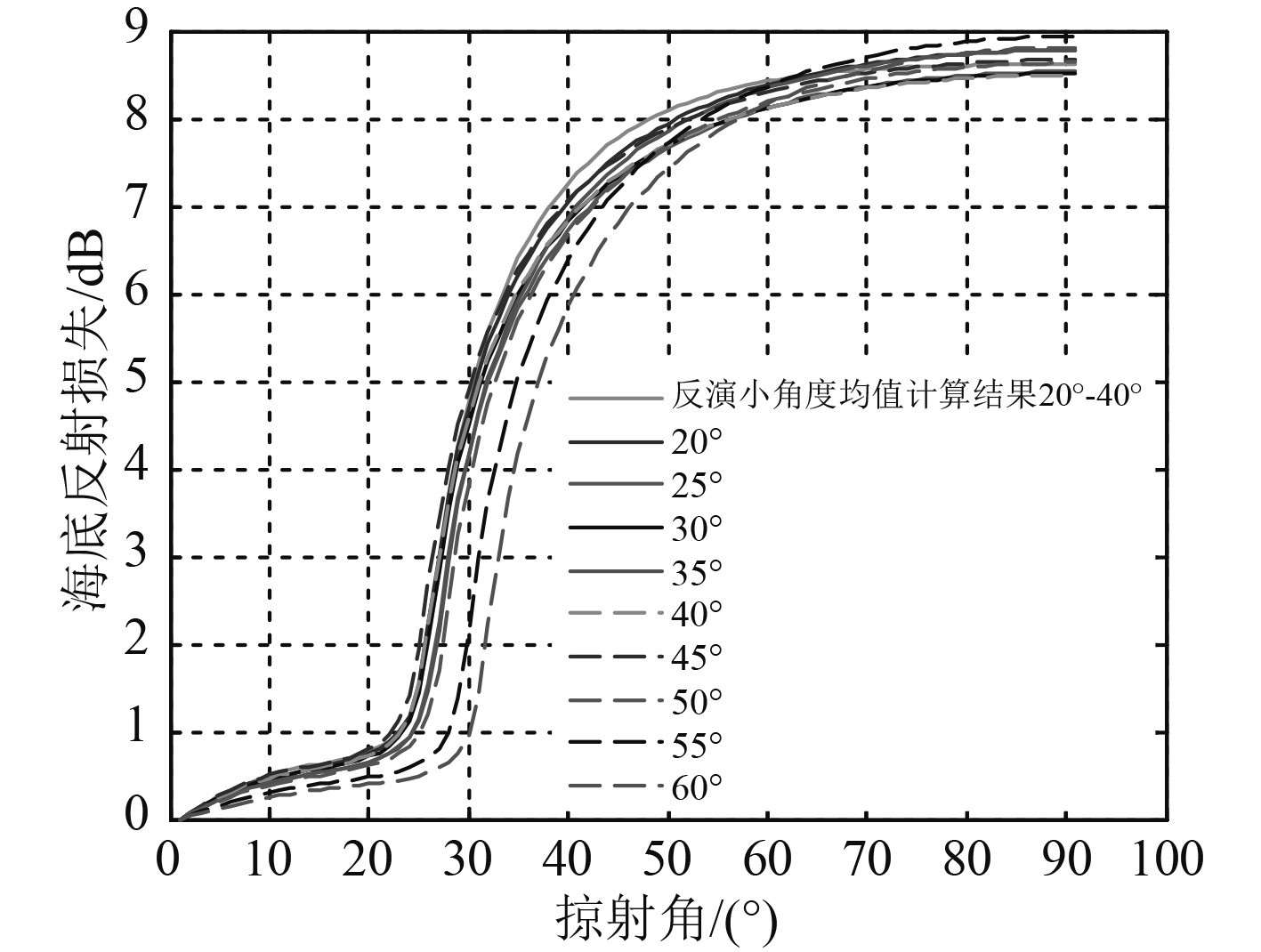
|
图 7 反演最终结果与各角度计算结果的对比关系 Fig. 7 Comparison between the final inversion results and the calculated results from various angles |
20°~40°掠射角区间的小角度均值,作为最终选定的反演参数集,其全掠射角计算结果与各曲线相应的掠射角对应反射损失吻合度较好,总体差异不超过1 dB,可以作为基于弹性模型的海底地声参数总体反演优化结果。
采用3层底质弹性模型对3层地声模型的一次反射过程进行反演试验,试验结果数据、参数反演结果如表3和图8所示。
|
|
表 3 试验结果及反演结果记录表(3层底质弹性模型) Tab.3 Records of test results and inversion results (elastic model of three-layer substrate) |
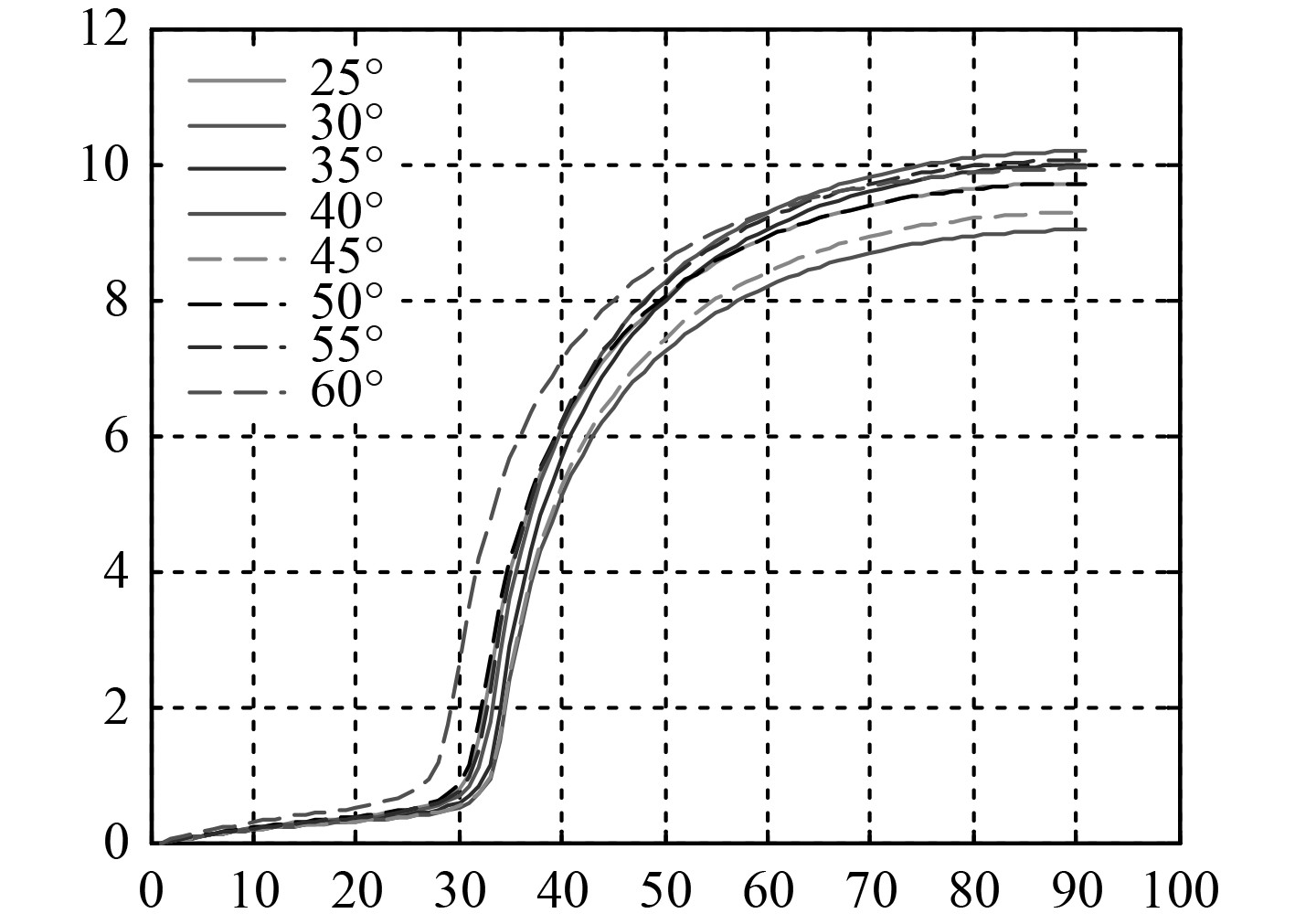
|
图 8 3层底质弹性模型试验反演结果 Fig. 8 Inversion results of elastic model test of three-layer substrate |
采用等效密度流体近似模型对3层地声模型的一次反射过程进行反演试验。等效密度表达式为:
| $ \frac{\rho_{eff}}{\rho_w}=\frac{1}{v^2_p[\beta +(1-\beta )K_w/K_g]}。$ | (10) |
式中:Vp为纵波速度,β为分数孔隙度,Kw为单个沉积物颗粒的体积模量,Kg为孔隙水的体积模量。试验结果数据、参数反演结果如表4和图9所示。
|
|
表 4 试验结果及反演结果记录表(3层底质EDFM模型) Tab.4 Record table of test results and inversion results (three-layer substrate EDFM model) |

|
图 9 3层底质EDFM模型试验反演结果 Fig. 9 Inversion results of EDFM model test on three-layer substrate |
本文依托海底地声学模型,建立3层海底地声模型。在实验室条件下构建浅海分层结构的海底缩比场仿真环境,以声学测试试验结果为数据样本,基于匹配场技术,采用全局优化算法实现不同分层结构的海底地声学参数的优化反演。试验结果证明,在缩比环境条件下,采用QPSO算法对不同底质特性的海底地声学模型参数反演结果所计算的海底反射损失系数均收敛在1~2dB,参数值符合其特性区间,正演计算一致性较好,验证了海底地声模型的正确性和可信性。
| [1] |
杨坤德, 马远良. 利用海底反射信号进行地声参数反演的方法[J]. 物理学报, 2009, 58(3): 1798−1805.
|
| [2] |
于盛齐, 黄益旺, 吴琼. 基于等效密度流体近似反射模型反演海底参数[J]. 声学学报, 2014, 39(4): 417−427.
|
| [3] |
YU Shengqi, HUANG Yiwang, WU Qiong. Geoacoustic inversion based on reflection model of effective density fluid approximation[J]. Chinese Journal of Acoustics. 2014, 33(3): 239−256.
|
| [4] |
纪震, 廖惠连, 吴青华. 粒子群算法及应用[M]. 北京: 科学出版社, 2009: 169−199.
|
| [5] |
TAROUDAKIS M I. Identifying modal arrivals in shallow water for bottom geoacoustic inversion[J]. Journal of Computational Acoustics, 2000, 8(2): 307−324.
|
| [6] |
Harrison C H, Nielsen P L. Separability of seabed reflection and scattering properties in reverberation inversion[J]. Journal of the Acoustical Socitety of America, 2007, 121(1): 108−119.
|
| [7] |
David R D, PETER H D. Properties of the acoustic intensity vector field in a shallow water waveguide[J]. Journal of the Acoustical Socitety of America, 131 (3): 2023−2035.
|
| [8] |
彭临慧, 郁高坤, 王桂波. 海底介质模型及其声能透入机理研究[J]. 船舶力学, 2007, 11(1): 128−135.
|
| [9] |
李艳华. 海底沉积物声学性质原位测量技术研究[D]. 北京: 中国科学院研究生院, 2010.
|
| [10] |
马黎黎, 王仁乾. 分层砂底对浅海信道声传播影响的研究[J]. 声学学报. 2003, 28(2): 145−150.
|
| [11] |
宋磊. 海底散射系数测量方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
| [12] |
薛婷. 基于T型乘积阵的海底散射系数测量方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
 2023, Vol. 45
2023, Vol. 45
