矢量水听器兼备声压通道和标量通道,能够空间共点地同步测量声场中的声压标量信号和振速矢量信号,具有低频性能好、灵敏度高、体积小、功耗低等特点[1],在海洋环境监测和水下目标探测等领域有着广泛的应用,其耐水压性能一直是限制其在大深度水下应用的制约因素[2]。
根据矢量水听器设计的基本原理,为获得更宽的工作频带和较高的灵敏度,还要求水听器具有小尺寸和低密度的特点[3],受制于材料和工艺水平,高耐压、小尺寸、低密度的设计要求无法同时满足,需要综合考虑各个因素的影响。本文设计一款耐20 MPa水压的矢量水听器,基于静力分析与响应面优化方法,对水听器耐压壳体进行尺寸优化,在满足耐高静水压的条件下,实现了水听器的低密度设计。
1 水听器设计与壳体耐压仿真 1.1 矢量水听器设计原理复合式矢量水听器包括声压通道和矢量通道,根据矢量通道的同振特性可知,水听器外形尺寸越小,其上限工作频率越大。水听器的平均密度越接近于水,其振速幅值与水听器振速幅值之比的绝对值越大,水听器的振速灵敏度越大[4]。在实际应用中,由于材料、结构和工艺的限制,水听器的密度很难小于水,常常追求将水听器的平均密度设计成趋近于水的密度。
因此,复合式矢量水听器在完成设计选型后,其主要难点在于结构尺寸小、耐水压强度高以及低密度等设计要求难以兼顾的问题,高耐水压强度和低密度是一对相互矛盾的设计要素。
1.2 矢量水听器设计选型根据薄壁壳体强度理论,在直径、压力相同的情况下,球形壳体的内部应力仅为圆筒形的一半,是一种更加合理的耐压结构[5]。因此,将水听器设计成球形壳体结构可以减轻重量,而且球形结构的水听器在声学性能上也具备较好的三轴一致性[6]。
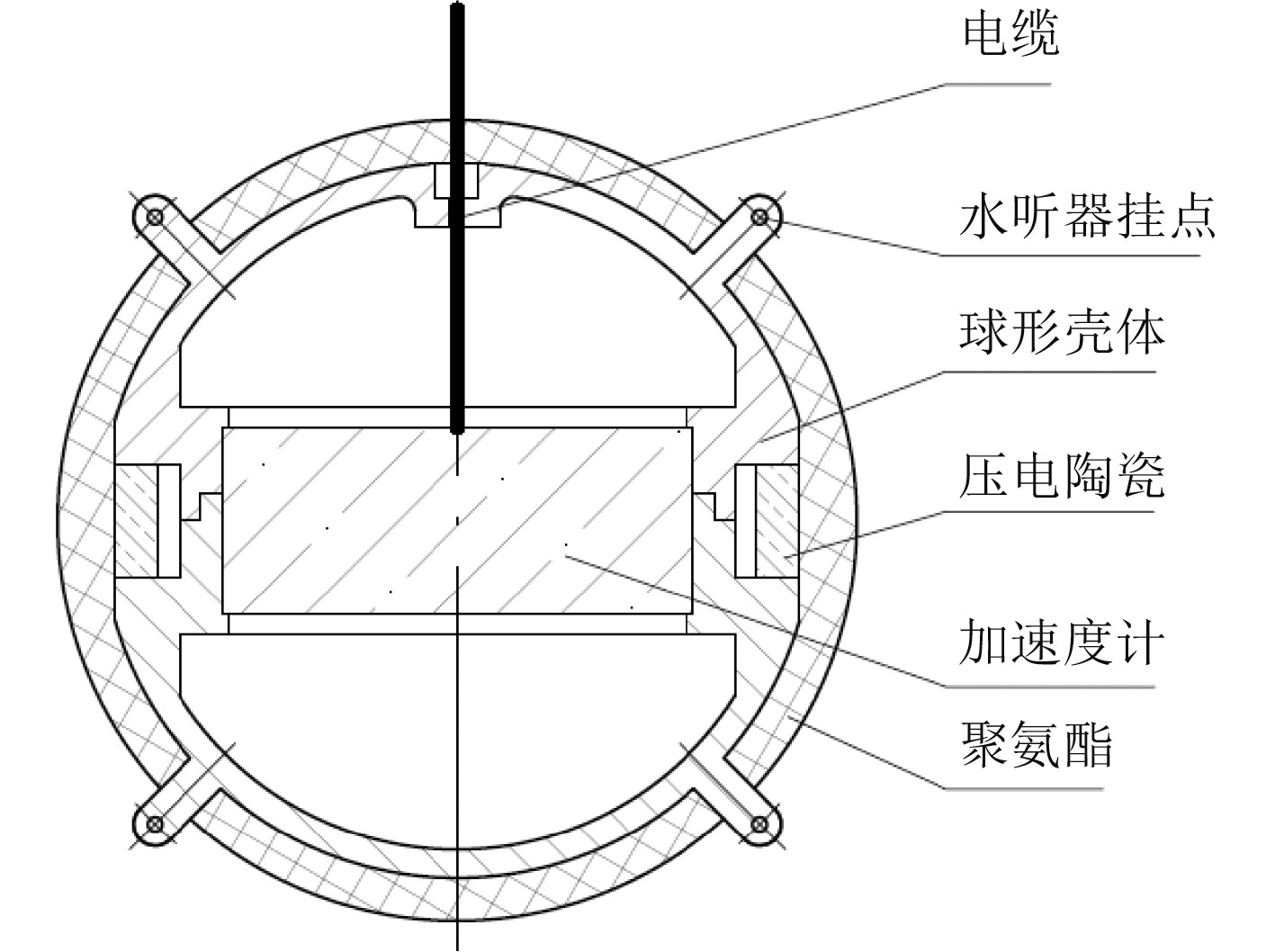
根据指标要求设计的矢量水听器结构形式如图1所示。声压通道和矢量通道分离,耐压壳体分为上、下2个半球形壳体,将加速度计卡紧悬空固定于中心位置,声压通道采用P5材质的径向极化压电陶瓷管,采用空气被衬结构,壳体外层用聚氨酯包覆水密。最大工作水压为20 MPa,要求水听器密度与水接近。
|
图 1 矢量水听器内部结构图 Fig. 1 Internal structure diagram of vector hydrophone |
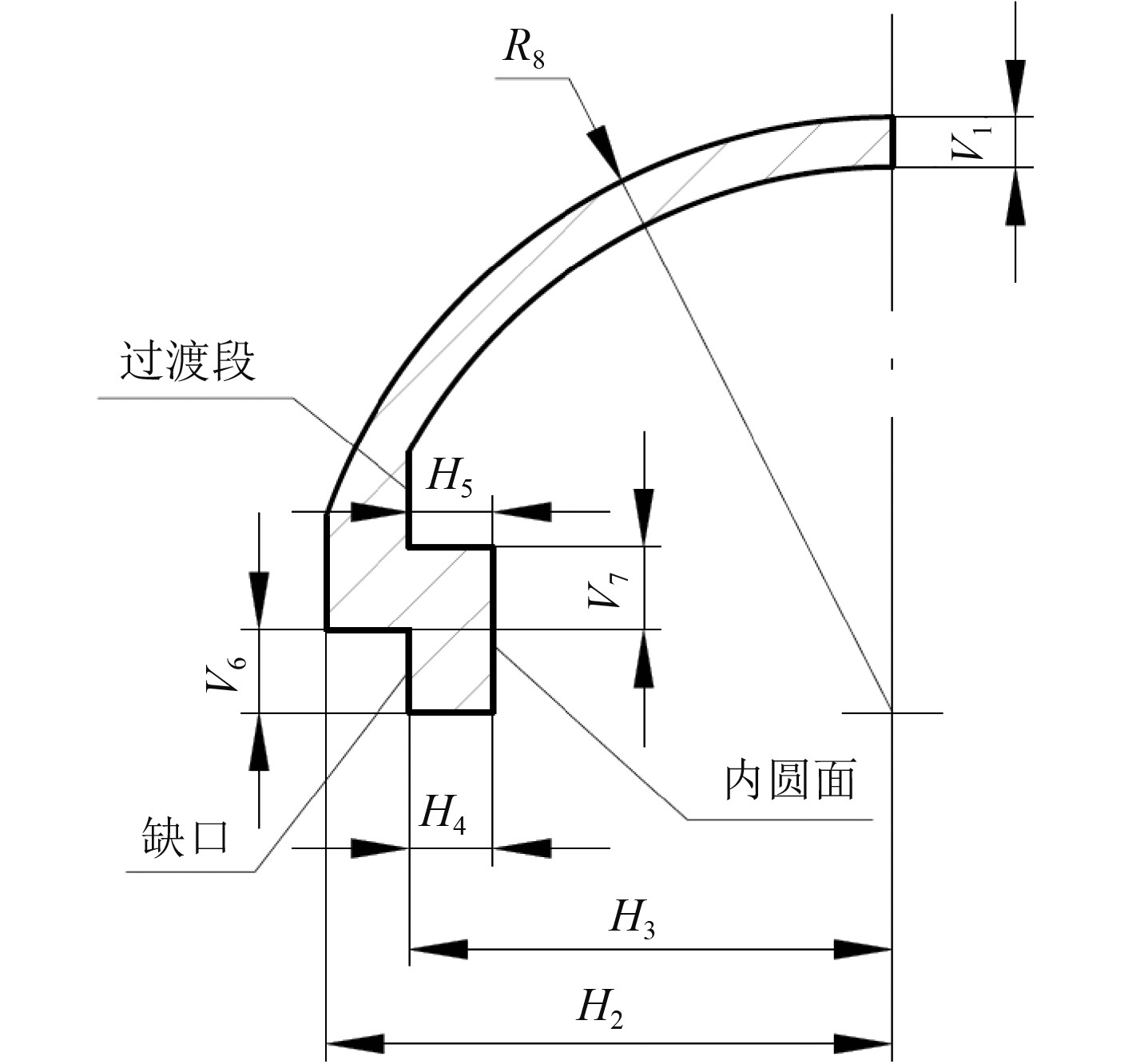
半球形壳体的尺寸剖视图如图2所示。R8为球形壳体半径,V1为壳体壁厚,H2为陶瓷外半径,H3为壳体缺口处半径,H4为缺口处壁厚,H5为内圆面与壳体过渡段间距,V6为缺口处高度,V7为缺口上部厚度。根据以上选型及设计,其初始设计值分别41 mm,3 mm,39 mm,34 mm,5 mm,4 mm,4 mm,5 mm。根据选型及计算,水听器各组成部分的质量如表1所示。水听器总重约415 g,排水量为332 g,平均密度为1.25 g/cm3,相比水的密度有较大差距。
|
图 2 壳体结构尺寸示意图 Fig. 2 Internal structure diagram of vector hydrophone |
|
|
表 1 矢量水听器质量构成 Tab.1 Mass composition of vector hydrophone |
壳体在静水压力作用下可能发生强度失效和稳定性失效,需要通过有限元分析对其进行静强度仿真和屈曲仿真[7]。为简化模型,减少设计参数,忽略上壳体顶部的电缆引出小孔,上、下壳体采用相同的三维模型,在模型中省去对壳体耐压强度没有影响的挂点等特征。
在静力分析模块中建模,壳体材料采用铝合金7075,其0.2%屈服强度约为460 MPa,在壳体底部平面施加固定约束,球形外表面及外圆面施加20 MPa静压力,求解后得到的应力云图如图3所示。可以看出,壳体内部最大应力为218 MPa,主要应力在壳体的内球面过渡处,这是因为过渡处的尺寸发生突变引起了应力集中。

|
图 3 壳体受压应力云图 Fig. 3 Pressure stress nephogram of shell |
在上述分析结果基础上进行线性屈曲分析,得到一阶屈曲模态的变形云图如图4所示。第一阶屈曲载荷因子为519,由于一阶屈曲因子最小,故其临界失稳压力为519 MPa,远大于水听器设计的工作压力。因此,当工作水深不断增大时,其可能发生的失效形式是强度失效而不是稳定性失效。

|
图 4 壳体线形屈曲变形云图 Fig. 4 Deformation nephogram of shell linear buckling |
设计方案不满足设计要求时,可以在当前基础上进行优化,使其在满足所有设计要求的条件下,求得某一项或几项参数的最大值或最小值。
2.1 优化设计基本原理和方法优化设计的原理是通过建立数学模型,运用优化方法,在满足设计要求的情况下进行迭代计算,从而求出目标函数在约束条件下的极值,得到最终的优化结果[8]。优化设计的三要素包括目标函数、约束条件和设计变量,优化设计的数学模型为:
目标函数
| $ f(x) = f({x_1},{x_2},\cdots,{x_n}),$ | (1) |
约束条件
| $ \begin{array}{ll} {g_i}(x) \leqslant 0,& i = 1,\cdots ,m,\\ {h_j}(x) \leqslant 0,& j = 1,\cdots ,m,\end{array} $ | (2) |
设计变量
| $ x_k^l \leqslant {x_k} \leqslant x_k^u,\quad k = 1,\cdots ,n。$ | (3) |
目标函数以设计变量表达各目标的性能,约束条件是限制设计变量取值范围和描述其对应关系的函数式[9],目标函数和约束条件从有限元分析中获得结构响应,设计变量从模型中提取,根据选定的优化方法,将需要优化的尺寸定义为设计变量。
响应面法(response surface method)是一种常用的优化设计方法,其原理是通过建立一系列在范围内的设计变量组合,建立与原设计相近的模型,进行重复试验和筛选,得到目标函数和约束条件的响应面模型,预测非试验点的响应值,再根据约束条件和收敛条件,求出满足要求的设计结果[10]。响应面法只需要确定输入条件和输出目标,即可对模型进行自动分析求解,而无需研究输入与输出之间的内在联系,其优点是模型精度高,能同时显示预测位置的误差和预测值[11],并通过不断迭代在相互矛盾的多个设计变量中求解出一组最优解。
通常情况下,响应面模型选用比较精准的二阶模型,多个设计变量的二次多项式模型可以表示为:
| $ D(x) = {\alpha _0} + \sum\limits_{i = 1}^n {{\alpha _i}} {x_i} + \sum\limits_{i = 1}^n {{\alpha _{ii}}} {x_i} + \sum\limits_{1 = i < j}^n {{\alpha _{ij}}} {x_i}{x_j} + \varepsilon 。$ | (4) |
式中:
从图1可以看出,壳体为上下对称的回转结构,水听器直径及压电陶瓷管尺寸选定后,图2中的R8,H2,H3,V6等4个尺寸即为常量,将V1,H4,H5,V7四个尺寸定义为设计变量,允许其在设计尺寸附近一定范围内变化,将壳体的质量设为优化目标,约束条件为壳体的最大内部应力应小于许用强度。因此,设计含有一个优化目标(质量)、4个设计变量(V1,H4,H5,V7)和一个约束条件(最大应力)。
由仿真结果可知,水听器壳体可能发生的失效是强度失效,因此,在静力学分析模块后添加响应面模块和优化模块[12]。进入响应面模块后,对响应面进行更新,系统自动得到25组不同的设计变量组合的取点及求解结果,根据响应面分析结果,系统自动生成各设计变量在模型中的局部敏感度,以及目标函数和约束条件相对于各设计变量取值变化的响应面图。
2.2.2 局部敏感度分析局部敏感度用来显示设计变量对目标函数和约束条件的影响程度,从本质上来说是目标函数和约束条件对于设计变量的偏导数,反映其对应关系。局部敏感度分析可以判断设计变量的总体变化趋势,为最终的优化方案提供支撑,保证设计变量与优化目标之间最大程度的匹配。响应面模型根据试验点求解结果生成的各设计变量局部敏感图如图5所示。可以看出,V1和H4与壳体质量正相关,而与壳体最大应力负相关,且敏感系数较大,这意味着其变大会导致壳体质量大幅增大,而最大应力会明显减小,H5则刚好相反,而V7对二者均呈正相关,敏感因素较小,说明V7增大会导致壳体质量和最大应力小幅增大。设计目标是在满足壳体耐压强度的条件下,求得质量的最小值。为达到预期的低密度效果,从设计变量优化的方向来看,V1,H4,V7应减小,H5应增大;从敏感系数来看,V1,H4,H5的取值范围应适当取得宽一些,V7敏感度较小,其取值范围应适当缩小。

|
图 5 各设计变量的局部敏感度 Fig. 5 Local sensitivity of each design variable |
响应图是通过对设计变量在上、下一定范围内进行插值,然后对目标函数和约束条件进行求解而获取的图表,可以在三维坐标系中更加直观地显示不同设计变量对于目标函数和约束条件变化趋势的影响。图6和图7为各设计变量与壳体质量及壳体最大应力的响应面关系。从图中不仅可以验证敏感度分析的结果,还可以直接读取设计变量取特定值时的壳体质量及最大应力,对下一步确定设计变量取值范围有指导意义。

|
图 6 质量与设计变量的响应面关系 Fig. 6 Response surface between mass and design variables |

|
图 7 最大应力与设计变量的响应面关系 Fig. 7 Response surface between maximum stress and design variables |
为满足水听器的低密度要求,在保持其他部件不变时,水听器的密度若降至1.05 g/cm3,则上、下壳体的总质量需要从232 g减小至170 g。根据水声换能器耐静水压的相关标准,换能器的最大耐压深度应不小于工作深度的1.5倍,壳体的耐压安全系数应不小于1.5,设定壳体最大内部应力不大于300 MPa。根据敏感度分析结果,综合水听器设计尺寸、约束条件及优化目标,本设计的目标函数为Mass≤85 g,约束条件为Stress≤300 MPa,设计变量的取值范围设定为:
| $ \left\{ \begin{array}{l} 1.5\geqslant {V}_1\geqslant 4.5,\\ 1\geqslant {H}_4\geqslant 7,\\ 1\geqslant {H}_5\geqslant 7,\\ 2\geqslant {V}_7\geqslant 6。\end{array}\right. $ |
在优化设计模块中分别输入上述设计变量、约束条件和目标函数的取值范围。由于设计变量较多,采用直接优化法求解点数多、效率较低。为快速精确求解,选用多目标遗传算法(multi-objective genetic algorithm)作为全局优算法求解Pareto可行域,初始样本设定为100组,每代前50组作为遗传算法选择样本进行迭代,最大允许遗传代数为20代,系统预计需要求解1050组设计变量组合,设置最大允许Pareto比例为70%,收敛稳定性为2%,进行求解计算,得到如表2所示的3组推荐参数组合。
|
|
表 2 求解结果推荐参数 Tab.2 Recommended solution results |
优化目标为在满足壳体最大应力小于许用强度的情况下获得最小的质量,显然采用第一组推荐参数减重效果最为明显。对推荐参数取整后重新计算求解,单个壳体质量为80 g,其内部应力云图如图8所示。优化后壳体内部最大应力为从218 MPa变为288 MPa,与图3相比,壳体内部应力分布更加均匀,应力集中效应有所降低,材料的强度得到更加充分地利用。

|
图 8 优化后的壳体受压应力云图 Fig. 8 Optimized pressure stress nephogram of shell |
表3为优化前后各项参数对比,从优化结果可以看出,设计变量V1和V7的取值变小,H4的取值不变,H5则有所增大,这与前文的分析基本一致。优化后的水听器质量为345 g,减小了17%,密度为1.03 g/cm3,接近于水下零浮力,达到了理想的水听设计效果。
|
|
表 3 优化前后参数对比 Tab.3 Parameters before and after optimization |
为验证水听器样机是否满足耐设计工作水压要求,在压力釜中进行20 MPa的静水压力试验。将压力釜缓慢加压至20 MPa并保持压力30 min,保压过程中压力表平稳,取出后观察,水听器外表无明显变化,经测试,水压试验后其灵敏度及指向性基本一致,表明该矢量水听器可以满足2000 m水深的工作要求。
3 结 语本文介绍矢量水听器设计原理与结构优化方法,运用有限元软件对水听器壳体耐压强度进行仿真分析,针对水听器的低密度要求,通过响应面优化方法对水听器壳体的尺寸进行优化设计,完成了水听器的试制和测试,得到结论如下:
1)随着工作水深的增大,水听器壳体会发生强度失效而不是稳定性失效。
2)尺寸V1和H4变大会导致壳体质量大幅增大,最大应力明显减小,H5则刚好相反,尺寸V7则对二者的影响较小。
3)壳体尺寸优化后,水听器的密度从原来的1.25 g/cm3降低至1.03 g/cm3,接近于水下零浮力。
| [1] |
杨德森, 洪连进. 矢量水听器原理及应用引论[M]. 北京: 科学出版社, 2009.
|
| [2] |
王文龙, 孙芹栋, 王超, 等. 大深度复合同振式矢量水听器设计[J]. 国防科技大学学报, 2021, 43(03): 149-158. DOI:10.11887/j.cn.202103018 |
| [3] |
葛松, 付昌, 卞加聪, 等. 用于水下目标监测的低频同振式矢量水听器研制[J]. 无损检测, 2022, 44(1): 70-73. |
| [4] |
陈洪娟, 杨士莪, 王智元, 等. 同振式矢量传感器设计方法的研究[J]. 声学技术, 2005, 24(2): 80-83. |
| [5] |
朱保国. 压力容器设计知识[M]. 北京: 化学工业出版社, 2016.
|
| [6] |
贾富志. 三维同振球型矢量水听器的特性及其结构设计[J]. 应用声学, 2001, 20(4): 15-20. |
| [7] |
高杰. 深海球形耐压壳体力学特性及试验研究[D]. 镇江: 江苏科技大学, 2017.
|
| [8] |
解可新, 韩建. 最优化方法[M]. 天津: 天津大学出版社, 2004.
|
| [9] |
孙靖民, 梁迎春. 机械优化设计[M]. 北京: 机械工业出版社, 2012.
|
| [10] |
曾漾, 周俊, 沈志远, 等. 基于响应面法的复合材料舱壁结构优化设计[J]. 重庆大学学报, 2020(6): 82-89. |
| [11] |
DI Meo C A, WAKEFIELD J R, CRAY S C. A new device for sampling small volumes of water from marine micro-environments[J]. Deep Sea Research Part I:Oceanographic Research Papers, 1999, 46(7): 1299. |
| [12] |
孟巧荣, 高立志, 王勇, 等. 基于SolidWorks与Workbench的纤维过滤器壁厚优化设计[J]. 太原理工大学学报, 2020, 51(4): 610-614. DOI:10.16355/j.cnki.issn1007-9432tyut.2020.04.019 |
 2023, Vol. 45
2023, Vol. 45
