0 引　言

船舶的动力定位系统主要由传感器、控制器、动力推进器等部件构成，其工作过程中需要采集环境的风浪流因素，通过控制器的动力分配，向推进器发送控制指令，产生抵抗外界环境干扰的作用力，使船舶在一定范围内保持定位。随着船舶大型化、控制程序复杂程度的提高，传统的动力定位系统精度已经难以满足要求，需要进行优化和升级。传统的动力定位方法一般是使用PID算法对船舶进行定位，通过调节PID的参数实现对船舶的闭环控制。但是调节的PID参数受到环境因素、船舶动力因素的影响，经常会出现超调的情况，同时在调节时间上也很容易出现长时间无法进入稳定状态的情况。

本文结合现有船舶的动力定位系统，建立船舶和干扰因素的数学模型，设计一种自抗扰控制算法的动力定位控制器。采用Simulink软件的仿真结果表明，基于自抗扰控制算法的船舶动力定位控制具有较高的精度。

1 船舶动力定位的数学建模

船舶动力定位过程受到的干扰力以波浪干扰力为主，本文在海浪干扰力建模时采用P-M波浪谱密度函数^[1]，如下式：

$\varGamma (X,Y,t) = A\cos \left( {\dfrac{{2\text{π} }}{\lambda }\left( {Y\cos \theta + X\sin \theta - {w_1}t + \varphi } \right)} \right)。$

式中： $\lambda$ 为波长； $\theta$ 为波浪倾角； ${w_1}$ 为波浪的频率； $\varphi$ 为相位。

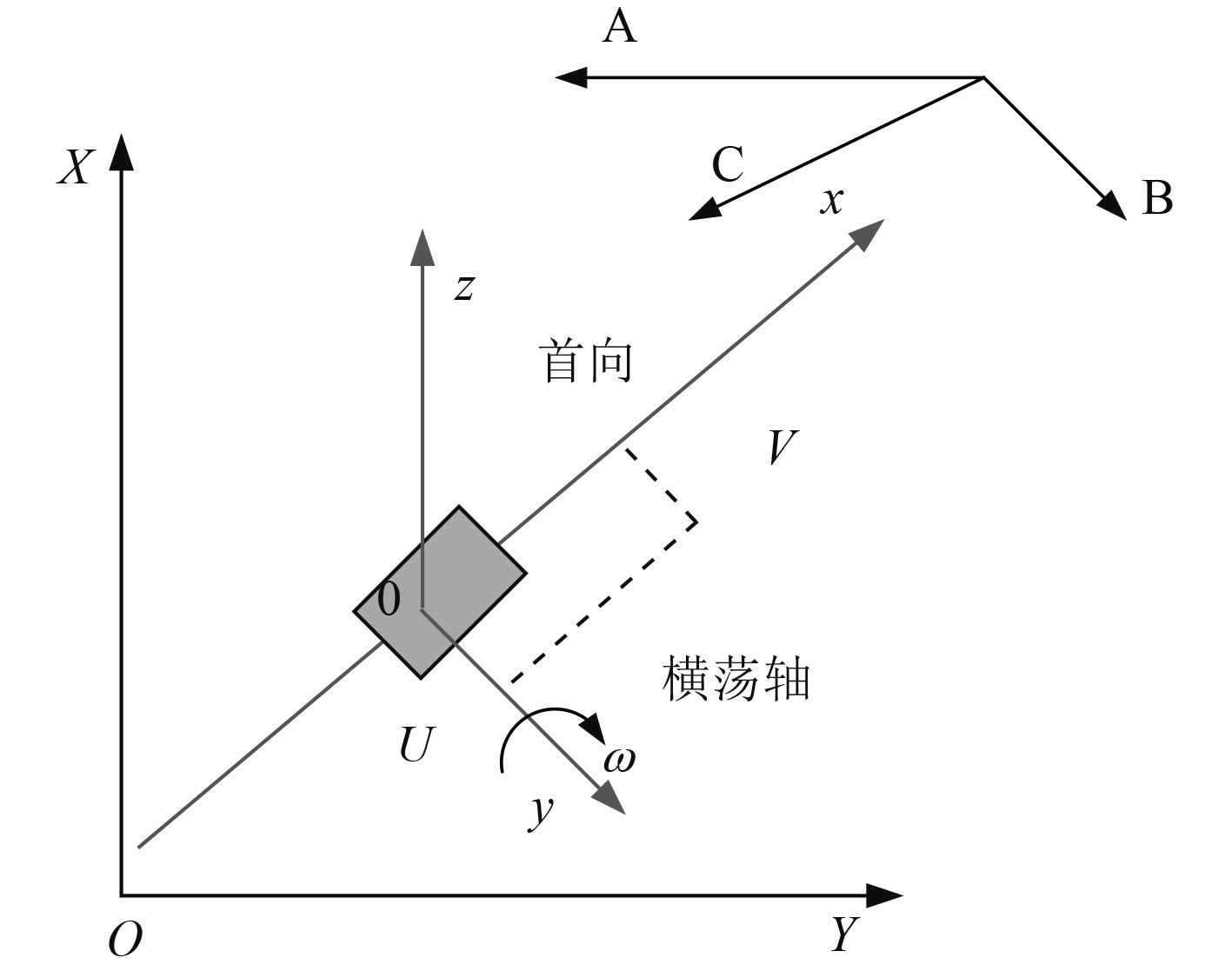
建立船舶动力定位过程的坐标系如图1所示。

图中， $(O,X,Y)$ 为地球坐标系，U为横向与波浪的相对速度，V为首向与波浪的相对速度， $\omega$ 为晃动角速度。

结合波浪谱密度函数^[3]，建立动力定位的波浪扰动载荷为：

$\left\{ {\begin{array}{*{20}{l}} {{F_{\text{h}}} = 0.025m{V_l}^2 + 1.9} ，\\ {{T_0} = - 0.0026m{V_l}^3 + 0.0046m{V_l}^2} \text{，} \\ {{T_1} = m\dfrac{4}{5}\sqrt {\left( {{V_l}^2 + {U^2}} \right)} \sqrt {{\lambda _{}}} } 。\end{array}} \right.$

式中： ${F_h}$ 为扰动作用力； ${V_l}$ 为波浪速度；T₀ ，T₁分别为2个方向的扰动力矩。

在该坐标系下建立动力定位运动方程如下式：

$\vec M = \vec J\left( M \right)\vec V 。$

式中： $\vec M$ 为船舶的位置向量、方向向量和横摇角度向量， $\vec M = {\left[ {x,y,\alpha } \right]^{\rm{T}}}$ ； $\vec V$ 为船舶的速度向量， $\vec V = {\left[ {u,v,r} \right]^{\rm{T}}}$ ； $\vec {\boldsymbol{J}} \left( M \right)$ 为关系矩阵，用下式表示：

$\vec {\boldsymbol{J}}\left( M \right) = \left[ {\begin{array}{*{20}{c}} { - \cos \alpha }&{\cos \alpha }&0 \\ 1&{\sin \alpha }&0 \\ { - \sin \alpha }&0&1 \end{array}} \right]。$

由于船舶动力定位过程的运动以低频运动为主，建模如下：

$\vec G{\vec V} + R\left( {{{\vec V}}} \right) + \vec F\left( {{{\vec V}} - {{\vec V}}_c} \right) = {\vec \tau _0} 。$

式中： ${\vec V_c}$ 为低频下的船舶动力定位运动速度分量， ${\vec V_c} = {\left[ {{u_c},{v_c},{r_c}} \right]^{\rm{T}}}$ ， $\vec {\boldsymbol{G }}$ 为船舶的惯性矩阵， $\vec{\boldsymbol{ F}}$ 为低频运动的系数矩阵。

$\overrightarrow {\boldsymbol{G}} = \left[ \begin{gathered} m - {X_r}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m - {Y_r} \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \\ \end{gathered} \right.\left. \begin{gathered} 0 \\ {\kern 1pt} {\kern 1pt} {Y_r} \\ {I_z} - {N_r} \\ \end{gathered} \right] \text{，}$

$\vec {\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} { - {X_r}}&0&0 \\ 0&{{Y_r}}&{ - {Y_r}} \\ 0&1&{ - {N_r}} \end{array}} \right] 。$

式中： $m$ 为舰船质量； ${I_z}$ 为转动惯量； ${X_r}$ ， ${Y_r}$ ， ${N_r}$ 分别为低频运动下的附加质量； $R\left( {{{\vec V}_{}}} \right)$ 为科里奥系数^[3]，表征惯性力对运动模型的影响； ${\vec \tau _0}$ 为低频运动的力矩向量，与船舶推力、海浪、海风干扰作用力矩有关。

2 船舶动力定位的自抗扰控制器数学建模

船舶动力定位系统控制器的工作原理是通过位置测量传感器测得船舶的位置、航向等信息，同时采集海浪、海流、海风干扰条件，获得动力定位的位置与角度偏差，并将偏差值作为控制器的输入信号，通过一系列的控制解算，将推进器的调整指令发送至动力定位推进器^[2]。

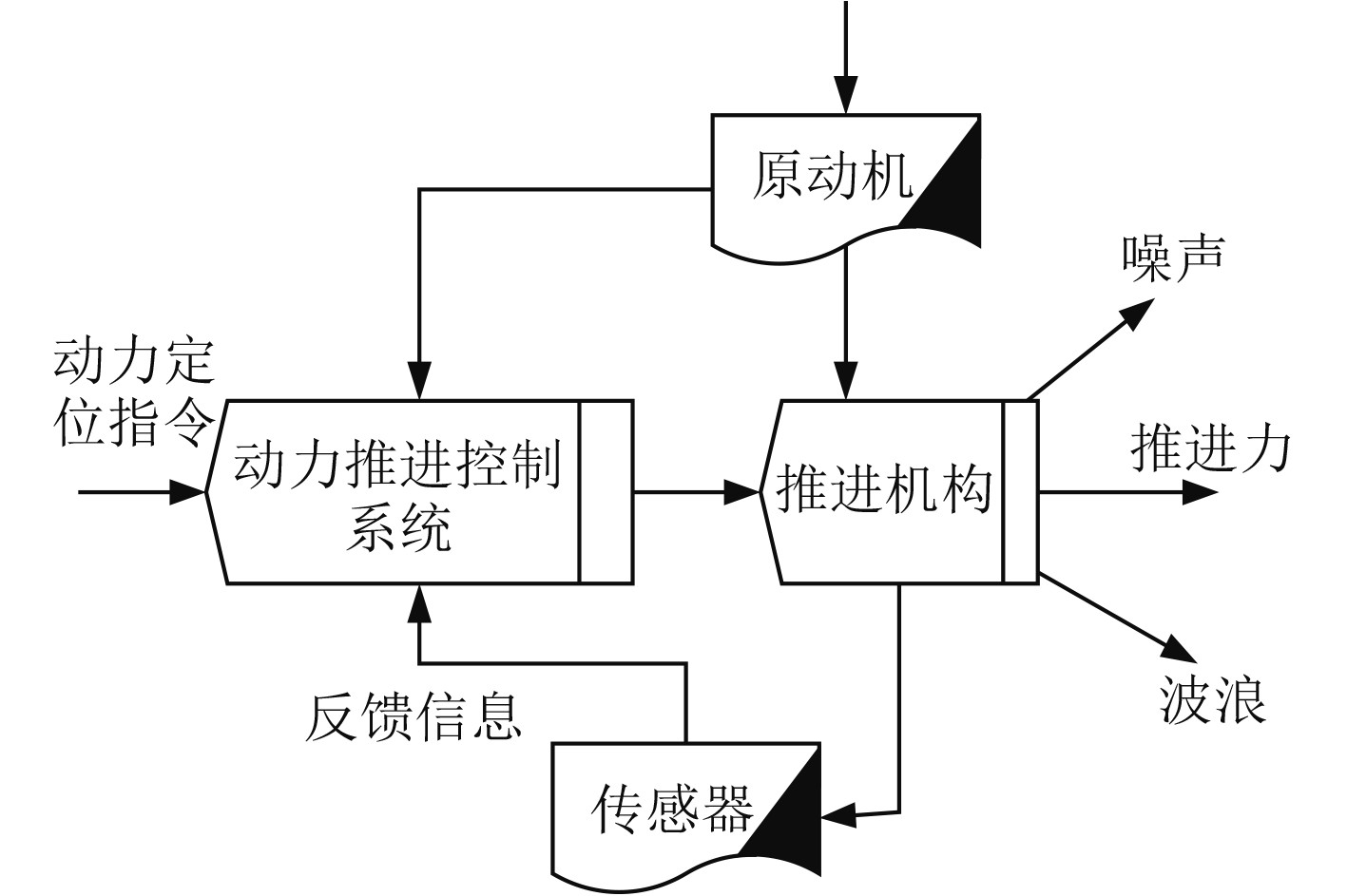
图2为船舶动力定位控制系统的工作原理。

在船舶动力定位控制系统中，传统的控制方法是PID等控制，这些控制方法存在的问题是无法进行系统误差的纠偏，只能将误差信号反馈给控制系统^[4]。不同于传统的控制方法，自抗扰控制器是一种误差观测和补偿的控制方法，可以将导致被控对象偏差的不确定性扰动进行补偿，正是因为自抗扰控制器具有观测和补偿的功能，在系统控制方面具有控制效果好和抗干扰能力强的特点，且自抗扰控制器不需要精确的数学模型。

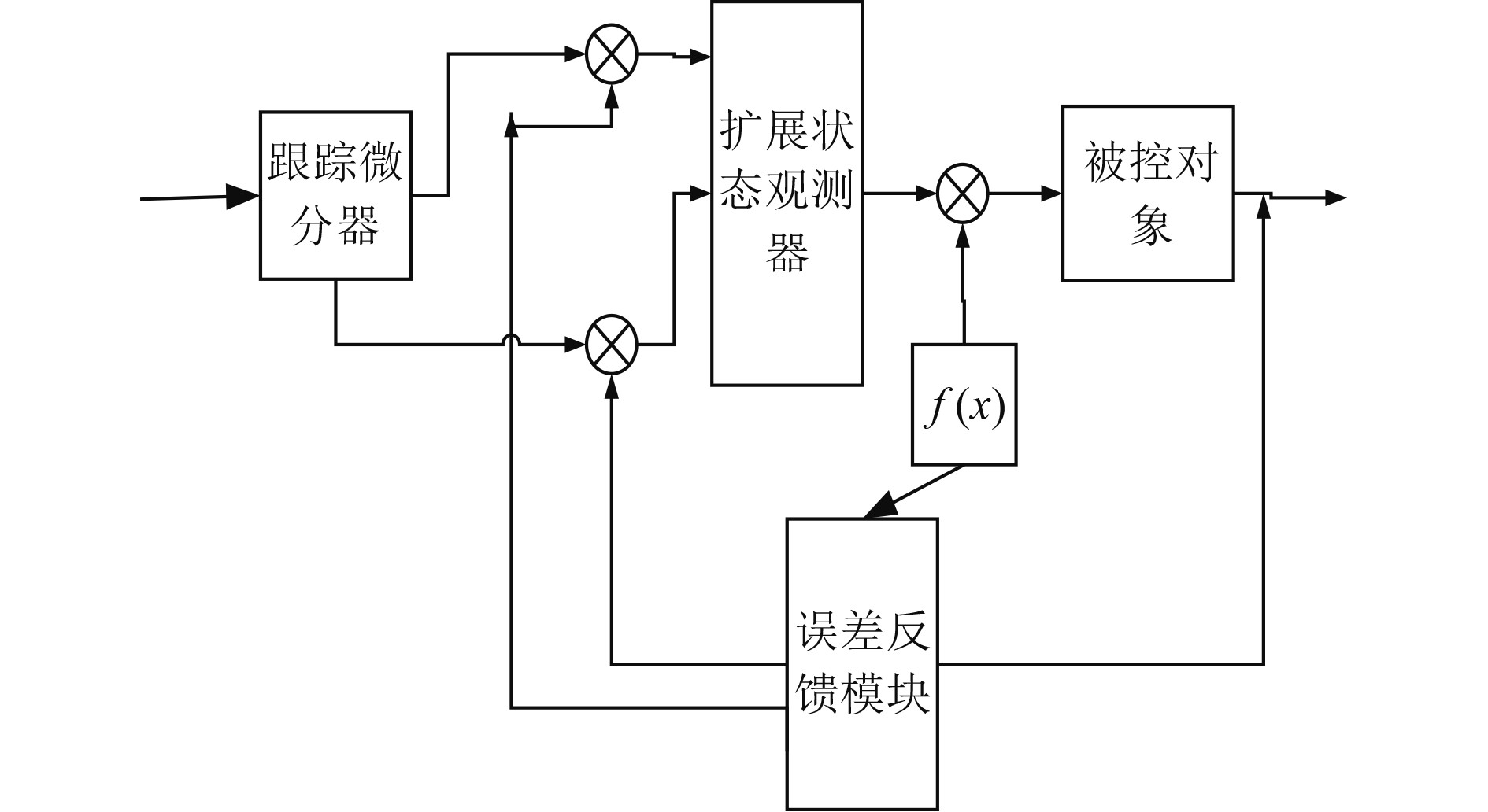
本文针对船舶动力定位的控制系统开发一种自抗扰控制器，该控制器由跟踪微分器、扩展状态观测器、误差反馈模块等组成，原理如图3所示。

1）跟踪微分器

跟踪微分器是自抗扰控制系统的输入调制模块，其功能是进行输入信号的过滤和调制，将调制后的信号发送至扩展状态观测器和系统的其他模块^[5]。

跟踪微分器的数学模型为：

$\left\{ {\begin{array}{*{20}{l}} {{x_1}(k + 1) = {x_1}(k) + h{x_2}(k)}，\\ {{x_2}(k + 1) = {x_2}(k) + h \cdot fh}，\\ {f = K\left( {{x_1}(k) - v(t),{x_2}(k),r,{h_0}} \right)} 。\end{array}} \right.$

式中： $h$ 为跟踪微分器的步长； $r$ 为输入信号的响应； ${h_0}$ 为输入信号的噪声，步长和噪声决定了跟踪微分器的性能， $h$ 越大，跟踪微分器的信号调制处理速度越快。

2）扩展状态观测器

扩展状态观测器接收来自跟踪微分器的信号，并通过扩展状态参数实时反映控制系统的特性。

状态扩展观测器的输入为：

$\begin{gathered} {d_1} = - {u_1}{G_i}\left( s \right) + \theta {Q_i}\left( s \right)p\left( s \right)，\\ {d_2} = - {u_2}q\left( s \right){Q_i}\left( s \right) - {f_d}\left( d \right)。\\ \end{gathered}$

其中： ${d_1}$ ， ${d_2}$ 分别为干扰信号值； ${u_1}$ ， ${u_2}$ 分别为动力定位系统的控制输入信号； $\theta$ 为输出的动力定位航向角。

经过状态观测器的误差补偿后，动力定位系统的输出为：

$\begin{gathered} {\theta _1} = {u_1}\frac{{{G_i}\left( s \right) + \theta {Q_i}\left( s \right)}}{{q\left( s \right){Q_i}\left( s \right)}} - \theta ，\\ {\theta _2} = \frac{{p\left( s \right){u_2} - {f_d}\left( d \right)}}{{{Q_i}\left( s \right)}} + \theta。\\ \end{gathered}$

式中： ${G_i}\left( s \right)$ 为自抗扰控制器的传递函数； ${Q_i}\left( s \right)$ 为跟踪微分器的传递函数； $p\left( s \right)$ 为信号低通滤波传递函数； $q\left( s \right)$ 为信号高通滤波传递函数； ${f_d}\left( d \right)$ 为扰动信号。

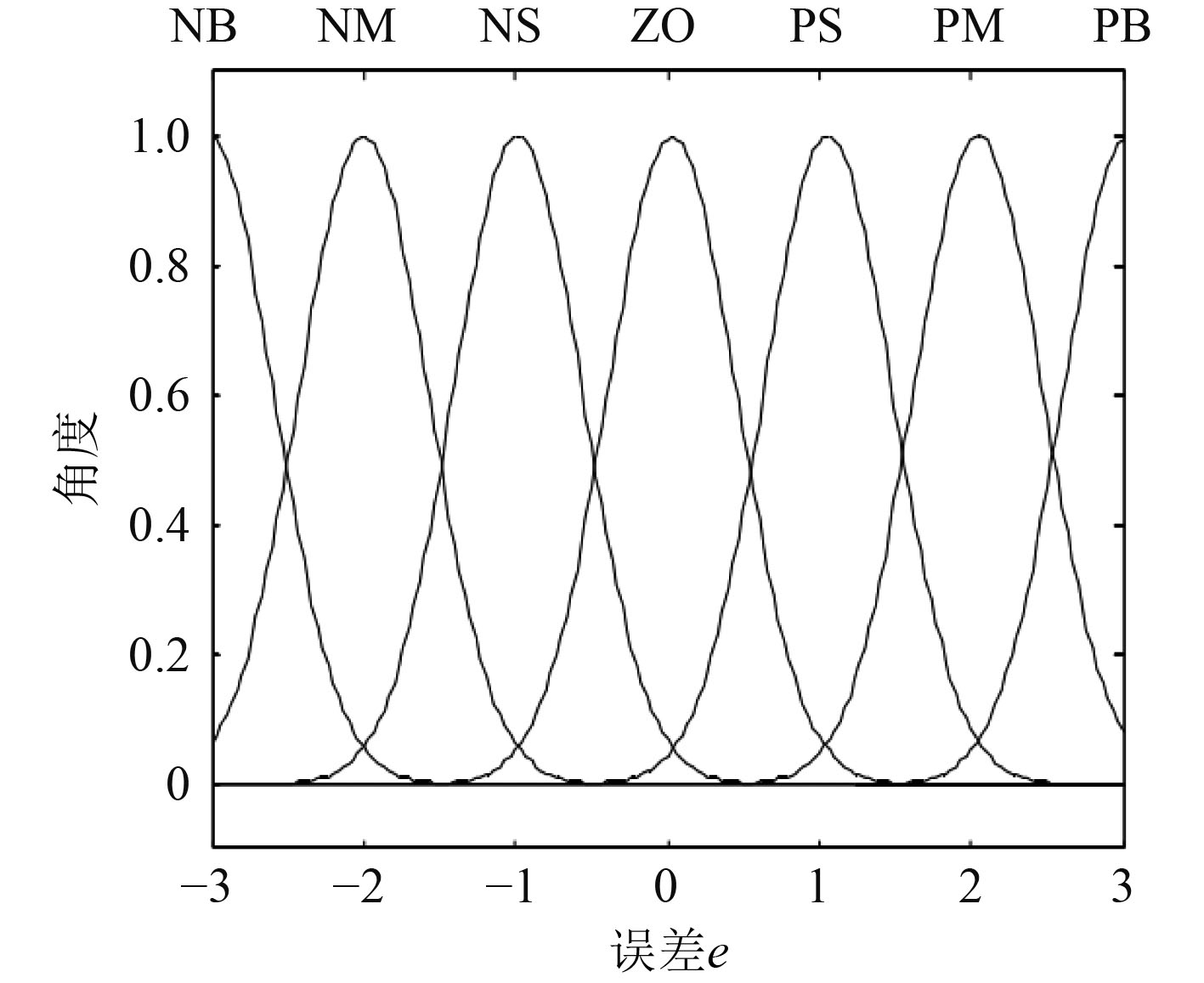
经过扩展状态观测器的补偿后，动力定位系统输出的航向角误差e的隶属度函数曲线如图4所示。

3 基于自抗扰控制器的船舶动力定位系统仿真分析

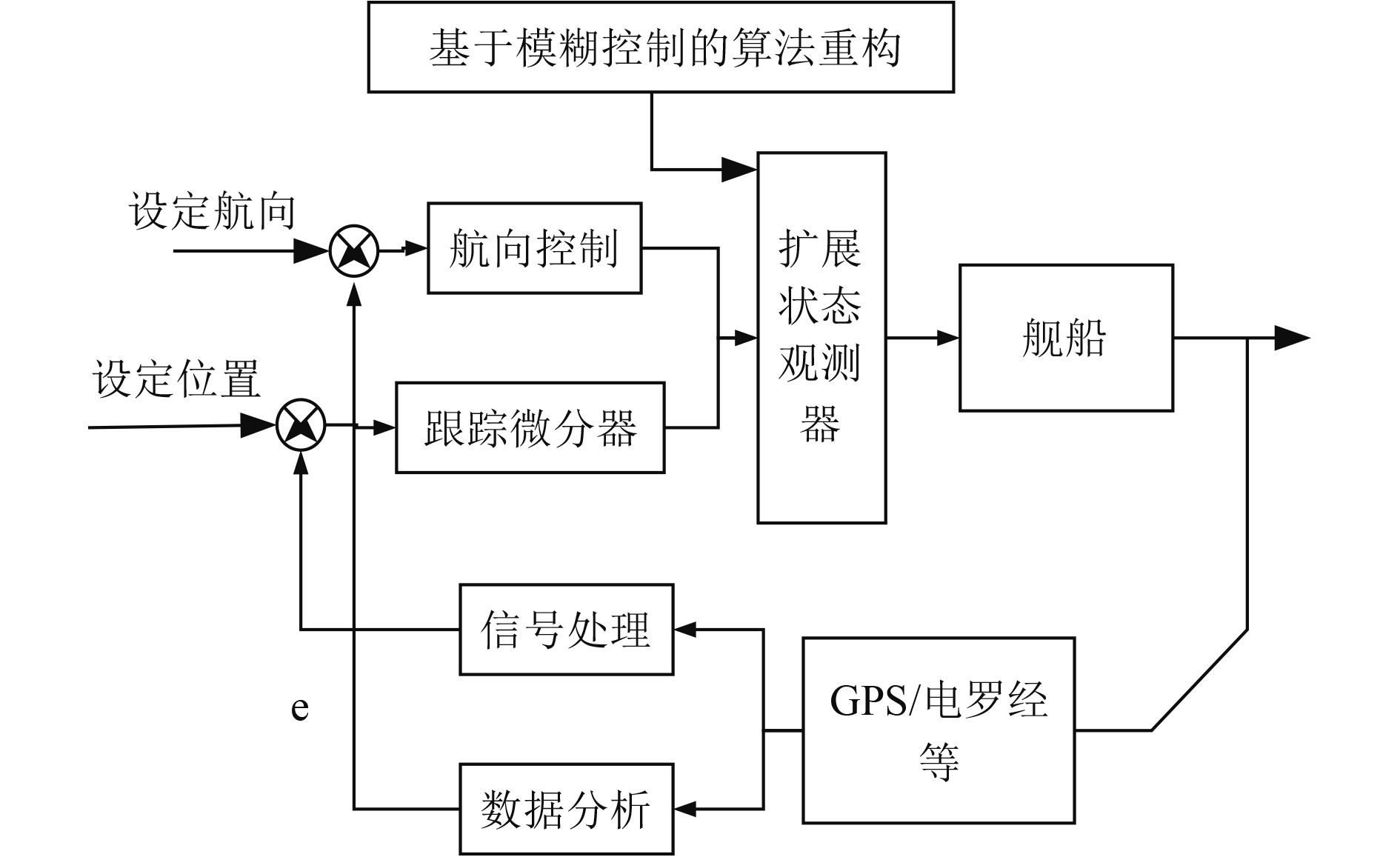
结合模糊算法，基于自抗扰控制器设计一种船舶动力定位控制系统，系统原理图如图5所示。

定义该自抗扰控制系统的控制模型为：

$\begin{array}{*{20}{l}} {\dot \mu = R\left( \psi \right)v}，\\ {M\dot v = - Dv + \tau + w}，\\ {\tau = 0.3 \times \dfrac{{\delta v}}{{\delta t}}}。\end{array}$

式中： $w$ 为动力定位的扰动；v为船舶与波浪的相对速度； $R\left( \psi \right)$ 为航向角函数； $\tau$ 为航向角变化角加速度。

动力定位系统的航向角误差反馈量为：

$\delta {\text{ = }}\eta - {\eta _0} \text{，}$

航向角误差反馈量的时间导数为：

$\frac{\rm d}{{{\rm{d}}t}}\delta {\text{ = }}\dot \eta - {\dot \eta _0} = R\left( \psi \right)v - \frac{{{\rm{d}}{{\dot \eta }_0}}}{{{\rm{d}}t}} 。$

可以得到模糊自抗扰控制器的函数表达式为：

$f\left( t \right) = \frac{{\displaystyle\sum\limits_0^{{n_1}} {\sum\limits_0^{{n_2}} {\left( {\left( {R\left( t \right)v - {\eta _0}} \right)} \right)} } }}{{\displaystyle\sum\limits_0^{{n_1}} {\sum\limits_0^{{n_2}} {\eta \left( t \right)} } }} 。$

其中： ${n_1},{n_2}$ 为自抗扰控制器的控制时间历程^[6]。

基于Simulink软件进行自抗扰船舶动力定位控制的仿真，采用的船舶参数如表1所示。

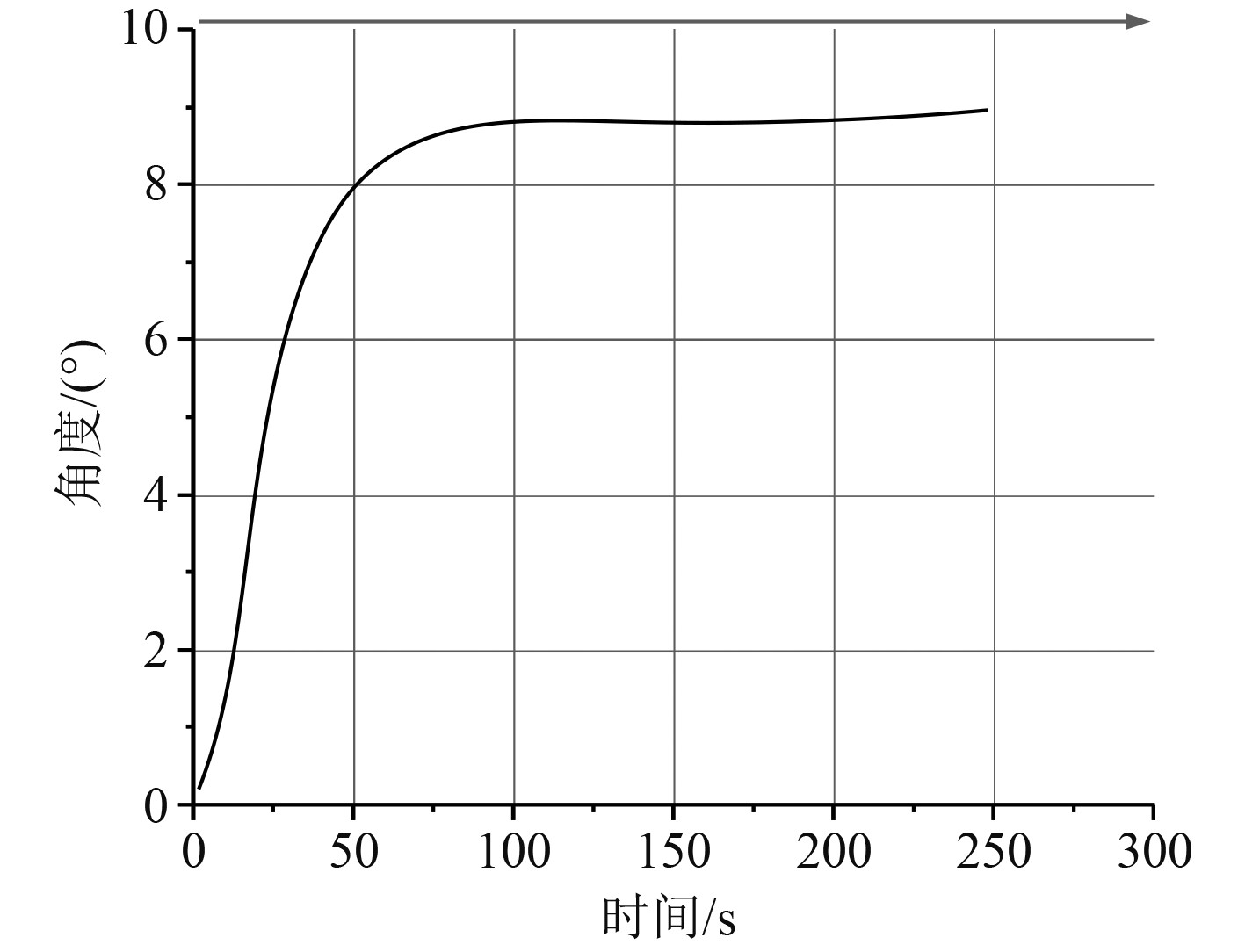
图6为输入信号为9.5°航向角下，Simulink软件仿真得到的船舶动力定位航向角变化曲线。

4 结　语

针对舰船动力定位过程的系统扰动信息，本文建立一种自抗扰船舶动力定位控制系统。通过建立动力定位模型和自抗扰控制器模型，在Simulink中完成了船舶动力定位的航向角控制仿真。仿真结果表明，基于自抗扰控制器的船舶动力定位系统的控制精度高、控制响应快。