压气机叶片是燃气轮机运行过程中完成能量转换的基本单元,也是燃气轮机关键部件中出现故障的最典型部件之一。裂纹是压气机叶片出现故障的常见形式之一,裂纹的存在将会改变叶片的模态特征和振动特性。燃气轮机压气机叶片工作环境恶劣,承受着离心载荷和气动载荷等复杂载荷的影响,特别是高压压气机,随着压比的升高,高压压气机周围气流的温度也不断升高,同时燃烧室通过传热等方式也会导致高压压气机温度升高。在高温的影响下,压气机叶片的材料和力学性能会发生变化,也会对压气机叶片的模态和振动特性产生影响。
压气机叶片可被看作悬臂梁,通过裂纹悬臂梁模型模拟含裂纹的压气机叶片。对于含裂纹梁的模态特征和振动特性,20世纪便有人开始进行了研究,并发展至今[1-9],可见研究含裂纹梁的模态特征和振动特性具有实际的工程意义。分析裂纹深度、裂纹位置、结构阻尼、刚度等因素对梁的模态特征和振动特性的影响,却很少考虑温度的影响[10-12]。然而在实际过程中,空气流过各级叶片时,由于受到压缩,压力和温度会逐级升高,位于后面级的压气机,温度产生的影响很难忽略,尤其是在迫切渴求实时监测和在线诊断的今天。若想在燃气轮机工作过程中得到压气机叶片的状态信息,其所处工况的环境温度应考虑在内。
本文通过含裂纹悬臂梁模型模拟含裂纹的压气机叶片,采用无质量扭转弹簧等效代替裂纹。通过弹性模量引入温度模块,推导出不同温度下含裂纹悬臂梁的模态特征方程,并通过梁的受迫弯曲振动方程,得到温度影响下梁的振动特性曲线。
1 模型建立和模态分析 1.1 含裂纹悬臂梁模型建立如图1(a)所示,建立一段长为L,宽为b,高为h的等截面矩形悬臂梁模拟裂纹叶片,并忽略裂纹尺寸随温度的变化。在该悬臂梁表面有一条深度为a的裂纹,该裂纹距离固定端的距离为R。

|
图 1 含裂纹叶片等效模型 Fig. 1 A equivalent model of cracked compressor blade |
如图1(b)所示,该含裂纹悬臂梁可以等效成由1条无质量扭转弹簧连接的2段无损弹性梁。对于该悬臂梁的弯曲振动,只考虑等效弹簧的刚度
| $ \frac{1}{{{K_{\text{T}}}}} = \frac{{72{\text{π}} L(1 - {\eta ^2})(1 - {\nu ^2})}}{{{E_{\text{T}}}b{h^2}}}\phi ,$ | (1) |
| $\begin{split} \phi =\; & 0.629{{\text{r}}^2} - 1.047{r^3} + 4.602{r^4} - 9.975{r^5} + 20.285{r^6}- \\&32.993{r^7} + 47.041{r^8} - 40.693{r^9} + 19.6{r^{10}} 。\end{split}$ | (2) |
式中:L为悬臂梁的长度,
|
|
表 1 TC11不同温度下的弹性模量 Tab.1 The elastic modulus at different temperature |
图1为各向同性的含裂纹等截面均质悬臂梁,则梁的自由振动微分方程为:
| $ {E}_{T}I\frac{{\partial }^{4}y(x,t)}{\partial {x}^{4}}+\rho A\frac{{\partial }^{2}y(x,t)}{\partial {x}^{2}}=0 。$ | (3) |
式中:ρ为材料密度,
假定有分离变量解存在,令
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}x}} - {k^4}y = 0 。$ | (4) |
其中:
| $ \left\{ {\begin{array}{l}\begin{split} {Y_1} \left( x \right) =& {A_1}{\rm cos}\left( {kx} \right) + {B_1}{\rm sin}\left( {kx} \right) + \\&{C_1}{\rm cos}h\left( {kx} \right) + {D_1}{\rm sin}h\left( {kx} \right) ,\end{split}\\\begin{split} {Y_2}\left( x \right) =& {A_2}{\rm{cos}}\left( {kx} \right) + {B_2}{\rm{sin}}\left( {kx} \right) +\\& {C_2}{\rm{cos}}h\left( {kx} \right) + {D_2}{\rm{sin}}h\left( {kx} \right)。\end{split} \end{array}} \right.$ | (5) |
Y(x)表示位移,A1,B1,C1,D1表示裂纹左侧梁与边界条件有关的未知参数,A2,B2,C2,D2表示裂纹右侧梁与边界条件有关的未知参数。
悬臂梁的边界条件为:
固定端(x=0)的挠度和挠角
| $ {Y_1}(0) = 0 \text{,} \frac{{\partial {Y_1}(x)}}{{\partial x}} = 0 。$ |
自由端(x=l)的弯矩和剪力
| $ \frac{{\partial Y_3^2(x)}}{{\partial {x^2}}} = 0 \text{,} \frac{{\partial Y_2^3(x)}}{{\partial {x^3}}} = 0 。$ |
假设裂纹所在位置为x=R,将裂纹等效成无质量扭转弹簧,因此,裂纹处的连续条件为:
裂纹两侧挠度相等
| $ {Y_1}(x) = {Y_2}(x) 。$ |
裂纹两侧挠角变化关系
| $ \frac{{\partial {Y_1}(x)}}{{\partial x}} + \frac{1}{{{K_{\text{T}}}}}\frac{{\partial {Y_1}(x)}}{{\partial {x^2}}} = \frac{{\partial {Y_2}(x)}}{{\partial x}} ,$ |
裂纹两侧弯矩相等
| $ \frac{{\partial Y_1^2(x)}}{{\partial {x^2}}} = \frac{{\partial Y_2^2(x)}}{{\partial {x^2}}} ,$ |
裂纹两侧剪力相等
| $ \frac{{\partial Y_1^3(x)}}{{\partial {x^3}}} = \frac{{\partial Y_2^3(x)}}{{\partial {x^3}}}。$ | (6) |
式中,KT为扭转弹簧刚度。由梁的自由振动方程解和梁的边界条件及弹簧连续条件,可得:
| $ \det ({\boldsymbol{S}}) = 0 ^{ } 。$ | (7) |
其中,矩阵S表达式为:
| ${\begin{split} S =& \left[ {\begin{array}{*{20}{c}} 1 & 0 & 1 \\ 0 & 1 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 0\\ {\cos (kR)} & {\sin (kR)} & {\cosh (kR)}\\ { - \sin (kR) - k/{K_T}\cos (kR)} & {\cos (kR) - k/{K_T}\sin (kR)} & {\sinh (kR) + k/{K_T}\cosh (kR)} \\ { - \cos (kR)} & { - \sin (kR)} & {\cosh (kR)} \\ {\sin (kR)} & { - \cos (kR)} & {\sinh (kR)} \end{array}} \right. \\ &\left. \begin{array}{*{20}{c}} 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & { - \cos (kl)} & { - \sin (kl)} & {\cosh (kl)} & {\sinh (kl)} \\ 0 & {\sin (kl)} & { - \cos (kl)} & {\sinh (kl)} & {\cosh (kl)} \\ {\sinh (kR)} & { - \cosh (kR)} & { - \sin (kR)} & { - \cosh (kR)} & { - \sinh (kR)} \\ {\cosh (kR) + k/{K_T}\sinh (kR)} & {\sin (kR)} & { - \cosh (kR)} & { - \sinh (kR)} & { - \cosh (kR)} \\ {\sinh (kR)} & {\cos (kR)} & {\sin (kR)} & { - \cosh (kR)} & { - \sinh (kR)} \\ {\cosh (kR)} & { - \sin (kR)} & {\cos (kR)} & { - \sinh (kR)} & { - \cosh (kR)} 。\end{array} \right] 。\end{split}}$ |
根据式(7)可得到k值,进而得到裂纹梁的固有频率ωg,将得到的k值代入到位移方程中,可得到含裂纹梁的模态振型。
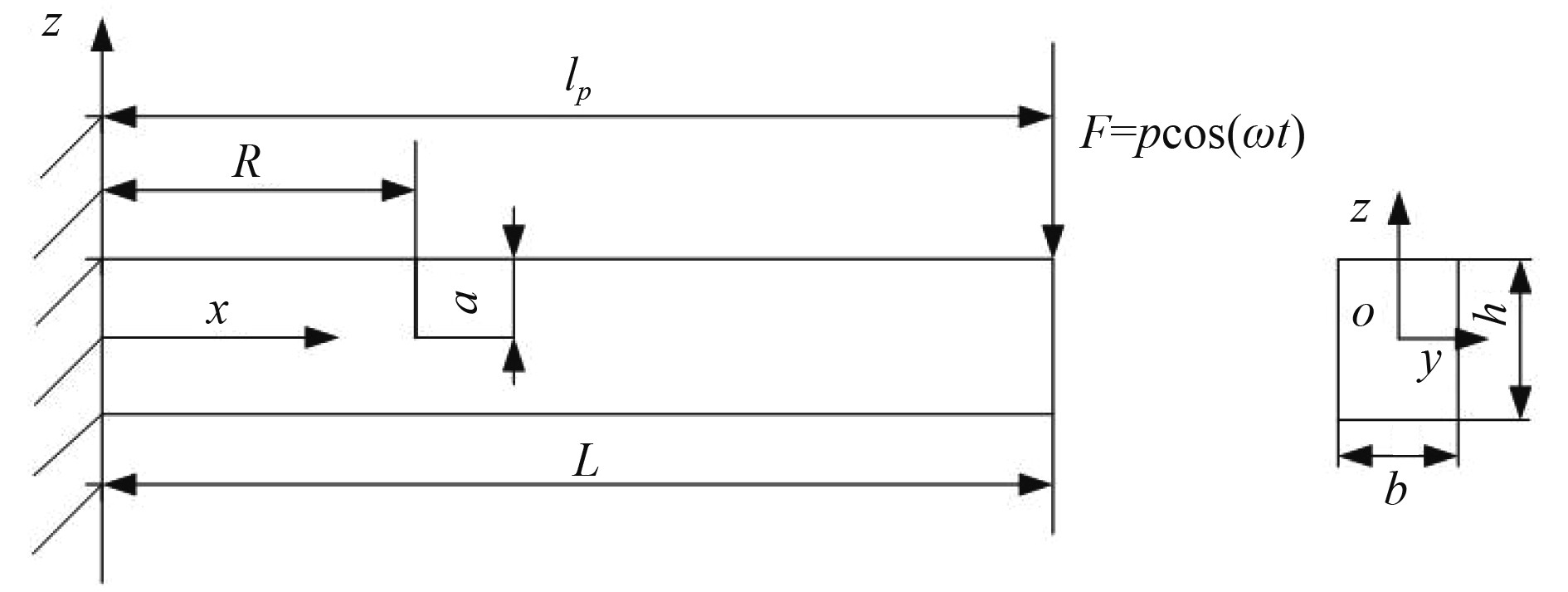
2 振动特性分析 2.1 建立呼吸式裂纹梁弯曲振动方程在图1(a)的基础上,距悬臂梁固定端lp处引入大小为F的余弦激振力,激振频率为ωJ,如图2所示。
|
图 2 含裂纹悬臂梁模型 Fig. 2 The cracked cantilever beam model |
忽略裂纹对悬臂梁振动的影响,横向力激励下梁的受迫弯曲振动方程为[14]:
| $ {E_T}I\frac{{{\partial ^4}y(x,t)}}{{\partial {x^4}}} + c\frac{{\partial y(x,t)}}{{\partial t}}dx + \rho A\frac{{{\partial ^2}y(x,t)}}{{\partial {t^2}}} = p\cos ({\omega _{\text{J}}}t)\delta (x - {l_{\text{p}}})。$ | (8) |
式中:c为阻尼系数,p为横向激励力的幅值,lp为激励力离固支端的距离,ωJ为外激励频率,
利用假设的裂纹梁横向固有振动形式
| $ Y(x) = \left[ {(\sin kx - \sinh kx) + {\alpha _n}(\cos kx - \cosh kx)} \right],$ | (9) |
式中,
将
| $ m^* \frac{\partial^{2} T(t)}{\partial t^{2}}+c^{*} \frac{\partial T(t)}{\partial t}+k^{*} T(t)=F^{*}。$ | (10) |
其中:
| $ {m^*} = \rho A\int_0^L {{Y^2}(x){\text{d}}x} ,$ | (11) |
| $ {c^*} = c\int_0^L {Y{}^2(x){\text{d}}x},$ | (12) |
| $ {k^*} = {E_T}I\int_0^L {\frac{{{\partial ^4}Y(x)}}{{\partial {x^4}}}Y(x){\text{d}}x}。$ | (13) |
| $ {F^*} = \cos (\omega t)\int_0^L {p\delta (x - {l_{\text{p}}})Y(x){\text{d}}x} 。$ | (14) |
式中:m*为广义质量;c*为广义阻尼;k*为无裂纹梁的广义刚度,即无损梁刚度;F*为广义力。其中k*用呼吸式裂纹刚度kbr替代,从而得到呼吸式裂纹梁的弯曲振动方程。
对于呼吸式裂纹刚度kbr,刘文光等[14]提出:
| $ {k_{{{br}}}} = {k_{{o}}} + \frac{{{k^*} - {k_{{o}}}}}{2}(1 + \cos (\omega t)) 。$ | (16) |
其中:
| $ {k_{\text{o}}} = \frac{{{k_{{T}}}{k^*}}}{{{k_{{T}}} + {k^*}}} 。$ | (17) |
式中,ko为张开式裂纹梁模型。当ωt=2nπ (n=1,2,…)时,裂纹完全闭合,此时呼吸梁模型等效为闭合梁模型,即kbr= k*;当ωt= (2n-1)π,(n=1,2,…)时,裂纹完全张开,此时呼吸梁模型等效为张开梁模型,即kbr=ko。
将式(10)的k*用式(16)中的呼吸式裂纹刚度kbr替代,从而得到呼吸式裂纹梁的弯曲振动方程:
| $ {m^*}\frac{{{\partial ^2}T(t)}}{{\partial {t^2}}} + {c^*}\frac{{\partial T(t)}}{{\partial t}} + {k_{{{br}}}}T(t) = {F^*} 。$ | (18) |
由式(13)可知,悬臂梁的广义刚度与弹性模量具有一定的关系,因此可知呼吸式裂纹刚度与弹性模量也具有关系。温度的变化通过对弹性模量的影响,导致呼吸式裂纹刚度发生变化,进而会对梁的振动位移响应造成影响。通过对梁的振动位移及其他振动特性与温度的变化之间的规律进行分析,得出相关结论。
3 结果与讨论以图1所示悬臂梁为例模拟含裂纹叶片,假设叶片的几何尺寸为:长度L= 0.09 m,宽度b= 0.055 m,高度h= 0.006 m;材料参数为:密度ρ= 4480 kg.m−3,泊松比v = 0.33,阻尼比ξ= 0.05,弹性模量ET随温度发生变化。
3.1 环境温度对裂纹梁模态特征的影响结合假设的含裂纹叶片的几何尺寸,取裂纹的相对位置为R/L= 1/9,相对深度为a/h∈

|
图 3 固有频率对环境温度变化曲线 Fig. 3 The natural frequency vs. ambient temperature |
可以看出,在悬臂梁裂纹位置和深度一定的情况下,当环境温度不断增大时,悬臂梁的固有频率不断减少。通过比较,可知悬臂梁在环境温度为600℃下的固有频率比在20℃下的降低70 Hz左右,大约为悬臂梁固有频率的12%左右。由此可见,环境温度对悬臂梁固有频率具有一定的影响。而当温度不变的情况下,梁的相对裂纹深度越大,固有频率越低。同时也可以看出,当梁的相对裂纹位置不变的情况下,环境温度对梁的一阶固有频率的影响明显比相对裂纹深度大。
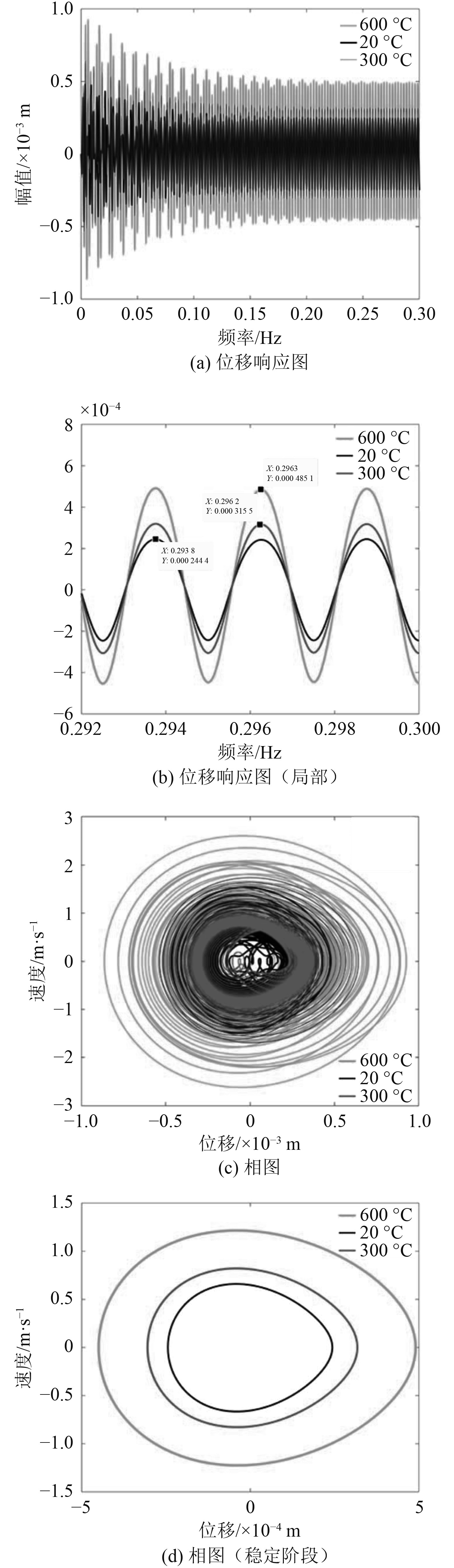
3.2 环境温度对裂纹梁振动特性的影响在假设的含裂纹叶片几何尺寸以及材料参数基础上,裂纹位置R= 0.01 m,裂纹深度为a= 0.000 5 m,引入外部简谐激振力F=pcos(ωt),其中激振力幅值为100 N,环境温度的变化为T∈{20℃ 300℃ 600℃} ,使梁分别在400 Hz、固有频率及4000 Hz下振动,通过数值计算得到环境温度与含裂纹梁的振动特性之间的关系如图4~图6所示。
|
图 4 400 Hz频率下振动特性图 Fig. 4 The vibration performance with 400 Hz frequency |
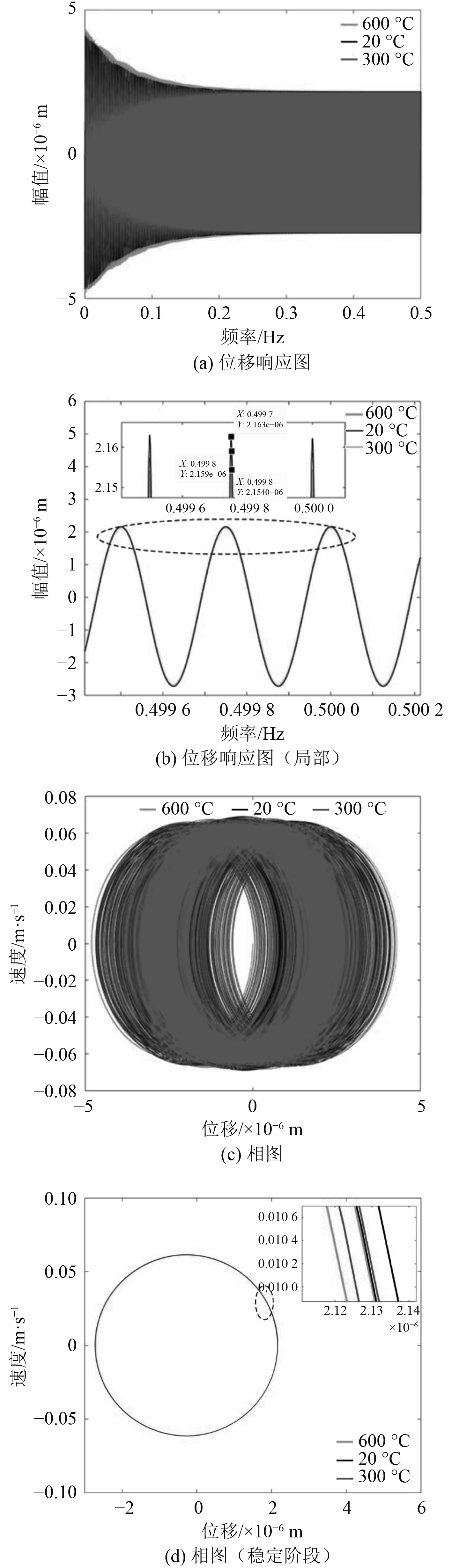
|
图 6 4000 Hz下振动特性图 Fig. 6 The vibration performance with 4000 Hz frequency |
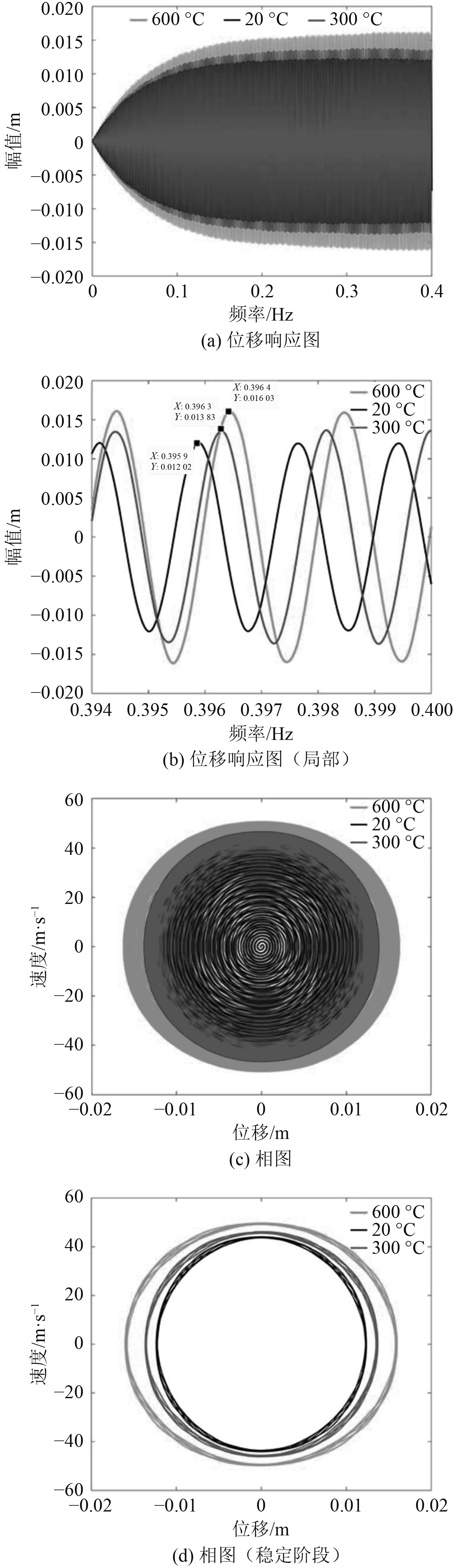
由图4和图5中的位移响应图可以看出,在选取的低频和固有频率作用下,温度越高,梁的振动幅值越大。这是因为随着温度的升高,梁的刚度和阻尼会出现减小的情况,在相同激振力幅值的影响下,刚度和阻尼越小,梁的位移响应越大。从图4和图5的相图也可以看到相关现象,反映出选取的呼吸式裂纹刚度所作用的效果。同时,从图5(b)可以看到在共振情况下阻尼产生明显的响应滞后效应。
|
图 5 固有频率下振动特性图 Fig. 5 The vibration performance with natural frequency |
在选取的高频作用下,为温度越高,梁的振动幅值越大,与低频作用下的现象不同,如图6所示。随着温度的升高,梁的刚度和阻尼减小,梁的位移响应增大。在相同阶数弯曲频率下,随着温度的升高,梁的固有频率下降,且下降幅度较大。在每一阶频率附近都存在一个幅值峰,各阶频率构成了连续的幅值峰。当梁处于300℃和600℃时,4000 Hz可能位于该温度下某一高阶幅值峰的中段,而位于20℃下某一高阶与临近低阶间的谷底。
4 结 语本文通过含裂纹悬臂梁模拟含裂纹压气机叶片,选取无质量扭转弹簧模拟裂纹,并引入呼吸式裂纹刚度模拟裂纹振动过程中的呼吸效应。通过弹性模量引入温度模块,研究环境温度对含裂纹压气机叶片的一阶固有频率和振动响应之间的关系,得出以下结论:
1)环境温度对梁的一阶固有频率具有一定的影响,随着环境温度的升高,梁的一阶固有频率下降,而且下降的幅度较裂纹深度带来的影响更大。
2)在低频及固有频率激振力作用下,随着环境温度的升高,梁的位移响应越大,但在高频激振力作用下,出现了不同的现象。这是所选激振频率处于不同温度下各阶频率的距离远近导致的。
由此可见,环境温度对叶片的模态特征和振动特性具有一定影响。若想在实际工作过程中实现实时监测和在线诊断,应选取合适的工作频率,需要后续进行研究得到。
| [1] |
OSTACHOWICZ W M, KRAWCZUK M. Analysis of the effect of crack on the natural frequencies of a cantilever beam[J]. Journal of Sound and Vibration, 1991, 150(2): 191-201. DOI:10.1016/0022-460X(91)90615-Q |
| [2] |
王术新, 姜哲. 裂缝悬臂梁的振动特性及其裂缝参数识别[J]. 振动与冲击, 2003, 22(3): 83-85. DOI:10.3969/j.issn.1000-3835.2003.03.025 |
| [3] |
QIAN G L, GU S. N, JIANG J. S, The dynamic behavior and crack detection of a beam with a crack[J]. Journal of Sound and Vibration, 1990, 138(2): 233-243.
|
| [4] |
董广明, 陈进, 邹剑. 裂纹转子的振动特性与裂纹参数识别[J]. 上海交通大学学报, 2004, 38(6): 857-861. |
| [5] |
CHEN L H, DUAN J W, SUN Y, et al. The study of the vibration characteristics of the cantilever beam with a surface C[J]. Applied Mechanics and Materials, 2013(394): 121-127. |
| [6] |
杨海燕, 杨秉玉, 刘启州. 疲劳裂纹叶片振动的非线性特性研究[J]. 西北工业大学学报, 1999, 17(2): 198-204. |
| [7] |
胡家顺, 冯新, 周晶. 呼吸裂纹梁非线性动力特性研究[J]. 振动与冲击, 2009, 28(1): 76-80,87. |
| [8] |
刘文光, 陈国平. 含裂纹悬臂梁的振动与疲劳耦合分析[J]. 振动与冲击, 2011, 30(5): 140-144. |
| [9] |
XIE J, ZI Y, ZHANG M, et al. A novel vibration modeling method for a rotating blade with breathing cracks[J]. Science China: Technology Sciences, 2019, 62(2): 333-348. |
| [10] |
马一江, 陈国平. 不同温度下裂纹悬臂梁的模态和疲劳寿命分析[J]. 振动与冲击, 2017, 36(8): 132-137+163. |
| [11] |
孙强, 张忠平, 柴桥,等. 航空发动机压气机叶片振动频率与温度的关系[J]. 应用力学学报, 2004, 21(4): 137-139. |
| [12] |
王振清, 刘兵, 韩玉来. 高温下含裂纹铝合金梁自由振动频率分析[J]. 哈尔滨工程大学学报, 2012, 33(3): 320-324. DOI:10.3969/j.issn.1006-7043.201103012 |
| [13] |
中国标准出版社. 中国航空材料手册——钛合金、铜合金[M]. 2001, 2 (3).
|
| [14] |
刘文光, 陈国平. 呼吸式裂纹梁的振动疲劳裂纹扩展耦合分析[J]. 中国机械工程, 2010, 21(23): 2798-2802. |
| [15] |
辛格雷苏. S. 拉奥. 机械振动[M]. 李欣业, 杨理诚译. 北京: 清华大学出版社, 2016.
|
 2023, Vol. 45
2023, Vol. 45
