振动噪声问题不仅关系到船舶的舒适性,也关系到船舶的声目标特征。动力装置是船舶最主要的振动激励源和噪声源,而这其中进排气系统的噪声会沿管路传播,影响舷外的噪声等级,产生很大整体声目标特征。
船上的管路形式多样,包括圆管、方管,直管、弯管以及直角弯管、圆角弯管。由于船舶进排气管路长度长、分布广且形式复杂的特点,一直以来对船上管路噪声的控制都是一个难点。在以往的研究中,动力装置的进排气系统噪声预测多集中在进排气出口管口声辐射,鲜有研究关注管道壁面本身的声辐射问题。
但是对于大型船舶的主动力进气管道,管壁声辐射问题不容忽视。主要原因如下:1)大型船舶若主动力采用舷外进气而非舱内进气的形式,则必然采用较长的进气管道穿过上层建筑,这导致管壁辐射源离舱室空间距离近,容易造成较大的舱室噪声。2)进气管路尺寸大(最大可达2 m以上),且进气管路截面为矩形截面,结构的等效刚度小,容易被管内噪声激励而引管壁结构振动。而管壁的结构振动会引起二次声辐射,进而在与进气管道相连的舱室内引起噪声。3)从热绝缘的角度考虑,排气管路外包覆有多孔隔热材料,能起到一部分隔声作用。而进气管路外部一般是裸露的,更容易辐射噪声。
管道会在噪声的激励作用下发生受迫振动,管内噪声通过与管壁的声振耦合作用辐射到环境中,这一过程被称为“breakout”,Webb[1]对这一过程进行了描述。
国内外学者对于管道声辐射机制进行了大量研究,并提出了有效的计算方法。Cremer[2]和 Heckl [3]研究了通过圆形截面管道壁的高频传递损失。Brown等[4]和Kuhn 等[5]研究了通过圆形管道壁的低频传递损失。
Allen[6]引用的1个非常简单的公式计算管道声辐射,但该方法只在高频下取得比较可靠的结果,无法用于低频管道噪声的预测。Cummings[7-8]针对低频范围内矩形管道声辐射的管壁传递损失计算问题提出了wave solution的计算方法,并且和实验结果吻合良好。在更高频率范围内,Guthrie[9]和Cummings[10]等学者通过实验和解析等方法均观察到,当管道内存在高阶模态的声传播时,管壁的传递损失曲线呈现以斜率为
本文以某船燃气轮机进气管路为研究对象,首先使用wave solution计算方法研究一段简单燃机进气管道的声辐射特征,在此基础上给出能维持舱室噪声不超标的最小壁面厚度。其次考虑壁面耦合和腔室负载的作用,利用商业有限元软件计算燃机进气管口声辐射和临近舱室声辐射的响应。最后,基于计算结果给出控制舱室噪声的建议措施。
1 简单管道声辐射解析估算在管道设计中,通过管壁辐射到环境中的噪声程度可根据下式计算:
| $ {L}_{w,out}={L}_{w,in}+10\mathrm{log}\left(\frac{S}{A}\right)-T{L}_{out} 。$ |
式中:
对于矩形截面管道,有
因此,对于矩形管道的传递损失计算采用wave solution方法,通过建立管道内噪声以平面波形式传播情况下管壁与噪声的声振耦合模型,计算得到管壁的传递损失。在更高频率范围内,根据低频范围的计算结果,以3 dB/octave的斜率向高频方向拓展,估算管壁的传递损失。
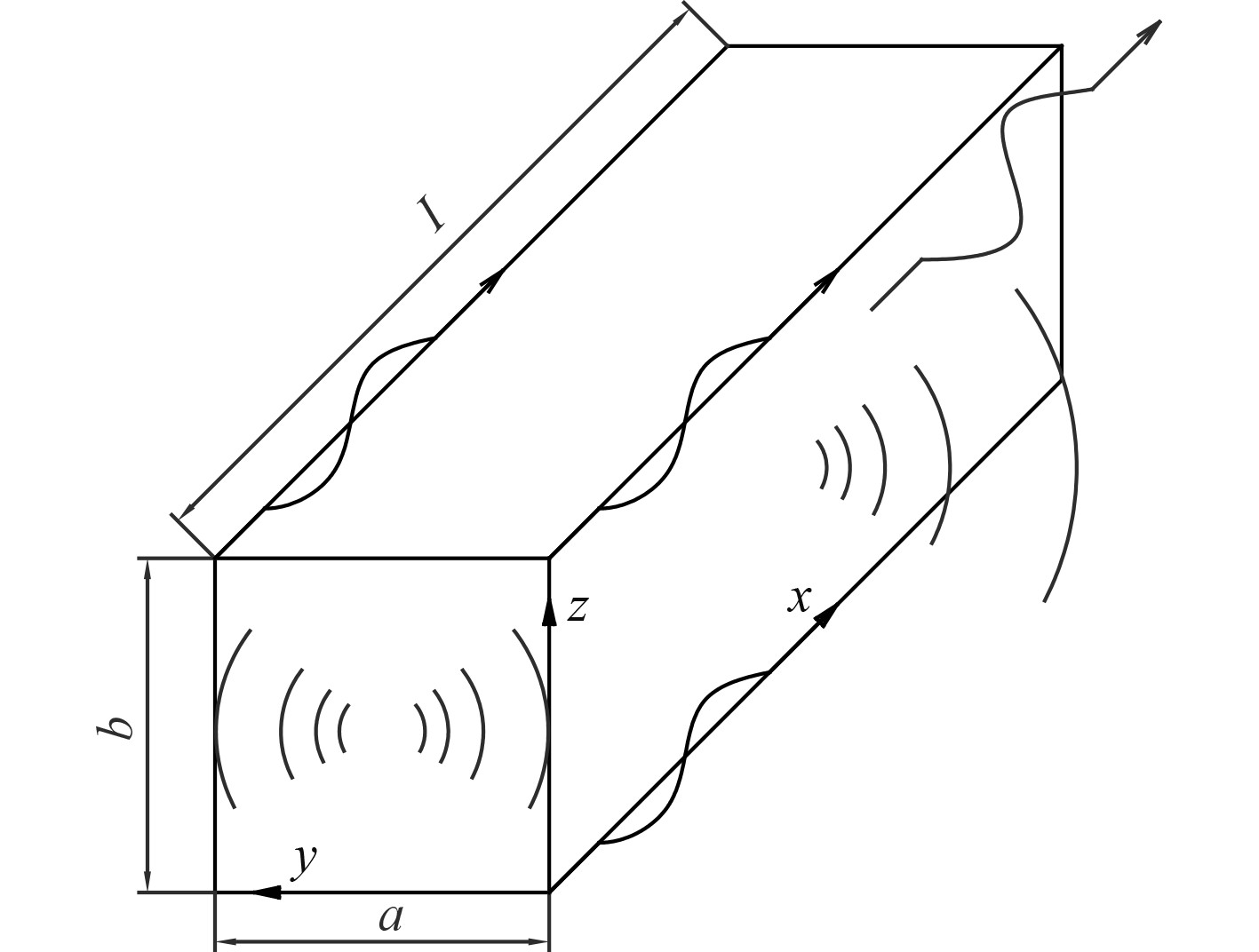
|
图 1 wave solution方法计算模型 Fig. 1 wave solution method calculation model |
令管内气体介质密度为c,入射激励频率为f,则管内波数为:
| $ {k}_{i}=\frac{2{\text{π}} f}{c},$ |
| $ K=\frac{12(1-{\sigma }^{2})}{E{h}^{3}},$ |
| $ {\gamma }^{4}={\omega }^{2}mK 。$ |
由于
| $ {\alpha }_{1}=\sqrt{{\gamma }^{2}-{k}_{x}^{2}},$ |
| $ {\alpha }_{2}=\sqrt{{\gamma }^{2}+{k}_{x}^{2}}。$ |
令与xy平面平行的管壁在z方向上的振动:
| $\begin{split} D\left(x,y\right)=&\Biggr[{A}_{1}\mathrm{cos}\left({\alpha }_{1}y\right)+{A}_{2}\mathrm{sin}\left({\alpha }_{1}y\right)+{A}_{3}\mathrm{cosh}\left({\alpha }_{2}y\right)+\\ &{A}_{4}\mathrm{sinh}\left({\alpha }_{2}y\right)+\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}}\Biggr]{e}^{-i{k}_{x}x}。\end{split} $ |
与xz平面平行的管壁在y方向上的振动:
| $\begin{split} D\left(x,z\right)=&\Biggr[{B}_{1}\mathrm{cos}\left({\alpha }_{1}z\right)+{B}_{2}\mathrm{sin}\left({\alpha }_{1}z\right)+{B}_{3}\mathrm{cosh}\left({\alpha }_{2}z\right)+\\ &{B}_{4}\mathrm{sinh}\left({\alpha }_{2}z\right)+\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}}\Biggr]{e}^{-i{k}_{x}x} ,\end{split}$ |
| $\begin{split} Y\left(y\right)=&{A}_{1}\mathrm{cos}\left({\alpha }_{1}y\right)+{A}_{2}\mathrm{sin}\left({\alpha }_{1}y\right)+{A}_{3}\mathrm{cosh}\left({\alpha }_{2}y\right)+\\ &{A}_{4}\mathrm{sinh}\left({\alpha }_{2}y\right)+\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}} ,\end{split}$ |
| $ \begin{split}Z\left(z\right)=&B_{1}\mathrm{cos}\left({\alpha }_{1}z\right)+{B}_{2}\mathrm{sin}\left({\alpha }_{1}z\right)+{B}_{3}\mathrm{cosh}\left({\alpha }_{2}z\right)+\\ &{B}_{4}\mathrm{sinh}\left({\alpha }_{2}z\right)+\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}},\end{split} $ |
| $ \begin{split} {Y}'\left(y\right)=&{-A}_{1}{\alpha }_{1}\mathrm{sin}\left({\alpha }_{1}y\right)+{A}_{2}{\mathrm{\alpha }}_{1}\mathrm{cos}\left({\alpha }_{1}y\right)+\\ &{A}_{3}{\alpha }_{2}\mathrm{sinh}\left({\alpha }_{2}y\right)+{A}_{4}{\mathrm{\alpha }}_{2}\mathrm{cossh}\left({\alpha }_{2}y\right) ,\end{split} $ |
| $\begin{split} {Z}'\left(y\right)=&{-B}_{1}{\alpha }_{1}\mathrm{sin}\left({\alpha }_{1}z\right)+{B}_{2}{\mathrm{\alpha }}_{1}\mathrm{cos}\left({\alpha }_{1}z\right)+\\ &{B}_{3}{\alpha }_{2}\mathrm{sinh}\left({\alpha }_{2}z\right)+{B}_{4}{\mathrm{\alpha }}_{2}\mathrm{cossh}\left({\alpha }_{2}z\right),\end{split} $ |
| $ {M}_{y}\left(x,y\right)=-\frac{1}{K}\left(\frac{{\partial }^{2}}{\partial {y}^{2}}+\frac{{\partial }^{2}}{\partial {x}^{2}}\right)D(x,y),$ |
| $\begin{split} {M}_{y}\left(x,y\right)=&-\frac{1}{K}\Biggr\{{-A}_{1}{\mathrm{\alpha }}_{1}^{2}\mathrm{cos}\left({\alpha }_{1}y\right)-{A}_{2}{\mathrm{\alpha }}_{1}^{2}\mathrm{sin}\left({\alpha }_{1}y\right)+\\ &{A}_{3}{\mathrm{\alpha }}_{2}^{2}\mathrm{cosh}\left({\alpha }_{2}y\right)+{A}_{4}{\mathrm{\alpha }}_{2}^{2}\mathrm{sinh}\left({\alpha }_{2}y\right)+\\ &{k}_{x}^{2}\Biggr[{A}_{1}\mathrm{cos}\left({\alpha }_{1}y\right)+{A}_{2}\mathrm{sin}\left({\alpha }_{1}y\right)+{A}_{3}\mathrm{cosh}\left({\alpha }_{2}y\right)+\\ &{A}_{4}\mathrm{sinh}\left({\alpha }_{2}y\right)+\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}}\Biggr]\Biggr\}{e}^{-i{k}_{x}x},\end{split} $ |
| $\begin{split} {M}_{z}\left(x,z\right)=&-\frac{1}{K}\Biggr\{{-B}_{1}{\mathrm{\alpha }}_{1}^{2}\mathrm{cos}\left({\alpha }_{1}z\right)-{B}_{2}{\mathrm{\alpha }}_{1}^{2}\mathrm{sin}\left({\alpha }_{1}z\right)+\\ &{B}_{3}{\mathrm{\alpha }}_{2}^{2}\mathrm{cosh}\left({\alpha }_{2}z\right)+{B}_{4}{\mathrm{\alpha }}_{2}^{2}\mathrm{sinh}\left({\alpha }_{2}z\right)+\\ &{k}_{x}^{2}[{B}_{1}\mathrm{cos}\left({\alpha }_{1}z\right)+{B}_{2}\mathrm{sin}\left({\alpha }_{1}z\right)+{B}_{3}\mathrm{cosh}\left({\alpha }_{2}z\right)+\\ &{B}_{4}\mathrm{sinh}\left({\alpha }_{2}z\right)+\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}}]\Biggr\}{e}^{-i{k}_{x}x}。\end{split} $ |
管壁的受迫振动满足边界条件,如下式:
| $ \left\{\begin{array}{l}Y\left(0\right)=0,Y\left(0\right)=0,Y\left(0\right)=0,Y\left(0\right)=0,\\ {Y}'\left(0\right)={Z}'\left(0\right),{M}_{y}\left(0\right)={M}_{z}\left(0\right),\\ {Y}'\left(\dfrac{a}{2}\right)=0,{Z}'\left(\dfrac{b}{2}\right)=0。\end{array}\right. $ |
| $ Y\left(0\right)=0,$ |
| $\begin{split} {A}_{1}\mathrm{cos}\left({\alpha }_{1}0\right)+&{A}_{2}\mathrm{sin}\left({\alpha }_{1}0\right)+{A}_{3}\mathrm{cosh}\left({\alpha }_{2}0\right)+\\ &{A}_{4}\mathrm{sinh}\left({\alpha }_{2}0\right)=-\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}}。\end{split} $ |
| $ Y\left(a\right)=0 ,$ |
| $ \begin{split}{A}_{1}\mathrm{cos}\left({\alpha }_{1}a\right)+&{A}_{2}\mathrm{sin}\left({\alpha }_{1}a\right)+{A}_{3}\mathrm{cosh}\left({\alpha }_{2}a\right)+\\ &{A}_{4}\mathrm{sinh}\left({\alpha }_{2}a\right)=-\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}} 。\end{split}$ |
| $ Z\left(0\right)=0 ,$ |
| $\begin{split} {B}_{1}\mathrm{cos}\left({\alpha }_{1}0\right)+&{B}_{2}\mathrm{sin}\left({\alpha }_{1}0\right)+{B}_{3}\mathrm{cosh}\left({\alpha }_{2}0\right)+\\ &{B}_{4}\mathrm{sinh}\left({\alpha }_{2}0\right)=-\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}}。\end{split} $ |
| $ Z\left(b\right)=0 ,$ |
| $\begin{split} {B}_{1}\mathrm{cos}\left({\alpha }_{1}b\right)+&{B}_{2}\mathrm{sin}\left({\alpha }_{1}b\right)+{B}_{3}\mathrm{cosh}\left({\alpha }_{2}b\right)+\\ &{B}_{4}\mathrm{sinh}\left({\alpha }_{2}b\right)=-\frac{K{P}_{0}}{{k}_{x}^{4}-{\gamma }^{4}} 。\end{split}$ |
| $ {Y}'\left(0\right)={-Z}'\left(0\right)or{Y}'\left(0\right)+{Z}'\left(0\right)=0 ,$ |
| $ \begin{split}{-A}_{1}{\alpha }_{1}\mathrm{sin}\left({\alpha }_{1}0\right)+&{A}_{2}{\mathrm{\alpha }}_{1}\mathrm{cos}\left({\alpha }_{1}0\right)+{A}_{3}{\alpha }_{2}\mathrm{sinh}\left({\alpha }_{2}0\right)+\\ &{A}_{4}{\mathrm{\alpha }}_{2}\mathrm{cossh}\left({\alpha }_{2}0\right){-B}_{1}{\alpha }_{1}\mathrm{sin}\left({\alpha }_{1}0\right)+\\ &{B}_{2}{\mathrm{\alpha }}_{1}\mathrm{cos}\left({\alpha }_{1}0\right)+{B}_{3}{\alpha }_{2}\mathrm{sinh}\left({\alpha }_{2}0\right)+\\ &{B}_{4}{\mathrm{\alpha }}_{2}\mathrm{cossh}\left({\alpha }_{2}0\right)=0 ,\end{split}$ |
| $ {Y}'\left(\frac{a}{2}\right)=0,$ |
| $\begin{split} &{-A}_{1}{\alpha }_{1}\mathrm{sin}\left(\frac{{\alpha }_{1}a}{2}\right)+{A}_{2}{\mathrm{\alpha }}_{1}\mathrm{cos}\left(\frac{{\alpha }_{1}a}{2}\right)+\\ &{A}_{3}{\alpha }_{2}\mathrm{sinh}\left(\frac{{\alpha }_{2}a}{2}\right)+{A}_{4}{\mathrm{\alpha }}_{2}\mathrm{cossh}\left(\frac{{\alpha }_{2}a}{2}\right)=0\end{split} ,$ |
| $ {Z}'\left(\frac{b}{2}\right)=0 ,$ |
| $ \begin{split}&{-B}_{1}{\alpha }_{1}\mathrm{sin}\left(\frac{{\alpha }_{1}b}{2}\right)+{B}_{2}{\mathrm{\alpha }}_{1}\mathrm{cos}\left(\frac{{\alpha }_{1}b}{2}\right)+\\ &{B}_{3}{\alpha }_{2}\mathrm{sinh}\left(\frac{{\alpha }_{2}b}{2}\right)+{B}_{4}{\mathrm{\alpha }}_{2}\mathrm{cossh}\left(\frac{{\alpha }_{2}b}{2}\right)=0,\end{split} $ |
| $ {M}_{y}\left(0\right)={M}_{x}\left(0\right),$ |
| $\begin{split} -&A_{1}{\mathrm{\alpha }}_{1}^{2}\mathrm{cos}\left({\alpha }_{1}0\right)-{A}_{2}{\mathrm{\alpha }}_{1}^{2}\mathrm{sin}\left({\alpha }_{1}0\right)+{A}_{3}{\mathrm{\alpha }}_{2}^{2}\mathrm{cosh}\left({\alpha }_{2}0\right)+\\ &{A}_{4}{\mathrm{\alpha }}_{2}^{2}\mathrm{sinh}\left({\alpha }_{2}0\right)+{k}_{x}^{2}[{A}_{1}\mathrm{cos}\left({\alpha }_{1}0\right)+{A}_{2}\mathrm{sin}\left({\alpha }_{1}0\right)+\\ &{A}_{3}\mathrm{cosh}\left({\alpha }_{2}0\right)+{A}_{4}\mathrm{sinh}\left({\alpha }_{2}0\right)]={-B}_{1}{\mathrm{\alpha }}_{1}^{2}\mathrm{cos}\left({\alpha }_{1}0\right)-\\ &{B}_{2}{\mathrm{\alpha }}_{1}^{2}\mathrm{sin}\left({\alpha }_{1}0\right)+{B}_{3}{\mathrm{\alpha }}_{2}^{2}\mathrm{cosh}\left({\alpha }_{2}0\right)+\\ &{B}_{4}{\mathrm{\alpha }}_{2}^{2}\mathrm{sinh}\left({\alpha }_{2}0\right)+{k}_{x}^{2}[{B}_{1}\mathrm{cos}\left({\alpha }_{1}0\right)+\\ &{B}_{2}\mathrm{sin}\left({\alpha }_{1}0\right)+{B}_{3}\mathrm{cosh}\left({\alpha }_{2}0\right)+{B}_{4}\mathrm{sinh}\left({\alpha }_{2}0\right)] 。\end{split}$ |
式中:令
计算xy,xz平面上壁面导纳:
| $\begin{split} {\bar {\beta }_{y}}=&\frac{i\omega {\rho }_{i}{c}_{i}}{a{P}_{0}}\Biggr[\frac{{A}_{1}}{{\alpha }_{1}}\mathrm{sin}\left({\alpha }_{1}a\right)-\frac{{A}_{2}}{{\alpha }_{1}}\mathrm{cos}\left({\alpha }_{1}a\right)+\frac{{A}_{3}}{{\alpha }_{2}}\mathrm{sinh}\left({\alpha }_{2}a\right)+\\ &\frac{{A}_{4}}{{\alpha }_{2}}\mathrm{cossh}\left({\alpha }_{2}a\right)+\frac{{A}_{2}}{{\alpha }_{1}}-\frac{{A}_{4}}{{\alpha }_{2}}\Biggr]+\frac{i\omega {\rho }_{i}{c}_{i}K}{{k}_{x}^{4}-{\gamma }^{4}},\end{split} $ |
| $\begin{split} {\bar{\beta }_{z}}=&\frac{i\omega {\rho }_{i}{c}_{i}}{b{P}_{0}}\Biggr[\frac{{B}_{1}}{{\alpha }_{1}}\mathrm{sin}\left({\alpha }_{1}b\right)-\frac{{B}_{2}}{{\alpha }_{1}}\mathrm{cos}\left({\alpha }_{1}b\right)+\frac{{B}_{3}}{{\alpha }_{2}}\mathrm{sinh}\left({\alpha }_{2}b\right)+\\ &\frac{{B}_{4}}{{\alpha }_{2}}\mathrm{cossh}\left({\alpha }_{2}b\right)+\frac{{B}_{2}}{{\alpha }_{1}}-\frac{{B}_{4}}{{\alpha }_{2}}\Biggr]+\frac{i\omega {\rho }_{i}{c}_{i}K}{{k}_{x}^{4}-{\gamma }^{4}} 。\end{split}$ |
计算壁面的平均导纳:
| $ \bar{\beta }=\frac{a{\bar{\beta }_{y}}+b{\bar{\beta }_{y}}}{a+b}。$ |
计算管内轴向波数:
| $ {k}_{x}={k}_{i}\sqrt{1-\frac{iL\bar{\beta }}{{k}_{1}S}} 。$ |
声辐射系数:
| $ {C}_{r}=-\frac{1}{\text{π} }\mathrm{arctan}\left(\frac{\text{π} }{6}l{k}_{x}\left(1-\frac{{k}_{e}}{{k}_{x}}\right)\right)+0.5 。$ |
上式是通过曲线拟合,并非声辐射系数的定义式。
| $ {c}_{x}=\frac{2\text{π} f}{{k}_{x}} 。$ |
管道传递损失:
| $ TL=10\mathrm{log}\left(\frac{ab{\rho }_{i}{c}_{i}}{{C}_{r}{k}_{i}{\rho }_{e}{c}_{x}\left|a{\bar{\beta }_{y}}+b{\bar{\beta }_{y}}\right|}\right) 。$ |
计算的噪声源输入如表1所示。
|
|
表 1 燃机进气管路噪声源计算输入 Tab.1 Input for calculation of noise source in the combustion engine intake pipe |
几何输入参数为:
当管道外为自由空间时,按照wave solution方法计算得到的燃机进气管外辐射声压级如图2和图3所示。从图2可看出,随着板厚的增加,管外辐射声压逐渐降低。这是由于厚度增加时,既能在低频区域增加控制刚度,也能在高频区域增加等效质量,提高了管壁的隔声效果,降低了管壁周围的辐射声压。当壁面厚度为4 mm,6 mm,8 mm时,壁面辐射总声压级分别为76.2 dBA,74.5 dBA,73.2 dBA。按照IMO《船上噪声等级规则》中的要求,机器控制室的工作面声压级应低于75 dB。因此,为了满足IMO标准,所采用的进气管壁面厚度应至少为6 mm。虽继续增加壁面厚度有助于隔声,但过厚会增大整个进气系统的质量,不利于全船轻量化设计。
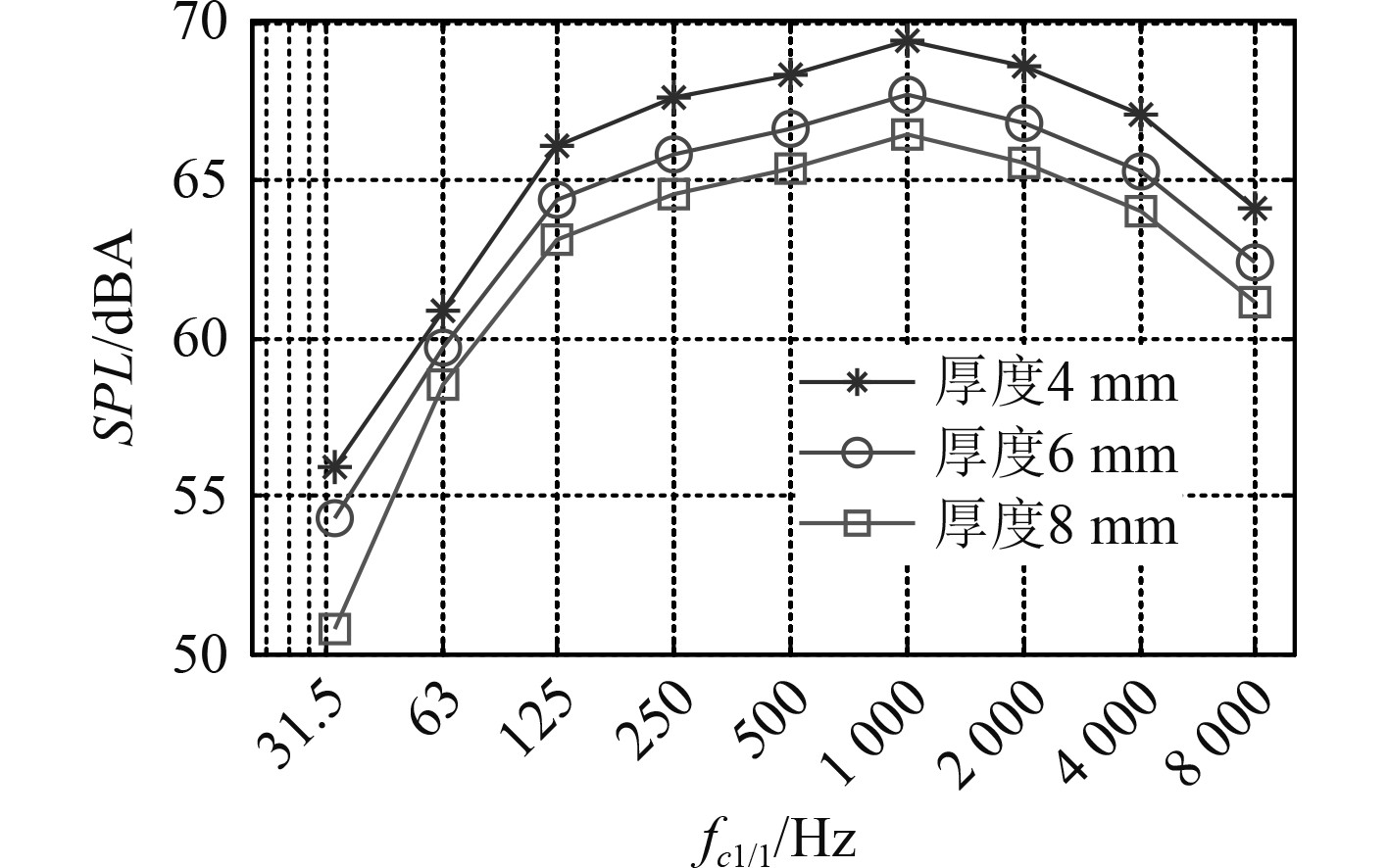
|
图 2 不同厚度下的壁面辐射声压级 Fig. 2 Radiated sound pressure levels for different thicknesses |

|
图 3 不同管道截面下的壁面辐射声压级 Fig. 3 Radiated sound pressure levels for different pipe sections |
从图3可看出,随着管道尺寸的减小,壁面外的辐射声压级会增大。另外,管道尺寸减小也会增大管内气体流速,进而增大进气阻力。因此,在噪声源声功率级不变的情况下,应当尽量使用截面较大的进气管道,但继续增加进气管道会带来重量增加的问题,根据实船需要选定合适的管道尺寸。
wave solution方法可以在设计之初给出管壁辐射声压的解析估算结果,但该方法也存在以下问题:
首先,该方法适用的模型过于简单和理想化,难以直接用于评估实船复杂管路辐射噪声,仅能给出一部分定性分析;其次,该方法没有考虑到外部封闭腔室的辐射阻抗,无法在受限空间中准确评估声辐射效果。最后,该方法无法考虑到壁面声振耦合的高阶模态。
在利用解析方法完成估算后,有必要利用成熟的数值计算方法对结果进行验证。综合考虑计算精度和计算效率,使用有限元方法建立进气管道的声固耦合模型,计算进气管的管口声辐射效果和壁面辐射效果。
2 燃气轮机进气管道声辐射数值计算燃气轮机进气管路几何模型如图4所示。模型的声学计算域包括进气管路、进气消声器、进气集箱等。为了模拟管道壁面的二次声辐射情况,在燃机进气管路的第1个弯头处建立周围的舱室模型。同时,建立进气管路和舱室之间的结构壁面模型,管道内声学域、管道结构壁面和舱室内声学域三者之间采用双向耦合模型。考虑到模型的计算规模和计算效率,仅建立和进气管路第1个弯头相邻的舱室模型作为典型例子,分析管道的辐射特性。模型的边界设定如下:入口边界根据燃气的进气噪声谱施加声源入射条件。考虑到噪声出口的开孔截面大,为使出口处噪声充分发展,故在进气百叶窗周围建立附加计算域,并设定辐射边界条件。根据计算频率上限,划分计算网格,确保每个波长内至少有6个单元,共划分四面体网格共560万。
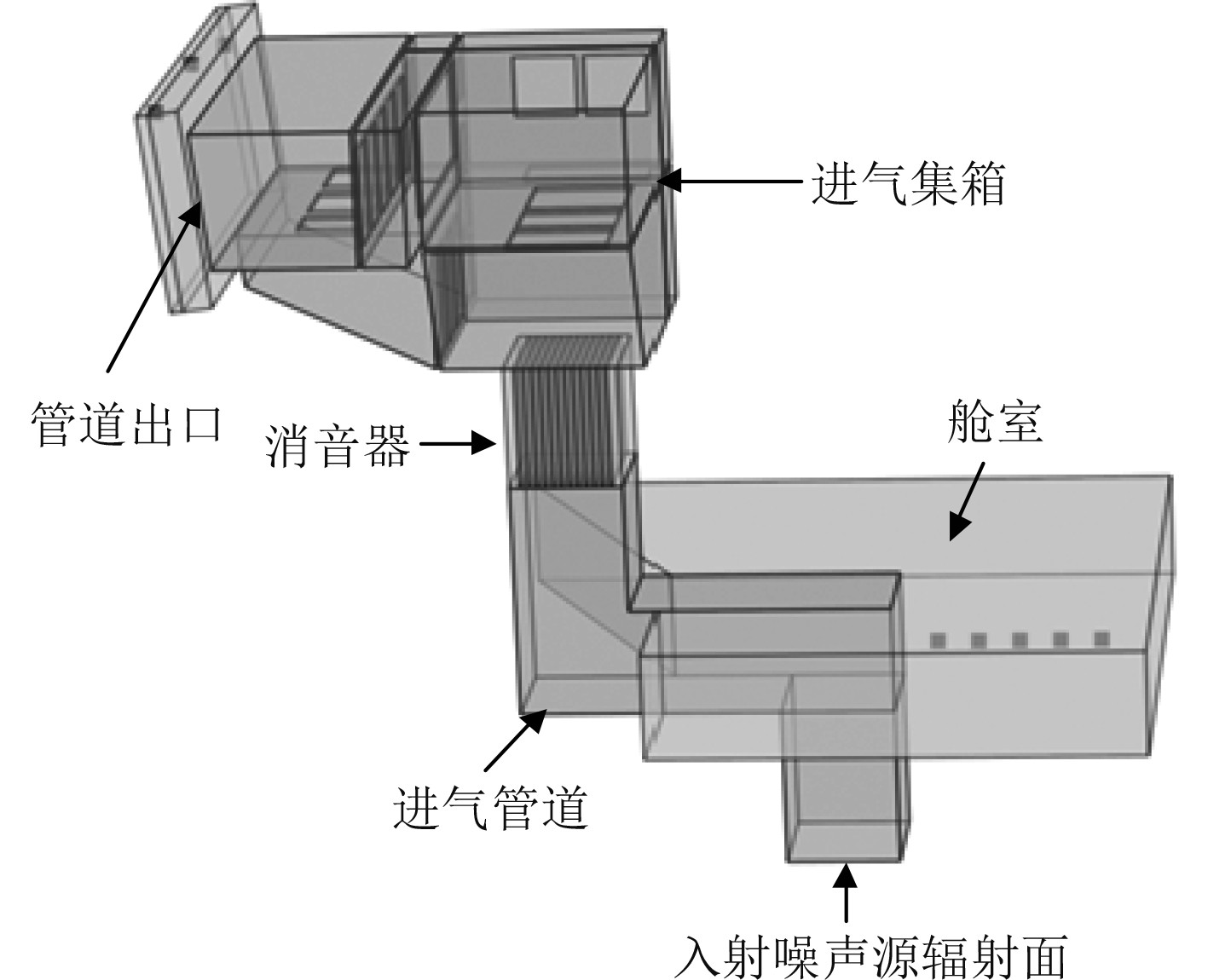
|
图 4 燃气轮机进气管路计算模型 Fig. 4 Calculation model of gas turbine intake pipeline |
图5给出了燃气轮机进气噪声源和经过进气管路出口辐射的噪声声压级对比。图6~图10给出了部分频率下的燃机进气管路和相邻舱室内的声压级分布。
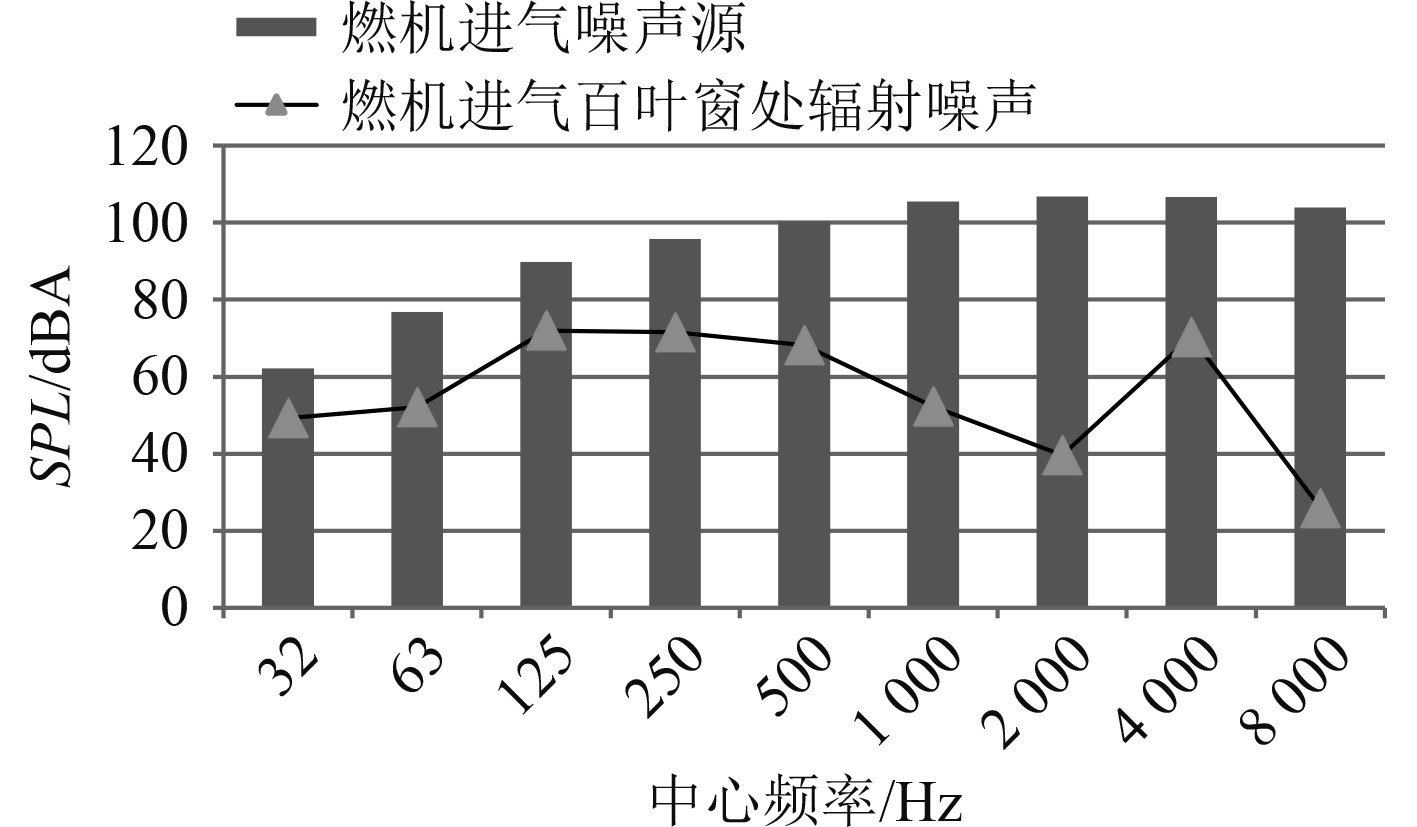
|
图 5 燃气轮机进气噪声源与百叶窗处辐射噪声对比 Fig. 5 Comparison of gas turbine intake noise sources and radiated noise at louvers |

|
图 6 频率为31.5 Hz时声压级分布 Fig. 6 Sound pressure level distribution at 31.5 Hz |
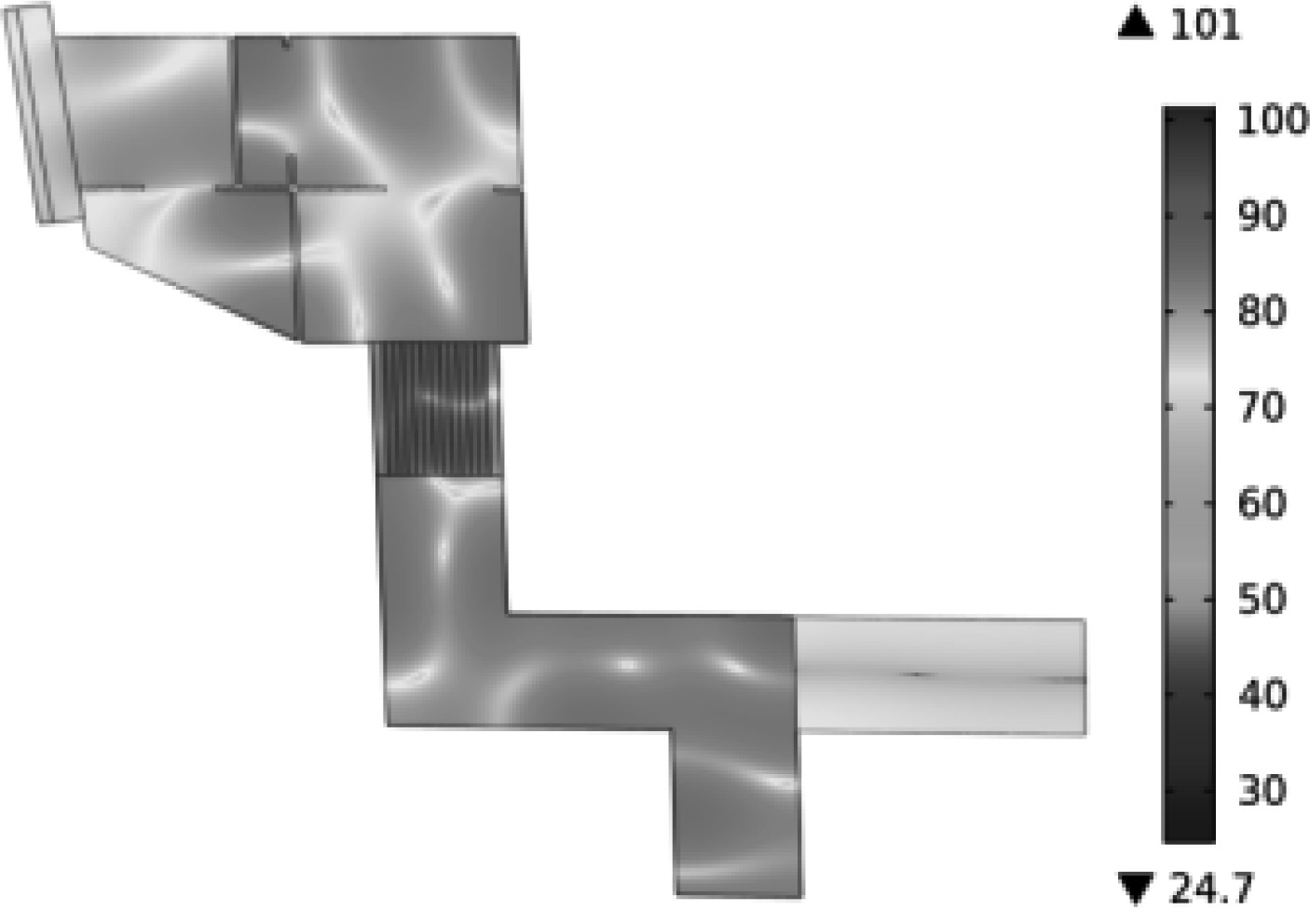
|
图 7 频率为125 Hz时声压级分布 Fig. 7 Sound pressure level distribution at a frequency of 125 Hz |
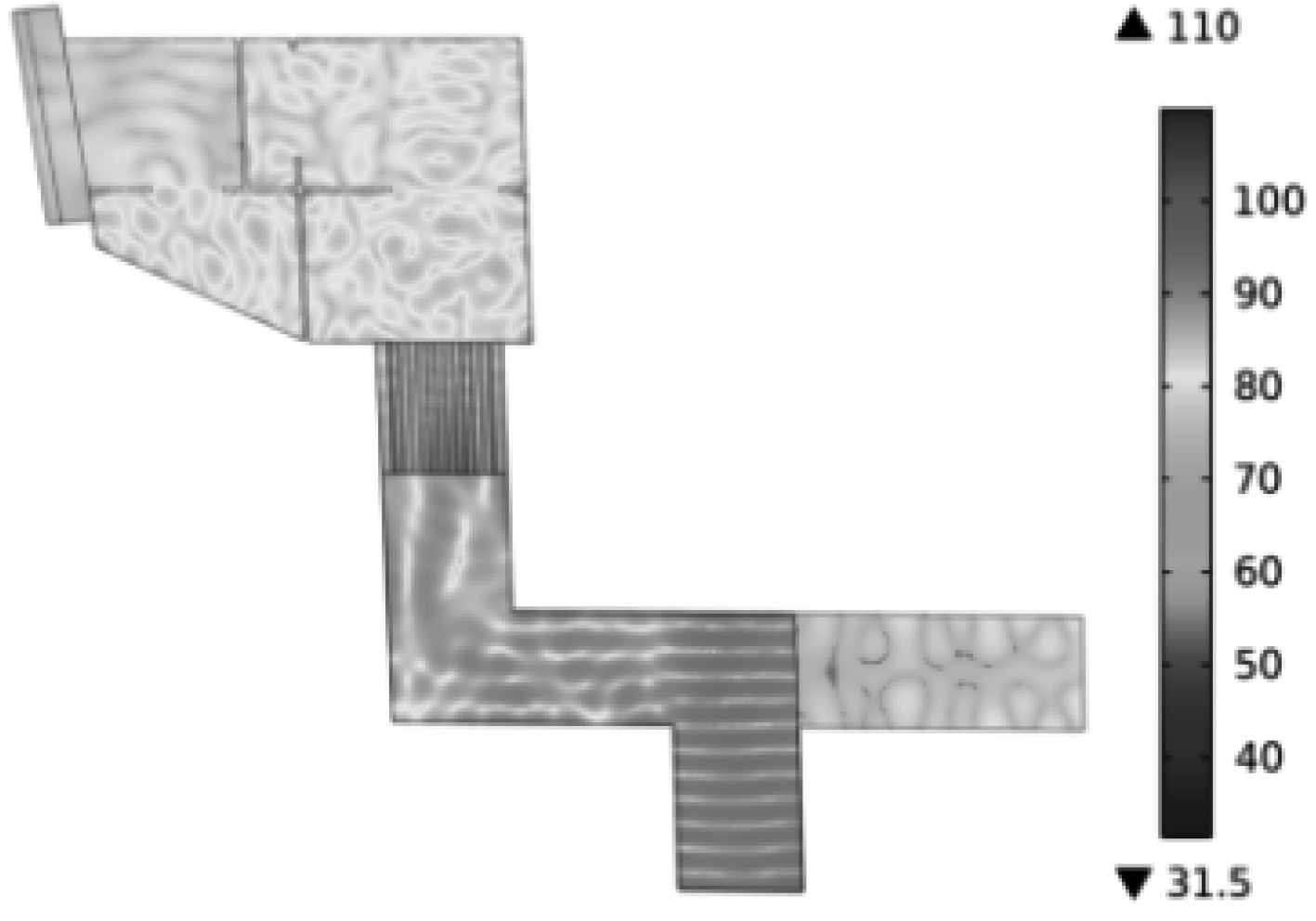
|
图 8 频率为500 Hz时声压级分布 Fig. 8 Sound pressure level distribution at a frequency of 500 Hz |
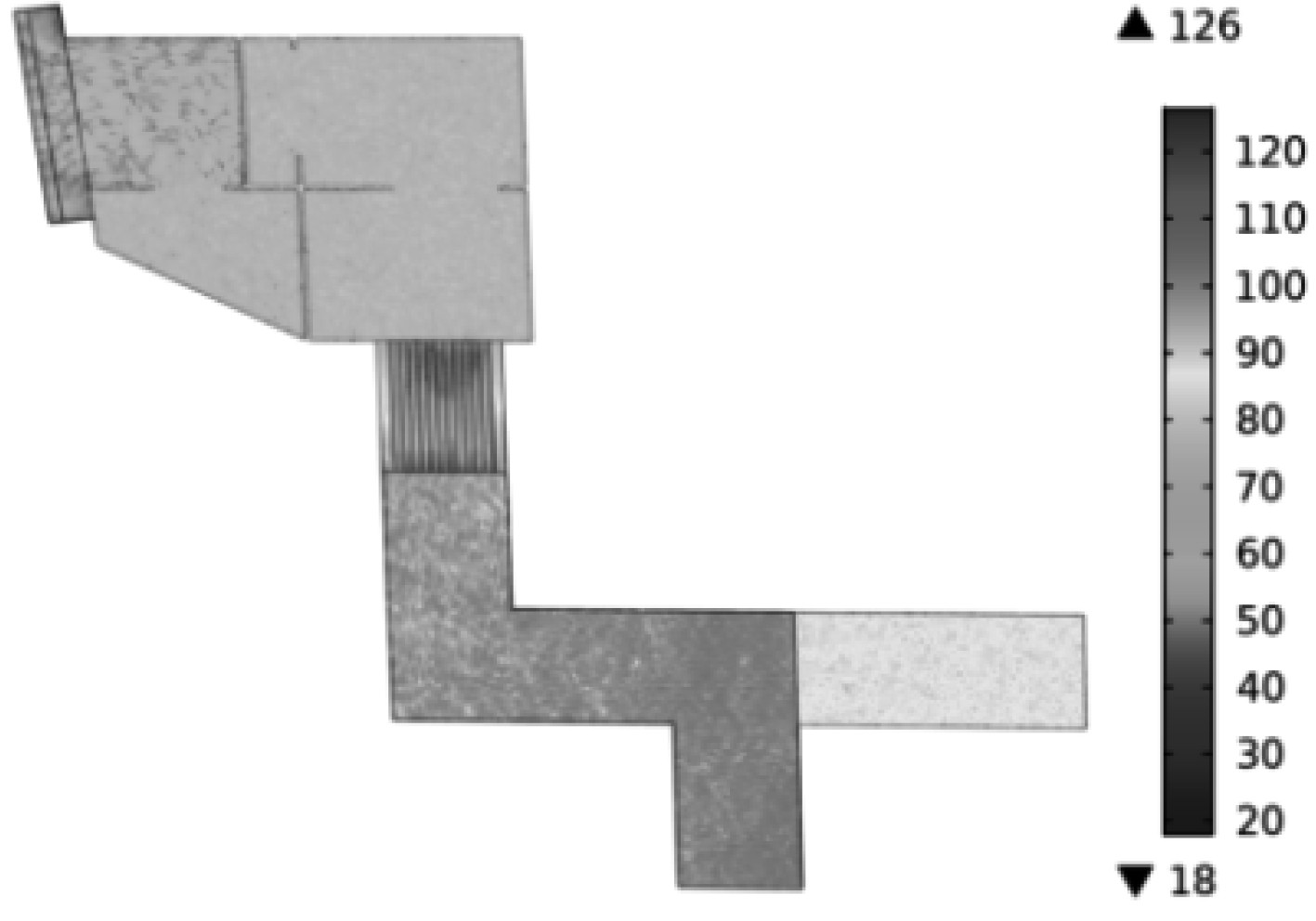
|
图 9 频率为2000 Hz时声压级分布 Fig. 9 Sound pressure level distribution at a frequency of 2000 Hz |

|
图 10 频率为8000 Hz时声压级分布 Fig. 10 Sound pressure level distribution at a frequency of 8000 Hz |
可知,进气噪声的总声压级为112.3 dBA,与柴油机不同,燃气轮机的进气噪声呈现出随着频率的增高而逐渐上升的趋势。500 Hz~8 kHz的各个频带上A声级均可达到100 dBA以上,说明其叶片旋转噪声和气流噪声占比很大。管口辐射的总声压级为76.8 dBA。其中管路出口监测点距离进气百叶窗1 m,和百叶窗端面法向呈45°。
当频率低于500 Hz时,对管道声衰减起主要作用的是进气集箱,其内部较大的中空结构相当于一个膨胀腔消声器,阻止了进气噪声向舷外传播。当频率高于500 Hz以后,随着频谱的增加,抗式结构逐渐出现高频失效现象。而消声器中吸声材料的高频吸声特性逐渐体现,从云图上可能看到,当频率高于500 Hz后,声波经过消声后有很大的衰减。
经过进气集箱和消声器的双重降噪后,进气噪声得到了很大的衰减,距离进气百叶窗1 m处的总声压级降低至76.8 dBA。在舱室内距离进气管路1 m取了监测点,计算得到的舱室内平均声压级结果如图11所示。可以发现,进气管道相邻的舱室噪声主要集中在500 Hz以上,这一方面跟燃气轮机的噪声源特性有关(500 Hz以上噪声源较高),另一方面也受到了腔室和管道之间的声固耦合固有特性的影响。另外,由于舱室壁面这是为刚性壁,声波在舱室内形成混响。
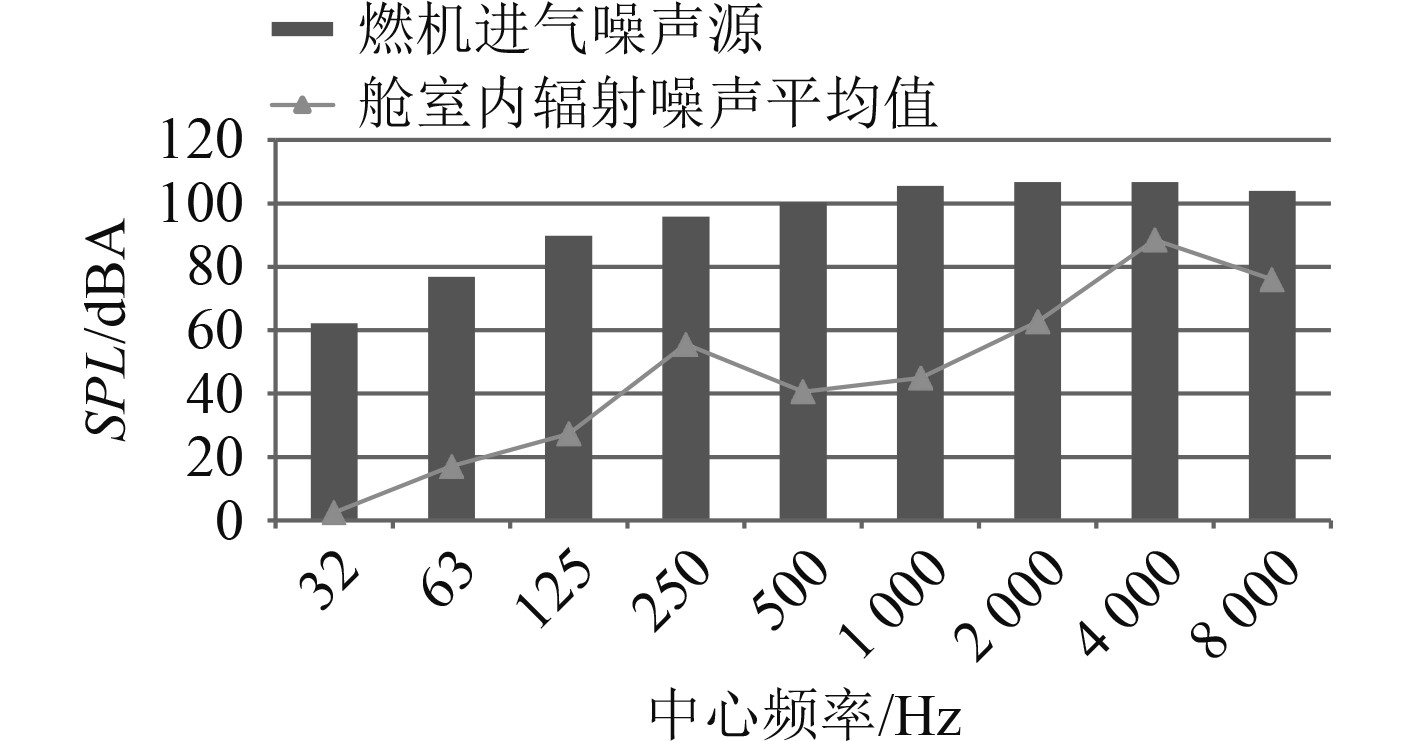
|
图 11 不同频率下舱室声压级大小 Fig. 11 Cabin sound pressure level at different frequencies |
在2000 Hz以上管壁的隔声效果明显下降。该现象的出现可用平板隔声理论进行解释。在质量控制区,当入射声波的频率继续增加时,材料内部传播的与频率相关的弯曲波波长会逐步接近空气中的声波波长。吻合(波长相等)首先发生在掠入射,即入射角为90°。吻合发生时,入射波与平板中的弯曲波互相加强。平板振动的结果是导致板传递损失的大幅降低[11]。根据吻合频率的计算公式
按照IMO《船上噪声等级规则》中的要求,机器控制室的工作面声压级应低于75 dB。因此,有必要对燃机进气管路进行包覆,以减小其向周围舱室内的噪声辐射。一般使用多孔吸声材料进行包覆。阻性吸声材料一般用来达到宽频降噪效果。吸声材料是多孔介质,由于排气中的气体分子与吸声材料空隙之间有摩擦、黏滞力和热传导作用,导致声波的能量转化为其他形式的能量,进而达到降噪的作用。吸声材料的声学模型包括局部反应模型和体积反应模型,其中局部反应模型仅考虑表面声阻抗,不考虑声波在吸声材料内的驻波效应,适用于流阻率高或厚度比较小的吸声材料。进气管道的尺寸比较大,因此内部敷设的吸声材料比较厚。显然,考虑声波在吸声材料内传播的体积反应模型更适用于其性能预测。在这种声学模型内,可将吸声材料看作是一种等效流体,该流体具有特定的复声速和复密度。准确描述复声速和复密度是预测阻性消声器声学性能的关键。本文采用Delany-Bazley经验模型来描述上述复特性。
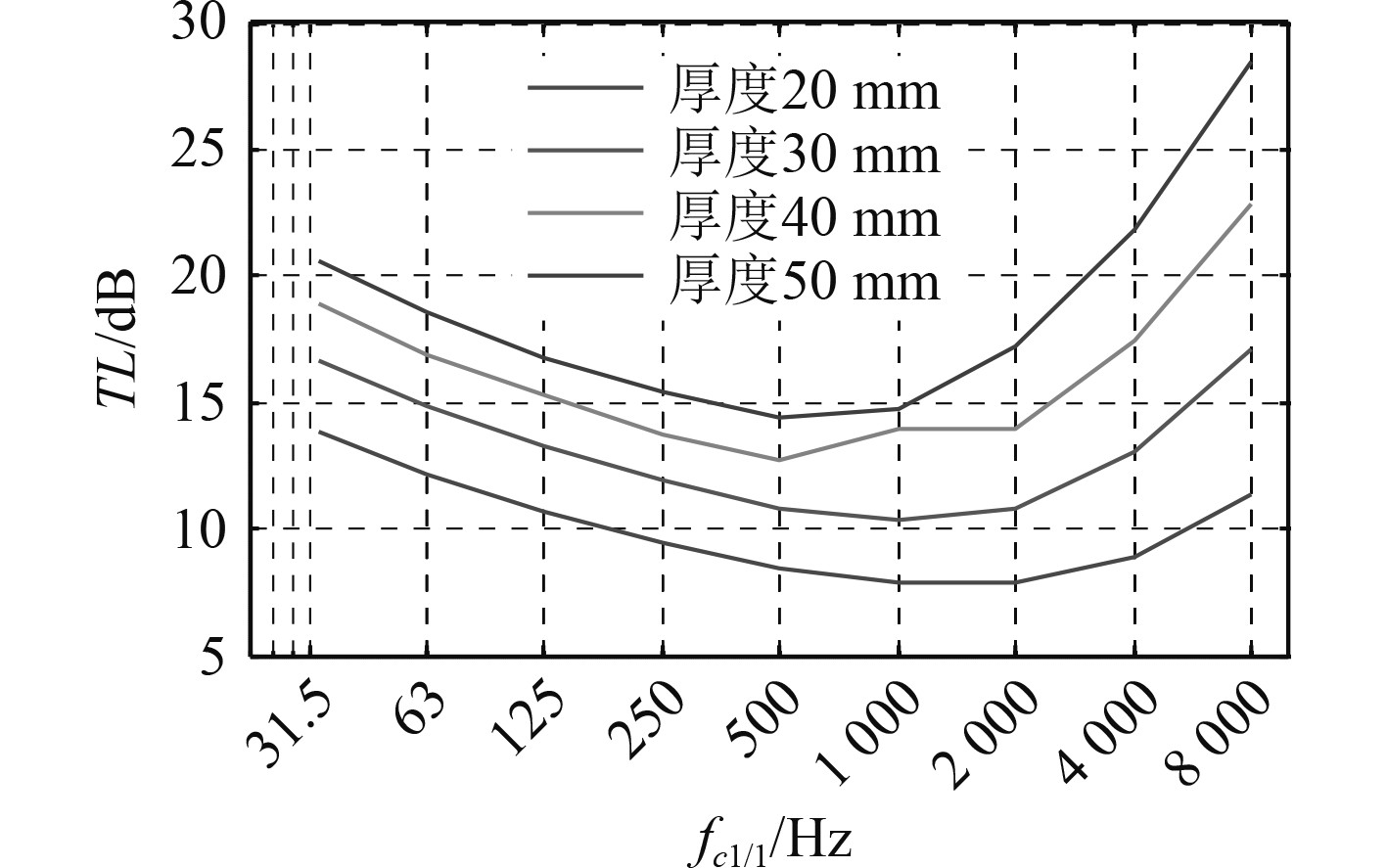
所用的吸声材料为90g/L的硅酸铝吸声棉,按照上述理论计算,得到不同厚度吸声面包覆后的传递损失如图12所示。由于吸声棉的吸声系数会随着吸声棉厚度的增加而增加,而且吸声系数会随着频率的升高而增大。另外,由于舱室内2000 Hz以上噪声占主导,因此选择吸声棉厚度时应当至少要求其在2000 Hz以上有不小于15 dB的降噪量。
|
图 12 不同厚度吸声材料的传递损失 Fig. 12 Transmission loss of sound absorbing materials with different thicknesses |
包覆不同厚度的吸声材料后,舱室内预估平均声压级如表2所示。
|
|
表 2 包覆不同吸声材料后舱室内平均声压级(dBA) Tab.2 Average sound pressure level in the cabin after covering with different sound absorbing materials (dBA) |
可以发现,包覆吸声材料可以有效降低舱室内的噪声,为满足《船上噪声等级规则》中,并机器控制室的工作面声压级低于75 dB。因此,必须保证包覆的吸声材料厚度在40 mm以上,由于实际情况复杂,可考虑包覆厚度在50 mm左右。
4 结 语1)对于船用燃机进气管道而言,由于其噪声源激励幅值高、管道尺寸大,这导致管壁声激振动引起的二次辐射噪声不容忽视。
2)解析估算表明:随着板厚的增加,管外辐射声压逐渐降低。随着管道尺寸的减小,壁面外的辐射声压级会增大。对于本文研究的高度、宽带均为2.56 m的大尺寸进气管段,管道壁面取6 mm以上才可使进气消声器和燃气轮机之间的管道辐射噪声降低到75 dBA以下。
3)数值计算表明,对燃气轮机进气管道低频声衰减起主要作用的是进气集箱,其内部较大的空腔结构相当于一个膨胀腔消声器,阻止了进气噪声向舷外传播。当频率高于500 Hz以后,随着频谱的增加,消声器中吸声材料的高频吸声特性逐渐体现。经过进气集箱和消声器的双重降噪后,进气噪声得到了衰减。距离燃机进气百叶窗1 m处的总声压级降低至76.8 dBA。但在管道表面未采取控制措施的情况下,舱室内监测点的总噪声平均声压级可达到89 dBA。
4)依据声学包覆的隔声特性以及舱室环境要求可知,进气管道的声学包覆厚度为40mm时,可使该船燃机进气管道相邻舱室内的管道辐射噪声降低到75 dBA以下。
| [1] |
WOODS R I , WEBB J D . Noise control in mechanical services[J]. Journal of Sound and Vibration, 1972.
|
| [2] |
CREMER L. Theory of sound transmission through cylindrical shells[J]. Journal of Sound and Vibration, 1955, 5: 245-256. |
| [3] |
HECKL M. Experimental investigation of sound transmission through cylinders[J]. Journal of Sound and Vibration, 1958, 8: 259-265. |
| [4] |
BROWN G L, RENNISON D C. Sound radiation from pipes excited by plane acoustic waves[C]//Proceedings of the Noise, Shock and Vibration Conference, Monash University, Melbourne. 1974: 416–425.
|
| [5] |
KUHN G F, MORFEY C L. Transmission of low-frequency internal sound through pipe walls[J]. Journal of Sound and Vibration, 1976, 47(2): 147-161. DOI:10.1016/0022-460X(76)90714-8 |
| [6] |
ALLEN C H. Noise reduction[J]. Journal of Sound and Vibration, 1960: 545.
|
| [7] |
CUMMINGS A. Low frequency acoustic transmission through the walls of rectangular ducts[J]. Journal of Sound and Vibration, 1978, 61(3): 327-345. DOI:10.1016/0022-460X(78)90384-X |
| [8] |
CUMMINGS A. Design charts for low frequency acoustic transmission through the walls of rectangular ducts[J]. Journal of Sound and Vibration, 1981, 78(2): 269-289. DOI:10.1016/S0022-460X(81)80038-7 |
| [9] |
GUTHRIE A. Low frequency acoustic transmission through the walls of various types of ducts[J]. Journal of Sound and Vibration, 1979.
|
| [10] |
CUMMINGS A. Higher order mode acoustic transmission through the walls of rectangular ducts[J]. Journal of Sound and Vibration, 1983, 90(2): 193-209. DOI:10.1016/0022-460X(83)90528-X |
| [11] |
BARRON R F. Industrial noise control and acoustics[M]. CRC Press, 2002.
|
 2023, Vol. 45
2023, Vol. 45
