2. 天津大学 水利仿真与安全国家重点实验室,天津300072
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China
风力发电机是将风能转化为电能的大型工程设施,海上浮式风力机是风力发电的一种重要形式。由于海洋环境相较陆地更为复杂,与固定式风机相比,浮式风机会发生大范围运动,从而影响风机叶片气动载荷。因此采用耦合的分析方法对整个浮式风力机系统进行动力分析很有必要。
目前有许多有关浮式风力机系统的建模及分析方法,主要包括刚体动力学方法和刚-柔耦合的多体动力学方法。李焱等[1]基于刚体动力学理论,考虑气动力与浮式基础运动的耦合,建立了Spar型风机系统动力学模型,并分析了浮式风机系统动力特性。Minu等[2]与Shen等[3]分别使用涡格法与势流理论建立刚体模型计算了风机的非定常空气动力学响应。Jonkman等[4]采用气动-水动-伺服-弹性全耦合方法初步分析了5 MW风机动力响应特性。Roberson等[5]在此基础上应用该仿真程序对几种不同形式的浮式风机进行分析,对比研究了不同环境载荷下系统的动力响应。肖昌水等[6]基于Jourdain原理和有限元离散方法研究了风机系统的动力响应。叶江舟等[7]研究了刚-柔耦合理论模型及其数值原理。陈嘉豪等基于OC3平台建立了时域耦合分析程序并加以验证[8],并对比研究了半潜式风机的气动阻尼响应特性[9]。不同的建模方法具有不同的精度、速度与稳定性,单刚体模型的计算速度快,但计算精度相对较低。相对而言,刚-柔耦合模型的计算精度高,同时其计算成本也很高。如何权衡并合理使用2种不同的方法成为亟待解决的问题。
基于此,本文采用单刚体和刚-柔耦合[6]2种不同建模方法,在保证气动力、水动力、系缆等外载荷相同算法的前提下,研究浮式分机系统动力响应,对比分析浮式风机系统刚体模型和刚-柔耦合模型对计算产生的影响。
1 浮式风机系统动力学方程以5 MW浮式风机系统为例进行分析,其中,浮式基础为OC4基础,上部为NERL-5 MW风力机,具体参数见文献[10]。
1.1 单刚体动力学方程将浮式风机系统处理为一个刚体,建立系统动力学方程。采用笛卡尔-右手坐标系,取其整体重心为惯性系原点,z轴由塔柱中垂线竖直向上,x轴由盘面法向在z轴法平面投影方向,与无穷远处来流方向保持一致,如图1所示。
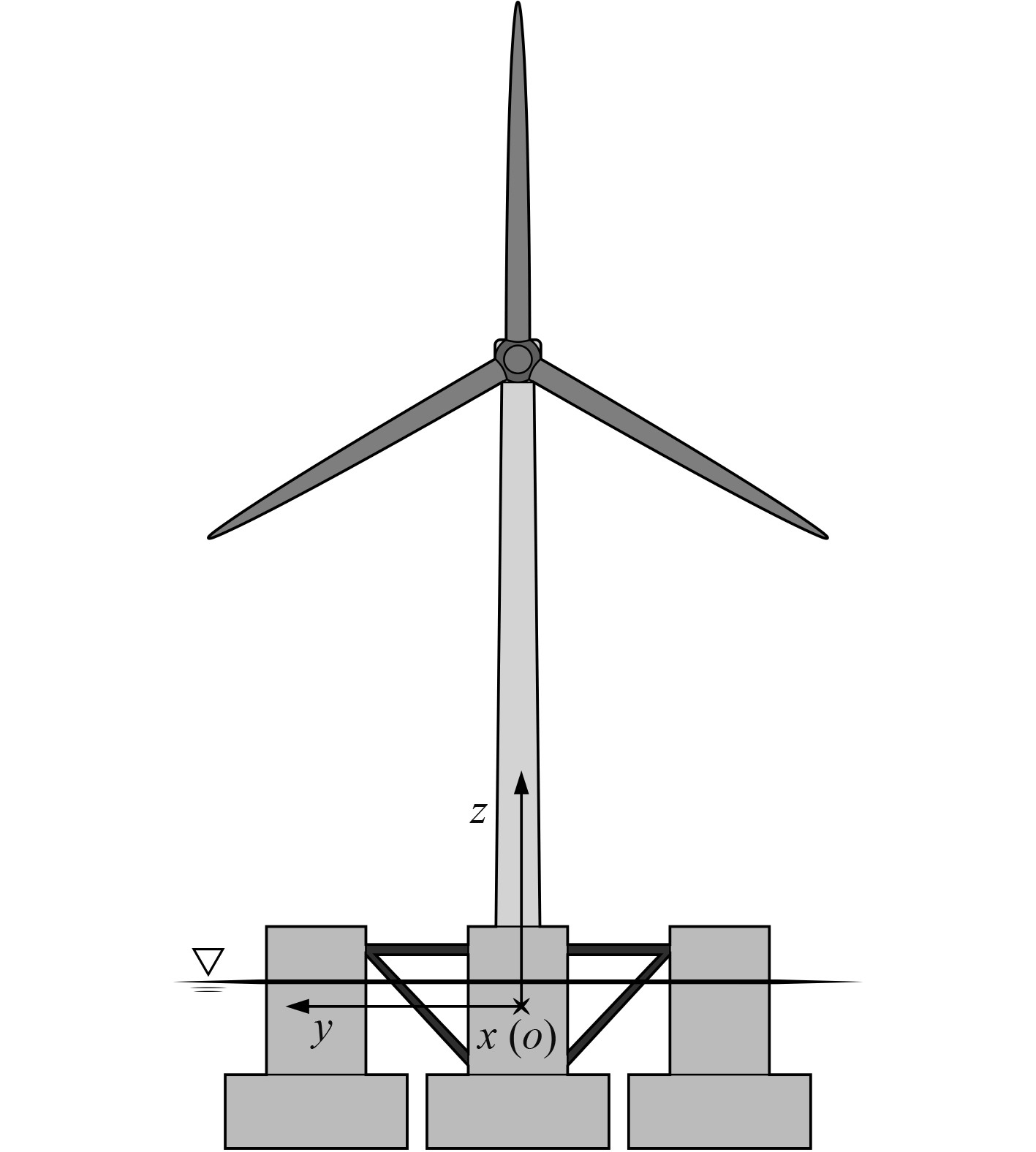
|
图 1 刚体模型坐标系 Fig. 1 Coordinate system of rigid body |
考虑浮式风机系统叶片受到的气动载荷(
| $\begin{aligned} & ({M} + {{m}_\infty }){\ddot X}(t) + {C\dot X}(t) + {KX}(t) + \int_0^t {{R}(t - \tau )} {\dot X}(\tau ){\rm{d}}\tau =\\ & {{F}_{{\rm{blade}}}} + {{F}_{{\rm{tower}}}} + {{F}_{{\rm{wave}}}}+{{F}_{{\rm{moor}}}} 。\end{aligned}$ | (1) |
式中:
| $ {R}(t) = \frac{2}{{\text{π}} }\int_0^\infty {{B}(\omega ){e^{i\omega t}}{\rm{d}}} \omega = \frac{2}{\text{π} }\int_0^\infty {i\omega ({m}(\omega ) - {{m}_\infty }){e^{i\omega t}}{\rm{d}}} \omega 。$ | (2) |
基于Jourdain速度变分原理,考虑刚-柔耦合建立浮式风机系统动力学方程,其中浮式基础处理为刚体,考虑六自由度运动;将塔柱和叶片处理成弹性体,采用有限元方法进行离散;机舱处理为塔柱末端的集中质量;轮毂处理为刚体。浮式风力机系统模型如图2所示。
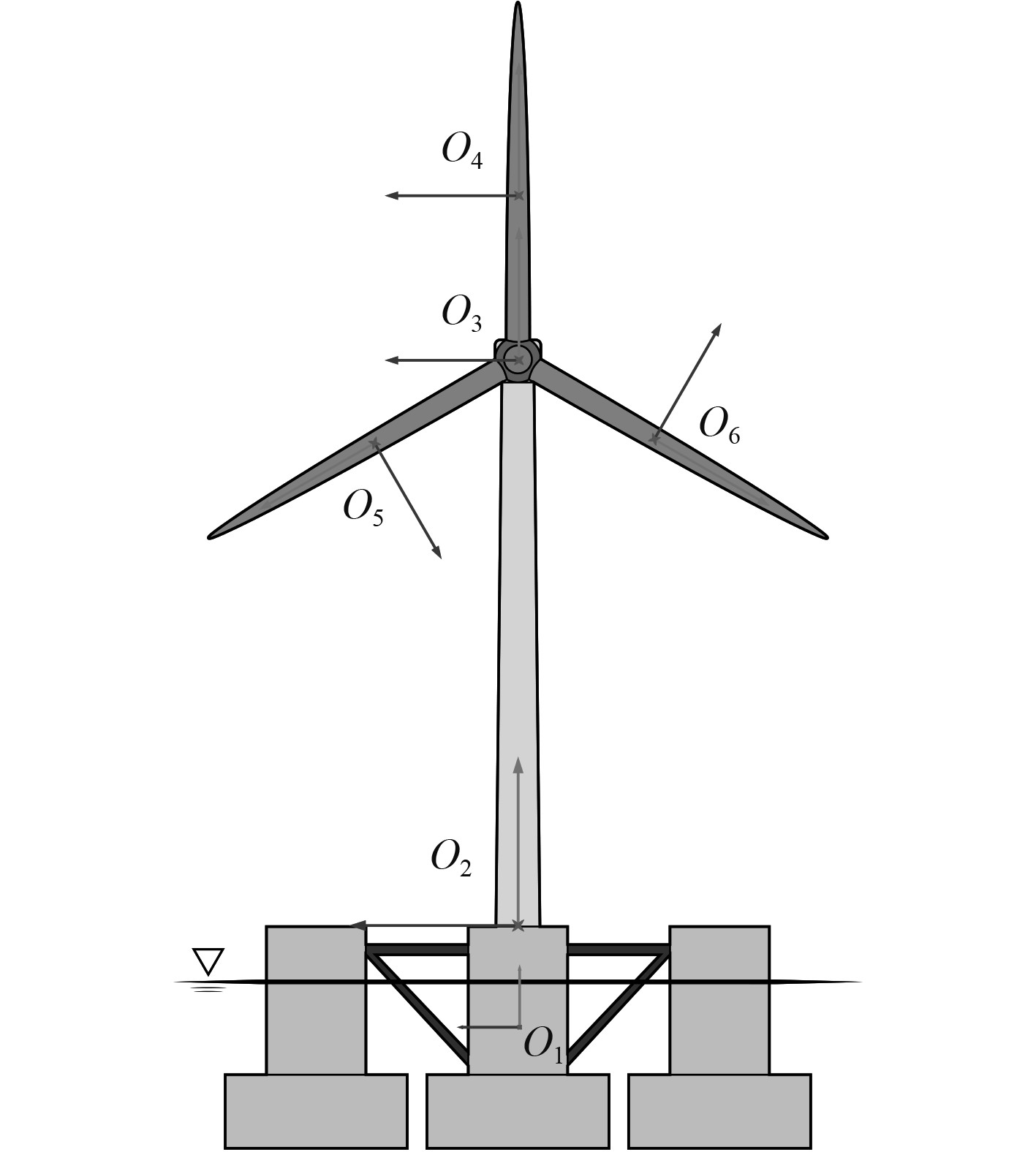
|
图 2 刚-柔耦合模型坐标系 Fig. 2 Coordinate system of R-F coupling body |
建立多体系统坐标系如下:大地坐标系(
根据卡尔丹角坐标转换定理,物体的旋转可分解为先绕x轴,再绕y轴,最后绕z轴的三维旋转运动,故从一坐标系转换到另一坐标系时,需左乘卡尔丹角方向余弦矩阵:
| $ {A = }\left[ {\begin{array}{*{20}{c}} {c\beta c\gamma }&{ - c\beta s\gamma }&{s\beta } \\ {c\alpha s\gamma + s\alpha s\beta c\gamma }&{c\alpha c\gamma - s\alpha s\beta s\gamma }&{ - s\alpha c\beta } \\ {s\alpha s\gamma - c\alpha s\beta c\gamma }&{s\alpha c\gamma + c\alpha s\beta s\gamma }&{c\alpha c\beta } \end{array}} \right] ,$ | (3) |
不同坐标系上的角速度相互转换时也需要左乘相应的角速度转换矩阵:
| $ {D = }\left[ {\begin{array}{*{20}{c}} {c\beta c\gamma }&{s\gamma }&0 \\ { - c\beta s\gamma }&{c\gamma }&0 \\ {s\beta }&0&1 \end{array}} \right] 。$ | (4) |
式中:
利用有限元原理对塔柱与叶片进行离散。根据材料平断面假定,柔性梁上任一点k处的变形位移
| $ {{\mathbf{u}}_k} = \left[ {\begin{array}{*{20}{c}} {{u_1}} \\ {{u_2}} \\ {{u_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{w_1} - y\dfrac{{\partial {w_2}}}{{\partial x}} - z\dfrac{{\partial {w_3}}}{{\partial x}} + {u_g}} \\ {{w_2}} \\ {{w_3}} \end{array}} \right]。$ | (5) |
式中,
据连续介质力学理论,k点处的纵向正应变为:
| $ \varepsilon = \frac{{\partial {w_1}}}{{\partial x}} - y\frac{{{\partial ^2}{w_2}}}{{\partial {x^2}}} - z\frac{{{\partial ^2}{w_3}}}{{\partial {x^2}}},$ | (6) |
由式(5)和式(6)即可得到柔性梁各方向应变及变形。
通过Jourdain速度变分原理推导出系统空间变形动力学方程。对于柔性体变形为:
| $ {r = }{{r}_0} + {A\rho ' = }{{r}_0} + {A}\left( {{{{\rho '}}_0} + {u'}} \right), $ | (7) |
对于刚体,根据动量矩定理有:
| $ {J} \cdot {\dot \omega + \omega } \times \left( {{J} \cdot {\omega }} \right) = {M}, $ | (8) |
得到浮式风机系统的动力学方程为:
| $ \int_V \delta {{\dot r}^{\rm{T}}}\hat \rho {\ddot r}{\rm{d}}V + \delta P - \delta {W_e} = 0 。$ | (9) |
其中:
| $\begin{split} \delta P = & \int_0^{\text{l}} {[EA\delta \left(\frac{{\partial {{\dot w}_1}}}{{\partial x}}\right)\frac{{\partial {w_1}}}{{\partial x}} + E{I_{yy}}\delta \left(\frac{{{\partial ^2}{{\dot w}_1}}}{{\partial {z^2}}}\right)\frac{{{\partial ^2}{w_1}}}{{\partial {z^2}}}} +\\ & E{I_{yy}}\delta \left(\frac{{{\partial ^2}{{\dot w}_1}}}{{\partial {z^2}}}\right)\frac{{{\partial ^2}{w_1}}}{{\partial {z^2}}}]dz 。\end{split}$ | (10) |
考虑不同结构之间的约束条件,最终得到离散后的刚-柔耦合动力学方程:
| $ \begin{split} & {M\ddot q + }\lambda {\varPsi }_q^{\rm{T}} = {Q},\\ & {{\varPsi }_q}{\ddot q} = - [{({{\varPsi }_q}{\dot q})_q}{\dot q} + 2{{\varPsi }_{qt}}{\dot q} + {{\varPsi }_{tt}}] 。\end{split} $ | (11) |
其中:
广义力列阵可表示为:
| $ {\boldsymbol{Q}} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_{{\rm{plat}}}}}&{{{\boldsymbol{F}}_{{\rm{tower}}(i)}}}&{{{\boldsymbol{F}}_{{\rm{hub}}}}}&{{{\boldsymbol{F}}_{{\rm{blade}}(j,i)}}} \end{array}} \right]^{\rm{T}}}。$ | (12) |
其中,平台外力列阵
| $ {{\boldsymbol{F}}_{{\rm{tower}}(i)}}|{{\boldsymbol{F}}_{{\rm{blade}}(j,i)}} = \int_{{l_i}} {{f_i}{\rm{d}}l}。$ | (13) |
式中,
在海洋环境中,影响风机运动响应的外载荷主要为风载荷、波浪载荷、系缆力等。
2.1 风载荷所有位于水面以上的浮体结构均受到风载荷的影响。对于塔柱及停机状态的叶片,采用绕流理论计算风压,即
| $ {f_{L,D}} = \frac{{\rho {v_w}^2{C_{L,D}}}}{2}。$ | (14) |
式中:
| $ {F_{L,D}} = \int_l {{f_{L,D}}{\rm{d}}l}。$ | (15) |
对于一般作业工况下的叶片,风载荷主要表现为气动载荷,本文使用经典叶素动量理论来解决此问题,具体求解过程与理论可参考文献[4]。
2.2 波浪载荷对于波浪载荷,基于三维势流理论计算,采用Sesam/Wadam模块进行模拟。在Sesam软件中建模计算,得到一阶波浪力、平均漂移力、附加质量、静水恢复刚度、势流阻尼的水动力传递函数后,将频域结果转换为时域结果,并将其分别代入刚体程序与刚-柔耦合程序中,之后进行浮式风机系统动力响应的时域计算。
2.3 系缆载荷风机的系泊系统由3根系泊缆组成,间隔120°设置,如图3所示。锚泊点处于水下200 m,导缆孔的位置在浮体水下14 m的位置处,整体的锚链未被拉伸时长837.6 m,具体的系缆参数见文献[10]。
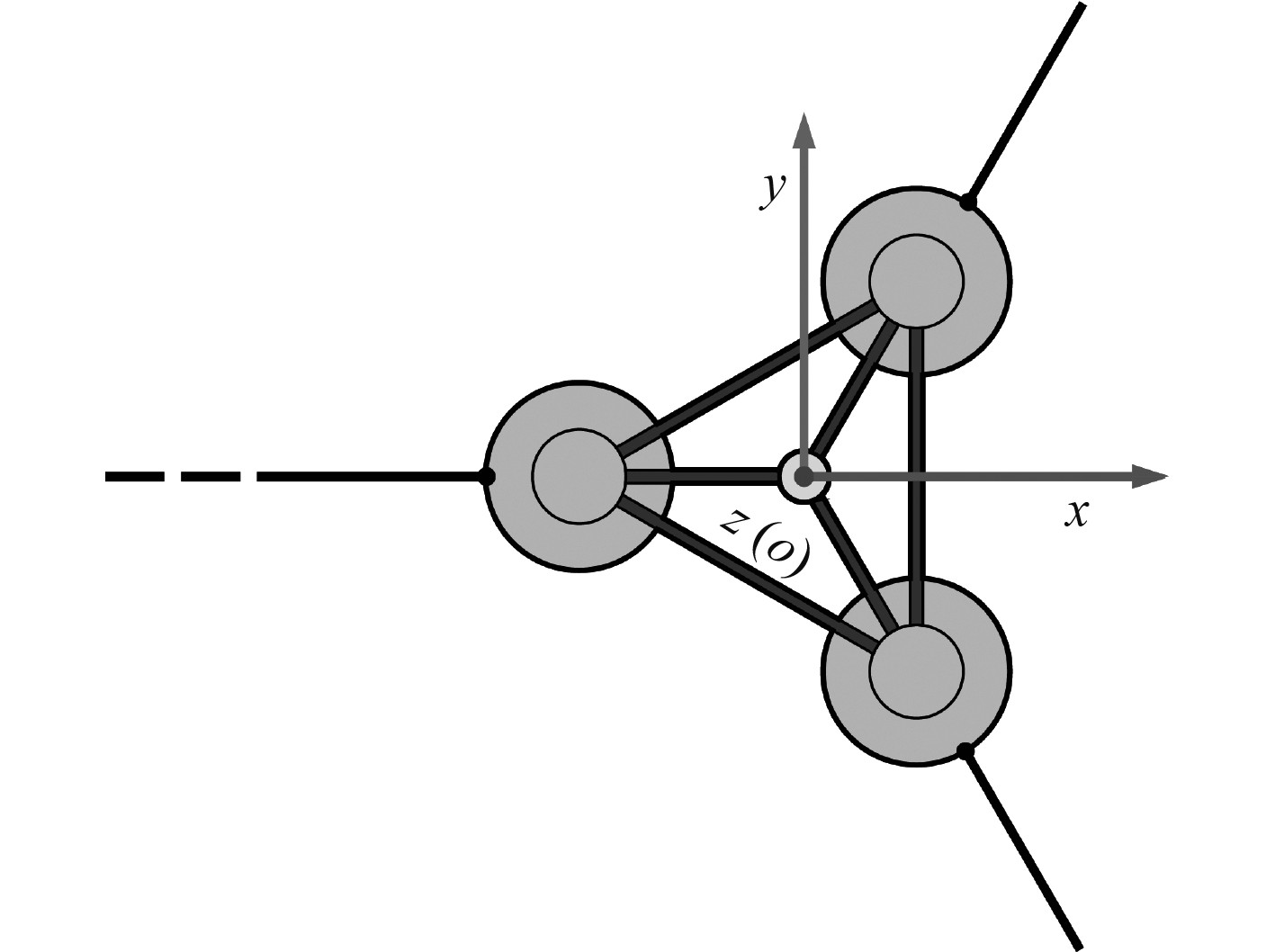
|
图 3 系缆布置方式 Fig. 3 Mooring arrangement |
使用准静态悬链线理论[3]求解系缆载荷,通过分类讨论判别锚链躺底状态并使用迭代方法求解。
2.4 变桨控制策略依照参考规范[10]中的桨距角-风速控制策略得到低风速下的桨距,并根据计算结果优化拟合得到高风速下的桨距,从而得到各个风速下的最佳桨距,结果如表1所示。
|
|
表 1 桨距角控制 Tab.1 Pitch control |
通过使用桨距角控制,浮式风机可以在较低风速下达到最高输出功率的同时,在较高风速下又不至于叶片损坏、系缆断裂或基础位移过大,从而实现在各种环境条件下浮式风机系统的数值模拟。
2.5 浮式风机系统运动响应计算过程对于单刚体计算,每一迭代步计算风机气动载荷,之后考虑气动载荷影响计算浮式风机整体运动,而浮式基础运动又影响下一时刻步的气动载荷计算,从而实现浮式风机系统气动力和浮式基础运动的相互耦合。
对于刚-柔耦合计算,每一步迭代计算风机气动载荷,之后考虑气动载荷影响计算浮式基础运动、叶片/塔柱振动,而浮式基础运动、叶片/塔柱振动又影响下一时刻的气动载荷计算,实现浮式风机系统气动力-浮式基础运动-叶片/塔柱振动的相互耦合。
单刚体计算程序和多刚体计算程序都采用相同的风载荷、波浪载荷、系缆力计算方法及变桨控制策略。对2种程序的正确性做了大量的验证,见参考文献[6,11],本文直接采用2种程序开展计算分析。
3 响应结果与分析参考规范[10]中给出的切入、额定、切出、极限4个工况对单刚体建模方法与刚-柔耦合建模方法分别得到的系统运动响应进行对比分析,各个工况的环境参数如表2所示。
|
|
表 2 工况环境参数 Tab.2 Working conditions |
风、浪作用方向同系缆1的布置方向,即作用在浮式风机系统的纵荡方向,因此主要针对浮式风机整体运动较为明显的纵荡、纵摇自由度以及直接影响输出功率的气动转矩进行分析。
3.1 不同工况的响应对比分别采用单刚体算法和刚-柔耦合算法对不同工况下浮式风机系统响应进行计算。其中,对于切出工况,风机从稳定运行状态到降速乃至停机状态的转捩点,但为防止叶片受损或因机械功率过大导致电机受损,风机叶片需要进行较大的变桨,依照规范,在23°桨距下对单刚体及耦合2种程序进行模拟计算;对于极限工况,风轮停转,桨距角调整为90°附近(顺桨)。得到浮式风机系统纵荡、纵摇及气动转矩的时间历程和频谱图,如图4~图15所示。对不同工况的响应结果进行统计,得到其平均值和标准差,并进行对比,结果如图16~18所示。
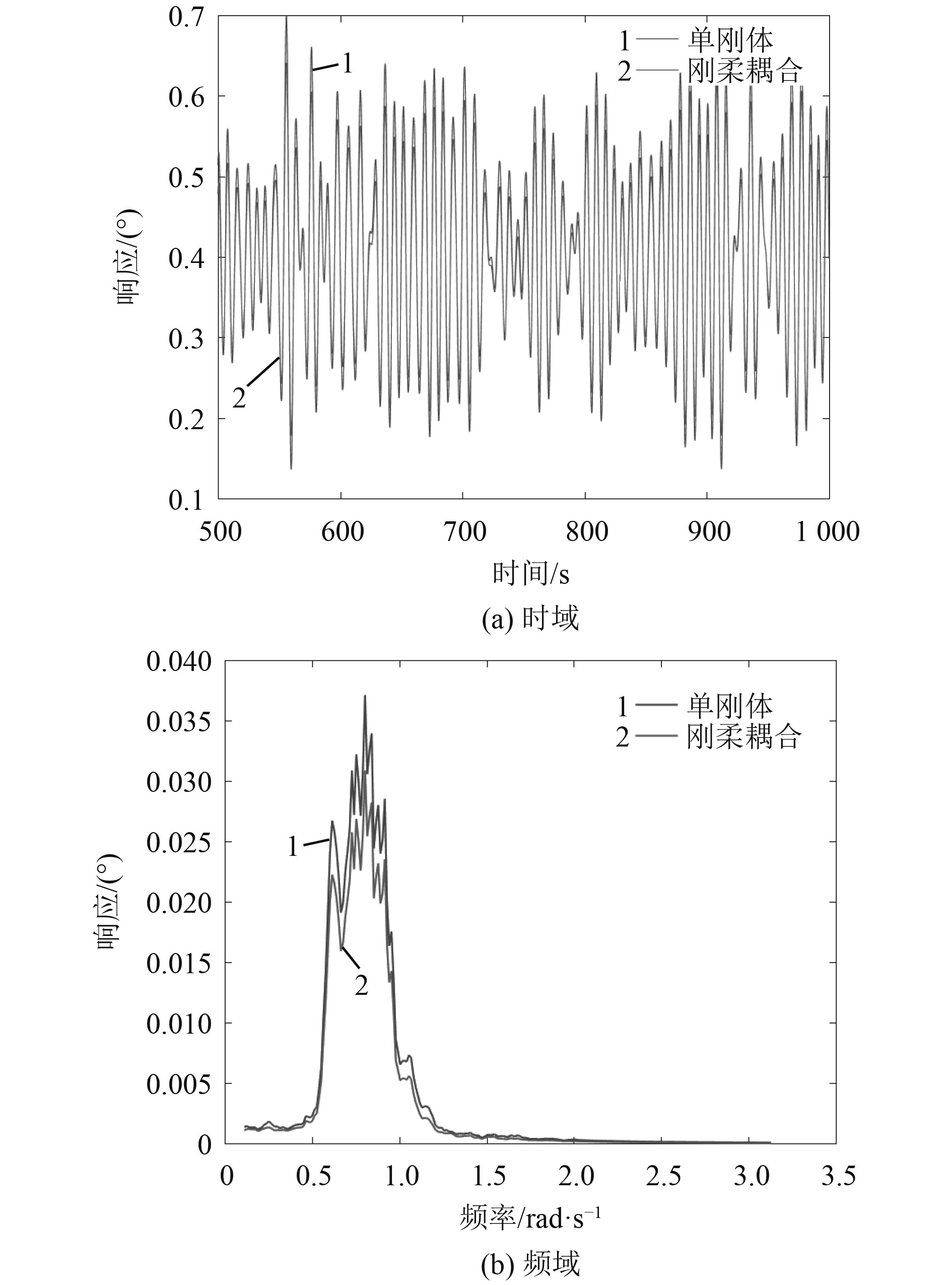
|
图 4 切入工况纵荡响应 Fig. 4 Surge, LC1 |
|
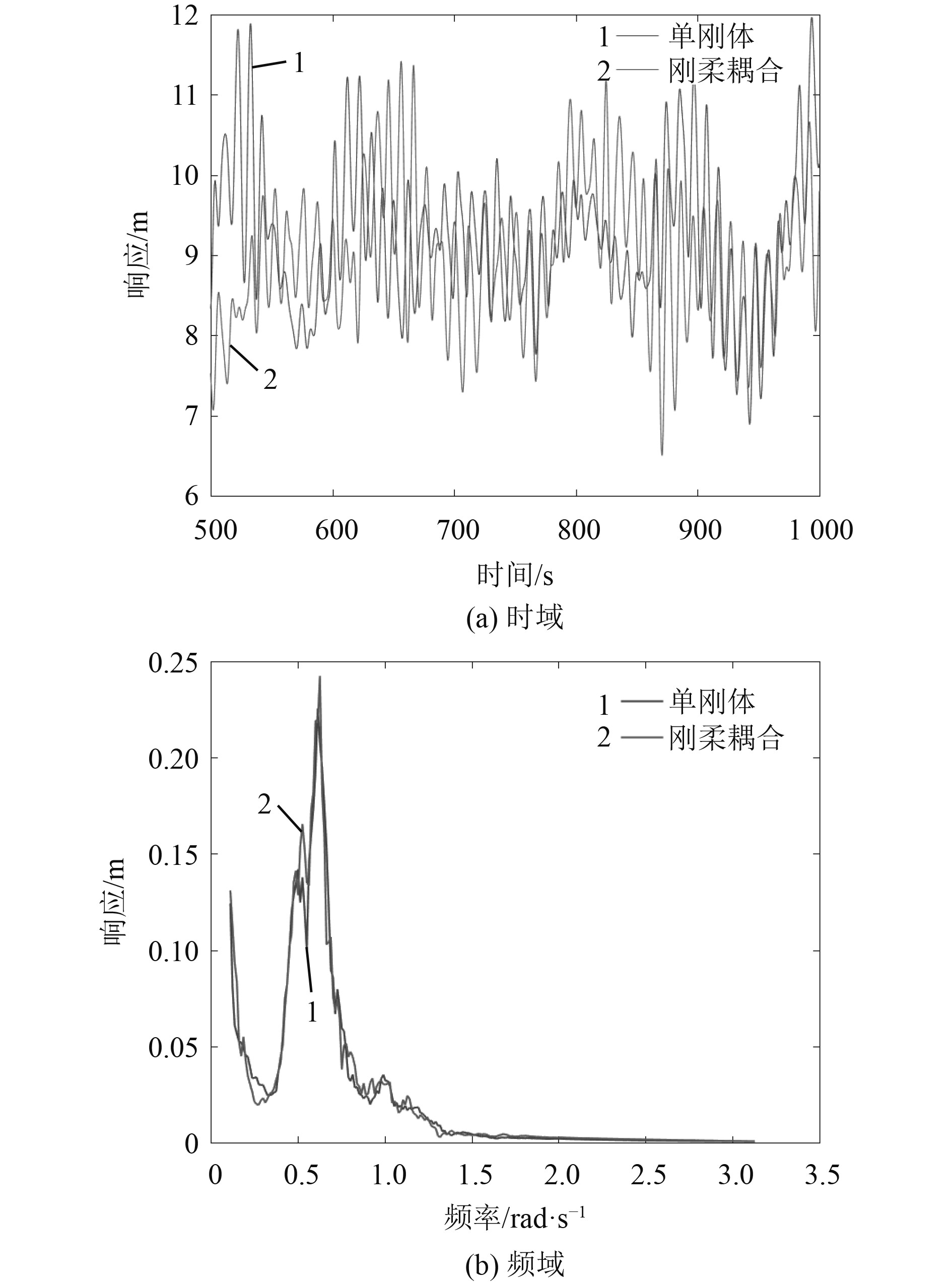
图 5 切入工况纵摇响应 Fig. 5 Pitch, LC1 |
|
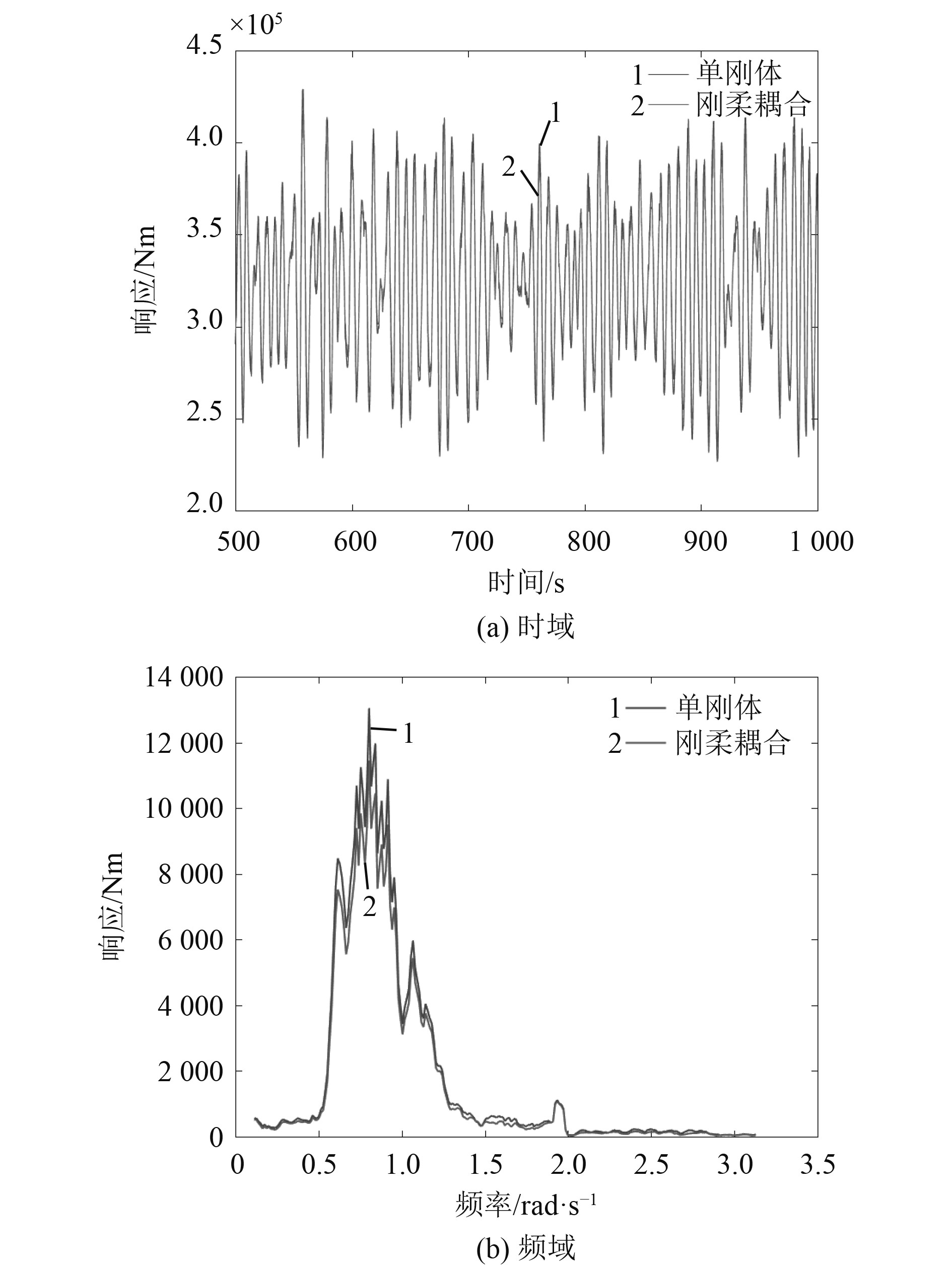
图 6 切入工况气动转矩 Fig. 6 Torque, LC1 |
|
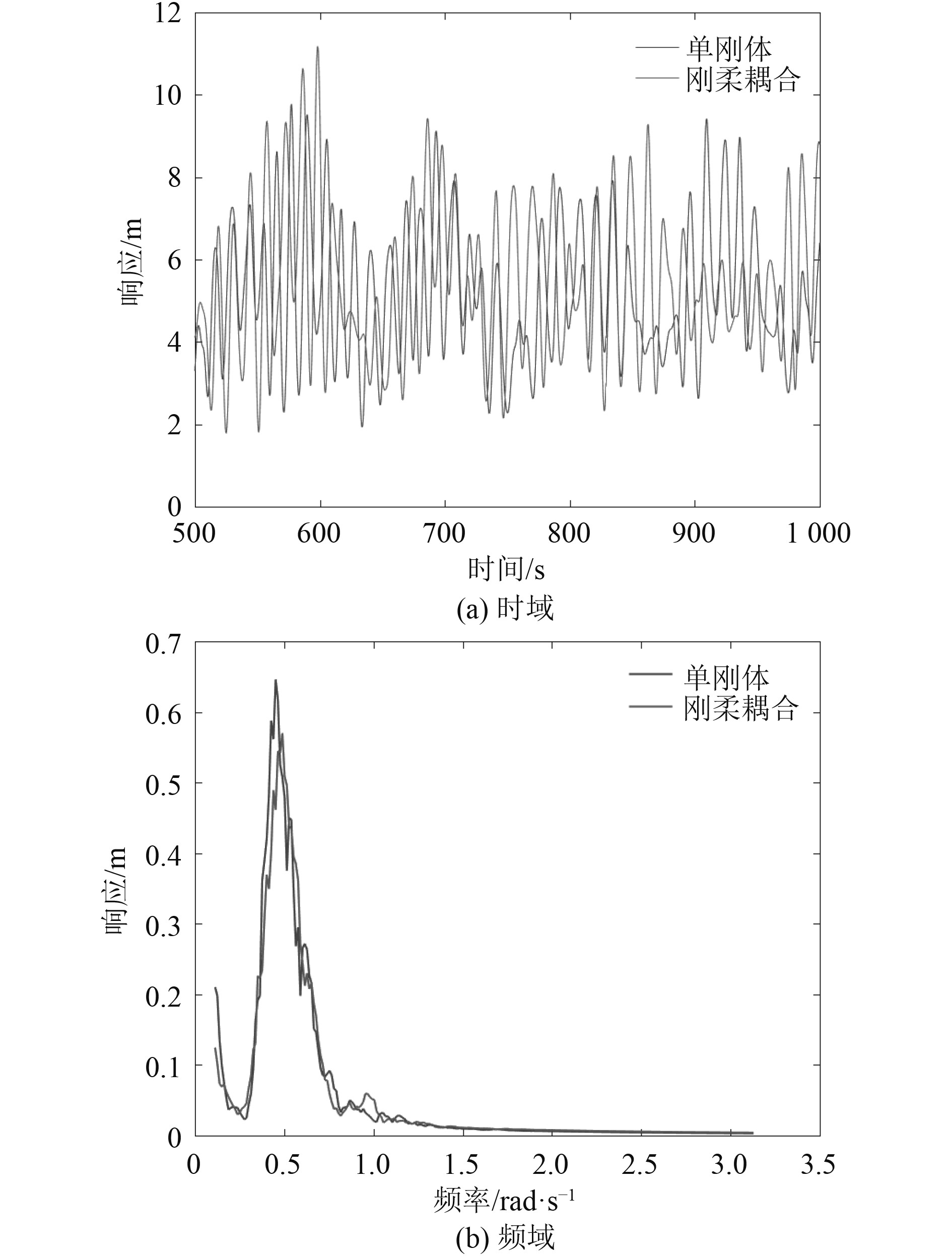
图 7 额定工况纵荡响应 Fig. 7 Surge, LC2 |

|
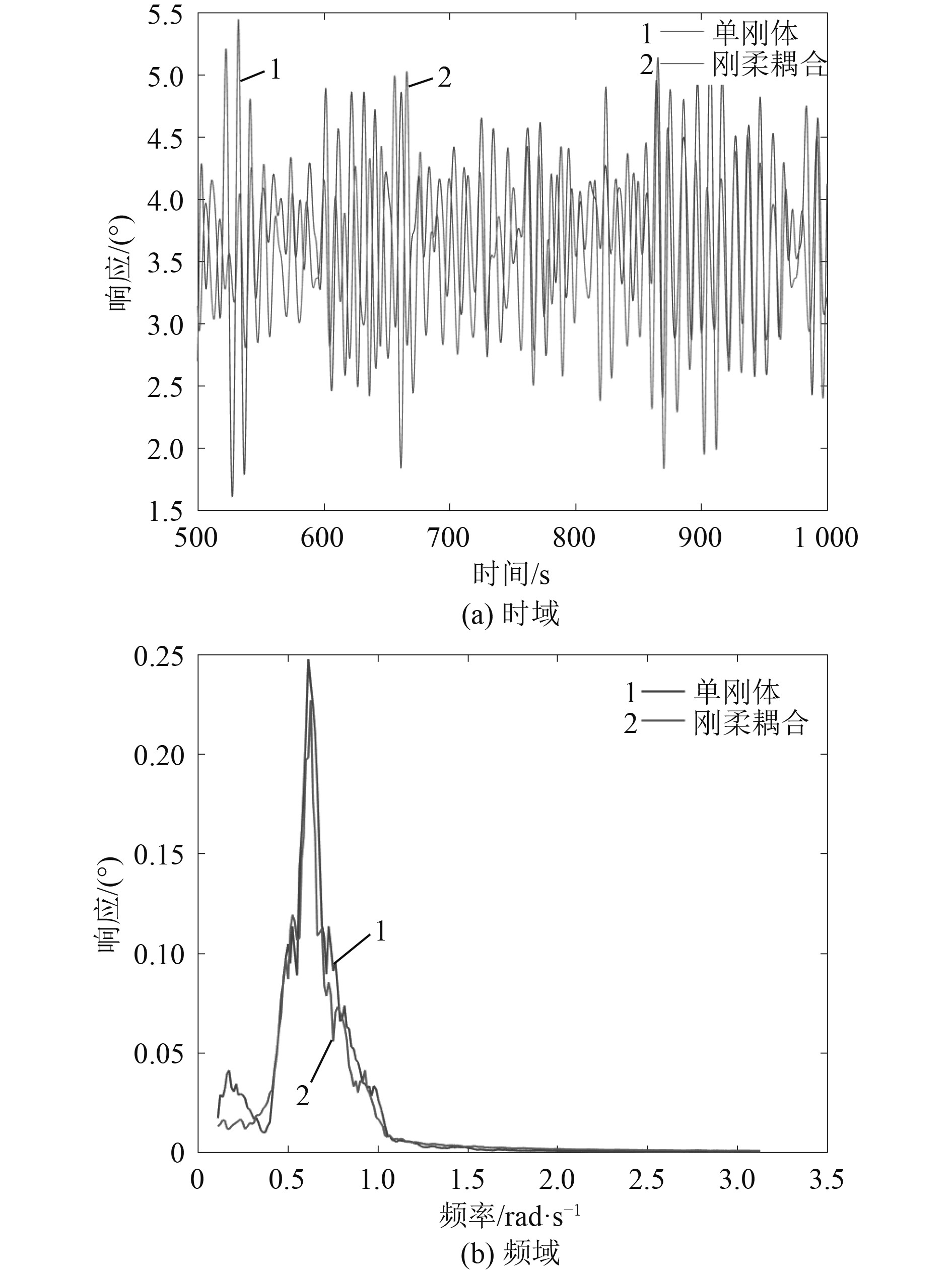
图 8 额定工况纵摇响应 Fig. 8 Pitch, LC2 |
|
图 9 额定工况气动转矩 Fig. 9 Torque, LC2 |

|
图 10 切出工况纵荡响应 Fig. 10 Surge, LC3 |
|
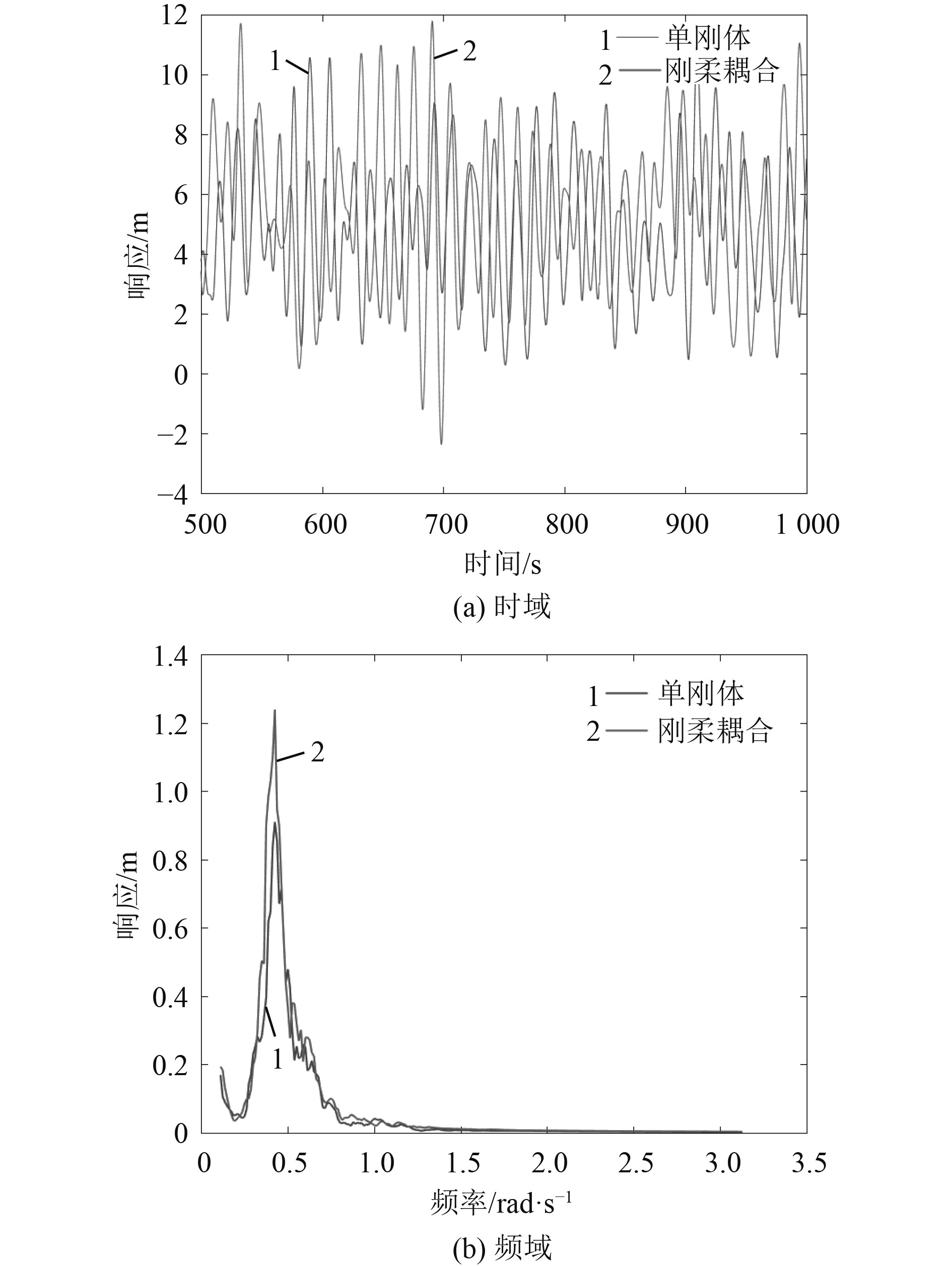
图 11 切出工况纵摇响应 Fig. 11 Pitch, LC3 |
|
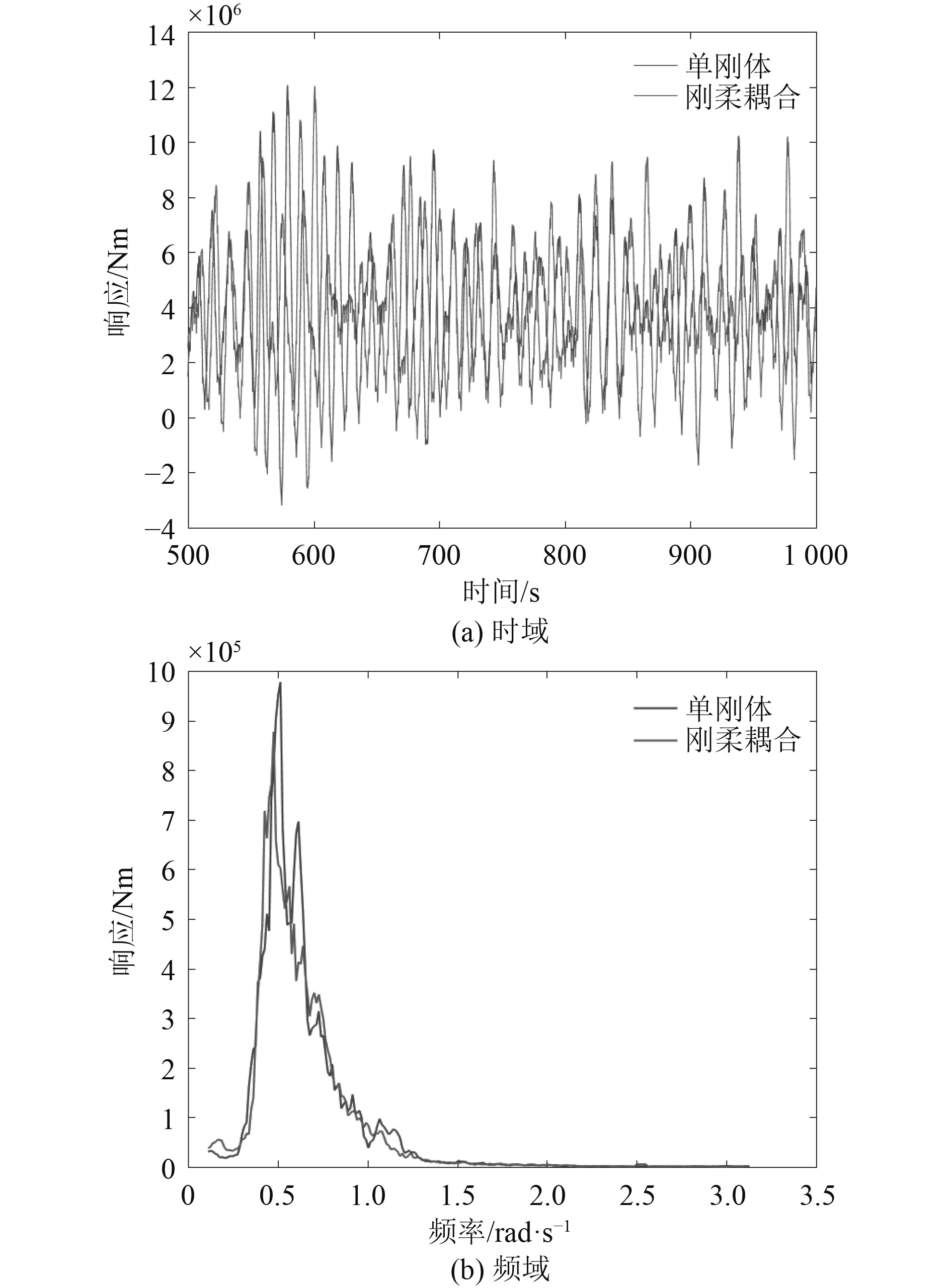
图 12 切出工况气动转矩 Fig. 12 Torque, LC3 |
|
图 13 极限工况纵荡响应 Fig. 13 Surge, LC4 |

|
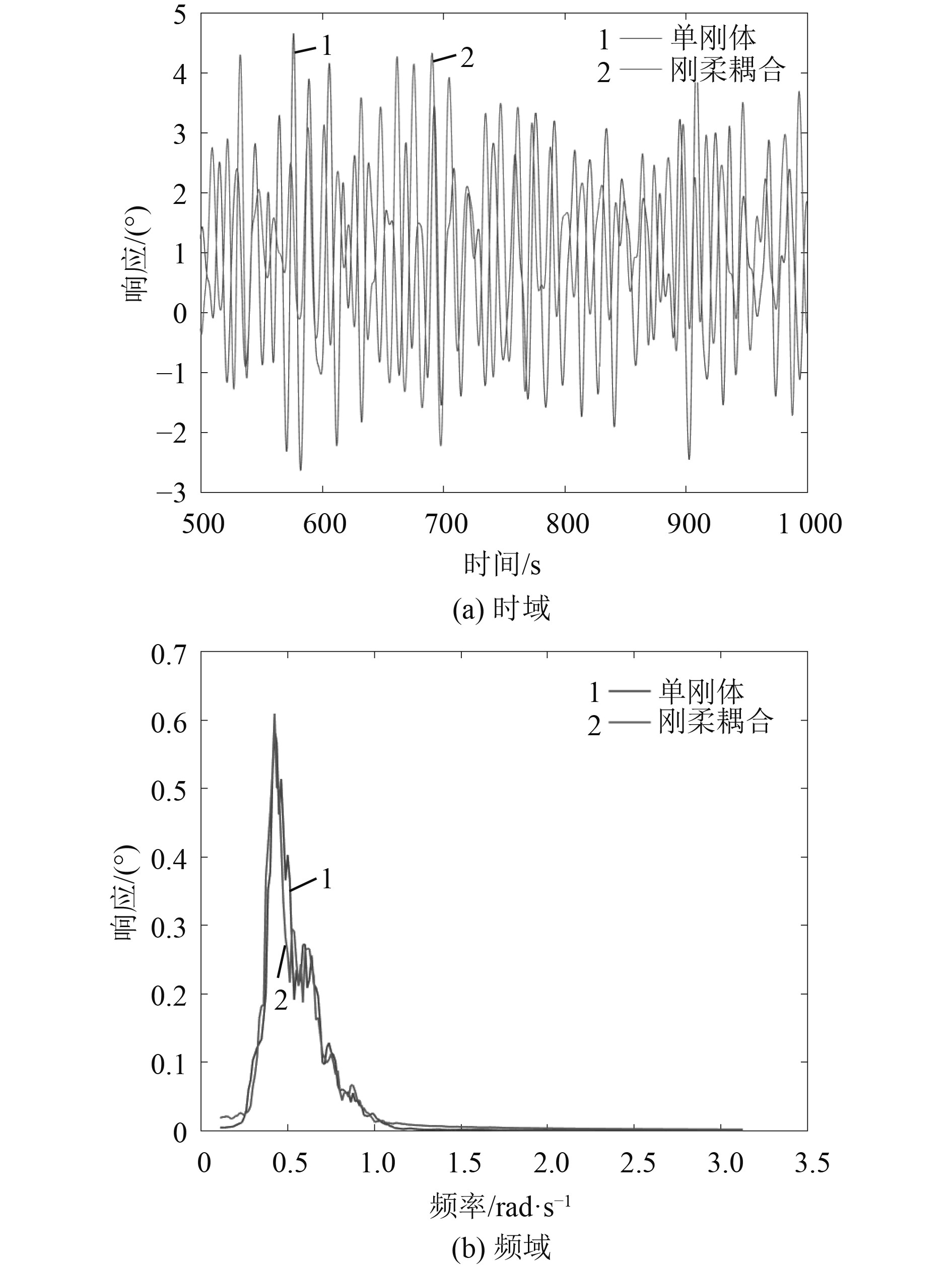
图 14 极限工况纵摇响应 Fig. 14 Pitch, LC4 |
|
图 15 极限工况转矩 Fig. 15 Torque, LC4 |
|
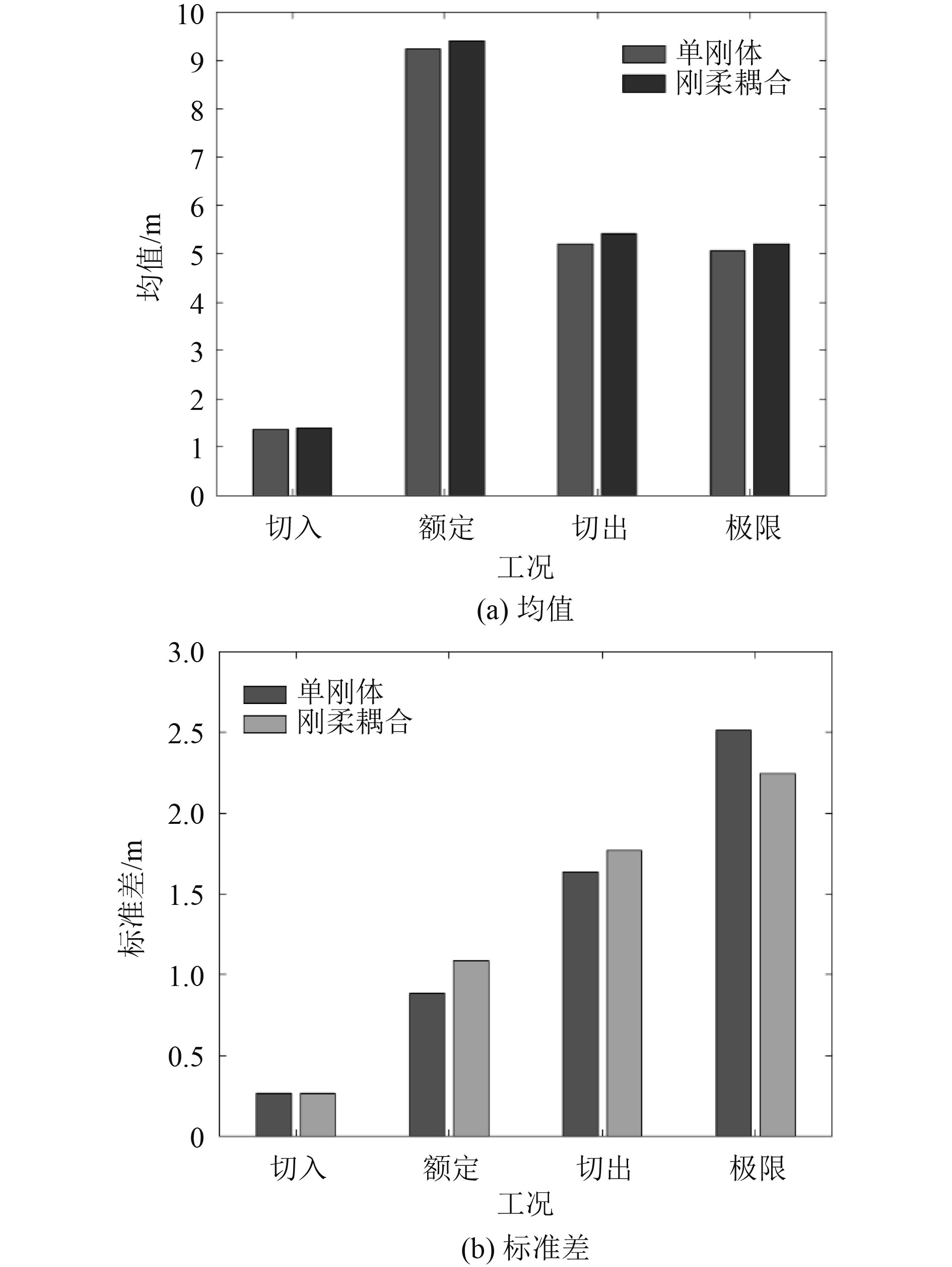
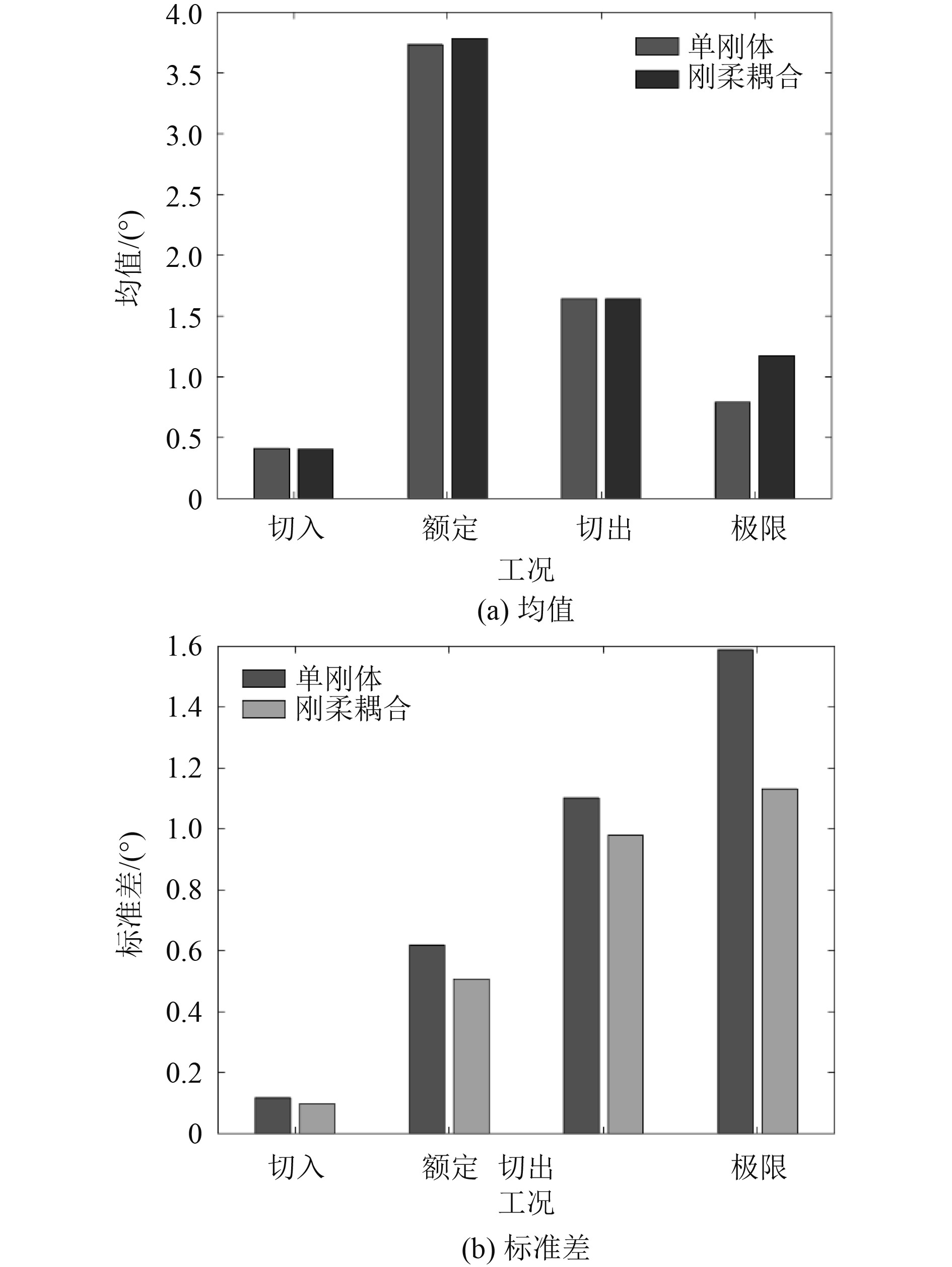
图 16 各工况纵荡统计值对比 Fig. 16 Surge comparison |
|
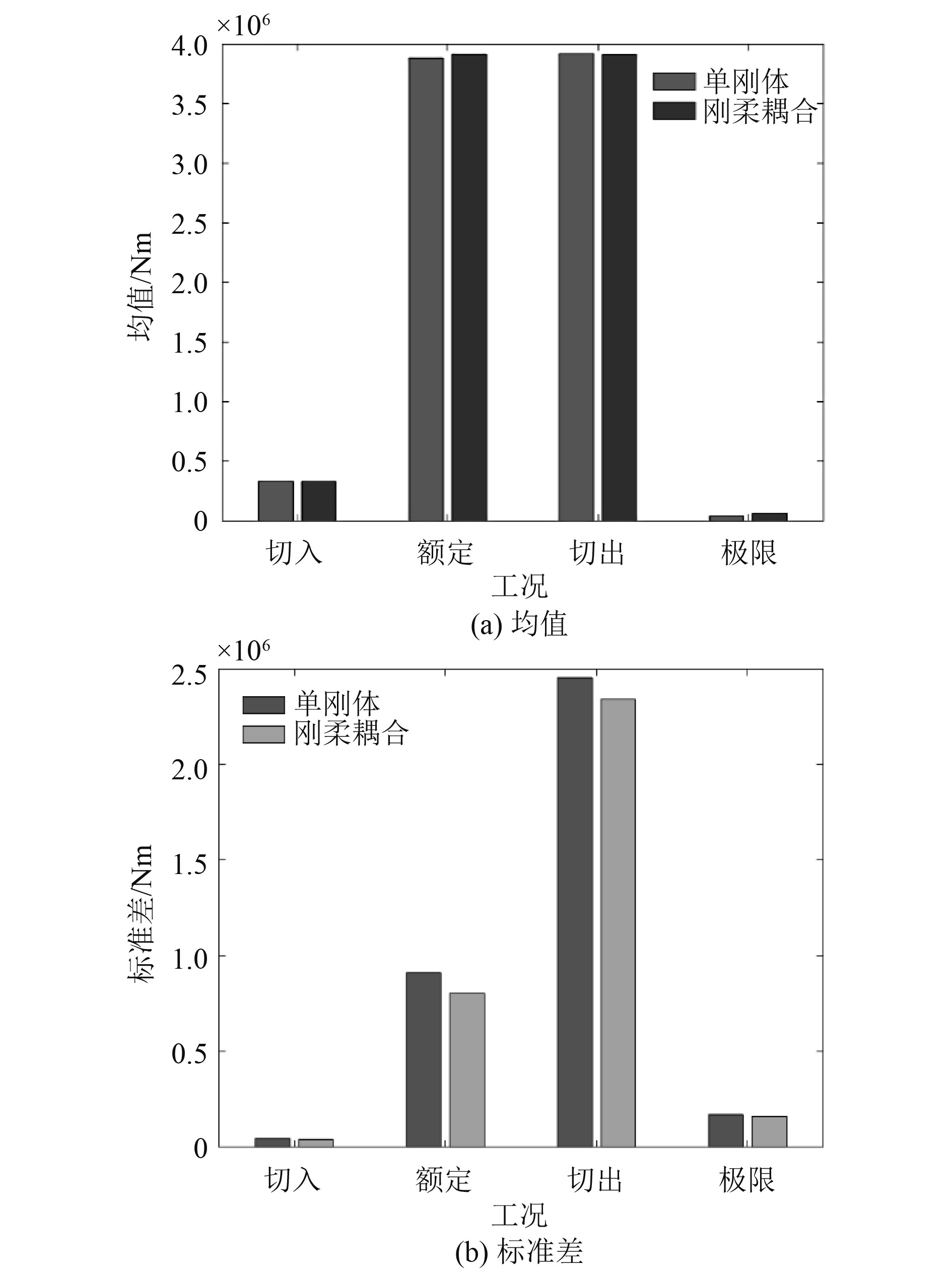
图 17 各工况纵摇统计值对比 Fig. 17 Pitch comparison |
|
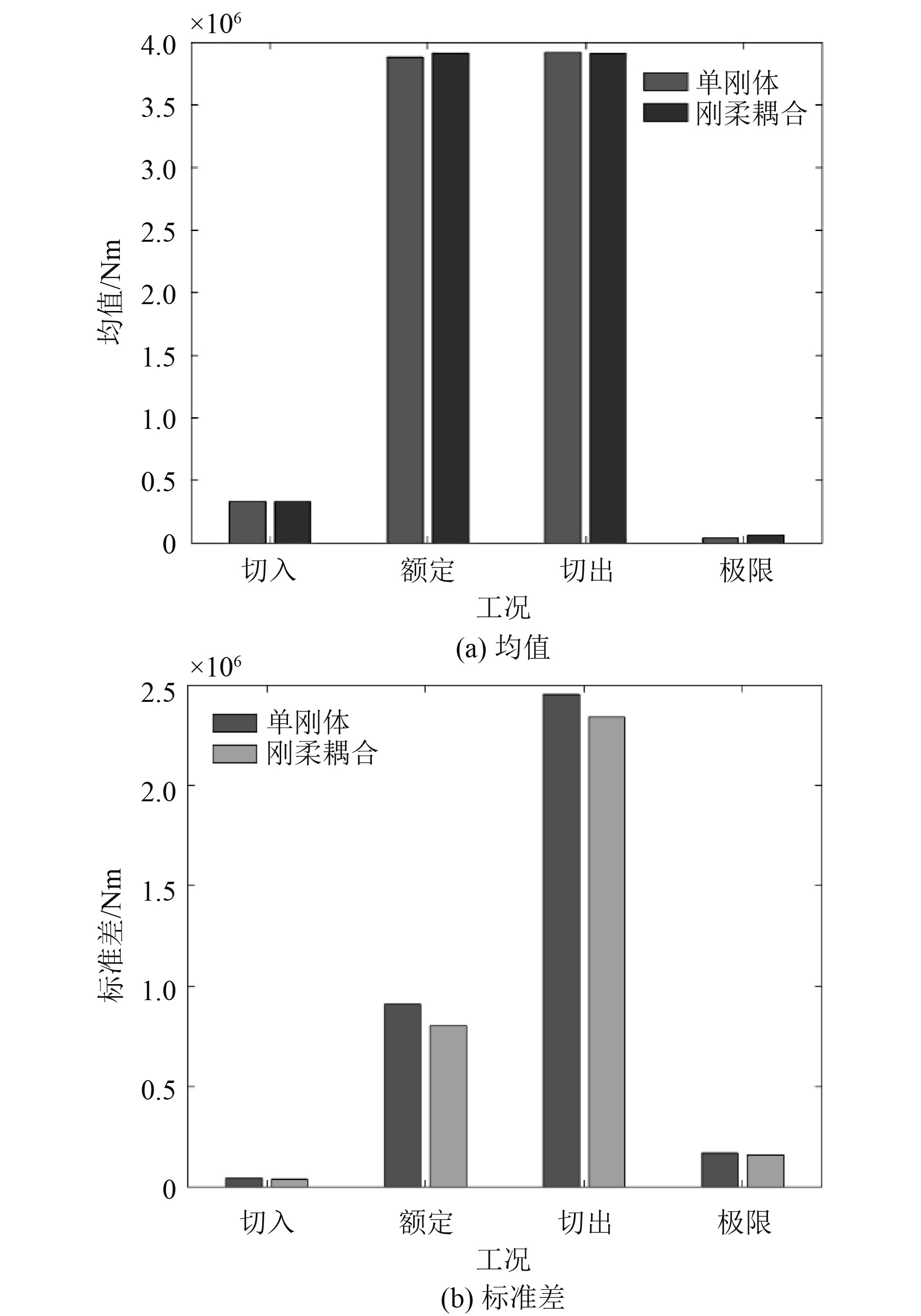
图 18 各工况转矩统计值对比 Fig. 18 Torque comparison |
针对不同工况进行分别分析,分析中用到的相对差异均指刚-柔耦合方法相对于单刚体方法的差异,即
1)对于切入工况,风浪环境条件较为温和,风机以低功率转动,桨距角为0°,浮式风机的纵荡、纵摇运动较小,2种方法所得气动转矩略有差异,而纵荡和纵摇运动一致性较好,以下重点分析另外3个工况。
2)浮式风机纵荡/纵摇运动及风机气动转矩的平均值采用两种不同模型得到的结果非常接近;对于极限工况,2种模型得到的浮式风机纵摇平均值相对差异较大,但绝对差异仅为0.5°。因此,浮式风机系统的纵荡/纵摇运动及风机气动转矩的平均值非常接近,两种不同模型的计算结果差异很小。
3)2种不同模型计算得到的浮式风机纵荡/纵摇及气动功率标准差的相对差异较为显著。对于浮式风机的纵荡运动,在额定和切出工况,2种模型的纵荡标准差相对差异较小,刚体模型结果略小于刚-柔耦合模型结果;而极限工况结果相反,和刚体模型结果相比,刚-柔耦合模型得到的纵荡标准差减小约20%。对于浮式风机的纵摇运动,刚体模型得到的纵摇运动标准差均大于刚-柔耦合模型的结果,相对差异最大为极限工况约为30%。这是由于柔性叶片和塔柱的振动吸收了部分外载荷能量,使得刚-柔耦合模型的结果小于刚体模型的结果。对于气动转矩,2种模型得到的标准差差异较小,额定工况的相对差异最大为10%左右。
3.2 计算效率统计为研究不同计算方法的计算效率,本文各工况均选用Matlab算法进行数值模拟,模拟时长均为1000 s,最终得到的计算效率统计对比如表3所示。
|
|
表 3 计算效率对比 Tab.3 Efficiency comparison |
可知:切入工况耗时最长,这是由于在低风速时BEM方法迭代收敛需要的时间较长;刚体模型相对刚-柔耦合模型的计算效率优势极为明显,如切入工况,刚体模型的计算时间仅为刚-柔耦合模型计算时间的10%左右。这是由于刚-柔耦合程序不仅计算了整体载荷、位移,还在每个时间步中计算塔柱与叶片变形,并将此变形代入气动模块进行耦合。这一过程使得结构动力学矩阵维度陡增,从而求解难度与消耗时长激增。
实际设计中,应充分考虑2种计算模型的特点,合理使用2种计算模型。在浮式风机系统的动力学参数设计初始阶段,由于刚体模型计算的快速性,可以用来获得浮式风机系统运动及气动转矩,通过大量参数组合计算及方案筛选,确定初步的浮式风机系统动力学设计参数。之后,针对已有的浮式风机系统设计参数,采用刚-柔耦合模型开展进一步的校核,以获得更为精确的计算结果。
4 结 语本文以OC4-NERL5 MW浮式风机为例,建立浮式风机系统刚体动力学模型及刚-柔耦合动力学模型;考虑不同工况,对比研究了刚体模型及刚-柔耦合模型2种方法在计算浮式风机系统纵荡/纵摇及气动转矩的差异,分析了2种模型的实用性。研究结论如下:
1)对于浮式风机系统纵荡/纵摇运动,切入工况下浮式风机的运动较小,2种方法所得的风机系统纵荡/纵摇的平均值和标准差都非常接近;对于其他工况,采用2种不同模型得到的浮式风机纵荡/纵摇的平均值结果也非常接近。
2)除去切入工况,2种模型计算得到的浮式风机运动标准差的差异较为显著,相对差异最大为极限工况。和刚体模型结果相比,刚-柔耦合模型的纵荡标准差最大减小约20%,纵摇标准差最大减小约30%。弹性叶片和塔柱振动可吸收部分外载荷能量,使得刚-柔耦合模型得到的运动标准差小于刚体模型结果。
3)对于所有的工况,2种模型得到的气动转矩均值几乎相同;标准差略有差异,额定工况气动转矩标准差的相对差异最大,约10%左右。
4)实际设计中应合理使用2种计算模型,刚体模型可用于浮式风机系统的动力学参数设计初始阶段,进行多组参数组合及方案筛选的大规模计算;刚-柔耦合模型可用于后续的动力学参数校核,以获得更为精确的计算结果。
本文计算中,为防止桨距角不同对2种模型计算产生的影响,采用了定桨计算,与实际情况存在一定差异。另外,本文计算中,只考虑了风浪同向的情况,后续将进一步研究风浪异向的情况。
| [1] |
李焱. Spar型浮式风力机系统耦合动力响应特性研究[D]. 天津: 天津大学, 2018.
|
| [2] |
MINU J, SEUNGMIN L, SOOGAB L. Unsteady aerodynamics of offshore floating wind turbines in platform pitching motion using vortex lattice method[J]. Renewable Energy, 2014, 65(5): 207-212. |
| [3] |
SHEN X, CHEN J G, HU P, et al. Study of the unsteady aerodynamics of floating wind turbines[J]. Energy, 2018, 145(c): 793-809. |
| [4] |
JONKMAN J M. Dynamic modeling and loads analysis of an offshore floating wind turbine[D]. University of Colorado, 2007.
|
| [5] |
ROBERTSON A N, JONKMAN J M. Loads analysis of an offshore floating wind turbine concepts[C]//Proceedings of the Twenty-first International Offshore and Polar Engineering Conference. Maul, Hawaii, USA, 2011.
|
| [6] |
刘利琴, 肖昌水, 郭颖, 等. 基于Jourdain原理和有限元离散的浮式风机动力响应分析[J]. 哈尔滨工程大学学报, 2020, 41(3): 309-317. DOI:10.11990/jheu.201810068 |
| [7] |
叶江舟, 胡志强, 王晋. 张力腿式浮式风机耦合动力响应理论模型与数值实现[J]. 海洋工程, 2018, 36(2): 100-107. DOI:10.16483/j.issn.1005-9865.2018.02.012 |
| [8] |
陈嘉豪, 刘格梁, 胡志强. 海上浮式风机时域耦合程序原理及其验证[J]. 上海交通大学学报, 2019, 53(12): 50-59. DOI:10.16183/j.cnki.jsjtu.2019.12.006 |
| [9] |
陈嘉豪, 胡志强. 半潜式海上浮式风机气动阻尼特性研究[J]. 力学学报, 2019, 51(4): 293-303. |
| [10] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW Reference Wind Turbine for Offshore System Development[R]. National Renewable Energy Laboratory (NREL), 2009.
|
| [11] |
刘利琴, 肖昌水, 郭颖. 海上浮式水平轴风力机气动特性研究[J]. 太阳能学报, 2021, 42(1): 302-309. DOI:10.19912/j.0254-0096.tynxb.2018-0866 |
 2023, Vol. 45
2023, Vol. 45
