水下航行器的动力推进装置由低速无刷电机组成,低速无刷电机在适应水下航行器螺旋桨负载特征的同时,其高效率工作范围也较宽[1-2]。水下航行器低速无刷电机的推进方式为2个螺旋桨互为反方向旋转产生推力而前进。但在不同水域以及航行任务需求情况下,需要对水下航行器低速无刷电机速度进行调整[3],以满足航行需求。目前有很多学者研究低速无刷电机调速控制方法,仲伟正等[4]提出直流无刷电机驱动系统调速方法,通过计算不同调制方法情况下低速无刷电机换相转矩脉动,以其为基础设计调速控制策略,将该策略写入复杂可编程逻辑器件内,通过启动复杂可编程逻辑器件实现低速无刷直流电机调速控制。徐会风等[5]提出零矢量的二三导通无刷直流电机调速控制方法,利用二三导通的驱动方式,将低速无刷直流电机转矩划分为12个分区,再利用零矢量控制低速无刷直流电机调速。上述2种方法虽可实现低速无刷直流电机调速控制,但二者均存在调速控制精度不足和反应时间过长问题。为此本文提出水下航行器低速无刷直流电机调速控制方法,提升水下航行器航行速度控制水平。
1 低速无刷直流电机调速控制方法 1.1 水下航行器低速无刷直流电机数学模型构建以水下航行器低速无刷直流电机相变量为基础,建立数学模型,该模型在构建前,设置模型假设条件为:1)水下航行器低速无刷直流电机的三相绕组为对称状态,且每个绕组的电阻、互感等参数均相同[6]。2)低速无刷直流电机控制开关均为正常状态。3)忽略低速无刷直流电机齿槽效应、磁芯饱和、涡轮损耗等[7]。4)低速无刷直流电机的反电动势为平顶,且呈梯形波状态分布。
以上述水下航行器低速无刷直流电机特性为基础,构建低速无刷直流电机电压方程。令
| $ \begin{split} \left[ \begin{gathered} {u_A} \\ {u_B} \\ {u_C} \\ \end{gathered} \right] = &\left[ \begin{array}{*{20}{l}} {R_A}& 0& 0 \\ 0&{R_B}& 0 \\ 0& 0& {R_C} \end{array} \right]\left[ \begin{gathered} {i_A} \\ {i_B} \\ {i_C} \\ \end{gathered} \right] + \frac{\rm d}{{{\rm d}t}}\left[ \begin{array}{*{20}{l}} {Q_A}& {Q_{AB}}& {Q_{AC}} \\ {Q_{BA}}& {Q_B}& {Q_{BC}} \\ {Q_{CA}}& {Q_{CB}}& {Q_C} \end{array} \right] \times \\ & \left[ \begin{gathered} {i_A} \\ {i_B} \\ {i_C} \\ \end{gathered} \right] + \left[ \begin{gathered} {g_A} \\ {g_B} \\ {g_C} \\ \end{gathered} \right] + \left[ \begin{gathered} {u_n} \\ {u_n} \\ {u_n} \\ \end{gathered} \right]。\\[-30pt] \end{split} $ | (1) |
式中:
当水下航行器低速无刷直流电机满足假设条件时[8],绕组之间的互感、电流等均相同,利用
| $ \begin{split} {\left[ \begin{gathered} {u_A} \\ {u_B} \\ {u_C} \\ \end{gathered} \right]^\prime } = &\left[ \begin{array}{*{20}{l}} R & 0 & 0 \\ 0 & R & 0 \\ 0 & 0 & R \end{array} \right]\left[ \begin{gathered} {i_A} \\ {i_B} \\ {i_C} \\ \end{gathered} \right] + \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ \begin{array}{*{20}{c}} Q - M & 0 & 0 \\ 0 & Q - M & 0 \\ 0 & 0 & Q - M \end{array} \right] \times \\ & \left[ \begin{gathered} {i_A} \\ {i_B} \\ {i_C} \\ \end{gathered} \right] + \left[ \begin{gathered} {g_A} \\ {g_B} \\ {g_C} \\ \end{gathered} \right] + \left[ \begin{gathered} {u_n} \\ {u_n} \\ {u_n} \\ \end{gathered} \right]。\\[-30pt] \end{split} $ | (2) |
令
| $ {P_e} = \left( {{g_a} \times {i_a} + {g_b} \times {i_b} + {g_c} \times {i_c}} \right) \times {\left[ \begin{gathered} {u_A} \\ {u_B} \\ {u_C} \\ \end{gathered} \right]^\prime }。$ | (3) |
式中:
假设
| $ {M_X} = {h_e} + {h_L} + \frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} \times J + {B_v} \times {P_e}。$ | (4) |
式中:
模糊PID控制参数是传统PID控制参数与模糊控制参数相结合的一种控制参数,能够在保证控制稳定性的前提下,解决控制过程中的误差、鲁棒性等问题。
利用PID控制参数控制水下航行器低速无刷直流电机调速时,需要检测并获取该电机的转速和电流误差,同时需要记录误差值的变化率,以便进行控制参数调整并保证控制的精度和稳定性。模糊PID控制参数输入模糊子集论域表达公式如下:
| $ {E_R} = {M_X} \times \left( {{W_1} + {W_2}} \right) \times W'。$ | (5) |
式中:
以式(5)结果为基础,则模糊PID控制参数的校正量论域表达公式如下:
| $ \Delta {K_p} = {E_R} \times {\left[ \begin{gathered} {u_A} \\ {u_B} \\ {u_C} \\ \end{gathered} \right]^\prime } 。$ | (6) |
PID控制参数运算过程简单,具备较好的适应性和可靠性。PID控制参数通过调节输入值和实际反馈值的偏差,实现目标的控制。使用PID控制参数实现水下航行器低速无刷直流电机的调速控制,PID控制参数数学表达式如下:
| $ e(t) = \Delta {K_p} \times \left[ {y^*(t) - y(t)} \right] \times \kappa 。$ | (7) |
式中:
在使用模糊PID算法控制水下航行器低速无刷直流电机调速时,受其参数影响,其输出控制量不够准确,需对其参数实施整定。使用麻雀搜索算法对模糊PID控制参数进行整定,其详细过程如下:
将模糊PID控制参数看作麻雀集合矩阵,表达式为:
| $ X = e(t) \times {\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right]^{\rm{T}}} 。$ | (8) |
式中:
以式(8)结果为基础,建立麻雀的适应度数值矩阵,表达式为:
| $ {{F}_x} = X + {\left[ {f({x_1}),f({x_2}), \cdots ,f({x_n})} \right]^{\rm{T}}}。$ | (9) |
式中:
对麻雀种群进行初始化,表达式为:
| $ {x_{n + 1}} = \cos (k \times \arccos {x_n} \times {{\boldsymbol{F}}_x})。$ | (10) |
式中:
将式(10)结果映射成
| $ {x_{id}} = {l_d} + (1 + {y_{id}}) \times ({u_d} - {l_d})/{x_{n + 1}}。$ | (11) |
式中:
依据自适应分布方法,更新麻雀位置,整定模糊PID控制参数,表达式为:
| $ x_i^t = \left\{ \begin{array}{ll} {x_i} + {x_{id}} \times t(\lambda ),&{\rm{rand}} < p,\\ {x_i},& {\rm{otherwise}}。\\ \end{array} \right. $ | (12) |
式中:
以上述公式为基础,利用麻雀算法整定模糊PID控制参数流程如下:
步骤1 对麻雀种群进行初始化,并设置迭代次数、种群数量、问题维数等参数。确定模糊PID控制的基本参数。
步骤2 利用式(10)、式(11)对麻雀种群进行映射处理,建立起PID控制参数在不同控制环节下的初始参数值。
步骤3 利用式(9)计算所有麻雀的适应度数值,并对计算结果进行降序排列。
步骤4 对麻雀种群添加扰动,并对麻雀种群进行更新处理后,再次计算麻雀种群内每只麻雀的适应度数值。然后对比随机数数值是否大于麻雀密度概率,若大于选择添加扰动后的适应度数值,反之则选择添加扰动前的适应度数值。
步骤5 判断当前迭代次数是否达到迭代次数阈值,若是,则输出当前最优解,反之返回步骤4。
步骤6 根据最终的控制参数进行验证和性能测试,检验设计方案的有效性和控制参数的稳定性。
经过上述过程,得到模糊PID控制参数整定结果,利用控制参数控制水下航行器低速无刷直流电机调速。
2 实验分析以某水下航行器作为实验对象,该航行器配备型号为HXL70-8的低速无刷直流电机,应用本文方法对该水下航行器低速无刷直流电机调速进行控制,分析本文方法实际应用效果。
以低速无刷直流电机电磁功率作为指标,使用本文方法计算该水下航行器低速无刷直流电机电磁功率,计算结果如表1所示。
分析表1可知,应用本文方法计算水下航行器低速无刷直流电机电磁功率的计算结果和实际结果之间最小差值为0 W,最大差值也仅为0.2 W,说明本文方法计算水下航行器低速无刷直流电机电磁功率精度较高,可有效为水下航行器低速无刷直流电机调速控制提供数据基础。
|
|
表 1 水下航行器低速无刷直流电机电磁功率(W) Tab.1 Electromagnetic power of low speed brushless dc motor for underwater vehicles (W) |
测试在不同迭代次数时,输出全局最优结果的收敛情况,测试结果如图1所示。
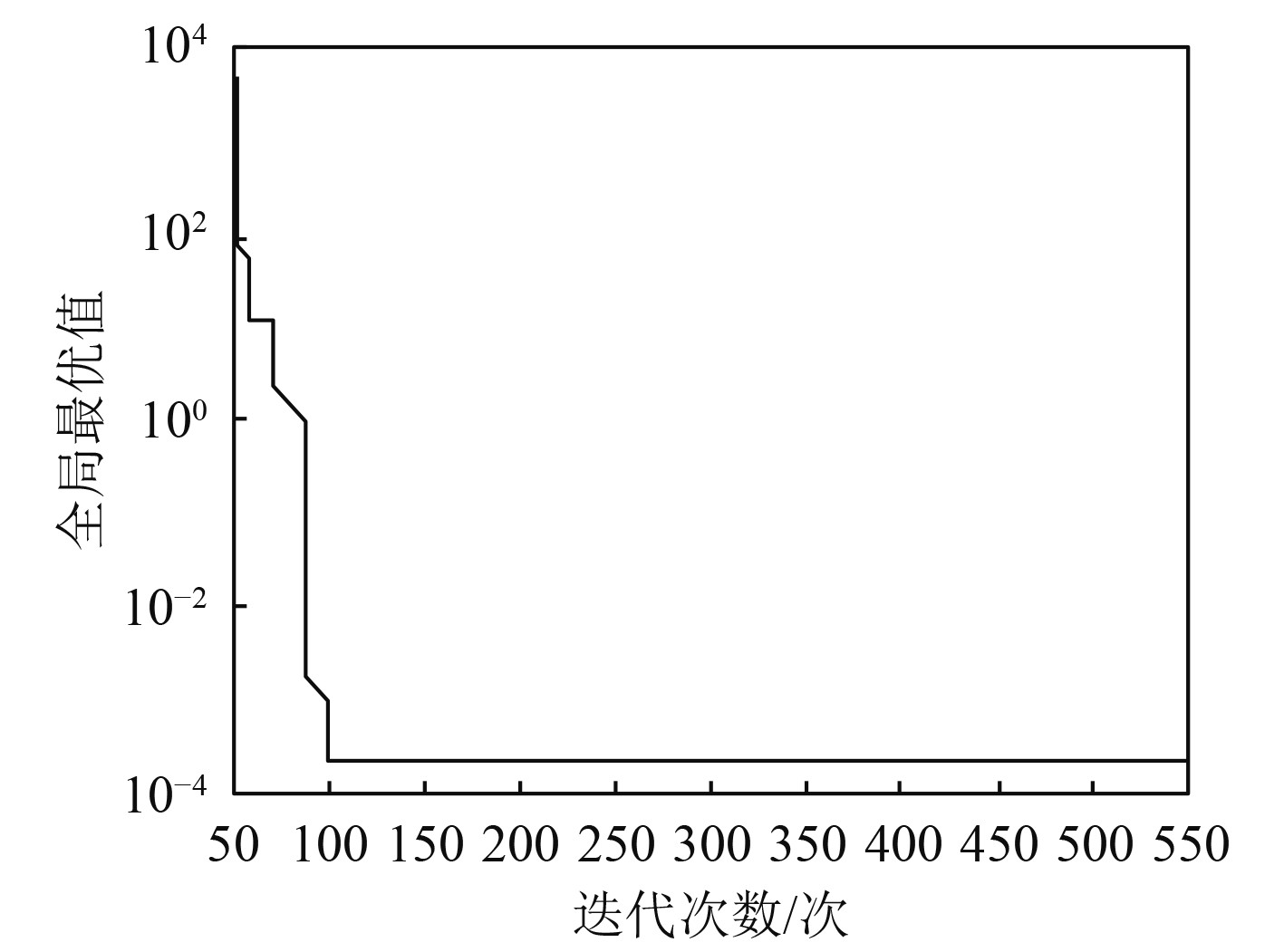
|
图 1 收敛测试结果 Fig. 1 Convergence test results |
分析图1可知,在输出模糊PID控制参数整定全局最优结果时,在迭代次数为50次时,全局最优数值接近104,但随着迭代次数增加,全局最优结果输出函数呈现迅速下降趋势,并在迭代次数为100次时,全局最优结果输出函数数值接近10−4。该结果说明应用本文方法输出模糊PID控制参数整定时,其全局最优函数可迅速达到收敛状态,其输出结果较为准确,从侧面说明本文方法对水下航行器低速无刷直流电机进行调速控制效果较好。
使用本文方法控制该水下航行器低速无刷直流电机调速,控制结果如图2所示。
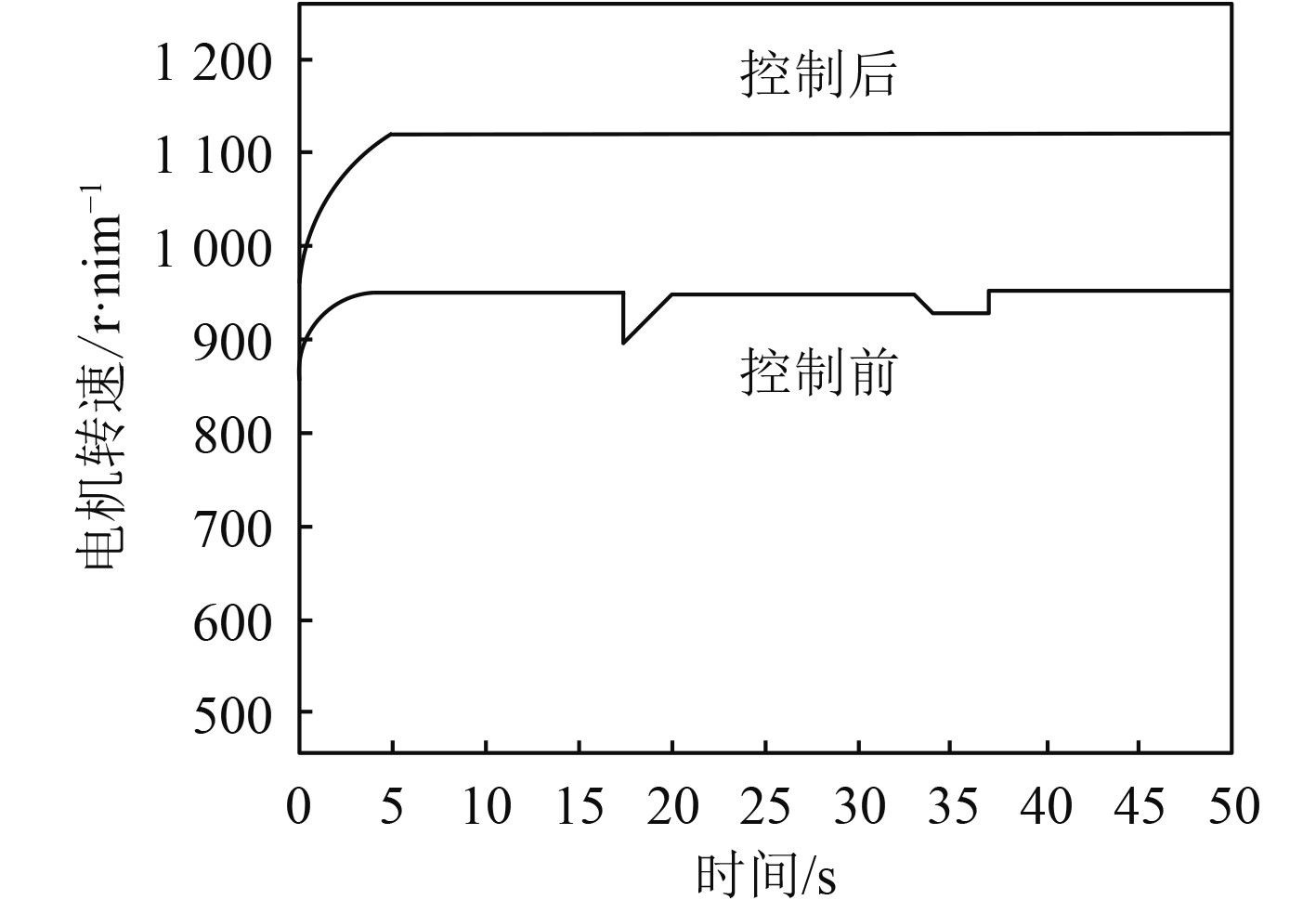
|
图 2 水下航行器低速无刷直流电机调速控制结果 Fig. 2 Speed control results of low speed brushless dc motor for underwater vehicles |
分析图2可知,该水下航行器在航行过程中,其电机转速不够稳定,出现骤降和骤升情况,而应用本文方法对低速无刷直流电机进行调速控制后,其电机转速得到提升,且电机转速曲线呈现平衡状态。说明本文方法,可有效控制水下航行器低速无刷直流电机调速,具备较好的应用效果。
设置水下航行器低速无刷直流电机转速为900 r/min,测试其控制水下航行器低速无刷直流电机调速时的响应能力,测试结果如图3所示。
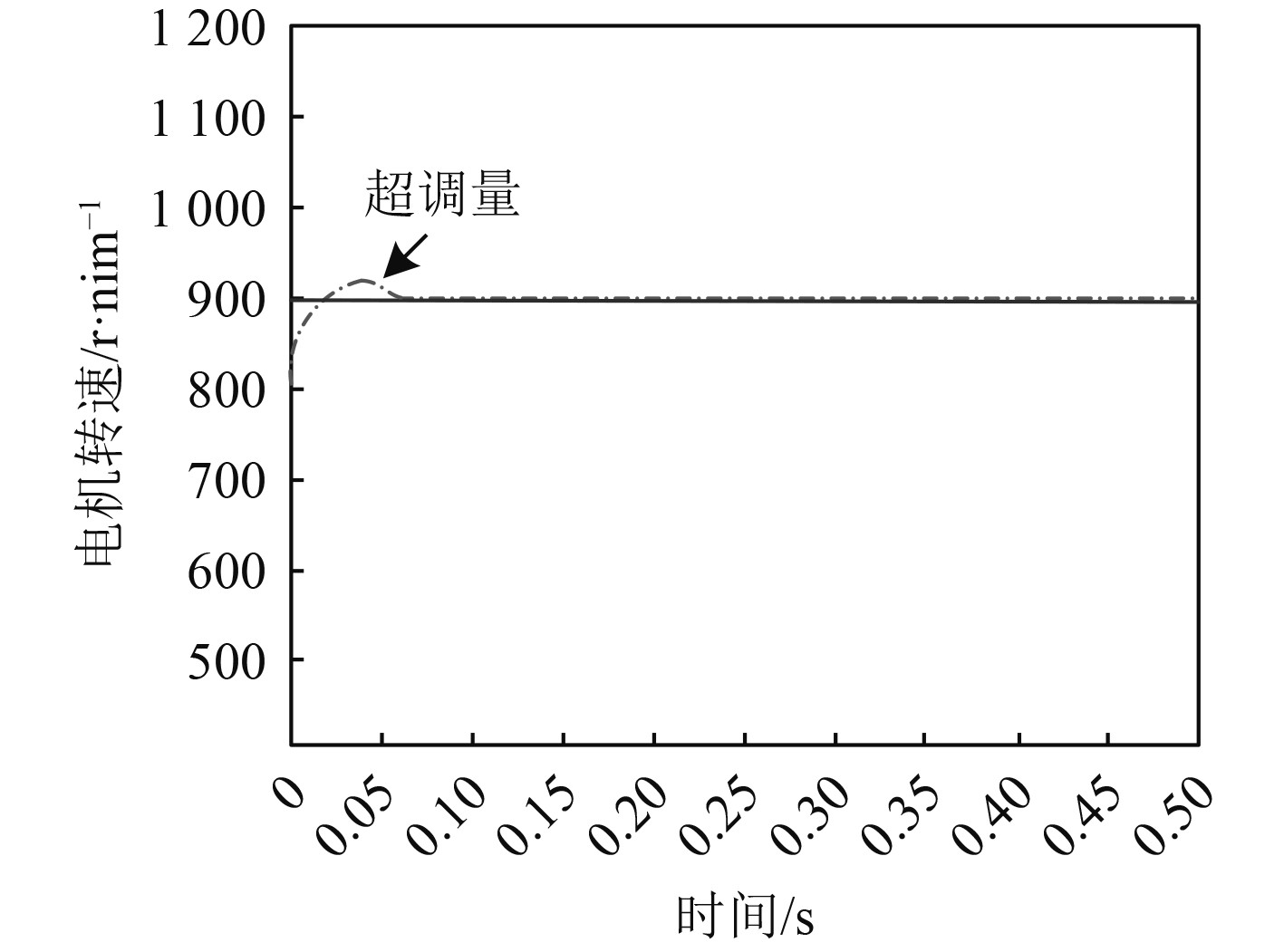
|
图 3 控制水下航行器低速无刷直流电机调速响应 Fig. 3 Control the speed control response of low speed brushless DC motor for underwater vehicles |
分析图3可知,应用本文方法对水下航行器低速无刷直流电机调速进行控制时,其在0.05 s时即可实现水下航行器低速无刷直流电机调速控制,且其超调量极小,说明本文方法控制水下航行器低速无刷直流电机调速响应较为迅速,控制能力强。
3 结 语本文研究水下航行器低速无刷直流电机调速控制方法,应用模糊IPD控制参数实现低速无刷直流电机调速控制,使用麻雀搜索算法解决模糊PID参数整定问题。多角度验证表明,该方法应用效果较好,未来可在航海、海底勘探等方面应用。
| [1] |
张娟, 孙彦超, 高杨, 等. 基于花授粉算法的无刷直流电动机速度控制研究[J]. 微特电机, 2020, 48(3): 58-60,64. ZHANG Juan, SUN Yanchao, GAO Yang, et al. Research on Speed Control of Brushless DC Motor Based on Flower Pollination Algorithm[J]. Small & Special Electrical Machines, 2020, 48(3): 58-60,64. DOI:10.3969/j.issn.1004-7018.2020.03.013 |
| [2] |
唐伟, 王立忠, 庄健, 等. 无刷直流电机的模糊自整定MRPID转速控制方法研究[J]. 中国机械工程, 2021, 32(15): 1786-1792,1800. DOI:10.3969/j.issn.1004-132X.2021.15.003 |
| [3] |
尹洪桥, 易文俊, 李璀璀, 等. 基于速度环模糊参数自适应PID算法的弹载无刷直流电机控制系统研究[J]. 兵工学报, 2020, 41(1): 30-38. |
| [4] |
仲伟正, 刘曰涛, 毛薪然, 等. 基于CPLD直流无刷电机驱动系统的调速控制分析[J]. 机床与液压, 2021, 49(1): 7-12. DOI:10.3969/j.issn.1001-3881.2021.01.002 |
| [5] |
徐会风, 苏少平, 杜庆诚. 一种新型零矢量的二三导通无刷直流电机直接转矩控制系统研究[J]. 西安交通大学学报, 2020, 54(4): 85-92. DOI:10.7652/xjtuxb202004011 |
| [6] |
汪宗彪, 龚纯, 姜淑忠, 等. 深海推进用永磁无刷电机温度场分析[J]. 电机与控制应用, 2022, 49(2): 47-53. DOI:10.12177/emca.2021.176 |
| [7] |
曹晓明, 魏勇, 尹岳昆, 等. 欠驱动UUV的动态面轨迹跟踪抗干扰控制[J]. 计算机仿真, 2022, 39(12): 17-22,33. CAO Xiaoming, WEI Yong, YIN Yuekun, et al. Underactuated UUV Dynamic Surface Tracking Based on Disturbance Rejection Control[J]. Computer Simulation, 2022, 39(12): 17-22,33. DOI:10.3969/j.issn.1006-9348.2022.12.004 |
| [8] |
刘金刚, 张聪悦, 傅兵, 等. EHB用无刷直流电机齿槽转矩电流补偿控制策略研究[J]. 机械科学与技术, 2022, 41(9): 1327-1333. LIU Jin'gang, ZHANG Congyue, FU Bing, et al. Exploring Current Compensation Control Strategy for Reducing Cogging Torque of Brushless DC Motor in EHB[J]. Mechanical Science and Technology for Aerospace Engineering, 2022, 41(9): 1327-1333. |
 2023, Vol. 45
2023, Vol. 45
