水下无人航行器(UUV)自主、智能、灵活且能长时间工作需要具备良好的控制性能,。但是因为水下环境复杂,水流多变,干扰不可控制,航向稳定性及其精度无法得到保证仍是一个需要解决的问题。
目前实现UUV航向控制的主要方法包括PID控制、反步法控制、模糊控制及滑模控制等[1]。PID控制算法较为简便且控制性能较强,在航向控制方面受到广泛应用。但对于模型复杂的控制对象而言,PID控制无法满足其设计需求,通常需要与其他的控制方法相结合来实现较复杂系统的控制,这会使得其设计变得更为复杂[2]。反步法控制的本质是先拆分,再集成,其主要思想是将高复杂度、高阶数的非线性系统逐一拆分成若干个低阶数子系统,再根据李雅普诺夫稳定性原理对每个子系统分别设计模拟控制量,再将各部分子系统集成,最终实现总体系统控制[3]。该方法针对模型较为简单的系统设计精确,而且当系统存在不确定项时,可以放宽匹配条件。但是设计过程较为繁琐,在航向控制问题中,系统控制量求解时随着系统阶数的增加,微分计算越来越复杂,较难在实际控制中应用。模糊控制方法是一种借助模糊规则和论域分割来实现将复杂系统简单化的控制方法,其不完全依赖于系统数学模型,从而具有较强鲁棒性[4],但由于模糊控制自身局限性,难以实现复杂系统的稳定性分析及整体化设计,使得无法精确控制系统,使得其动态品质变差。
滑模控制相较于其他控制方法而言,其系统结构可以根据当前的状态有针对性地不断优化,且其对外界干扰及模型参数变化不敏感,从而表现出较强的自适应能力和鲁棒性[5]。本文采用滑模控制方法,在模糊运动学模型的基础上,采用干扰观测器模拟外界干扰,对系统进行干扰补偿,结合连续滑模控制器实现水下无人航行器的航向跟踪。
1 水下无人航行器建模 1.1 坐标系构建将UUV的空间运动分解成两部分,第1部分忽略其形变将其看成在空间中运动的质点,第2部分为UUA自身绕重心定点转动。此次建模主要应用了地面坐标系[6](固定坐标系)和潜航器坐标系(运动坐标系)对其空间运动进行分析。
1.1.1 地面坐标系(固定坐标系)为了分析UUV在整个空间中的运动,首先建立一个地面坐标系。在地面适合处选择固定点E将其设置为坐标原点,ζ轴垂直于水平面向下,称为铅垂轴;ξ轴平行于水平面,且UUV前进方向为正方向;η轴垂直于另外两轴,整个坐标轴满足右手系,如图1所示。
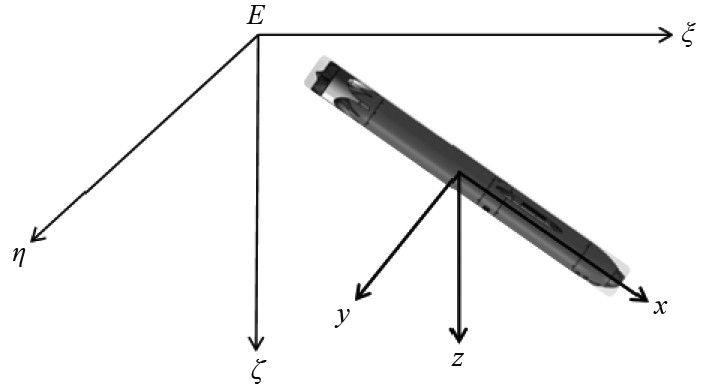
|
图 1 固定坐标与运动坐标系 Fig. 1 Fixed and moving coordinates |
为了分析UUV在水下的俯仰、首摇、转动问题,建立一个UUV坐标系[7](运动坐标系)。坐标原点设置在UUV的重心处,x轴水平于UUV艇身,前进方向为正方向;z轴垂直x轴,下为正方向;y轴与另两轴垂直且整个坐标系满足右手系。
1.2 运动参数 1.2.1 姿态角偏航角
俯仰角
横滚角
一般UUV运动问题需要用到2个坐标系之间相互转换,适用于航向追踪问题的坐标系转换满足方程[8]
| $ \left[\begin{array}{c}\xi \\ \eta \\ \zeta \end{array}\right] ={{T}} \left[\begin{array}{c}x\\ y\\ z\end{array}\right], $ | (1) |
| $\begin{split} {\rm{T}}=&\left[\begin{array}{ccc}{\rm{cos}}\varPsi {\rm{cos}}\theta & {\rm{cos}}\varPsi {\rm{sin}}\theta {\rm{sin}}\phi -{\rm{sin}}\varPsi {\rm{cos}}\varPsi \\ {\rm{sin}}\varPsi {\rm{cos}}\theta & {\rm{sin}}\varPsi {\rm{sin}}\theta {\rm{sin}}\phi +{\rm{cos}}\varPsi {\rm{cos}}\phi\\ -{\rm{sin}}\theta & {\rm{cos}}\theta {\rm{sin}}\phi \end{array}\right. \\ & \left.\begin{array}{ccc}{\rm{cos}}\varPsi sin\theta {\rm{cos}}\varPsi +{\rm{sin}}\varPsi {\rm{sin}}\phi \\ {\rm{sin}}\varPsi {\rm{sin}}\theta {\rm{cos}}\phi -{\rm{cos}}\varPsi {\rm{sin}}\phi \\ {\rm{cos}}\theta{\rm{cos}}\phi \end{array}\right] 。\end{split}$ | (2) |
式中:T=[n s a]=
在UUV系统中,依然满足牛顿第二定律。忽略UUV的形变将其看做一个刚体,并对其整体进行分析,满足基础动力学方程:
| $ \sum _{i}{m}_{i}\frac{{{\rm{d}}v}_{i}}{{\rm{d}}t} = \sum _{t}{F}_{i}。$ | (3) |
式中:
UUV行器通常有6个自由度,并且它的运动可以看做是刚体运动[9]。在UUV运动过程中,令
将上式转化为广义向量的矩阵形式为:
| $\begin{split} \left[\begin{array}{c}\dot{x}\left(t\right)\\ \dot{y}\left(t\right)\\ \dot{z}\left(t\right)\\ \dot{\varphi }\left(t\right)\\ \dot{\theta }\left(t\right)\\ \dot{\varPsi }\left(t\right)\end{array}\right]= &\left[\begin{array}{c}{\rm{cos}}\varPsi {\rm{cos}}\theta \\ {\rm{sin}}\varPsi {\rm{cos}}\theta \\ -{\rm{sin}}\theta \\ 0\\ 0\\ 0\end{array}\right]{v}_{x}+ \left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\\ 0\end{array}\right]{\mathrm{\omega }}_{x}+ \\ &\left[\begin{array}{c}0\\ 0\\ 0\\ {\rm{sin}}\phi {\rm{tan}}\theta \\ {\rm{cos}}\phi \\ {\rm{sin}}\phi {\rm{sec}}\theta \end{array}\right]{\mathrm{\omega }}_{y}+ \left[\begin{array}{c}0\\ 0\\ 0\\ {\rm{cos}}\phi {\rm{t}}an\theta \\ -{\rm{sin}}\phi \\ {\rm{cos}}\phi {\rm{sec}}\theta \end{array}\right]{\mathrm{\omega }}_{z} ,\end{split} $ | (4) |
由于UUV运动学模型是在线速度存在非完整约束的条件下得到的[10],减少了速度的维数。统有2个非完整约束,分别为绕y轴的线速度和绕z轴的线速度。因为速度维度的减少,所以速度在这2个方向为0。这2个约束可表示为:
| $ {s}^{{\rm{T}}}\dot{p}=0 ,$ | (5) |
| $ {a}^{{\rm{T}}}\dot{p} =0,$ | (6) |
将s,a,p展开并且用A(q)
| $ \begin{split}{{A(q)}} = &\left[ \begin{array}{*{20}{c}} {\rm{cos}}\varPsi {\rm{sin}}\theta {\rm{sin}}\phi - {\rm{sin}}\varPsi {\rm{cos}}\phi\\ {\rm{cos}}\varPsi {\rm{sin}}\theta {\rm{cos}}\phi + {\rm{sin}}\varPsi {\rm{sin}}\phi\end{array}\right.\\ & \left.\begin{array}{*{20}{c}} {\rm{sin}}\varPsi {\rm{sin}}\theta {\rm{sin}}\phi +{\rm{cos}}\varPsi {\rm{cos}}\phi & {\rm{cos}}\theta sin\phi & 0 & 0 & 0\\ {\rm{sin}}\varPsi {\rm{sin}}\theta {\rm{cos}}\phi -{\rm{cos}}\varPsi {\rm{sin}}\phi & {\rm{cos}}\theta {\rm{cos}}\phi & 0 & 0 & 0\end{array} \right]。\end{split} $ | (7) |
用向量场f1(g),f2(g),f3(g)和f4(g)线性组合称行的矩阵A(q)来描述速度,则建立如下运动模型:
| $ \dot{q}\left(t\right)= {f}_{1}\left(q\right){v}_{1} + {f}_{2}\left(q\right){v}_{2}+ {f}_{3}\left(q\right){v}_{3}+ {f}_{4}\left(q\right){v}_{4} 。$ | (8) |
式中:
| $ \left\{\begin{array}{*{20}{l}} {f}_{1}\left(q\right)=[{\rm{cos}}\varPsi {\rm{cos}}\theta \;\; {\rm{cos}}\theta {\rm{sin}}\varPsi \;\; -{\rm{sin}}\theta \;\; 0 \;\; 0 \;\; 0],\\ {f}_{2}\left(q\right)=[0 \;\; 0 \;\; 0 \;\; 1 \;\; 0 \;\; 0],\\ {f}_{3}\left(q\right)=[0 \;\; 0 \;\; 0 \;\; {\rm{sin}}\phi \mathrm{tan}\theta \;\; {\rm{cos}}\phi \;\; {\rm{sin}}\phi sec\theta ],\\ {f}_{4}\left(q\right)=[0 \;\; 0 \;\; 0 \;\; {\rm{cos}}\phi \mathrm{tan}\theta \;\; -{\rm{sin}}\phi \;\; {\rm{cos}}\phi \mathrm{sec}\theta ]。\end{array}\right. $ | (9) |
对于UUV,纵向运动可独立存在,将UUV纵向运动单独拆分出来,为空间的垂直平面运动。对于纵向运动,依然遵循牛顿定律和基础动力学方程[11],则有:
| $ {m}\dot{v}={-A}_{x}{v}^{2}+{T}\mathrm{cos}\alpha -{P}\mathrm{sin}\varTheta,$ | (10) |
| $\begin{split} {m}{v}\dot{\varTheta }=&{A}_{y}^{2}{v}^{2}\mathrm{\alpha }+{A}_{y}^{\delta }{v}^{2}{\mathrm{\delta }}_{\mathrm{e}}{+A}_{y}^{\omega }v{\omega }_{{z}_{1}}+\\ & {\lambda }_{22}\left(\dot{v}\alpha +v\dot{\alpha }\right)-{\lambda }_{26}{\dot{\omega }}_{{z}_{1}}+{T}\mathrm{sin}\mathrm{\alpha }-{P}\mathrm{cos}\varTheta,\end{split}$ | (11) |
| $\begin{split} {J}_{{z}_{1}}{\dot{\omega }}_{{z}_{1}}=&{A}_{{m}_{z}}^{a}{v}^{2}a-{A}_{y}^{\delta }{x}_{e}{v}^{2}{\delta }_{e}-{A}_{{m}_{z1}}^{\omega }v{\omega }_{{z}_{1}}+\\ &{\lambda }_{26}\left(\dot{v}a+v\dot{a}\right)-{\lambda }_{66}{\dot{\omega }}_{{z}_{1}}- \\&B\left(h\mathrm{sin}\theta -{x}_{b}\mathrm{cos}\theta \right)-Th。\end{split}$ | (12) |
式中:
由于纵向参数在任何时候都不会完全为0,所以侧向运动并不会单独存在。假设UUV是理想的直鳍舵上下对称,那么此时的侧向运动不含横滚,此时的侧向运动方程为:
| $ m{v}_{0}\dot{\kappa } = \left({A}_{z}^{\beta }{v}_{0}^{2} + T\right)\beta + {A}_{z}^{\delta }{v}_{0}^{2}{\delta }_{r} + {A}_{z}^{\omega }{v}_{0}{\omega }_{{y}_{1}} + {\lambda }_{33}{v}_{0}\dot{\beta } + {\lambda }_{35}{\dot{\omega }}_{{y}_{1}},$ | (13) |
| $\begin{split} {J}_{{y}_{1}}{\dot{\omega }}_{{y}_{1}}=&{A}_{{m}_{y}}^{\beta }{v}_{0}^{2}\beta -{A}_{z}^{\delta }{x}_{r}{v}_{0}^{2}{\delta }_{r}-{A}_{{m}_{y1}}^{\omega }{v}_{0}{\omega }_{{y}_{1}}-\\ &{\lambda }_{55}{\dot{\omega }}_{{y}_{1}}-{\lambda }_{35}{v}_{0}\dot{\beta }+T{z}_{b}。\end{split}$ | (14) |
式中:
UUV绕x轴转动被称之为横滚,用滚角
| $\begin{split} & {J}_{{y}_{1}}{\dot{\omega }}_{{y}_{1}}+\left({J}_{{z}_{1}}{-J}_{{y}_{1}}\right){\omega }_{{y}_{1}}{\omega }_{{z}_{1}}={A}_{{m}_{x}}^{\beta }{v}^{2}\beta -{A}_{{m}_{x}}^{\delta }{v}^{2}{\delta }_{d}-\\ & {A}_{{m}_{x1}}^{\beta }v{\omega }_{{x}_{1}}+{A}_{{m}_{x}p}{v}^{2}-{\lambda }_{44}{\dot{\omega }}_{{x}_{1}}-\\& B\left({Z}_{b}\mathrm{cos}\phi +h\mathrm{sin}\phi \right)\mathrm{cos}\theta,\end{split} $ | (15) |
| $ \dot{\phi }={\omega }_{{x}_{1}}-\left({\omega }_{{y}_{1}}{{\rm{cos}}}\phi -{\omega }_{{z}_{1}}{{\rm{si}}n}\phi \right){{\rm{tan}}}\theta ,$ | (16) |
| $\begin{split} {{\rm{cos}}}\varTheta {{\rm{sin}}}\mathrm{\varPhi }=& {{\rm{cos}}}\beta {{\rm{cos}}}\theta {{\rm{sin}}}\phi -{{\rm{sin}}}\alpha {{\rm{sin}}}\beta {{\rm{cos}}}\theta {{\rm{cos}}}\phi +\\ & {{\rm{cos}}}\alpha {{\rm{sin}}}\beta {{\rm{sin}}}\theta。\end{split}$ | (17) |
式中,
航向控制可以不考虑横滚运动,但侧向运动不能单独存在[13],所以将UUV看做一个以重心为质点的刚体,考虑其纵向及包含横滚的侧向运动。
将简化模型中的纵向运动模型和包含横滚的侧向运动模型合并,得
| $\begin{aligned} & u={J}_{{z}_{1}}{\dot{\omega }}_{{z}_{1}}+{J}_{{y}_{1}}{\dot{\omega }}_{{y}_{1}}+\left({J}_{{z}_{1}}{-J}_{{y}_{1}}\right){\omega }_{{y}_{1}}{\omega }_{{z}_{1}} ={A}_{{m}_{z}}^{a}{v}^{2}a-\\ & {A}_{y}^{\delta }{x}_{e}{v}^{2}{\delta }_{e}-{A}_{{m}_{z1}}^{\omega }v{\omega }_{{z}_{1}}+{\lambda }_{26}\left(\dot{v}a+v\dot{a}\right)-{\lambda }_{66}{\dot{\omega }}_{{z}_{1}} -\\ & B\left(h{{\rm{sin}}}\theta -{x}_{b}\mathit{{\rm{cos}}}\theta \right)-Th+{A}_{{m}_{x}}^{\beta }{v}^{2}\beta -{A}_{{m}_{x}}^{\delta }{v}^{2}{\delta }_{d}-{A}_{{m}_{x1}}^{\beta }v{\omega }_{{x}_{1}}+\\ & {A}_{{m}_{x}p}{v}^{2}-{\lambda }_{44}{\dot{\omega }}_{{x}_{1}}-B\left({Z}_{b}\mathrm{cos}\phi +h\mathrm{sin}\phi \right)\mathrm{cos}\theta ,\\[-10pt]\end{aligned}$ | (18) |
航向控制问题[14]可以表现为:
| $ {\ddot{x}}_{1}=-b{\dot{x}}_{1}+au-F。$ | (19) |
式中:
建立一个标称模型[15],把建模误差,噪声,还有实际的外部干扰都给增广为一个新的状态变量,将新的状态变量等效输入到控制端,进行干扰补偿,实现对干扰的完全控制。
| $ \left\{\begin{array}{l}\dot{\widehat{F}}={k}_{1}\left(\widehat{\omega }-{\dot{x}}_{1}\right),\\ \dot{\widehat{\omega }}=-\widehat{F}+au-{k}_{2}\left(\widehat{\omega }-{\dot{x}}_{1}\right)-b{\dot{x}}_{1}。\end{array}\right. $ | (20) |
式中:
| $ F=-{\ddot{x}}_{1}-b{\dot{x}}_{1}+au ,$ | (21) |
| $ \widehat{F}=-\dot{\widehat{\omega }}-b{\dot{x}}_{1}+au-{k}_{2}\left(\widehat{\omega }-{\dot{x}}_{1}\right),$ | (22) |
则
定义Lyapunov函数:
| $ {V}_{1}=\frac{1}{2{k}_{1}}{\stackrel{~}{F}}^{2}+\frac{1}{2}{\stackrel{~}{\omega }}^{2},$ | (23) |
| $ \stackrel{~}{F}=F-\widehat{F}\text{,}\stackrel{~}{\omega }={\dot{x}}_{1}-\widehat{\omega }。$ | (24) |
合适的参数选取能够更加精准实现外界干扰补偿[16],增强系统鲁棒性。取a=5,b=0.15,d=150 sin(0.1 t),
图2为设计的干扰观测器干扰及观测仿真结果,虚线为实际干扰值,点线为观测器估计值。仿真结果显示虚线与点线很好的贴合,说明设计的干扰观测器可以很好实时估计干扰值。
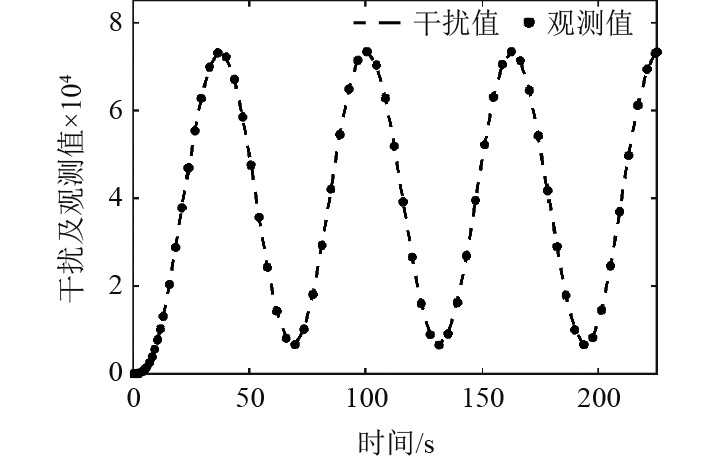
|
图 2 干扰及观测结果 Fig. 2 Interference and results of their observations |
将期望航向角设为
| $ S={\dot{Z}}_{1}+c{Z}_{1}\text{,} c > 0,$ | (25) |
| $ \dot{{S}}={\ddot{Z}}_{1}+c{\dot{Z}}_{1} ={\ddot{x}}_{d}-{\ddot{x}}_{1}+c{\dot{Z}}_{1} = {\ddot{x}}_{d}+b{\dot{x}}_{1}-au+F+c{\dot{Z}}_{1},$ | (26) |
基于干扰补偿的滑模控制器设计为:
| $ {\rm{U}}=\frac{1}{a}\left[{\ddot{x}}_{d}+b{\dot{x}}_{1}+c{\dot{Z}}_{1}+\widehat{F}+\eta {\rm{sgn}}\left(s\right)\right] ,$ | (27) |
其中
选择Lyapunov函数为:
| $ {V}_{2}=\frac{1}{2}{S}^{2},$ | (28) |
| $ \begin{aligned} & {\dot{V}}_{2}=S\dot{S}=\\ & S\left({\ddot{x}}_{d}+b{\dot{x}}_{1}-au+F+c{\dot{Z}}_{1}\right)=\\ &{\rm{S}} \left({\ddot{x}}_{d}+b{\dot{x}}_{1}-\left({\ddot{x}}_{d}+b{\dot{x}}_{1}+c{\dot{Z}}_{1}+\widehat{F}+\eta {\rm{sgn}}\left(s\right)\right)+F+c{\dot{Z}}_{1}\right) =\\ &{\rm{S}} \left(F-\widehat{F}-\eta {\rm{sgn}}\left(s\right)\right)= \widehat{F}S-\eta \left|S\right|\leqslant 0 ,\end{aligned}$ | (29) |
| $ {{V}}={{V}}_{1}+{{V}}_{2}=\frac{1}{2{K}_{1}}{\stackrel{~}{F}}^{2} + \frac{1}{2}{\stackrel{~}{\omega }}^{2}+\frac{1}{2}{S}^{2}。$ | (30) |
仿真中,用
图3为干扰值及其误差对比图。可以看出,实际干扰值越大,那么观测器估计值就越精确,实际干扰值越小,观测器估计值的偏差越大,但误差最大不超过5%,符合设计要求。
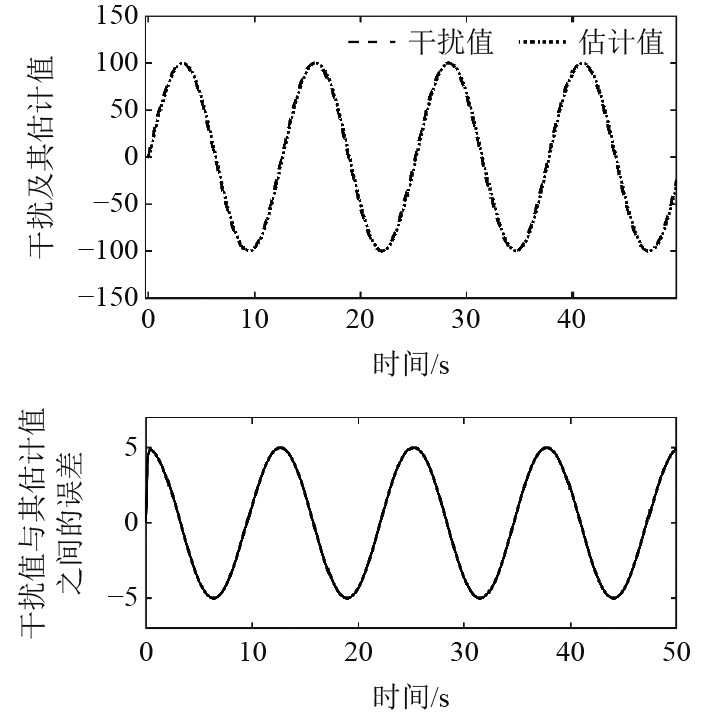
|
图 3 干扰及其估计值之间的误差 Fig. 3 Error between the interference and its estimate |
当预设航向为一个固定值即为一条直线

|
图 4 预设定航向及航向跟踪 Fig. 4 Pre-set heading and course tracking |
当预设航向角设为一个正弦波
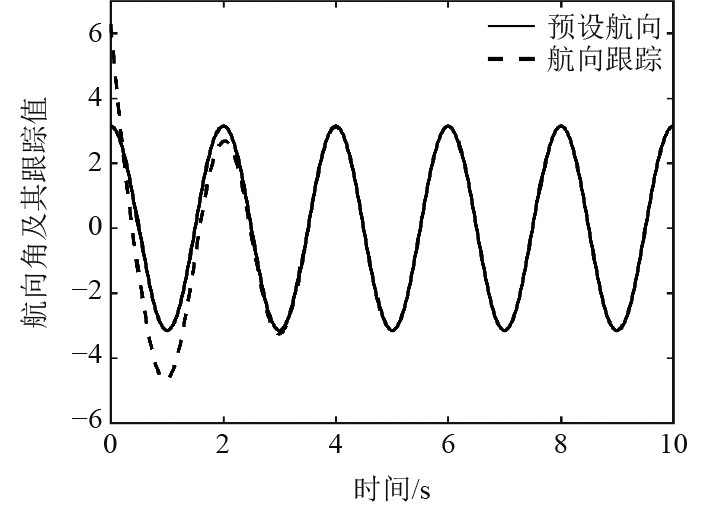
|
图 5 预设正弦航向及航向跟踪 Fig. 5 Preset sinusoidal heading and course tracking |
当预设航向为一个自定函数xd= acot(cot(θ)/sin(Ψ)+tan(Ψ)/sin(θ)),Ψ=atan(xact(2,: )),

|
图 6 预设自定义航向及航向跟踪 Fig. 6 Preset custom heading and course tracking |
本文对水下无人航行器进行模糊运动学建模,并对包含不确定因素的系统模型设计一种变结构控制和干扰补偿的连续滑模控制器进行航向跟踪仿真研究。当预设航线为一条直线时,系统可以快速调整航向,并与预设航向重合。接着以正弦波预设航向,改变固定频率时,系统能够快速调整航向与预定航向重合,虽然其间会产生一定误差但在系统可控范围。最后设置自定义无规律预设航向,若预设航向变化速度过快或变化角度过大时,系统由于反馈控制信号的不连续性导致无法及时调整航向,但随着时间增加最终会与预设航向重合。以上3个仿真实验证明基于干扰补偿的滑模控制器可以实现对于航向的稳定跟踪,并且具有较强的鲁棒性。
| [1] |
吕厚权, 郑荣, 杨斌, 等. 水下自主机器人航向控制算法应用研究[J]. 舰船科学技术, 2020, 42(2): 7. LV Houquan, ZHENG Rong, YANG Bing, et al. Research on the application of underwater autonomous robot heading control algorithm[J]. Ship Science and Technology, 2020, 42(2): 7. DOI:10.3404/j.issn.1672-7649.2020.02.021 |
| [2] |
罗伟林, 李新宇. 水下机器人航向模糊PID控制[C]//第二十届中国系统仿真技术及其应用学术年会(20th CCSSTA 2019). LUO Weilin, LI Xinyu. Underwater robot heading fuzzy PID control[C]// The 20th Annual China Conference on System Simulation Technology and its Applications (20th CCSSTA 2019). |
| [3] |
王永涛. 基于粒子群优化反步法的船舶航向控制器设计[J]. 中国航海, 2020, 43(1): 78-82. WANG YT. Design of ship heading controller based on particle swarm optimization backstepping method[J]. China Navigation, 2020, 43(1): 78-82. DOI:10.3969/j.issn.1000-4653.2020.01.015 |
| [4] |
刘志强, 叶曦, 钱同惠. 基于变论域的无人艇航向模糊控制策略[J]. 江汉大学学报: 自然科学版, 2022. LIU Zhiqiang, YE Xi, QIAN Tonghui. Fuzzy control strategy of unmanned boat heading based on variable theory domain[J]. Journal of Jianghan University: Natural Science Edition, 2022. |
| [5] |
袁昌斌, 董升亮, 李超. 滑模变结构在AUV航向控制中的应用[J]. 现代电子技术, 2012, 35(20): 117-120. YUAN Changbin, DONG Shengliang, LI Chao. Application of sliding mode variable structure in AUV heading control[J]. Modern Electronics Technology, 2012, 35(20): 117-120. DOI:10.3969/j.issn.1004-373X.2012.20.035 |
| [6] |
曾俊宝, 李硕, 刘鑫宇, 等. 便携式自主水下机器人动力学建模方法研究[J]. 计算机应用究, 2018, 35(6): 1747-1750. ZENG Junbao, LI Shuo, LIU Xingyu, et al. Research on dynamic modeling method of portable autonomous underwater robot[J]. Journal of computer applications, 2018, 35(6): 1747-1750. |
| [7] |
魏延辉, 杜振振, 陈巍, 等. 多翼自治水下机器人动力学建模与姿态控制[J]. 华中科技大学学报:自然科学版, 2015, 43(6): 106-111. WEI Yanhui, DU Zhenzhen, CHEN Wei, et al. Dynamic modeling and attitude control of multi-wing autonomous underwater vehicle[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2015, 43(6): 106-111. |
| [8] |
齐强, 陈志刚, 周源. 航行器水中运动数学模型及数值仿真[J]. 舰船科学技术, 2014, 36(5): 80-83. QI Qiang, CHEN Zhigang, ZHOU Yuan. Mathematical model and numerical simulation of underwater vehicle motion[J]. Ship Science and Technology, 2014, 36(5): 80-83. |
| [9] |
CHEN W H, BALLANCE D J. A nonlinear disturbance observer for robotic manipulators[J]. Industrial Electronics IEEE Transactions on, 2000, 47(4): 932-938. DOI:10.1109/41.857974 |
| [10] |
乔冰, 刘鑫, 袁龙. 大深度潜航器水下空间运动建模与仿真[J]. 数字海洋与水下攻防, 2020, 3(1): 65-70. QIAO Bing, LIU Xing, YUAN Long. Modeling and simulation of underwater space motion for deep underwater vehicle[J]. Digital Ocean & Underwater Attack and Defense, 2020, 3(1): 65-70. DOI:10.19838/j.issn.2096-5753.2020.01.012 |
| [11] |
LAKHEKAR G V , ROY R G. Heading control of an underwater vehicle using dynamic fuzzy sliding mode controller[C]// International Conference on Circuit. IEEE, 2015.
|
| [12] |
于靖, 陈谋, 姜长生. 基于干扰观测器的非线性不确定系统自适应滑模控制[J]. 控制理论与应用, 2014(8): 993-999. YU Jing, CHEN Mou, JIANG Changsheng. Adaptive sliding mode control for nonlinear uncertain systems based on disturbance observer[J]. Control Theory & Applications, 2014(8): 993-999. DOI:10.7641/CTA.2014.30920 |
| [13] |
ZHOU H, LIU K, LI Y, et al. Dynamic sliding mode control based on multi-model switching laws for the depth control of an autonomous underwater vehicle[J]. International Journal of Advanced Robotic Systems, 2015, 12(7): 106. DOI:10.5772/61038 |
| [14] |
刘青, 黄茹楠, 陈勇, 等. 水下航行器智能航向滑模控制[J]. 电子技术应用, 2017, 43(7): 117-121. LIU Qing, HUANG Runan, CHEN Yong et al. Intelligent heading sliding mode control for underwater vehicle[J]. Application of Electronic Technique, 2017, 43(7): 117-121. |
| [15] |
闫茂德, 许化龙, 贺昱曜. 自主水下潜航器的自适应反演变结构控制器设计[J]. 火力与指挥控制, 2005, 30(3): 18-21. YAN Maode, XU Hualong, HE Yuyao. Design of adaptive anti-evolution structure controller for autonomous underwater vehicle[J]. Fire Control & Command Control, 2005, 30(3): 18-21. DOI:10.3969/j.issn.1002-0640.2005.03.002 |
| [16] |
YANG I, BYUN S, SEO B, et al. Robust dynamic inversion based on sliding mode control for autonomous underwater vehicles - sciencedirect[J]. IFAC Proceedings Volumes, 2013, 46(10): 79-84. DOI:10.3182/20130626-3-AU-2035.00074 |
| [17] |
WANG D, SHEN Y, WAn J, et al. Sliding mode heading control for AUV based on continuous hybrid model-free and model-based reinforcement learning[J]. Applied Ocean Research, 2022, 118: 102960. DOI:10.1016/j.apor.2021.102960 |
 2023, Vol. 45
2023, Vol. 45
