2. 深海技术科学太湖实验室,江苏 无锡 214082;
3. 深海载人装备国家重点实验室,江苏 无锡 214082
2. Taihu Laboratory of Deepsea Technological Science, Wuxi 214082, China;
3. State Key Laboratory of Deep-sea Manned Vehicles, Wuxi 214082, China
水下无人航行器(autonomous underwater vehicle,AUV)具有自主决策和控制能力,在海洋安全、海洋开发、海洋科研等领域发挥重要作用,是世界海洋强国竞相发展的重要装备之一[1]。航行控制,特别是航行过程中对航向和深度的控制是AUV高效执行水下任务的重要基础。国内多位学者在AUV航向和深度控制方面做了一系列研究工作,罗建超[2]、雷江航[3]、饶志荣[4]、李泽宇[5]、梅新华[6]等采用垂直面运动数学模型对AUV的深度控制进行研究,胡坤[7]、聂为彪[8]、于浩洋[9]、陈恳[10]等采用水平面运动数学模型对AUV的航向控制进行了研究。
水平面/垂直面运动数学模型是在平面运动假设的前提下简化分解而得到的,详细推导见文献[11]。平面/运动数学模型认为只改变航向而不改变深度,或只改变深度而不改变航向,并忽略2个平面之间的耦合作用。但AUV由于外伸信标、天线、推力器、舵翼、起吊点等多种附体,整体外形复杂,导致其空间运动具有非线性、强耦合的特点,AUV在前进、变向的同时,还将伴随变深、姿态的变化,此时单平面的运动数学模型将不再适用。因此,采用六自由度空间运动数学模型研究航行控制更能反映AUV水下空间运动的真实情况,具有重要意义。本文以某AUV为研究对象,基于六自由度空间运动数学模型,对AUV进行受力分析。应用工程应用中常用的增量式PID控制方法,通过仿真计算对比分析不同运动数学模型计算AUV航向和深度控制时的运动规律,为AUV的水动力及操纵面设计提供参考。
1 空间运动数学模型 1.1 坐标系研究AUV的水下空间运动时,采用通用的2个右手坐标系,如图1所示。一个是固定坐标系E-ξηζ,固定于地球;另一个是随体坐标系G-xyz,固定于AUV。

|
图 1 坐标系 Fig. 1 Coordinate system |
在建立六自由度空间运动数学模型时,认为AUV是一个刚体,AUV在水下的空间运动可以看作一个刚体在流体中的空间机动。通过惯性坐标系与AUV随体坐标系的转换,即可得到AUV的空间运动模型[12]。
| $ \left\{ \begin{gathered} m(\dot u + qw - rv - {x_G}\left( {{q^2} + {r^2}} \right) + \\ {y_G}\left( {pq - \dot r} \right) + {z_G}\left( {pr + \dot q} \right)) = X,\\ m(\dot v + ru - pw - {y_G}\left( {{r^2} + {p^2}} \right)+ \\ {z_G}\left( {qr - \dot p} \right) + {x_G}\left( {pq + \dot r} \right)) = Y ,\\ m(\dot w + pv - qu - {z_G}\left( {{p^2} + {q^2}} \right) + \\ {x_G}\left( {pr - \dot q} \right) + {y_G}\left( {qr + \dot p} \right)) = Z,\\ {I_x}\dot p + ({I_z} - {I_y})qr - \left( {\dot r + pq} \right){I_{xz}} + \\ \left( {{r^2} - {q^2}} \right){I_{yz}} + \left( {pr - \dot q} \right){I_{xy}}+ \\ m\left[ {{y_G}\left( {\dot w - uq + vp} \right) - {z_G}\left( {\dot v - wp + ur} \right)} \right] = K,\\ {I_y}\dot q + ({I_x} - {I_z})rp - \left( {\dot p + qr} \right){I_{xy}} + \\ \left( {{p^2} - {r^2}} \right){I_{xz}} + \left( {pq - \dot r} \right){I_{yz}} + \\ m\left[ {{z_G}\left( {\dot u - vr + wq} \right) - {x_G}\left( {\dot u - vr + wq} \right)} \right] = M,\\ {I_z}\dot r + ({I_y} - {I_x})pq - \left( {\dot q + rp} \right){I_{yz}} + \\ \left( {{q^2} - {p^2}} \right){I_{xy}} + \left( {rq - \dot p} \right){I_{zx}} + \\ m\left[ {{x_G}\left( {\dot v - wp + ur} \right) - {y_G}\left( {\dot w - uq + vp} \right)} \right] = N。\\ \end{gathered} \right. $ | (1) |
其中:X,Y,Z,K,M,N为AUV所受的外力和外力矩,包括重力、浮力、推力器推力、水动力及力矩等,具体的受力情况和所研究的对象相关,需要具体分析。
1.2.2 受力分析本文以某AUV(见图2)为研究对象。

|
图 2 某AUV外观图 Fig. 2 Appearance of an AUV |
AUV的主要参数如表1所示。
|
|
表 1 某AUV主要参数 Tab.1 Main parameters of an AUV |
该AUV通过尾部设置的推力器和十字舵实现水下空间运动的操纵与控制,通过对其受力分析,可得其所受外力和外力矩的数学模型如下:
| $ \begin{split}X=&\dfrac{\rho }{2}{L}^{4}\left[{{X}^{\prime }}_{qq}{q}^{2}+{{X}^{\prime }}_{rr}{r}^{2}+{{X}^{\prime }}_{rp}rp\right]+\\ &\dfrac{\rho }{2}{L}^{3}\left[{{X}^{\prime }}_{\dot{u}}\dot{u} + {{X}^{\prime }}_{vr}vr+{{X}^{\prime }}_{wq}wq\right] + \dfrac{\rho }{2}{L}^{2}\left[{{X}^{\prime }}_{vv}{v}^{2} + {{X}^{\prime }}_{ww}{w}^{2}\right] +\\ &\dfrac{\rho }{2}{L}^{2}\left[{{X}^{\prime }}_{{\delta }_{r}{\delta }_{r}}{u}^{2}{\delta }_{r}{}^{2}+{{X}^{\prime }}_{{\delta }_{s}{\delta }_{s}}{u}^{2}{\delta }_{s}{}^{2}\right]-\left(W-B\right)\mathrm{sin}\theta +{X}_{T},\end{split} $ | (2) |
| $ \begin{split}Y=&\dfrac{\rho }{2}{L}^{4}\left[{{Y}^{\prime }}_{\dot{r}}\dot{r}+{{Y}^{\prime }}_{\dot{p}}\dot{p}+{{Y}^{\prime }}_{p\left|p\right|}p\left|p\right|+{{Y}^{\prime }}_{pq}pq\right]+\\ &\dfrac{\rho }{2}{L}^{3}\left[{{Y}^{\prime }}_{\dot{v}}\dot{v}+{{Y}^{\prime }}_{r}ur+{{Y}^{\prime }}_{wp}wp+{{Y}^{\prime }}_{p}up\right]+\\ &\dfrac{\rho }{2}{L}^{2}\left[{{Y}^{\prime }}_{*}{u}^{2}+{{Y}^{\prime }}_{v}uv+{{Y}^{\prime }}_{v\left|v\right|}v\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+\\ &\dfrac{\rho }{2}{L}^{2}\left[{{Y}^{\prime }}_{{\delta }_{r}}{u}^{2}{\delta }_{r}\right]+\left(W-B\right)\mathrm{cos}\theta \mathrm{sin}\phi ,\end{split} $ | (3) |
| $ \begin{split}Z=&\dfrac{\rho }{2}{L}^{4}\left[{{Z}^{\prime }}_{\dot{q}}\dot{q}+{{Z}^{\prime }}_{pp}{p}^{2}+{{Z}^{\prime }}_{rr}{r}^{2}+{{Z}^{\prime }}_{rp}rp\right]+\dfrac{\rho }{2}{L}^{3}\left[{{Z}^{\prime }}_{\dot{w}}\dot{w}+\right.\\ &\left.{{Z}^{\prime }}_{q}uq+{{Z}^{\prime }}_{vr}vr+{{Z}^{\prime }}_{vp}vp\right]+\dfrac{\rho }{2}{L}^{2}\left[{{Z}^{\prime }}_{*}{u}^{2}+{{Z}^{\prime }}_{w}^{}uw+\right.\\ &\left.{{Z}^{\prime }}_{vv}^{}{v}^{2}\right]+ \dfrac{\rho }{2}{L}^{2}\left[{Z}_{{\delta }_{s}}{u}^{2}{\delta }_{s}\right]+\left(W-B\right)\mathrm{cos}\theta \mathrm{cos}\phi ,\\[-15pt]\end{split} $ | (4) |
| $ \begin{split}K=&\dfrac{\rho }{2}{L}^{5}\left[{{K}^{\prime }}_{\dot{p}}^{}\dot{p}+{{K}^{\prime }}_{\dot{r}}^{}\dot{r}+{{K}^{\prime }}_{qr}^{}qr+{{K}^{\prime }}_{pq}^{}pq\right]+\\ &\dfrac{\rho }{2}{L}^{4}\left[{{K}^{\prime }}_{\dot{v}}^{}\dot{v}+{{K}^{\prime }}_{p}^{}up+{{K}^{\prime }}_{r}^{}ur+{{K}^{\prime }}_{vq}^{}vq+\right.\\ &\left.{{K}^{\prime }}_{wp}^{}wp+{{K}^{\prime }}_{wr}^{}wr\right]+\\ &\dfrac{\rho }{2}{L}^{3}\left[{{K}^{\prime }}_{*}{u}^{2}+{{K}^{\prime }}_{v}uv+{{K}^{\prime }}_{vw}vw\right]+\\ &\dfrac{\rho }{2}{L}^{3}\left[{{K}^{\prime }}_{{\delta }_{r}}{u}^{2}{\delta }_{r}\right]+\left({y}_{G}W-{y}_{B}B\right)\mathrm{cos}\theta \mathrm{cos}\phi -\\ &\left({z}_{G}W-{z}_{B}B\right)\mathrm{cos}\theta \mathrm{sin}\phi ,\end{split} $ | (5) |
| $ \begin{split} M =& \dfrac{\rho}{2}{L^5}\left[ M'_{\dot q} \dot q + M'_{pp}{p^2} + M'_{rr}{r^2} + M'_{rp}rp \right] + \\ & \dfrac{\rho}{2}{L^4}\left[ M'_{\dot w}\dot w + M'_{vr}vr + M'_{vp}vp + M'_quq \right] + \\ & \dfrac{\rho }{2}{L^3}\left[ {{{M'}_*}{u^2} + {{M'}_w}uw + {{M'}_{vv}}{v^2}} \right] + \\ & \dfrac{\rho }{2}{L^3}\left[ {{{M'}_{{\delta _s}}}{u^2}{\delta _s}} \right] - ({x_G}W - {x_B}B)\cos \theta \cos \varphi - \\ & ({z_G}W - {z_B}B)\sin \theta,\end{split} $ | (6) |
| $ \begin{split} N = &\dfrac{\rho }{2}{L^5}[N'_{\dot r}\dot r + N'_{pq}pq + N'_{qr}qr]+ \\ & \dfrac{\rho }{2}{L^4}\left[ N'_{\dot v}\dot v + N'_{wr}wr + N'_{wp}wp + N'_{vq}vq + {{N'}_p}up + N'_rur \right] + \\ &\dfrac{\rho }{2}{L^3}\left[ {N'_*{u^2} + N'_vuv + N'_{vw}vw} \right] + \dfrac{\rho }{2}{L^3}\left[ {{{N'}_{{\delta _r}}}{u^2}{\delta _r}} \right] +\\ & \left( {{x_G}W - {x_B}B} \right)\cos \theta \sin \varphi + \left( {{y_G}W - {y_B}B} \right)\sin \theta 。\\[-10pt] \end{split} $ | (7) |
AUV在固定坐标系中的位置参数可表示为:
| $ \left\{ \begin{array}{l} \dot \varphi = p + q\tan \theta \sin \varphi + r\tan \theta \cos \varphi ,\\ \dot \theta = q\cos \varphi - r\sin \varphi ,\\ \dot \psi = \left( {q\sin \varphi + r\cos \varphi } \right)/\cos \theta,\\ {{\dot \xi }_G} = u\cos \psi \cos \theta + v\left( \cos \psi \sin \theta \sin \varphi - \sin \psi \cos \varphi \right) + \\ \qquad w\left( {\cos \psi \sin \theta \cos \phi + \sin \psi \sin \varphi } \right) ,\\ \dot \eta {}_G = u\sin \psi \cos \theta + v\left( \sin \psi \sin \theta \sin \varphi + \cos \psi \cos \varphi \right) + \\ \qquad w\left( {\sin \psi \sin \theta \cos \varphi - \cos \psi \sin \varphi } \right),\\ {{\dot \zeta }_G} = - u\sin \theta + v\cos \theta \sin \varphi + w\cos \theta \cos \varphi 。\\ \end{array} \right. $ | (8) |
自动控制采用工程应用中常用的增量式PID控制方法实现AUV的自动定向和自动定深。增量式PID通过对系统偏差进行比例、几分、微分操作并线性组合成控制量,以减小系统误差,提高系统响应速度和响应效果。增量式PID控制模型如下:
| $ \Delta u(k) = {K_P}\Delta e(k) + {K_I}e(k)+ {K_D}[\Delta e(k) - \Delta e(k - 1)]。$ | (9) |
其中:
| $ \Delta e(k) = e(k) - e(k - 1) 。$ | (10) |
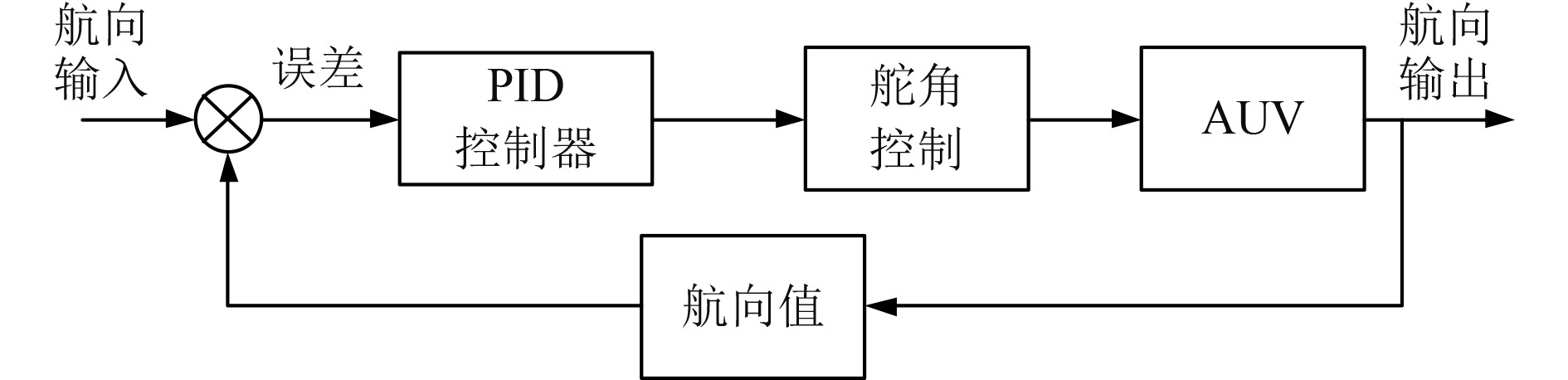
航向控制结构如图3所示。
|
图 3 自动航向保持结构 Fig. 3 Automatic heading angle-holding structure |
航向控制结构如图4所示。

|
图 4 自动深度保持结构 Fig. 4 Automatic depth-holding structure |
针对某型AUV,分别通过式(1)~式(8)建立空间运动数学模型以及平面运动数学模型,对AUV典型的空间运动进行仿真计算和对比分析。
3.1 Z形操舵运动仿真计算Z形操舵运动采用10°/10°操舵方法,采用空间运动数学模型和水平面运动数学模型分别进行仿真计算。其中,采用空间运动数学模型进行仿真计算时,对深度采用增量式PID控制方法进行控制。仿真计算过程中,AUV的航行速度为1.5 m/s,初始深度30 m,采样间隔为0.5 s,结果如图5所示。

|
图 5 10°/10°Z形操舵特征曲线图 Fig. 5 Characteristic curves of Z-shaped steering motion |
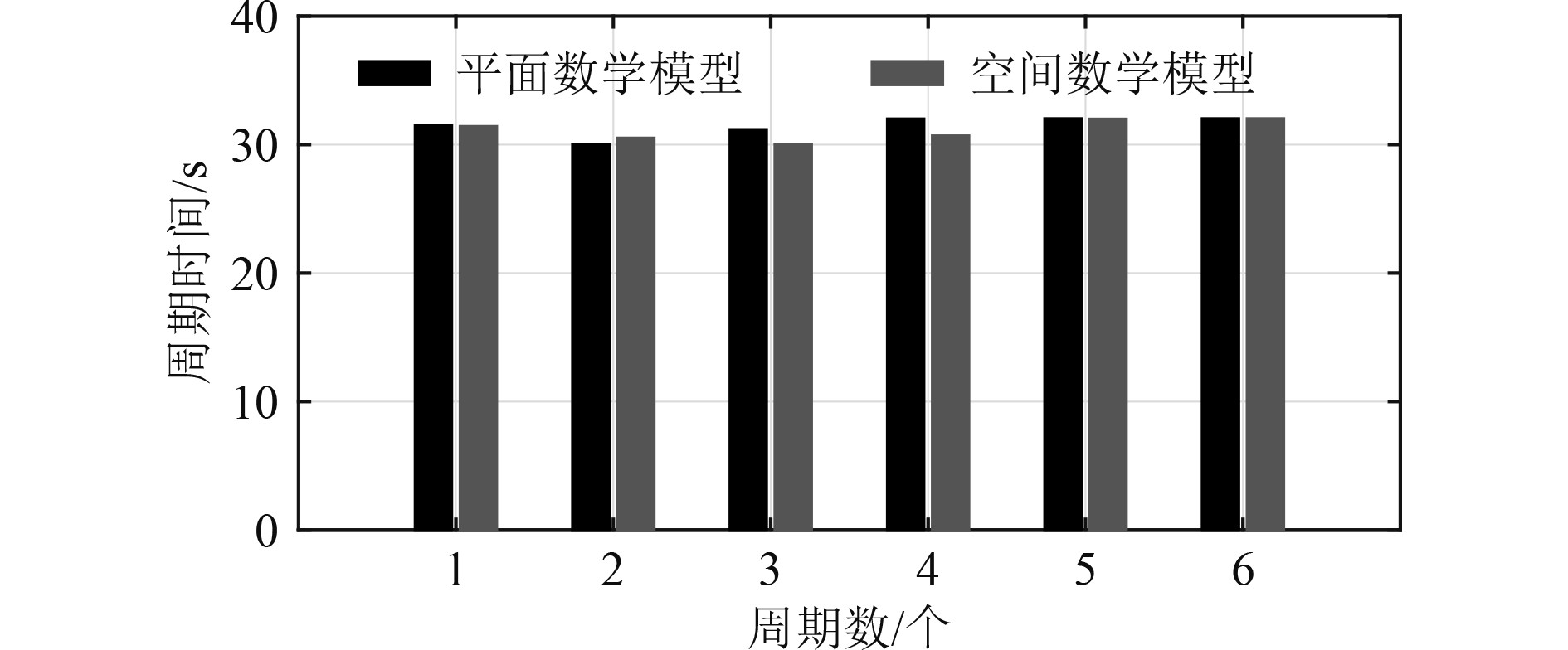
可知,当采用空间运动数学模型进行仿真计算时,前2个周期中,AUV的操舵规律和首向角变化规律与水平面运动数学模型的计算结果基本一致。从第3个周期开始,AUV的操舵规律和首向角变化规律发生变化,如图6~图8所示。

|
图 6 初转期对比图 Fig. 6 Comparison of initial turnaround periods |
|
图 8 周期时间对比图 Fig. 8 Comparison of cycle times |
由图6可知,在前2个周期中,2种数学模型计算得到的初转期一致。从第3个周期开始,空间运动数学模型比平面运动数学模型计算得到的初转期小,其中第3个周期小0.48 s。同时,空间运动数学模型计算的艏向角比平面运动数学模型提前1.1 s达到10°;第4个周期中初转期小0.42 s,提前2 s达到10°。到第5个周期时,2种数学模型计算得到的初转期恢复一致,保持在4 s左右,但空间运动数学模型计算的首向角始终比平面运动数学模型提前1.1 s达到10°。
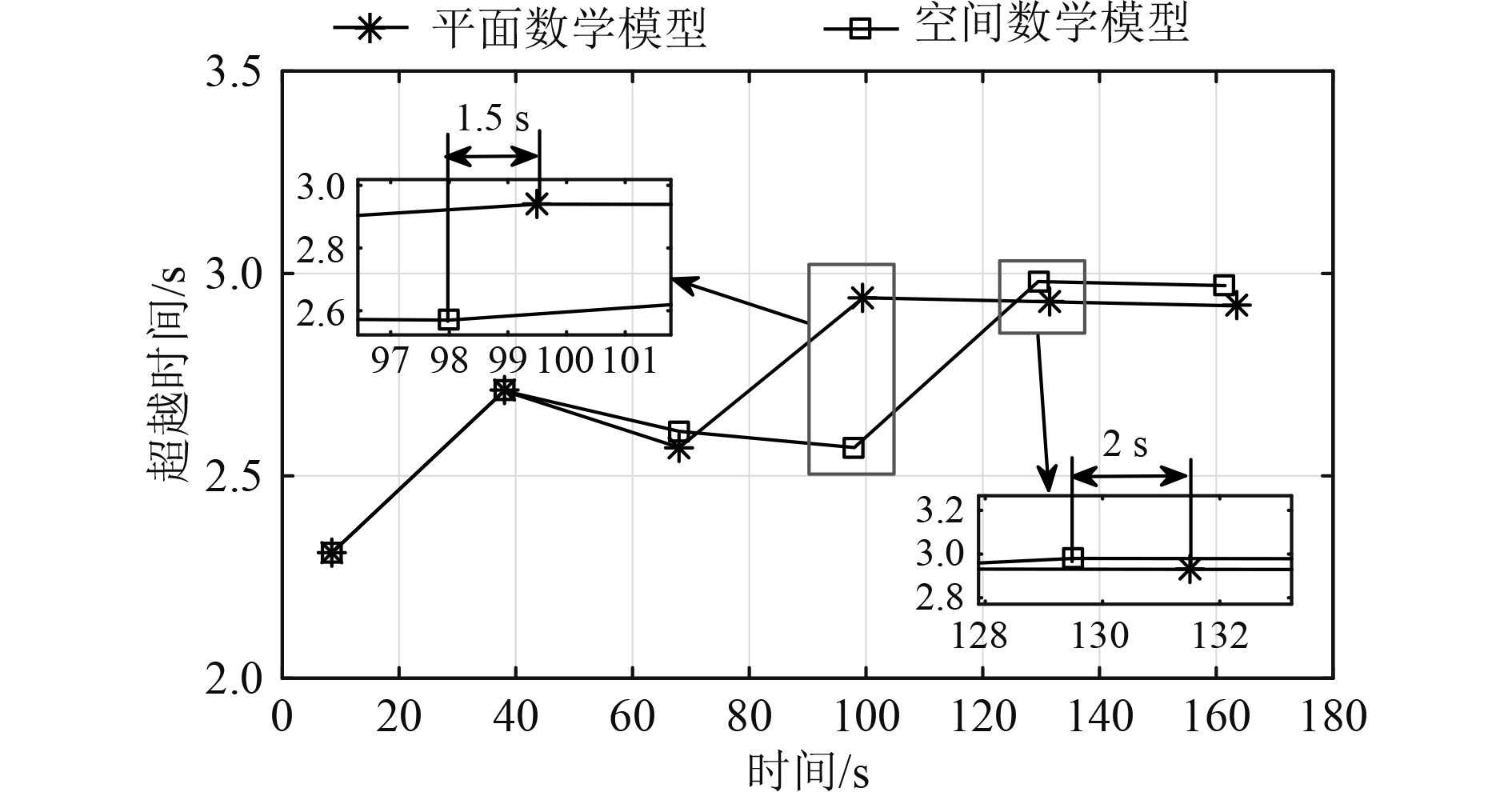
由图7可知,在前3个周期中,2种数学模型计算得到的超越时间一致。第4个周期中,空间运动数学模型比平面运动数学模型计算得到的超越时间小0.36 s。同时,空间运动数学模型计算的超越角比平面运动数学模型提前1.5 s达到峰值。到第5个周期时,2种数学模型计算得到的超越时间恢复一致,保持在3 s左右,但空间运动数学模型计算的首向角始终比平面运动数学模型提前2 s达到峰值。
|
图 7 超越时间对比图 Fig. 7 Comparison of beyond times |
由图8可知,在前2个周期中,2种数学模型计算得到的周期时间一致。从第3个周期开始,空间运动数学模型比平面运动数学模型计算得到的周期时间小,其中第3个周期小1.16 s。同时,空间运动数学模型计算的艏向角比平面运动数学模型提前0.72 s进入下一个周期;第4个周期中周期时间小1.33 s,提前2 s进入下一个周期。到第5个周期时,2种数学模型计算得到的周期时间恢复一致,保持在32 s左右,但空间运动数学模型始终比平面运动数学模型提前2 s进入下一个周期。
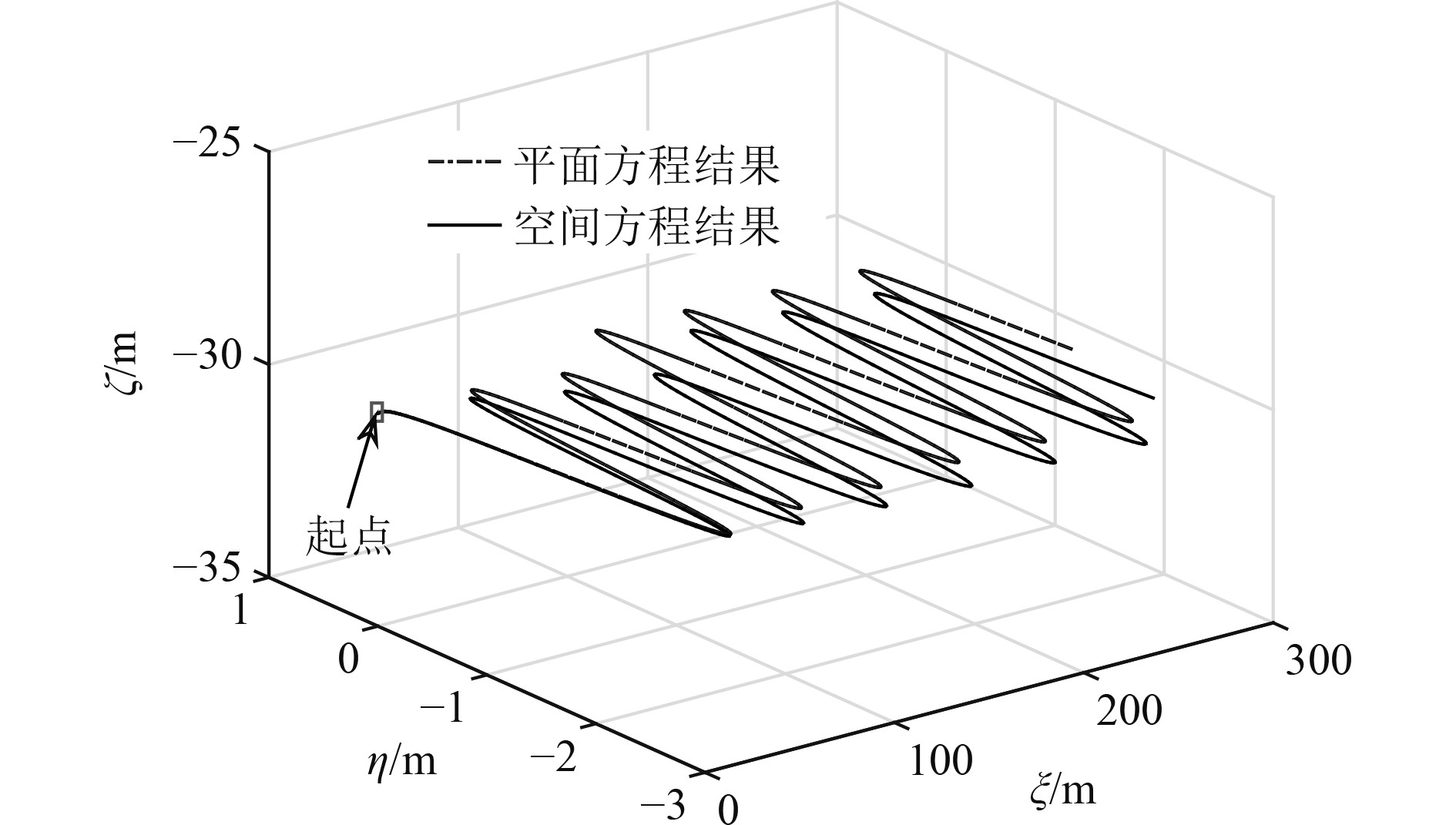
上述操舵规律和首向角变化规律的不同将导致运动轨迹的不同,运动轨迹对比如图9所示。
|
图 9 运动轨迹对比图 Fig. 9 Comparison of movement trajectories |
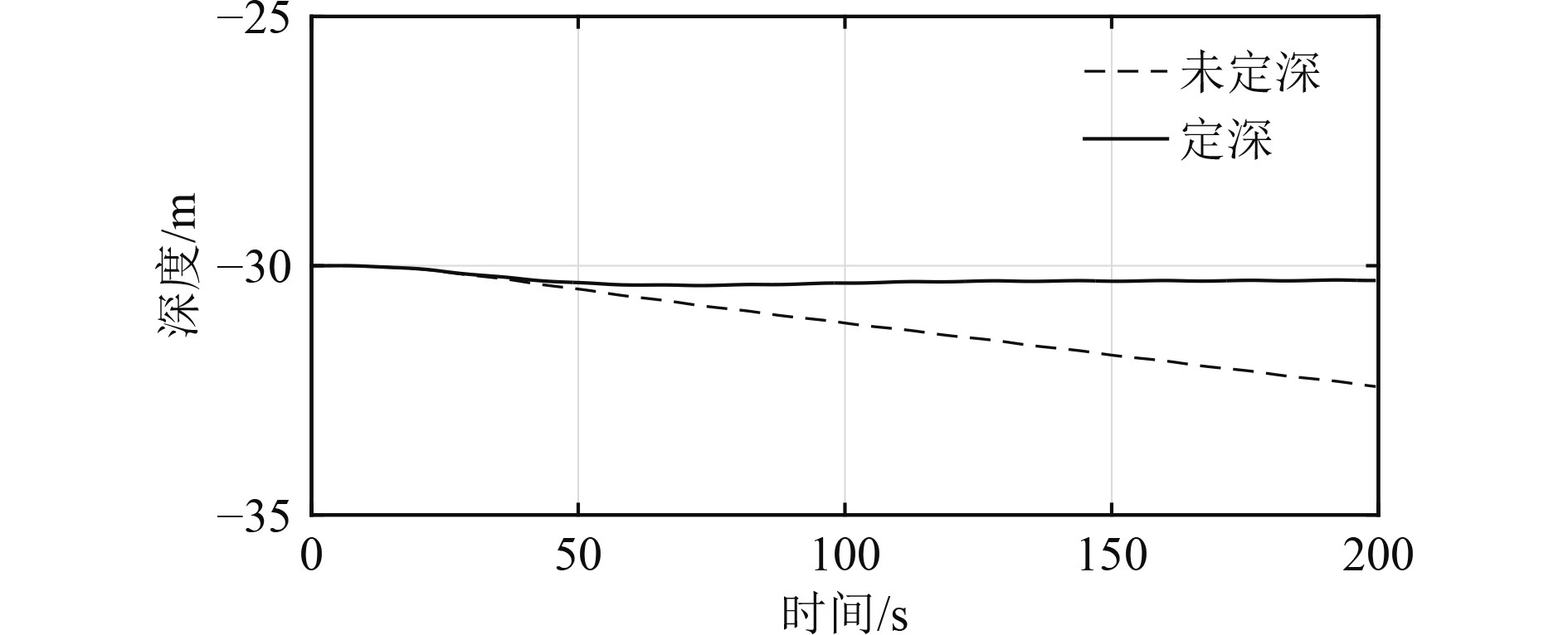
可知,采用2种数学模型仿真得到的AUV运动轨迹并不重合,存在一定的差别。因为AUV整体外形的不对称,导致AUV在水平面内运动时伴随着垂直面内的运动,为保证AUV水平面运动的稳定性,需要对垂直面内的运动进行控制。在使用空间运动数学模型进行仿真计算时,对深度采用增量式PID控制方法进行控制,PID参数值为KP=0.7,KI=1.1×10−4,KD=0.01。深度控制结果如图10所示,水平舵操舵如图11所示。
|
图 10 深度变化图 Fig. 10 Depth with time |

|
图 11 水平舵舵角变化图 Fig. 11 Horizontal rudder angle with time |
由图10可知,如果AUV在进行Z形操舵运动时不对深度进行控制,则AUV将由于整体外形不对称产生的力及力矩而同时向更深的方向运动,该运动将反向影响AUV水平面内的运动。因此,AUV在进行水平面内的运动时,同时需要对垂直面内的运动进行控制,转动水平舵抵消整体外形不对称产生的力及力矩引起的深度变化。由图11可知,水平舵舵角最终稳定在0.26°左右,AUV深度保持在30.15 m左右,AUV实现水平面内运动的稳定。
3.2 航向与深度保持仿真计算AUV在实际航行过程中,航向与深度往往需要同时保持,这也是AUV空间机动能力的体现。本文分别采用空间运动数学模型和平面运动数学模型进行航向与深度保持仿真计算,计算类型划分如表2所示。
|
|
表 2 计算类型 Tab.2 Type of calculation |
仿真计算过程中,AUV的航行速度为1.5 m/s,初始航向0°,初始深度0 m,采样间隔为0.5 s,3种模型采用相同的控制律。其中,航向控制的PID参数为KP=0.15,KI=1.0×10−4,KD=0.01,深度控制的PID参数为KP=0.7,KI=1.1×10−4,KD=0.01。计算结果如图12~图15所示。
|
图 12 航向角控制对比图 Fig. 12 Comparison of heading angle control |

|
图 15 水平舵舵角变化对比图 Fig. 15 Comparison of horizontal rudder angle |
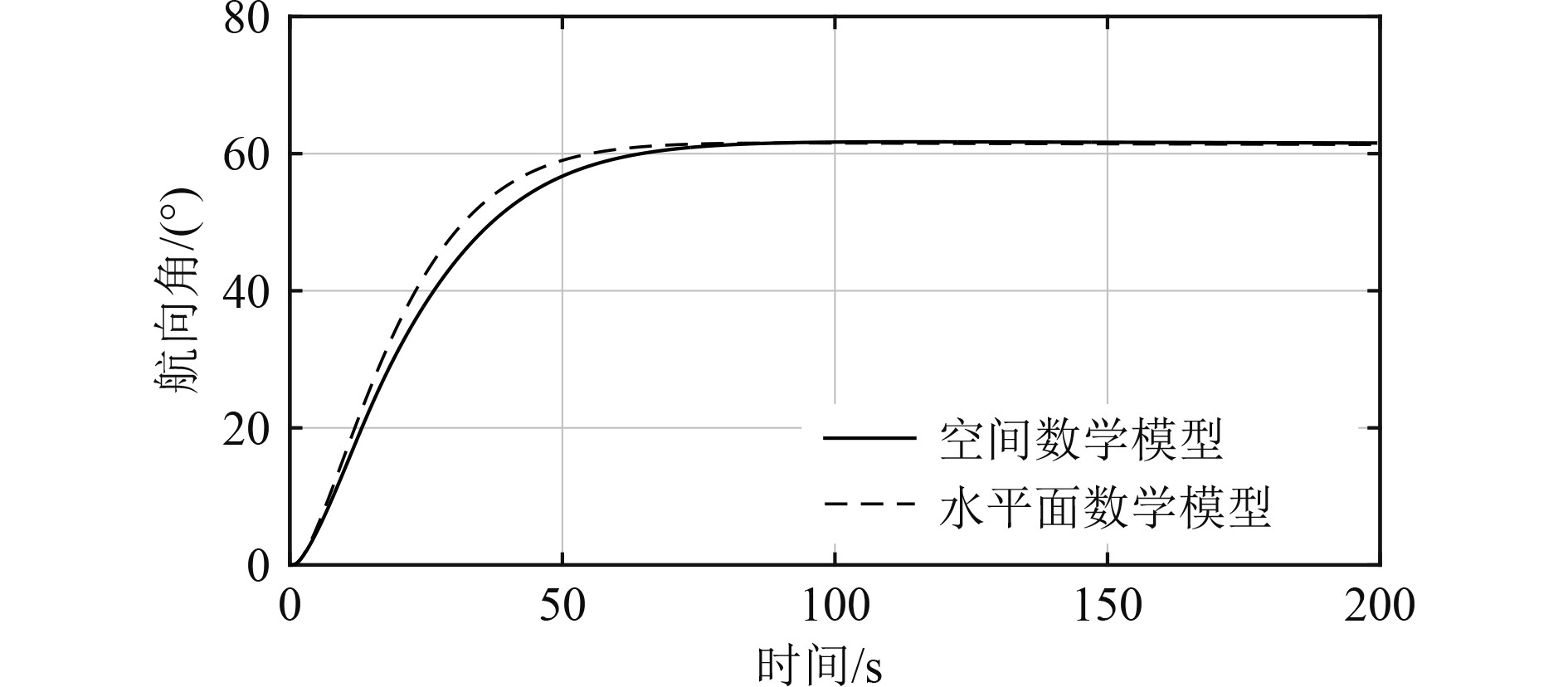
通过图12和图13可以看出,对于航向的机动与保持,在相同控制律的情况下,采用空间运动数学模型比水平面运动数学模型的上升时间长9 s,采用空间运动数学模型计算的航向角最终稳定在61.6°,采用水平面运动数学模型计算的航向角最终稳定在61.3°,基本一致。也就是说,当AUV在水下进行空间机动时,深度机动会导致航向机动响应变缓,但对最终的控制效果无影响。

|
图 13 垂直舵舵角变化对比图 Fig. 13 Comparison of vertical rudder angle |
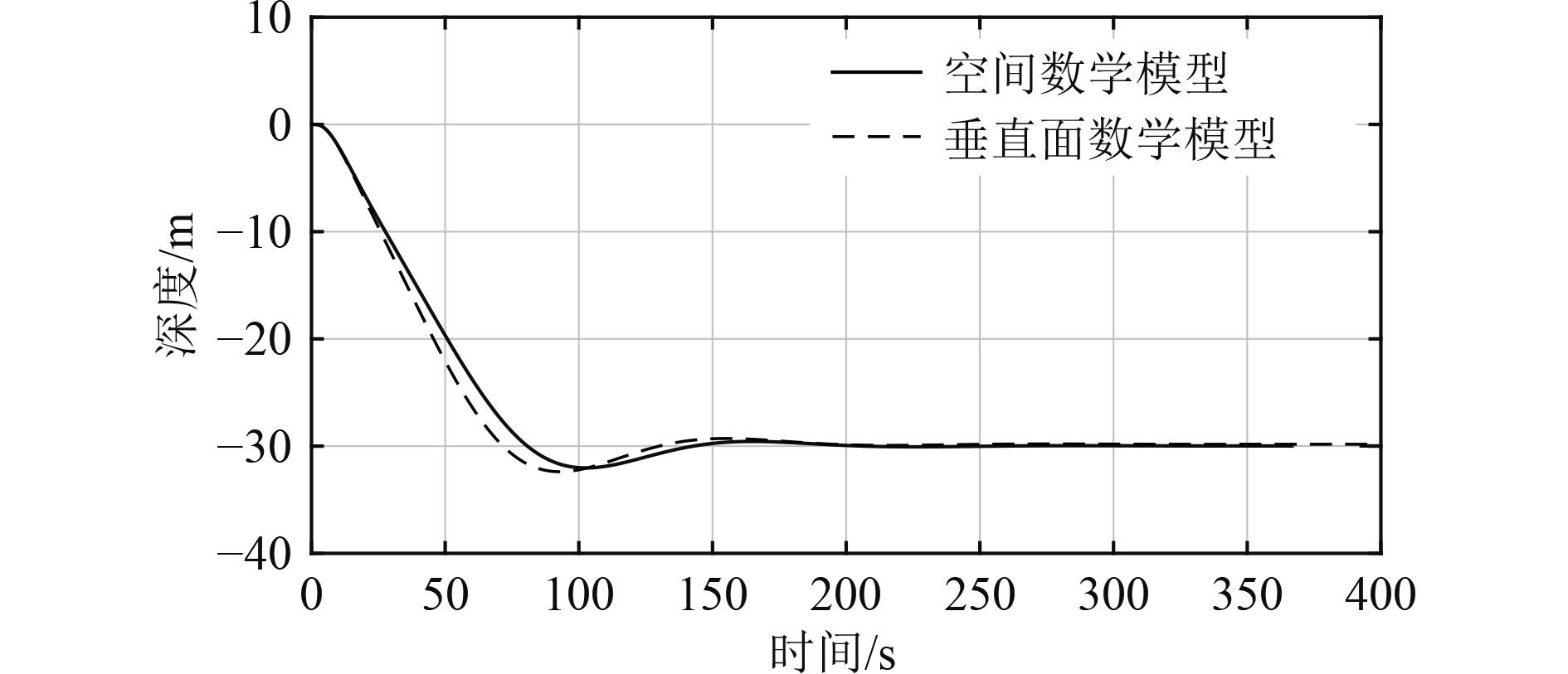
通过图13和图14可以看出,对于深度的机动与保持,在相同控制律的情况下,采用空间运动数学模型比垂直面运动数学模型的上升时间长9 s,超越深度小0.35 m,采用空间运动数学模型计算的深度最终稳定在29.9 m,采用垂直面运动数学模型计算的深度最终稳定在29.8 m,基本一致。也就是说,当AUV在进行水下空间机动时,航向机动会导致深度机动响应变缓,超越深度变小,但对最终的控制效果无影响。
|
图 14 深度控制对比图 Fig. 14 Comparison of depth control |
本文以某AUV为研究对象,基于六自由度空间运动数学模型,对AUV进行受力分析,应用工程中常用的增量式PID控制方法,形成AUV水下空间运动自动控制仿真计算的数学模型。分别采用空间运动数学模型和平面运动数学模型进行典型空间运动仿真计算。通过对比分析可以看出,当AUV在水下进行空间运动时,其水平面运动与垂直面运动之间的耦合作用不可忽略,该耦合作用将直接影响AUV的操纵律和空间运动的控制律。本文研究结果可为AUV水下空间运动的自动控制研究提供参考,具有一定的工程价值。
| [1] |
吴有生, 赵羿羽, 郎舒妍, 等. 智能无人潜水器技术发展研究[J]. 中国工程科学, 2020, 22(6): 26-31. |
| [2] |
罗建超, 朱心科. 基于改进粒子群优化算法的自主水下航行器深度控制[J]. 舰船科学技术, 2022, 44(8): 64-68. LUO Jianchao, ZHU Xinke. Depth control of autonomous underwater vehicle based on improved particle swarm optimization algorithm[J]. Ship Science and Technology, 2022, 44(8): 64-68. DOI:10.3404/j.issn.1672-7649.2022.08.013 |
| [3] |
雷江航, 姜向远, 栾义忠, 等. 基于L1自适应理论的AUV深度控制器设计[J]. 中国舰船研究, 2021, 16(5): 150-157. LEI Jianghang, JIANG Xiangyuan, LUAN Yizhong, et al. Design of AUV depth controller based on L1 adaptive theory[J]. Chinese Journal of Ship Research, 2021, 16(5): 150-157. DOI:10.19693/j.issn.1673-3185.02114 |
| [4] |
饶志荣, 董绍江, 王军, 等. 基于干扰观测器的AUV深度自适应终端滑模控制[J]. 北京化工大学学报(自然科学版), 2021, 48(1): 103-110. DOI:10.13543/j.bhxbzr.2021.01.014 |
| [5] |
李泽宇, 刘卫东, 申高展, 等. 水下航行器空间机动滑模变结构控制仿真[C]// 2015年中国西部声学学术交流会论文集, 2015: 4.
|
| [6] |
梅新华, 周祥龙. 基于BP神经网络的双舵型AUV深度控制算法应用[J]. 水雷战与舰船防护, 2017, 25(3): 79-82. |
| [7] |
胡坤, 何斌, 张建华, 等. 波浪环境下潜艇近水面操纵特性仿真分析[J]. 舰船科学技术, 2017, 44(2): 6-11. HU Kun, HE Bin, ZHANG Jian-hua, et al. Simulation analysis of submarine maneuvering characteristics near water surface in wave environment[J]. Ship Science and Technology, 2017, 44(2): 6-11. DOI:10.3404/j.issn.1672-7619.2017.02.002 |
| [8] |
聂为彪, 钱治强, 吴铭, 等. 水下航行器横向操纵性运动预报设计与仿真[J]. 舰船科学技术, 2021, 43(S1): 22-26. NIE Weibiao, QIAN Zhiqiang, WU Ming, et al. Analysis on navigation scheme and key technology of the underwater vehicle[J]. Ship Science and Technology, 2021, 43(S1): 22-26. |
| [9] |
于浩洋, 李普强. 无缆自主式水下机器人航向的模糊控制[J]. 黑龙江工程学院学报, 2017, 31(5): 33-36. |
| [10] |
陈恳, 刘涛, 杜新光, 等. 基于自适应神经网络滑模控制的常压潜水装具航向控制器设计[J]. 中国造船, 2018, 59(1): 187-196. CHEN Ken, LIU Tao, DU Xinguang, et al. Design of course controller for atmospheric diving suit(ads) based on sliding mode control with adaptive neural network[J]. Shipbuilding of China, 2018, 59(1): 187-196. |
| [11] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [12] |
魏延辉. UVMS系统控制技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2017.
|
 2023, Vol. 45
2023, Vol. 45
