0 引　言

振动主动控制技术在舰船低频振动抑制方面有着明显优势，2005年Mathias Winberg等^[1]对瑞典游艇上2台柴油机进行振动主动控制，使得舱室噪声在120 Hz以下有超过10 dB的减弱。Filter -x least mean square (FxLMS)算法结构简单，控制精度高，是振动主动控制自适应算法的经典算法。但在复杂的噪声环境下，该算法的收敛性和稳定性往往不能满足实际要求，因此学者们对传统的FxLMS算法进行改进。其中次级通道在线辨识技术能够对次级通路参数进行实时更新，保证了降噪算法的实时性和稳定性，更符合实际控制中有时变特性的次级通道^[2-3]。

在线辨识次级通道的主动控制系统中，保证对时变的次级通道快速精确辨识是该算法减小控制误差的关键因素。提高次级通道辨识精度、减少初级通道和次级通道间的相互干扰是在线辨识次级通道算法优化改进的重点方向^[4-5]。

Eriksson^[6]提出引入随机白噪声作为次级通道的参考信号，但引入的白噪声信号会进入到控制通道中，对控制结果产生干扰，导致系统不稳定甚至发散。

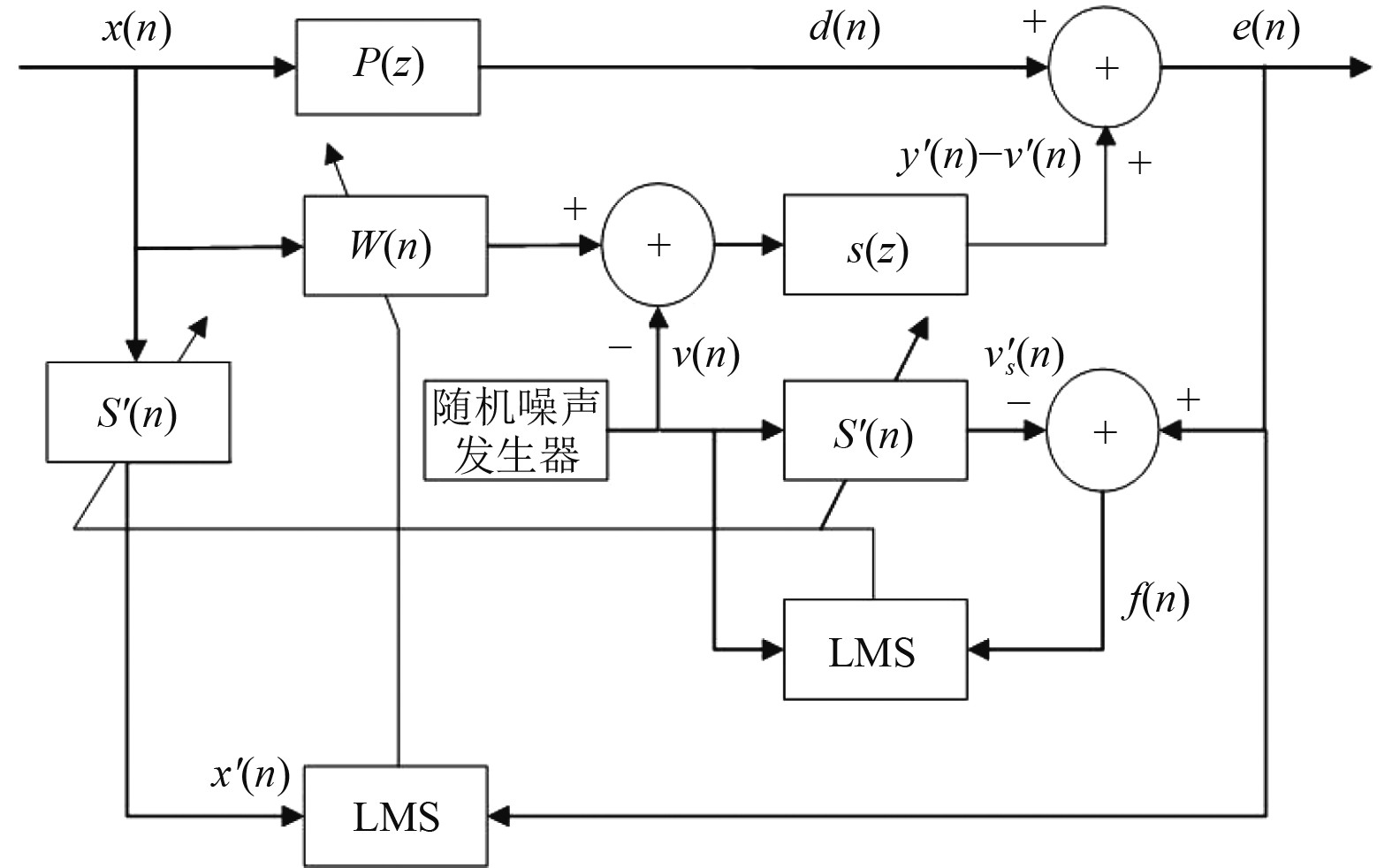
Eriksson算法见图1， $ P\left(z\right) $ 为初级通道，指振源到目标控制点的传递函数； $ S\left(z\right) $ 为次级通道，指控制信号发生到目标控制点的传递函数； $ x\left(n\right) $ 为振源信号，作为初级通道的参考信号； $ e\left(n\right) $ 为误差信号； $ v\left(n\right) $ 为引入的随机白噪声信号，作为次级通道的参考信号。

由FXLMS算法推算，可得控制通道权系数 $ W\left(n\right) $ 和次级通道辨识结果 $S'\left(n\right)$ 系数迭代公式为：

$ w \left(n+1\right)=w\left(n\right)+{\mu }_{w}{x}'\left(n\right)e\left(n\right)，$

(1)

$ {s}'(n+1)={s}'\left(n\right)+{\mu }_{s}v\left(n\right)f\left(n\right)。$

(2)

式中： $ {\ \mu }_{w} $ ， $ {\ \mu }_{s} $ 为收敛步长。

$ f\left(n\right)=e\left(n\right)-{v}_{s}'\left(n\right)，$

(3)

$ {x}'\left(n\right)={{S}'}^{\rm{T}}\left(n\right){{X}}_{{L}}\left(n-1\right)，$

(4)

$ {{X}}_{{L}}(n-1)=[x\left(n\right),x\left(n-1\right),\cdots ,x(n-L+1){]}^{\rm{T}}。$

(5)

附加随机噪声 $ v\left(n\right) $ 经 ${S}'\left(n\right)$ 的输出为：

$ {v}_{s}\left(n\right)={{S}'}^{\mathbf{T}}\left(n\right){V}\left(n\right) ，$

(6)

$ \mathit{V}\left(n\right)=\left[v\right(n)\cdots v(n-L+1){]}^{\mathrm{T}} 。$

(7)

误差信号 $ e\left(n\right) $ 中也会存在因引入的随机白噪声而产生的误差，即

$ e\left(n\right)=\left[d\left(n\right)+{y}'\left(n\right)\right]-{v}'\left(n\right)。$

(8)

进一步推导有

$ e\left(n\right)=\left[P\left(n\right)X\left(n\right)+S\left(n\right)Y\left(n\right)\right]-\left[s\left(n\right)v\left(n\right)\right]，$

(9)

式中： $ s\left(n\right)v\left(n\right) $ 为在线辨识环节中引入的附加随机噪声流入控制通道后经由次级通道后产生的误差。当系统收敛后， $ W\left(n\right) $ 逼近 $ {W}_{opt} $ ，前一项趋近于0，噪声信号为误差的主要来源。

对辨识通道误差分析得

$ f\left(n\right)=\left[S\left(n\right)V\left(n\right)-{S}'\left(n\right)V\left(n\right)\right]+\left[d\left(n\right)-{y}'\left(n\right)\right] 。$

(10)

式中： $ d\left(n\right)-{y}'\left(n\right) $ 为控制通道对辨识通道的影响，前一项在系统收敛后趋近于0。由上述可知，2个通道间存在的相互影响直接关系到系统的控制效果。

为解决2个通道间相互影响的问题，Bao等^[7]引入一个自适应滤波器用以产生有源控制的误差信号，减小了该信号对建模滤波器的影响，但没有消除建模信号对控制通道的影响。张明^[8]、杨铁军^[9-10]等在Bao的基础上附加第3个维纳滤波器，进一步拟合并消除建模通道中的控制信号，降低了通道间的相互影响，提高了整体性能，但由于附加的滤波器，算法框架及参数设置更为复杂，计算量也更大。Akhtar^[11]提出在次级通道中采用时变的收敛步长算法，该方法的算法框架与原算法几乎一致，减小了在线辨识算法中控制通道对辨识通道的干扰影响，但没有解决辨识通道对控制通道的影响。Shakeel Ahmed^[12]提出通过在线调节引入噪声信号功率的方法减小控制误差。控制初期，噪声信号的输出功率由次级通道的误差信号功率决定；控制收敛后，噪声信号的输出功率由2个次级通道的辨识滤波器误差信号相关估计值决定。整体提高了控制精度，但采用了结构更复杂的归一化最小均方算法，稳定性和收敛速度低于Akhtar算法。

本文基于已有算法，在不增加算法结构复杂程度基础上，提出块处理的变步长次级通道在线辨识主动控制算法，旨在减小在线辨识中2个通道的相互影响，加快算法收敛速度，提高算法稳定性。

1 基于块处理的改进型变步长LMS算法 1.1 变步长控制通道算法

通常根据参考信号 $ x\left(n\right) $ 或者振动期望信号 $ e\left(n\right) $ 及其功率变化作为变步长更新算法建模的误差信号，但信号采集中的异常值会导致步长更新存在突变而影响算法的稳定性和收敛性。

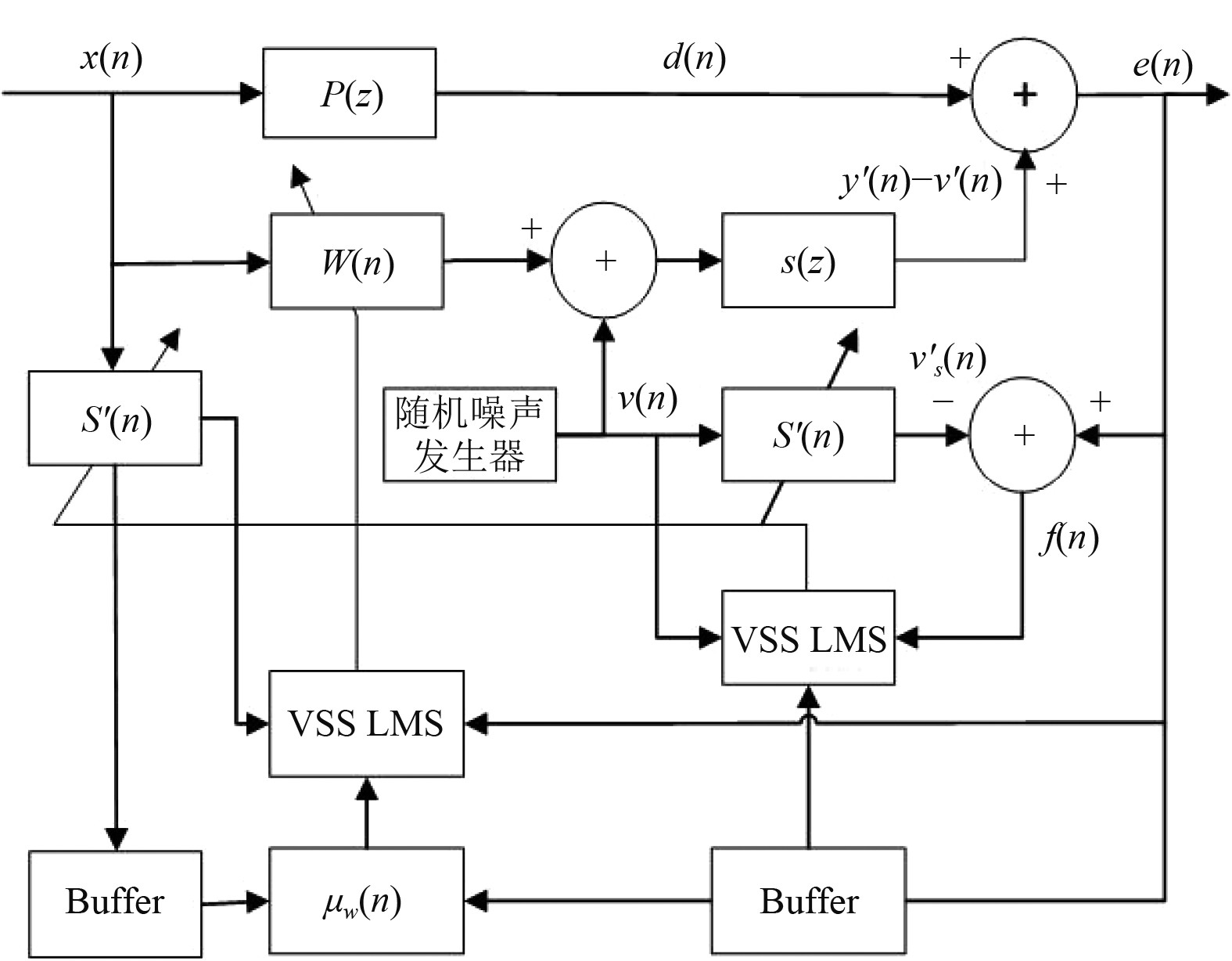
本文提出块处理的思路，将参考信号存入一定长度的寄存器进行范数平均化，降低异常值的影响，提出改进的控制算法。算法框图如图2所示。

主动控制环节的步长根据系统状态在线调整，进一步改善系统的收敛速度和稳态误差。参考信号功率增加会导致系统趋于发散，保持较小的步长有利于系统的稳定。随着控制进行，期望信号逐步减小，辨识误差对系统影响变小，此时步长可适当增大以加快控制收敛速度；当系统收敛完毕处于稳态后，适当减小步长，来得到更低的稳态误差。

以参考信号的欧几里得范数为误差信号进行评价，定义误差因子为：

$ \tau \left(n\right)=\frac{\parallel \mathit{X}\left(n\right)\parallel }{\alpha +\sqrt{\parallel \mathit{X}\left(n\right)\parallel \cdot \parallel \mathit{e}\left(n\right)\parallel }}。$

(11)

根据定义的迭代步长变化特性，进行归一化及参数调整，此时步长调整表达式为：

$ {\mu }_{w}\left(n\right)=\frac{\beta {\tau \left(n\right)}^{2}}{\sqrt{1+{\tau \left(n\right)}^{4}+\gamma {\tau \left(n\right)}^{2}}}。$

(12)

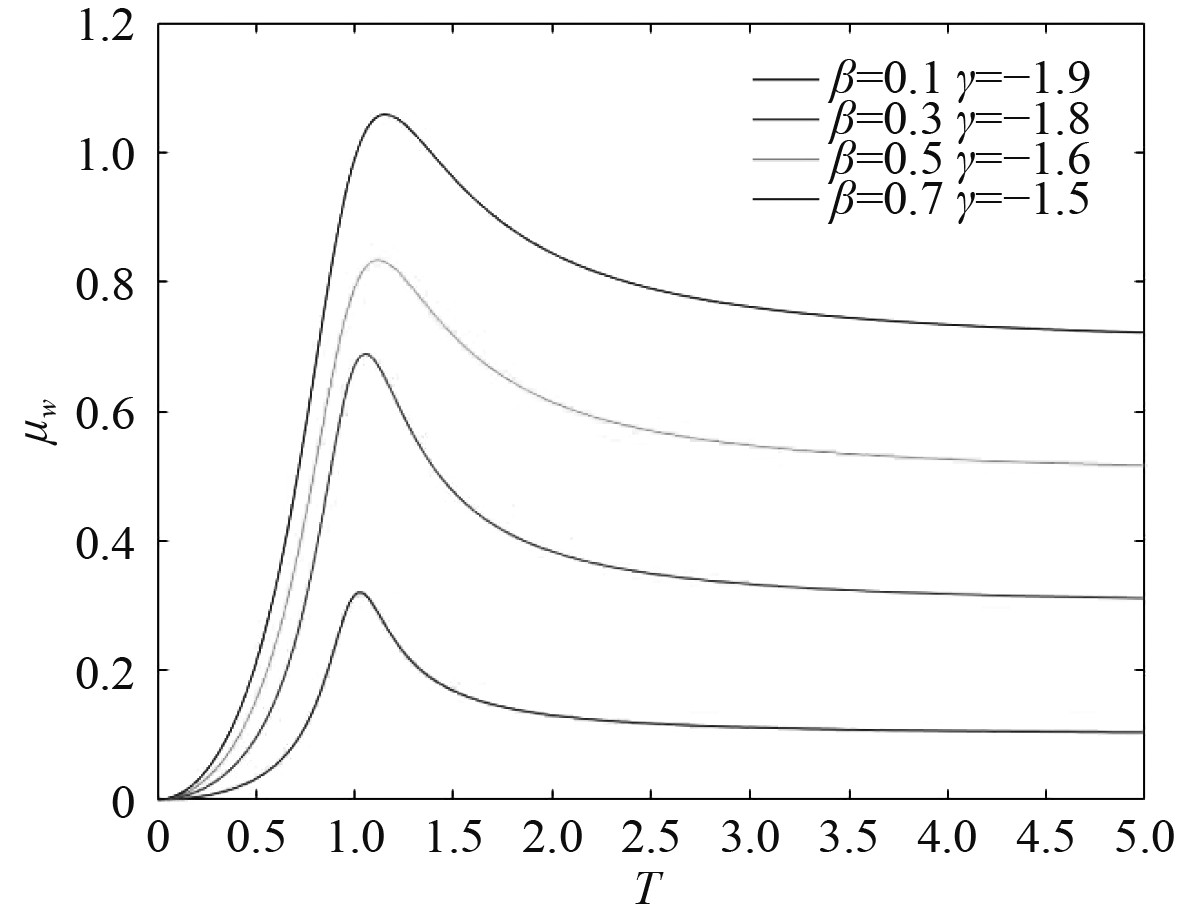
$ {\mu }_{w}\left(n\right) $ 与 $ \tau \left(n\right) $ 关系如图3所示，可根据控制对象和控制策略对步长上下限和调整速度快慢进行优化参数调整。

1.2 变步长辨识通道算法

辨识通道误差由式（10）计算，其中 $ \left[d\left(n\right)-{y}'\left(n\right)\right] $ 为控制通道对建模通道的影响。在控制未收敛时，反馈的期望信号较大，辨识通道的步长只能取较小值，以保证辨识通道的稳定性。随着控制逐渐收敛， $ \mathit{e}\left(n\right) $ 快速减小，此时可以取较大的步长进行快速收敛。但在系统收敛后，较大的步长值不能保证更好的稳态误差和控制效果，因此需要再次减小步长。

迭代步长调整策略为先上升后降低的2个过程。

第1阶段：辨识初始阶段， $\left[d\left(n\right)-{y}'\left(n\right)\right]$ 是干扰因素的主要来源，需要考虑辨识误差 $ \Delta S $ 的大小，即可将干扰信号剔除，引入 $ \rho \left(n\right) $ 能量因子：

$ \rho \left(n\right)=\frac{{P}_{v}\left(n\right)}{{P}_{e}\left(n\right)}，$

(13)

其中， $ {P}_{v}\left(n\right) $ 和 $ {P}_{e}\left(n\right) $ 分别为参考信号 $ \mathit{v}\left(n\right) $ 和期望信号 $ \parallel \mathit{e}\left(n\right)\parallel $ 的功率估计函数，并用指数平滑预测方法计算：

$ {P}_{v}(n+1)=a{P}_{v}\left(n\right)+\left(1-a\right){v}^{2}\left(n\right)，$

(14)

$ {P}_{e}(n+1)=a{P}_{e}\left(n\right)+\left(1-a\right){\parallel \mathit{e}\left(n\right)\parallel }^{2} 。$

(15)

其中， $ a $ 为遗忘因子（ $ 0.9 < a < 1 $ ）。

在控制开始时，期望信号约等于输入信号远大于附加噪声， $ \rho \left(n\right) $ 为趋于0的小值；当控制通道逐渐收敛后， $\left[d\left(n\right)-{y}'\left(n\right)\right]$ 趋于0， $ \rho \left(n\right) $ 逐渐增大到某一定值。由此可见 $ \rho \left(n\right) $ 与 $\left[d\left(n\right)-{y}'\left(n\right)\right]$ 呈负相关性，而 $ f\left(n\right) $ 为 $ \Delta S $ 与 $\left[d\left(n\right)-{y}'\left(n\right)\right]$ 加和，所以 $ \rho \left(n\right)f\left(n\right) $ 与 $ \Delta S $ 呈正相关性，可用 $ \rho \left(n\right)f\left(n\right) $ 近似估计辨识误差，考虑到附加噪声与期望信号能量比不确定的情况，需要限制步长上下限，步长调整表达式修改为：

$ {\mu }_{s1}\left(n\right)=\rho \left(n\right){\mu }_{min}+[1-\rho (n\left)\right]{\mu }_{max}。$

(16)

其中： $ {\mu }_{min} $ ， $ {\mu }_{max} $ 为辨识步长的上下限。

第2阶段：当辨识通道辨识完成后，需要将辨识步长调整到较小值，进一步降低辨识误差。当 $ {\mu }_{s1}\left(n\right) > \phi {\mu }_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 时，采用第2阶段步长变化规律，并设置第2阶段初始步长 $ {\mu }_{s2}\left(n\right)=\phi {\mu }_{max} $ ，该阶段的步长调整表达式为：

$ {\mu }_{s2}\left(n\right)=b{\mu }_{s2}(n-1)+c\left(1-\mathrm{e}\mathrm{x}\mathrm{p}\left({\rho }^{2}\left(n\right)\right)\right) 。$

(17)

其中： $ b,c $ 为预设参数。

2 算法仿真

对Akhtar算法和本文改进算法进行仿真实验，采用主动控制算法中常用的权系数辨识误差和控制系统的减振性能作为评价指标。

定义辨识通道辨识误差为^[11]：

$ \mathrm{\Delta }S\left(n\right)=10\mathrm{lg}\left\{\frac{{∥S\left(n\right)-{S}'\left(n\right)∥}^{2}}{\parallel S\left(n\right){\parallel }^{2}}\right\}，$

(18)

定义系统减振标准为：

$ R\left(n\right)=10\mathrm{l}\mathrm{g}\left\{\frac{\sum e(n{)}^{2}}{\sum d(n{)}^{2}}\right\}。$

(19)

$ \mathrm{\Delta }S\left(n\right) $ 的值越小，表征辨识精度越高， $ R\left(n\right) $ 的值越小，表征系统的减振性能越好。

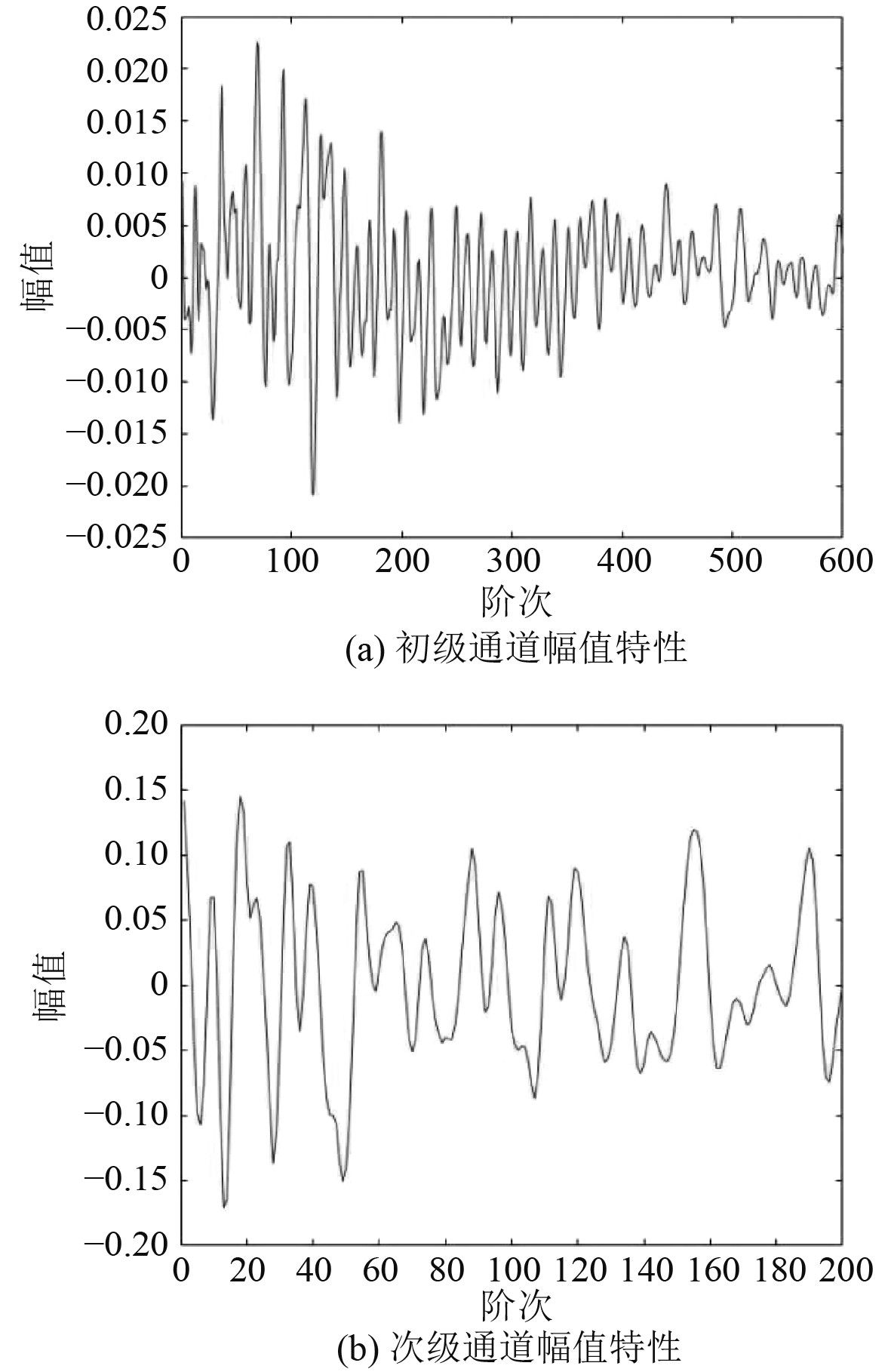
搭建单通道在线辨识主动振动控制模型，对Akhtar和本文所提算法进行验证。初级通道和次级通道的传递函数由实际主动隔振实验的数据分别转化为600阶和200阶的FIR滤波器系数而来，其幅值特性如图4所示，控制通道和建模通道的建模FIR滤波器长度均设置为200阶。

其中，仿真采样频率设置为10kHz，辨识通道初始参数为0，相关参数设置如表1所示。

2.1 双频振动信号控制算例仿真

设参考信号为频率分别为60 Hz与100 Hz的正弦信号与高斯白噪声的合成信号，信噪比为30 dB。辨识通道的建模信号为均值为0、方差为0.001的高斯白噪声。

仿真结果如图5所示。图5(a) 和图5(b)为本文算法与Akhtar算法控制前与控制后在时域上的对比效果，可见2种算法在本仿真模型中均能达到预期的控制目的。为定量分析2种算法的优劣，按上述评价标准分析仿真数据可得。

图5(c)是在线建模辨识误差 $ \mathrm{\Delta }S $ 的比较，在迭代30000次左右时，Akhtar算法辨识基本收敛，在辨识误差 $\mathrm{\Delta }S=-64\;{\rm{dB}}$ 处小幅波动；本文算法在迭代20000次左右时，即可完成算法收敛，平均辨识误差 $\mathrm{\Delta }S= -68\;{\rm{dB }}$ ，辨识速度提升了50%，辨识精度提升了4%。图5(d)表示振动控制系统的减振性能，可以发现，整个控制阶段中本文算法相比于Akhtar算法，在减振量和算法收敛速度方面都有明显的优势，控制收敛后，减振性能高5 dB。

图5(f)为本文算法与Akhtar算法在仿真中，辨识通道迭代步长 $ {\mu }_{s} $ 的在线调整对比情况。图5(e)表示本文算法在控制通道中迭代步长 $ {\mu }_{\omega } $ 的在线调整情况。在控制初期，主动控制系统还未产生效果，误差信号较大，2种算法的迭代步长都保持较小，保证算法不会发散。随着误差信号在主动控制下逐步减小，辨识步长值都逐渐增大，以加快收敛速度。Akhtar算法在迭代10000次后达到最大值，本文算法在迭代13000次时达到更大的最大值后，逐步减小步长，并于20000次时减小到最小值。控制通道的步长Akhtar算法保持在定值，本文算法按控制策略在控制初始阶段由小增大，减小辨识通道对控制的影响，加快收敛速度，在控制逐步收敛后步长减小，降低稳态误差。

2.2 次级通道突变算例仿真

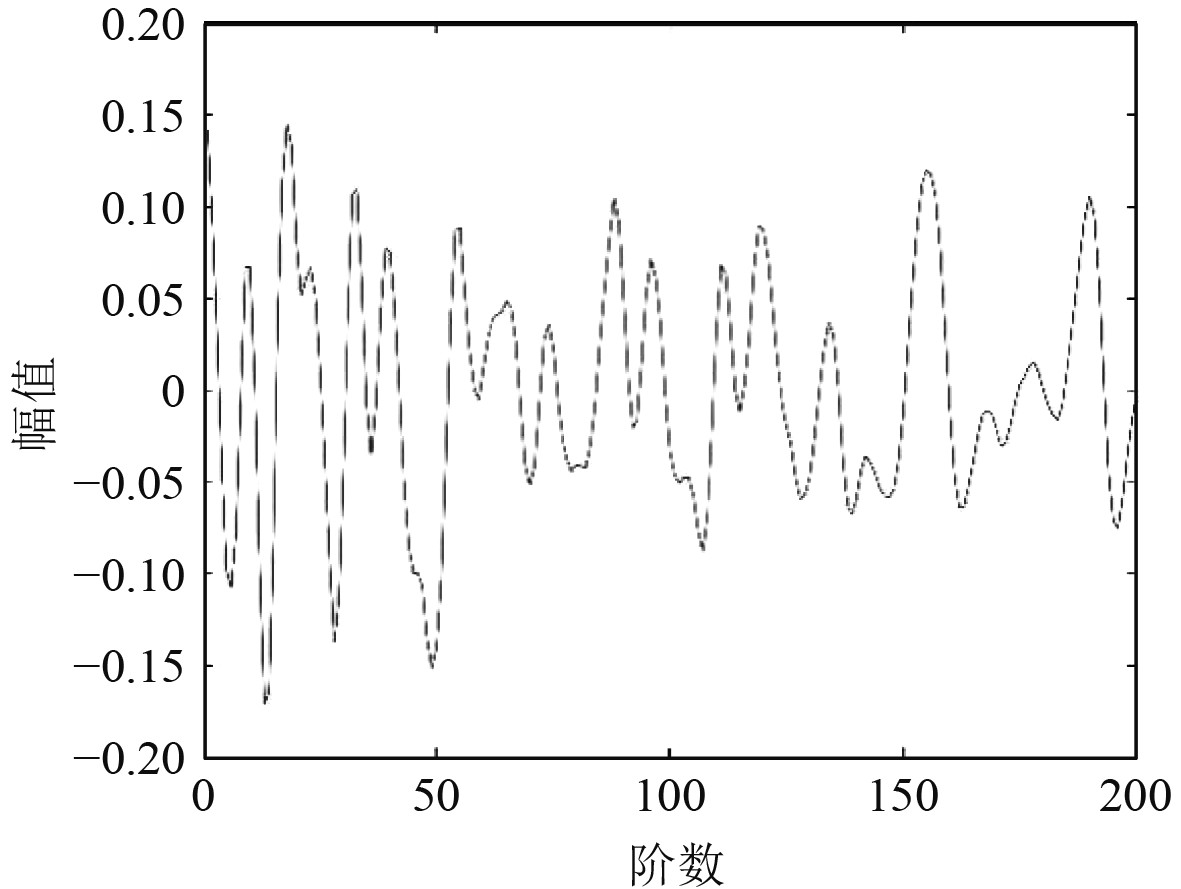
在实际条件下，次级通道往往会随着时间不断变化，为检验算法在次级通道变化情况下的控制情况，设置次级通道突变的仿真实验，在迭代40000次时，次级通道发生突变，突变后的次级通道幅值特性如图6所示。

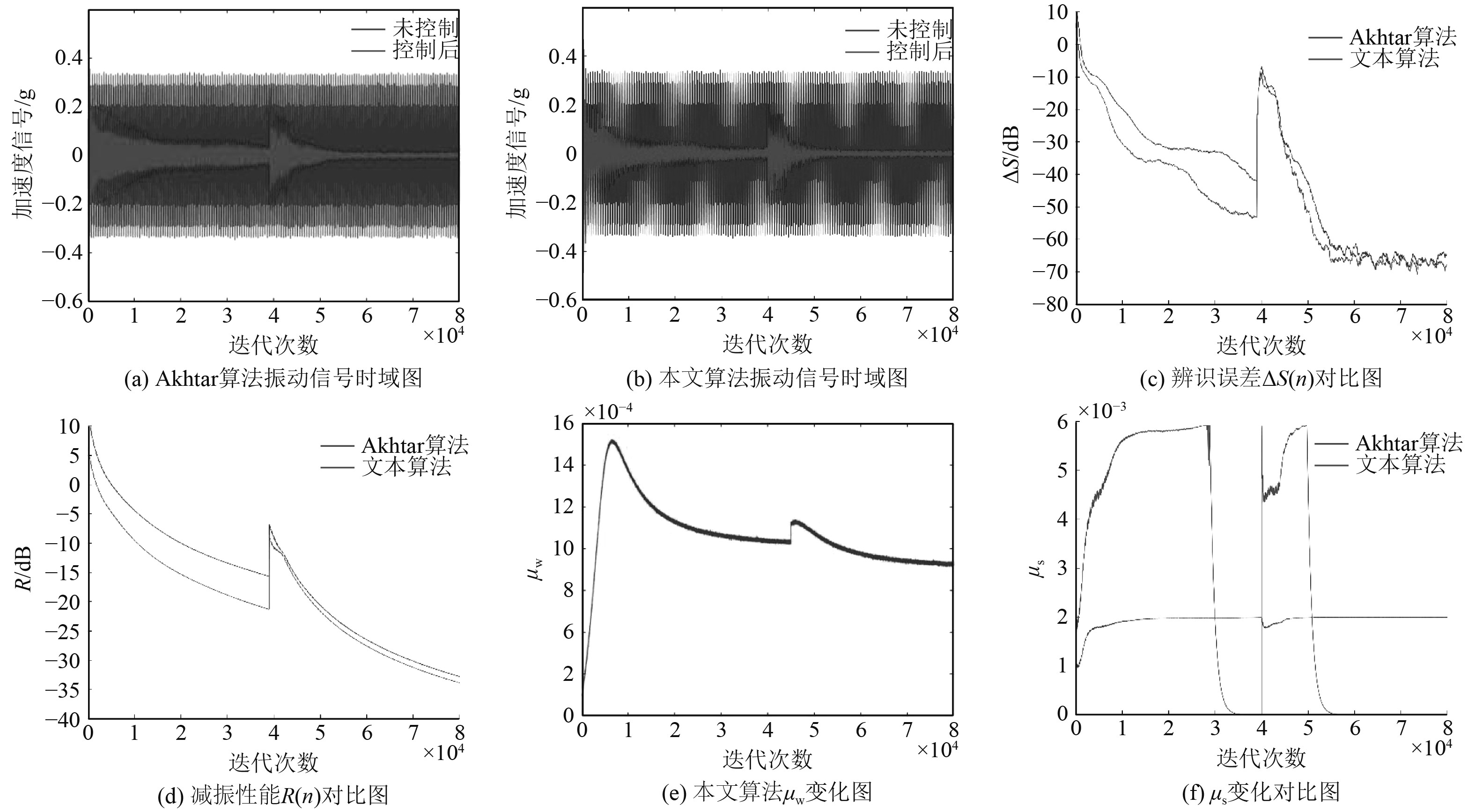
图7(a)和图7(b)分别为次级通道发生突变，2种算法的控制前后的时域对比图。图7(c)和图7(d)为建模辨识误差和减振效果，可看出算法迭代到稳定时，本文算法提前4000次左右，辨识精度整体高10 dB，减振性能高5 dB。图7(e)和图7(f)表示在考虑次级通道的时变特性后，本文算法能按照预定策略在线调整迭代步长，提高振动主动控制的整体性能。

3 实验研究

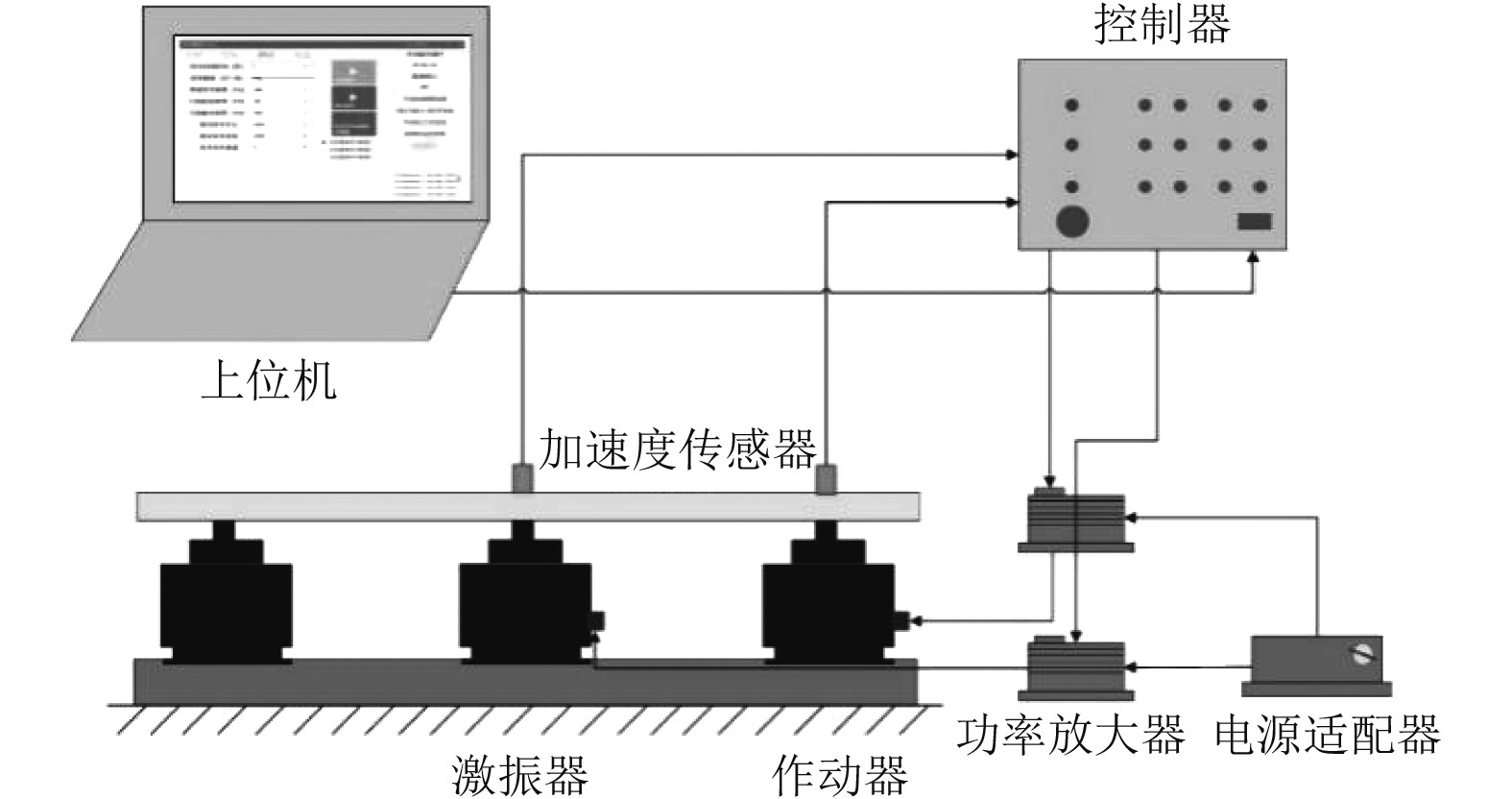
为了验证本文提出算法的有效性，基于中科振声公司自主研发的DSP控制器，进行单层隔振平台振动主动控制实验。实验基本原理如图8所示，由控制器中的信号发生模块模拟并输出振源信号，作为参考信号，经功率放大器适配放大后传给激振器产生初级振动。加速度传感器位于上层平台的目标控制区，在采集到平台的振动信号后，传输至控制器中的数据采集模块进行A/D转换，作为误差信号。输出的控制信号经输出模块D/A转换后到功率放大器及作动器，产生主动控制力作用于上层平台，产生次级振动，与初级振动叠加实现对控制点的减振功能。上位机通过TPC/IP通信线与控制器连接，将算法程序配置到下位控制器中。采用PCB加速度传感器，输入输出模块均集成与DSP控制器中，作动器和激振器采用中科振声公司自主研发的主被动一体化电磁隔振器。

上层平台由5个隔振器支撑，由螺栓连接，平台几何中心1个，四角各1个，隔振器下方刚性连接在一块钢板上。中央的隔振器视为激振器，其余隔振器按控制策略视为主动隔振器或被动隔振器。加速度传感器均设置在上层平台对应的隔振器上方。

实验开始由信号发生模块产生频率为60 Hz和80 Hz，幅值为2的双频叠加的正弦信号，激励上层平台产生初级振动。设置各自适应滤波器阶数均为512阶，初值为零，收敛步长参数调整至最佳值，控制步长变化范围在0.0001～0.001之间，采样频率2 kHz，内部控制算法产生的附加随机白噪声与正弦信号叠加作为输入信号。为方便2种算法的对比研究，设置通道4采用Akhtar算法，通道2采用本文算法。

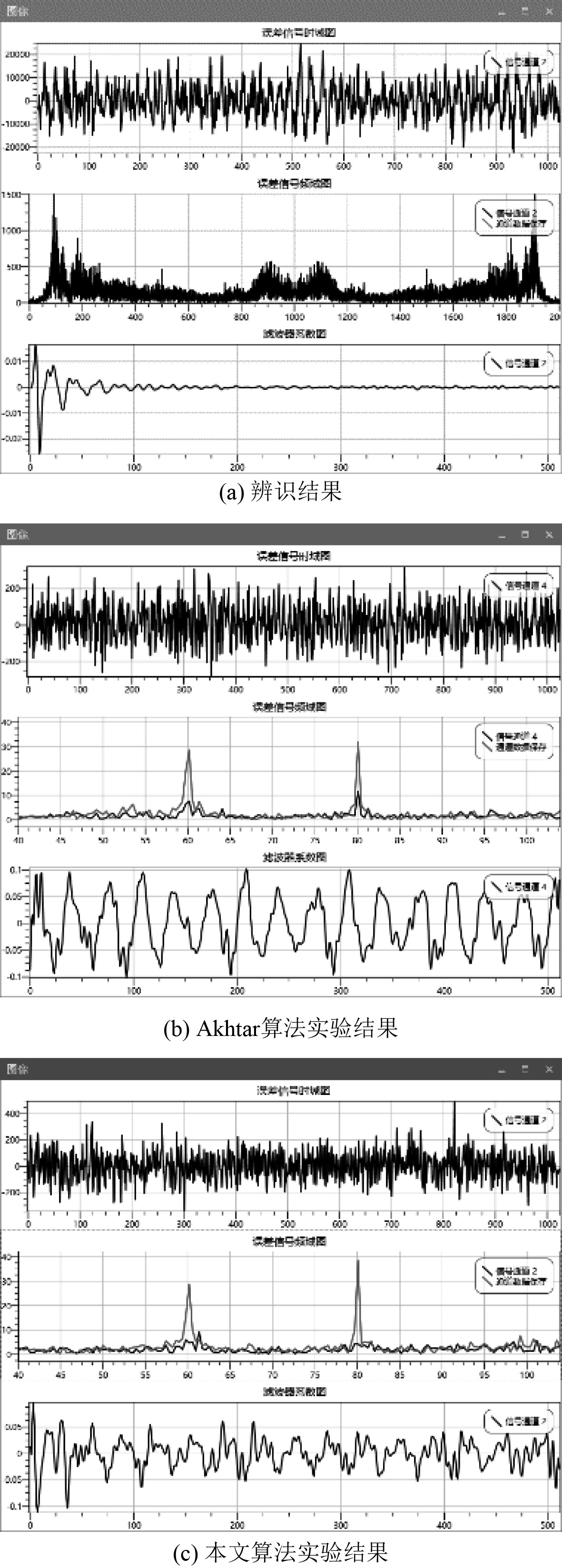
图9(a)为控制收敛后，辨识通道的辨识结果。图9(b)和图9(c)分别为开启控制5 s后采用Akhtar算法，和采用本文算法的误差信号时域图、频域图以及控制通道滤波器辨识结果图。2种算法均能有效减弱控制点的振动响应，频谱中60 Hz和80 Hz的线谱均明显下降，但Akhtar算法还未完全收敛，滤波器系数还有较大波动，振动响应幅值较高；本文算法已到达稳态，振动响应幅值下降更大。

4 结　语

针对在线辨识中2个通道间的相互影响，输入信号存在杂波的问题，本文在已有在线辨识主动控制算法基础上，提出一种变步长次级通道在线建模的振动主动控制算法，通过范数化参考信号采集，同时引入能量因子对迭代步长进行在线调整。结合仿真和实验对本文算法进行验证，结果表明，本文算法相比于原算法，步长调节范围跨度大，步长变化稳定可控，控制收敛速度快，稳态误差小，稳定性高。但本文算法为达到最佳控制效果需要设置较多参数值，当系统发生较大变化时，需要重新调整算法参数，下一步需要对此进行深入研究。