2. 郑州大学 管理学院,河南 郑州 450001;
3. 国防科技大学 智能科学学院 装备综合保障技术重点实验室,湖南 长沙 410073
2. School of Management, Zhengzhou University, Zhengzhou 450001, China;
3. Laboratory of Science and Technology on Integrated Logistics Support, College of Intelligence Science andTechnology, National University of Defense Technology, Changsha 410073, China
船舶在海面航行时,会遇到各种不同的水域,需要调整船舶的浮力,船舶的压载水系统能够调整船舶的排水量[1]。船舶的压载水系统由多种不同的阀门、水泵组成,结构复杂,各组件分布船舶的不同区域,故障排查困难。由于船舶在航行的过程中所处环境复杂,压载水系统需要进行不停的压载、卸载工作,频繁的操作会降低各组件的可靠性。
船舶的压载水系统结构复杂,通过对船舶压载水系统的可靠性分析,能够帮助了解压载水系统的故障原因,更快地进行维修。张迪等[2]利用模糊集合论建立故障树,并对压载水系统进行可靠性分析及优化。李佩昌等[3]提出了模糊动态故障树分析方法,对船舶系统可靠性进行分析。白旭等[4]提出将系统故障树转化为贝叶斯网络,考虑节点的正常、一般故障、严重故障3种状态,进行计算系统可靠度。易静[5]引入贝叶斯网络对系统可靠性进行分析。苏艳琴等[6]引入粗糙集和贝叶斯网络,对系统故障进行分析。姚成玉等[7]提出一种新型连续时间贝叶斯网络分析方法,计算子节点的故障概率。Mamdikar等[8]提出了一个使用故障树和动态贝叶斯网络的动态可靠性评估框架。王晓明等[9]采用基于连续时间贝叶斯网络的建模及分析方法对系统的动态特性进行可靠性分析。Codetta-Raiteri等 [10]采用广义的连续贝叶斯网络对系统进行可靠性分析。张大信等[11]分析了4种动态故障树顶事件概率的计算方法。Lei等[12]利用动态故障树对不同的系统进行可靠性建模。
上述研究并没有考虑分析船舶压载水系统随时间变化的系统可靠性,并且基于连续贝斯网络的系统可靠性分析的研究较少。本文利用动态故障树分析了船舶压载水系统故障原因,基于现有的连续贝叶斯网络可靠性分析方法,将动态故障树转化为连续贝叶斯网络,分析系统的可靠性以及剩余寿命。
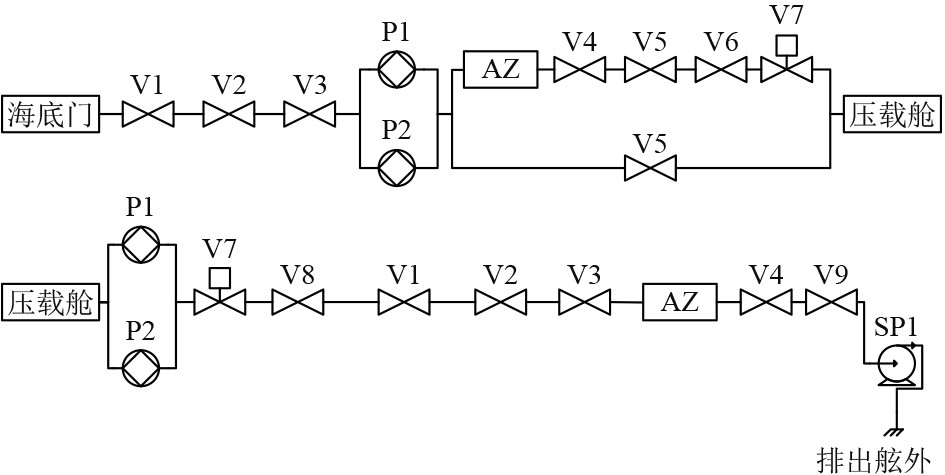
1 船舶压载水系统故障分析船舶压载水系统能够保证船舶在海上运行过程中保持稳定。压载水系统结构复杂,设备众多,因此故障原因众多,故障分析困难[12]。图1所示为简化后船舶压载水系统的组件结构图[13]。
|
图 1 船舶压载水系统结构图 Fig. 1 Structure drawing of ship ballast water system |
图中,V1和V2等分别代表止水阀,P1和P2代表压载水泵,SP1代表扫舱泵。可以看出,压载水系统包括压载水泵、阀门、扫舱泵,管道等。压载水的调驳包括压载和卸载两个过程。
压载即为系统吸水,压载的流程为打开海底门,1号压载水泵工作,海水通过1,2,3号阀门,进入AZ(压载水处理装置)进行海水的净化。海水净化后,依次通过4,5,6号阀门以及7号压载舱隔离阀件,进入压载舱,压载工作完成。如遇紧急情况,或者阀门损坏,海水可不通过AZ,直接经由7号阀门进入压载舱。其中2号压载泵为备用,如遇紧急情况,1号压载泵和2号压载泵同时工作。
卸载即为系统排水,卸载流程为打开4号压载隔离阀件,1号压载泵开始工作,将水抽出,经7,8,1,2,3号阀门进入AZ,水质达标后排除舷外。当压载水低于某一容量时,需扫舱系统将剩余压载水排除,即关闭1号压载泵,通过扫舱泵将压载水排出。
通过对于压载水系统工作流程的介绍,可以得到压载水系统故障事件,如表1所示。
|
|
表 1 故障事件 Tab.1 Fault event |
动态故障树为包含动态逻辑门的故障树。由于故障事件间具有关联关系,所以采用动态故障树来分析故障原因。以压载水系统为顶端事件来建立故障树。为了方便分析故障事件的关系,引入部分中间事件作为过渡。
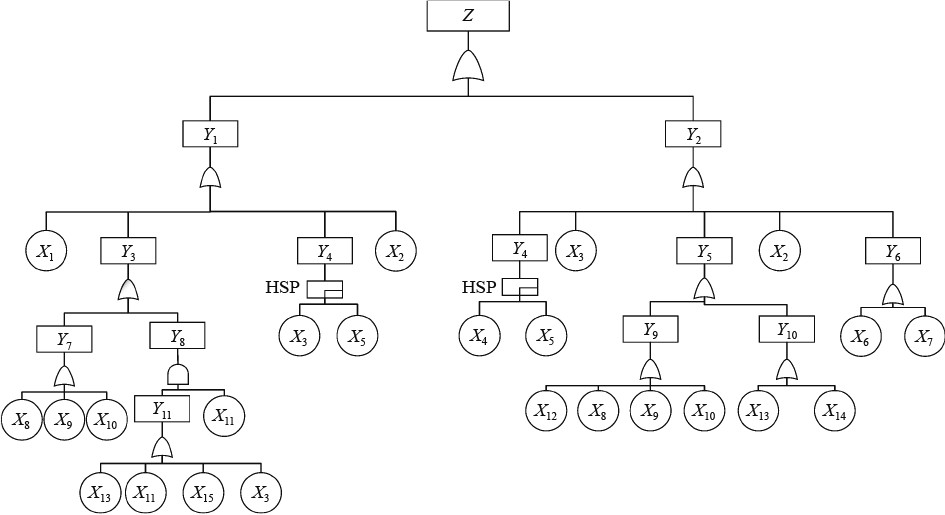
由图2可以看出,故障事件由逻辑门连接起来。以压载水系统失效Z为顶端事件,其中Y1和Y2分别为失效事件,只要吸水不成功或者排水不成功,压载水系统即失效。对于Y1来说,X1,Y3,Y4、X2只要有一个事件失效,Y1即失效,所以逻辑门关系为或门。同理其余类似事件的逻辑门关系也应为或门。但对于事件Y4压载泵失效来说,在特殊情况下2号水泵与1号水泵,均要工作,所以事件X4、X5的逻辑门应为热备门。事件Y11和X11同时失效,事件Y8才失效,应为与门。
|
图 2 压载水系统故障树 Fig. 2 Ballast water system fault tree |
连续贝叶斯网络能够表示系统在连续时间下的性能。由于船舶压载水系统组件众多,系统性能随时间变化较为明显,因此连续贝叶斯网络能够较好的刻画系统性能。船舶压载水系统故障树转化为贝叶斯网络的过程中,需要借助单位阶跃函数和冲激函数[9]实现转化。
单位阶跃函数为:
| $ v\left( {t - \eta } \right) = \left\{ \begin{gathered} 1 \quad t \gt \eta ,\\ \frac{1}{2} \quad t = \eta ,\\ 0 \quad t \lt \eta 。\\ \end{gathered} \right. $ | (1) |
冲激函数为:
| $ \zeta \left( {t - \eta } \right) = \left\{ \begin{gathered} 0 \quad t \ne \eta ,\\ \infty \quad t = \eta 。\\ \end{gathered} \right. $ | (2) |
其中,变量t和η分别表示事件的失效时间。
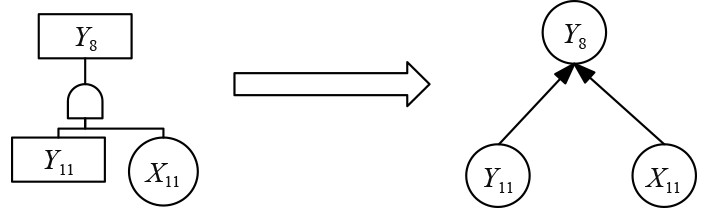
图3为逻辑与门的故障树结构和转化后的贝叶斯网络。当事件Y11和事件X11同时失效后,事件Y8才失效。根据逻辑或门的失效机理和贝叶斯网络的性质,可以得到事件Y8的失效条件概率为:
|
图 3 与门转化为贝叶斯网络 Fig. 3 AND gate is converted to Bayesian networks |
| $ \begin{split} {f_{{Y_8}|{Y_{11}},{X_{11}}}}\left( {{y_8}|{y_{11}},{x_{11}}} \right) =& v\left( {{x_{11}} - {y_{11}}} \right)\zeta \left( {{y_8} - {x_{11}}} \right) + \\ & v\left( {{y_{11}} - {x_{11}}} \right)\zeta \left( {{y_8} - {y_{11}}} \right) ,\end{split}$ | (3) |
其中,y11、x11、y8 分别表示事件Y8 、事件Y11、事件X11的发生失效的时间。
根据贝叶斯网络的性质可知,该逻辑与门的联合概率密度函数为:
| $\begin{split} & {f_{{Y_{11}}{X_{11}}{Y_8}}}\left( {{y_{11}},{x_{11}},{y_8}} \right) = \\ & {f_{{Y_8}|{Y_{11}},{X_{11}}}}\left( {{y_8}|{y_{11}},{x_{11}}} \right){f_{{Y_{11}}}}\left( {{y_{11}}} \right){f_{{X_{11}}}}\left( {{x_{11}}} \right) ,\end{split}$ | (4) |
将此联合概率密度函数对y11和x11积分,得到事件Y8的概率密度函数为以及概率分布函数为:
| $ \begin{split} &{f_{{Y_8}}}\left( {{y_8}} \right) =\int_0^\infty {\int_0^\infty {v\left( {{x_{11}} - {y_{11}}} \right)\zeta \left( {{y_8} - {x_{11}}} \right)} } \\ & {f_{{Y_{11}}}}\left( {{y_{11}}} \right){f_{{X_{11}}}}\left( {{x_{11}}} \right){\rm{d}}{x_{11}}{\rm{d}}{y_{11}} + \\ &\int_0^\infty {\int_0^\infty {v\left( {{y_{11}} - {x_{11}}} \right)\zeta \left( {{y_8} - {y_{11}}} \right)} } {f_{{Y_{11}}}}\left( {{y_{11}}} \right){f_{{X_{11}}}}\left( {{x_{11}}} \right){\rm{d}}{x_{11}}{\rm{d}}{y_{11}} =\\ & \frac{{{\rm{d}}\left[ {{F_{{Y_{11}}}}\left( {{y_8}} \right){F_{{X_{11}}}}\left( {{y_8}} \right)} \right]}}{{{\rm{d}}{y_8}}},\\[-17pt] \end{split} $ | (5) |
| $ {F_{{Y_8}}}\left( t \right) = P\left( {{Y_8} \leqslant t} \right) = {F_{{Y_{11}}}}\left( t \right){F_{{X_{11}}}}\left( t \right) 。$ | (6) |
图4为逻辑或门的故障树结构和转化后的贝叶斯网络。事件X6和事件X7,只要有一个事件失效后,事件Y6则失效,根据逻辑与门的失效原理和贝叶斯网络的性质,可以得到事件Y6的失效条件概率为:

|
图 4 或门转化为贝叶斯网络 Fig. 4 Or gate is converted to Bayesian networks |
| $\begin{split} {f_{{Y_6}|{X_6},{X_7}}}\left( {{y_6}|{x_6},{x_7}} \right) = &v\left( {{x_6} - {x_7}} \right)\zeta {y_6}\left( {{y_7} - {x_7}} \right) + \\ & v\left( {{x_7} - {x_6}} \right)\zeta \left( {{y_6} - {x_6}} \right)。\end{split}$ | (7) |
其中:x6,x7,y6 分别为事件X6 、事件X7、事件Y6的发生失效的时间。
根据贝叶斯网络的性质可知,该逻辑或门的联合概率密度函数为:
| $ {f_{{X_6}{X_7}{Y_6}}}\left( {{x_6},{y_7},{y_6}} \right) = {f_{{Y_6}|{X_6},{X_7}}}\left( {{y_6}|{x_6},{x_7}} \right){f_{{X_6}}}\left( {{x_6}} \right){f_{{X_7}}}\left( {{x_6}} \right) ,$ | (8) |
将此联合概率密度函数对x6和x7积分,得到事件Y6的边缘概率密度函数为以及概率分布函数为:
| $ \begin{split} & {f_{{Y_6}}}\left( {{y_6}} \right) = \\ & \int_0^\infty {\int_0^\infty {{f_{_{{Y_6}}|{X_6},{X_7}}}} } \left( {{y_6}|{x_6},{x_7}} \right){f_{{X_6}}}\left( {{x_6}} \right){f_{{X_7}}}\left( {{x_7}} \right){\rm{d}}{x_6}{\rm{d}}{x_7}= \\ & {f_{{X_6}}}\left( {{y_6}} \right) + {f_{{X_7}}}\left( {{y_6}} \right) - \frac{{{\rm{d}}\left[ {{F_{{X_6}}}\left( {{y_6}} \right){F_{{X_7}}}\left( {{y_6}} \right)} \right]}}{{d{y_6}}} 。\end{split} $ | (9) |
因此,在
| $ {F_{{Y_6}}}\left( t \right) = P\left( {{Y_6} \leqslant t} \right)t = {F_{{X_6}}}\left( t \right) + {F_{{X_7}}}\left( t \right) - {F_{{X_6}}}\left( t \right){F_{{X_7}}}\left( t \right) 。$ | (10) |
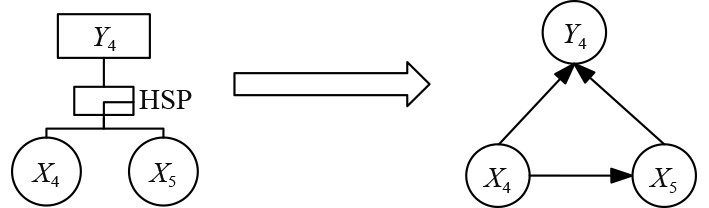
图5为热备门的故障树结构和转化后的贝叶斯网络。压在水泵1工作时,压载水泵2也工作,当压载水泵1和2均失效时,事件Y4才失效。根据动态贝叶斯网络的性质,X4在X5失效的条件下,失效的概率为:
|
图 5 热备门转化为贝叶斯网络 Fig. 5 Hot spare gate is converted to Bayesian network |
| $ {f_{{X_5}|{X_4}}}\left( {{x_5}|{x_4}} \right) = {f_{{X_5}}}\left( {{x_5}} \right) ,$ | (11) |
又因为只有事件X4、事件X5均发生失效时,事件Y4才失效,因此,事件Y4失效的条件概率函数可由动态逻辑与门的条件概率得到,其条件概率可以表示为:
| $\begin{split} & {f_{{Y_4}|{X_4},{X_5}}}\left( {{y_4}|{x_4},{x_5}} \right) = v\left( {{x_5} - {x_4}} \right)\zeta \left( {{y_4} - {x_5}} \right) + \\ & v\left( {{x_4} - {x_5}} \right)\zeta \left( {{y_4} - {x_4}} \right) 。\end{split}$ | (12) |
根据贝叶斯网络的性质可知,该热备门的联合概率密度函数为:
| $ \begin{split} &{f_{{X_4}{X_5}{Y_{\text{4}}}}}\left( {{x_4},{x_5},{y_4}} \right) = {f_{{Y_4}|{X_{\text{4}}},{X_5}}}\left( {{y_4}|{x_4},{x_5}} \right){f_{{X_{\text{5}}}{\text{|}}{X_4}}}\left( {{x_5}{\text{|}}{x_4}} \right),\\ &{f_{{X_4}}}\left( {{x_4}} \right) = {f_{{Y_4}|{X_{\text{4}}},{X_5}}}\left( {{y_4}|{x_4},{x_5}} \right){f_{{X_5}}}\left( {{x_5}} \right){f_{{X_4}}}\left( {{x_4}} \right)。\\[-10pt] \end{split} $ | (13) |
上述联合概率密度函数对变量x4和x5积分,可得下级事件Y4的边缘概率密度函数和概率分布函数为:
| $ \begin{split} &{f_{{Y_1}}}\left( y \right) = \\ & \int_0^\infty {\int_0^\infty {{f_{{Y_{\text{1}}}|{X_{\text{1}}},{X_{\text{2}}}}}\left( {y|{x_{\text{1}}},{x_{\text{2}}}} \right){f_{{X_{\text{2}}}}}\left( {{x_{\text{2}}}} \right){f_{{X_1}}}\left( {{x_1}} \right)} } {\rm{d}}{x_2}{\rm{d}}{x_1} =\\ & \frac{{{\rm{d}}\left[ {{F_{{X_{\text{1}}}}}\left( y \right){F_{{X_2}}}\left( y \right)} \right]}}{{{\rm{d}}y}} 。\\[-10pt] \end{split} $ | (14) |
| $ {F_{{Y_4}}}\left( t \right) = P\left( {{Y_4} \leqslant t} \right) = {F_{{X_4}}}\left( t \right){F_{{X_5}}}\left( t \right) 。$ | (15) |
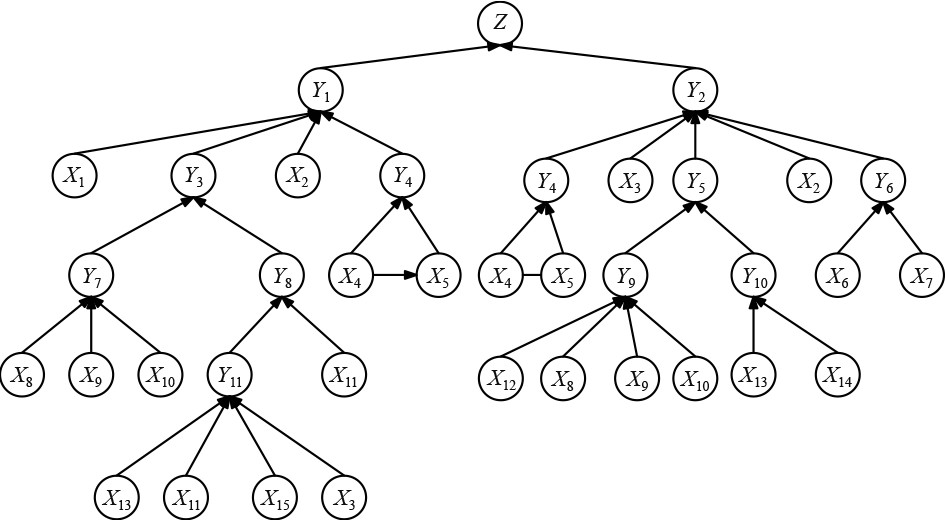
船舶压载水系统结构复杂,故障形式多样,故障事件间具有错综复杂的关系。借用上述分析,将压载水系统动态故障树转化为连续贝叶斯网络模型,以便于分析压载水系统的可靠性和剩余寿命。基于图2中的船舶压载水系统故障树,可以得到系统的连续贝叶斯网络模型,如图6所示。
|
图 6 连续贝叶斯网络模型 Fig. 6 Continuous Bayesian network model |
通过转化后的贝叶斯网络,基于表1中的数据,利用式(6)、式(10)、式(15),可以得到船舶压载水系统可靠度随时间的变化,如图7所示。

|
图 7 系统可靠性变化曲线 Fig. 7 System reliability change curve |
可以看出,船舶压载水系统随着时间的变化,可靠度逐渐降低,当t=153h,系统可靠度已经降低到0.4955;当系统运行到t=348 h时,系统的可靠度降低为0.207。系统可靠度下降的速度逐渐变缓。
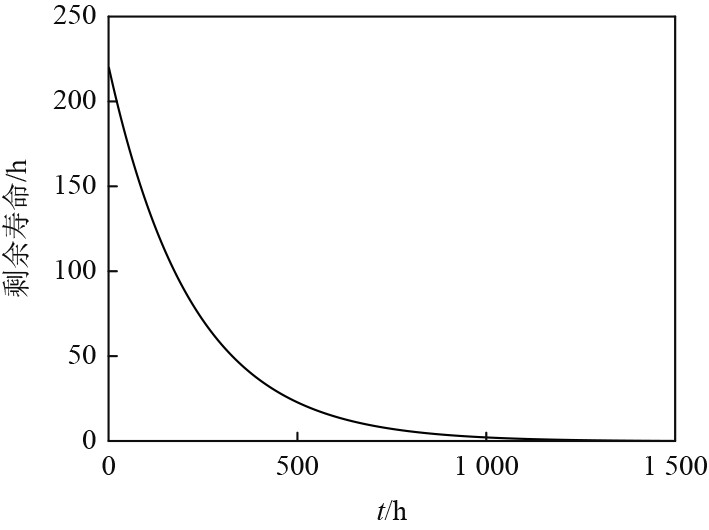
利用船舶压载水系统的可靠度,通过对系统可靠度在
|
图 8 系统寿命变化曲线 Fig. 8 System life curve |
根据图8以及仿真计算,船舶压载水系统,在0时刻剩余寿命为219.76 h,随着时间的递增,剩余寿命逐渐变短;在t=348 h剩余寿命为45.54 h。系统的剩余寿命随时间变化的速度逐渐递减。
4 结 语针对船舶压载水系统结构复杂,可靠性难以分析的问题。本文基于船舶压载水系统的故障机理,建立了压载水系统的动态故障树模型。然后基于连续时间的贝叶斯网络,通过算例分析了船舶压载水系统的可靠性。
| [1] |
杨泽宇, 乔红宇. 基于 InTouch 的船舶压载水监控系统[J]. 中国造船, 2010, 51(3): 185-190. YANG Z Y, Q H Y. Design of ship ballast monitor based on intouch[J]. Shipbuilding of China, 2010, 51(3): 185-190. |
| [2] |
张迪, 朱发新, 雷建, 等. 基于模糊故障树的压载水系统可靠性分析[J]. 造船技术, 2012(5): 20-23. DOI:10.3969/j.issn.1000-3878.2012.05.006 |
| [3] |
李佩昌, 周海军, 周国敬. 基于专家综合评估的模糊动态故障树分析[J]. 舰船科学技术, 2019, 41(19): 192-197. |
| [4] |
白旭, 汤荣铿, 罗小芳, 等. 基于故障树分析和贝叶斯网络方法的半潜式钻井平台系统多状态可靠性分析[J]. 中国造船, 2020, 61(2): 220-228. DOI:10.3969/j.issn.1000-4882.2020.02.021 |
| [5] |
易静. 基于贝叶斯网络的舰船故障建模方法研究[J]. 舰船科学技术, 2019, 41(4): 43-45. |
| [6] |
苏艳琴, 徐廷学, 张文娟. 粗糙集和贝叶斯网络融合故障诊断方法[J]. 舰船科学技术, 2013, 35(3): 91-93. SU Y Q, XU T X, ZHANG W J. Research on one fusion fault diagnosis method based on rough set theory and bayesian network[J]. Ship Science and Technology, 2013, 35(3): 91-93. |
| [7] |
姚成玉, 韩丁丁, 陈东宁, 等. 考虑共因失效的新型连续时间动态贝叶斯网络可靠性分析方法[J]. 仪器仪表学报, 2022, 43(6): 174-184. |
| [8] |
MAMDIKAR M R, KUMAR V, SINGH P. Dynamic reliability analysis framework using fault tree and dynamic Bayesian network: A case study of NPP[J]. Nuclear Engineering and Technology, 2022, 54(4): 1213-1220. DOI:10.1016/j.net.2021.09.038 |
| [9] |
王晓明, 李彦锋, 李爱峰, 等. 模糊数据下基于连续时间贝叶斯网络的整流回馈系统可靠性建模与评估[J]. 机械工程学报, 2015, 51(14): 167-174. DOI:10.3901/JME.2015.14.167 |
| [10] |
CODETTA-RAITERI D, PORTINALE L. Generalized continuous time bayesian networks as a modelling and analysis formalism for dependable systems[J]. Reliability Engineering & System Safety, 2017, 167: 639-651. |
| [11] |
张大信, 郭基联. 动态故障树顶事件概率计算流程[J]. 信息工程大学学报, 2021, 22(5): 566-570+605. DOI:10.3969/j.issn.1671-0673.2021.05.008 |
| [12] |
LEI X, MACKENZIE C A. Assessing risk in different types of supply chains with a dynamic fault tree[J]. Computers & Industrial Engineering, 2019, 137: 106061. |
| [13] |
隆奇芮, 郭智威, 白秀琴, 等. 大型邮轮压载水系统设计技术研究[J]. 舰船科学技术, 2020, 42(5): 85-91. LONG Q R, GUO Z W, BAI X Q, et al. Research on the design technology of ballast water system for large cruise ships[J]. Ship Science and Technology, 2020, 42(5): 85-91. DOI:10.3404/j.issn.1672-7649.2020.05.017 |
 2023, Vol. 45
2023, Vol. 45
