近年来,随着人民生活质量和消费水平不断提高,邮轮旅游已成为我国新型的消费产业,预计到2030年,我国邮轮出入境游客人数将达1750万人次[1],成为邮轮产业最大的消费市场之一。同时,旅游方式也将从旅游观光为主向休闲娱乐的转变,因此邮轮旅游的舒适性与多样性变得尤为重要[2]。
其中,邮轮泳池多布置在船首以及尾部,并附带多功能如烧烤台,海滩派对,日光浴场等,是游客休闲放松的主要区域。然而,泳池的自由液面会影响船舶稳性降低舒适性,同时泳池的晃荡也会对乘客造成不适与危险,所以一般船舶泳池布置在船舶中心线附近[3],其尺寸也会受到限制。许多邮轮还规定在3级海况时禁止开放游泳池。为提高乘客舒适性,减少高海况对乘客旅游观光的不利影响,本文将对不同形状泳池进行晃荡分析,研究影响泳池晃荡的因素,提出舒适性更高的泳池形状。
对于晃荡问题,国内外专家学者开展了大量的分析研究。早期的液舱晃荡问题大多依赖于模型试验的方法。Nasar等[4]对波浪中单液舱浮箱进行试验研究,设置不同波高、周期等参数和载液量,研究晃荡现象。卫志军等[5]开展了单个矩形液舱晃荡的大尺度模型试验,研究不同载液量下舱内液体晃荡冲击荷载的特性。
随着理论方法与数值方法的不断完善,基于数值计算的研究方法不断被采用。Jiang等[6]针对某型双液舱船舶,采用VOF法(volume of fluid)和IRF法(impulse response function)求解船舶与液舱晃荡间的耦合响应,研究了不同载液工况下船舶运动响应与液舱晃荡间的耦合效应。丁刚[7]采用非结构混合网格,基于Fluent软件中的VOF模型、Segregated,以及压力速度祸合的PISO算法,模拟三维条件下具有自由液面的、不互溶的、油一水一气三相不可压缩非定常流动。徐博等[8]基于CFD软件STAR-CCM+建立一种二维黏性流体数值模型,研究了矩形液舱在特定水平余弦激励下舱内液体的晃动问题。Stephen等[9]建立考虑液舱耦合效应的时域运动方程,求解了规则波作用下矩形浮体的液舱晃荡问题,研究不同载液量对浮体水动力响应的影响。DongmingLiu等[10]基于CFD方法,采用大涡模拟(LES)研究了三维液舱晃荡液面变化情况,采用VOF追踪自由液面,计算结果与试验吻合度高。
目前研究液舱晃荡问题多以模型试验结合数值仿真为主,经验证CFD方法能够与试验结果很好吻合,尤其对于非线性现象能够准确预测。基于势流理论的方法可在时域范围内求解液舱与浮体耦合运动,在线性条件下可以很好预测响应结果且效率较高。当浮体出现抨击:液面破碎等强非线性现象时势流理论将不再适用。因此,根据这一结论,本文在求解大型邮轮水动力响应时采用势流理论,将得到的结果作为液舱的强迫运动,基于CFD方法模拟液舱晃荡,得到更多流动细节。在此基础上对不同形状泳池进行晃荡分析,研究影响泳池晃荡的因素,提出舒适性更高的泳池形状。
1 邮轮水动力分析 1.1 模型建立以某大型邮轮为例,其主尺度参数如图1所示。采用势流软件Ansys-AQWA对其水动力性能进行分析,由于船舶排水量与泳池重量相差甚大,故计算忽略泳池对邮轮运动响应的影响。参照目前研究方法,邮轮三维模型及网格图如图1所示,总网格数为7902,坐标系原点建立在船体中纵剖面与水线面的交线尾部。考虑到此类船舶纵向摇动远小于横向摇动,本文仅考虑横向最危险工况,即重点研究横浪作用下船舶在固有周期时的横摇及其造成的液舱晃荡。

|
图 1 船体模型 Fig. 1 Model of ship hull |
|
|
表 1 主尺度参数 Tab.1 Main scale parameters |
根据经验公式,横摇惯性半径选取0.36B,按规范增加人工阻尼。计算邮轮横浪作用时的横摇RAO,为节约计算时间去除主甲板以上上层建筑。
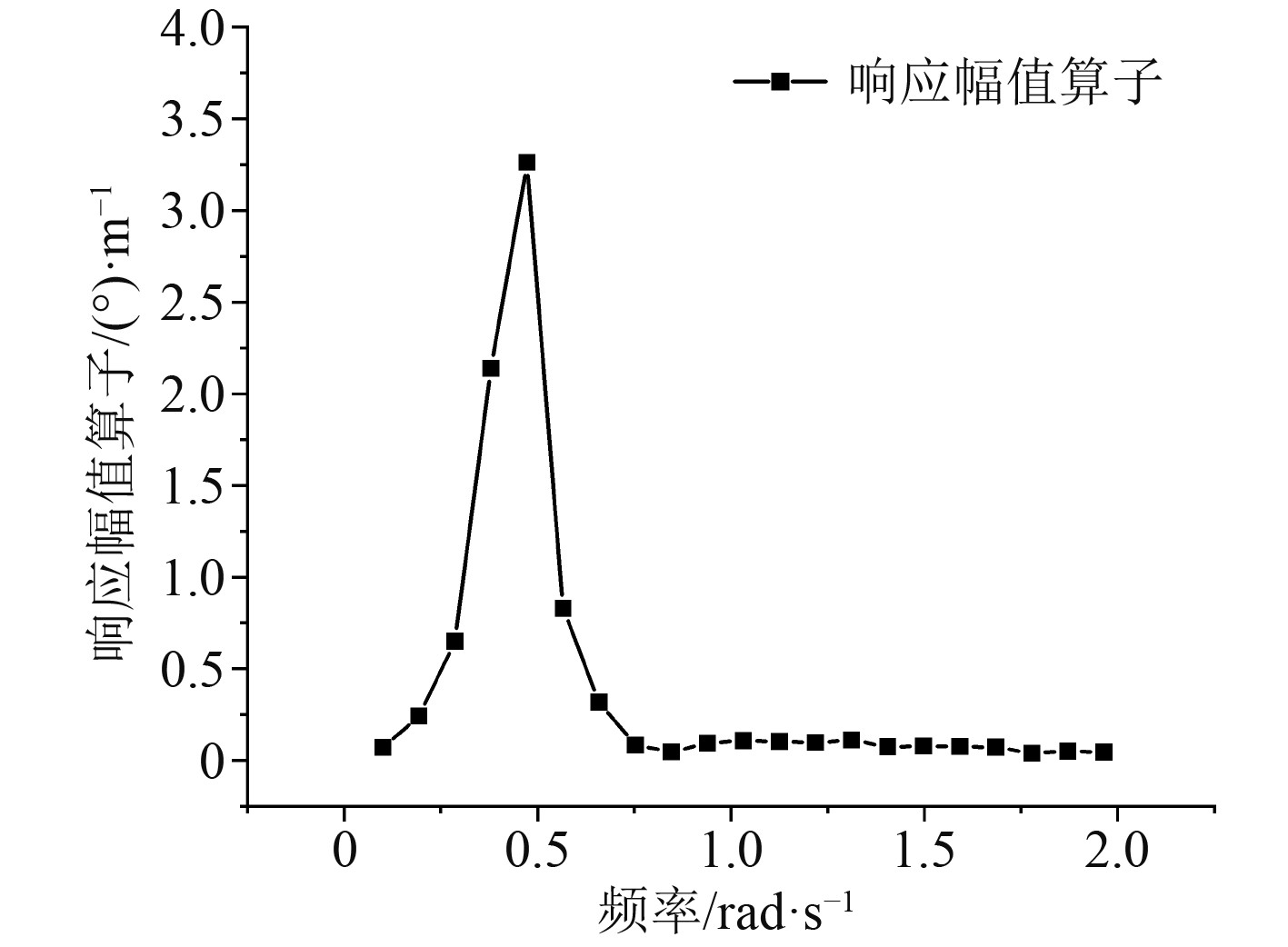
1.2 计算结果考虑横浪作用下,船舶横摇响应幅值算子如图2所示。
|
图 2 横浪作用下邮轮横摇RAO Fig. 2 Rolling RAO under transverse waves |
图2为邮轮横摇RAO曲线。可看出单位波幅下邮轮最大响应幅值可达3.3°,此时波浪激励力频率为0.5 rad/s。考虑到大型邮轮尺寸较大,单位波幅作用时满足线性微幅波条件,当波高提升至1.25 m(对应3级最高海况)时,邮轮最大响应幅值可达2.3°,对应频率仍为0.5 rad/s。因此,考虑最危险工况,即邮轮横向受频率为0.5 rad/s的规则波,则邮轮上任一点绕重心旋转角度为:
| $ \theta = 0.04 \cdot \cos (0.5t){\text{rad}}/{\text{s}}。$ | (1) |
将式(1)作为泳池绕重心的强迫运动输入CFD软件即可得到3级海况下不同形状泳池内液面升高及压力变化情况。
2 泳池晃荡分析为深入研究泳池晃荡性能,基于CFD软件Fluent计算不同形状泳池3级海况下液面变化情况,为泳池设计及提高舒适性措施提供参考。CFD具有丰富的物理模型,功能强大,精度比较高,用来捕捉液面变化规律具有较强的优势。
2.1 基础理论 2.1.1 流体的运动控制方程根据连续介质假设,流体质量守恒方程(又称为连续性方程)可表达为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {v_x})}}{{\partial x}} + \frac{{\partial (\rho {v_y})}}{{\partial y}} + \frac{{\partial (\rho {v_z})}}{{\partial z}} = 0 ,$ | (2) |
式中:
动量守恒方程(Navier-Stokes方程)可表达为:
| $\left\{ \begin{split} & \frac{{\partial (\rho {v_x})}}{{\partial t}} + \nabla \cdot (\rho {v_x}\nu ) = - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + {f_x} ,\\ & \frac{{\partial (\rho {v_y})}}{{\partial t}} + \nabla \cdot (\rho {v_y}\nu ) = - \frac{{\partial p}}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} + {f_y} ,\\ & \frac{{\partial (\rho {v_z})}}{{\partial t}} + \nabla \cdot (\rho {v_z}\nu ) = - \frac{{\partial p}}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} + {f_z} 。\end{split} \right. $ | (3) |
式中:
1)指定加速度。Fluent中可以指定流体运动加速度,并将加速度以体积力的形式施加到计算域中的流体上。然而Fluent并没有提供变加速度的直接添加,若要计算变加速度情况,则需要手工分段计算。
2)指定计算域速度。将加速度或位移数据转化为速度添加到计算域上。可以通过DEFINE_ZONE_MOTION宏或PROFILE文件的方式进行指定。2021版Ansys-Fluent可通过函数直接定义域的运动此方式要比加速度方式更加灵活,本文采用此方法。
2.2 数值计算 2.2.1 模型建立以矩形泳池为例,参数设置与实际情况一致,四周采用固壁边界条件,顶部设置大气压力出口,计算模型如图3所示。网格总数为190万(经无关性验证),自由液面处加密。启用moving mesh,设置泳池绕重心的强迫运动,为保证计算精度采用PISO压力、流速耦合算法。保证面积不变,改变泳池形状采用相同设置,如图3所示。

|
图 3 计算域网格模型 Fig. 3 Computational domain |
采用VOF模型,时间步长经验证可兼顾效率与准确性,RNG
|
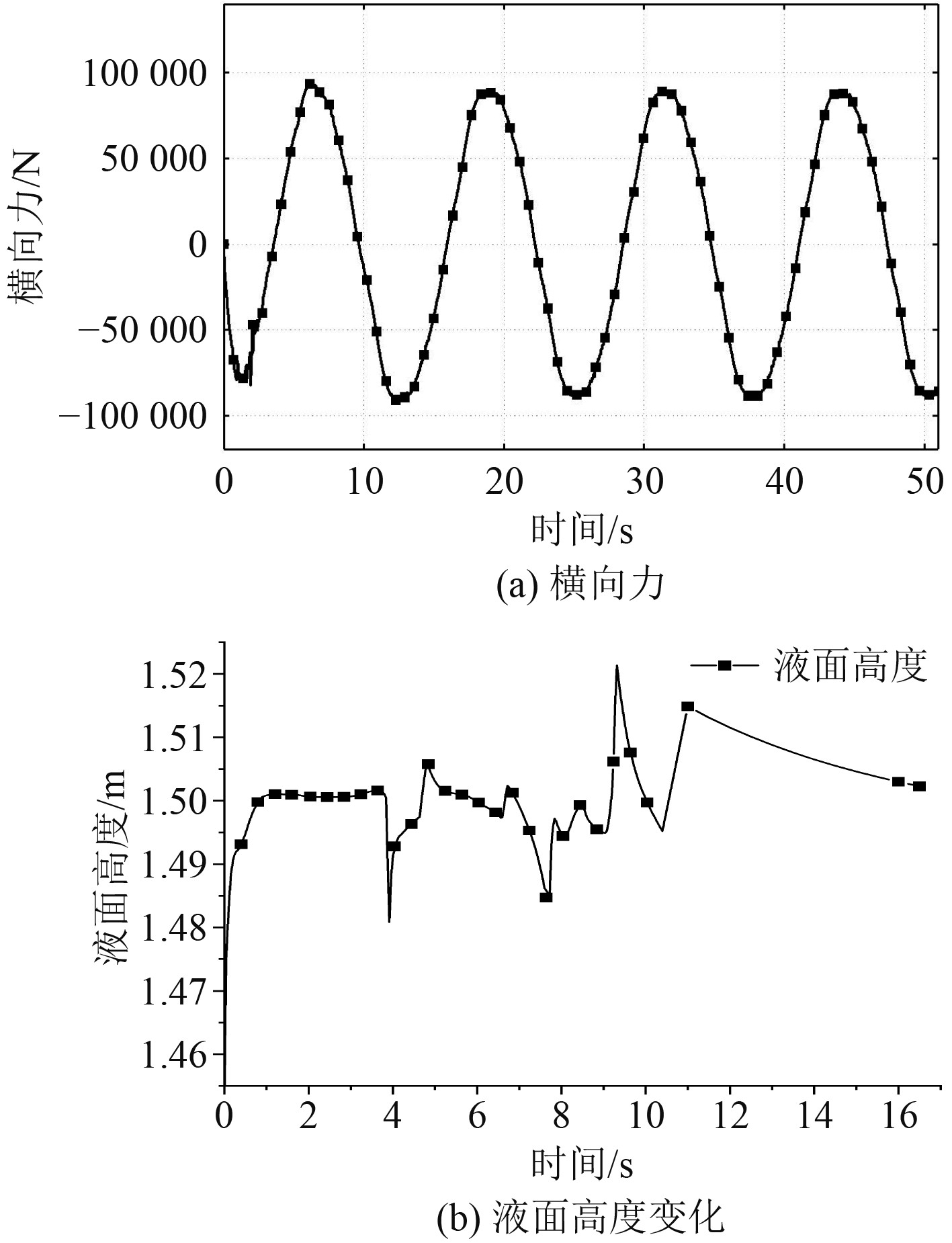
图 4 矩形泳池计算结果 Fig. 4 Calculation results of rectangular pool |
可知,由于重心距泳池垂向距离较小,泳池内液面升高不明显,泳池两侧受到的压力交替变化可比较明显地看出晃荡带来的影响,横向力变化频率与波浪激励力保持一致符合实际。监测点位于泳池壁面液面在1.480~1.522 m之间,游客受到影响较小。
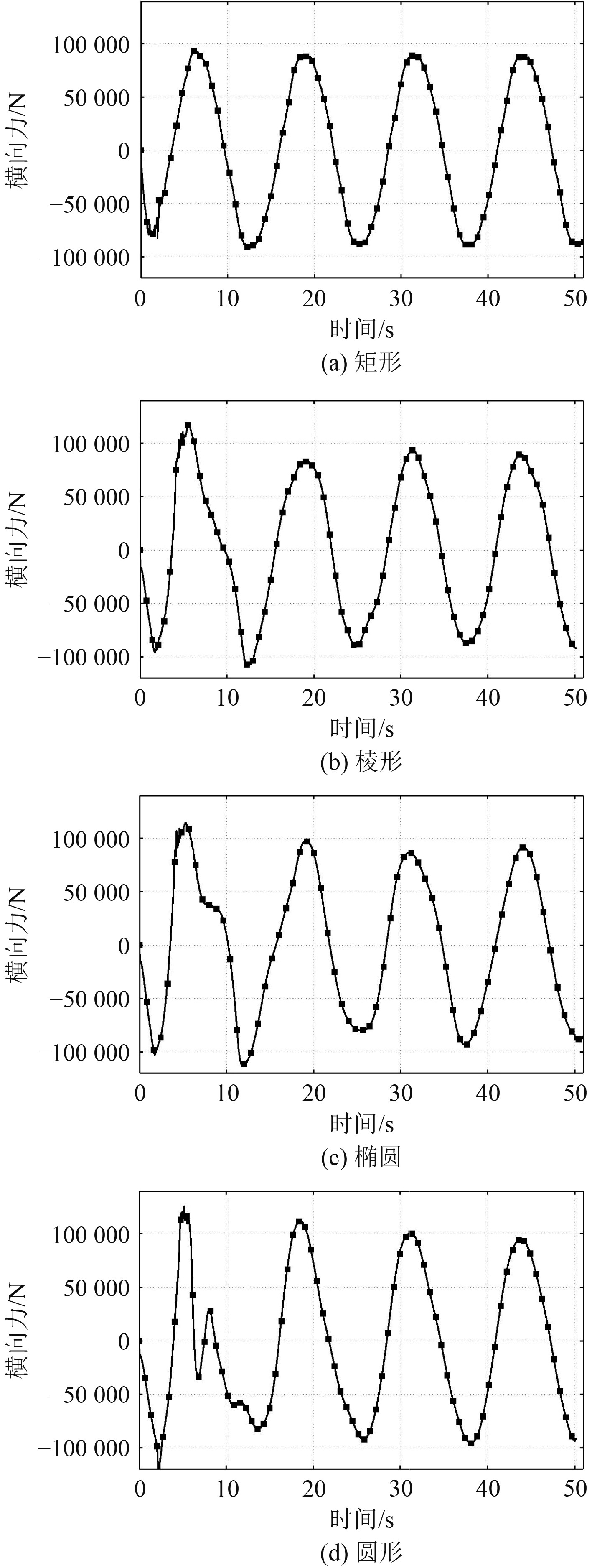
3 不同形状泳池晃荡对比为进一步提高泳池舒适性,对目前市内泳池形状进行总结,通过上述方法研究不同形状泳池晃荡性能,通过对比分析最终确定有利于乘客舒适性的截面形状。不同形状泳池横向力曲线如图5所示。
|
图 5 不同形状泳池横向力曲线 Fig. 5 Transverse force of swimming pools with different shapes |
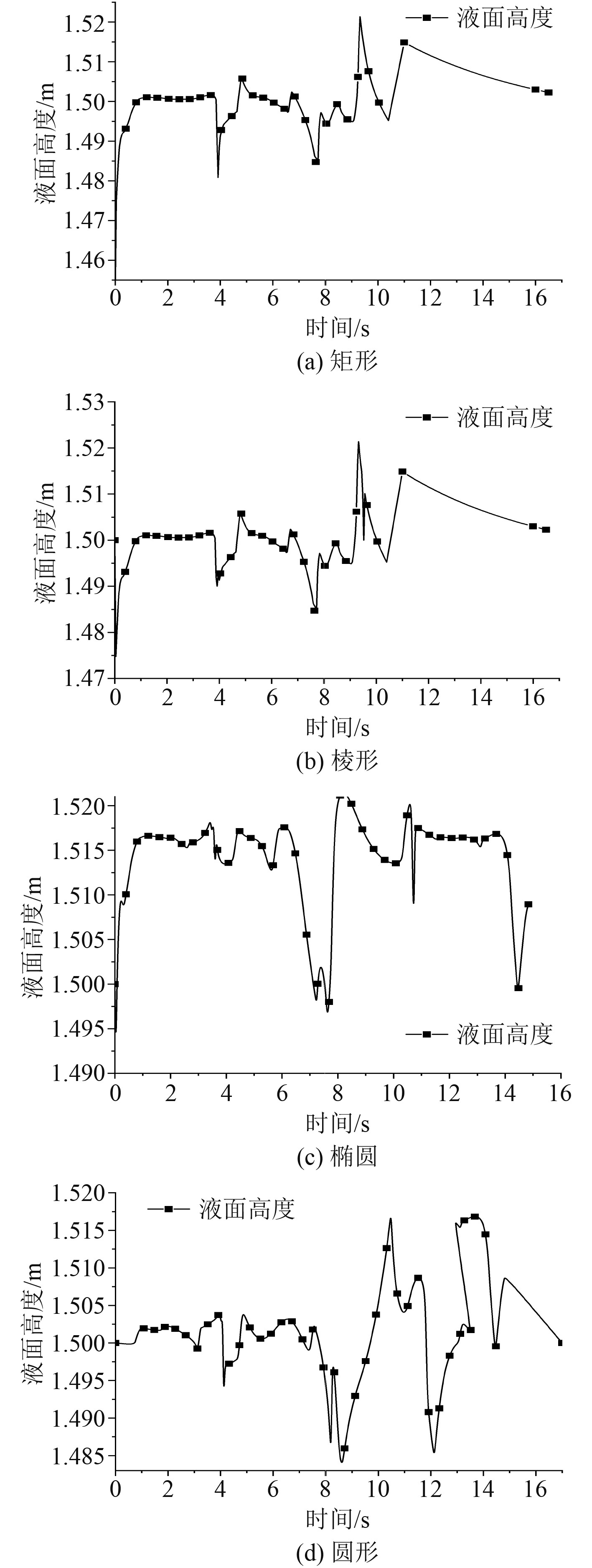
图6为不同形状泳池晃荡结果。可以看出:
|
图 6 不同形状泳池晃荡结果 Fig. 6 Surface height of swimming pools with different shapes |
1)受力曲线总体上变化规律一致,均在晃动开始6~8 s后达到最大值。稳定后矩形、棱形与椭圆受到横向力较小,圆形最大。
2)液面变化曲线波动规律性较差,这主要是因为泳池整体晃荡较小任何一点小的扰动都会引起液面高度发生变化。对4种形状液面高度峰值进行分析,菱形和圆形液面升高较大,且升高最大值均出现在横向最远点,容易出现溢出泳池的现象,造成乘客的不适与危险。
进一步分析,圆形截面不管是横向力还是液面升高都是最大的,这主要是因为相同面积时圆形截面直径大于其他形状的宽度,其横向尺度最大,因此晃荡引起的液面变化最大。菱形与圆形沿横向纵截面收缩明显,流速随之增大最终导致液面爬升高度增加。
4 结 语国内外大多邮轮对泳池的舒适性研究较少,3级海况时通常关闭泳池给游客带来不便。本文对波浪环境下泳池晃荡进行研究,结合势流与粘流理论研究3级海况下邮轮泳池晃荡情况。以此方法为基础,研究不同形状泳池的晃荡特性。通过对比分析,得到以下结论:
1)通过势流与粘流理论的结合可快速准确得到泳池或液舱晃荡细节;
2)3级海况下大型邮轮泳池晃荡不明显,可视情况开放;
3)横向大尺度是引起横向冲击力的主要原因,纵截面面积沿横向变化情况是导致液面升高的主要因素;
4)矩形与椭圆泳池舒适性最好,结构布置允许时尽量采用。
| [1] |
姜杰. 大型邮轮外观设计的本土化研究[D]. 武汉: 武汉理工大学, 2018.
|
| [2] |
吴卫国, 潘长学. 大型豪华邮轮设计研发关键技术探析[J]. 船舶工程, 2020, 42(1): 18-21. |
| [3] |
王俊, 林贤恒. 邮轮游泳池设计初探[J]. 广船科技, 2020, 40(2): 18-22. DOI:10.3969/j.issn.2095-4506.2020.02.005 |
| [4] |
NASAR T, SANNASIRAJ S A, SUNDAR V. Motion responses of barge carrying liquid tank[J]. Ocean Engineering, 2010, 37(10): 935-946. DOI:10.1016/j.oceaneng.2010.03.006 |
| [5] |
卫志军, 岳前进, 阮诗伦, 等. 矩形液舱晃荡冲击载荷的试验机理研究[J]. 船舶力学, 2012, 16(8): 885-892. DOI:10.3969/j.issn.1007-7294.2012.08.007 |
| [6] |
JIANG S C, TENG, B, BAI W, et al. Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action[J]. Ocean Engineering, 2015, 108: 140-154. DOI:10.1016/j.oceaneng.2015.07.044 |
| [7] |
丁刚. 基于FLUENT的破舱船舶溢油的数值模拟[D]. 武汉: 武汉理工大学, 2010.
|
| [8] |
徐博, 姜胜超, 刘浩, 等. 基于STAR-CCM+的液舱晃荡数值研究[C]//中国海洋工程学会. 第十九届中国海洋(岸)工程学术讨论会论文集(上). 中国海洋工程学会: 中国海洋学会海洋工程分会, 2019: 178−183.
|
| [9] |
STEPHEN J J, SANNASIRAJ S A, SUNDAR V. Numerical modeling of nonlinear sloshing of liquid in a container coupled with barge subjected to regular excitation[J]. Journal of Hydrodynamics, 2019, 31(5): 999-1010. DOI:10.1007/s42241-019-0073-6 |
 2023, Vol. 45
2023, Vol. 45
