0 引　言

目前，陆地发射仍是各国主要的火箭发射方式，火箭在太空中依次进行舱段分离，在规划火箭运行线路时，避开居民区会牺牲火箭运载能力和增加成本^[1-2]。另外，从赤道上发射可以最大限度地利用地球自转，同时也能够减少卫星进入地球同步轨道的路程，但是赤道上的陆地较少，因此海上火箭发射的概念受到船舶工程和航天工程等领域的专家学者广泛关注^[3-4]。海上火箭发射不需要支付高昂的发射场地建设费用，而且海上火箭发射平台能规避可知的风险，总体上能够有效降低火箭发射的服务和运营成本。海上火箭发射已经走过了五十多年的历程，已有很多成功发射的经验，但从起步到成熟是个漫长的过程，目前海上发射仍存在着许多工程和技术上的问题^[5-6]。例如，海上发射面临许多复杂的海洋环境问题，发射平台受到风浪流的作用会产生六自由度运动，因此发射之前须根据海域情况分析发射平台的耐波性能，以保障火箭的安全发射^[7]。此外，海上火箭在发射时对平台产生巨大的瞬时冲击力，会放大发射平台的六自由度运动幅值和运动变化模态，还会对平台附近波浪的波高产生很大的瞬态影响，甚至会出现甲板上浪的现象，增大波浪砰击载荷，影响发射平台和火箭的安全^[8]。因此，在进行海上火箭发射之前，需要准确预报发射时平台的运动响应、开展针对海上火箭发射平台运动响应的相关研究^[9]。

综上，对于海上发射来说，要保证火箭安全高效发射，发射平台的性能极为重要。为此，国内外学者对船舶的性能进行了多学科和单学科优化，主要包括耐波性、操纵性和阻力。Lawrenced^[10]研究了不同船型参数对船舶阻力的影响，研究表明最重要的参数是长细比，并且其越大阻力越小。Scamardella^[11]以棱形系数、方形系数和浮心纵向位置为参数，应用参数化建模，将乘客晕船率作为优化目标，优化后的晕船率大大降低。冯佰威^[12]以船型参数为变量，以阻力、稳性和耐波性为优化目标，建立了一个多学科优化平台。刘畅等^[13]开发了一个海上发射平台耐波性优化系统，该系统由发射平台、船体型线和耐波性优化构成，通过该系统可以实现发射平台的耐波性优化。吴贝尼等^[14]提出了一种基于遗传算法的双向渐进算法，该算法能解决之前因参数设置不当而无法求得全局最优解的问题，仿真结果表明该算法能得到全局最优解且计算效率较高。Vernengo等^[15]基于全局收敛遗传算法对双体船在不同航速下的耐波性和阻力进行优化，研究表明双体船的阻力降低15%，垂荡加速度降低30%。Warren^[16]以船长、船宽和水线面面积为变量，以滑行艇的稳性、耐波性和操作性为优化目标，通过saea和idea算法求解，但没有给出三者综合优化的结果。Miao^[17]将NM理论与CFD技术相结合，创建了一个水动力优化系统，大大降低了计算成本。Jeroen等^[18]通过自适应网格加密对船舶在静水中的阻力进行模拟，与实验结果对比效果良好，且与传统方案相比降低了成本。Dunarea^[19]用商业软件FineMarine评估船体附近的流场，并评估船舶附体对船舶水动力性能的影响，与水池实验结果相比仅差2 %。Yang等^[20]通过非光滑离散元方法建立了数学模型，研究浮冰形状与船舶阻力的关系，并通过聚丙烯制成的人工冰进行实验对比，研究结果表明数值模型计算的阻力与试验结果和半经验公式计算的结果吻合度都很好。Cheng等^[21]提出一种新的船舶表面修改方法，把遗传算法和CFD方法相结合用于船舶的多目标性能优化，并通过该方法对1300TEU集装箱船的首部进行了优化，结果表明该参数化修改方法对于工程应用是实用的。Nam-Kyun^[22]提出一种船舶完整稳性评估模型，该模型由稳定性指标计算和稳定性评估模块组成。对2艘船舶模型在多种工况下进行了稳性计算，表明所提出的模型在稳性评估方面比以往研究更精准。以上研究在提高船舶性能方面取得了明显成果，但缺少针对海上发射船性能优化的案例。本文建立基于模糊层次分析的海上发射船性能优化模型，填补这一空缺。

1 性能优化基本原理 1.1 模糊数学基础理论

对于常规的集合理论而言，元素和集合之间的关系是一一对应的，只存在属于和不属于2种情况，用数学的语言描述就是元素和集合的关系只有0和1两个值。然而实际中，往往存在一些模糊不清的概念。例如，高矮这一概念是有模糊性的，没有明确的界线来划分，高和矮存在中间过渡的模糊区域。模糊数学便是用数学方法解决存在模糊现象的数学，模糊数学中，把元素和集合从只有0和1的隶属关系扩展成为了[0，1]的连续区间。

1.1.1 隶属函数的定义

若对于定义域上的任意一个u 都有唯一一个结果与之对应，即存在映射关系：

$ {{{V}}}\left({{{u}}}\right)\to {{U}} \to \left[\mathrm{0,1}\right]，$

(1)

式中：V为U上的模糊集， ${{{V}}}\left({{{u}}}\right)$ 为u对模糊集V的隶属度函数。当u变化时， ${{{V}}}\left({{{u}}}\right)$ 对应唯一变化，隶属度函数的值越接近于1，则表示u属于U的程度越高。隶属函数是普通集合函数的推广，利用隶属函数可以表示出事物之间的模糊性，即把元素对集合的隶属程度表示出来。这就有了一种可行的方法对模糊问题进行描述和评价。

1.1.2 隶属函数的确定

隶属函数实际上是对客观事物的反映，但为研究方便，可以在满足实际情况和利用过去经验的前提下，人为地确定隶属函数，几种确定隶属函数的方法如下：

1）模糊统计法

有一些模糊集合在某一准则中可以由集合的投影来表示，这种模糊集合的隶属函数可以用模糊统计法来确定。

2）德尔菲法

对于一些难以进行模糊统计的集合，可以用德尔菲法，利用专家的意见和经验确立隶属函数。

3）对比排序法

有些模糊集合的隶属关系难以用具体的数字表示，但可以确定模糊集合中各个元素的相对隶属度。这种情况下，可以通过隶属度的相对大小来排序，再通过特定的数学方法推导隶属函数。

实际应用时，应结合具体情况选择合适的分布函数，并且函数中的参数也要根据要表达的模糊集合确定，本文所使用的模糊层次分析模型用到了德尔菲法和对比排序法。

1.2 模糊层次分析法 1.2.1 层次分析法概述

其基本原理是把一个复杂的问题划分为组成它的元素，根据不同元素的重要程度构造标度为1~9的两两比较模糊判断矩阵，通过矩阵求解各元素对目标的权重。虽然层次分析法是一种十分有效有优势的决策工具，表现为系统性、适用性等，但还是存在一些问题：

1）衡量两两重要程度的判断矩阵以1~9为衡量标度可能过于精准，不符合人为判断的模糊性，因此计算结果可能不够精准。

2）对于非一致判断矩阵的修正较为复杂，并且有可能违背了实际情况。

1.2.2 模糊层次分析法

针对上述层次分析法存在的问题，基于模糊理论提出了模糊层次分析法。模糊层次分析法从模糊集出发，构造元素两两比较的模糊判断矩阵，充分考虑人为因素，通过大量专家样本数据得到较为可靠的结果，模糊层次分析步骤如下：

1）构建层次结构

将待分析的问题根据组成元素的层次结构依次形成递阶结构，为了方便计算每个层次的元素数量一般不超过9个，图1为一个典型的递阶结构示意图。

2）构建两两模糊判断矩阵

判断矩阵是模糊层次分析法最基本的元素，判断矩阵的建立就是将一种元素下面所支配的所有因素进行两两比较，通过专家经验法以矩阵的形式给出。

3）判断矩阵的一致性检验

因为人为的判断存在主观性，会出现A比B重要，B比C重要，C比A重要的现象，因此需要对判断矩阵进行一致性检验。若判断矩阵满足如下条件，则称该判断矩阵满足一致性检验。

$ a_{ij}=\frac{a_{ik}}{a_{jk}}\quad i,j={1,2},{3,4}\cdots {{{n}}}。$

(2)

矩阵有且仅有一个不为0的最大特征值根 $ {\mathrm{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ ，并且其越接近n矩阵的一致性越好。由此，引用一致性标准CI判断矩阵的一致性程度，其越接近0矩阵的一致性越好。

$ CI=\frac{{{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}-n}{n-1} 。$

(3)

平均随机一致性指标 $RI$ 是重复很多次计算矩阵特征值取平均值得到的，实验数据见表3。

将 $RI$ 与 $RI$ 比较得到一致性比率 $CR$ ，当 $CR＜$ 0.1时，则判断矩阵的一致性标准可以接受，如不满足，需要对判断矩阵进行调整，直到满足一致性标准。

4）依据判断矩阵计算各因素的权重

$ {\boldsymbol{A}}=\left(\begin{array}{cccc}{\mathit{a}}_{11}& {\mathit{a}}_{12}& \cdots & {\mathit{a}}_{1\mathit{n}}\\ {\mathit{a}}_{21}& {\mathit{a}}_{22}& \cdots & {\mathit{a}}_{2\mathit{n}}\\ \cdots & \cdots & \ddots & \cdots \\ {\mathit{a}}_{\mathit{n}1}& {\mathit{a}}_{\mathit{n}2}& \cdots & {\mathit{a}}_{\mathit{n}\mathit{n}}\end{array}\right)，$

(4)

其中， $ {a}_{ij}=\dfrac{1}{{a}_{ji}} $ ， $ {a}_{ij}＞0 $ ， $ {a}_{ii}=1 $ ，计算该层因素相对于上一层因素的权重就是求解该矩阵最大特征值根 $ {\lambda }_{max} $ 对应的特征向量 $ M $ 。

$ {\boldsymbol{A}}M={\lambda }_{{\rm{max}}}{\boldsymbol{A}} 。$

(5)

2 基于模糊层次分析的海上发射船性能优化 2.1 评价体系建立

影响海上发射船性能的指标很多，有些指标影响较小，评价指标的选取直接影响到优化结果，在选择评价指标时要保证全面且不相容。借鉴国内外研究，选取4个对海上发射性能影响较大的指标。

1）火箭的弯矩

发射船受到风浪的作用会产生六自由度运动，火箭竖起后，将随发射船的运动而运动，火箭重心很高、转动惯量大。因此，火箭会产生巨大的弯矩，如果超过允许值，会影响火箭的安全发射。

2）发射船稳性

发射船在航行的过程中，当其遇到恶劣天气的干扰时船舶的平衡状态会受到破坏。因此，平台应具备足够的稳性，以通过船舶重力和浮力产生的力矩抵抗风浪产生的力矩而不至倾覆。

3）发射船阻力

船舶节能减排已成为船舶行业研究和关注的重要问题，其不仅仅影响着船舶的经济效益，也是保护生态环境和减少环境污染的重要举措。减小航行阻力是节能减排最有效的方式。

4）发射船造价

从船舶经营效益的角度看，降低成本是一个重要指标。

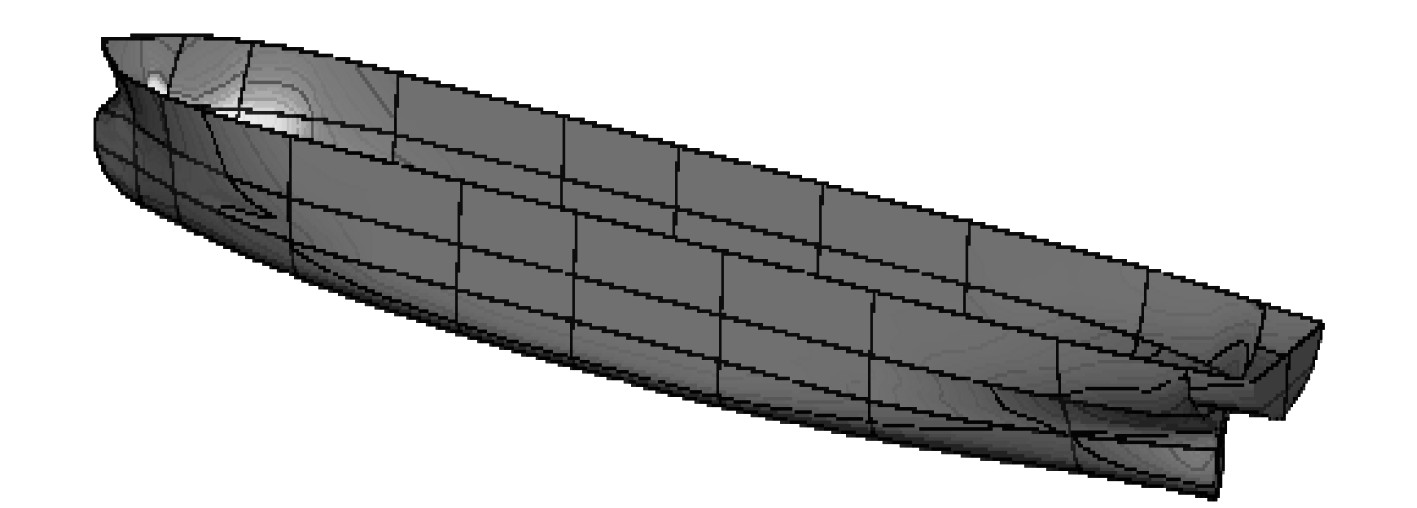
2.2 评价指标计算

根据火箭发射的要求，船长范围为105≤L≤110，船宽为30≤B≤35,并且发射船应能够承受火箭发射对其造成的冲击力，发射船的吨位应在8000 t 以上。油船吨位大、纵向强度高、稳定性好，并且甲板足够大，有利于火箭发射的安全和配套设施的布置。因此，以油船作为母型船，母型船模型如图2所示，母型船主要参数如表4所示。船长选取104，106，108，110，船宽30，31，32，33，方形系数0.6，0.64，0.68，0.72，0.76，0.8进行全因子试验，96个样本点参数如表5所示。

1）火箭弯矩的计算

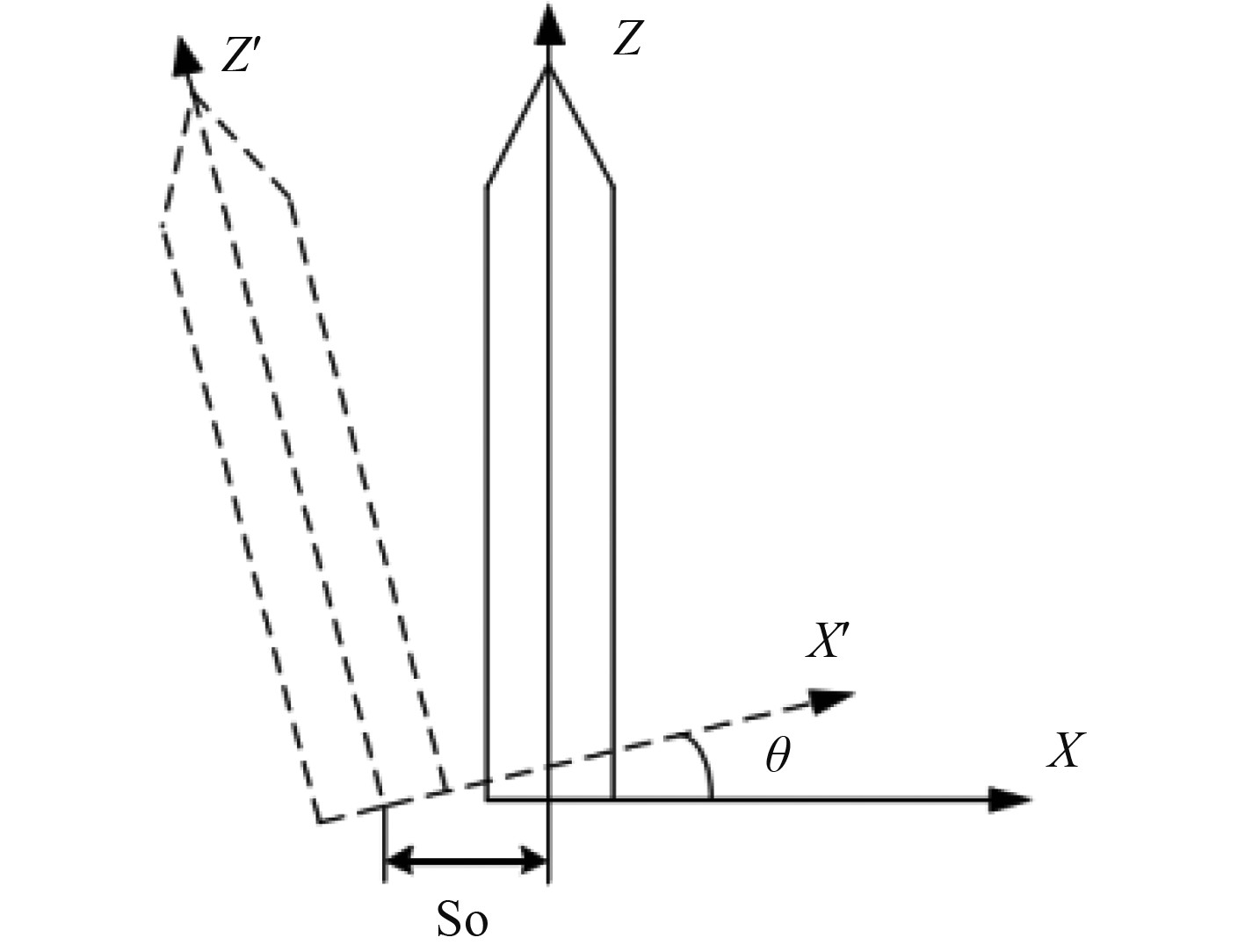
建立火箭力学模型如图3所示，火箭参数如表6所示。推导火箭的弯矩函数。建立三维空间坐标系，Y轴沿船长方向，X轴向右，Z轴指向火箭方向^[23]。

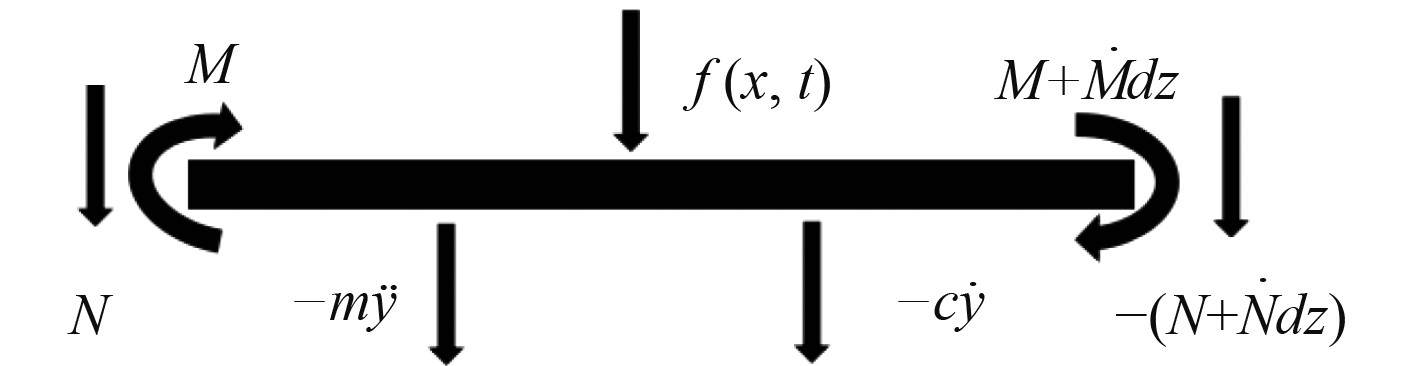
火箭微元受力分析如图4所示。只考虑纵摇、横摇和垂荡运动对火箭弯矩的影响，考虑到火箭的安全，竖起时应使发射船处于迎浪或背浪状态。可以将火箭视为一端固定于刚性端、一端自由的非均匀弹性悬臂结构，以此计算火箭的运动和受力情况。

$ S = {\theta z\sin\lambda t} ，$

(6)

$ a = \ddot S = {{\theta z}}{{\text{λ }}^{\text{2}}}\sin {\text{λ t}} ,$

(7)

$ f(x,t) = m(z)a = m(z)\ddot S = m(z){\theta z}{{\text{λ }}^{\text{2}}}\sin {\lambda t} 。$

(8)

式中： $s$ 为火箭的位移， $a$ 为火箭加速度； $ f\left(x,t\right) $ 为火箭的惯性力。取火箭微元段 $ d\mathrm{z} $ 进行受力分析。

由力的平衡方程 $ \sum {F = 0} $ 得：

$ N + \dot Ndz - N + m\ddot ydz - Fdz + c\dot y = 0 ，$

(9)

即

$ \dot N{\rm{d}}z + m\ddot ydz - F{\rm{d}}z + c\dot y = 0 ,$

(10)

考虑火箭材料的非弹性阻尼，应力应变关系可以表示为：

$ {\varepsilon } = {{y}} \cdot {\ddot y}, $

(11)

$ {\text{σ }} = {{E\varepsilon }} + {{\text{c}}_{\text{s}}}{{\dot \varepsilon }}, $

(12)

通过截面应力积分得到弯矩：

$ M = \int\limits_A {\sigma y{\rm{d}}A}, $

(13)

对火箭全长进行积分得到总弯矩：

$\begin{split} {My_\theta } =& {\lambda ^2}\theta \sin \lambda t\int_0^{L} m (z) \cdot {z^2}{\rm{d}}z + \\ & \dfrac{\eta }{{{{m}_\eta }}}\int_0^L f (z) \cdot m(z){\rm{d}}z\int_0^L f (z) \cdot {z^2} \cdot m(z){\rm{d}}z ，\end{split}$

(14)

$M{y_L} = (g + \ddot z)\sin \alpha \int_0^{{L}} {\rm{m}} ({\rm{z}}) \cdot {{\rm{z}}^2}{\rm{d}}z,$

(15)

$M = M{y_\theta } + M{y_L},$

(16)

$\sin \alpha = \frac{{\theta \int_0^L f (z) \cdot z \cdot m(z){\rm{d}}z}}{{{L}}} \cdot \frac{\eta }{{{{\rm{m}}_\eta }}},$

(17)

$\eta = \dfrac{{{{\left( {\dfrac{\lambda }{{\rm{p}}}} \right)}^2}}}{{\sqrt {{{\left( {1 - \dfrac{{{\lambda ^2}}}{{{{\rm{p}}^2}}}} \right)}^2} + 4\varphi {{\left( {\dfrac{\lambda }{{\rm{p}}}} \right)}^2 }} }} ，$

(18)

$ {m_{\text{η }}} = \int_0^L {{f^2}(z)} \cdot m(z){{{\rm{d}}}}z 。$

(19)

根据火箭参数，积分得到总弯矩函数表达式：

$ M = 2278322.838 \cdot {\theta_{}} + 103495.6558 \cdot {\theta_{}} \cdot \ddot {{z}}。$

(20)

式中： $ {\text{λ }} $ 为波浪圆频率； $ \theta $ 为纵摇幅值； $ z $ 为沿火箭方向的垂向高度； $ m(z) $ 为火箭的质量分布函数； $ f(z) $ 为火箭的一阶阵型； $ \ddot z $ 为垂向加速度； $ {\text{α }} $ 为弹性变形角； $ p $ 为火箭的一阶固有频率； $ g $ 为重力加速度， $ {My}_{\theta } $ 和 $ {My}_{L} $ 分别为由纵摇和垂荡运动所引起的弯矩；L为火箭长度； $ \phi $ 为火箭无因次阻尼比。

使用Maxsurf计算母型船及样本点的纵摇幅值和垂荡加速度，计算时选取JONSWAP谱。有义波高取为4 m，跨零周期为8 s，浪向角为0°，将纵摇幅值和垂荡加速度代入火箭弯矩公式结果如表7所示。

2）稳性的计算

发射船在风浪的作用下会产生倾斜，水线面也会发生变化，重力和浮力会产生一个恢复力矩。评价船舶稳性最合理的指标是稳性消失角，各样本计算结果如表8所示。

3）阻力的计算

Maxsurf的Hullspeed模块计算粘性阻力时采用ITTC-57计算，航速取为12 kn，粘性阻力计算公式如下：

$ {R}_{v}={C}_{F}\left(1+k\right)\frac{1}{2}\rho {v}^{2}S。$

(21)

式中： $ v $ 为航速； $ S $ 为湿面积； $ {C}_{F} $ 为摩擦系数。各样本阻力计算结果如表9所示。

4）造价的估算

船舶造价对船舶营运费用影响甚大，船舶造价受世界经济变化、市场供需等很多因素的影响，是不断变化的，没有什么固定的函数曲线能准确表达船舶的造价。本文对发射船进行总体优化，无须计算出每个样本点的具体造价，用体积这一参数表示船舶的相对造价，各样本造价计算结果如表10所示。

2.3 计算结果归一化

计算结果归一化的方法通常有2种，一种是令单个因素的最优值为1，最差的为0，中间的因素通过差分得到。

$ x_{ij}^{*}=\left|\frac{{x}_{ij}-\mathrm{min}x}{\mathrm{max}x-\mathrm{min}x}\right|，$

(22)

另一种是以单个因素的最优值为1，其他因素按比例进行调整。

${x}_{ij}^* = \frac{{x}_{ij}}{{\mathop{{\rm {max}}x}\nolimits }}{或}x_{ij}^* = \frac{{{\mathop{{\rm {min}}x}\nolimits} }}{{\rm{{\rm{x}}}}_{ij}}。$

(23)

本文采用第2种计算方式。

2.4 建立判断矩阵

共统计问卷17份，问卷专家均为硕博学历。其中男性14份，女性3份，工作年限均10年以上。中级职称6位，副高级职称4位，高级职称7位。根据专家问卷的实际情况，取均数并四舍五入调整，判断矩阵如下：

$ {\boldsymbol{A}}=\left[\begin{array}{cccc}1& 3/2& 2& 3\\ 2/3& 1& 6/5& 4/3\\ 1/ 2& 5/6& 1& 11/10\\ 1/3& 3/4& 10/11& 1\end{array}\right]。$

2.5 计算各样本点综合评分

各因素的权重即矩阵A最大特征值 ${\lambda }_{{\rm{max}}}$ 所对应的特征向量，计算得权重向量W=[ 0.4072，0.23822，0.1924，0.1622]，且CI=0.0057，CR=0.0064<0.1，进一步得到各样本点评分，结果如表11所示。

计算结果表明：78号样本点综合评分最高，船长为110 m，船宽30 m，方形系数0.8。弯矩、稳性、造价和阻力的评分分别为0.983，0.962，0.746和0.786。相比于母型船，火箭承受弯矩的评分提高了19.87%，稳性评分提高了2.99%，阻力评分提高了23.19%，造价评分降低了8.35%。

3 结　语

本文针对海上发射船性能优化中影响因素较多且指标参数难以定量评估现状，建立火箭竖起时的弯矩模型，以方形系数、船长和船宽为优化变量，设计了基于模糊层次分析法的海上火箭发射船性能优化方案。通过专家问卷调查确定判断矩阵的方法给出了各性能指标的权重，并对各个指标单独进行分析计算，最后计算了母型船和96个样本点的综合评分，得到如下结论：

1）相比于母型船，火箭承受弯矩的评分提高了19.87%，稳性评分提高了2.99%，阻力评分提高了23.19%，造价评分降低了8.35%。造价提高9.13%，验证了该模型在火箭发射船性能优化方面的适用性，为海上发射船性能优化提供了一种研究思路。

2）计算结果表明，为了保证火箭发射的安全，应采用较大的方形系数以减少火箭承受的弯矩。长细比对阻力影响很大，应采用较大的长细比以减少航行阻力。