2. 中国船舶信息中心,北京 100101;
3. 江南造船(集团)有限责任公司,上海 201913
2. China Ship Information Center, Beijing 100101, China;
3. Jiangnan Shipbuilding (Group) Co., Ltd., Shanghai 201913, China
摆线推进器(cycloidal propeller)也称直翼推进器,它是由一组数量不等的叶片等间距分布组成,叶片从船体表面伸向水中并与船体表面垂直,同时绕某特定点做圆周运动,由于叶片在空间上的运动轨迹是一条摆线,因此被称之为摆线推进器。摆线推进器在保持回转箱转速恒定的情况下也能快速改变推力的大小和方向,其高效的操纵性使得船舶能实现侧向移动、原地回转等一系列高难度的动作,安装了摆线推进器的船舶在低速航行状态下的控制力也大大提高。
摆线推进器近些年来的研究主要分为理论研究和实验研究2个阶段。在实验研究阶段,张洪雨[1]利用设计的偏心盘-偏心率-连杆机构实验装置研究了不同方向角、偏心率等工况下摆线推进器的水动力性能变化。段瑞[2]设计了一种偏角可控直叶片摆线推进器的试验装置,计算了叶片在不同状态下的推力系数,扭矩系数,并依据叶片的非定常效应以及叶片之间的相互干扰,对计算结果进行修正。陈先进[3]提出了一种曲柄滑块机构,并将其应用在摆线推进器上,相比于传统的摆线推进器,其具有高效、结构简单、螺距连续可调的优点。在理论研究阶段,谷口中[4]提出一套适用于实际应用中的理论模型,并利用动量定理,对诱导速度的计算公式进行了经验补充。Nakonechny等[5]通过对大量实验值的分析,得出谷口中法的适用范围为中小进速系数,当进速系数较大时,得到的计算值与实验值误差偏大。朱典明[6]以此为基础,对谷口中的计算方法进行了优化,从而提高了计算结果的准确度。顾欣星[7]利用滑移网格建立摆线推进器的水动力性能模拟方案,依靠研究的结果对摆线推进器的叶片翼型等结构参数进行优化,总结叶片翼型变化对推进器推进效率的影响。
本文选取和NSRDC实验中翼型相近的NACA 3412翼型,对仿真方法的可靠性进行验证,基于验证的CFD的数值模拟方法,分析进速系数以及偏心率变化对摆线推进器的性能影响,并总结不同初相位下叶片之间的受力变化趋势。
1 摆线推进器的工作原理摆线推进器工作过程中,叶片随着推进器叶轮做圆周运动,叶片本身还在做升沉摆动,摆动运动的中心点是叶片的自转中心点,2种运动的合运动为摆线运动。
叶片随着摆线推进器转轮旋转时,所有叶片弦线的垂线始终汇交于一个点,即满足“法线相交定律”,如图1所示。相交的这个点称为偏心点N。摆线推进器叶片的受力是升力与阻力的叠加,2个力的合方向垂直于偏心ON,所以通过移动偏心点N的位置,可以改变叶片和来流方向之间的角度,这就是调节摆线推进器推力方向的原理。
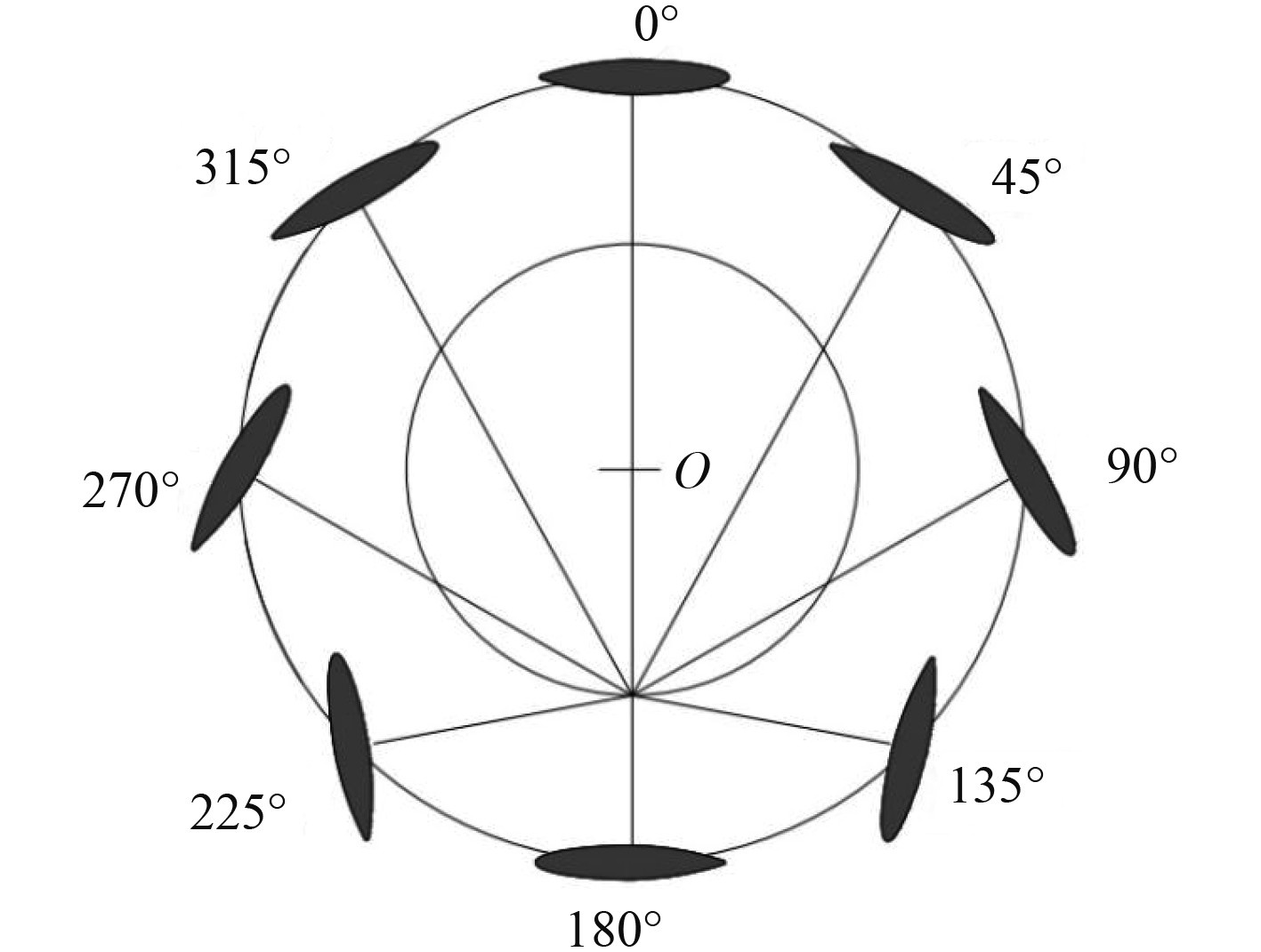
|
图 1 摆线推进器叶片运动原理 Fig. 1 Motion principle of cycloid propeller blades |
若当叶片的弦线始终与摆线圆周轨迹的切线方向保持同向,摆线推进器将不会产生推力,此时推进器转动1周前进的距离称为摆线推进器的螺距。当改变偏心点N的方向时,相当于在叶片与轨迹线的夹角上增加或减小了1个角度,从而可以改变推力的大小和方向,叶片在1个周期内的运动轨迹如图2所示。
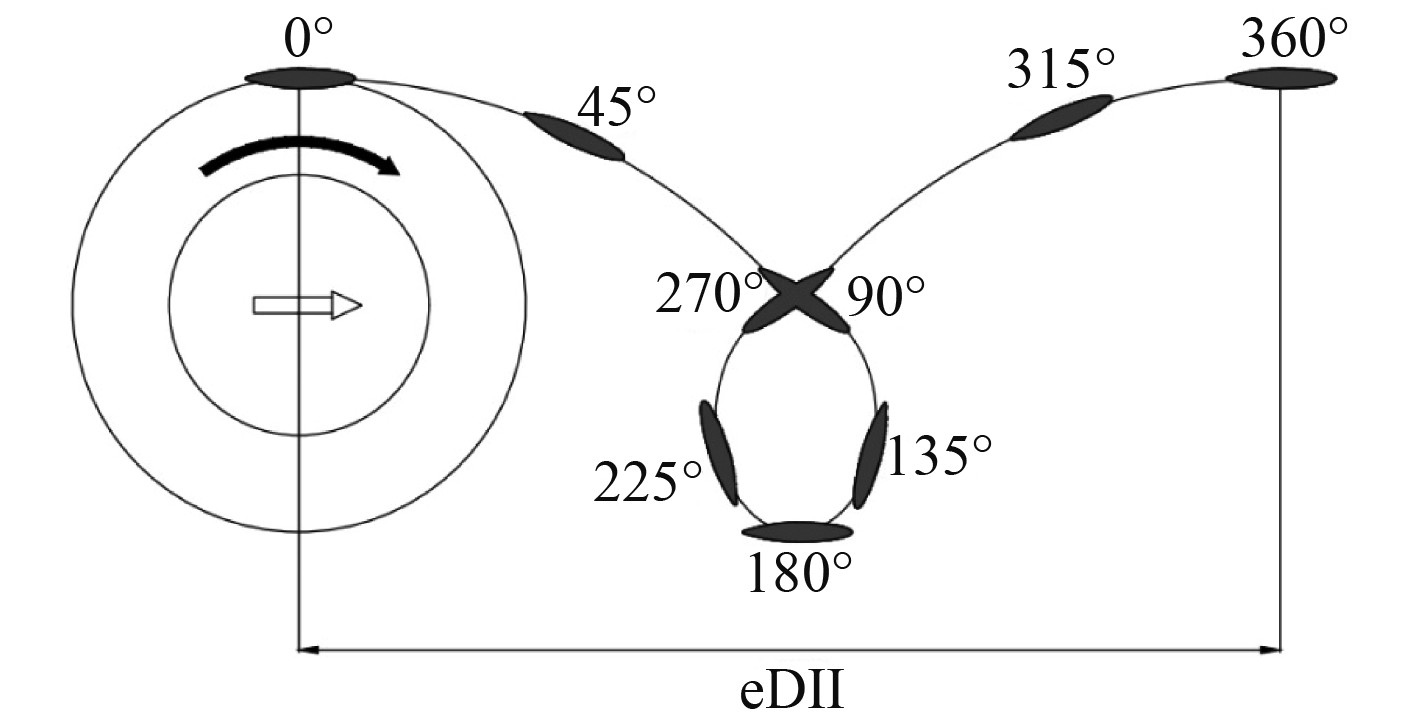
|
图 2 摆线推进器叶片轨迹示意图 Fig. 2 Geoid propeller blade track schematics |
摆线推进器旋转中心点为O点,点O和点N之间ON的距离称为偏心距。叶片弦线与叶片自转中心点处圆周切线之间的夹角为
| $ \theta = \alpha + \beta,$ | (1) |
通过数学关系求解可得:
| $ \beta = \arccos \left\{ {\frac{{e + \cos \theta }}{{\sqrt {1 + {e^2} + 2e\cos \theta } }}} \right\}。$ | (2) |
根据定义,角
| $ \alpha ' = - \omega \frac{{{e^2} + e\cos \theta }}{{1 + {e^2} + 2e\cos \theta }}。$ | (3) |
其中:偏心率

|
图 3 摆线推进器的运动模型 Fig. 3 Motion model of cycloid propeller |
选取NACA 0012翼型作为摆线推进器叶片模型,叶片最大厚度位于29.6%的翼弦处,最大弯度位于0.0%翼弦处,叶片翼型如图4(a)所示。选取CATIA软件对推进器进行建模,摆线推进器模型如图4(b)所示,推进器模型的主要参数如表1所示。
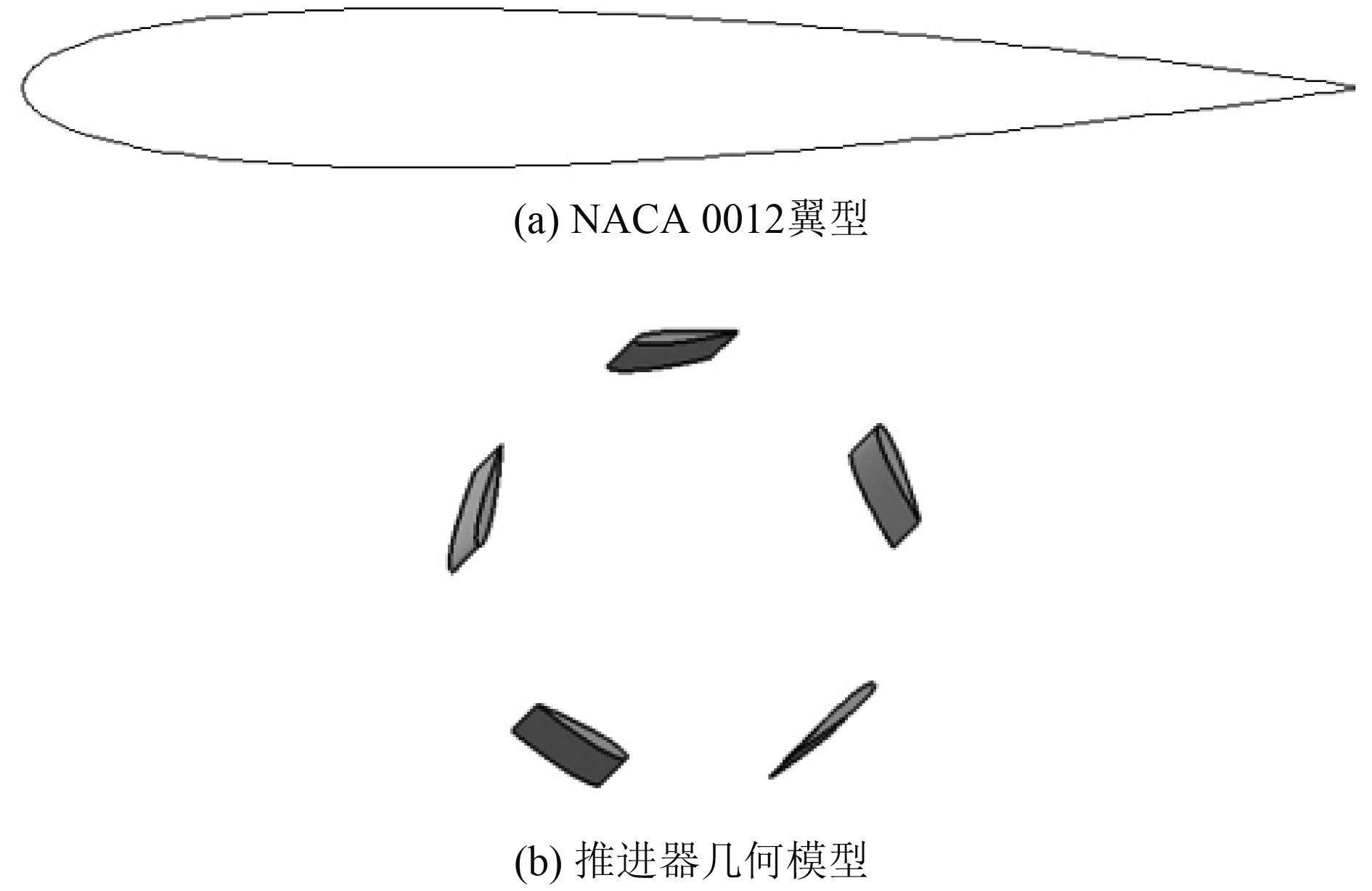
|
图 4 叶片翼型及推进器几何模型 Fig. 4 Geometric model of blade airfoil and propeller |
|
|
表 1 推进器模型参数 Tab.1 Propeller model parameters |
摆线推进器前进时的运动速度较小,其周围的流体可看作不可压缩流体,其满足质量守恒定律的同时,也满足N-S方程。
| $ \frac{{\partial }u}{{\partial}x} + \frac{{\partial} v}{{\partial} y} + \frac{{\partial}w}{{\partial} z} = 0, $ | (4) |
| $ \left. \begin{aligned} & \frac{{\partial u}}{{\partial t}} + \frac{{\partial \left( {{u^2}} \right)}}{{\partial x}} + \frac{{\partial \left( {uv} \right)}}{{\partial y}} + \frac{{\partial \left( {uw} \right)}}{{\partial z}} = X - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + v{\nabla ^2}u\\ & \frac{{\partial v}}{{\partial t}} + \frac{{\partial \left( {vu} \right)}}{{\partial x}} + \frac{{\partial \left( {{v^2}} \right)}}{{\partial y}} + \frac{{\partial \left( {vw} \right)}}{{\partial z}} = Y - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + v{\nabla ^2}v\\ & \frac{{\partial w}}{{\partial t}} + \frac{{\partial \left( {wu} \right)}}{{\partial x}} + \frac{{\partial \left( {wv} \right)}}{{\partial y}} + \frac{{\partial \left( {{w^2}} \right)}}{{\partial z}} = Z - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + v{\nabla ^2}w \end{aligned} \right\} 。$ |
其中:
摆线推进器叶片的运动是自转和公转的叠加运动,较为复杂,因此需要优化CFD计算方案研究摆线推进器的敞水性能。利用STAR-CCM+中重叠网格模拟叶片自转和绕叶轮公转的运动。选取的计算域为一圆柱体,计算域的范围是以推进器的公转轴为中心,靠前端5 m,靠后端12 m,计算域半径为5 m,计算域的边界选取的足够大,以减小边界效应对计算精度的影响。摆线推进器的计算域由静止域和旋转域组成,静止域用于模拟流体的平面流动,旋转域用于模拟摆线推进器叶片复杂的运动。
有关边界条件的设定如图5所示,边界类型分为速度进口、压力出口、对称平面。流场的入口设定为速度进口,流场出口设定为压力出口,流场侧边界设定为对称平面,叶片的表面类型设定为壁面,5个圆柱面区域边界类型设定为重叠网格,并创建静止域和各圆柱表面的界面,类型设定为重叠网格。

|
图 5 计算域示意图 Fig. 5 Calculation domain schematics |
考虑到叶片翼型以及叶片壁面剪切力的影响,选取
计算域的网格尺寸为0.5 m,叶片自转中心设置在叶片弦线的中点,叶片的网格尺寸设置为0.03 m,并对各叶片的导边和随边进行加密。以5个叶片各自的自转轴为中心,半径为0.5 m创建6个小圆柱体。以各个小圆柱体为目标零部件,与对应的叶片进行减运算得到单个叶片旋转域。以整个推进器叶轮的旋转轴为中心轴,对称建立一个边长为3.5 m,高度为2.2 m的方形网格加密区,以保证数据交换的稳定和计算结果的精确。网格加密区域包括了摆线推进器的5个叶片及其旋转域,加密区的布局如图6所示。通常在进行CFD仿真分析时,网格越密计算得出的结果就更精确,与此同时工况计算量会加大,相应的仿真时间也会更长。综合计算结果的精度以及运行时间等因素考虑,加密区的网格尺寸设置为0.03 m,和5个叶片旋转域的网格尺寸相同,以保证数据传输过程中不会出现太大的波动落差。

|
图 6 叶片加密区网格划分 Fig. 6 Grid division in blade-encrypted area |
沿着各个叶片前进方向分解各叶片所受外力,即可得到某瞬态时刻下的摆线推进器主推力,对一个周期内的平均主推力进行叠加[9],得
| $ T = \sum\limits_{i = 1}^z {\frac{1}{{2{{\text{π}}} }}} \int_0^{2{\text{π}} } {{t_i}} \left( \theta \right){\rm{d}}\theta 。$ | (6) |
同理,把各桨叶旋转1周的平均转矩进行叠加,得
| $ Q = \sum\limits_{i = 1}^z {\frac{1}{{2{\text{π}} }}} \int_0^{2{\text{π}} } {{q_i}\left( \theta \right)} {\rm{d}}\theta 。$ | (7) |
其中:
对以上公式进行无因次化,即可得到推力系数,扭矩系数,推进器效率。
| $ {K_T} = \frac{T}{{\rho {n^2}{D^3}L}},$ | (8) |
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^4}L}},$ | (9) |
| $ \eta = \frac{J}{{2{\text{π}} }}{\text{ }}\frac{{{K_T}}}{{{K_Q}}}。$ | (10) |
式中:
| $ J = \frac{{{V_A}}}{{nD}} 。$ | (11) |
为了对仿真方法可行性进行验证,采取和NSRDC实验中翼型相近的NACA 3412,其他参数与其相同。经过对摆线推进器的建模、网格划分、边界条件划分等一系列操作,将所得的仿真值与实验值进行比较,结果如图7所示。

|
图 7 计算结果与实验结果对比下的主推力系数 Fig. 7 Main thrust coefficient compared with experimental results |
分析可知,当偏心率不变时,主推力系数KT随着进速系数J的增大而减小,同一进速系数下主推力系数KT随着偏心率e的增大也逐渐增大,当偏心率变化时,KT也会发生相应的变化,这也是通过改变偏心率进而改变推力的大小和方向的原理。由于偏心率的这个特性,摆线推进器因此具备优越的操控性能。同时由于旋转的叶片翼型和实验中的叶片截面有所区别,导致数值模拟的结果较实验数据偏大,当偏心率e=0.6、进速系数J=1.6时,两者差值最大,出现的一个最大误差为6.32%,这可能是由于流体的扰动导致的。计算整体结果平均误差为3.14%,仿真结果与实验值整体变化趋势相近,且两者误差在允许范围内,表明仿真方法模拟效果较好,可靠性较高。
4.2 数值模拟分析在仿真计算和实验数据对比的基础上,将摆线推进器的叶片翼型NACA 3412更改为本文所选取的NACA 0012翼型,摆线推进器的转速为42 r/min,进速系数的范围为0.5~2.0,同样在保持偏心率e=0.8,0.7,0.6等其他参数不变的情况下,对摆线推进器的敞水性能进行仿真,仿真所得的主推力系数KT随进速系数J变化的曲线如图8所示。
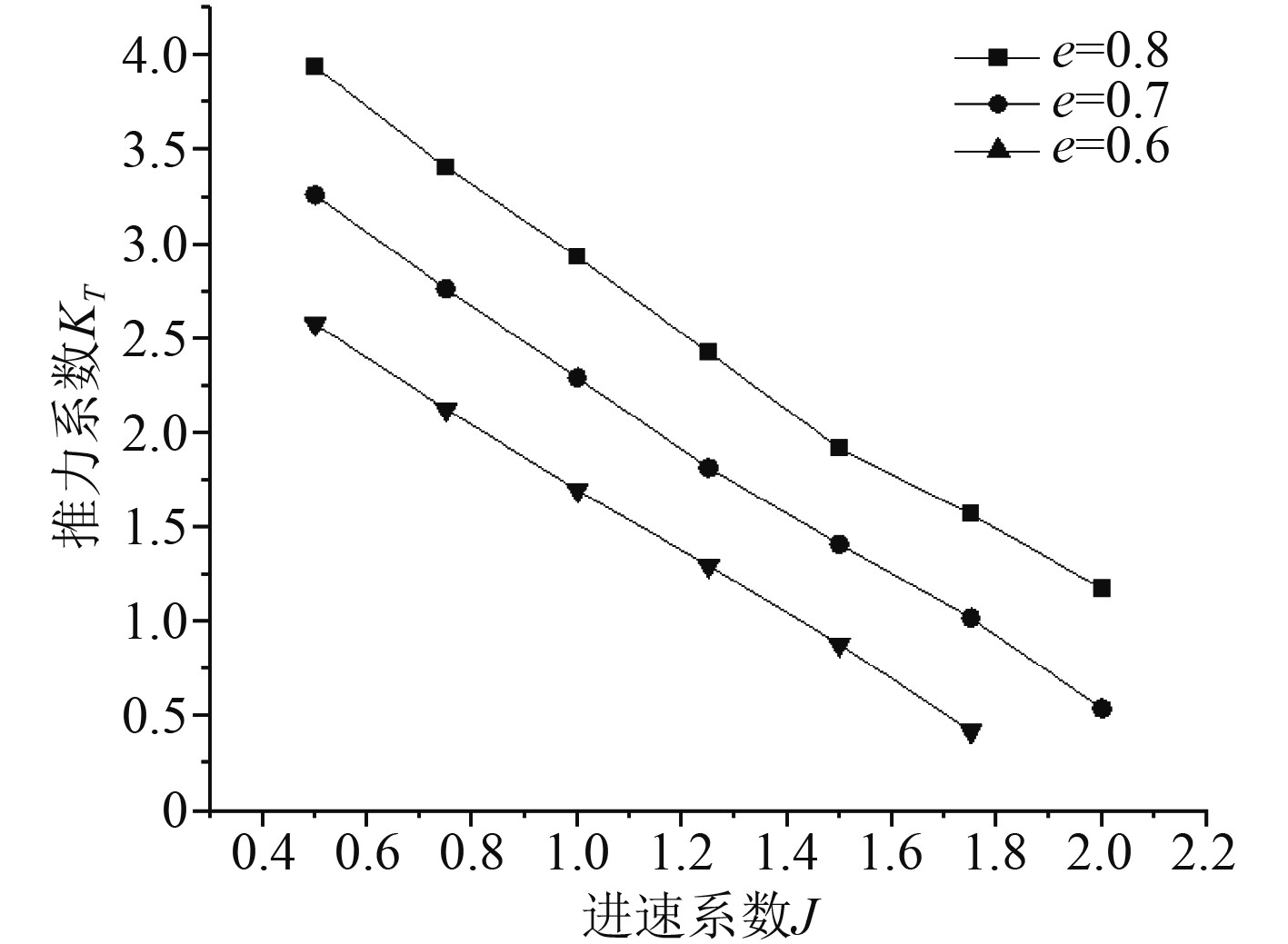
|
图 8 不同偏心率下的推力系数曲线 Fig. 8 Thrust coefficient curves at different eccentricities |
可知,当进速系数J相同时,KT随着偏心率e的增大而增大,当偏心率相同时,KT随着进速系数J增大而减小。
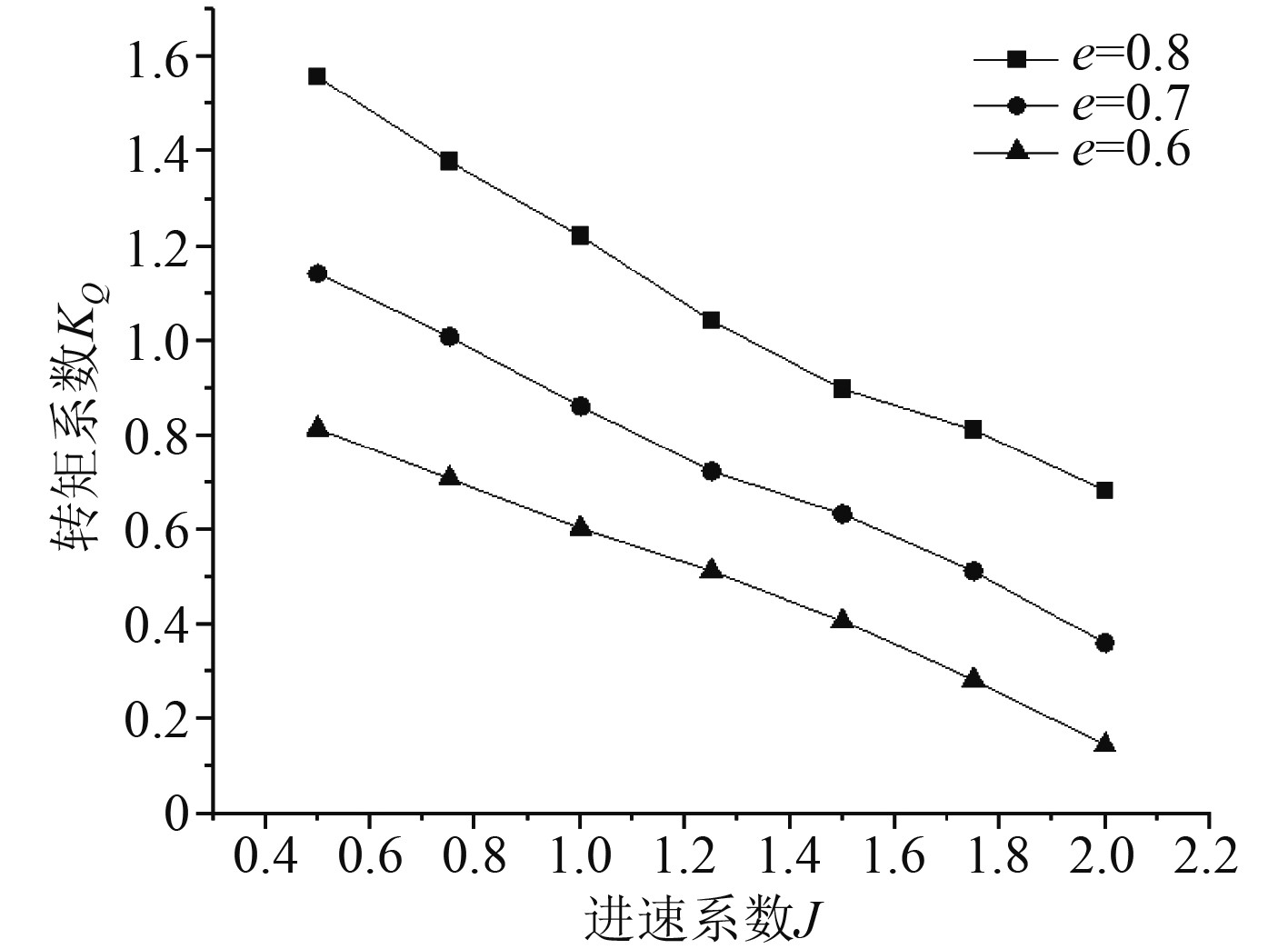
保持偏心率e分别为0.8,0.7,0.6,其他参数不变的情况下,仿真所得转矩系数KQ随进速系数J变化的曲线如图9所示。
|
图 9 不同偏心率下的转矩系数曲线 Fig. 9 Torque coefficient curves at different eccentricities |
可知,KQ的变化趋势和KT类似,当进速系数J相同时,KQ随着偏心率e的增大而增大,当偏心率相同时,KQ随着进速系数J增大而减小。
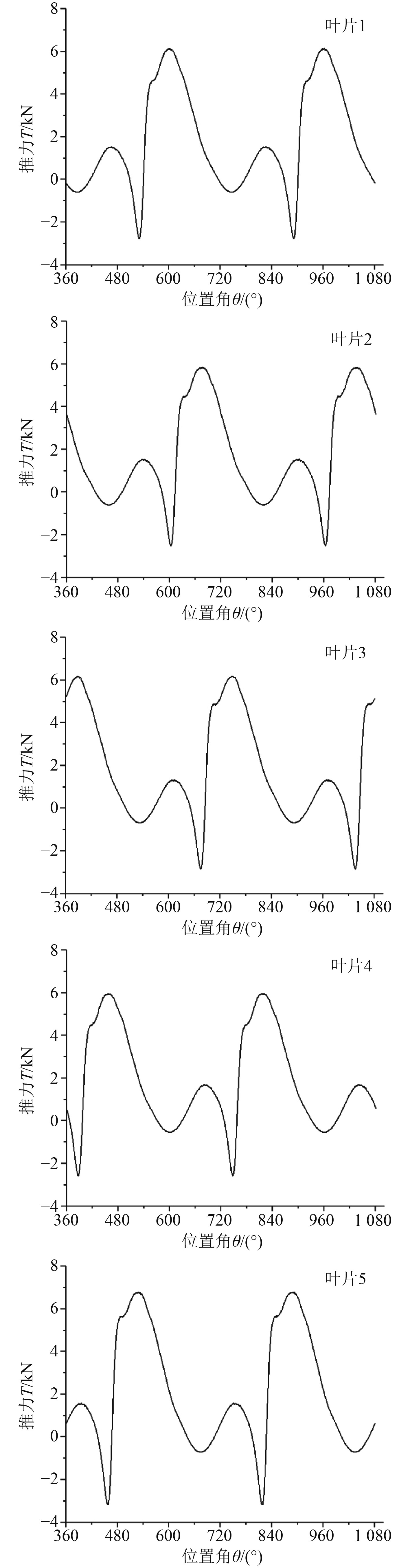
为了研究不同初相位下叶片的受力变化规律,在上述结果里随机选取一个工况进行分析。选取的工况参数为:摆线推进器偏心率e=0.7,进速系数VA=2.1 m/s。此工况下,各叶片瞬时推力变化幅值曲线如图10所示。考虑到计算收敛需要一定的时间,在达到收敛之前推力变化没有达到稳定状态,误差较大,因此选取第2个旋转周期即位置角为360°时开始监测。
|
图 10 e=0.7时各叶片瞬时推力变化曲线 Fig. 10 Transient thrust curve of each blade at e=0.7 |
由图10可知,5个叶片的受力波动趋势大致相同,只是由于5个叶片各自存在一个初始相位角差值,导致变化趋势曲线也间隔一个相位,这个相位正好等于叶片初始相位角差值72°。同时叶片之间的流场存在相互干扰以及叶片自身旋转的差异性,各推力峰值会产生一定的波动,但整体的变化趋势依旧相同。
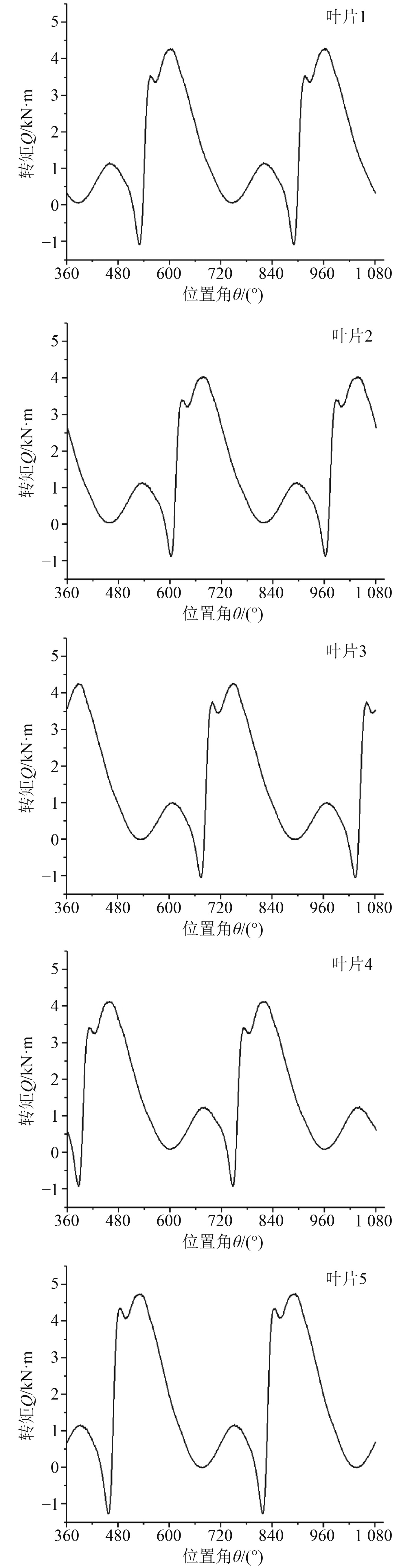
摆线推进器在偏心率e=0.7,进速系数VA=2.1 m/s时,各叶片瞬时转矩变化曲线如图11所示。规律与推力变化趋势曲线相近,5个叶片受到的转矩变化趋势相同,但同样存在72°的相位差。
|
图 11 e=0.7时各叶片瞬时转矩变化曲线 Fig. 11 Transient torque curve of each blade at e=0.7 |
在某些角度范围内,叶片的推力及转矩会存在负值,但在大部分角度下叶片的推力及转矩是正值。在1个旋转周期内叶片的推力和转矩均会存在1个峰值,且正向的峰值较大,此时的瞬时值可以作为叶片强度校核的依据,同时叶片所受的推力及转矩都是随叶轮转角的变化而变化,变化的周期为360°。
5 结 语本文对摆线推进器水动力性能的数值仿真方法进行探讨,并采用NACA 3412翼型为推进器叶片模型对仿真方法验证,得出的结果与NSRDC实验值进行比较,两者之间的误差在允许范围内,表明仿真得到的计算结果精度较高,验证了仿真方法的可行性。在此基础上以自主选用的叶片翼型作为摆线推进器叶片模型,分析偏心率和进速系数对摆线推进器敞水性能的影响,同时研究了不同初始角叶片之间所受的推力及转矩变化规律,得出以下结论:
1) 进速系数一定时,偏心率越大,推进器的KT,KQ值越大;偏心率一定时,进速系数越大,推进器的KT,KQ越小。
2) 不同初相位下叶片所受的推力和转矩变化规律相同,只是相差了一个初始相位角,同时由于叶片之间的流场存在相互干扰以及叶片自身旋转的差异性,各推力峰值会产生一定的波动,但整体的变化趋势依旧相同。
| [1] |
张洪雨. 摆线推进器水动力性能研究[D]. 哈尔滨: 哈尔滨工程大学, 1999.
|
| [2] |
段瑞. 摆线式推进器水动力性能试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
| [3] |
陈先进. 摆线推进器结构及性能优化研究[D]. 杭州: 浙江大学, 2013.
|
| [4] |
谷口中. トロコィダルプロペテ江关する研究[D]. 东京: 东京大学, 1960.
|
| [5] |
NAKONECHNY BV. Experimental performance of a six-bladed vertica axis propeller [J]. 1961.
|
| [6] |
朱典明. 摆线推进器的理论计算方法[J]. 哈尔滨船舶工程学院学报, 1982(1): 1-27. |
| [7] |
顾欣星. 全向直翼推进器水动力性能研究及优化[D]. 杭州: 浙江大学, 2016.
|
| [8] |
施培丽, 邵雪明. 高密实度H型风力机气动性能的数值分析[J]. 机电工程, 2013, 30(3): 277−280+291.
|
| [9] |
章丽丽, 李锋, 孙寒冰, 等. 船舶摆线推进器敞水性能优化仿真研究[J]. 计算机仿真, 2017, 34(3): 19−24.
|
 2023, Vol. 45
2023, Vol. 45
