极地地区自然资源种类丰富,其中包括淡水资源、海洋生物资源、矿产资源和潜在资源,具有重要的科考价值和战略价值[1]。北极航线的开通可以减少我国对常规航线的依赖,降低运输的成本与风险[2]。船舶在极区开展科考活动和航运的过程中,所处寒冷多雾的环境易造成桅杆积冰。桅杆积冰会导致船体重心上移,航行不稳,严重时会导致船体翻覆,船毁人亡。因此,为了减少类似事故的发生,提高船舶在极区航行的稳定性和安全性,需要对船舶桅杆进行积冰预报。
现代舰船上的桅杆已不再是桁架式桅杆,而是更加注重隐身性能和作战性能的集成桅杆[3]。但现今对桅杆积冰的研究较少,大多数关于积冰的研究均集中在航空航天领域,尤其是机翼积冰。Pouryoussefi等[4]研究了展向脊冰、角冰和回流冰对NACA 23012翼型空气动力特性的影响。Janjua等[5]研究了在机翼生长界面上以固体雾凇冰颗粒和水的结合形式沉积的过冷液滴的局部冻结形成混合冰的过程;Bhatia等[6]使用SST
桅杆属于舰船上层建筑,其积冰过程与机翼相似,二者均属于大气积冰,所以机翼积冰的分析方法适用于桅杆积冰。本文借鉴荷兰Holland级巡逻舰桅杆进行建模,通过求解Navier-Stokes方程获得空气流场,使用欧拉法求解水滴的撞击特性,基于Messinger模型研究桅杆表面积冰生长情况,进而研究气象条件对桅杆积冰分布的影响。
1 积冰数值模拟计算方法 1.1 空气流场计算方法过冷水滴的运动轨迹与撞击物面的特性很大程度上取决于物体周围的流场情况,流场计算是水滴轨迹计算与积冰生成计算的首要条件与重要步骤。目前大多数CFD软件都采用求解Navier-Stokes方程(N-S方程)的方法求解空气流场。N-S方程的张量形式表示如下:
连续性方程
| $ \frac{{\partial \rho }}{{\partial {t}}} + \frac{{\partial \rho {u_j}}}{{\partial {x_j}}} = 0,$ | (1) |
动量方程
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\tau _{ij}}} \right) ,$ | (2) |
能量方程
| $ \begin{split} & \frac{\partial }{{\partial t}}\left( {\rho H - p} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}H} \right) = \\ & \frac{\partial }{{\partial {x_j}}}\left( {{u_i}{\tau _{ij}}} \right) - \frac{\partial }{{\partial {x_j}}}\left( {\frac{\mu }{{Pr }}\frac{{\partial h}}{{\partial {x_j}}}} \right)。\end{split} $ | (3) |
其中,
当求解的流体模型为湍流模型时,无法直接求解N-S方程对空气流场进行计算。通常采用雷诺平均法进行求解,即先将参数时均化,再模化,形成雷诺时均方程再进行求解。其张量形式为:
连续性方程
| $ \frac{{\partial \overline \rho }}{{\partial t}} + \frac{{\partial \rho {{\widetilde u}_j}}}{{\partial {x_j}}} = 0,$ | (4) |
动量方程
| $ \begin{split} &\frac{\partial }{{\partial t}}\left( {\overline \rho \widetilde ui} \right) + \frac{\partial }{{\partial xj}}(\overline \rho {\widetilde u_i}\widetilde uj + \overline p {\delta _{ij}}) = \\ & \frac{\partial }{{\partial {x_j}}}\left[ {(u + {u_t})\left( {\frac{{\partial \widetilde ui}}{{\partial xj}} + \frac{{\partial {{\widetilde u}_j}}}{{\partial {x_i}}}} \right) + \lambda \frac{{{{\widetilde u}_k}}}{{{x_k}}}{\delta _{ij}}} \right] ,\end{split} $ | (5) |
能量方程
| $ \begin{split} & \frac{\partial }{{\partial t}}\left( {\overline \rho \widetilde H - \overline p } \right) + \frac{\partial }{{\partial {x_j}}}\left( {\overline \rho {{\widetilde u}_j}\widetilde H} \right) = \\ & \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\frac{\mu }{{\Pr }} + \frac{{{\mu _t}}}{{{{\Pr }_t}}}} \right)\frac{{\partial \widetilde h}}{{\partial {x_j}}}} \right] + \\ &\frac{\partial }{{\partial {x_j}}}\left\{ {{{\widetilde u}_i}\left[ {\left( {\mu + {\mu _i}} \right)\left( {\frac{{\partial {{\widetilde u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\widetilde u}_j}}}{{\partial {x_i}}}} \right) + \lambda \frac{{\partial {{\widetilde u}_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right]} \right\} - \\ & \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right]。\end{split} $ | (6) |
在对参数时均化的过程中,引入了雷诺应力和湍流热2个未知参数,从而导致方程中未知数的个数多于方程的个数,无法对其进行求解。这时则需要引入湍流模型进行补充,使方程封闭。针对本文所计算的模型,采用RNG
在用欧拉法进行水滴撞击特性计算前,做出如下假设:
1)水滴在运动过程中始终为球体;
2)水滴在运动过程中只受到重力和空气阻力;
3)水滴在运动过程中,不考虑水滴的传质传热;
4)水滴在撞击壁面时,不发生反弹与飞溅现象。
对流场中的单个水滴应用牛顿第二定律可以得到水滴的运动轨迹方程:
| $ \dfrac{{{\rm{d}}u}}{{{\rm{d}}t}} = \frac{{18{\mu _a}{C_D}{Re} }}{{24\rho d_p^2}}({u_a} - u) + \frac{{\rho - {\rho _a}}}{\rho }g。$ | (7) |
其中:t为时间;u为水滴速度;
| $ {Re} = \frac{{{\rho _a}\left| {u{}_a - u} \right|{d_p}}}{{{\mu _a}}}。$ | (8) |
欧拉法将水滴看作连续相,建立水滴的连续性方程和动量方程如下:
| $ \begin{split} & \frac{{\partial \left( {\alpha u} \right)}}{{\partial t}} + \nabla \cdot \left( {\alpha uu} \right) = \\ & \frac{{18{\mu _a}{C_D}{Re} }}{{24\rho d_p^2}}\alpha \left( {{u_a} - u} \right) + \alpha \frac{{\rho - {\rho _a}}}{\rho }g,\end{split} $ | (9) |
| $ \frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot \left( {\alpha u} \right) = 0 。$ | (10) |
式中,
| $ \alpha = \frac{{LWC}}{\rho }。$ | (11) |
其中,LWC为空气中液态水含量。通过欧拉法得到的水滴收集系数
| $ \beta = \frac{{\left( {{u_n} \cdot {\boldsymbol{n}}} \right){\alpha _n}}}{{\left| {{u_\infty }} \right|{\alpha _\infty }}} 。$ | (12) |
式中:
积冰生成计算就是利用传质传热过程中的守恒定律模拟物体表面的积冰方法。Messinger提出了一个完整的积冰数学模型,并一直沿用至今。Messinger模型中的控制体单元如图1所示。
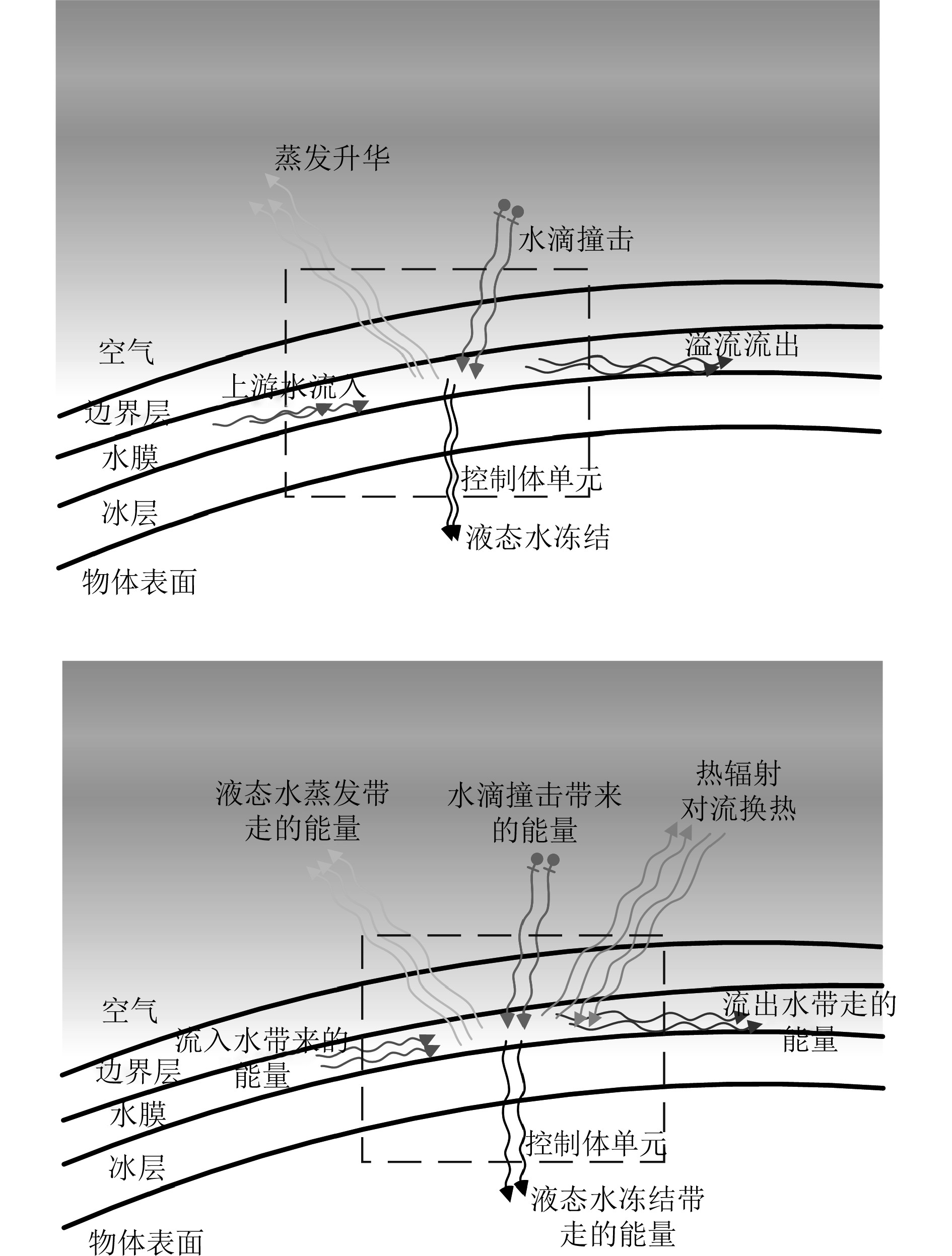
|
图 1 控制单元内的质量和能量交换示意图 Fig. 1 Schematic diagram of mass and energy exchange within a control unit. |
建立该控制体单元的质量守恒方程和能量守恒方程如下:
| $ {M_{in}} + {M_{im}} + {M_{ev}} + {M_{out}} + {M_{ice}} = 0 ,$ | (13) |
| $ {Q_{in}} + {Q_{im}} - {Q_{ev}} - {Q_{out}} - {Q_{fre}} - {Q_{conv}} = 0。$ | (14) |
其中:
为了求解积冰量,引入冻结系数
| $ f = \frac{{{M_{ice}}}}{{{M_{in}} + {M_{im}}}}。$ | (15) |
结合式(10)可以得出紧靠驻点的第1个控制体单元的冻结系数为:
| $ {f_1} = \frac{{{M_{ice,1}}}}{{{M_{im,1}}}}。$ | (16) |
当
每个控制体单元的冻结系数计算出来后,相应的积冰量就可以计算得出:
| $ {M}_{ice}=f\cdot\left({M}_{in}+{M}_{im}\right) 。$ | (17) |
桅杆积冰的研究方法共有3种:海上试验、冰风洞试验和数值模拟。海上试验可以直接观测到积冰过程,能反映最真实的积冰情况,但相对来说投资大,周期长,并且对试验条件也有一定的限制。冰风洞试验的显著优点为便捷、安全,可以在理想的环境下进行试验,但冰风洞在我国发展较晚,技术不成熟且造价高昂,无法进行大批量试验。随着计算机技术以及计算流体力学(CFD)的发展,数值模拟方法由于其经济、高效和可重复性等优点受到广泛的认可与推广[11]。本文采用数值模拟方法对极地船舶桅杆进行积冰预报。
选择引射式冰风洞[12]内圆柱体的积冰试验数据作为数值模拟验证依据。试验条件如下:圆柱体直径d=25.4 mm,风速v=30 m/s,温度T=258.15 K,液态水含量LWC=1.2 g/m3,平均水滴直径MVD=20 μm,积冰时间t=100 s。图2为圆柱体的网格划分情况。其中,inlet为流体入口,outlet为流体出口,wall为无滑移壁面。
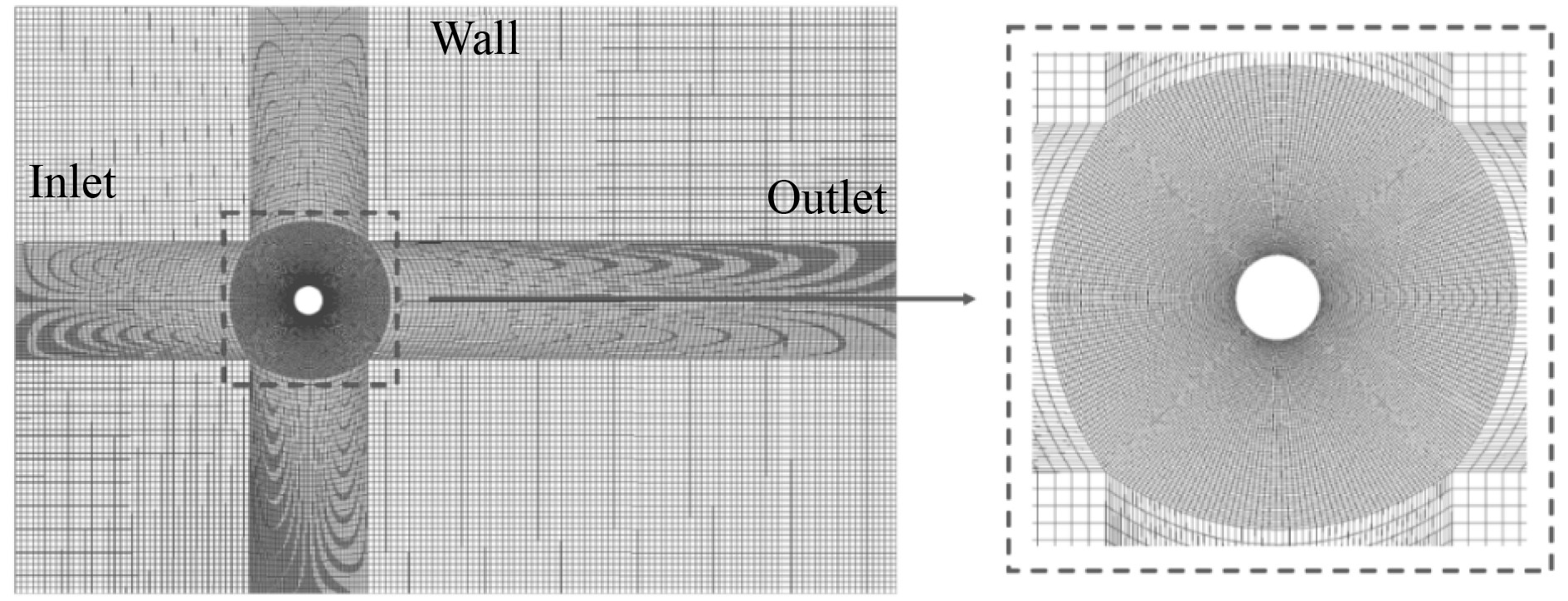
|
图 2 圆柱体网格划分情况 Fig. 2 Cylinder meshing situation. |
图3为数值模拟结果与试验结果的对比图。图中,x/d和y/d分别为x轴和y轴相对于圆柱直径的无量纲坐标,实线为通过冰风洞试验所得到的积冰轮廓,虚线为数值模拟的结果。由图3可知,数值模拟计算的冰型与冰风洞试验所得到的冰型基本一致。可以证明本文所采用的积冰数值模拟理论是可行的。

|
图 3 数值模拟结果与冰风洞试验结果对比 Fig. 3 Comparison between numerical simulation results and ice wind tunnel experimental results. |
为了解桅杆的积冰过程,借鉴荷兰Holland级巡逻舰进行建模。图4为通过SolidWorks创建的桅杆模型,比例尺为1∶100。模型总高度130 mm,划分为3个区域:Ⅰ 区域为球体,直径为20 mm;Ⅱ 区域为圆柱体,高度为15 mm;Ⅲ 区域为棱台,底边长与高度均为80 mm,斜边与垂直方向的倾斜角为30

|
图 4 模型建立 Fig. 4 Model establishment. |
图5为外流场及桅杆网格划分情况。其中,Inlet为空气入口,Outlet为空气出口,Wall为无滑移壁面,Symm为对称面,Mast为桅杆。为保证模拟的准确性,外流场在长度方向上是桅杆长度的20倍,宽度方向和高度方向是桅杆的10倍。
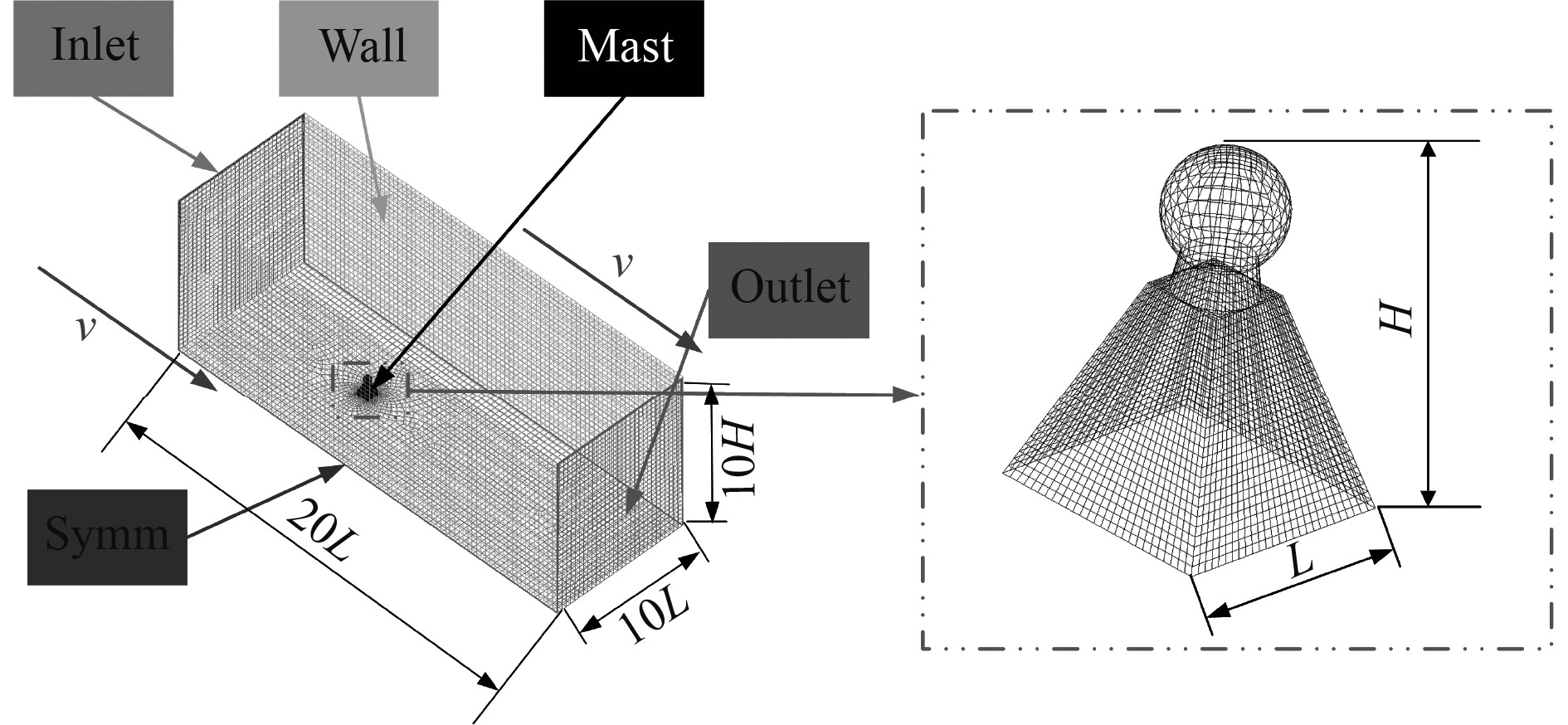
|
图 5 桅杆及外流场网格划分情况 Fig. 5 Meshing of mast and outer flow field. |
气象条件的变化会导致桅杆周围空气流场和水滴运动轨迹发生变化,从而改变了桅杆表面水滴的撞击特性,最终影响冰层在部件表面的积冰质量分布和冰形。影响桅杆积冰的气象条件主要为风速、空气中的液态水含量以及过冷水滴直径。
3.1 风速对桅杆积冰的影响模拟工况如下:T=239.15 K,LWC=0.8 g/m3,MVD=20 μm,v的取值为2 m/s,4 m/s,6 m/s,8 m/s和10 m/s。数值模拟结果如图6所示。图中纵坐标为桅杆表面的水滴收集系数,横坐标表示桅杆高度。由图可知,随着风速的增加,桅杆的最大液滴收集效率从0.13增加至0.57。其原因是在忽略重力和浮力的情况下,液滴在自由气流中的运动受其阻力和惯性的影响。如果阻力主导惯性,液滴遵循流线,而对于惯性主导的情况,液滴会与桅杆表面碰撞。液滴惯性与阻力之比取决于风速。风速越大,水滴受惯性的影响越大,撞击在桅杆表面的水滴越多,水滴收集系数增大。
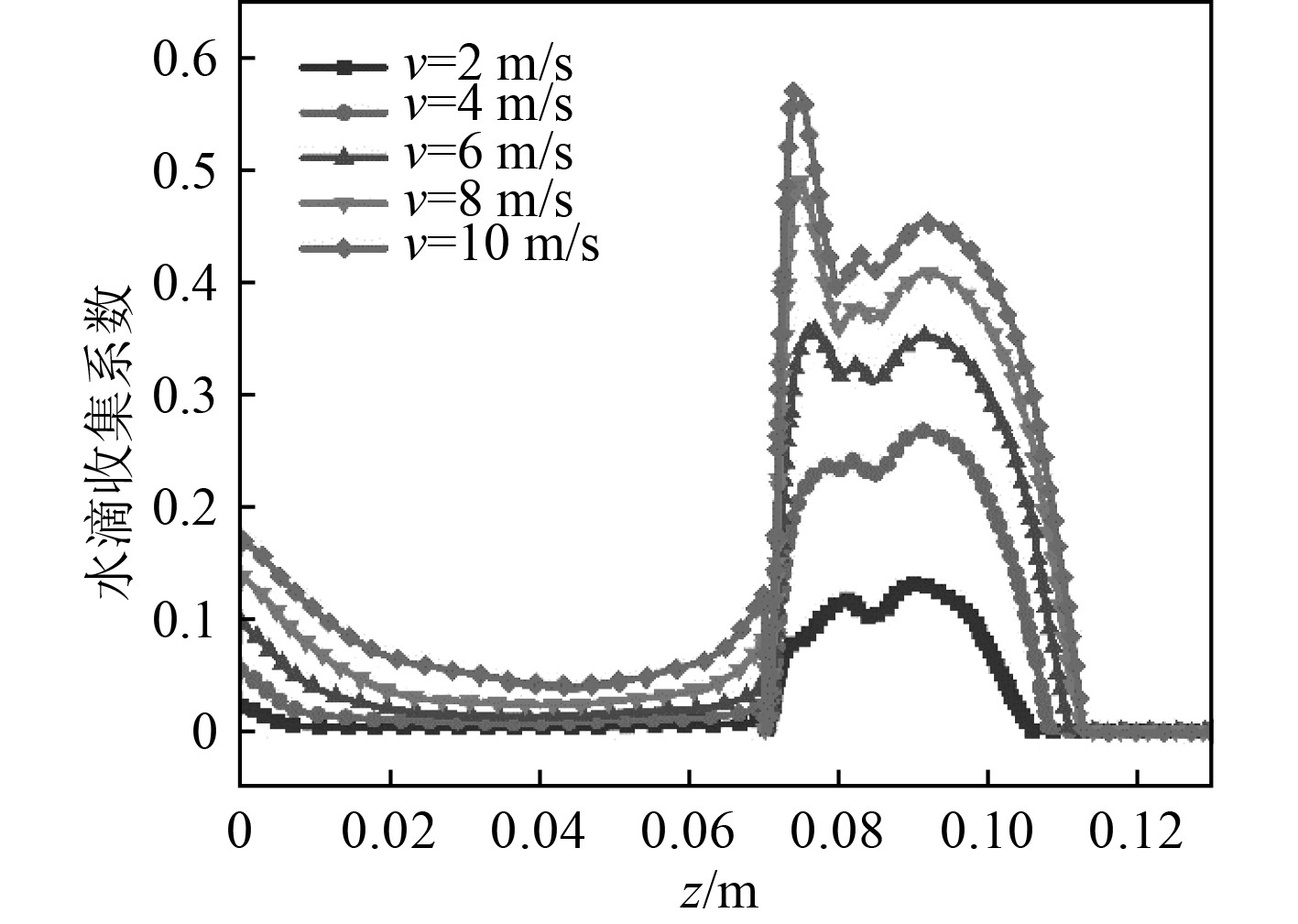
|
图 6 不同风速条件下桅杆表面水滴收集系数 Fig. 6 Collection coefficient of water droplets on the mast surface under different wind speeds. |
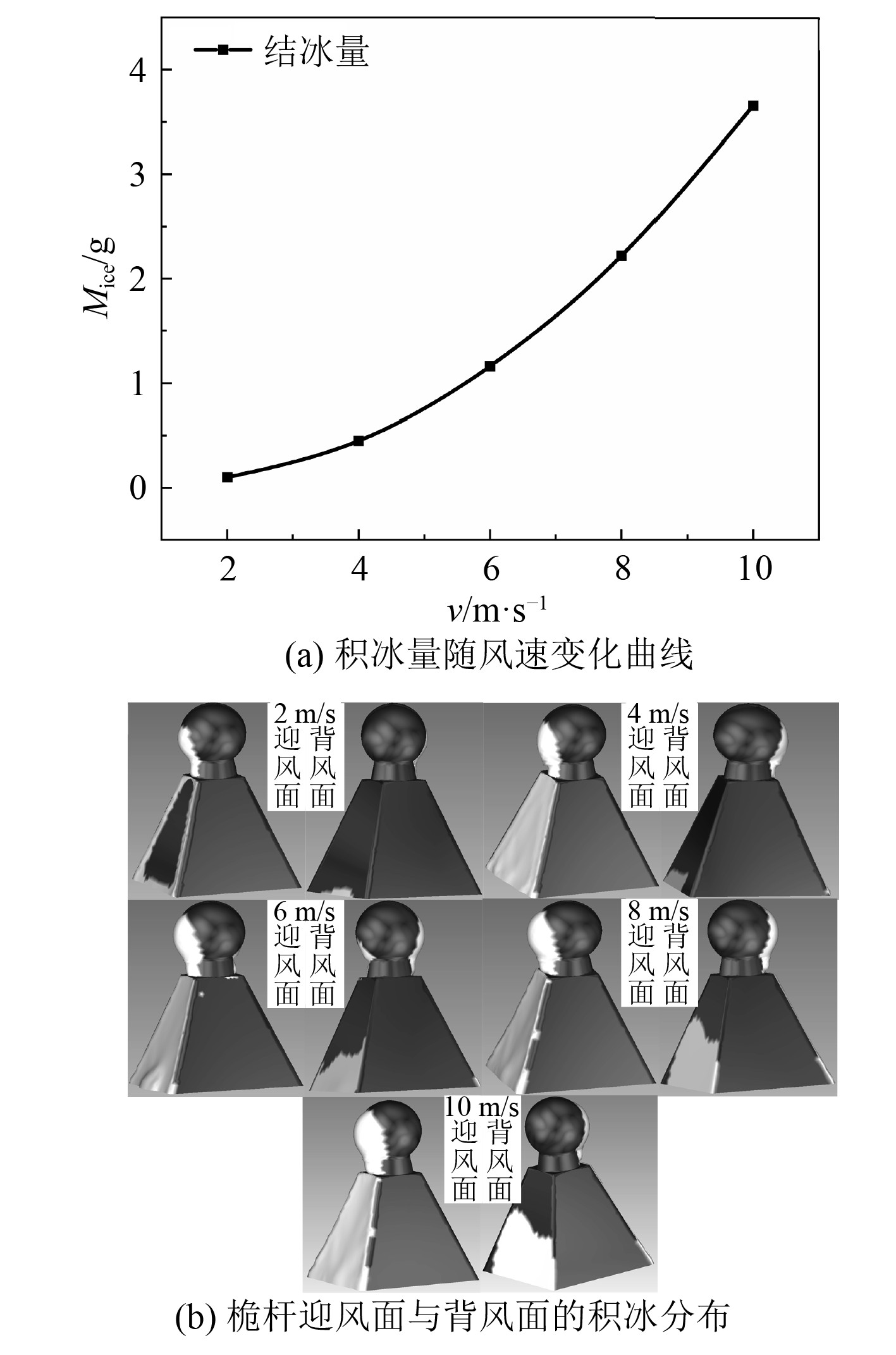
图7 (a)为桅杆表面积冰量随风速变化的趋势图。风速从2 m/s增加至10 m/s,桅杆表面积冰量从0.1 g增加至3.66 g。图7 (b)为桅杆的迎风面与背风面的积冰对比图,随着风速的增加,桅杆迎风面与背风面的积冰区域均显著增加。其原因是风速越大,单位时间内空气所携带的水滴数量增多,撞击到桅杆迎风面的水滴质量增加,水滴收集效率增加,所以桅杆表面的积冰量增大。而随着风速的增加,桅杆背风面回流现象加剧,越来越多的水滴随着回流撞击在桅杆的背风面,使背风面的水滴收集量增加,积冰厚度与范围也相应地增加。
|
图 7 不同风速条件下桅杆表面积冰 Fig. 7 Ice accretion on mast surface under different wind speeds. |
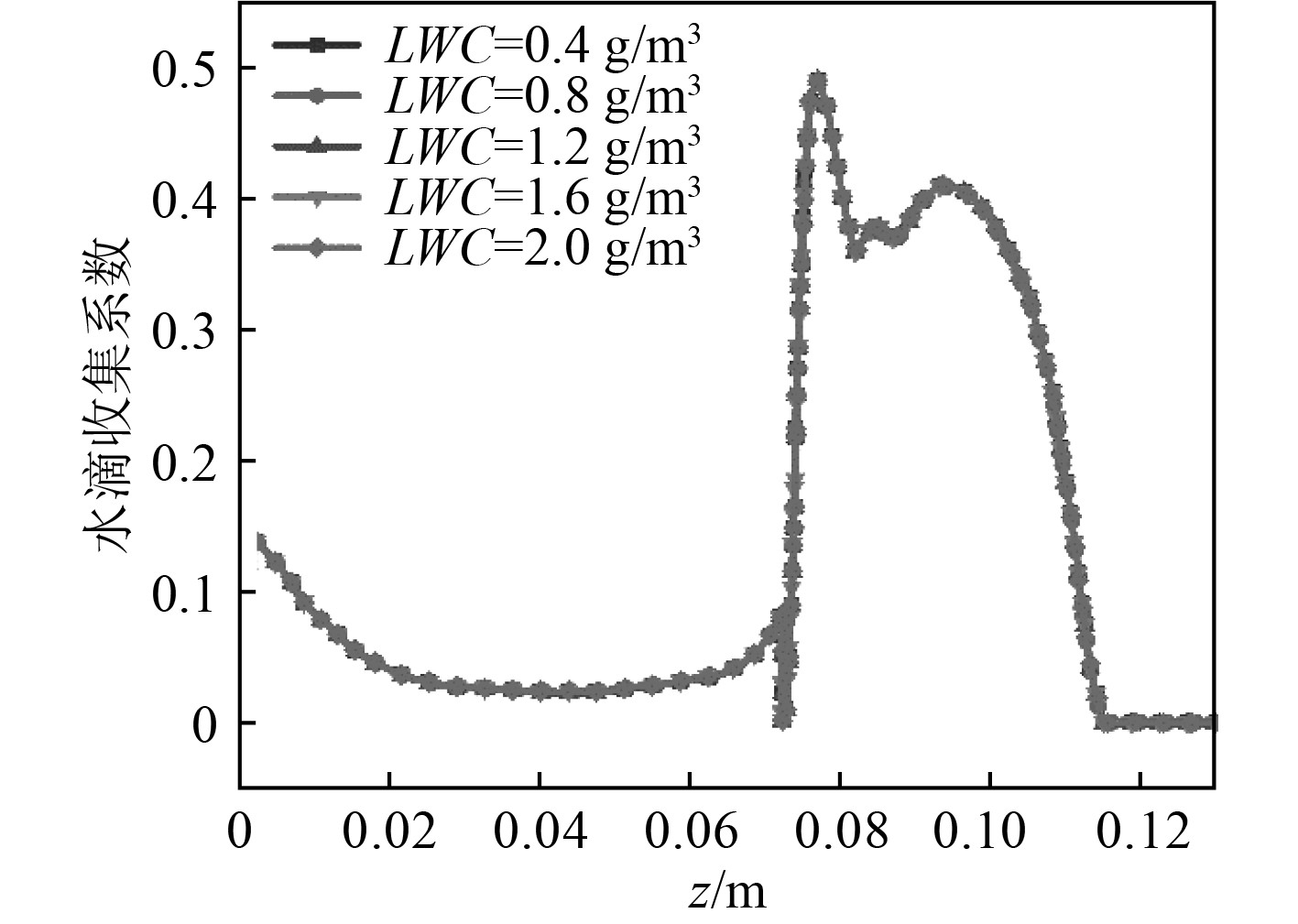
模拟工况如下:T=239.15 K,v=8 m/s,MVD=20 μm,LWC的取值为0.4 g/m3,0.8 g/m3,1.2 g/m3,1.6 g/m3和2.0 g/m3。数值模拟结果如图8所示。可知,空气中液态水含量的变化不会使桅杆的水滴收集系数发生改变。这是因为通过欧拉法计算水滴收集系数时,在计算过程中将“LWC”这一项略去,所以水滴收集系数与液态水含量无关。
|
图 8 不同液态水含量条件下桅杆表面水滴收集系数 Fig. 8 Collection coefficient of water droplets on mast surface under different liquid water content. |
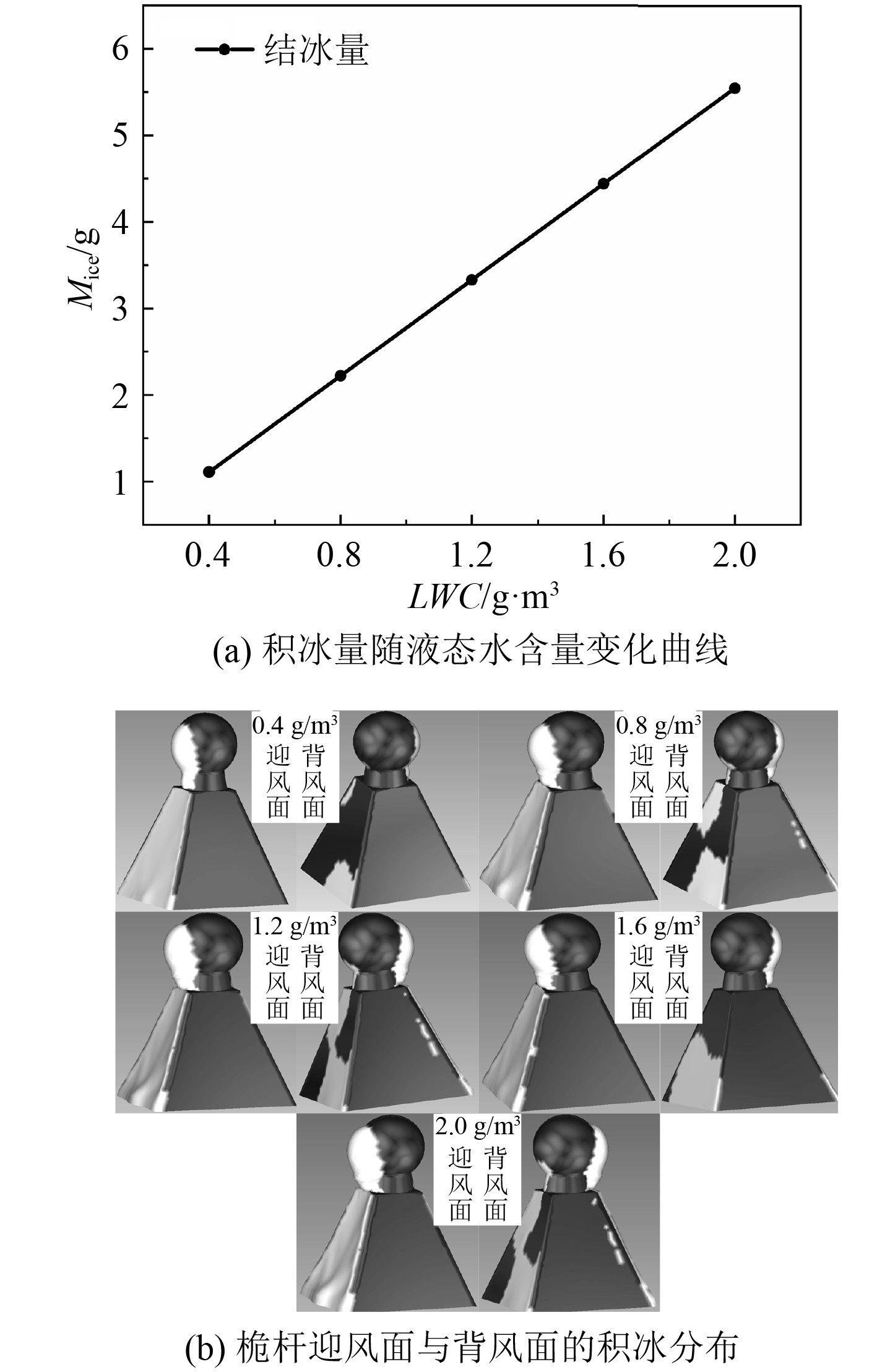
图9 (a)为桅杆表面积冰量随液态水含量变化曲线。可知,LWC从0.4 g/m3增加到2.0 g/m3,桅杆表面的积冰量从1.11 g增加到5.55 g,并且积冰量随着液态水含量线性增加。图9 (b)为桅杆的迎风面与背风面的积冰对比图,随着液态水含量的增加,桅杆迎风面与背风面的积冰厚度与积冰范围均增加。这是因为液态水含量的增加会导致单位时间内桅杆表面收集到的液态水量增多,同时使绕流到桅杆背风面的水滴数量增加,积冰范围扩大。
|
图 9 不同液态水含量下桅杆表面积冰 Fig. 9 Ice accretion on mast surface under different liquid water content. |
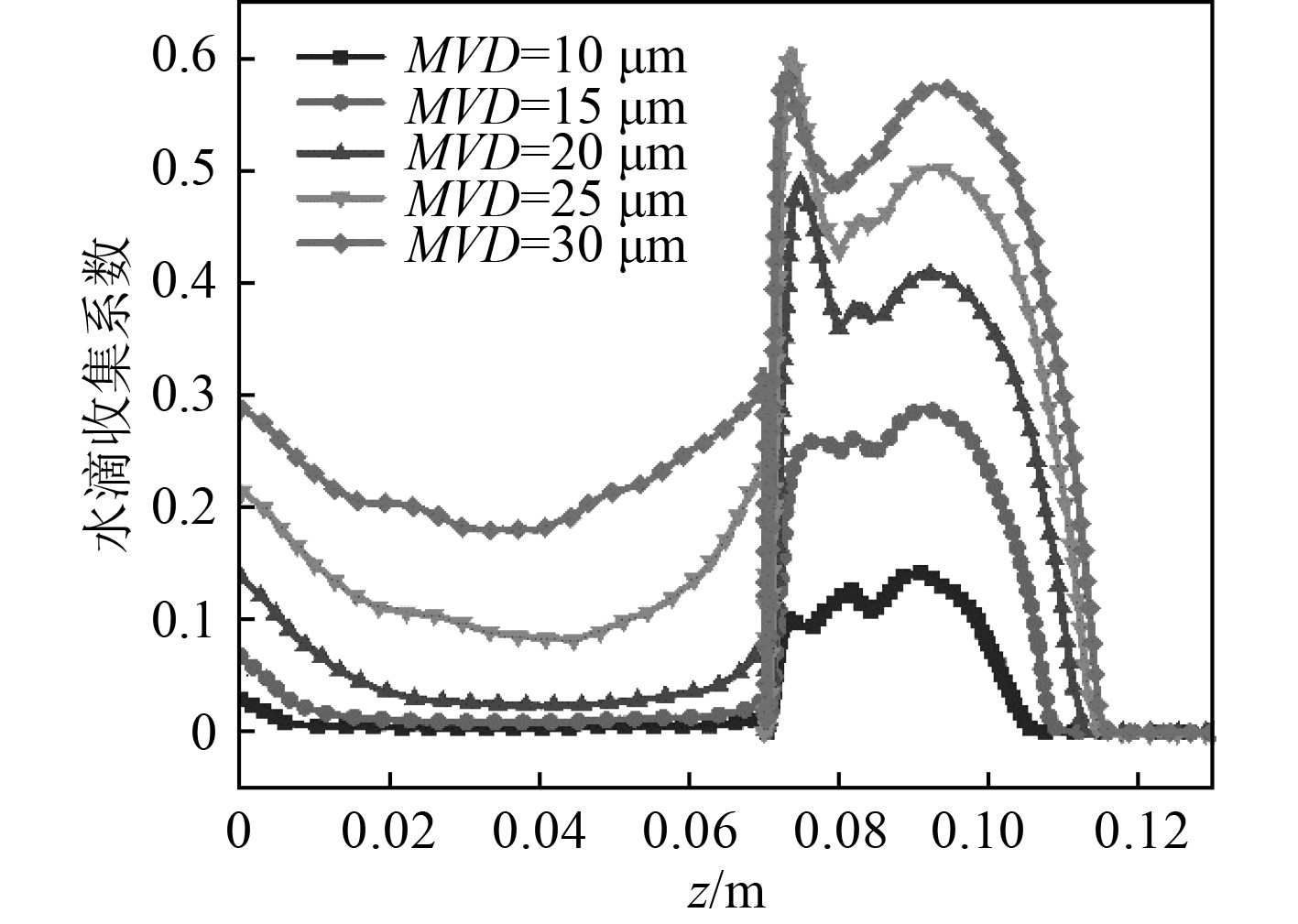
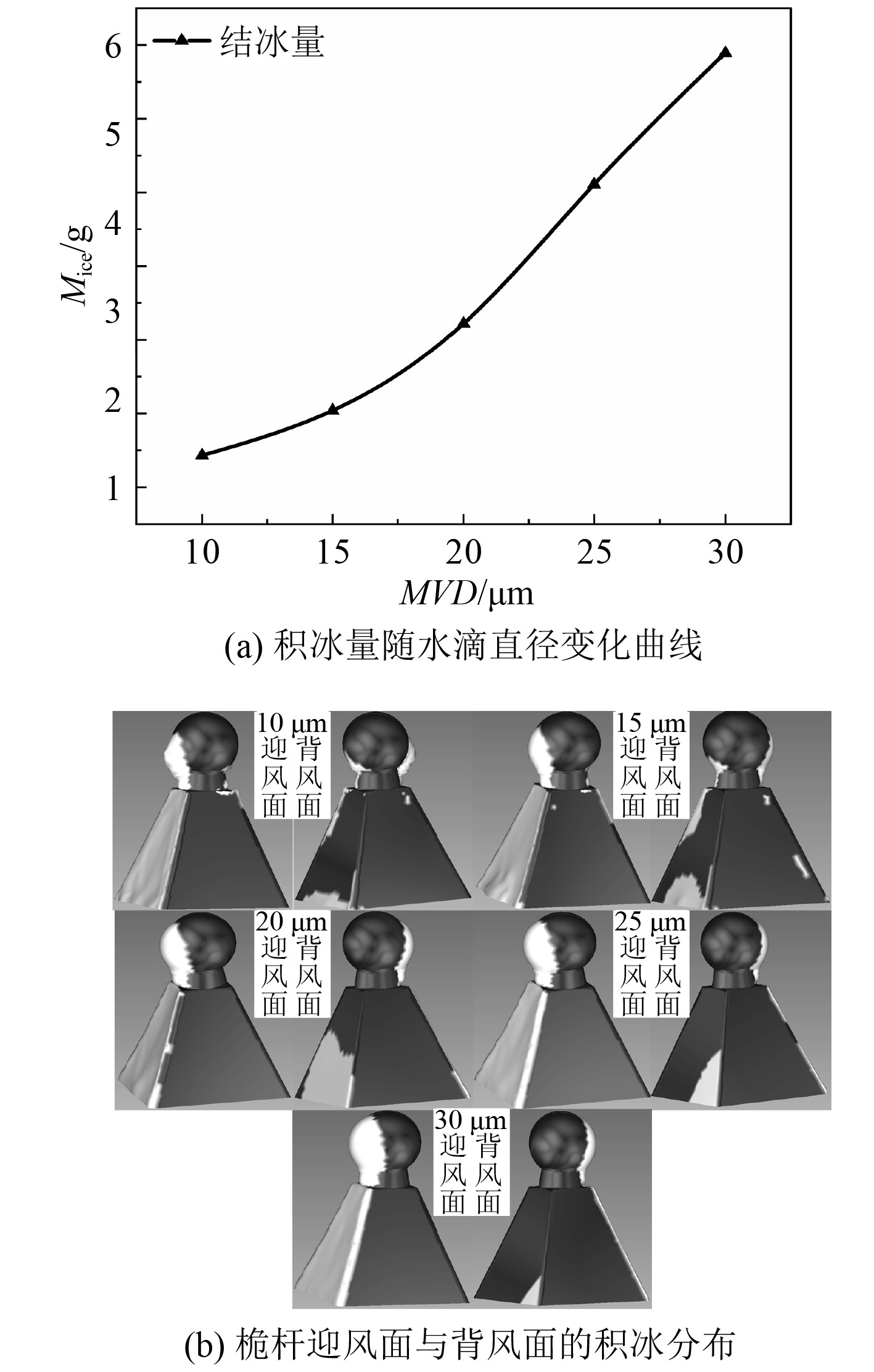
模拟工况如下:T=239.15 K,v=8 m/s,LWC=0.8 g/m3,MVD的取值为10 μm,15 μm,20 μm,25 μm和30 μm。数值模拟结果如图10所示。可知,随着平均水滴直径从10 μm增加至30 μm,桅杆表面的最大水滴收集系数从0.14增加到0.61。该现象是由于实际收集的水滴量增大导致的。
|
图 10 不同水滴直径条件下桅杆表面水滴收集系数 Fig. 10 The collection coefficient of water droplets on the mast surface under the condition of different droplet diameters. |
图11 (a)为桅杆表面积冰量随水滴直径变化的曲线图。随着水滴直径的增加,桅杆表面的积冰量增加。其主要原因是,与较小的液滴相比,较大直径的液滴具有较大的惯性。因此,大液滴的运动受气流影响较小,更多的水滴与桅杆表面碰撞。图11 (b)为桅杆的迎风面与背风面的积冰分布图。可知,桅杆迎风面的积冰范围随着水滴直径的增加而增加,而背风面的积冰范围先增加后减小。产生该现象的原因是随着回流所携带的水滴直径增加,水滴撞击在桅杆的范围增加,但当水滴的直径增加到一定程度时,水滴便会脱离自由来流的轨迹,撞击到桅杆的迎风面上,使得参与回流水滴数量减少,所以积冰范围变小。
|
图 11 不同水滴直径条件下桅杆表面积冰 Fig. 11 Ice accretion on mast surface under different droplet diameters. |
本文以极地船舶桅杆为研究案例,利用Fluent和Fensap-Ice模拟桅杆表面的积冰分布情况,研究气象条件对桅杆积冰的影响,得到如下结论:
1)所选桅杆的Ⅰ 区域与Ⅱ 区域是积冰最为严重的部位,在进行积冰防护与清理时,尤其要注意该部位。
2)随着风速从2 m/s增加到10 m/s,桅杆表面的最大水滴收集系数从0.13增加到0.57,积冰质量从0.10 g增加到3.66 g。同时,背风面的积冰厚度和范围增加。
3)随着液态水含量的增加,积冰质量从1.11 g增加到5.55 g,并且是呈线性增加。但液态水含量不会改变桅杆表面的水滴收集系数。
4)随着水滴直径的增加,撞击到桅杆表面水滴的质量增加,桅杆迎风面积冰范围和积冰质量增加,但水滴直径越大,水滴和空气一起运动时偏离气流流线的能力越强,参与回流的水滴数量减少,导致桅杆背风面的积冰范围减少。
| [1] |
谢强, 陈海龙, 章继峰. 极地船舶及海洋平台防冰和除冰技术研究进展[J]. 中国舰船研究, 2017, 12(1): 45-53. |
| [2] |
NG A K Y, ANDREWS J, BABB D, et al. Implications of climate change for shipping: Opening the Arctic seas[J]. Wiley Interdisciplinary Reviews:Climate Change, 2018, 9(2): e507. |
| [3] |
刁端信, 陈豪. 国外海军集成桅杆技术发展浅析[J]. 船舶, 2015, 26(3): 6.
|
| [4] |
POURYOUSSEFI S G, MIRZAEI M, NAZEMI M, et al. Experimental study of ice accretion effects on aerodynamic performance of an NACA 23012 airfoil[J]. Chinese Journal of Aeronautics, 2016, 29(3): 585-595. DOI:10.1016/j.cja.2016.03.002 |
| [5] |
JANJUA Z A, TURNBULL B, HIBBERD S, et al. Mixed ice accretion on aircraft wings[J]. Physics of Fluids, 2018, 30(2): 027101. DOI:10.1063/1.5007301 |
| [6] |
BHATIA D. A numerical investigation into the impact of icing on the aerodynamic performance of aerofoils[C]//IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2020, 831(1): 012007.
|
| [7] |
KALYULIN S L, MODORSKII V Y, CHEREPANOV I E. Numerical modeling of the influence of the gas-hydrodynamic flow parameters on streamlined surface icing[C]//AIP Conference Proceedings. AIP Publishing LLC, 2018, 2027(1): 030180.
|
| [8] |
JIN J Y, VIRK M S. Study of ice accretion along symmetric and asymmetric airfoils[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 179: 240-249. DOI:10.1016/j.jweia.2018.06.004 |
| [9] |
TAKAHASHI T, FUKUDOME K, MAMORI H, et al. Effect of characteristic phenomena and temperature on super-cooled large droplet icing on NACA0012 airfoil and axial fan blade[J]. Aerospace, 2020, 7(7): 92. DOI:10.3390/aerospace7070092 |
| [10] |
WANG J Y, HU X J. Application of RNG k-ε turbulence model on numerical simulation in vehicle external flow field[C]//Applied Mechanics and Materials. Trans Tech Publications Ltd, 2012, 170: 3324-3328.
|
| [11] |
沈杰, 白旭. 风速对寒区船舶杆件结构霜冰结冰的影响分析[J]. 舰船科学技术, 2020, 42(9): 56-60. |
| [12] |
孟繁鑫, 陈维建, 梁青森, 等. 引射式积冰风洞内圆柱积冰试验[J]. 航空动力学报, 2013, 28(7): 1467-1474. |
 2023, Vol. 45
2023, Vol. 45
