2. 上海外高桥造船海洋工程有限公司,上海 200131
2. Shanghai Waigaoqiao Shipbuilding and Offshore Engineering Co., Ltd, Shanghai 200131, China
浮式钻井生产储卸油装置(floating drilling production storage and offloading system,FDPSO)是21世纪海上油气开采的重要装备之一[1],具有建造成本低、储油能力强、能适应多种海况、转移方便可重复使用等优点[2]。我国南海存在许多储量不高、分布散乱的边际油田,FDPSO能够极大改善我国对边际油田开发不足的状况[3]。
从结构类型上可以将FDPSO分为船型和圆筒形,但是船型FDPSO存在垂荡和横摇运动性能差、船体疲劳问题严重、经常需要维修保养影响生产效率等缺点,而圆通型FDPSO能够改善横摇和纵摇运动性能,在运动性能上圆筒型FDPSO要优于船型FDPSO,但两者垂荡性能都较差[4]。在抑制圆筒型FDPSO垂荡运动方面,曲志森等[5-6]提出了一种带通海延伸筒体和减动结构的新型FDPSO,能够有效抑制其垂荡运动,但是在利用水动力计算软件分析其阻尼系数时,由于通海孔尺寸远远小于FDPSO基本尺寸,在数值仿真计算时存在局部网格加密区域多、网格数量大大增加导致计算效率低、计算结果误差增大等问题。
本文提出用无通海孔
在只考虑浮体单自由度运动的情况下,基于达朗贝尔原理的直接平衡法建立FDPSO运动方程[7]:
| $ {{m}}\ddot y + c\dot y + ky = F。$ | (1) |
式中:
当FDPSO做垂荡自由衰减运动时,干扰力
| $ F = {F_{\text{v}}} + {F_a},$ | (2) |
| $ {F_{{a}}} = - {{\text{m}}_a}\ddot y 。$ | (3) |
式中,
将式(2)和式(3)代入式(1),可得到FDPSO垂荡衰减运动方程为:
| $ (m + {m_a})\ddot y + c\dot y + ky = {F_{{v}}},$ | (4) |
有通海孔FDPSO垂荡衰减运动方程为:
| $ ({m_1} + m_a^1)\ddot y + c\dot y + ky = F_v^1 ,$ | (5) |
无通海孔FDPSO垂荡衰减运动方程为:
| $ ({m_2} + m_a^2)\ddot y + c\dot y + ky = F_v^2。$ | (6) |
式中:
| $ 令 m + {m_a} = {m_\delta }。$ | (7) |
式中,
FDPSO固有周期的表达式可表示为[8]:
| $ {T_j} = 2\text{π} \sqrt {\frac{{{M_j}}}{{{K_j}}}} 。$ | (8) |
在计算FDPSO各自由度的固有周期时,都可以按照式(8)计算。其中,j取1~6分别为了垂荡、纵荡、纵摇、横荡、横摇、首摇;
以一种带通海结构的圆筒型FDPSO为分析对象,如图1所示。在传统圆筒型FDPSO主筒体下部增加延伸筒体和减动结构。有通海孔FDPSO如图1(a)和图1(c)所示,通海孔直径为2 m,通海孔位于减动结构顶部、底部以及延伸筒体底部,通气孔贯穿主筒体连通延伸筒体,减动结构上下通海孔以及延伸筒体上通气孔和下通海孔在垂直方向上不在同一条直线上。在进行水动力数值计算时,有通海孔FDPSO下部延伸筒体和减动结构视为中空透水结构,排水量可以忽略不记。无通海孔FDPSO如图1(b)和图1(d)所示,在进行数值计算时可将整体构型视为实体结构,排水量较大,使浮体质量大大增加。2种模型的基础参数如表1所示。

|
图 1 FDPSO模型示意图 Fig. 1 Schematic diagram of FDPSO model |
|
|
表 1 物理参数 Tab.1 Physical parameters |
在水动力仿真软件Aqwa中对有通海孔和无通海孔的新型圆筒型FDPSO进行频域分析。频域计算时,取波浪周期5~64 s,间隔1 s,共60个波浪周期。计算结构垂荡运动的附加质量和运动响应传递函数。结果如图2和图3所示。

|
图 2 运动响应传递函数(RAOs) Fig. 2 Motion response transfer function (RAOs) |
|
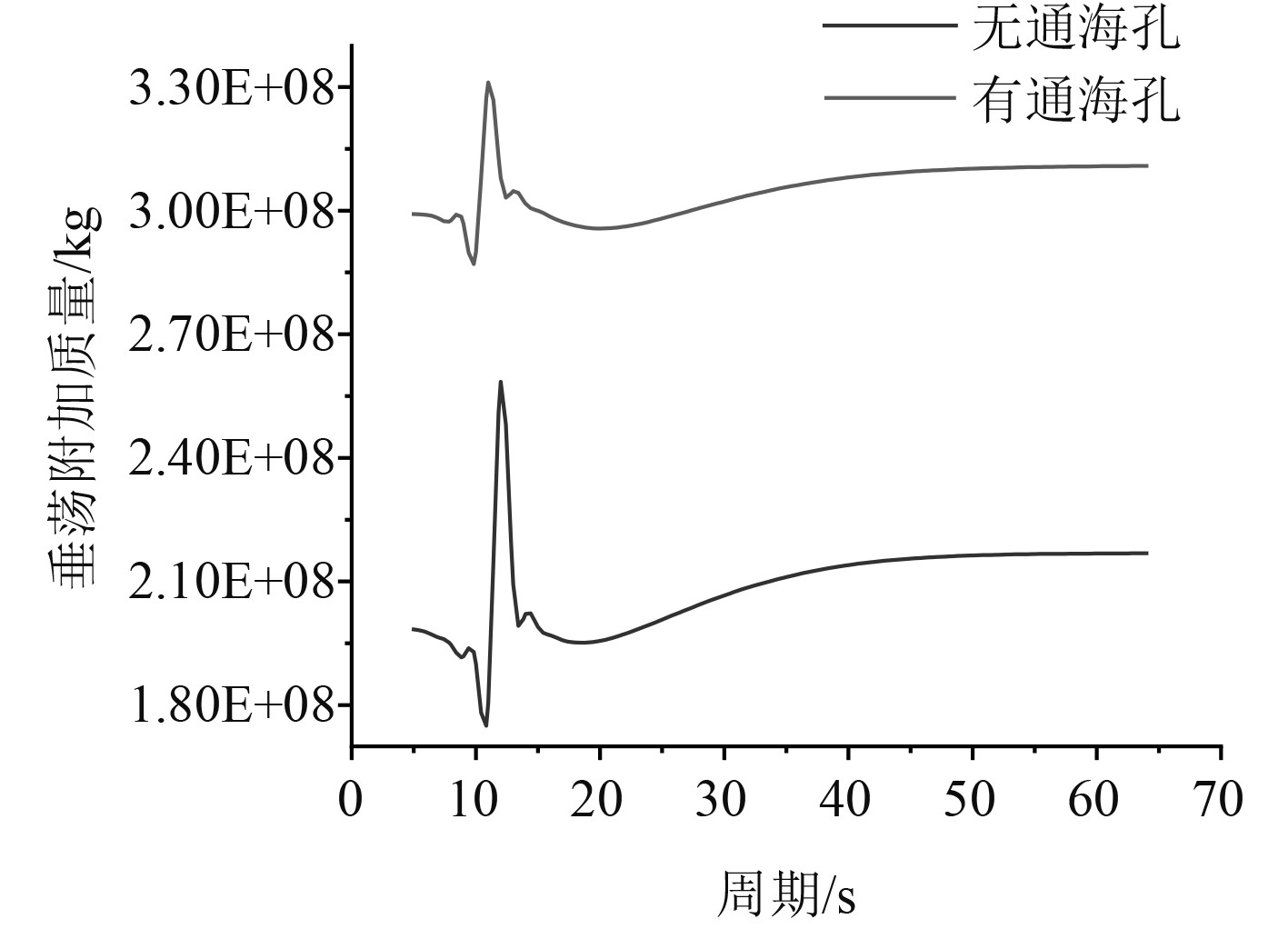
图 3 垂荡附加质量 Fig. 3 Heave additional mass |
运动响应传递函数(RAOs)和垂荡附加质量计算结果,如表2所示。
|
|
表 2 频域计算结果分析 Tab.2 Analysis of frequency domain calculation results |
可知,无通海孔的FDPSO垂荡附加质量
当有通海孔FDPSO和无通海孔FDPSO的基础尺寸一致时,由于通海孔处流体流动对整体结构水动力
| $ F_v^1 \approx F_v^2 。$ | (9) |
结合以上2种模型垂荡等效质量和固有周期的分析结果,可以得出2种模型的垂荡衰减运动控制方程几乎是等效的。因此,在后续采用计算流体力学方法分析有通海孔FDPSO的阻尼系数时,可选择分析更简单、准确度更高的无通海孔FDPSO代替有通海孔FDPSO。
3 FDPSO垂荡阻尼分析利用水动力仿真软件STAR-CCM+对新型圆筒型FDPSO的垂荡方向上运动衰减过程进行仿真计算,分析其运动情况和受力情况,通过自由衰减时历图分析其阻尼系数[9]。在分析有通海孔FDPSO的阻尼系数时,选择更简单、准确度更高的无通海孔FDPSO代替有通海孔FDPSO。
3.1 分析模型为了与文献[5]曲志森的试验测量结果进行对比,以无通海孔FDPSO实际尺寸按照1∶77.8的缩尺比建立模型,模型尺寸如表3所示。基于SolidWorks建立的平台三维几何模型如图4所示。
|
|
表 3 物理参数 Tab.3 Physical parameters |

|
图 4 FDPSO几何建模 Fig. 4 FDPSO geometric modeling |
使用计算流体力学软件STAR-CCM+对FDPSO模型进行研究,计算水域是以模型质心为中心建立,其长10.0 m、宽4.0 m、高5 m,如图5所示。

|
图 5 计算域尺寸 Fig. 5 Calculation domain size |
在FDPSO垂荡阻尼系数的计算中,采用粘性流体的基本理论计算FDPSO的水动力,即求解不可压缩流体的连续性和Navier-Stokes方程[10]。计算域内的水和空气两相流体采用欧拉-欧拉模型(Euler-Euler Model)进行描述,并采用求解基于VOF方法的流体体积输运方程来捕捉水和空气的界面位置,即
| $ \frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot ({\boldsymbol{U}}\alpha ) + \nabla \cdot ({{\boldsymbol{U}}_r}(1 - \alpha )\alpha ) = 0。$ |
式中:
| $ \left\{ \begin{gathered} \alpha = 0,{\text{ air}},\\ 0 < \alpha < 1,{\text{ interface}},\\ \alpha = 1,{\text{ water}} 。\\ \end{gathered} \right. $ |
网格划分采用动网格技术,主要涉及计算区域和运动区域2个区域的网格划分。计算区域的网格划分采用切割体棱柱层体网格技术,同时对流场复杂区域的网格进行细化加密。对自由液面进行3层加密,其网格尺寸x方向和y方向均为基础尺寸的20%,z方向分别为基础尺寸的5%,10%,15%,如图6(a)所示。对减动结构间隙处的网格单独细化加密,网格尺寸x,y,

|
图 6 网格划分 Fig. 6 Meshing |
计算中,使浮体初始位置低于其质心0.1 m,即初始液面比浮体标定水线高0.1 m,让浮体能够在不受外力的条件下做垂荡自由衰减运动。
3.3.1 数值计算结果FDPSO上升过程和下降过程中速度最大时的局部流场如图7所示。

|
图 7 FDPSO上升和下降过程速度最大时局部流场图 Fig. 7 Local flow field diagram of FDPSO at maximum speed during rising and falling process |
可以看出:上升时,减动结构外侧和通海间隙下方存在涡;下降时,减动结构外侧和通海间隙上方存在涡。运动过程中,流体从减动结构间隙通过,与间隙外流场产生速度差,形成涡。当FDPSO在流体中运动时,由于流体存在粘性,带动周围流体一起运动,此时会受到流体的粘性剪切力,粘性剪切力方向与其运动方向相反,并随着其运动速度增大而增大,所以流体的粘性剪切力有抑制运动的效果[11],导致FDPSO垂向运动持续衰减。
FDPSO垂荡自由衰减运动位移和受力如图8所示。

|
图 8 FDPSO垂荡衰减运动位移图和受力图 Fig. 8 FDPSO heave attenuation motion displacement diagram and stress diagram |
物体在自由衰减振动过程中,振动频率是不变的,并且一直沿着中心位置做振荡运动。所以可以通过衰减振动曲线计算出系统的阻尼系数ζ。
如图9所示,为阻尼比计算理论[7],设相邻2两个周期的位移峰值为

|
图 9 阻尼比计算理论 Fig. 9 Damping ratio calculation theory |
| $ \frac{{{y_i}}}{{{y_{i + 1}}}} = \frac{{A{e^{ - \zeta \lambda {t_i}}}\cos ({\lambda _d} + \beta )}}{{A{e^{ - \zeta \lambda ({t_i} + {T_d})}}\cos \left[ {{\lambda _d}({t_i} + {t_d}) + \beta } \right]}}。$ |
因为:
| $ {\lambda _d}{T_d} = 2{\text{π}} $ |
所以:
| $ \frac{{{y_i}}}{{{y_{i + 1}}}} = {e^{\zeta \lambda {T_d}}}。$ |
两边取对数得:
| $ \delta = \ln \frac{{{y_i}}}{{{y_{i + 1}}}} = \zeta \lambda {T_d} = \zeta \lambda \frac{{2{\text{π}} }}{{{\lambda _d}}} \approx \zeta 2{\text{π}} 。$ | (10) |
于是得到阻尼系数为:
| $ \zeta \approx \frac{1}{{2{\text{π}} }}\delta。$ | (11) |
式中:δ称为对数衰减率。利用式(11)即可计算得到阻尼系数。如果利用间隔N个周期的位移峰值之比来计算对数衰减率,则可得到N个周期位移峰值对数衰减率的平均值,从而可以得到更接近振动系统实际的阻尼系数。间隔N个周期的位移峰值之比为:
| $ \frac{{{y_i}}}{{{y_{i + N}}}} = {e^{\zeta \lambda N{T_d}}},$ |
两边取对数得:
| $ \ln \frac{{{y_i}}}{{{y_{i + N}}}} = \zeta \lambda N{T_d} = \zeta N\lambda \frac{{2{\text{π}} }}{{{\lambda _d}}} \approx \zeta N2{\text{π}} = N\delta ,$ |
即有
| $ \delta = \frac{1}{N}\ln \frac{{{y_i}}}{{{y_{i + N}}}}。$ | (12) |
将式(12)代入式(11)计算阻尼系数,可提高阻尼系数精度。
3.3.3 阻尼系数和周期计算通过式(12)和式(11)计算FPDSO的阻尼系数。分别计算前2个、3个和4个周期的阻尼系数,最后求其平均值作为阻尼系数ζ。
取前2个周期做计算,第1个峰值为0.075 7 m,第2个峰值为0.045 9 m,代入计算可得阻尼系数ζ1为0.0795。
取前3个周期做计算,第1个峰值为0.075 7 m,第3个峰值为0.026 2 m,代入计算可算得阻尼系数ζ2为0.0844。
取前4个周期做计算,第1个峰值为0.075 7 m,第4个峰值为0.015 7 m,代入计算可算得阻尼系数ζ3为0.0835。
求其平均数可得阻尼系数:
| $ \zeta = \frac{{{\zeta _1} + {\zeta _2} + {\zeta _3}}}{3} = 0.082\;5。$ |
采用FFT计算FDPSO的垂荡固有周期,选取图8(a)中前9个波峰对应的时间点,分别为:1.12 s,3.44 s,5.73 s,7.91 s,10.09 s,12.19 s,14.37 s,16.62 s,18.88 s,可得到其垂荡固有周期:
| $ T = 2.22\;{\rm{s}} 。$ |
曲志森以相同尺寸的FDPSO做水池实验,得到的阻尼系数为0.087,垂荡固有周期为2.29 s。通过本文的计算方法得到的阻尼系数与水池实验所得的阻尼系数仅相差5.17%,垂荡固有周期与水池实验所得的垂荡固有周期仅相差3.06%,验证了本文的计算思路和计算方法的可行性。
4 结 语本文分析圆筒型FDPSO的通海孔对计算其阻尼系数是否有影响,计算圆筒型FDPSO的垂荡固有周期,并对其垂荡衰减运动进行了数值模拟,通过数值计算结果分析其阻尼系数,得到以下结论:
1)南海海况谱峰周期通常在12~18 s之间[6],传统FDPSO的垂荡固有周期很难避开南海海况谱峰周期,通过计算,本文研究的圆筒型FDPSO垂荡固有周期为19 s,远离南海波浪能量集中范围,相较于传统FDPSO其运动性能得到较大改善。
2)通过理论公式推导和数值计算,得到有通海孔FDPSO和无通海孔FDPSO的垂荡等效质量相等,验证了通海孔对求解FDPSO阻尼系数几乎没有影响。
3)在尺寸一致的情况下,本文求解的阻尼系数与文献[5]水池实验得出的阻尼系数仅相差5.17%,垂荡固有周期仅相差3.06%,从实验角度也验证了本文思路和方法的正确性,为在求解阻尼时存在类似问题提供了一种分析思路。
| [1] |
王天英, 冯永训. 新概念FPSO最新研究进展[J]. 船海工程, 2011, 40(5): 184-188+192.
|
| [2] |
吴家鸣. FPSO的特点与现状[J]. 船舶工程, 2012, 34(S2): 1-4.
|
| [3] |
李茂. 南海西部海域边际油田开发浅谈[J]. 石油钻采工艺, 2007(6): 61-64.
|
| [4] |
谭家翔. 深水FPSO发展现状与趋势[J]. 船海工程, 2016, 45(5): 65-69+75.
|
| [5] |
曲志森. 新型FDPSO减动结构开发及运动响应分析[D]. 天津: 天津大学, 2018.
|
| [6] |
白杰, 李焱, 曲志森等. 新型圆筒型FPSO垂荡抑制结构优化设计[J]. 海洋工程, 2020, 38(1): 20-29.
|
| [7] |
唐友刚. 高等结构动力学[M]. 天津: 天津大学出版社, 2002.
|
| [8] |
盛振邦. 船舶静力学[M]. 北京: 国防工业出版社, 1979.
|
| [9] |
张玉龙, 李红霞, 王文华等. 船舶横摇阻尼确定方法研究[J]. 中国造船, 2015, 56(S1): 155-160.
|
| [10] |
GRANDMONT C, HILLAIRET M. , MATIN S, et al. Self-propelled motion of a rigid body inside a density dependent incompressible fluid*[J]. Mathematical Modelling of Natural Phenomena, 2021, 16.
|
| [11] |
沙毅. 流体力学[M]. 合肥: 中国科学技术大学出版社, 2016.
|
 2023, Vol. 45
2023, Vol. 45
