0 引　言

随着现代智能控制理论被广泛应用于各行各业，船舶控制研究也进入了智能控制时代。船舶运动控制是其中的核心问题，轨迹跟踪问题是船舶运动控制的基础，其含义是在所有控制时刻内使船舶达到对应时刻的参考位置。欠驱动水面船舶是远洋运输的重要船舶类型，其特点是船舶缺少侧推装置，仅依靠船尾推进装置提供的纵向推力和舵提供的旋转扭矩控制船舶运动^[1]。

在研究确定期望轨迹的轨迹跟踪问题时，Serret-Frenet坐标系（以下简称SF坐标系）是常用的一种坐标构建方法。其原理是在运动的每一时刻都在期望轨迹上建立一个随时间变化的坐标构架，构架的坐标原点及坐标轴方向均随曲线上期望点的移动而变化。齐雪等^[2]针对水下机器人的运动问题引入了SF坐标系，采用反步法，通过灵活设置虚拟路径上的参考点放宽了控制器的初始条件，提高了系统的鲁棒性。王宏健等^[3]结合SF坐标系对船舶轨迹跟踪进行研究，运用反步法设计了动力学控制器，使得航行器能够精准地跟踪曲线路径。王威等^[4]在SF坐标系下对智能车辆的路径跟踪问题进行了研究，运用模型预测控制，将速度设为定值，解决了控制延时的问题。综合上述文献可以看出，由于SF坐标系的建立具有时变特性，所以现有研究多结合反步法，而在模型预测控制当中难以解决预测问题，现有研究则选择了设置固定速度来简化速度控制精度的问题。

对USV的轨迹跟踪控制，经典控制方法有滑模控制、反步法（Backstepping）、神经网络法和模型预测控制法（model predictive control，MPC）等此外众多学者也在不断提出改进算法。张成举等^[5]基于反步法和自适应技术，提出一种非线性鲁棒轨迹跟踪控制策略，有效减小了反步法中虚拟变量直接求导的复杂性问题。葛科奇^[6]提出了一种动态神经模糊网络的水面欠驱动船舶运动控制算法，算法描述了船舶动力系统的受力特性，以黑箱形式模拟了船舶非线性模型，并对算法进行了仿真验证。相较而言，模型预测控制方法采用滚动优化机制，且能够显式处理约束，所以解决船舶运动非线性系统及多约束问题具有独特优势^[1]。轨迹跟踪控制算法在不断进步，但现有研究方向都聚焦于船舶位置控制的精度，而缺少对其航速控制效果的关注。本文提出一种Serret-Frenet坐标系下USV的时变参考状态轨迹跟踪模型预测控制方法。

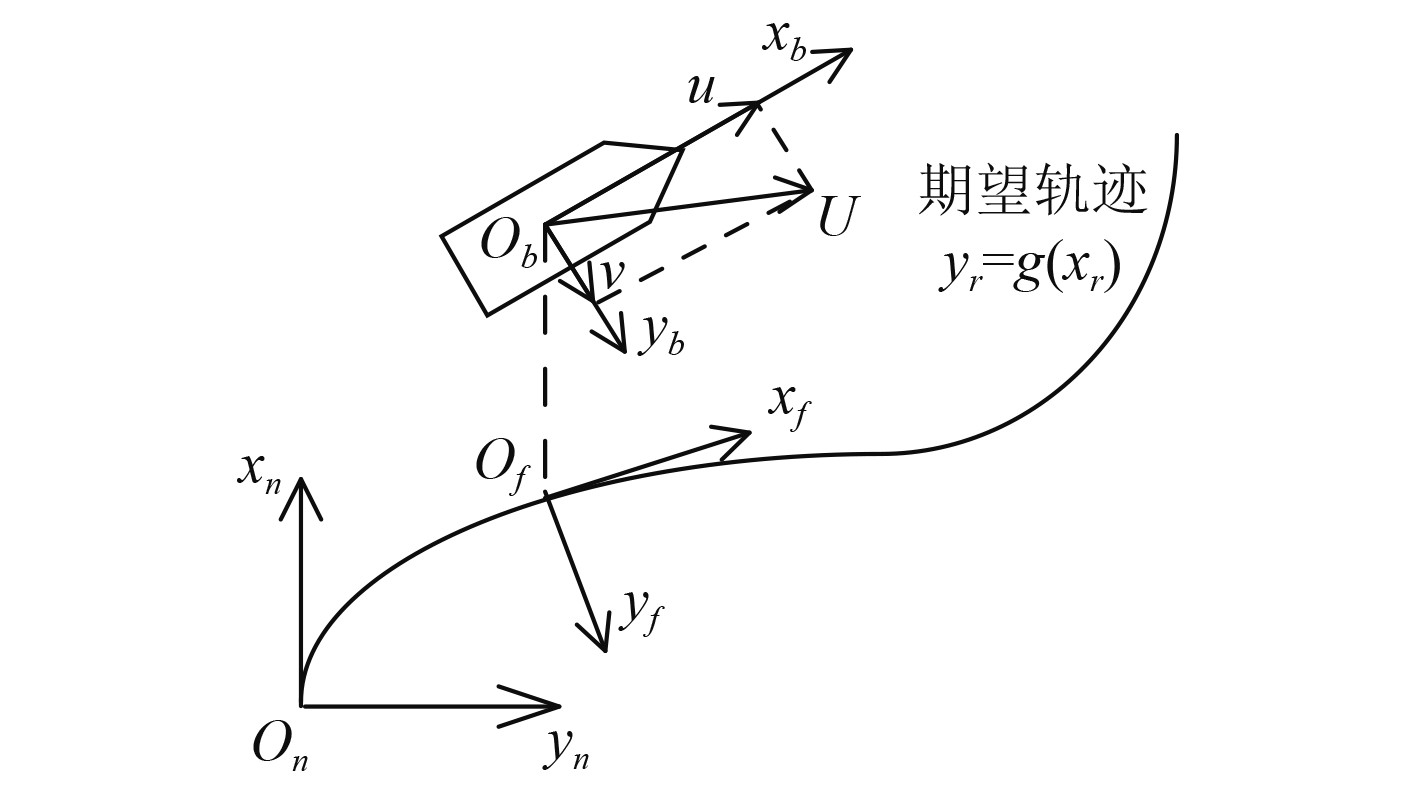
1 坐标系与模型

USV水面运动模型的建立需要依托相应的坐标系，通常运动学特征依托于惯性坐标系，记作 $ \left\{n\right\}= \left({x}_{n},{y}_{n}\right) $ ；动力学特征依托于附体坐标系，记作 $ \left\{b\right\}=\left({x}_{b},{y}_{b}\right) $ ，描述参考状态依托于SF坐标系，记作 $ \left\{f\right\}=\left({x}_{f},{y}_{f}\right) $ 。惯性坐标系定义为：原点 $ {O}_{n} $ 位于期望轨迹起点， $ {O}_{n}{x}_{n} $ 指向正北， $ {O}_{n}{y}_{n} $ 指向正东；附体坐标系定义为：原点 $ {O}_{b} $ 位于船舶重心， $ {O}_{b}{x}_{b} $ 沿船舶对称剖面指向船首， $ {O}_{b}{y}_{b} $ 指向右舷；SF坐标系定义为：原点 $ {O}_{f} $ 位于期望路径上当前时刻的目标参考点， $ {O}_{f}{x}_{f} $ 指向期望轨迹的切线方向， $ {O}_{f}{y}_{f} $ 指向垂线方向。水面坐标系关系如图1所示。

基于Fossen提出的船舶水动力建模方法构建欠驱动船舶的动力学模型，其状态空间方程表示为：

$ \dot{\mathit{x}}\left(t\right)=f(\mathit{x}\left(t\right),\mathit{u}\left(t\right),\mathit{e}(t\left)\right) 。$

(1)

式中： $ {{\boldsymbol{x}}}\left(t\right)={\left[x,y,\phi ,u,v,r\right]}^{\mathrm{T}} $ 为系统状态变量； $ {{\boldsymbol{u}}}\left(t\right)= {\left[{\tau }_{\mathrm{u}},0,{\tau }_{\mathrm{r}}\right]}^{\mathrm{T}} $ 为模型输入控制量； $ {{\boldsymbol{e}}}\left(t\right)={\left[{e}_{u},{e}_{v},{e}_{\mathrm{r}}\right]}^{\mathrm{T}} $ 设定为干扰； $ x,y,\phi $ 为船舶位置及首向； $ {\tau }_{\mathrm{u}},{\tau }_{\mathrm{r}} $ 分别为船尾推力及转向力矩； $ {e}_{u},{e}_{v},{e}_{\mathrm{r}} $ 分别为3个自由度上的干扰， $ f $ 表示映射关系，表示为：

$ \dot{\boldsymbol{x}}=\left[\begin{array}{c}{{\boldsymbol{T}}}\left({\boldsymbol{q}}_{1}{{\boldsymbol{x}}}\right)\\ {\boldsymbol{M}}^{-1}(-\boldsymbol{C}\left({\boldsymbol{q}}_{1}{{\boldsymbol{x}}}\right)-\boldsymbol{D}\left({\boldsymbol{q}}_{1}{{\boldsymbol{x}}}\right)+{{\boldsymbol{u}}}+{{\boldsymbol{e}}})\end{array}\right]，$

(2)

式中： $ \boldsymbol{M} $ 表示惯性矩阵； $ \boldsymbol{C} $ 表示科式向心矩阵； $ \boldsymbol{D} $ 表示阻尼矩阵，上述矩阵均由水动力导数构成，水动力导数可由经验公式法求得； $ \boldsymbol{T} $ 为坐标变换矩阵，用于附体坐标系下变量向惯性坐标系转化：

$ \boldsymbol{T}=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\psi \right)& -\mathrm{s}\mathrm{i}\mathrm{n}\left(\psi \right)& 0\\ \mathrm{s}\mathrm{i}\mathrm{n}\left(\psi \right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\psi \right)& 0\\ 0& 0& 0\end{array}\right] \text{，} $

$ {\boldsymbol{q}}_{1}=\left[\begin{array}{c}\begin{array}{ccc}0& 0& 0\end{array}\begin{array}{ccc}1& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}\begin{array}{ccc}0& 1& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\end{array}\begin{array}{ccc}0& 0& 1\end{array}\end{array}\right] 。$

现已知船舶期望轨迹表示为函数 ${{{y}}}_{{r}}=g\left({x}_{\mathrm{r}}\right)$ ，将船舶实际位置用其重心位置点Q表示，则Q点在惯性坐标系下坐标为（ $ x,y $ ）,同时定义其在SF坐标系下坐标为（ $ a,d $ ）；引入合速度 $ U=\sqrt{{u}^{2}+{v}^{2}} $ ，其与 $ {O}_{n}{y}_{n} $ 轴的夹角 $ \theta $ 表示为 $ \theta ={{\rm{tan}}}^{-1}\left(\dfrac{u}{v}\right)+\phi $ 。那么基于坐标可将轨迹跟踪问题的控制目标描述为以下两点：

1）控制船舶重心靠近期望点，即

$ \underset{k\to {i+N}_{p}}{\mathrm{lim}}\left(\left|a\left(k\right)\right|+\left|d\left(k\right)\right|\right)=0。$

(3)

式中： $ i $ 表示当前仿真时刻； $ {N}_{\mathrm{p}} $ 表示控制器预测步长。

2）控制船舶合速度方向趋近于期望轨迹在期望点的切线方向，切线方向通过对期望轨迹求一阶导数得到，即

$ \underset{k\to i+{N}_{p}}{\mathrm{lim}}\left(\theta \left(x\right(k\left)\right)-{tan}^{-1}\left(g{'}\left(x\right(k\left)\right)\right)\right)=0 。$

(4)

为了对曲线有更好的描述，建立从期望轨迹起点到当前期望点的弧长 $ s $ 对坐标 $ x $ 的变上限积分对应关系:

$ s=I\left(x\right)={\int }_{0}^{x}\sqrt{1+{g\text{'}}^{2}\left(x\right)}\mathrm{d}x 。$

(5)

利用式(5)可将式(3)和式(4)中的自变量 $ x $ 转换为 $ s $ 。

2 控制器设计 2.1 预测模型

为了减轻控制器计算负担，保证控制实时性，采用线性模型预测控制器。运用船舶运动模型作为控制器预测迭代模型，将模型代入控制器还需要对其进行线性化和离散化处理。

首先利用近似线性化方法对模型进行线性化处理，将任意时刻的船舶运动状态空间方程以上一控制时刻平衡点 $ {({\boldsymbol{x}}_{\mathrm{r}},\boldsymbol{u}}_{\mathrm{r}}) $ 作为参考点进行Taylor展开，并与平衡点做差，得到线性差值表达式如下：

$ \dot{\tilde{\boldsymbol{x}}}={{\boldsymbol{A}}}\left(t\right)\tilde{\boldsymbol{x}}+{{\boldsymbol{B}}}\left(t\right)\tilde{\boldsymbol{u}} ，$

(6)

式中： $\tilde{\boldsymbol{x}}={{\boldsymbol{x}}}-{\boldsymbol{x}}_{\mathrm{r}} $ ， $\tilde{\boldsymbol{u}}={{\boldsymbol{u}}}-{\boldsymbol{u}}_{\mathrm{r}} $ ， $ {{\boldsymbol{A}}}\left(t\right)={\left.\dfrac{\partial f}{\partial {\boldsymbol{x}}_{\mathrm{l}}}\right|}_{\begin{array}{c}x={\boldsymbol{x}}_{r}\\ u={\boldsymbol{u}}_{r}\end{array}} $ ， ${{\boldsymbol{B}}}\left(t\right)={\left.\dfrac{\partial f}{\partial {\boldsymbol{u}}_{\mathrm{l}}}\right|}_{\begin{array}{c}x={\boldsymbol{x}}_{r}\\ u={\boldsymbol{u}}_{r}\end{array}} $ 。

对其进行近似离散化，引入步长 $ {T}_{\mathrm{s}} $ ，则A，B变化可分步表示为：

$ \left\{\begin{array}{l}{\boldsymbol{A}}_{\mathrm{d}\mathrm{i}\mathrm{s}}\left(k\right)=I+{T}_{\mathrm{s}}A\left(k\right)，\\ {\boldsymbol{B}}_{\mathrm{d}\mathrm{i}\mathrm{s}}\left(k\right)={T}_{\mathrm{s}}B\left(k\right)。\end{array}\right. $

经过离散化后得到的预测模型为：

$ \tilde{\boldsymbol{x}}\left(i+k\right)={\boldsymbol{A}}_{\mathrm{dis}}\tilde{\boldsymbol{x}}\left(i+k-1\right)+{\boldsymbol{B}}_{\mathrm{dis}}\tilde{\boldsymbol{u}}\left(i+k-1\right)。$

(7)

式中： $ k=1,2,\cdots ,{N}_{p} $ 为预测步数。

2.2 参考量设计

设计控制系统参考量。首先需要在期望轨迹上找到每一控制时刻对应的期望点 $ {({x}_{\mathrm{e}},g(x}_{\mathrm{e}}\left)\right) $ ，选取船舶当前位置在期望轨迹上的投影点作为期望点，则其可通过求解方程得到：

$ \left(g\left({x}_{\mathrm{e}}\right)-y\left(i\right)\right)g'\left({x}_{\mathrm{e}}\right)=-({x}_{\mathrm{e}}-x(i\left)\right) 。$

(8)

引入对船舶的速度控制，将其设定为关于 $ s $ 的函数：

$ {v}_{\mathrm{r}}=h\left(s\right) ，$

(9)

则根据期望速度，期望点在期望轨迹上的弧长变化量可表示为下式：

$ \Delta s\left(k\right)={v}_{\mathrm{r}}{T}_{\mathrm{s}} 。$

(10)

在预测步长 $ {N}_{p} $ 内得到期望点惯性坐标序列为下式：

$\begin{split}& {\mathit{P}}_{1}\left(i\right)=\left[\begin{array}{c}\begin{array}{c}({x}_{\mathrm{p}1},\;{y}_{\mathrm{p}1})\\ ({x}_{\mathrm{p}k},\;{y}_{\mathrm{p}k})\end{array}\\ \dots \dots \\ ({x}_{\mathrm{p}{N}_{\mathrm{p}}},\;{y}_{\mathrm{p}{N}_{\mathrm{p}}})\end{array}\right]=\\ &\left[ \begin{array}{c}{(I}^{-1}\left(s\left(i\right)\right),\;g\left({I}^{-1}\left(s\left(i\right)\right)\right))\\ {(I}^{-1}\left(s\left(i\right)+\Delta s\left(k\right)\right),\;g\left({I}^{-1}\left(s\left(i\right)+\Delta s\left(k\right)\right)\right))\\ \dots \dots \\ \left({I}^{-1}\left(s\left(i + {N}_{\mathrm{p}} - 1\right) + \Delta s\left({N}_{\mathrm{p}}\right)\right),\;g\left({I}^{-1}\left(s\left(i + {N}_{\mathrm{p}} - 1\right) + \Delta s\left(k\right)\right)\right)\right)\end{array} \right]。\end{split}$

(11)

对应期望点坐标序列的合速度参考量序列由期望轨迹的一阶导数得到，表示为下式：

$ {\mathit{P}}_{2}\left(i\right)=\left[ \begin{array}{c}\begin{array}{c}{U}_{\mathrm{p}1}\\ {U}_{\mathrm{p}k}\end{array}\\ \dots \dots \\ ({U}_{\mathrm{p}{N}_{\mathrm{p}}},{U}_{\mathrm{p}{N}_{\mathrm{p}}})\end{array} \right]=\left[ \begin{array}{c}\begin{array}{c}{tan}^{-1}\left(g'({(I}^{-1}\left(s\left(i\right)\right)\right)\\ {tan}^{-1}\left(g'\left({(I}^{-1}\left(s\left(i+k\right)\right)\right)\right)\end{array}\\ \dots \dots \\ {tan}^{-1}\left(g'\left({(I}^{-1}\left(s\left(i+{N}_{\mathrm{p}}\right)\right)\right)\right)\end{array} \right]。$

(12)

2.3 目标函数及约束设计

为完成可变航速轨迹跟踪控制的目的，基于以下4个方面设置目标函数：

1）使预测到船舶位置点的投影点靠近期望点序列位置；

2）使船舶当前位置靠近期望点位置；

3）使船舶合速度方向靠近期望点的切线方向；

4）使控制系统输出控制量尽可能小。

由此设计的目标函数表示为：

$ \begin{split} J\left(i\right)=&\sum _{k=1}^{{N}_{\mathrm{p}}}{(\|x(i+k)-{x}_{\mathrm{p}k}\|}_{{Q}_{1}}^{2}+\|y(i+k)-\\ &{y}_{\mathrm{p}k}\|_{{Q}_{2}}^{2}+\|\theta (i+k)-{U}_{\mathrm{p}k}\|_{{Q}_{3}}^{2}+{\|{x}_{\mathrm{e}}-{x}_{\mathrm{p}k}\|}_{{Q}_{4}}^{2}+\\ &{\|{g(x}_{\mathrm{e}})-{y}_{\mathrm{p}k}\|}_{{Q}_{5}}^{2}+ \sum _{k=0}^{{N}_{\mathrm{c}}-1}{\|\mathit{u}(i+k)\|}_{\mathit{R}}^{2}。\end{split}$

(13)

式中： $ {Q}_{n}(n=\mathrm{1,2},\dots ,5) $ 和 $ \mathit{R} $ 为权值和权重矩阵； $ {N}_{\mathrm{c}} $ 为控制步长； $ \mathit{u} $ 为系统控制量。

通过目标函数的设置，可变航速的轨迹跟踪控制的优化问题转化为求解所设约束下目标函数最小值对应的控制量问题。依据禁止船舶倒航、动力机构性能设置约束条件为：

$ \left\{\begin{split}&u > 0，\\ &{\boldsymbol{u}}_{\min}\left(i+k\right)\leqslant {{\boldsymbol{u}}}\left(i+k\right)\leqslant {\boldsymbol{u}}_{\max}\left(i+k\right)，\\ & {\Delta \boldsymbol{u}}_{\min}\left(i+k\right)\leqslant \Delta \boldsymbol{u}\left(i+k\right)\leqslant \Delta {\boldsymbol{u}}_{\max}\left(i+k\right)。\end{split}\right. $

(14)

3 仿真实验 3.1 仿真模型

选择Cybership Ⅱ模型船作为研究对象^[7]，该船是一艘以1∶70的比例建造的补给船模型，其长度为 $ {L}_{\mathrm{C}}=1.255\;\mathrm{m} $ ，宽度为 $ {B}_{\mathrm{C}}=0.29\;\mathrm{m} $ ，最大推进力为2 N，最大推力下的平衡船速为0.58 m/s，最大转向力矩为 $1.5\;\rm{N}\cdot \rm{m}$ 。其对应矩阵 $ \boldsymbol{M} $ 和 $ \boldsymbol{D} $ 大小分别为：

$ \boldsymbol{M}=\left[\begin{array}{ccc}25.8& 0& 0\\ 0& 33.8& 1\\ 0& 1& 2.8\end{array}\right] \text{，} $

$ \boldsymbol{D}=\left[\begin{array}{ccc}0.72& 0& 0\\ 0& 0.89& 0.03\\ 0& 0.03& 1.9\end{array}\right] \text{。} $

3.2 控制器参数设置

期望轨迹函数及期望速度设置为：

$ {{y}}_{\mathrm{r}}=4\mathrm{s}\mathrm{i}\mathrm{n}\left(0.4{x}_{\mathrm{r}}\right) ，$

$ {v}_{\mathrm{r}}=0.1-0.005s。$

USV初始状态向量设置为：

$ {\mathit{x}}_{0}=[0 \quad 0.1 \quad \text{π}/4 \quad 0 \quad0\quad 0]^{\mathrm{T}} 。$

权重及权重矩阵设置为：

$ {Q}_{1}={Q}_{2}=10，$

$ {Q}_{3}={Q}_{4}=100，$

$ {Q}_{5}=3，$

$ \mathit{R}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right] 。$

根据所选船型的动力机构性能，将约束设置为：

$ u > 0$ (m/s)； ${\left[-\mathrm{2,0},-1.5\right]}^{\mathrm{T}}\leqslant {{\boldsymbol{u}}}\left(i+k\right)\leqslant {\left[\mathrm{2,0},1.5\right]}^{\mathrm{T}}\left(\mathrm{N}\right) $ ； $ {[-\mathrm{0.7,0},-0.5]}^{\mathrm{T}}\leqslant \Delta \mathit{u}\left(i+k\right)\leqslant {\left[\mathrm{0.7,0},0.5\right]}^{\mathrm{T}}\left(\mathrm{N}\right) $ 。

预测步长和控制步长设置为：

$ {N}_{\rm{p}}={N}_{\rm{c}}=10\text{，} {T}_{\rm{s}}=1\rm{s} \text{，} $

基于风、浪、流等设置随机干扰：

$ \mathit{e}\left(i\right)=\left[\begin{array}{c}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(-\mathrm{0.1,0.1}\right)\\ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(-\mathrm{0.1,0.1}\right)\\ \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(-\mathrm{0.1,0.1}\right)\end{array}\right]\left(\mathrm{N}\right) 。$

式中， ${\rm{rand}}i(\cdot)$ 表示均匀分布的随机整数。

3.3 结果分析

对USV运动进行210步仿真，以文献[1]所用轨迹跟踪方法作为实验对比组，将每一仿真时刻的期望点惯性坐标序列 $ {\mathit{P}}_{1}\left(i\right) $ 以及期望速度序列 $ {\mathit{P}}_{2}\left(i\right) $ 的第一项组合成矩阵 $ {\mathit{P}}_{210\times 2} $ ，并将 $ \mathit{P} $ 作为文献[1]所用方法的参考量矩阵，其余参数均与本文方法设置相同。得到的运行对比结果如图2～图5所示。

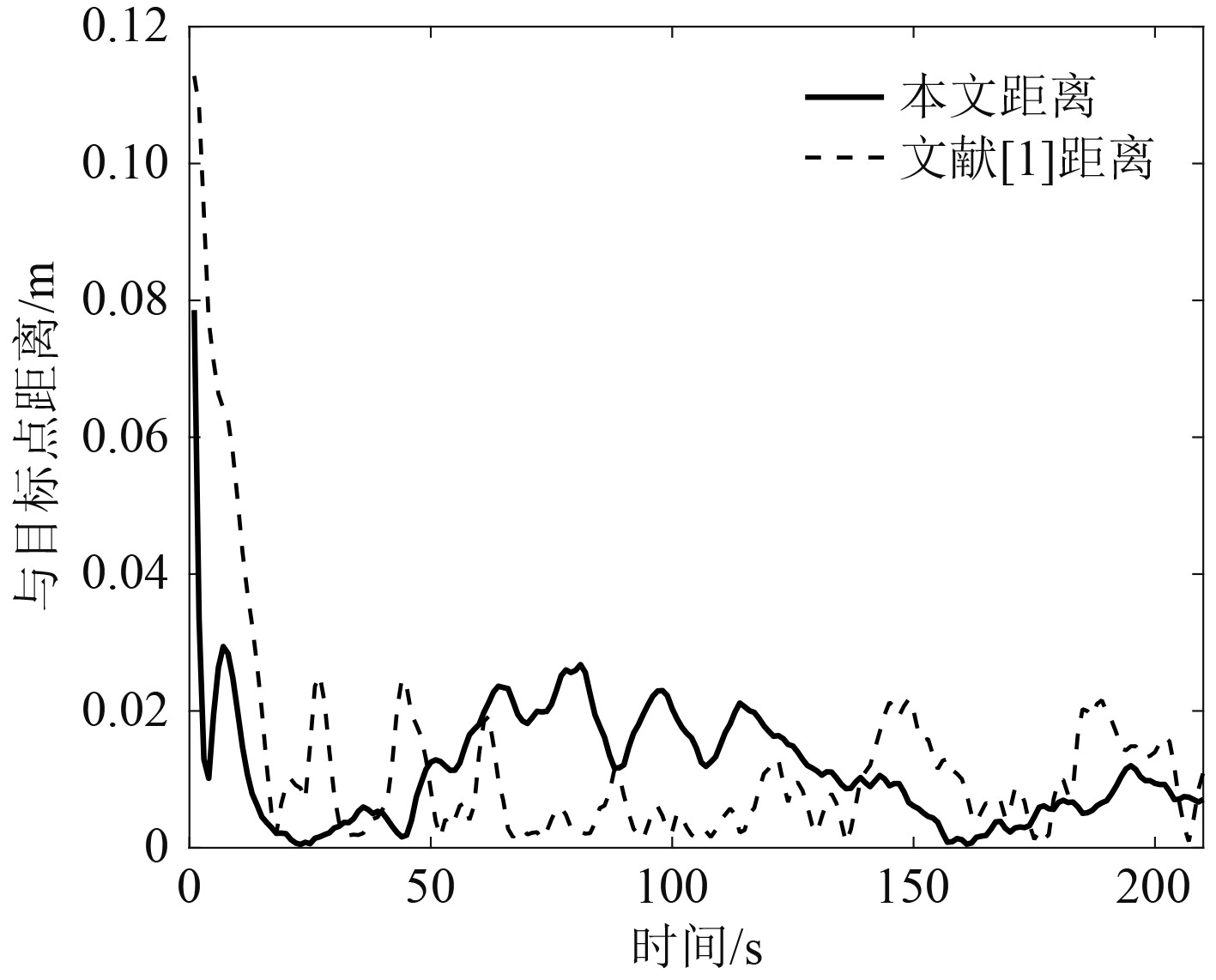
由图2和图3可知，本文设计的控制方法良好地完成了轨迹跟踪任务，初始位置与期望轨迹的偏差使得USV在航行初与投影点存在较大距离，20 s后能够与期望轨迹贴合，此后仿真过程最大距离为0.023 m，与对比组进行对比可以看出，本文方法在调整初始位置误差时，超出量更少且收敛速度更快，但总体而言，2种方法位置点与目标点的距离保持能力相差不大。由图4可以看出，USV航速从0 m/s开始，经过15 s后能够跟随期望航速曲线，此后在干扰的作用下有小幅的波动，对比组表现出的航速波动大，本文方法具有更好的航速控制效果。由图5可以看出，轨迹跟踪初期，控制器输出较大推力以追逐期望曲线，在完成追逐后迅速保持较小的控制输出，输出推力和转矩均由随干扰的小幅度震荡，相较而言，干扰对扭矩输出的影响更为明显，对比而言，本文提出的控制方法控制量的波动较小，控制更为稳定。

4 结　语

本文以Serret-Frenet坐标系为基础，建立USV三自由度运动模型，针对轨迹跟踪航速时变控制问题，提出了一种基于模型预测控制算法的USV轨迹跟踪控制方法，通过仿真得到的结论如下：

1）在Serret-Frenet坐标系下利用投影法寻找当前船舶位置在期望轨迹上对应的期望点；

2）引入随航行路程而变的期望速度，用对应控制时刻的期望速度构建参考位置序列作为系统参考量；

3）控制方法对USV轨迹跟踪和速度控制均有良好的效果。本文设计的控制方法可为USV航行行为控制提供参考。