舰船的工作环境非常恶劣,不仅要承受海上的波浪冲击载荷和船体内部机械设备的振动等载荷,还需要具有一定的抗撞击能力,因此舰船的主体结构需要采用优质的高强度钢材,如Q460等[1]。通常,舰船机械结构的失效形式有以下几种:
1)极限载荷下的塑性屈服或者屈曲变形
这种载荷往往出现在舰船发生碰撞、搁浅、水下爆炸等事故时,此时的冲击载荷会对船体钢材结构产生破坏效果。
2)疲劳载荷损伤
舰船结构长期处于振动等疲劳载荷工况下,材料会在载荷作用下产生裂纹损伤,随着疲劳载荷的不断施加,裂纹损伤会进一步扩展,最终导致船体机械结构的断裂。
大量的统计数据表明,高强度钢材的裂纹扩展失效是主要的失效形式[1],因此,从线弹性力学和断裂力学的角度出发,结合疲劳损伤理论,进行舰船高强度钢材结构的裂纹分析和力学特性评估,并结合有限元仿真软件Ansys进行钢材的力学特性仿真分析。
1 舰船高强度钢材的线弹性力学与断裂力学分析高强度钢材的静强度特性很好,相对应的在抵抗极限冲击载荷作用时,不容易发生失效,因此疲劳断裂是高强度钢材发生失效的主要形式,其原因多为结构内部的缺陷在疲劳载荷下发生裂纹,且裂纹逐渐扩展,形成断裂。
高强度钢的裂纹形式分为3种[2],裂纹长度用2a表示,深度方向用2c表示,宽度用B表示,图1为高强度钢材3种裂纹形式的示意图。

|
图 1 高强度钢材3种裂纹形式的示意图 Fig. 1 Schematic diagram of three crack forms of high-strength steel |
根据弹性力学理论,对于含有长度为2a裂纹的平板,垂直于裂纹面的拉应力
| $ {\sigma _{ij}} = \frac{{{K_1}}}{{\sqrt {2\text{π} r} }}{\phi _i}(\theta ) 。$ |
式中:
| $ {K_1} = \sigma \sqrt {\text{π} a} f(a,W, \cdots ) \text{,} $ |
式中:
断裂力学研究表明,材料的应力强度因子与裂纹尺寸、材料韧性等共同决定了材料是否会发生断裂,断裂时的应力强度因子用
在线弹性条件下,材料的断裂韧性
| $ {K_c} = \sigma \sqrt {\text{π} a} f\left(\frac{a}{W}, \cdots \right) 。$ |
对于结构中裂缝的任意一点
| $ \begin{gathered} {\sigma _p} = \frac{1}{{2\text{π} }}{\left( {\frac{{{K_1}}}{{{\sigma _w}}}} \right)^2} ,\\ {\delta _p} = \frac{1}{{2\text{π} }}{\left( {\frac{{{K_1}}}{{{\sigma _{\text{w}}}}}} \right)^2}{(1 - 2v)^2} 。\\ \end{gathered} $ |
式中:
当结构受到的应力为恒力
| $ R=\frac{1}{\alpha \text{π} }{\left(\frac{{K}_{1}}{{\sigma }_{H}}\right)}^{2},\alpha =\Bigg\{\begin{array}{l}1\text{,}应力,\\ 2\sqrt{2}\text{,}应变。\end{array} $ |
在线弹性条件的假定下,材料的裂纹扩展与材料的应力强度因子有关,只有当裂纹尺寸相对于塑性变形尺寸较小时,断裂力学才受到限制。
定义高强度钢的裂纹扩展速率为
| $ \Delta K = {K_{\max }} - {K_{\min }} \text{。} $ |

|
图 2
裂纹扩展速度与
|
对于小裂纹的疲劳扩展,需要利用弹塑性断裂力学分析。
将整个裂纹扩展分为低速、中速和高速3个区域:
1)低速扩展区域
在该区域内,裂纹扩展速率
2)中速扩展区域
在该区域内,裂纹扩展速率
3)高速扩展区域
在该区域内,裂纹扩展速率
针对船舶高强度钢结构的裂纹失效特性,将舰船结构的疲劳载荷分布划分为连续型正态/瑞利分布和连续型威布尔分布2种。
1)连续型正态/瑞利分布
高强度钢材受到的连续型瑞利分布载荷以风浪载荷为主,建立风浪载荷的正态分布概率密度函数为:
| $ F(\zeta ) = \frac{1}{{\sqrt {2\text{π} {\sigma _x}} }}\exp \left[ { - \frac{{{{\left( {\zeta - {\mu _x}} \right)}^2}}}{{2\sigma _x^2}}} \right] 。$ |
式中:
当波浪载荷的瞬时值服从正态分布,峰值服从瑞利分布时,建立其概率密度函数为:
| $ f(y) = \frac{{2y}}{R}\exp \left[ { - \frac{{{y^2}}}{R}} \right],0 \leqslant y < + \infty 。$ |
式中:
波浪载荷的连续型正态/瑞利分布曲线如图3所示。

|
图 3 波浪载荷的连续型正态/瑞利分布曲线图 Fig. 3 Continuous normal/Rayleigh distribution curve of wave loading |
2)连续型威布尔分布
大量的实测数据表明,舰船的浪涌载荷在长期情况下可用威布尔分布表示,威布尔分布的概率和概率密度函数如下式:
| $ \begin{gathered} F(\Delta \sigma ) = 1 - \exp \left[ { - {{\left( {\frac{{\Delta \sigma }}{q}} \right)}^h}} \right]0 ,\leqslant \Delta \sigma < + \infty ,\\ f(\Delta \sigma ) = \frac{h}{q}{\left( {\frac{{\Delta \sigma }}{q}} \right)^{h - 1}}\exp \left[ { - {{\left( {\frac{{\Delta \sigma }}{q}} \right)}^h}} \right]0,\leqslant \Delta \sigma < + \infty 。\\ \end{gathered} $ |
式中:q和h为威布尔分布的尺度参数和形状参数。
浪涌载荷的连续型威布尔分布曲线如图4所示。
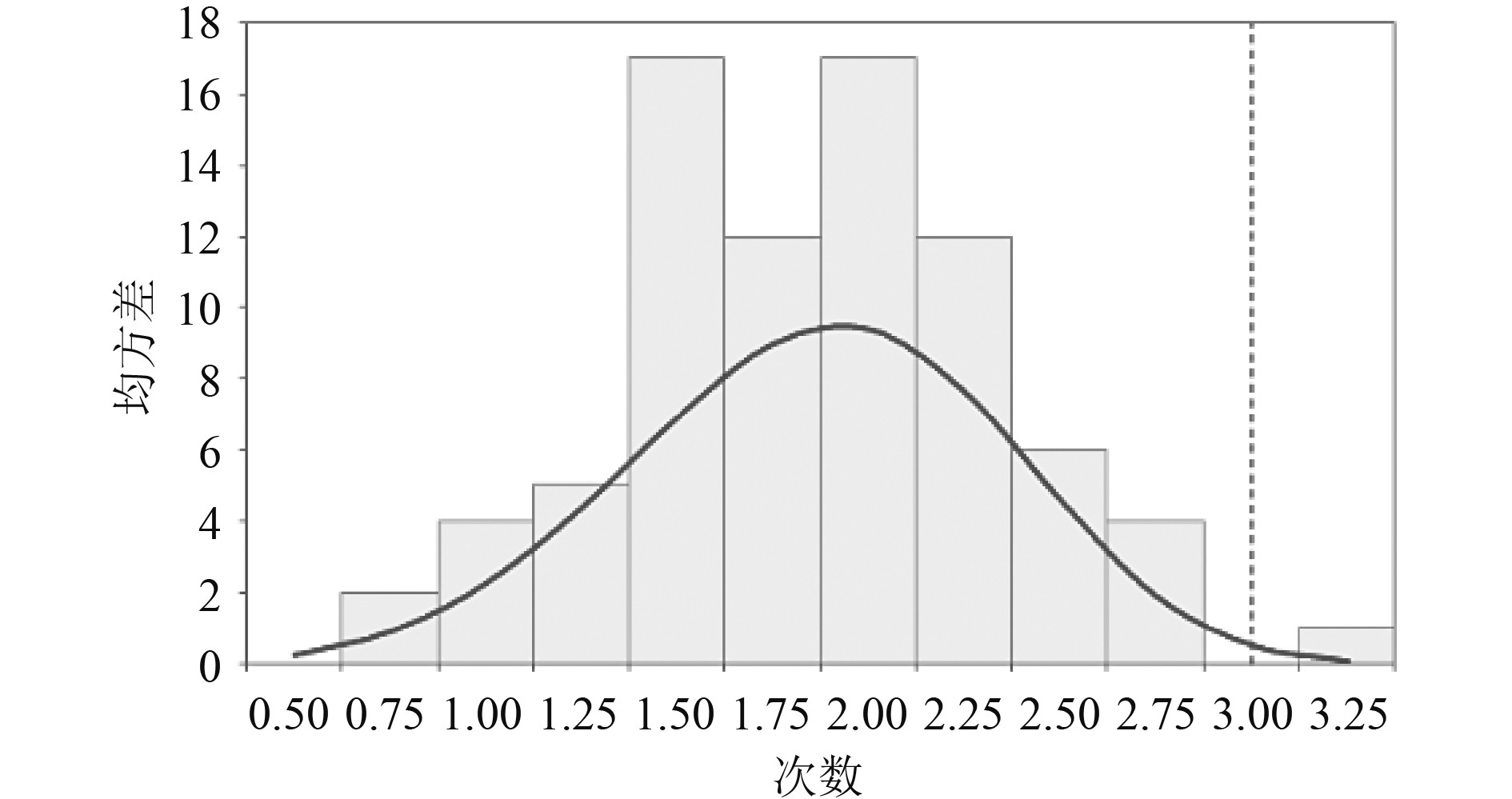
|
图 4 浪涌载荷的连续型威布尔分布曲线 Fig. 4 Continuous Weibull distribution curve for surge loads |
舰船高强度钢结构在疲劳载荷的作用下发生裂纹扩展和断裂,因此,需要建立高强度钢结构的疲劳载荷特性。
P-miner线性累积损伤理论[4]是目前针对疲劳载荷常用的一种评估方法,定义应力为
| $ {D_i} = \frac{{{n_i}}}{{{N_i}}} \text{。} $ |
假设结构承受了K级应力,则根据P-miner线性累积损伤理论,得到结构的总损伤为:
| $ D = \sum\limits_{i = 1}^k {} \frac{{{n_i}}}{{{N_i}}} \text{。} $ |
当D<1时,证明材料在该疲劳载荷下不发生失效。
定义舰船高强钢的材料S-N曲线如图5所示。

|
图 5 舰船高强钢的材料S-N曲线 Fig. 5 Material S-N curve of ship high-strength steel |
结合疲劳损伤理论和静强度理论,对舰船高强度钢材的力学特性进行仿真分析,主要分为以下环节:
1)有限元模型建立
选取舰船船舱腹板的高强度钢结构为分析对象,以船舶的质心为坐标系原点,采用六面体单元进行建模,有限元模型共包括25489个六面体单元,结构材料为Q460,材料的力学特性如表1所示
|
|
表 1 Q460力学特性表 Tab.1 Q460 mechanical characteristics table |
有限元模型示意图如图6所示。

|
图 6 舰船高强度钢结构的有限元模型 Fig. 6 Finite element model of high-strength steel structure of ships |
2)加载和求解
将多个疲劳载荷工况进行耦合,定义结构的自重为500 kg,载荷曲线为:
| $ {F_s} = {P_0}{\beta _z}{\chi _0}K 。$ |
式中:
在Ansys中得到舰船高强度钢结构的强度特性仿真如图7所示。

|
图 7 舰船高强度钢结构的强度特性仿真结果 Fig. 7 Simulation results of strength characteristics of high-strength steel structure of ships |
本文从断裂力学和疲劳累积损伤角度对舰船高强度钢结构进行力学分析,阐述了钢材裂纹扩展和断裂的原理,结合Ansys进行了舰船高强度钢结构的强度特性仿真。
| [1] |
张宇, 李大永, 唐伟琴. 高强钢电阻点焊TS试样疲劳寿命预测[J]. 机械强度, 2016, 38(5): 962-966. ZHANG Yu, LI Da-yong, TANG Wei-qin. Fatigue life prediction of TS specimen with high strength steel resistance spot welding[J]. Mechanical Strength, 2016, 38(5): 962-966. DOI:10.16579/j.issn.1001.9669.2016.05.011 |
| [2] |
辛克贵, 郭佳, 何铭华. 高强钢的应力强度因子分析[J]. 清华大学学报(自然科学版), 2010, 50(12): 1901-1905. XIN Ke-gui, GUO Jia, HE Ming-hua. Stress intensity factor of high strength steel Journal of Tsinghua University(Natural Science Edition), 2010, 50(12): 1901-1905. |
| [3] |
褚武扬, 姚玉琴, 林实, 等. 高强钢螺桩应力腐蚀断裂研究[J]. 中国腐蚀与防护学报, 1982(1): 18-26+68-69. CHU Wu-yang, YAO Yu-qin, LIN Shi, et al. Study on stress corrosion fracture of high strength steel screw pile[J]. Journal of Chinese Society for Corrosion and Protection, 1982(1): 18-26+68-69. |
| [4] |
钟勇. 断裂力学在一些单位的应用情况介绍[J]. 冶金建筑, 1978(1): 70. ZHONG Yong. Introduction to the application of fracture mechanics in some units[J]. Metallurgical Construction, 1978(1): 70. |
 2023, Vol. 45
2023, Vol. 45
