2. 兰州理工大学石油化工学院,甘肃 兰州 730050
2. School of Petrochemical Engineering, Lanzhou University of Technology, Lanzhou 730050, China
三通流量调节阀作为工艺管路中重要的控制元件,在船舶系统各领域有着广泛的应用。为实现调节阀流量调节的准确性,对其流量特性特别是流量系数的研究尤为重要。
随着(计算流体力学 (Computational fluid dynamics, CFD) 计算方法的发展,数值模拟已经成对阀门内部流动研究的一种重要方法。国内外很多研究人员对阀内流动特性进行数值模拟,并与试验结果进行了对比,证明了模拟的精确性[1~5]。Tao等[6]研究了不同V型角度对调节阀性能和内部流动特性的影响,发现无论是V角还是阀门开度的增加,都会导致阀门出口附近出现较大的压力波动,从而导致较长的压力稳定距离。Gao等[7]对原有V型调节阀进行了改进,结果表明改进后流量系数与附加间隙的流量截面积近似线性关系,满足了特殊工况的可调性。章茂森等[8]采用CFD数值模拟方法对典型工况下的三通调节阀的内部流动进行了分析,研究发现阀芯节流锥面可以降低阀门内部湍动能和耗散率,有利于介质流动的稳定性。李树勋等[9]采用遗传算法对三通调节阀节流盘开口型线进行了优化,并通过CFD与试验相结合的方法验证了优化后的流量调节特性满足要求。现有文献对三通阀主、旁通流量特性的研究较少,且大多为标准低压工况,目前仍缺少对高压工况下三通调节阀流量特性的研究。
因此,本文以PN50 DN250船用三通流量调节阀为研究对象,采用 CFD数值模拟方法对其低、高压工况下流量特性进行数值模拟、求解修正流量系数。基于结合流态变化的高、低压流量系数对比分析,提出了一种修正低压试验工况流量系数得到高压实际工况下流量系数的方法。通过高压工况下的主旁通流量特性试验,验证了该方法的精度。
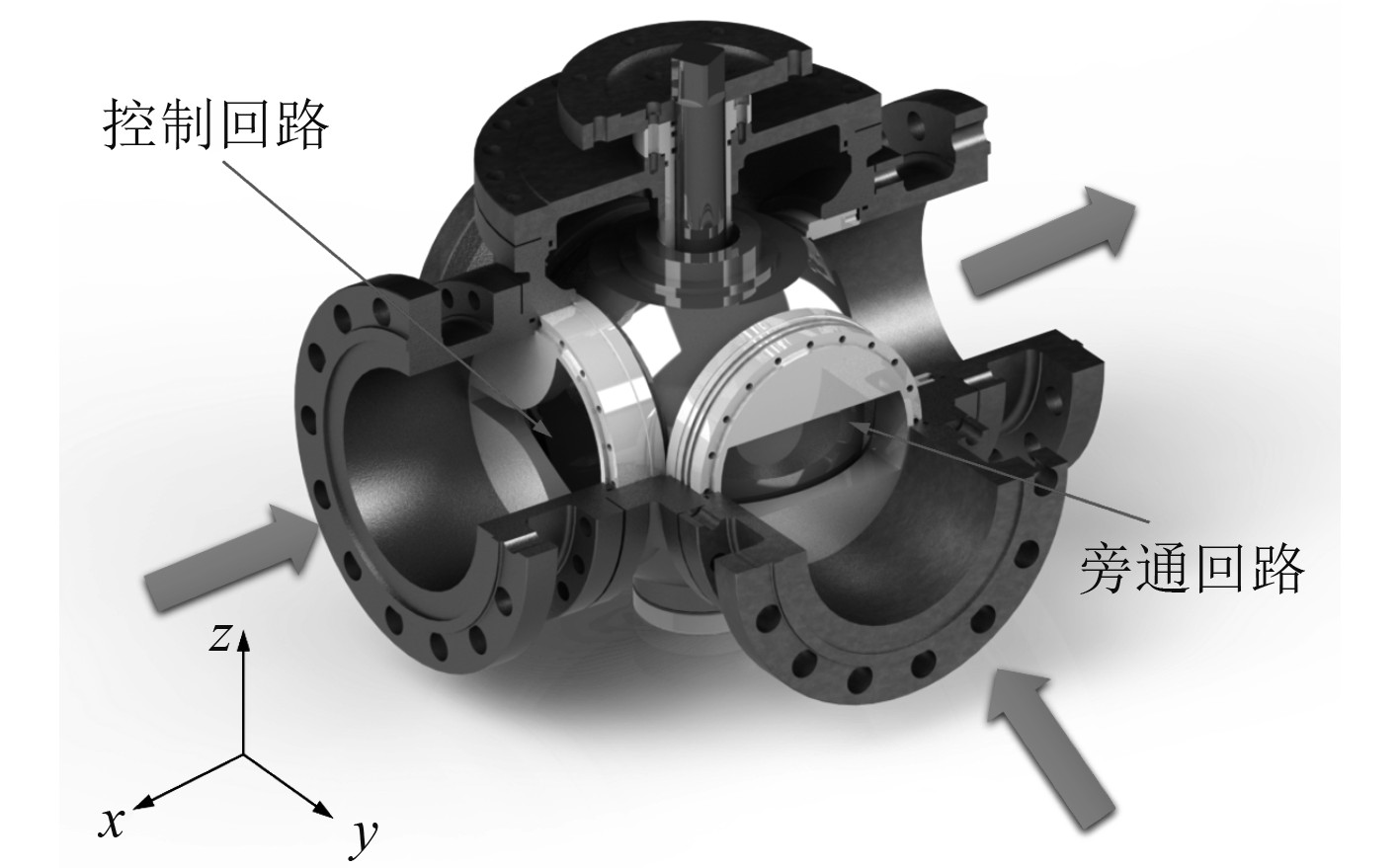
1 结构原理本文研究的PN50 DN250三通调节球阀主要由阀体、阀杆、阀盖、球芯、节流盘、底座等组成,调节精度高、结构紧凑、动作稳定可靠等特点。其中,主控制回路与旁通回路分别安装了带有特殊开口形状的节流盘,以满足流量特性调节要求,在流量变化范围内实现连续、稳定、精确调节[10]。其三维结构模型如图1所示。
|
图 1 DN250三通调节阀三维模型 Fig. 1 3D model of DN250 three-way regulating valve |
调节阀的流量特性分为快开流量特性、线性流量特性、等百分比流量特性和抛物线流量特性4种[11],不同阀门流量特性曲线如图2所示。

|
图 2 不同阀门流量特性曲线 Fig. 2 Flow characteristic curve of different valves |
可知,不同流量特性的阀门开度与流量之间的变化关系不同。本文研究的DN250三通调节阀,其主控制回路与旁通回路分别需要满足等百分比流量调节特性和等线性流量调节特性的要求。其中线性流量特性阀门流量与开度为直线关系,而等百分比型阀门回路流量特性在小开度时流量变化较慢,大开度下流量变化快。
3 三通调节阀流场的数值模拟 3.1 计算模型根据三维模型建立流道模型。分别取三通调节阀前后管段长度5倍和10倍的公称直径,使流场充分发展。将三维模型导入Ansys Workbench DM中反向建模生成三通调节阀主控制回路和旁通回路三维内部流道模型。
3.2 网格划分三通调节阀流道模型网格由Ansys Workbench Mesh软件划分生成,采取不均匀网格划分策略使计算结果更加精确。主控制回路全开和旁通回路全开的网格结构如图3和图4所示。

|
图 3 主控制回路流道网格 Fig. 3 Main control loop runner grid |

|
图 4 旁通回路流道网格 Fig. 4 Bypass loop runner grid |
模拟计算中流量值是求解的重要结果,因此选取计算流量值为目标进行网格无关性检验。在压差为100 kPa的边界条件下,计算3种不同网格的流体流量值,如表1所示。
|
|
表 1 三通调节阀阀网格无关性检验 Tab.1 Grid independence test of three-way regulating valve |
可知:从网格1到网格2流量的变化值为0.47%,从网格2到网格3流量的变化值为0.19%,流量变化值很小。因此在考虑模拟计算精度、时间成本和工作量的情况下,最终确定三通调节阀流道全开网格节点数为549956,单元数为1458569。
3.3 边界条件及数值计算方法流体流动遵循纳维斯托克斯方程(N−S),对于可压缩粘性流体流动求解应用的控制方程如下:
质量守恒方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w} \right)}}{\partial z} = 0 ,$ | (1) |
动量守恒方程
| $ \frac{{\partial \left( {\rho u} \right)}}{{\partial t}} + \nabla \left( {\rho uu} \right) = - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + {F_x},$ | (2) |
| $ \frac{{\partial \left( {\rho v} \right)}}{{\partial t}} + \nabla \left( {\rho vu} \right) = - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} + {F_y} ,$ | (3) |
| $ \frac{{\partial \left( {\rho w} \right)}}{\partial t} + \nabla \left( {\rho wu} \right) = - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} + {F_z} ,$ | (4) |
能量守恒方程
| $ \frac{{\partial \left( {\rho T} \right)}}{{\partial t}} + \nabla \left( {\rho uT} \right) = \nabla \left( {\frac{k}{{{c_p}}}gradT} \right) + {S_T} 。$ | (5) |
分别选取高压实际工况海水和低压试验工况标准大气压下常温淡水作为模拟介质,其进出口边界条件如表2和表3所示。
|
|
表 2 双回路实际工况模拟计算边界条件 Tab.2 Boundary conditions for simulation calculation of actual operating conditions of two loops |
|
|
表 3 低压工况下模拟计算边界条件 Tab.3 Boundary conditions of simulation calculation under low pressure condition |
采用Fluent仿真软件对三通调节阀阀内流场进行模拟计算,分别对三通调节阀主控制回路和旁通回路的每一个典型开度(10%,20%,30%,…,100%)进行CFD数值模拟计算,当残差曲线达到收敛值且监测的变量保持不变时,计算结束。以RANS方程为流体流动基本控制方程,采用无滑移壁面边界条件,在近壁面区采用标准壁面函数,以标准k−ε双方程为湍流模型,通过SIMPLE算法进行流场的速度及压力的求解并对入口流量和出口流量进行监测。
3.4 数值计算结果分析选取低压试验工况100%,80%和60%开度3个常用开度为例,对三通调节阀低、高压的控制回路和旁通回路的流动状况进行分析。分别对每个开度下的压力场及流线分布进行后处理可视化,以分析三通调节阀真实的流动状况。
低压试验工况下三通调节阀主、旁通回路流动信息如图5和图6所示。分析可知三通调节阀主、旁通回路流量特性有着相同的变化规律:阀前压力和速度分布均匀,流动平稳;随着流体流经节流件,速度逐渐增大,流线开始紊乱,伴随有涡流的出现;节流件后出现局部低压区,出口处压力分布均匀,流速也逐渐平稳。随着阀门开度的减小,流线紊乱程度增大。

|
图 5 低压工况不同开度下三通调节阀主控制回路流场图 Fig. 5 Flow field diagram of control loop of three-way regulating valve with different openings under low pressure condition |

|
图 6 低压工况不同开度下三通调节阀旁通回路流场图 Fig. 6 Flow field diagram of bypass loop of three-way regulating valve with different openings under low pressure condition |
高压实际工况下三通调节阀主、旁通回路流动信息如图7和图8所示。分析可知,高压工况下的压降要大于低压工况,且随着开度的减小,压降逐渐增大。相同开度下,旁通回路压降大于主控制回路压降。主控制回路80%开度下的压降就已经达到了170 kPa旁通回路60%开度时,压降更是达到了310 kPa,远大于标准规定的100 kPa压差。

|
图 7 高压工况不同开度下三通调节阀主控制回路流场图 Fig. 7 Flow field diagram of the main control loop of the three-way regulating valve under different opening degrees under high pressure conditions |

|
图 8 高压工况不同开度下三通调节阀旁通控制回路流场图 Fig. 8 Flow field diagram of the bypass loop of the three-way regulating valve under different opening degrees under high pressure conditions |
流量系数Kv计算公式为:
| $ {K_V} = \frac{Q}{{{N_1}}}\sqrt {\frac{{{{{\rho _1}}/{{\rho _0}}}}}{{\Delta P}}} 。$ | (6) |
式中:Q为被测体积流量,m3/h;ΔP为阀门的静压差,kPa;N1为数学常数,10×10−1;ρ1为流体的密度,单位kg/m3;ρ0为15℃时的水密度,kg/m3,水在常温时,取ρ1/ρ0的值为1。
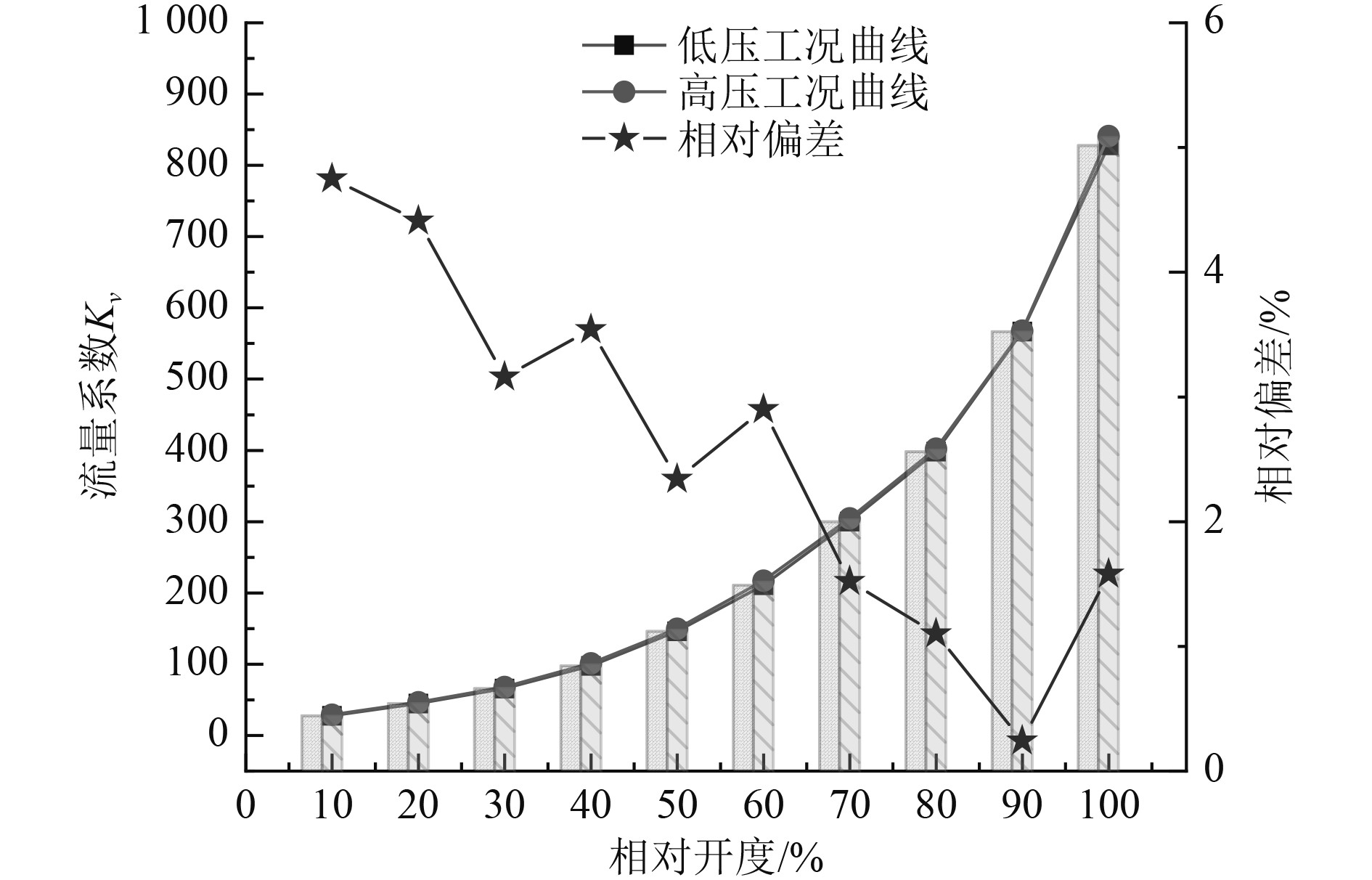
通过式(6)对由CFD模拟计算得到的DN250三通调节阀高、低压试验工况流量系数并求解2种工况模拟结果的相对偏差如图9和图10所示。
|
图 9 主控制回路流量系数模拟曲线 Fig. 9 Simulation curve of flow coefficient of main control loop |

|
图 10 旁通回路流量系数模拟曲线 Fig. 10 Simulation curve of flow coefficient of bypass loop |
可以看出,模拟得到的高、低压工况流量系数有所偏差,主控制回路和旁通回路流量系数模拟值最大偏差不超过6%,且开度越小,偏差越大。这是由于高压实际工况下的压力、压差很大,流体由不可压缩转变为可压缩,密度、粘度等流体特性发生改变,雷诺数增大,流体流态发生改变。此时测得的流量特性不再与其固有的流量特性完全相符,因此需要对低压工况下试验测得的流量系数进行修正。
4.2 流量系数修正方法在较低压下,三通阀内开始的流动状态为层流可视为理想流动,阀内流体随着压降的增大,导致边界层受到破坏,流动方式也开始发生转变。从流量−压差特性出发,结合试验研究和理论分析,研究从较低压差下得到的三通调节阀主控制回路、旁通回路的理想流量特性换算在实际工作压力下三通调节阀主控制回路、旁通回路的工作流量特性。
根据伯努利方程:
| $ {L_{corr}} = 10\lg \left( {{{10}^{{{{L_{{\text{meas}}}}} / {10}}}}-{{10}^{{{{L_{{\text{resid}}}}} / {10}}}}} \right) ,$ | (7) |
流体由静止状态经阀门流道至出口时,入口处的压力能全部转换为出口处的动能,即压力损失转换为出口的速度头,可得:
| $ {v_2} = \sqrt {\frac{{2\left( {{p_2} - {p_1}} \right)}}{\rho }}。$ | (8) |
式中:H1和H2分别为流道入口、出口的压头,m;p1和p2分别为入口、出口的压力,Pa;g为重力加速度,取9.8 N/kg;v1,v2分别为入口、出口的流速,m/s;ρ为流体密度,kg/m3。
雷诺数是一种可用来表征流体流态变化情况的无量纲数:
| $ R{e_v} = \rho vd/\eta 。$ | (9) |
式中:v为流体的流速,m/s;ρ为流体的密度,kg/m3;η为流体黏性系数,d为管径尺寸,m。
根据式(9)计算不同流态时的流量系数:
| $ {K_{v,req}} = {F_R}\cdot{K_v}。$ | (10) |
式中:Kv,req为阀门在某一紊流状态时的流量系数;FR为低压试验工况与高压实际工况的修正系数。
每个开度的修正系数为:
| $ {F_R} = 1 + e 。$ | (11) |
式中,e为高压工况与低压试验工况模拟结果的相对偏差,此相对偏差与雷诺数Rev有关,故式(11)可以写为:
| $ {F_R} = 1 + e\left( {R{e_v}} \right) 。$ | (12) |
利用式(6)求得Kv后代入式(10),得到实际工作压力下的流量:
| $ {K_{v{\text{,req}}}} = F{}_R \times 10 \times Q \times \sqrt {\frac{\rho }{{\Delta {p_v} \times {\rho _0}}}}。$ | (13) |
式中:Q为测得的介质流量,m3/h;Δpv为被试验阀门的净压差,kPa;ρ为介质密度,kg/m3;ρ0为15℃的水密度,kg/m3。
5 试验与验证 5.1 试验为验证修正后的流量系数的精确性,针对现行国际、国内标准[12]没有明确给出三通调节阀流量特性试验方法和高压下流量调节阀的流量特性试验方法,结合三通调节阀特点和相关标准开展三通调节阀流量特性试验。试验时,对三通调节阀2个回路分别进行试验:控制回路类似于一台直通式阀门,其流量特性试验以直通式试验方法进行测试;旁通回路类似于一台角通式阀门,其流量特性试验以角通式试验方法进行测试。
被测三通调节阀安装于标准试验管段上,分别在阀前2倍和阀后6倍阀门公称直径处[13]设置取压口。上下游节流阀共同作用控制试验段前后的压差,并使下游压力保持一个特定值。试验时通过安装在取压口的压力传感器读取试验段前后的压差,通过流量仪表读取对应流量,经过多次试验后得到被测阀门不同开度下的压差及流量,依据调节阀流通能力试验标准处理试验数据即可得到对应开度下的流量系数。
试验具体步骤如下:
步骤1 将被测阀门固定在试验管路中,调试电装,排除可能发生的运行故障及安全隐患。
步骤2 为保证试验过程中管道内介质充满管路,试验管路内无残留的空气,控制系统的变频泵频率为40 Hz(调节范围为0~60 Hz),让流量试验系统稳定运行一段时间后进行试验。
步骤3 待系统稳定运行后,分别调节待测阀门开度为100%,90%,80%,70%,60%,50%,40%,30%,20%和10%,待检测到的流量和压力数据稳定后,采集流量和压差信息,同一开度重复3次。
步骤4 关闭试验系统,切断电源。
5.2 试验验证对低压试验工况和高压实际工况进行现场试验。监测得到DN250三通调节阀主控制回路及旁通回路不同工况和开度下的压差、流量,代入式(6)得到试验流量系数,修正得到的高压工况流量系数如表4所示。
|
|
表 4 DN250三通调节阀修正的流量系数(Kv) Tab.4 Corrected flow coefficient (Kv) of DN250 three-way regulating valve |
根据修正后的流量系数绘制流量特性曲线并与试验获得的高压实际工况流量系数进行对比验证,对比结果如图11和图12所示。

|
图 11 三通调节阀控制回路流量特性曲线 Fig. 11 Flow characteristic curve of the control loop of the three-way regulating valve |

|
图 12 三通调节阀旁通回路流量特性曲线 Fig. 12 Flow characteristic curve of bypass circuit of three-way regulating valve |
由图11可知,主控制回路修正得到的流量系数曲线其流量特性接近等百分比流量特性,与试验流量系数曲线趋势一致。在10%~100%开度范围内模拟值与试验值的平均偏差为8.01%,修正值与试验值的平均偏差为2.35%。
由图12可知,旁通回路修正得到的流量系数曲线其流量特性接近线性流量特性,与试验流量系数曲线趋势一致。在10%~100%开度范围内模拟值与试验值的平均偏差为8.79%,修正值与试验值的平均偏差为2.29%,认为CFD数值模拟有着较高的精度,模拟修正后的流量系数更符合试验值,可用于预测及修正三通调节阀高压实际工况流量系数。
6 结 语利用CFD计算流体力学方法对某型船用三通调节阀高低压工况进行数值模拟,根据模拟结果提出的高低压工况流量系数修正转化关系,对低压工况下的试验流量系数进行修正,得到高压实际工况流量系数,并进一步通过试验加以验证,结论如下:
1)该型阀门主控制回路流量特性曲线接近等百分比流量特性、旁通回路流量特性曲线接近线性流量特性,均与试验流量系数曲线趋势一致。
2)模拟得到的主控制回路和旁通回路流量系数与试验结果的平均偏差不超过6%,证明CFD数值模拟计算结果有着较高的精度。
3)基于高低压工况CFD数值模拟结果,提出并得到了转化修正系数,修正后的高压工况流量系数与试验得到的高压流量系数平均偏差在2.35%以内,本方法可用于指导三通阀高压实际工况流量系数的预测。
| [1] |
孙彩珍, 李红, 汤攀. 三通调节阀分流比及内部流动特性分析[J]. 排灌机械工程学报, 2019, 37(5): 441–446.
|
| [2] |
王冠, 邓建飞, 寇琳媛, 等. 多级降压调节阀阀芯流阻特性及参数分析[J]. 流体机械, 2021, 49(12): 70–77.
|
| [3] |
石娟, 姚征, 马明轩. 调节阀内三维流动与启闭过程的数值模拟及分析[J]. 上海理工大学学报, 2005(6): 498–502.
|
| [4] |
QIAN J, WU J, GAO Z, et al. Effects of throttling window on flow rate through feed-water valves[J]. ISA transactions, 2020, 104: 393-405. DOI:10.1016/j.isatra.2020.05.017 |
| [5] |
魏丹, 宋花平, 赵军. 新型压力调节阀内部流场的数值模拟[J]. 化工进展, 2015, 34(5): 1264–1268.
|
| [6] |
TAO J Y, LIN Z, MA C J, et al. An experimental and numerical study of regulating performance and flow loss in a V-port ball valve[J]. Journal of Fluids Engineering, 2020, 142(2): 9-15. |
| [7] |
GAO Z X, YUE Y, YANG J M, et al. Numerical Study of the Microflow Characteristics in a V-ball Valve[J]. Micromachines, 2021, 12: 155.
|
| [8] |
章茂森, 李忠, 靳淑军, 等. 某冷却系统用三通调节阀内部湍流动能和耗散率分析[J]. 流体机械, 2019, 47(3): 37–41.
|
| [9] |
李树勋, 李忠, 周爱民, 等. 三通调节球阀节流盘开口型线优化及试验研究[J]. 华中科技大学学报(自然科学版), 2017, 45(2): 61–66.2
|
| [10] |
游超, 杨振彪, 刘浩, 等. 大口径流量调节阀模型试验研究[J]. 给水排水, 2020, 56(6): 27–32.
|
| [11] |
王佳星, 赵家睿, 李斯特, 等. 不同放汽阀流量特性对弹射过程的影响规律[J]. 化工学报, 2021, 72(S1): 318–325.
|
| [12] |
GB/T 17213.9-2005,. 工业过程控制阀第2-3部分流通能力试验程序[S]. 2005
|
| [13] |
张万年. 大口径活塞式流量调节阀CFD模拟与流噪音预测研究[D]. 兰州理工大学, 2020.
|
 2023, Vol. 45
2023, Vol. 45
