0 引　言

船舶在离靠码头时有多种方式，其中一种简便有效的方式是采用侧推器，侧推器的使用弥补了航速较小时主推进器舵效不足的问题，这使得大型船舶不需要拖船也能自行离靠港。此外，随着时代的发展出现了功能多样的载人潜水器、AUV和ROV，其在海底航行时对操纵性和定位有着更高的要求，因此除了在前后安装推进器，通常也要安装侧推器，“蛟龙”号深海载人潜水器，为达到深海操纵性要求，在首尾部安装了6台侧推器。因此研究侧推器的水动力性能具有重要意义。

槽道侧推器是出现最早也是目前应用最广泛的侧推器，其主要特点是在船首或船尾横向开槽，在槽道内部通过安装T形轴联动螺旋桨或者直接采用轮缘驱动式叶片。对于槽道侧推器研究主要采用理论和试验的方法。Taniguch^[1]采用敞水模型试验对定距桨和调距桨的槽道侧推器水动力性能进行了较为详细的研究，采用操纵试验检验侧推器的转向能力。该试验是目前公布的最为详细的侧推器敞水性能试验。沈国鉴等^[2]根据模型试验的结果得出了槽道侧推器的设计图谱，据此可初步确定所需功率和转速，对于侧推器的设计有很好的指导性作用。Ridley, Donald E.^[3]研究了隧道入口结构对推力产生和船体阻力增强的影响。Beveridge, John L^[4]的研究报告中提出船首侧推器的水动力性能计算经验公式，并从设计角度对管道布置、管道形状和叶轮的选择做了研究。

20世纪90年代，CFD开始广泛进入工业设计领域，目前已成为推进器研究设计的方法之一^[5]。熊鹰等^[6]基于混合网格的RANS方法准确预报螺旋桨敞水性能。相对于敞水螺旋桨，侧推器CFD方法研究目前较少，近年来国内外学者利用商用软件CFX，STAR –CCM+，Fluent等对侧推器的不同特征尺寸、工况，船速下的水动力性能和流场特性进行了模拟计算^[7-10]。郁程等^[11-12]基于MRF模型和混合网格技术对试验中^[1]部分调距桨做了数值计算，水动力性能误差在10%以内。Yukun等^[13]采用试验结合数值仿真的方法对船首侧推器进行了研究，主要研究单个首侧推器在不同船型，不同来流、不同开口圆角影响下的水动力性能，还研究了多个首侧推器互相影响以及开口圆角对叶片压力分布不均匀的改善作用,利用CFD方法从流场方面解释了各参数对侧推器水动力影响的原因。

目前采用CFD方法对侧推器仿真计算仍然有很多不确定性，本文对照公开的试验条件和数据^[1]，基于STAR-CCM+中的RANS方法和SST $ k - \omega $ 模型，采用高质量结构网格，对调距桨进行仿真计算。通过对计算域、网格数量和时间步长进行比较，验证CFD方法的可靠性，并对不同叶数的调距桨侧推器流场特性和水动力性能做了计算分析。

1 研究对象

本文以文献[1]试验中装有1308桨和1308-B桨的槽道侧推器为研究对象，1308桨是1个4叶平板调距桨，1308-B桨是1个3叶桨，其叶片参数与1308相同。叶片的轮廓如图1所示。

1308桨和1308-B桨叶的主要参数如表1所示。

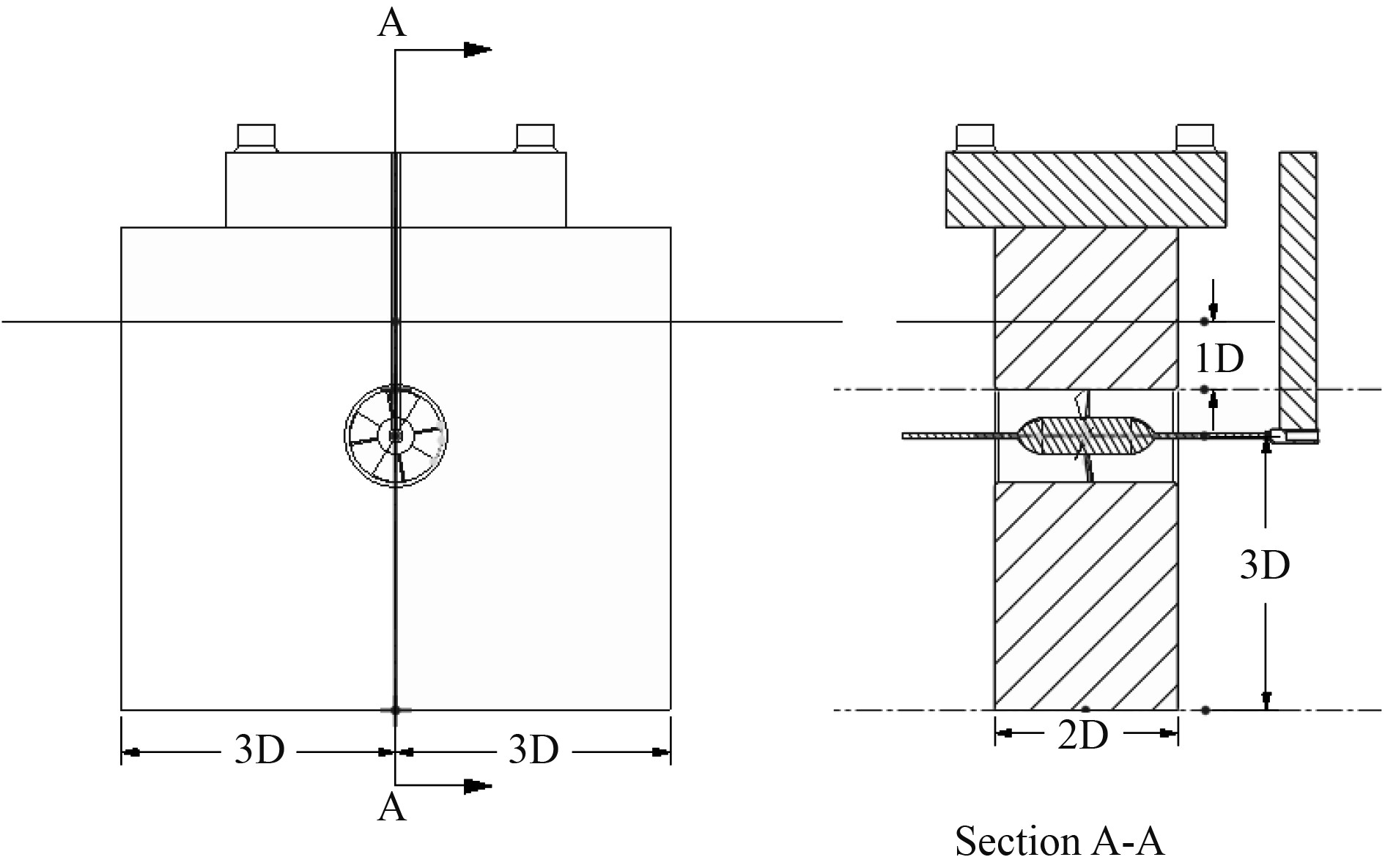
文献[1]试验中对1308桨和1308-B测试时使用的均是名义船体，船体槽道壁直径为203 mm，槽道进出口采用10 mm的圆弧倒角。试验的布置如图2所示。

据此采用Catia建立试验的几何模型，忽略露出水面的试验体和测量设备，仅对没入水下的名义船体和螺旋桨建模，如图3所示。

试验^[1]中数据采用无量纲化处理，由于侧推器工况属于系柱工况，进速系数为0，且名义船体推力占比较大，对此采用下列公式处理数据。

$ \left\{ \begin{gathered} {C_T} = \frac{T}{{\rho {n^2}{D^4}}}，\\ {C_F} = \frac{F}{{\rho {n^2}{D^4}}} ，\\ {C_{TF}} = \dfrac{{T + F}}{{\rho {n^2}{D^4}}} ，\\ {C_Q} = \dfrac{Q}{{\rho {n^2}{D^5}}}，\\ \eta = \dfrac{{{{\left( \dfrac{C_{TF}}{\text{π}} \right)}^{\frac{3}{2}}}}}{{{C_Q}}}。\\ \end{gathered} \right. $

(1)

式中： $ {C_T} $ ， $ {C_F} $ ， $ {C_{TF}} $ ，分别为螺旋桨，船体，侧推器整体的推力系数； $ {C_Q} $ 为螺旋桨扭矩系数； $ \eta $ 为侧推器整体效率； $ T $ ， $ F $ 分别为转子推力和船体推力 ${\rm{kg}}$ ； $ Q $ 为转子扭矩， ${\rm{kg}}\cdot{\rm{m}}$ 。 $ \ \rho $ 分别表示水的密度， ${\rm{kg}}\cdot{{\rm{s}}}^{2}/{m}^{4}$ ； $ n $ 为转子转速， ${\rm{ r}}/{\rm{s}} $ ， $ D $ 为转子直径， $ m $ 。试验中测试发现当结果以无量纲化方式表示时，转速对结果基本没有影响，本文计算时转速采用20 $ {\rm{r}}/{\rm{s}} $ 。

2 计算方法 2.1 计算域划分和边界设置

试验中没有给出水池的尺度，由于侧推器计算工况为系柱工况，为保证计算的收敛性和准确度，需划分大计算域。计算域初步设置为长度50D，宽度90D，深度40D的长方体，对结果影响最大的主要是长度，在后续计算中改变长度来检验计算域的影响。将名义船体置于计算域中央，其上表面与顶面平齐。由于槽道中心距离水面1.25D，螺旋桨浸深高于0.76D时可以不计算自由液面影响^[4]，因此外域顶面设置为对称平面，外域其他面设置为压力出口，其他表面均使用壁面条件处理，如图4所示。

2.2 网格划分

将计算域分为旋转域和外域2部分，采用结构网格对2个区域进行划分，区域之间采用交界面进行数据传递，在划分过程中在桨叶表面单独划分一层薄层用于边界层网格数量的控制，由于船体的压差主要来自于槽道进出口，此处的网格也需要加密。在后续计算中，主要改变这2处的网格数量来验证网格数量对于数值计算的影响。

2.3 计算模型

采用STAR-CCM+软件RANS方法，在流体不可压缩的条件下，流场的连续方程和动量方程如下：

$\begin{split} & \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 （2） \rho \frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial P}}{{\partial {x_j}}} + \rho {g_i} + \\ & \rho \frac{\partial }{{\partial {x_j}}}\left( {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \overline {{{u'}_i}{{u'}_j}} } \right)。\end{split}$

(3)

式中： $ {u_i} $ ， $ {u_j} $ 为各速度分量的时均值 $ \left( {i,\;j = 1,\;2,\;3} \right) $ ； $ P $ 为压力的时均值； $ \rho $ 为流体的密度； $ \mu $ 为流体的动力粘性系数； $ {g_i} $ 为重力加速度分量； $ - \rho \overline {{{u'}_i}{{u'}_j}} $ 为雷诺应力项。

为封闭控制方程引入SST $ k - \omega $ 湍流模型，该模型可以对边界层内的流动和边界层外的湍流进行更好的模拟，因此能够对翼型结构和含有分离流的流场进行准确的计算，但这需要较高的网格质量，符合本文计算需求。对于螺旋桨旋转的模拟目前主要有MRF和Sliding Mesh 2种方法，本文先采用MRF方法对旋转域的螺旋桨进行定常模拟，待计算稳定后再采用Sliding Mesh进行非定常计算。在计算中对非定常的时间步设置做了验证计算。

3 计算结果与分析 3.1 计算域、网格数量、时间步长对侧推器仿真计算的影响

对螺距比为0.8时的1308桨槽道侧推器水动力性能进行计算用来检验各因素的影响。首先对计算域的影响进行验证，构建出3个长度分别为30D，50D和80D的计算域，采用相同方法和过度率构建旋转域和外域的结构网格，取相同时间步长，即单位时间旋转2°，代入计算模型进行计算，结果如表2所示。

可看出计算域长度取30D时误差较大，取80D时误差较小，但其误差与50D时的误差差别不大。因此为减少计算时间，取50D作为计算域的长度，在后续计算中都使用该计算域。

对网格依赖性进行验证，旋转域内的叶片表面第1层网格高度分别取0.0005 mm，0.001 mm，0.005 mm。在能够反映出叶片形状的前提下，由低到高改变弦长方向网格数目和过度率，最终生成3种旋转域网格；选长度为50D的外域网格，采用相同的方式改变槽道进出口附近的网格数目，并保证区域网格过度平缓，得到3种外域网格，与旋转域组合成3套网格。网格划分情况如表3所示。

各组网格的计算结果和试验进行对比，如表4所示。

计算结果显示，当转子域和外域网格数量增至1240万、1800万时，继续增加网格数量对计算结果的影响较小，此后产生的误差与网格数量关系不大。因此采用Mesh2网格形式构建后续研究对象的网格。

转子单位时间步长内旋转角度分别设置为1°，2°，5°时，内部迭代采用10步，采用二阶时间离散，计算结果如表5所示。

结果显示时间步长采用5°时的误差最小，时间步长1°和2°的计算结果接近。分析其原因，5°误差小主要是因为时间步长过大对于非定常流场的计算粗糙，为了节省计算时间，在后续研究中采用2°时间步长。

3.2 不同螺距比的侧推器水动力计算结果

试验中没有明确调距方式，在数值计算中采用工程实践中的调距方式，从设计螺距比 $ \gamma = 0 $ 出发，调整到虚拟螺距角 $ \gamma ' $ ，虚拟螺距变化为 $ \Delta \gamma = \gamma ' - \gamma $ ，令桨叶绕设计转动轴转动 $ \Delta \alpha = \Delta \gamma $ ，并认为转动 $ \Delta \alpha $ 后，新调距桨是具有螺距角 $ \gamma ' $ 及对应螺距比(P/D)的桨^[14]。据此对1308桨和1308-B桨叶的0.8，1.0，1.2螺距进行建模和计算，计算域、网格和计算设置采用已验证的结果进行构建，计算结果如图9所示。

对比CFD计算结果和试验数据，发现CFD计算的水动力性能与试验基本相符，随着螺距的增大，水动力系数呈现上升的趋势。不同螺距的螺旋桨推力系数 $ {C_T} $ 误差在−2%～3%左右，船体的推力系数 $ {C_F} $ 误差在4%～6%， $ 10{C_Q} $ 的误差在−2%～4%左右，可见误差主要来自于船体推力的计算。

根据试验报告中采用的效率计算公式，对计算结果进行换算，CFD计算效率和试验测试效率结果如图10所示。

可以看出CFD的效率计算结果与试验基本相同，1308-B和1308桨随着螺距的增加效率逐渐增加。不同叶片数的敞水螺旋桨效率在系柱情况下基本相同^[15]，与敞水螺旋桨不同的是试验中叶片数多的槽道侧推器效率较高，这主要是因为叶片数量的增减影响了槽道内部的流速。虽然叶型相同，而1308桨的槽道侧推器流速较快，因此具有更高的效率点。

3.3 不同叶数的侧推器流场特性分析

取槽道中部横截面的轴向速度进行分析，如图11所示。可以看出，1308槽道侧推器不同螺距下的流速均稍高于1308-B槽道侧推器的流速，这使得1308槽道侧推器的推进效率略高于1308-B的效率。另外可以看出1308槽道侧推器的流场不均匀性更大，其产生稍隙泄流的流速更大。

取1308槽道侧推器和1308-B槽道侧推器不同螺距下叶片的吸力面压力分布进行对比分析，如图12所示。可以看出，叶片的压力分布呈“波浪式”分布，低压集中于高半径的导边附近.这主要是因为槽道侧推器采用的叶片是无拱度的叶片，且该桨叶剖面的螺距角均相同。这使得叶片高半径处的负载较重，因此在导边高半径部分的低压明显。对比可知1308槽道侧推器不同螺距下的吸力面最低压力都低于1308-B，特别是螺距P/D=1.2时，最低压力达到−270 kPa左右，容易产生明显的面空化问题。

4 结　语

本文验证CFD方法计算槽道侧推器水动力性能的可靠性，研究螺距比和叶片数对侧推器水动力性能的影响，并对流场特性进行了分析，得到以下结论：

1）槽道侧推器的水动力性能计算对计算域的要求较高，需选择较长的计算域，长度应不小于30D，采用结构网格时在对叶片、叶间隙、槽道口附近网格进行加密后，选择2°以内时间步长的非定常计算可以较为准确计算出槽道侧推器的水动力性能。本文计算误差主要来自于船体推力，误差在6%以内。

2）1308和1308-B槽道侧推器的水动力系数随螺距变化趋势相同，但1308的效率较高，主要是因为相同螺距下1308桨的槽道内部流速较快，使得叶片处于更高的效率点。

3）采用等螺距和无拱度叶型的槽道侧推器叶片压力分布呈“波浪式”分布特点，其低压集中于导边的高半径部分，容易产生空化问题。叶梢部分的流动不均性较大，叶顶间隙有明显的回流速度。

总体而言，CFD计算中URANS模型能够准确预报槽道侧推器水动力性能和流场特性，可以作为设计研究侧推器的辅助工具。