国际海事组织(IMO)为保护大气环境,对国际运输制定了温室气体和气体污染物排放相关的技术规则,以激励造船商和船东选择更高效且更环保的船舶(IMO2020[1])。随着IMO2020限硫令的实施,航运为减少船舶排放,积极寻求船舶减阻措施。船舶纵倾优化作为IMO提出的减小阻力的高效、节能的新方法,获得了更多关注且已进行很多研究。纵倾优化的研究是基于船模试验或计算流体动力学[2](CFD)方法模拟进行的。Sun等[3]将采用商用RANS计算软件获得的纵倾优化仿真结果应用于实际船舶,节油效果显著。Islam等[4]使用RANS模拟预测了集装箱船在3种不同的傅汝德数和吃水条件下的阻力,并证明了最佳纵倾角度随速度和吃水的变化而变化。宋磊等[5]运用Fluent软件对散货船进行纵倾优化,得出纵倾优化对总阻力的影响变化。马儒昆等[6]系统地提供了KVLCC2在斜向运动时的模拟数据分析。通过控制速度和纵倾条件,童骏等[7]采用Fluent对船模进行分析,得出纵倾优化对减小船舶阻力有非常显著的效果。这些研究是基于船舶直航状态,而在船舶实际航行时,很多时候处于斜航状态。王化明等[8]对船模斜航运动中运用多个自由度进行计算分析,而斜航状态下船舶纵倾对阻力的影响,研究较少。
本文以KCS标准船模为研究对象,运用商用RANS求解器STAR-CCM+软件,对斜航状态下船舶进行纵倾对船舶阻力影响的数值研究,探究船舶斜航状态下阻力最佳纵倾条件,对不同漂角条件下船舶纵倾减阻机理进行分析。
1 数值方法 1.1 控制方程用STAR-CCM+对模型进行数值模拟。在笛卡尔坐标下,用张量形式给出无外力不可压缩流的平均连续性和动量方程[9-10]如下:
| $ \frac{{\partial \left( {\rho \overline {{u_i}} } \right)}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{{\partial \left( {\rho {{\overline u }_i}} \right)}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}(\rho \overline {{u_i}} \overline {{u_j}} + \rho \overline {u_i'u_j'} ) = - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{{\partial {{\overline \tau }_{ij}}}}{{\partial {x_j}}}。$ | (2) |
其中,
| $ {\overline \tau _{ij}} = \mu \left( {\frac{{\partial {{\overline u }_i}}}{{\partial {x_j}}} + \frac{{\partial {{\overline u }_j}}}{{\partial {x_i}}}} \right)。$ | (3) |
式中:
流体体积(VOF)方法用于自由表面的计算。
体积分数的方程为:
| $ \frac{{\partial \alpha }}{{\partial t}} + \nabla \left( {\alpha U} \right) = 0 。$ | (4) |
其中:U为速度场;α为试验水池内水的体积分数,设置2相流,分别从0到1,不断注水直至充满水池。
选择具有壁面函数的Realizable k-ε湍流模型封闭方程,采用Simple方法进行速度-压力耦合,动量项和体积分数项均采用2阶迎风差分格式,扩散项的离散采用中心差分格式。
1.2 船舶模型采用无附体的KRISO集装箱船(KCS)模型。该模型的几何形状如图1所示,主要船舶参数见表1。

|
图 1 KCS模型的几何形状 Fig. 1 Geometry of the KCS model |
|
|
表 1 KCS船舶主要参数 Tab.1 Main parameters of KCS ship |
图2为计算域设置与网格划分。计算域按照ITTC(2011)的指导建议进行设置,计算域入口边界距船首1.5L,出口边界距船尾2.5L,侧边界距船中纵剖面2L,顶边界距自由液面1.5L,底部边界距自由液面2L。网格为非结构网格,在船体周围和自由液面进行了加密,船体表面采用棱柱层网格,y+值为60。

|
图 2 计算领域和网格 Fig. 2 Computing domains and grids |
入口、顶部和底部边界设为速度入口,出口边界设为压力出口,侧边界和对称面边界设为对称边界,船舶表面设为壁面边界。在入口边界、出口边界和侧边界设置了波浪阻尼,抑制回波对计算的影响。
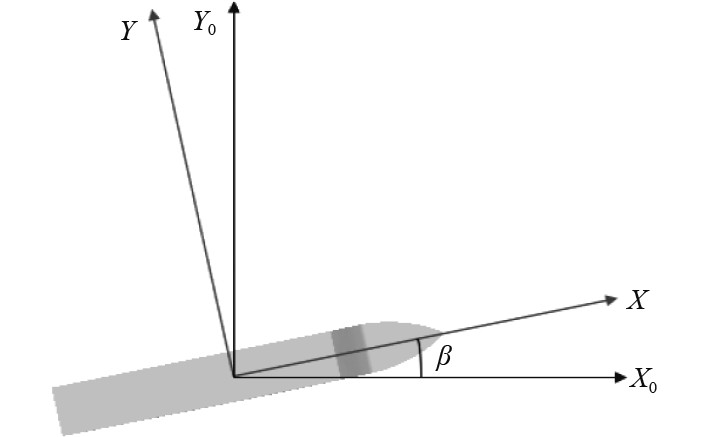
漂角设定为0°、6°和12°,船舶为斜航运动,船舶运动坐标系如图3所示。其中β表示漂角[11],船舶阻力为X方向受力,船舶纵倾角度为−0.5°~+0.5°,间隔为0.2°,船舶首倾为正,尾倾为负。
|
图 3 船舶倾斜运动示意图 Fig. 3 Diagram of ship tilting motion |
在 0°,6°,12°漂角下,对KCS船模进行阻力数值计算。为保证计算网格的划分合理,采用网格收敛指数(GCI)方法进行收敛性分析,网格尺寸按照细化比rG=1.41,创建粗、中和细3种网格。3种网格数量分别为246万(细)、126万(中)和66万(粗),并对Fr=0.26时船舶直航阻力进行计算。GCI方法分析如下:
| $ p = \frac{1}{{\ln ({r_{21}})}}\left. {\left| {\ln \left| {\left. {{\varepsilon _{32}}/{\varepsilon _{21}}} \right| + q(p)} \right.} \right.} \right| ,$ | (5) |
| $ q(p) = \ln \left( {\frac{{r_{21}^p - s}}{{r_{32}^p - s}}} \right) ,$ | (6) |
| $ s = 1 \cdot {{\rm{sgn}}} ({\varepsilon _{32}}/{\varepsilon _{21}}) 。$ | (7) |
其中:ε32=φ3−φ2,ε21=φ2−φ1。
外推值的计算方法如下:
| $ \phi _{ext}^{21} = (r_{21}^p{\phi _1} - {\phi _2})/(r_{21}^p - 1)。$ | (8) |
此外,近似相对误差和外推的相对误差分别由下式得到:
| $ e_a^{21} = \left| {\frac{{{\phi _1} - {\phi _2}}}{{{\phi _1}}}} \right|,$ | (9) |
| $ e_{est}^{21} = \left| {\frac{{\phi _{ext}^{21} - {\phi _1}}}{{\phi _{ext}^{21}}}} \right| ,$ | (10) |
最后,网格收敛指数计算如下:
| $ {{GCI}}_{{\text{fine}}}^{{\text{21}}} = \frac{{1.25e_a^{21}}}{{r_{21}^p - 1}}。$ | (11) |
结果如表2所示。计算结果表明,网格收敛性良好,符合ITTC建议的网格设置。
|
|
表 2 网格收敛性分析 Tab.2 Analysis of mesh convergence |
为了验证数值结果的准确性,将数值计算结果与船模试验数据进行比较,结果如表3所示。D%为相对误差,定义为
|
|
表 3 数值验证 Tab.3 The numerical validation |
基于验证过的数值方法,对船舶阻力进行计算。船舶在航行过程中会产生下蹲,以往有关纵倾对阻力影响的研究没有考虑船舶下蹲造成的影响,对于体型较大的船舶,下蹲也会影响船舶阻力。如图4所示,漂角为0°,Fr=0.26时,纵倾对船舶阻力的影响情况,Dt为总阻力变化比例,表达式为:

|
图 4 自由下蹲和约束下蹲状态对比 Fig. 4 Comparison of free squats and constrained squats |
| $ {D_t} = \frac{{{R_{tn}} - {R_{t0}}}}{{{R_{t0}}}}\times 100\text% 。$ | (12) |
其中:Rtn为各纵倾状态下阻力值,Rt0为此漂角下平吃水时阻力值。
可知,在约束下蹲和自由下蹲2种状态下,纵倾对船舶阻力的影响规律存在明显差异。为了数值模拟能更加接近船舶航行实际,数值模拟采用自由下蹲状态进行模拟。各漂角下纵倾对船舶阻力的影响如图5所示。

|
图 5 不同漂角下纵倾对船舶阻力影响 Fig. 5 Influence of trim on ship drag under different drift angles |
在不同漂角下,纵倾对船舶阻力的影响规律并不相同。当漂角为6°时,纵倾对阻力的影响与漂角为0°时接近,但最优阻力对应的纵倾值变为首倾0.1°;当漂角为12°时,纵倾对阻力的影响变化较大,出现较大波动,最优阻力对应的纵倾值变为0°,即船舶平吃水状态。同时,在各漂角下,船舶阻力是在尾倾时均大于首倾,在尾倾5°时,阻力最大。
2.3 阻力变化分析船舶阻力由摩擦阻力和剩余阻力2部分组成,为分析船舶纵倾变化后阻力变化的主导因素,将计算结果表述为不同倾角下分阻力变化率,如下式:
| $ {D_f} = \frac{{{R_{fn}} - {R_{f0}}}}{{{R_{f0}}}}\times 100\text% ,$ | (13) |
| $ {D_p} = \frac{{{R_{pn}} - {R_{p0}}}}{{{R_{p0}}}}\times 100\text% 。$ | (14) |
其中:Rfn为各纵倾状态下摩擦阻力值,Rf0为此漂角下平吃水时摩擦阻力值,Rpn为各纵倾状态下剩余阻力值,Rp0为此漂角下平吃水时剩余阻力值,结果如图6和图7所示。

|
图 6 摩擦阻力变化率 Fig. 6 Rate of change of friction resistance |

|
图 7 剩余阻力变化率 Fig. 7 Rate of change of residual resistance |
由图6可知,当漂角为0°和6°时,摩擦阻力变化不大,变化率不超过0.65%。漂角12°时,摩擦阻力变化出现明显波动,变化率不超过2.22%。由图7可知,在各漂角下,剩余阻力都出现明显变化,在尾倾时,剩余阻力变化率最大超过11.12%。当首倾时,剩余阻力变化率超过4.48%。说明在有漂角存在的情况下,纵倾对船舶阻力的影响主要因剩余阻力产生很大变化而引起。
图8左侧为算纵倾角度内阻力最优时,纵倾状态的兴波云图,右侧为阻力最大时纵倾状态的兴波云图。从左图和右图的对比可看出,右图中船舶兴波明显剧烈,兴波剧烈会导致船舶兴波阻力明显增加,继而导致剩余阻力增加。

|
图 8 兴波云图 Fig. 8 Wave-making cloud |
本文对集装箱船在有漂角的情况下船舶纵倾改变对船体阻力影响进行研究,计算阻力值与试验值的对比,验证网格和数值算法的合理性。计算有漂角情况下各纵倾状态阻力值,通过对比分析得出:
1) 集装箱船在有漂角的情况下直航时,纵倾对船舶阻力影响规律不一致;
2) 对于较大型船舶在预测阻力时,船舶下蹲变化不可忽略;
3) 比较不同纵倾状态总阻力可知,对于集装箱船在满载吃水状态下,尾倾时阻力增加;
4) 通过不同阻力成分比较可知,该集装箱船在纵倾改变时,剩余阻力变化较大,为阻力变化的主导因素。
| [1] |
International convention for the prevention of pollution from ships[R]. International Maritime Organisation (IMO), London.
|
| [2] |
倪崇本, 朱仁传, 缪国平, 等. 一种基于CFD的船舶总阻力预报方法[J]. 水动力学研究与进展A辑, 2010, 25(5): 579–586. NI C B , ZHU R C, MIAO G P, et al. A method for ship resistance prediction based on CFD computation[J]. Chinese Journal of Hydrodynamics, 2010, 25(5): 579–586. |
| [3] |
SUN J, TU H, CHEN Y, XIE D, ZHOU, J. A study on trim optimization for a container ship based on effects due to resistance Journal of Ship Research, 2016, 60, 30–47.
|
| [4] |
ISLAM H, SOARES C G. Uncertainty analysis in ship resistance prediction using OpenFOAM[J]. Ocean Engineering, 2019, 191: 105805. DOI:10.1016/j.oceaneng.2019.02.033 |
| [5] |
宋磊, 童骏, 孔斌. 散货船纵倾减阻及其成因分析[J]. 舰船科学技术, 2020, 42(5): 21-26. SONG L, TONG J, KONG B. Analysis of resistance change of bulk carriers trim optimization[J]. Ship Science and Technology, 2020, 42(5): 21-26. |
| [6] |
马儒昆, 胡义. 基于CFD的散货船纵倾优化研究[J]. 中国修船, 2019, 32(6): 21-25. MA R K, HU Y. Study on trim optimization of bulk carrier based on CFD[J]. China Shiprepair, 2019, 32(6): 21-25. DOI:10.13352/j.issn.1001-8328.2019.06.007 |
| [7] |
童骏, 涂海文, 孙江龙. 船舶纵倾优化减阻数值模拟研究[J]. 中国海洋大学学报, 2018, 48(7): 123-129. TONG J, TU H W, SUN J L. Analysis of resistance change of bulk carriers trim optimization[J]. Ship Science and Technology, 2018, 48(7): 123-129. DOI:10.16441/j.cnki.hdxb.20160049 |
| [8] |
王化明, 吕俊, 陈林, 等. 船舶多自由度斜航运动水动力数值研究(英文)[J]. 船舶力学, 2016, 20(9): 1083-1097. WAN H M, LV J, CHEN L, et al. Numerical study on hydrodynamics of ships in oblique motion with multi-degree of freedom[J]. Journal of Ship Mechanics, 2016, 20(9): 1083-1097. |
| [9] |
ISLAM H, SOARES C G. Effect of trim on container ship resistance at different ship speeds and drafts[J]. Ocean Engineering, 2019, 183: 106-115. |
| [10] |
ELSHERBINY K M, TERZIEV M, TEZDOGAN T, et al. Numerical and experimental study on hydrodynamic performance of ships advancing through different canals[J]. Ocean Engineering, 2019, 195.
|
| [11] |
伍海华, 邹早建. 船舶大漂角斜航运动水动力数值预报[J]. 水动力学研究与进展, 2019, 34(3): 339-345. WU H H, ZOU Z J. Numerical prediction of dynamic and hydrodynamic forces of ship with large drift Angle[J]. Chinese Journal of Hydrodynamics, 2019, 34(3): 339-345. |
 2023, Vol. 45
2023, Vol. 45

