2. 浙江大学 海洋学院,浙江舟山 316021;
3. 宁波大学 海运学院,浙江宁波 315211
2. Ocean College University, Hangzhou 316021, China;
3. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China
航母在海上执行任务时,风载荷是航母水面以上舰体受到的主要环境载荷。由于航母的飞行甲板和舰岛等结构的迎风面积较大,强烈的风场将对航母周围气流场造成显著影响,而舰载机起降的安全性和稳定性对气流场的依赖极高[1-2]。因此,对航空母舰的复杂气流场进行精确预报具有重要意义。
国内外对舰船气流场的预报进行了大量的试验及数值模拟工作。在国外,Polsky[3]对舰船气流场进行了大量的研究工作。先是计算了两栖攻击舰空气尾流的时间精确性,又进行了非稳态下的船体周围流场计算研究[4-5]。随后,Polsky[6]对核动力航母进行了尾流模拟,创建了F-18航母着陆时的气流场仿真,实现了对CFD模拟数据的二次开发。Rajagopalan[7]在NASA陆军研究中心的风洞中进行了两栖攻击舰的空气尾流测试,研究了V-22倾斜旋翼机舰载的空气动力学相互作用。Syms[8]使用格子-玻尔兹曼法计算了轻型护卫舰的气流场并获得了准确的气流场特征。Forreste[9]计算了2种不同型号护卫舰的气流场并与试验数据进行了对比。Kulkarni[10]使用标准k-ε模型进行了护卫舰烟囱气流场的参数研究。Yuan[11]使用DDES模型模拟了护卫舰的风场结构,并与实验进行了对比,计算结果与实验结果一致。Buchholz[12]采用PIV技术捕捉了ONR舰船甲板上方的气流场结构,并通过CFD研究了低雷诺数到高雷诺数转换过程中的舰船动力学行为。Dooley[13]基于CFD研究了实尺度下波浪和摇荡运动对舰船气流场及悬停在飞行甲板上方的直升机的影响。在国内,姜治芳[14-17]对航母气流场进行了大量的研究工作,包括上层建筑的布局和飞行甲板的形式对气流场的影响等。郜冶[18]研究了不同风向下航母甲板的涡结构特征,分析了影响船后涡旋强度和位置的因素。赵维义[19]通过CFD技术分析了舰船空气尾流特性。郜哲明[20]和秦江涛[21]采用DES模型分别对CVN71航母和“库兹涅佐夫”航母的气流场进行了数值模拟,研究了网格类型、网格密度以及湍流模型对气流场数值预报结果的影响。
因为具有特殊的外飘舷台和岛式上层建筑,航母舰面的气流形态较常规舰船有很大区别。本文采用RANS法对航母在风舷角0~360°范围的气流场进行数值模拟,研究不同风舷角下的航母气流场特征。
1 理论计算船舶风载荷经验公式法是在风洞试验的基础上,将数据回归分析并总结得到的一系列经验公式。通过代入被研究船舶的特定参数例如船长、船宽、投影面积等,就可求出对应风速下船舶风载荷系数。目前常用的方法主要有Hughes公式、Isherwood公式、Blendermann公式、Haddara公式和模块法等,其中Isherwood公式是常用的一种经验公式。Isherwood对大量的油船和散杂货船进行了模型风洞试验,经过多元线性回归分析后,给出了估算船舶纵向和横向风力及力矩分量的方程。
| $ \left\{ \begin{aligned} {C_x} = & {a_0} + {a_1}\frac{{2{A_L}}}{{L_{OA}^2}} + {a_2}\frac{{2{A_T}}}{{{B^2}}} + {a_3}\frac{{{L_{OA}}}}{{{B^2}}} + {a_4}\frac{S}{{{L_{OA}}}} +\\ &{a_5}\frac{C}{{L_{OA}^2}} + {a_6}M ,\\ {C_y} = & {b_0} + {b_1}\frac{{2{A_L}}}{{L_{OA}^2}} + {b_2}\frac{{2{A_T}}}{{{B^2}}} + {b_3}\frac{{{L_{OA}}}}{{{B^2}}} + {b_4}\frac{S}{{{L_{OA}}}} +\\ & {b_5}\frac{C}{{{L_{OA}}}} + {b_6}\frac{{{A_{ss}}}}{{{A_L}}},\\ {C_n} = & {c_0} + {c_1}\frac{{2{A_L}}}{{L_{OA}^2}} + {c_2}\frac{{2{A_T}}}{{{B^2}}} + {c_3}\frac{{{L_{OA}}}}{B} + {c_4}\frac{S}{{{L_{OA}}}} + {c_5}\frac{C}{{{L_{OA}}}}。\end{aligned} \right. \hspace{-10pt}$ | (1) |
式中:AL为侧投影面积;AT是正投影面积;ASS为上层建筑侧投影面积,LOA为船舶总长;B为船宽,C为侧向投影面积中心与船首之间的距离;S为侧向投影面积周长;M为侧向投影面积的中线面支柱或桅杆的数目;Cx为纵向风载荷系数;Cy为横向风载荷系数;Cn为首摇力矩系数。a0−a6,b0−b6和c0−c6分别是Isherwood常数,具体取值可参见文献[22]。Isherwood法是公认的一种较为准确的计算船舶风载荷系数的经验公式。本文的理论计算部分采用Isherwood法。
2 数值计算 2.1 计算方法 2.1.1 控制方程在航母气流场预报中,流场控制方程为三维不可压缩粘性流动的连续性方程和N-S方程,经过时均化处理后得到RANS(reynolds-averaged navier-stokes equations,RANS)方程组为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0 ,$ | (2) |
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_i}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \mu \frac{\partial }{{\partial {x_i}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right) + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {{u_i}{u_j}} } \right) 。$ | (3) |
式中:u为速度;p为静压;ρ气体密度;μ动力粘性系数。
2.1.2 控制方程湍流模型使用的是SST k-ω模型。k-ω系列湍流模型近壁面可采用直接离散求解,对于粘涡的分离效果较好,适用于近壁面流动和低雷诺数问题,但是这也导致了这种湍流模型更加依赖于较高的近壁面网格质量和计算机计算能力。SST k-ω模型合并了来源于ω方程中的交叉扩散项,同时考虑了逆压边界层中湍流剪切应力的传输效应。k方程和ω方程表示如下:
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k\overrightarrow {{u_i}} } \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + \widetilde {{G_k}} - {Y_k} + {S_k} ,$ | (4) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega \overrightarrow {{u_i}} } \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + \widetilde {{G_\omega }} - {Y_\omega } + {D_\omega } + {S_\omega } 。$ | (5) |
式中:Гk,Гω为湍动能k和比耗散率ω的有效扩散系数;Yk,Yω为k和ω的湍流耗散;
本文计算模型为近250 m长的常规轻型航空母舰,采用全通式甲板,并结合滑跃式跳台的设计,舰载机大多为直升机与短距起降飞机。舰岛安置在飞行甲板靠近右舷的后部,舰岛上装有飞行控制室、指挥塔、桅杆、雷达、通信天线等结构。
简化后的航母模型参数如表1所示。
|
|
表 1 航母主要参数 Tab.1 Main parameters of aircraft carrier |
航母受力和来流角度定义如图1所示。x轴指向舰首为正,y轴指向右舷为正。X为航母受到的纵向力,Y为航母受到的横向力。当舰首正前方来流时,定义风舷角β=0°。为全面考察航母模型的风载荷及气流场特性,计算中风舷角的变化范围取0°~360°,风速U=5 m/s,每个来流工况间隔的角度为30°。

|
图 1 航母受力方向和风舷角定义 Fig. 1 Force direction and wind angle |
定义纵向受力系数Cx、横向受力系数Cy和首摇力矩系数Cn为:
| $ {C_x} = \frac{X}{{\dfrac{1}{2}\rho {U^2}{A_T}}} ,{C_y} = \frac{Y}{{\dfrac{1}{2}\rho {U^2}{A_L}}} ,{C_n} = \frac{{{M_n}}}{{\dfrac{1}{2}\rho {U^2}{L_{OA}}{A_L}}}。$ | (6) |
计算过程中通过更改边界条件的方式控制气流方向,因此计算域各边界条件都需距离模型充分远。前后边界距离模型3LOA,左右边界距离模型2LOA,上边界距离模型2LOA,下边界与模型吃水线位于同一平面内。
速度进口1和速度进口2分别给定风速的分量,在计算域中心的模型处合成带有风舷角的最终风速。根据风向来自舰首或舰尾,图2中的速度进口1和压力出口1的位置适时互换。

|
图 2 计算域和边界条件 Fig. 2 Computational domain and boundary conditions |
网格划分是CFD计算中的关键步骤,直接决定了计算精度和效率。为探究适合航母气流场模拟的网格尺寸,进行网格收敛性研究。以
|
|
表 2 不同网格密度计算结果 Tab.2 Calculation results of different mesh densities |
由表2可知,低密度网格的风载荷系数与中密度相差约6.5%,而中密度的结果与高密度相差约2.7%,从低密度网格到高密度网格其风载荷系数呈现出收敛性。综合考虑计算精度和效率,本文的计算网格选取中等密度的网格,后续的不同风舷角计算均基于该网格尺寸。图3为中等密度网格的示意图。

|
图 3 计算网格 Fig. 3 Calculation meshes |
数值模拟采用瞬态RANS计算,时间步长0.005 s,采用二阶迎风格式离散,内部迭代次数10,计算10 s。压力速度耦合采用SIMPLE算法处理。压力和速度的亚松弛因子分别为0.4和0.7。
3 数值计算 3.1 风载荷系数图4为风载荷系数对比曲线。可知,Isherwood公式的纵向风载荷系数曲线与CFD结果虽然在部分风舷角下有一定偏差,但两者趋势和分布基本一致。从整体上看,3种风载荷系数中横向力系数Cy的契合度最高,纵向力系数Cx的契合度最低。观察0°~180°风舷角可知,对于纵向力系数,两者偏离较大的位置发生在0°风舷角和180°风舷角附近,这是纵风附近的风舷角。由于Isherwood所采用的船型和上层建筑均是严格关于中纵剖面对称的,公式中的参数也均是基于中纵剖面得到的,而航母舰岛的安放位置偏向于甲板右侧,因此在平行于中纵剖面附近的风舷角下,Isherwood公式的适用性表现出疲态。对于横向力系数,两者偏离较大的位置发生在90°风舷角附近,这是横风附近的风舷角。与船体表面的迎风面积相比,舰岛的迎风面积是一个小量,因此船型差异所带来的影响有所降低,Isherwood公式与CFD结果之间的横向力系数偏差要比纵向力偏差小,整个风舷角范围内横向力系数的契合度也相对较高。对于首摇力矩系数,Isherwood公式与CFD结果总体吻合较好,两者偏离较大的位置发生在120°风舷角附近。首摇力矩系数的偏差同样也是由于不对称分布的舰岛所引起的。由于航母与常规船舶结构的差异性,气流流经航母船体时会发生更加复杂的气流分离、漩涡等现象,流速和流向都会出现偏差。Isherwood限于当时的研究条件,对于上层建筑沿中纵剖面非对称分布的船舶以及带有超大型甲板的船舶缺乏相应的数据支持。尽管如此,Isherwood公式对于预报航母风载荷系数上仍具有一定的适用性,可以应用于航母的前期设计。

|
图 4 风载荷系数对比 Fig. 4 Comparison of wind load coefficient |
进一步观察航母风载荷系数曲线可发现,对于纵向力系数曲线,区别于常规舰船较光顺和沿180°风舷角对称分布的特征,航母纵向力系数曲线在整个风舷角范围内有多处小幅度波动和起伏,且沿180°风舷角呈非对称分布,这说明航母受到气流冲击后的纵向受力分布不均。纵向力系数曲线在0°~90°的范围内缓慢上升,说明纵向力在该区间内的变化较为平缓。这是由于该风舷角范围内的迎风面积较小,且飞行甲板外飘舷台结构能对来流起到一定的阻滞作用。90°~180°的范围内纵向受力的变化幅度较大。随着风舷角的增大,纵向力系数先是快速增大,在150°附近达到峰值后小幅度降低。一方面,航母的迎风面积在不断增大,另一方面,由于甲板后部和船尾之间有一较大空隙,气流在该处产生的涡旋现象也越来越明显。180°~360°的风舷角范围内,由于舰岛更靠近来流方向,舰岛对于风的阻碍作用更明显,因此除了300°的风舷角,其余风舷角纵向力系数比相应对称分布的风舷角纵向力更大。除此之外,在120°风舷角之前,纵向力系数都为负数,当风舷角大于120°后,纵向力系数才为正数。这说明即使在90°风舷角之后,风的方向已经是顺着航母航行的方向,风对航母的作用力却也不完全是有利于航母在纵向方向上减小阻力,如100°风舷角附近时,反而风在航母纵向上对航母航行起阻力作用。
航母的横向力系数曲线和首摇力矩系数曲线的走势较平缓,说明随着风舷角的变化,航母的横向受力和首摇力矩分布较为均匀。常规的集装箱船舶由于具有较多的。当风舷角为90°和270°时,风载荷作用于航母的横向力达到最大值,横向力系数Cy值达到最大。由于舰岛分布在飞行甲板的右侧,当风舷角在180°~360°之间时,航母遭遇以右舷为主导的气流,此时作用于舰岛上的力矩会与整船的力矩相互叠加,因此航母对于风的阻碍作用增大,首摇力矩比0°~180°范围内的首摇力矩更大。
3.2 船体表面风压图5为不同风舷角下的船体表面风压分布云图。风舷角的变化带来了船体表面风压的剧烈变化。航母受到的风阻绝大部分由航母的正迎风面和背风面的压力差引起的。当风舷角为0°时,航母的高压区主要集中在舰首、跳台和舰岛垂直的平直面上,而低压区发生在跳台的弧形结构、飞行甲板前部和舰岛的两侧等部位。随着风舷角的增大,整个飞行甲板和舰岛的高压区面积也在逐步增大,舰首处的高压区逐渐向舷侧和船尾移动。当气流以一定的风舷角冲击航母时,舷台和飞行甲板的角隅处的压力分布呈现射流状,靠近角隅处的压力较低,沿着气流的方向飞行甲板的风压逐渐升高。当风舷角为30°,60°,150°和330°时这种现象尤其明显。尾向来流时由于航母艉部的钝体受到绕流影响更明显,其风压分布尤其是高压区的分布更加复杂,在尾部形成更大的压差及首摇力矩。

|
图 5 不同风舷角下的船体表面风压分布云图 Fig. 5 Wind pressure under different wind angles |
图6为不同风舷角下航母周围的流线分布。可以看出,当风舷角为0°时,整体流线分布相对平顺,只有跳台和舰岛的桅杆处发生了小范围的流动分离。当航母处于30°风舷角的气流场时,由于舰岛是接近长方体的钝体结构,在舰岛的下风向存在比较明显的流动分离区。同时,由舰首和舰尾诱导出的流动分离区变得逐渐清晰。然而此时仍能地观察到舰首、舰尾和舰岛下游的流线,说明此时三者相互间的影响较小。随着风舷角的增大,船侧背风面的流动分离加剧,其尺度远大于小风舷角下的舰岛下游分离区。舰首、舰尾和舰岛各自的绕流场相互影响不断加剧,同时舰岛上游的流线也不再平整,由舷台诱导出的流线呈螺旋线状。当风舷角为90°时,航母周围流线变得更加紊乱,船体右舷的下游出现一个大尺度的D型分离区。当气流撞击到船体左舷一侧后,受到船体舷侧的阻碍,气流速度降低,原本的空气流向上抬起,翻过飞行甲板,与舷台及尾部的风交织在一起,在舰岛迎风侧上沿产生漩涡。部分气流遭遇舰岛后会向舰岛两侧进行分流,气流在经过迎风面的角隅结构时会产生分离,这部分气流在逆压差下产生回流,从而形成了背面一侧的漩涡。当风舷角大于90°时,由船体诱导出来的分离区逐渐减小,整个流场的流线逐渐趋于平顺。

|
图 6 不同风舷角下的整体流线分布 Fig. 6 Streamline under different wind angles |
舰岛作为航母唯一的上层建筑,包括舰长室、指挥中心等舱室,对于整艘航母的航行以及作战调度起着重要的指挥作用。研究舰岛周围气流场分布规律及特征的重要性不言而喻。图7为不同风舷角下舰岛周围的流线矢量分布情况。

|
图 7 不同风舷角下舰岛周围的流线矢量 Fig. 7 Streamline vector around Island under different wind angles |
可以看出,前方空气流经舰岛附近时,气流在舰岛迎风侧上沿发生分离,又因为壁面的粘性阻滞作用,流速有所降低,在临近舰岛背风侧上沿处发生再附着而形成漩涡。气流从前部绕到背风侧流向下游,在舰岛背风一侧形成分离涡,随后又与从其他处流过来的气流相互缠绕,影响着舰岛的背风侧流场。当远方气流形成一定风舷角(30°~150°)流向航母时,撞击到左舷的气流速度升高,原本的气流被向上抬升,翻过舰岛后在舰岛背后产生分离涡。随着风舷角的增大,舰岛背风区的漩涡尺度逐渐增大,逐渐从舰岛表面脱落出来,形成更大的尾涡区。桅杆、雷达等小尺度结构周围的气流越发密集,且雷达的背风侧更容易形成漩涡。风穿越过舰岛后形成了明显的涡流,湍流能量的损失加大,从而导致集装箱船前后压差增大,相应的风阻也增大。
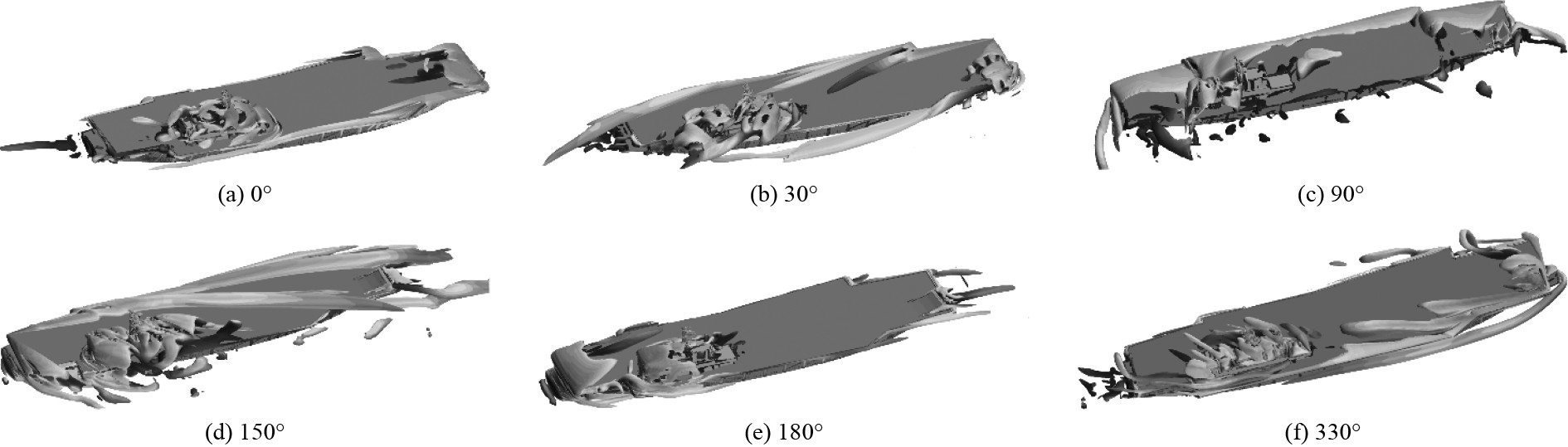
3.5 涡结构图8为采用Q准则捕捉到不同风舷角下的航母涡结构。
|
图 8 不同风舷角下的航母涡结构 Fig. 8 Vortex structure under different wind angles |
通过分析可知,航母遭遇不同风舷角的气流时,围绕航母舰体的绕流场通常存在舰首涡,侧舷涡、舰岛涡以及舰尾涡4大涡系。4种涡系独立存在且相互影响。当风舷角为0°时,舰首存在一个流动滞止区,此处的涡量较大,涡包围了整个舰首区域。由外飘舷台诱导出的侧舷涡沿舷侧细长且笔直地向舰尾方向延伸。舰岛遭遇气流后在正前方形成了一个较大的涡鼓包,小部分涡会向两侧延展,与向后不断发展的侧舷涡交汇融合。由于舰岛上存在外形和大小不一的钝体结构,因此各种结构诱导出的涡相互交错干扰,最终汇合成一个整体的舰岛涡。舰尾的涡量相对较少。当风舷角为30°时,从飞行甲板的角隅处分离出两股涡,一股涡笔直地沿飞行甲板向后延伸,另一股涡呈螺旋线状向后发展,两股涡之间会存在一个夹角。这就是典型的由绕钝体的流动分离引起的旋涡拖泄现象。侧舷涡和舰岛涡会跟随风舷角的变化向来流方向偏移。此时,由舰首尖部诱导出的弯曲涡仍不明显。随着风舷角的增大,侧舷涡和舰岛涡的角度随来流角度不断偏移,侧舷涡的涡量不断增大。尤其是当航母遭遇横风时,大量侧舷涡涌上甲板,覆盖了甲板近1/3的面积。由舰首尖部诱导出的弯曲涡也越发明显。此种情况极不利于舰载机的飞机和控制。风舷角为60°和90°的舰岛涡涡量反而有所降低,直至气流与航母重新形成一定风舷角后涡量才有所回升。风舷角180°~330°范围内的涡量明显比0°~150°范围内的更大,涡系也更复杂。
3.6 改善气流场的措施通过分析航母在不同风舷角下的气流场特征可知,改善航母气流场的主要措施,包括外形整体构型优化和局部细节部位优化2个方面。
航母因其特有的岛式上层建筑和外飘舷台外形对舰面气流场存在着较大影响。通过对航母的外形构型进行优化设计可有效改善航母气流场。如首部线型优化设计,可改善首部气流场的“回流”和“旋涡拖泄”现象,使流场更加均匀;在航母甲板和舷侧无法进行大面积优化修改的前提下,舰岛尽可能采用小型化设计,可减小其正迎风面积,并减少对上层建筑后部着舰区的影响;舰岛采用“钝头尖尾”,可有效改善上层建筑绕流流态,通过合理布置舰岛在飞行甲板上的纵向布置也可实现对航母舰尾气流场的改善。
通过局部细节部位优化可改善局部区域的气流流场形态。如飞行甲板前部设计成圆形或椭圆形,可减少首部流动分离;舰岛采用较为平缓的向后台阶状设计,可减小上层建筑后方的流动分离;设计平缓上升/下降的流线型舷台,可改善舷台涡结构形式。
4 结 语本文基于RANS法开展不同风舷角下的航空母舰气流场的数值模拟研究,对比RANS法和经验公式计算得到的风载荷系数,分析船体表面风压、流线以及涡结构在内的航母气流场特征,并给出改善航母气流场的措施。研究结论如下:
1)RANS法和Isherwood法得到的风载荷系数的变化规律基本一致,说明了数值模拟和Isherwood法在预报航母风载荷系数上的可行性。但限于船型结构,Isherwood法在部分风舷角下的适用性较差。
2)航母受到的风阻绝大部分原因是由于航母的正迎风面和背风面的压力差引起的。气流的分离及漩涡的产生是航母风阻增加的根本原因。
3)航母的绕流场特征整体上比较复杂,随风舷角的变化有着非常显著的不同。在任何风舷角下,流场中总存在流动分离区,航母各部分的绕流场会在一定风舷角下产生强烈的相互影响。
4)通过对航母整体外形构型和局部细节部位进行优化设计可以改善航母气流场,使气流场更加均匀,从而减小风阻。
| [1] |
全泽宇. 航母舰载机牵引车路径规划与轨迹跟踪研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [2] |
陈小飞, 时立攀, 毕玉泉. 美军航母舰载机出动回收能力和飞行甲板控制策略探讨[J]. 舰船科学技术, 2020, 42(21): 174-179. CHEN Xiao-fei, SHI Li-pan, BI Yu-quan. A discussion on the sortie generation capacity of embarked airwingsand the doctrine of flight deck control of U. S. aircraft carrier[J]. Ship Science and Technology, 2020, 42(21): 174-179. |
| [3] |
POLSKY S A, BRUNER C W. Time-accurate computational simulations of an LHA ship airwake[R]. AIAA 2000–4126.
|
| [4] |
POLSKY S A. A computational study of unsteady ship airwake[R]. AIAA, 2002: 10–22.
|
| [5] |
CZERWIEC R M, POLSKY S A. LHA airwake wind tunnel and CFD comparison with and without bow flap[R]. AIAA 2004: 48–32.
|
| [6] |
POLSKY S A, NAYLOR S. CVN airwake modeling and integration: initial steps in the creation and implementation of a virtual burble for F-18 carrier landing simulations[R]. AIAA 2005: 62–98.
|
| [7] |
RAJAGOPALAN G, SCHALLER D, WADCOSK A J, et al. Experimental and computational simulation of a model ship in a wind tunnel[R]. AIAA, 2005: 13–47.
|
| [8] |
SYMS G F. Simulation of simplified-frigate air wakes using a lattice-boltzmann method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 197-126. DOI:10.1016/j.jweia.2007.06.040 |
| [9] |
FORREST S, OWEN I. An investigation of ship airwakes using detached-eddy simulation[J]. Computers and Fluids, 2010, 29: 656-673. |
| [10] |
KULKARNI P R, SINGH S N, SESHADRI V. Parametric studies of exhaust smoke-superstructure interaction on a naval ship using CFD[J]. Computers and Fluids, 2007, 36: 794-816. DOI:10.1016/j.compfluid.2006.07.001 |
| [11] |
YUAN W, WALL A, LEE R. Combined numerical and experimental simulations of unsteady ship airwakes[J]. Computers & fluids, 2018, 172: 29-53. |
| [12] |
BUCHHOLZ J, MARTIN J, KREBILL A F, et al. Structure of a ship airwake at model and full scale[C]//2018 AIAA Aerospace Sciences Meeting. 2018: 1263.
|
| [13] |
DOOLEY G, MARTIN J E, BUCHHOLZ J H J, et al. Ship airwakes in waves and motions and effects on helicopter operation[J]. Computers & Fluids, 2020, 208: 104627. |
| [14] |
洪伟宏, 姜治芳, 王涛. 上层建筑形式及布局对舰船空气流场的影响[J]. 中国舰船研究, 2009(2): 53–58.
|
| [15] |
陆超, 姜治芳, 王涛. 不同工况条件对舰船舰面空气流场的影响[J]. 舰船科学技术, 2009, 31(9): 38–42.
|
| [16] |
陆超, 姜治芳, 王涛. 基于舰载机起降限制的舰船气流场特性评估方法初探[J]. 中国舰船研究, 2010, 5(1): 39–42.
|
| [17] |
陆超, 姜治芳, 王涛. 两种飞行甲板形式的舰船空气流场特性比较[J]. 舰船科学技术, 2009, 31(7): 29–31.
|
| [18] |
郜冶, 刘长猛, 贺征. 风向变化产生的航母甲板涡结构特征研究[J]. 空气动力学学报, 2013, 31(3): 310–315.
|
| [19] |
赵维义. 直升机旋翼与舰船复合流场试验方法研究[J]. 飞行力学, 2007(2): 72–74+77.
|
| [20] |
郜哲明. 航母甲板风场和火灾流场实验与数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [21] |
於菟, 秦江涛, 方乐. 航母气流场数值模拟方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(06): 1036–1040.
|
| [22] |
Wind resistance of merchant ship[J]. Trans. of RINA, 1972(112): 327–338.
|
 2023, Vol. 45
2023, Vol. 45

