燃气弹射过程先后经历火药药柱的燃烧、高温高压燃气的流动、燃气的膨胀做功以及武器在筒内的运动等多个问题,属于多学科交叉性研究课题。其中,筒内燃气流场的分布以及筒内复杂的力学作用是影响武器出筒运动的关键因素,对于整个筒内弹道及弹射过程的安全性具有非常重要的影响[1]。因此,研究燃气弹射过程中内弹道以及燃气流场的分布规律非常有必要。
随着CFD技术的发展成熟,学者们对流体的复杂流动现象开展了研究分析,目前,在武器发射领域,CFD方法应用广泛。谭大成等[2]建立燃气弹射的二维轴对称模型对内弹道过程进行计算研究,研究结果给出了弹射筒内低压室的流场分布情况,其有利于弹射过程的过载分析以及优化设计。白俊华等[3]利用CFD技术对燃气-蒸汽弹射的动力系统进行了相关研究。姜毅等[4-5]采用CFD方法,对同心筒发射装置的流场问题进行了全方位的研究分析,详细分析了弹底与筒底距离、同心筒间隙以及导流锥外形对于筒内流场的影响,其研究成果对同心筒发射装置的研制具有指导作用。Saha S等[6]利用CFD方法建立了多单元垂直发射装置的三维非定常流场模型,分析了燃气在排烟道的流动现象,研究结果表明在发射过程中冷空气的进入会对发射装置内气体聚集仓起到一定的降温作用。胡晓磊和李仁凤等[7-8]考虑到二次燃烧对于燃气弹射的影响,利用CFD方法对低压室初始时刻燃气的二次燃烧现象开展了详细的研究,其研究成果为同心筒发射及燃气弹射内弹道的优化设计提供理论基础。杨晓光等[9]基于CFD理论及动网格技术,对水下航行器的出水及入水过程进行了三维非定常的数值模拟。熊永亮等[10]研究了发射过程中筒内旁泄流产生的原因,并通过数值模拟,给出了如何避免外筒发射拥塞的相关解决方法。马讯等[11]基于二维轴对称的模型,计算并分析了活塞在燃气压力作用下温度场的分布,得出温度是造成活塞变形的主要原因。于勇等[12]对同心筒发射装置的燃气排导装置的流场进行了分析研究,对同心筒发射装置的结构优化提出了合理的方法。马艳丽等[13]针对同心筒垂直发射装置导弹底部燃气温度过高的问题,提出了一种在同心筒底部加装水室的方法来实现降温。
本文根据某武器燃气弹射装置结构,采用理论计算和试验验证相结合的方法,对燃气弹射筒内流场及武器受力特性开展研究,其研究成果对弹射装置的优化设计及实现武器安全稳定发射具有一定指导作用。
1 燃气弹射内弹道流场模型建立 1.1 基本假设燃气弹射过程是一个比较复杂的燃气流动问题,为了能够有效地对其进行数值模拟,在本文研究范围内,进行如下假设:
1)流场分析计算中,视燃气为理想气体;
2)忽略高压室燃气射流中固体颗粒对于流场的影响;
3)不考虑燃气射流中组分化学反应的影响;
4)忽略流体热辐射的影响。
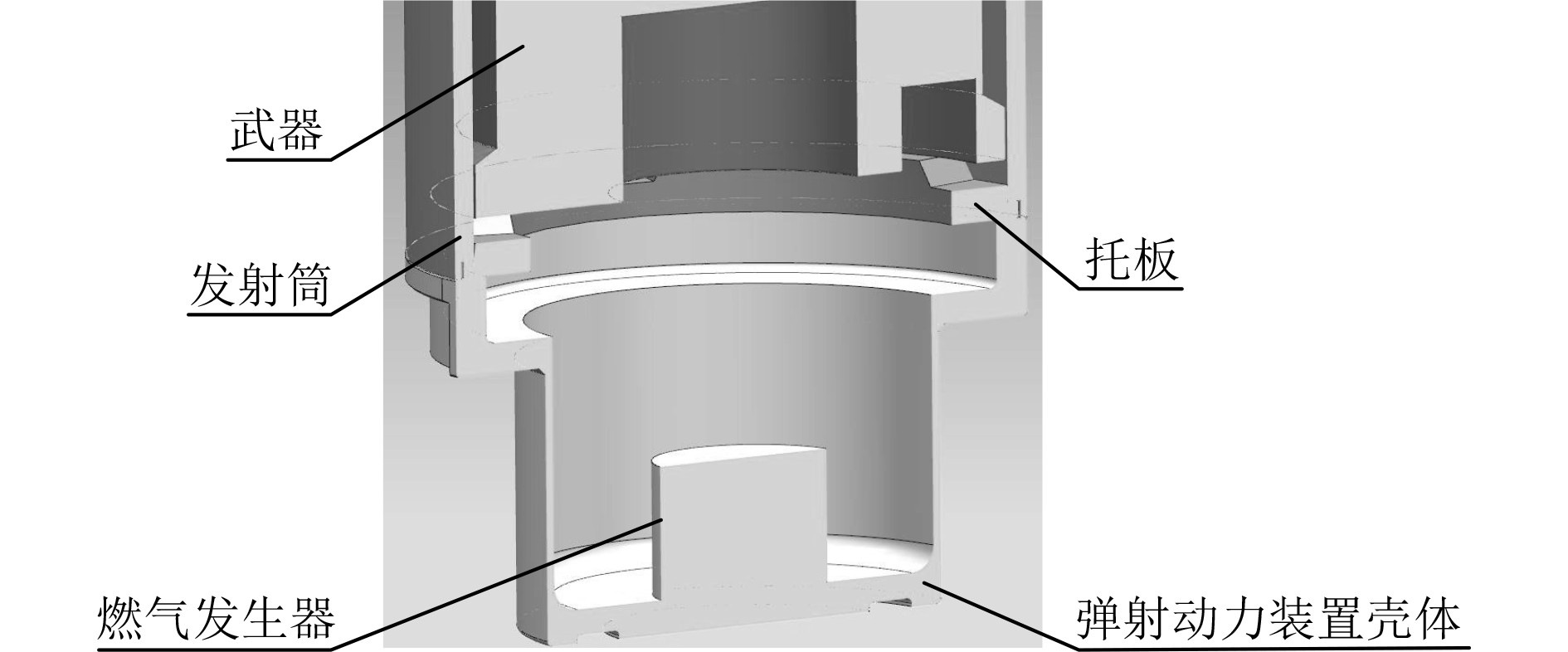
1.2 流场理论模型图1为某燃气弹射装置结构示意图,其中主要包括武器、发射筒、托板以及弹射动力装置,其弹射原理为:收到点火指令后,点火开关触发,燃气发生器开始工作,释放出大量的燃气,燃气在初始自由空间中不断积累并快速提升自由空间的压力,使武器得以克服重力等的束缚开始在筒内运动,进而在燃气压力作用下加速出筒。弹射过程中,所涉及的理论主要包括燃气流动控制方程及武器在发射筒内的运动。
|
图 1 燃气弹射装置三维结构图 Fig. 1 3D structure diagram of gas ejection device |
本文燃气弹射流场数值模拟采用欧拉方法描述,假设在某一时刻下,流场中某一固定位置选取一个控制体
| $ \frac{{\partial (\rho \phi )}}{{\partial t}} + {\rm{div}}(\rho u\phi ) = {\rm{div}}(\varGamma {\rm{grad}}\phi ) + S。$ | (1) |
式中:
燃气弹射过程中,武器总共受到4个力,分别为发射筒内燃气介质的推力、武器自身的重力、适配器与武器之间的摩擦力以及气密环与发射筒之间的摩擦力,由于适配器的固定,所以武器在发射筒内不会出现横向的摆动,在4个力的作用下,武器沿着发射筒轴向运动,根据牛顿第二定律,武器在筒内的运动方程可以表示为:
| $ Ma = {F_e} - {F_s} - {F_q} - G 。$ | (2) |
式中:
| $ {F_e} = pA;$ | (3) |
| $ {F_q} = {f_q}{A_q}\overline p。$ | (4) |
式中:
式(2)中,G为武器重力,
其中,武器在沿着发射筒轴向运动的过程中,任意时刻的速度及位移可以表示为:
| $ \begin{split} &{v_t} = {v_{t - \Delta t}} + \frac{F}{M} \cdot \Delta t ,\\ &{x_t} = {x_{t - \Delta t}} + {v_t} \cdot \Delta t 。\end{split} $ | (5) |
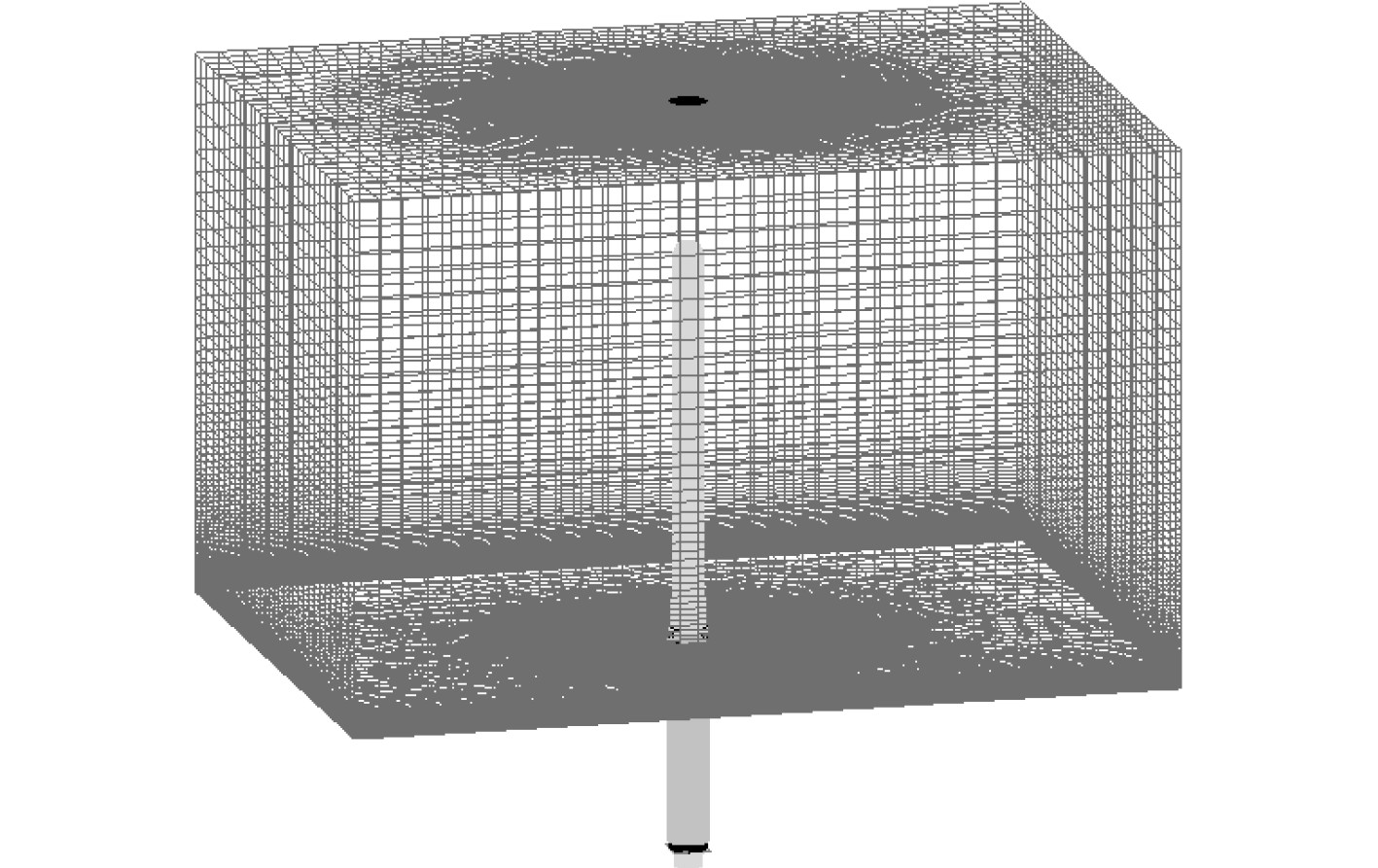
采用Gambit软件对计算流体域进行结构化网格划分,网格数量约为339万,图2为整个计算域网格模型。计算模型在Fluent中进行计算求解,采用标准的
|
图 2 计算域网格 Fig. 2 Computational domain grid |
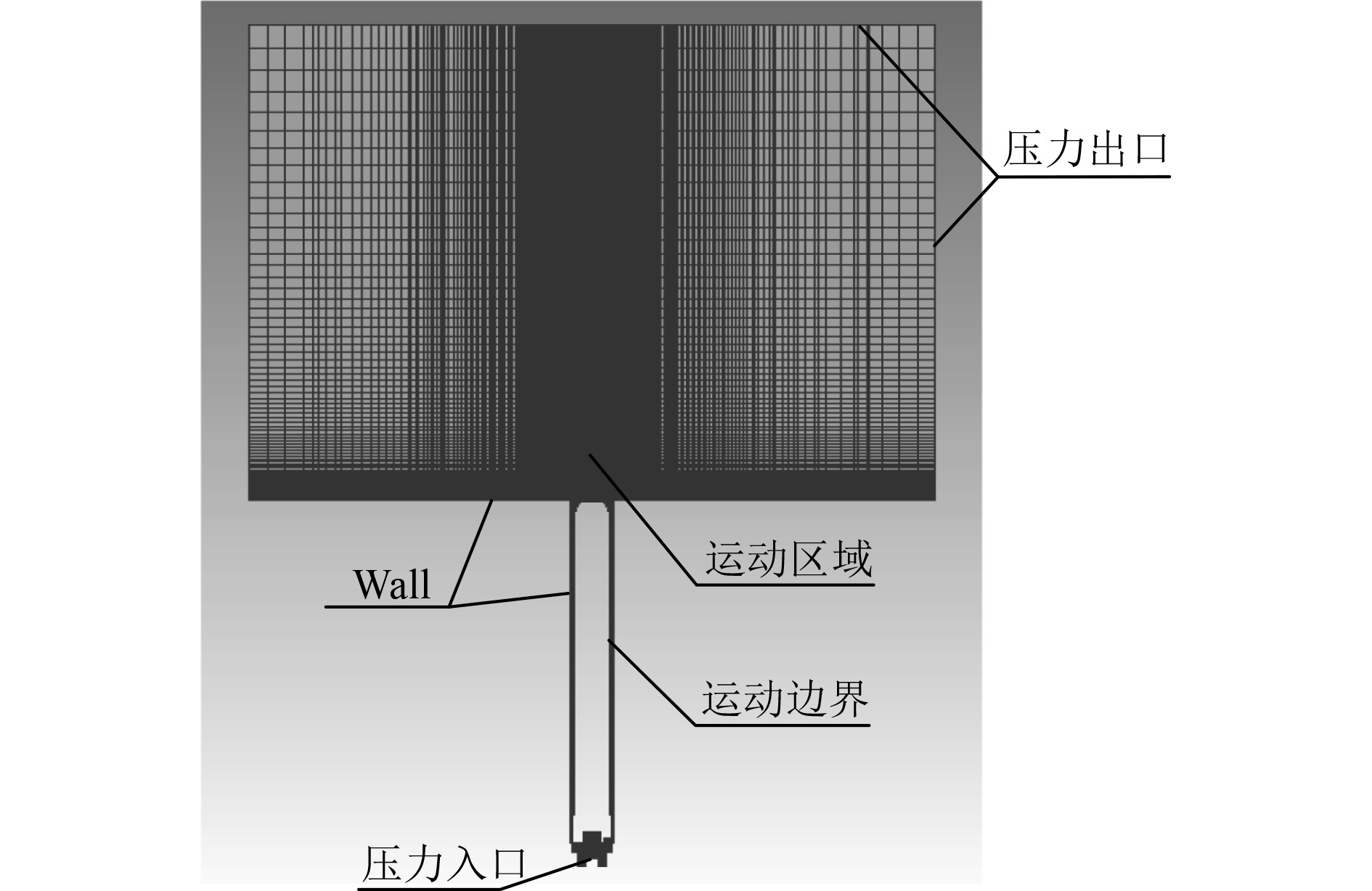
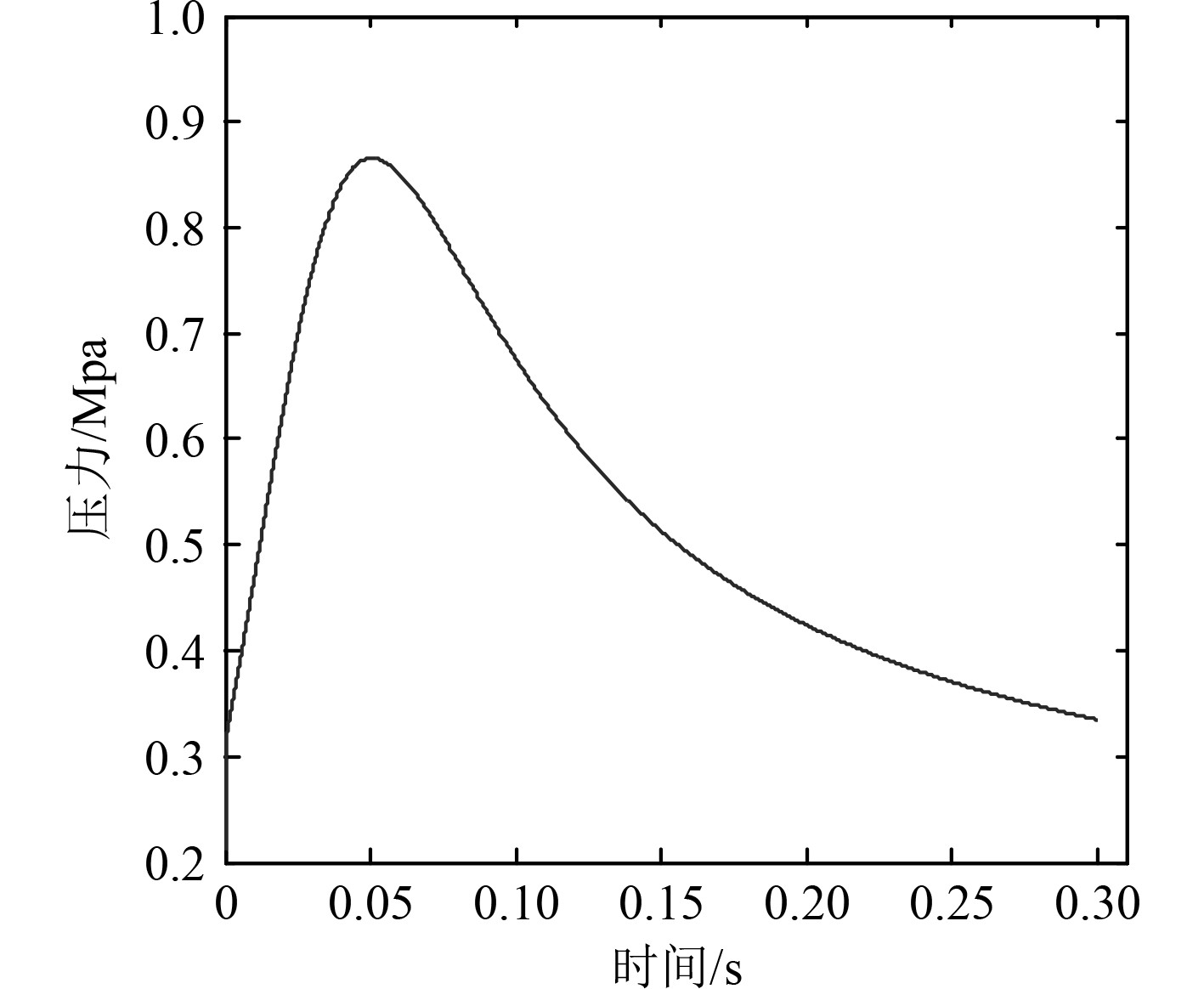
仿真模型中边界条件及初始条件的设置如图3、4所示。本文选择高压室燃气流出面为计算域入口,设置为压力入口,其总压曲线由高压室内弹道工程计算获得。图4为高压室内弹道压力数据,采用线性插值的方法编写用户自定义函数(UDF)实现变压力输入。高压室药柱燃烧总温为1 200 K,因为外部环境为大气,设置外部环境温度为300 K,出口压力设置为101325 Pa。
|
图 3 计算域边界设置 Fig. 3 Computational domain boundary setting |
|
图 4 高压室压力曲线 Fig. 4 High pressure chamber pressure curve |
武器运动边界的更新采用动态层的方法,在运动过程中,武器底部及侧面为运动边界,出口及入口为静止边界,当武器底部网格节点的位移增加量超过设定的计算网格拉伸高度时,武器尾部网格将产分裂,当武器头部网格节点位移压缩量小于设定的计算网格压缩高度时,头部网格将被压溃。设置网格更新的高度为1.5 mm。
2 结果及分析 2.1 压力分布规律基于以上流场数值建模,在Fluent中进行仿真计算,得到燃气弹射内弹道数值计算结果。为了方便观察弹射过程中筒内各时刻流场分布规律,将计算模型沿垂直面进行切分,图5为筒内各时刻的流场压力云图。

|
图 5 各时刻压力云图 Fig. 5 Pressure cloud map at each moment |
可以看出:随着燃气发生器的工作,0.01 s时弹底压力得以克服武器自身重量、摩擦力等的束缚,即将开始运动,到达0.051 s时,武器已在筒内运动,此时,燃气在弹底的压力分布呈现出正对燃气发生器顶部的位置压力较高,其余位置压力相对较低,燃气压力在弹底呈现出分布不均匀的现象,高压燃气对弹底中部造成明显的冲击,这种现象对武器筒内的运动是不利的,可能造成筒内推力不稳定的现象,对武器出筒的安全性造成影响。0.16 s后,武器在筒内作加速运动,随着武器速度的增加,筒内自由空间内的燃气呈现明显的梯度分布规律,靠近弹底的压力较小,靠近高压室的燃气压力较高。
2.2 武器受力及内弹道特性分析为了分析高压燃气是否对弹尾造成冲击,基于UDF技术,读取武器在筒内运动过程中的轴向受力数据,结果如图6所示。
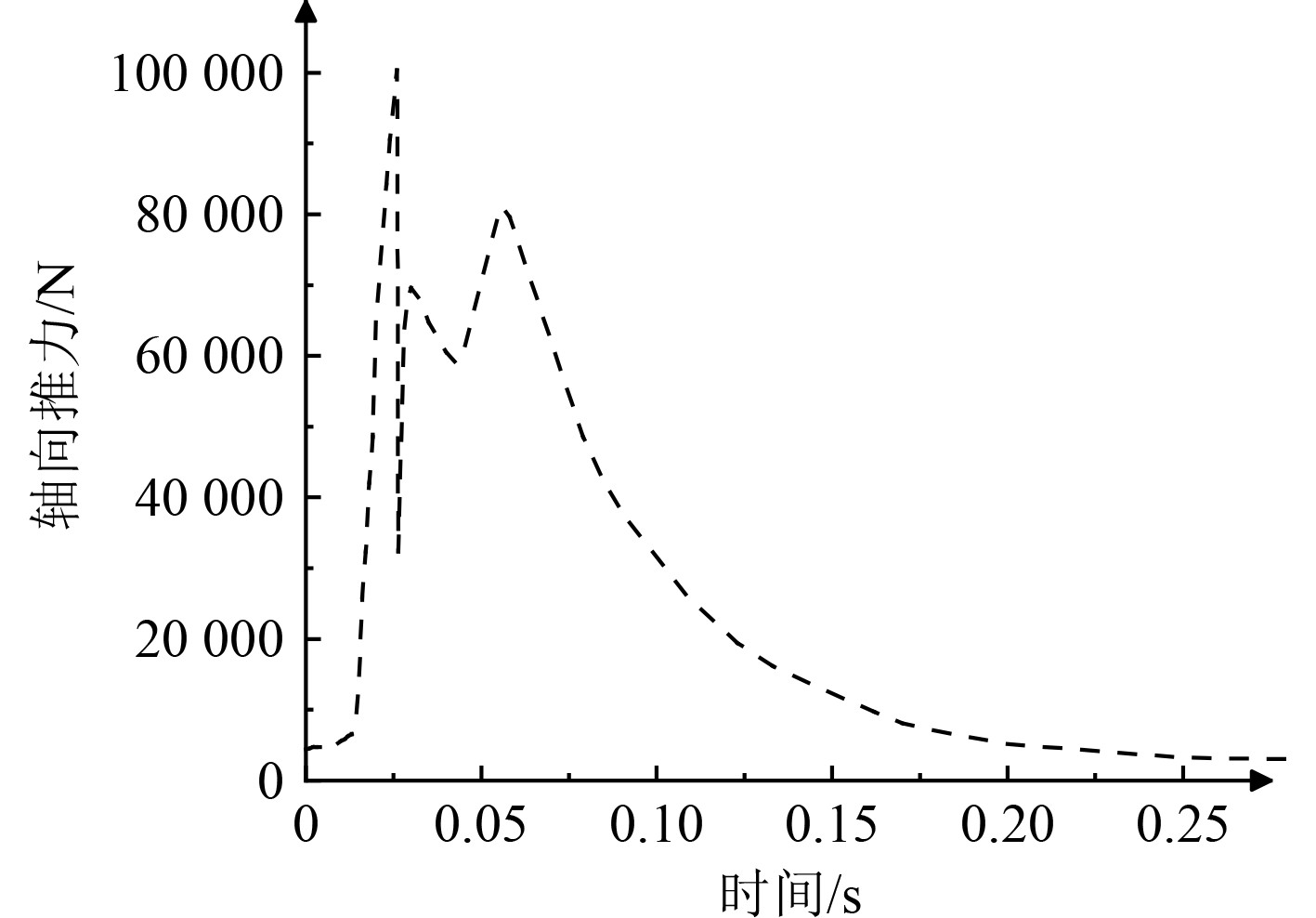
|
图 6 武器轴向受力 Fig. 6 Axial force on weapon |
轴向受力是武器筒内运动总的受力在轴向上的分力,通过编写UDF实现实时计算保存,通过以上轴向力的输出结果可以看出,在武器初始运动时刻,轴向力有一个突变的过程,这说明,武器初始运动时发射筒内燃气压力波动较大,武器尾部受到燃气的剧烈冲击,导致轴向推力不稳定,虽然武器可以在这种不稳定的推力作用下实现出筒,但是这对出筒安全性造成影响,不利于武器的安全稳定发射,存在一定的安全隐患。
图7与图8为武器在筒内运动的加速度曲线和速度曲线。由图7可知:武器初始运动时刻(0.05 s之前),武器加速度出现多个峰值,其中最大的峰值加速度达31.5 g,不利于武器的安全稳定发射;其次,运动前期武器加速度的突变将导致武器在筒内速度变化剧烈,速度的变化将使得筒内自由容腔的容积增大的速度变快,燃气压力在筒内呈现出明显的梯度分布,导致到达武器尾部的燃气压力变小。从图8可以看出,0.15 s之后武器加速度的值变得非常小,武器筒内运动速度变化平缓。
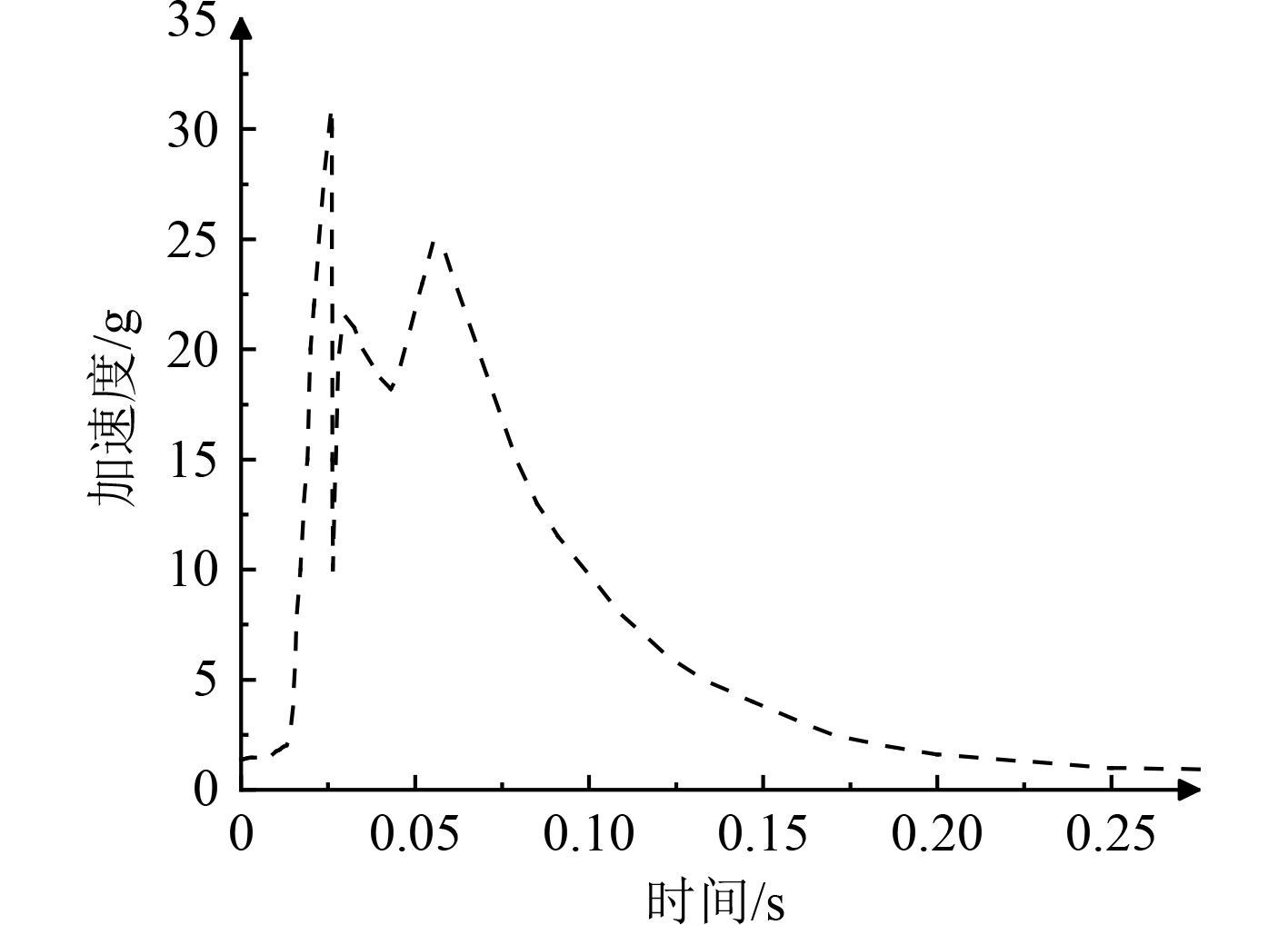
|
图 7 武器加速度曲线 Fig. 7 Weapon acceleration curve |
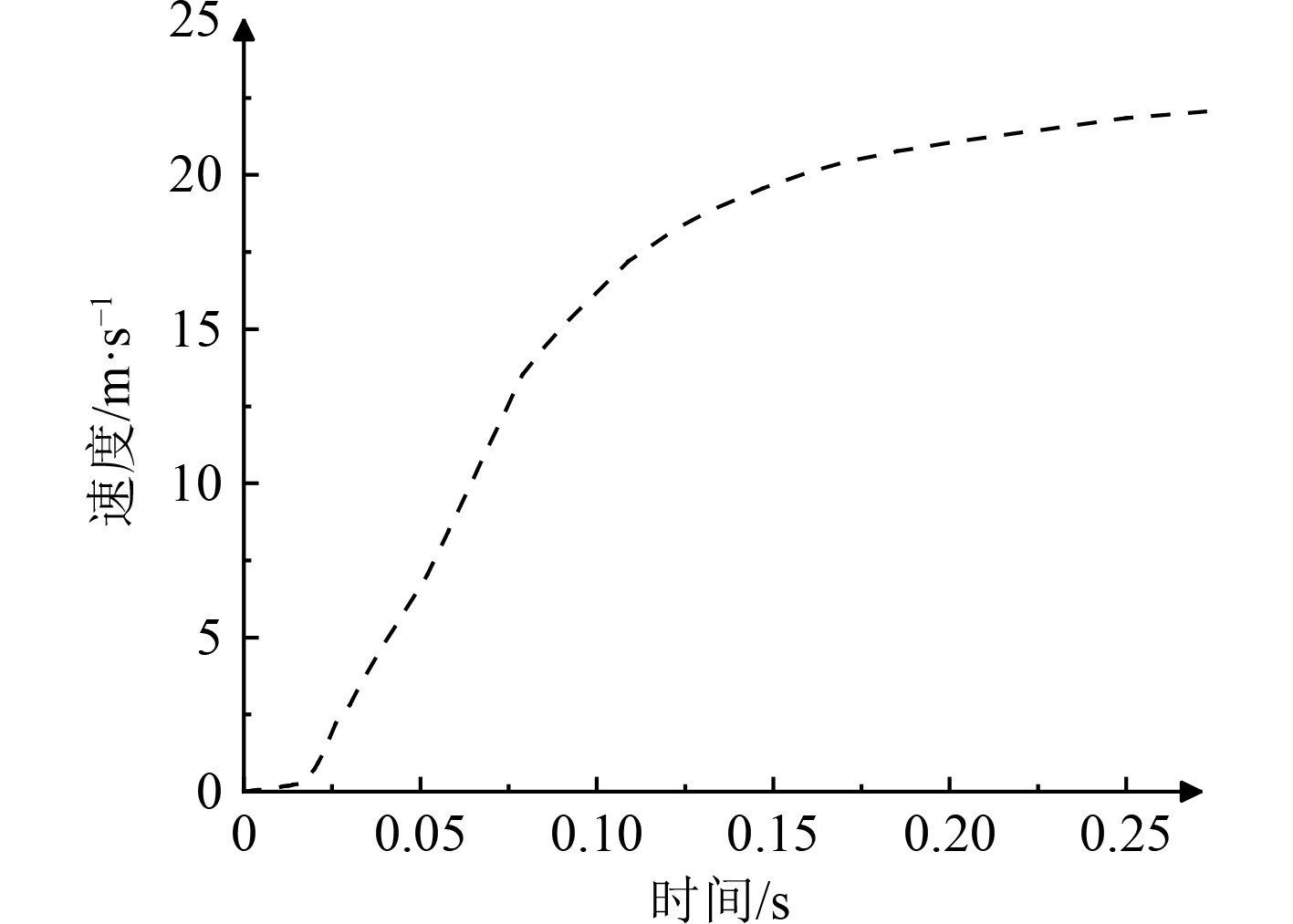
|
图 8 武器速度曲线 Fig. 8 Weapon velocity curve |
基于以上流场特性及武器内弹道特性分析,发现在武器起动的初始时刻,由于燃气发生器释放出大量的高温燃气,这些燃气直接作用于武器尾部,导致武器尾部局部位置受到燃气的冲击,这种现象导致武器的轴向推力发生突变,武器加速度形成多个峰值,对武器的稳定性发射及出筒安全性造成影响。
3 优化设计 3.1 方案设计及仿真针对以上燃气冲击造成的推力不稳定现象,本文考虑采用在燃气发生器与武器之间加装如图9所示的多孔钢板方法。其中,障碍物的存在可以抵挡高温燃气对武器尾部的直接冲击,钢板厚度设置为10 mm,开孔大小为10 mm,孔均匀的分布在圆盘上,共215个孔。
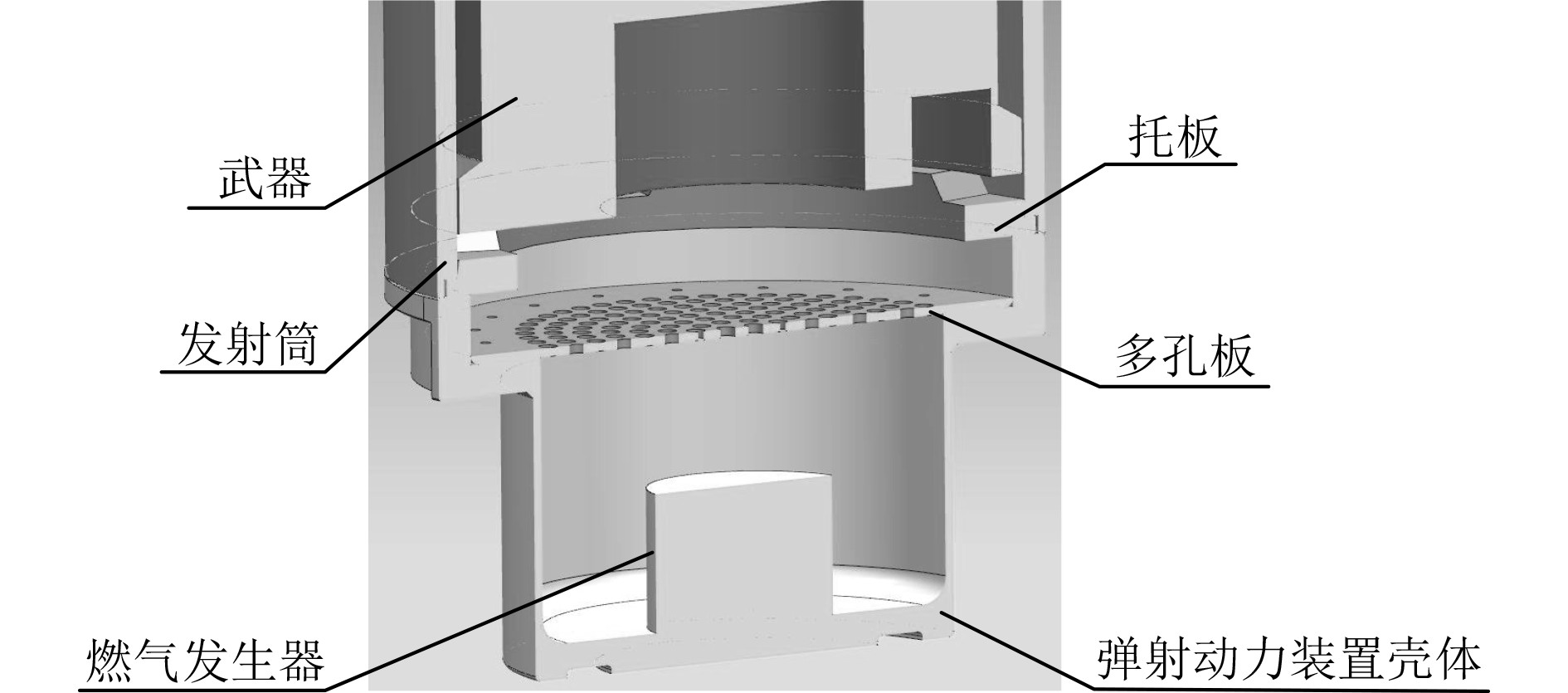
|
图 9 加装多孔板的三维模型 Fig. 9 3D model of adding perforated plate |
对以上加装多孔板之后的模型进行仿真计算,仿真计算结果如图10所示。
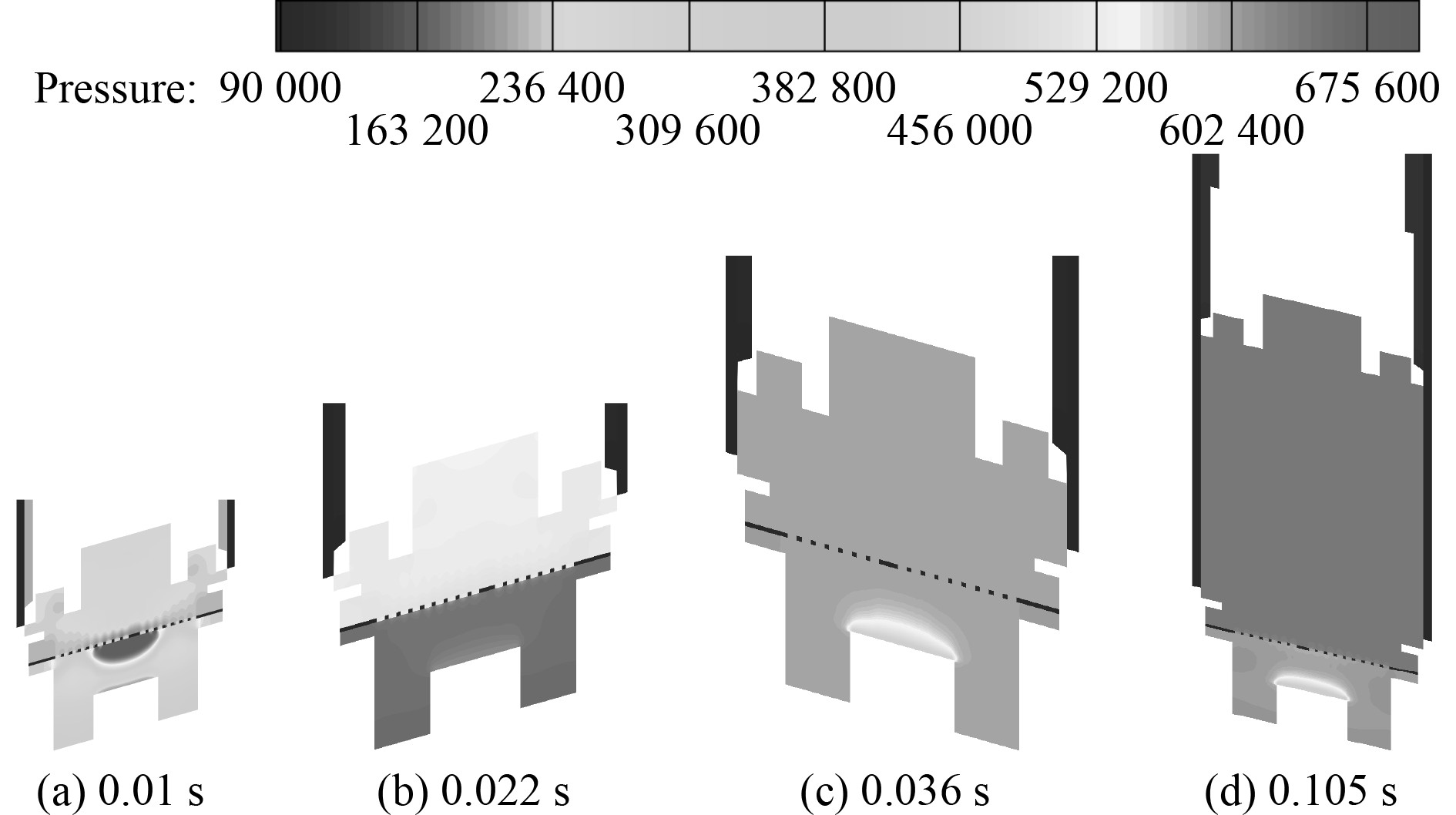
|
图 10 优化后各时刻压力云图 Fig. 10 Pressure cloud map at each moment after optimization |
可以看出,随着燃气发生器的工作,0.01 s时刻,高压燃气开始在动力装置中膨胀,由于多孔板的存在,燃气大部分被阻挡在动力装置内,没有对武器尾部造成直接的冲击。0.022 s时刻,燃气压力分布高压区大多分布于动力装置内,且位于多孔板下方,多孔板上方的燃气也比较均匀的作用于武器尾部。这进一步说明了多孔板的存在对于武器尾部的保护作用,防止其受到高温高压燃气的直接冲击。0.022 s之后,武器在燃气压力作用下开始向上运动,靠近武器尾部的燃气压力分布均匀,武器在稳定推力下开始作加速运动。
3.2 武器受力及内弹道特性分析基于优化后的方案,读取武器在筒内运动过程中的轴向受力数据,结果输出如图11所示。
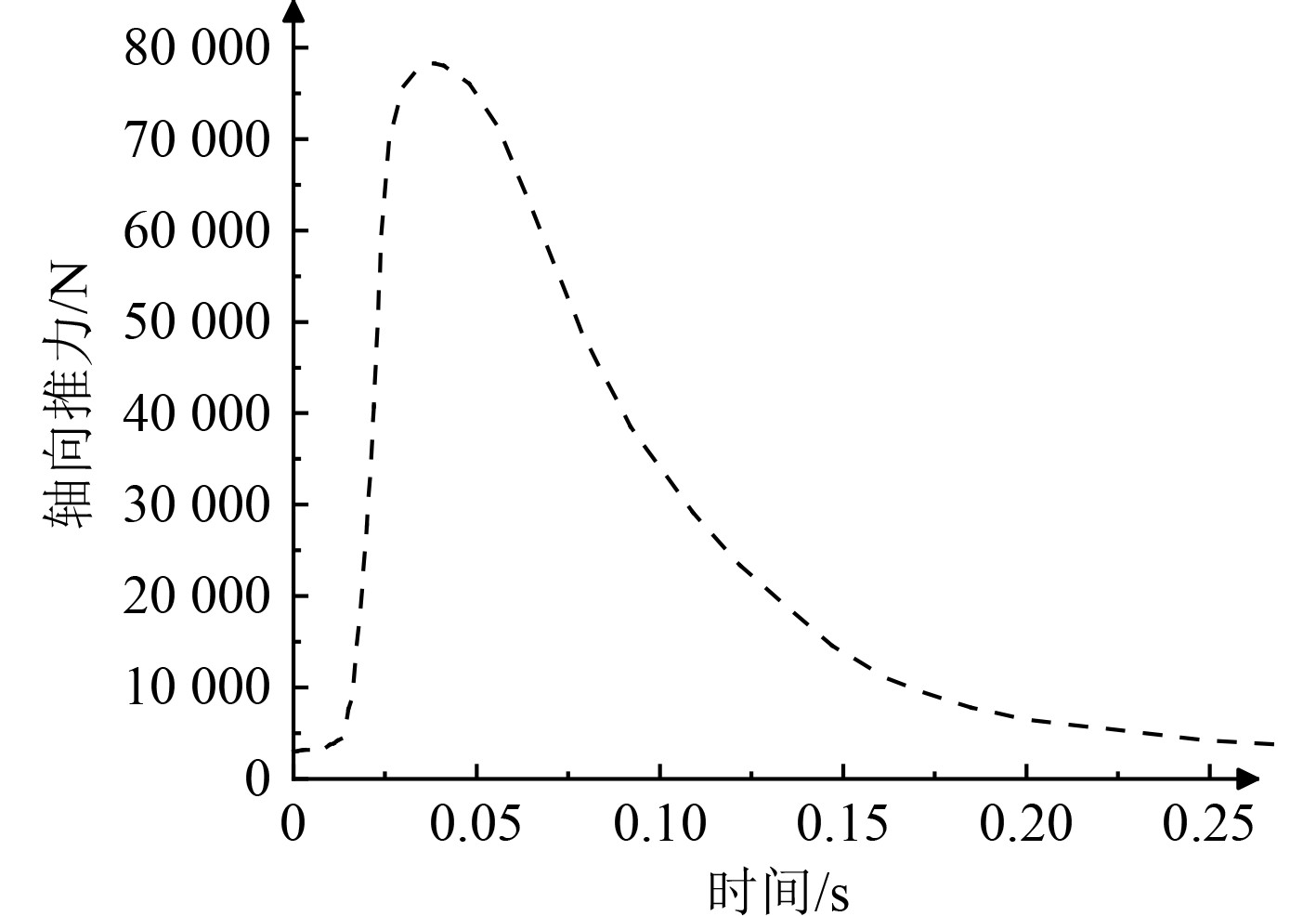
|
图 11 优化后武器轴向受力 Fig. 11 Axial force of weapon after optimization |
可以看出,初始时刻,燃气发生器虽已开始工作,但是其燃气流动并未到达武器尾部,因此,初始时刻武器尾部没有受到燃气压力作用。随着燃气发生器的继续工作,燃气在初始自由容腔中流动,武器受到燃气压力的作用,轴向推力不断增大,此时的推力可以看出无明显的波动现象。这是由于多孔板的存在使得高压燃气射流没有直接冲击武器尾部,而是通过多孔板小孔比较均匀的作用于武器尾部,推力呈稳定增长的趋势。
图12与图13分别为加装多孔板后仿真所得的武器内弹道数据。可以看出,武器在稳定的推力作用下呈现稳定增加的加速度,到达加速度峰值之后,随着武器在筒内运动速度的增大,筒内容腔燃气流动的自由容积不断增大,到达弹尾的燃气压力有所降低,武器加速度开始逐渐减小,武器速度变化逐渐平缓。
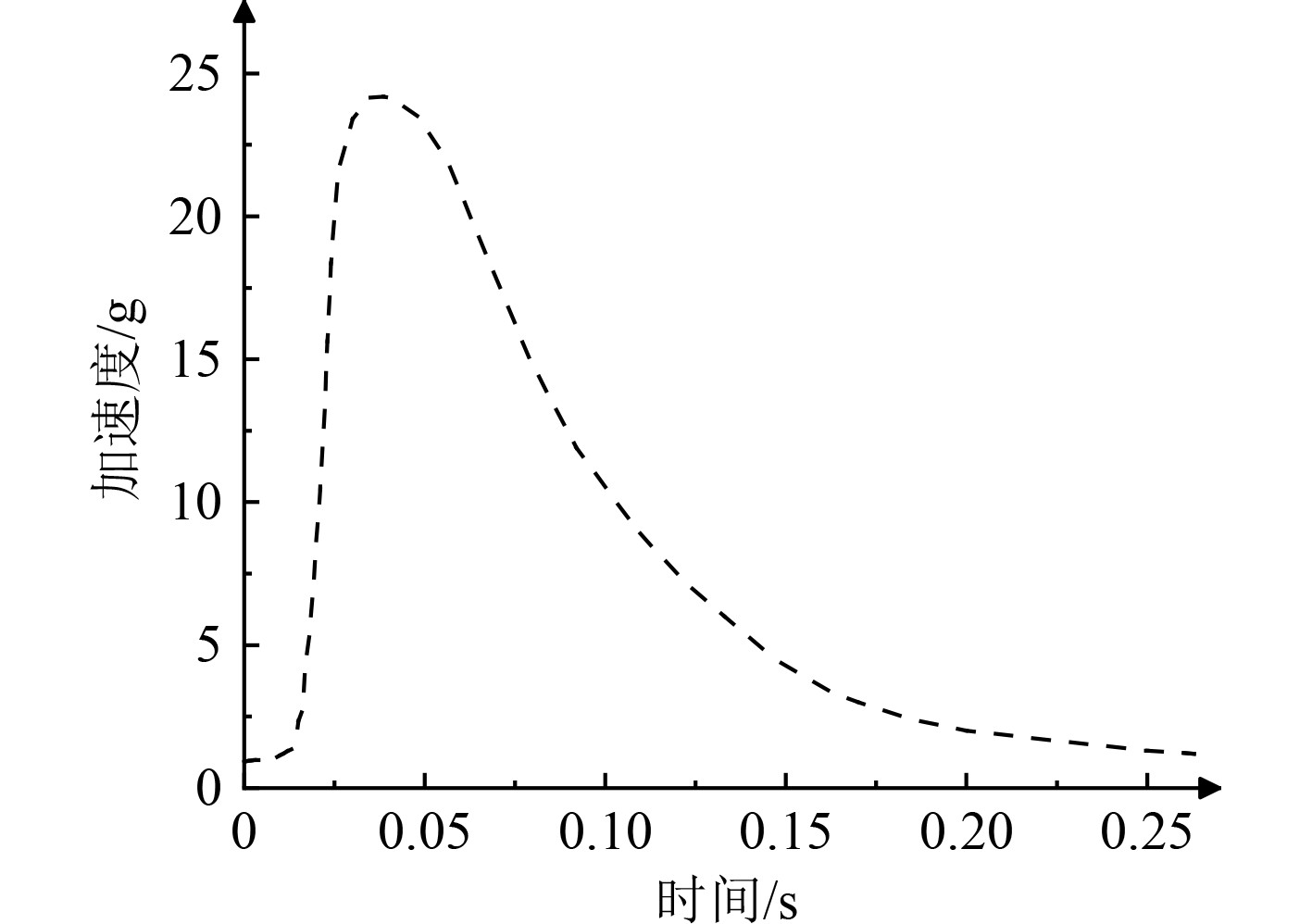
|
图 12 优化后加速度曲线 Fig. 12 The acceleration curve after optimization |
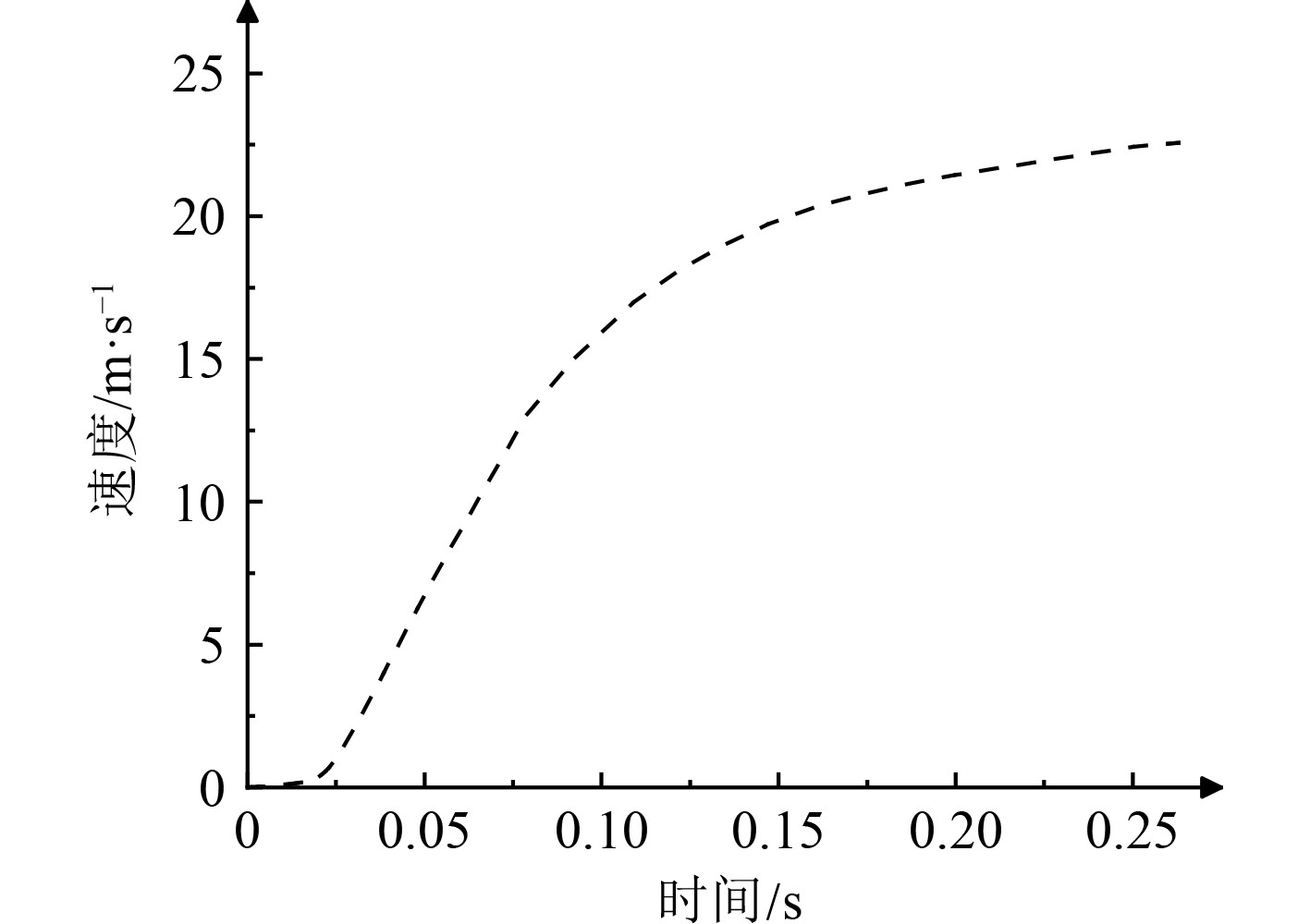
|
图 13 优化后速度曲线 Fig. 13 The speed curve after optimization |
基于以上优化设计方案进行相关试验,试验中保持试验条件与优化设计方案一致,在燃气发生器与武器之间加装多孔隔热板,高压室装药质量与以上优化仿真一致。采用加速度传感器用于测量武器在筒内的运动及受力情况。动力装置与发射筒连接位置无明显熏黑现象,这说明试验中不存在明显的漏气现象,工作完成之后的燃气发生器顶部滤网无明显堵塞,燃气发生器外形无明显变形,说明试验中燃气通道顺畅,试验条件良好。图14为武器加速度实测结果。
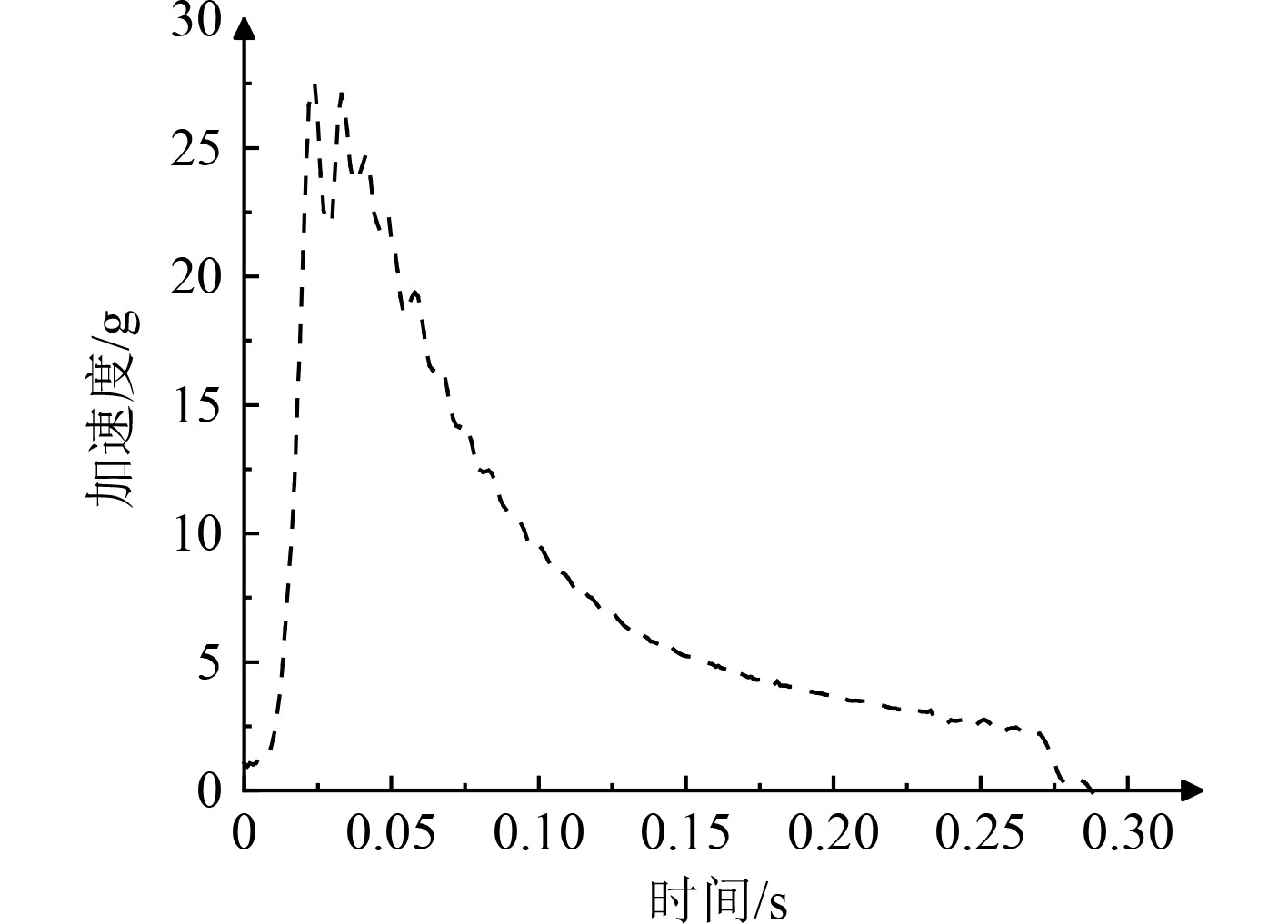
|
图 14 加速度实测数据 Fig. 14 Measured acceleration data |
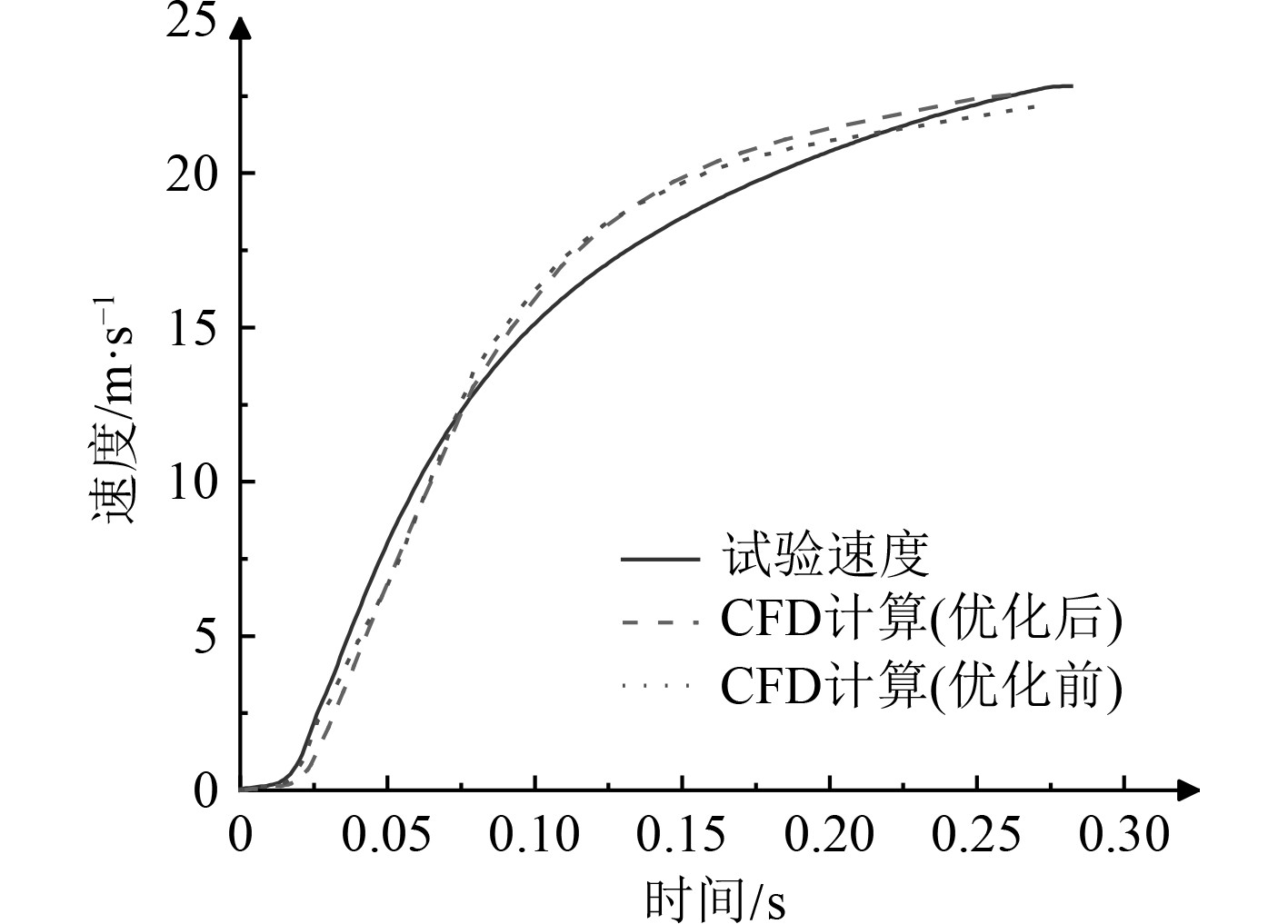
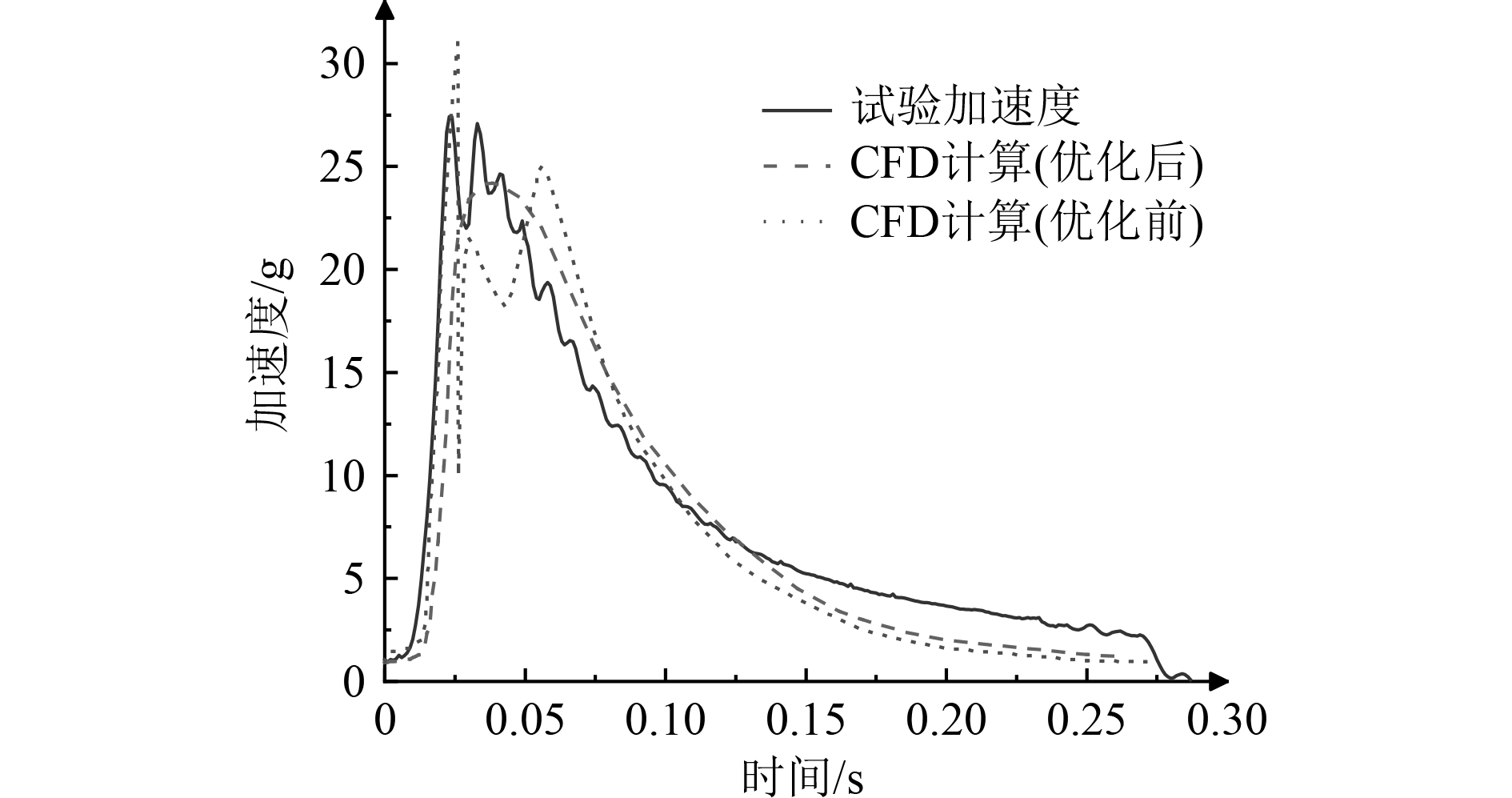
将试验速度曲线与CFD计算速度曲线进行对比,如图15所示。将试验所得加速度曲线与CFD计算加速度曲线进行对比,如图16所示。可以看出,试验所得速度曲线与CFD计算结果吻合较好,出筒速度基本一致,加速度变化存在不一致的的地方。具体表现为:试验中所测得加速度在武器运动前期存在明显的波动现象,而CFD计算的武器加速度变化相对平缓,不存在明显的突变现象。分析原因主要是由于燃气发生器的工作过程极其复杂,火药的燃烧更是瞬息万变,目前理论计算所得高压室压力数据不能够完全揭示火药的燃烧过程,采用理论计算高压室压力作为CFD计算的输入可能导致理论计算过于理想化,造成与实际测量之间的误差。另外,基于加速度传感器的内弹道数据测量可能存在一定误差,测量技术的精度极大的受限于传感器精度、灵敏度等因素的影响,合理可靠的测量方法是获得最真实数据的基础。
|
图 15 速度对比 Fig. 15 Speed comparison |
|
图 16 加速度对比 Fig. 16 Acceleration comparison |
表1为内弹道参数对比表。
|
|
表 1 内弹道参数对比 Tab.1 Comparison of internal ballistic parameters |
可以看出,结构优化后的CFD计算数据出筒速度为22.56 m/s,试验所得出筒速度为22.92 m/s,其误差仅为0.36 m/s,误差较小。尽管试验中测得加速度存在波动,且所测得的最大加速度比CFD计算所得结果大了2.72 g,但是其变化趋势基本与CFD计算一致,据此,可判定目前所用CFD计算方法能够满足工程实际的需要。经过对比优化前后的数据可知,加装多孔板之后,武器出筒速度从22.18 m/s增加到22.56 m/s,最大加速度从30.9 g降低到24.18 g,优化效果明显。此方法能够有效降低筒内过载并提高出筒速度,有利于武器发射的稳定性及安全性。
5 结 语本文以三维流场理论模型为基础,建立燃气弹射过程的三维流场计算模型,并利用Gambit软件为计算模型划分网格,采用Simple算法和标准的
| [1] |
谭大成. 弹射内弹道学[M]. 北京: 北京理工大学出版社, 2015.6.
|
| [2] |
谭大成, 苗佩云. 弹射器低压室二维内弹道模型及数值研究[J]. 弹箭与制导学报, 2006, 26(4): 224-226. DOI:10.3969/j.issn.1673-9728.2006.04.069 |
| [3] |
白俊华, 胡春波, 李佳明. 固体发动机喷管喉衬流固耦合换热规律数值研究[J]. 西北工业大学学报, 2014(1): 23-28. |
| [4] |
陈建伟, 姜毅. 同心筒发射装置燃气流场的三维数值计算[C]// 中国宇航学会发射工程与地面设备专业委员会学术会议, 2003: 184−188.
|
| [5] |
傅德彬, 姜毅, 陈建伟, 等. 同心筒自力发射燃气排导优化设计[J]. 弹箭与制导学报, 2004, 24(3): 42-45. DOI:10.3969/j.issn.1673-9728.2004.03.016 |
| [6] |
Saha S, Chakraborty D. Plume-ducting system design of vertical launcher using computational-fluid-dynamics tools[J]. Journal of Spacecraft and Rockets, 2013, 50(3): 715-718. DOI:10.2514/1.A32303 |
| [7] |
胡晓磊, 孙船斌, 郭佳肄, 等. 二次燃烧对燃气弹射初容室载荷影响数值研究[J]. 兵器装备工程学报, 2020, 41(11): 70-73. DOI:10.11809/bqzbgcxb2020.11.013 |
| [8] |
李仁凤, 乐贵高, 马大为. 燃烧产物特性对燃气弹射内弹道与载荷的影响研究[J]. 兵工学报, 2016, 37(2): 245–252.
|
| [9] |
杨晓光, 党建军, 王鹏, 等. 波面环境对高速入水载荷及弹道特性影响试验研究[J]. 西北工业大学学报, 2021, 39(6): 1259-1265. DOI:10.3969/j.issn.1000-2758.2021.06.011 |
| [10] |
熊永亮, 郜冶, 李燕良. 同心筒发射中旁泄流影响的数值研究[J]. 弹箭与制导学报, 2007, 27(4): 194-197. DOI:10.3969/j.issn.1673-9728.2007.04.059 |
| [11] |
马迅, 赵刚. 发动机活塞的热结构耦合分析[J]. 机械设计与制造, 2005(11): 40-42. DOI:10.3969/j.issn.1001-3997.2005.11.020 |
| [12] |
于勇, 徐新文, 傅德彬. 同心筒发射装置燃气排导的气体动力学原理分析[J]. 航空动力学报, 2012, 27(3): 501-507. DOI:10.13224/j.cnki.jasp.2012.03.007 |
| [13] |
马艳丽, 姜毅, 王伟臣, 等. 湿式同心筒自力垂直热发射技术降温效果研究[J]. 弹道学报, 2010, 22(4): 89-93. |
 2023, Vol. 45
2023, Vol. 45
