0 引　言

随着船舶航运规模的增大，航线的密集性越来越强，需要对航线进行优化调度和控制，结合航线数据趋势性预测和分析模型，通过对航线数据趋势性特征分析，构建船舶航线数据融合和适应度评价模型，实现对航线数据统计特征分析，提高对航线数据趋势性预测能力。研究航线数据趋势性预测方法，分析航线数据潜在特征和时间相关性特征，提高航线调度和规划能力^[1]。

当前，对航线数据趋势性预测方法主要采用分布式传感信息跟踪识别方法、Lyapunove指数预测方法以及BP神经网络预测方法等，通过航线数据传输控制和均衡配置，根据数据在低维空间的向量分布式融合调度模型，采用无线ZigBee组网控制协议进行航线调度^[2]，但传统方法进行船舶航线数据趋势性预测的实时性不好，时间偏差较大^[3]。

对此，本文提出基于深度学习的船舶航线数据趋势性预测方法。首先构建集中式访问和分布式传感结合的方式实现对航线数据采样和融合处理，然后采用深度学习和时间序列标签特征检测方法实现对航线数据的多元时间序列的分布重构，根据重构结果和数据聚类趋势性实现对船舶航线数据趋势性预测。最后进行实验测试，验证了本文方法在提高船舶航线数据趋势性预测精度方面的优越性能。

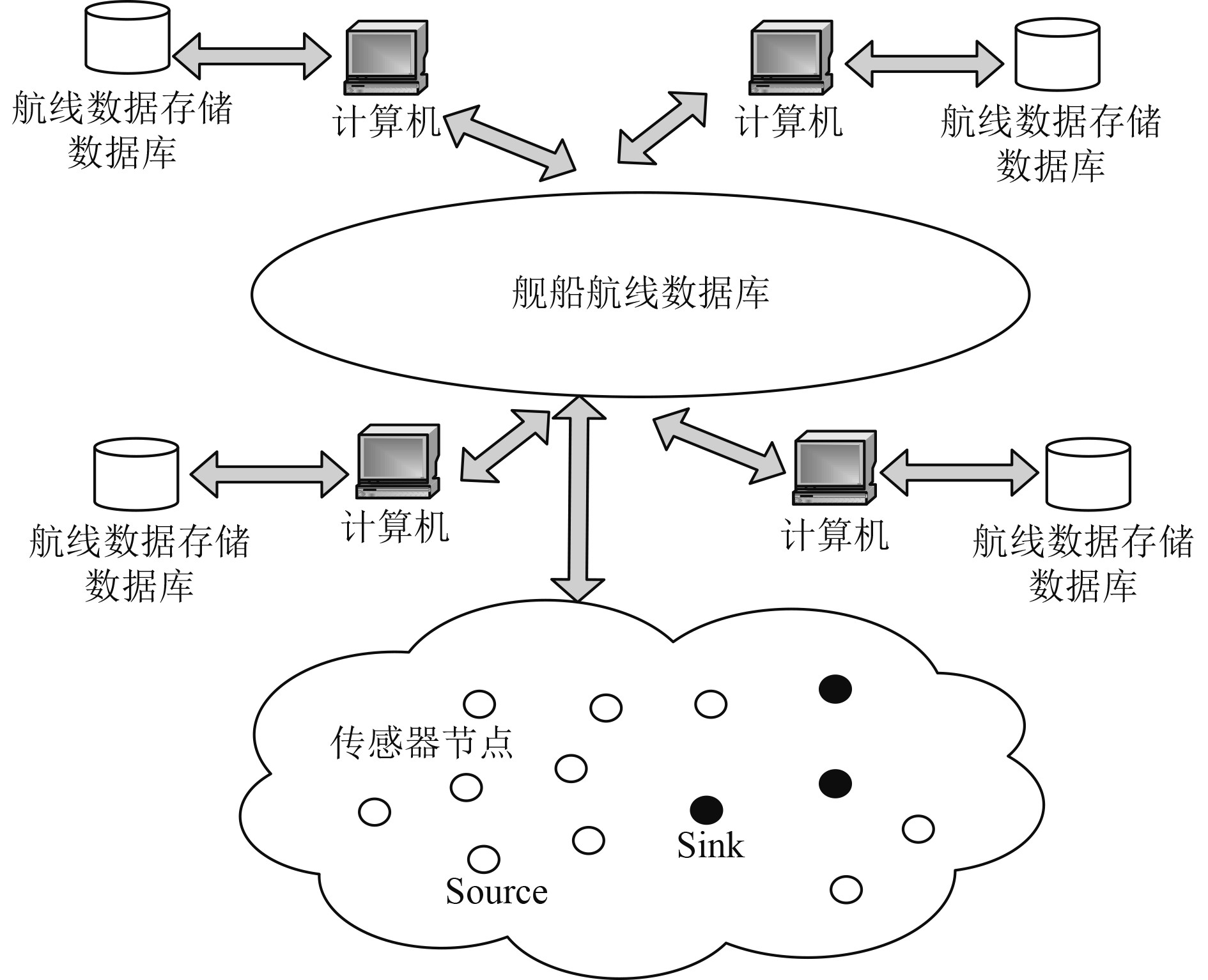
1 数据采样和特征分析 1.1 船舶航线数据采样

为了实现对船舶航线数据趋势性预测，首先构建船舶航线数据采集和特征分析模型，通过多元时间序列的分布式组合控制，采用信道均衡控制技术，构建航线数据趋势性预测的参数识别模型，采用模板特征匹配和交叉性组合编译控制方法，构建航线数据趋势性预测的参数融合模型^[4]，得到船舶航线数据分布结构模型如图1所示。

根据图1所示的船舶航线数据分布结构模型，得到进行船舶航线数据趋势性预测的模型参数构建^[5]，得到初始向量模型结构为：

$ {x_{ij}}^\prime = {x_i} - \rho + j\frac{{2\rho }}{n} 。$

(1)

式中： $ \rho $ 为船舶航线数据趋势性预测的内控系数， $ {x_i} $ 为船舶航线数据趋势性效果控制的解释变量。

结合模糊度融合，得到船舶航线数据趋势性误差评价函数为：

$ e(x) = \sum\limits_i {{d_{ei}}} {D_s}B(x).{d_e} 。$

(2)

式中： $ {d_{ei}} $ 为航线调度的训练参数， $ {d_e} $ 为航线数据趋势性知识讲授的动态参量 ， $ {D_s} $ 为自相关关联参数， $ B(x) $ 为航线的偏移特征值，用联合参数识别的方法，构建航线数据趋势性分布结构特征量，建立航线数据趋势性预测矩阵为：

$ B = \left[ {\begin{array}{*{20}{c}} { - 1}&0&0&{ - 1}&0&0 \\ 0&{6\xi /L}&{3\xi - 1}&0&{6\xi /L}&{3\xi - 1} \end{array}} \right] 。$

(3)

式中， $ \xi \in [ - 1,1] $ ，表示船舶航线节点异构性融合的覆盖系数。

采用多样本融合聚类的方法，建立船舶航线数据的关联规则数据库，得到第n+1和n步的评价模型为：

$ d\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {{\rm{arctan}}\left( {\dfrac{{X_2' \left( t \right)}}{{X_1' \left( t \right)}}} \right),} & {X_1' \left( t \right) > 0}，\\ {{\rm{arctan}}\left( {\dfrac{{X_2' \left( t \right)}}{{X_1' \left( t \right)}}} \right) + \pi } ，& {X_1' \left( t \right) < 0,t = 1,2,\cdots , T}，\\ {\pi /2}，& {X_1'\left( t \right) = 0}。\end{array}} \right. $

(4)

式中， $ X'_1(t) $ 为航线数据趋势性预测一阶统计特征量， $ X'_2(t) $ 为航线数据趋势性预测的二阶统计特征量。

采用相空间重构和特征压缩方法，建立船舶航线数据趋势性的特征聚类模型，得出航线数据趋势性的概念图结构参数特征值。

1.2 船舶航线数据聚类处理

采用决策寻优，得到船舶航线数据序列分布的特征解，结合自相关特征分析的方法，建立船舶航线数据趋势性预测的解释变量满足 ${x_0}$ ( ${x_0} = {[{\varphi _0},{\dot \varphi _0},{\theta _0}]^{\rm{T}}}$ )，联合关联检测特征量为 ${\ \mu _1}$ ， ${\ \mu _2}$ 和 ${\ \mu _m}$ ，分析航线数据调度的边界节点，得到航线数据趋势性挖掘的支撑构成集合定义为：

$ \begin{split} {d_{m + 1}}(m) =& {d_{k + 1}}(m) \pm \\ &\sqrt {{{({d_m}(0){e^{{\lambda _1}}} + 1)}^2} - \sum\limits_{i = 1}^{m - 1} {{{[{d_{m + 1}}(i) - {d_{k + 1}}(i)]}^2}} } \end{split} 。$

(5)

式中： $ {d_{m + 1}}(m) $ 为航线数据BIBD 的构造属性在第 $ m $ 点的预测值， $ {d_{k + 1}}(m) $ 为第 $ m $ 点处任意2个向量的位置参数。得到船舶航线数据趋势性质量特征向量 $ L{\left( {{Z_2} + {Z_3}} \right)^{ - 1}}{L^{\rm{T}}} $ 与 $ {M^{\rm{T}}}{\left( {{Z_2} + {Z_3}} \right)^{ - 1}}{M^{\rm{T}}} $ 的Bergmann核。采用负载均衡调度和数据块分组特征距离方法进行船舶航线数据趋势性相关特征检测，得到船舶航线数据聚类动态方程为：

$ K = \left(\frac{1}{2}(u_A^ + - u_A^ - ) - \frac{1}{2}{F_{{A_1}}},\frac{1}{2}(u_A^ + - u_A^ - ) - \frac{1}{2}({F_B} + {F_{{A_2}}})\right) 。$

(6)

式中： $ u_A^ - $ ， $ u_A^ + $ 分别为船舶航线数据趋势性动态聚类参数； $ {F_{{A_1}}} $ 和 $ {F_B} $ 分别为机器学习的聚类中心和模糊边缘特征量。

根据聚类结果进行趋势性动态分布检测。

2 船舶航线数据趋势性预测 2.1 预测深度学习模型

将船舶航线数据趋势性分布向量集合可以划分为 c 个不相交的正交子集，在有限射影平面内建立船舶航线数据趋势性分布的模糊度函数为：

$ {d_i} = \left[ {\begin{array}{*{20}{c}} {{k_b}}&{ - {k_b}} \\ { - {k_b}}&{{k_b} + {k_s}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{x_b}} \\ {{x_b}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{m_b}}&{} \\ {}&{{m_s}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_b}} \\ {{u_s}} \end{array}} \right\}{d_{ei}} 。$

(7)

式中： $ {x_b} $ 为编码映射到潜在空间的约束参数聚类参数， $ {u_b} $ 为航线数据趋势性序列相关性的贡献度， $ {u_s} $ 为编码器学习时间序列的特征， $ {m_b} $ 为生成样本和真实样的联合相似度， $ {m_s} $ 为周期一致性损失的相似特征量， $ {d_{ei}} $ 为第 k个生成器生成的样本， $ {k_b} $ 为学习数据相关性统计特征参数， $ {k_s} $ 为最小化输入特征，建立航线数据趋势性效果的重构误差分析模型，表示为：

$ p\left( r \right) = \frac{1}{{\sqrt {2\pi } {\sigma _s}}} = - 2E{\left({X_1}\cdot\frac{{\partial H}}{{\partial \tau }}\right)^{\rm{T}}} 。$

(8)

式中： $ {\sigma _s} $ 为航线数据趋势性的目标在属性， $ {X_1} $ 为时序数据采样周期性待估参数， $ H $ 为负载倾斜传递函数。

根据数据访问请求数量的差异性，得到航线数据趋势性预测的模糊控制方程为：

$ \begin{split} & \left[ {\begin{array}{*{20}{c}} {{m_b}}&{} \\ {}&{{m_s}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\ddot x}_b}} \\ {{{\ddot x}_s}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{c_b}}&{ - {c_b}} \\ { - {c_b}}&{{c_b} + {c_s}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\ddot x}_b}} \\ {{{\ddot x}_s}} \end{array}} \right\} + \\ & \left[ {\begin{array}{*{20}{c}} {{k_b}}&{ - {k_b}} \\ { - {k_b}}&{{k_b} + {k_s}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{x_b}} \\ {{x_b}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{m_b}}&{} \\ {}&{{m_s}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_b}} \\ {{u_s}} \end{array}} \right\} = 0 。\end{split} $

(9)

式中， $ {u_b} $ 为航线数据趋势性预测约束控制变量， $ {c_s} $ 为航线数据趋势性预测果的统计信息特征量， $ {k_b} $ 为负载均衡存储参数， $ {k_s} $ 为历史访问行为数据， $ {u_s} $ 为访问数据的缓存区间， $ {m_b} $ 为写入元数据缓存的状态特征值， $ {m_s} $ 为训练预测分类特征值。

2.2 船舶航线数据重组与预测

采用多队列调和联合特征解析方法，得到船舶航线数据趋势性分布的离散度函数， ${1 / {{\mu _i}}} \leqslant {1 / {{\mu _m}}} < {1/ {{\lambda _0}}} < {1 / {{\mu _j}}}$ ，船舶航线趋势性分布的最优决策函数为：

$ F = {X_2} - {X_1}\cdot H = \min \left(\sum\limits_i^N {{R_i}} \right) = \left\{ \begin{array}{cc} \dfrac{{{s_{ij}} - s(i,j)}}{{{s_{ij}}}}，& s(i,j) < {s_{ij}} ，\\ e(i,j)，& s(i,j) \geqslant {s_{ij}} 。\end{array} \right. $

(10)

式中， $s_{ij} $ 为航线数据趋势性分布的存储结构模型。

根据对航线数据趋势性空间分布结构分析，得到航线数据趋势性预测的自适应调度。设船舶航线趋势性分布的最优采样周期为 $T_s $ ，则每周期包含的航线趋势性分布数据点数 $ m = T/{T_s} $ ，航线数据趋势性分布特征检测的延迟函数为：

$ \begin{aligned} {\tau _{k + 1}} =&{\tau _k} + \mu ( - {{\hat G}_k}) = {t_{ACK}} + \\ &\sum\limits_{i = 0}^N {\left( {DIFS + C_R^{\left( i \right)} \times {t_{slot}} + {t_{DATA}} + SIFS + {t_{T - start}}} \right)}。\\ \end{aligned} $

(11)

式中， $ {\tau _k} $ 为冲激响应， $ {t_{ACK}} $ 为时间延迟， $ DIFS $ 为船舶航线趋势性分布模型化参数， $ SIFS $ 为最优解析融合参数， $t_{DATA} $ 为统计时间函数。

根据上述算法，实现对船舶航线数据趋势性预测。

3 仿真实验与结果分析

实验中设定航线数据采样条数为2400，训练样本集为120，采样时间延迟为1.2 ms，嵌入维数为8，深度学习为迭代次数为120，数据集规模分布如表1所示。

根据表1参数设定，进行航线趋势性预测的统计分析，得到描述性统计分析结果如表2所示。

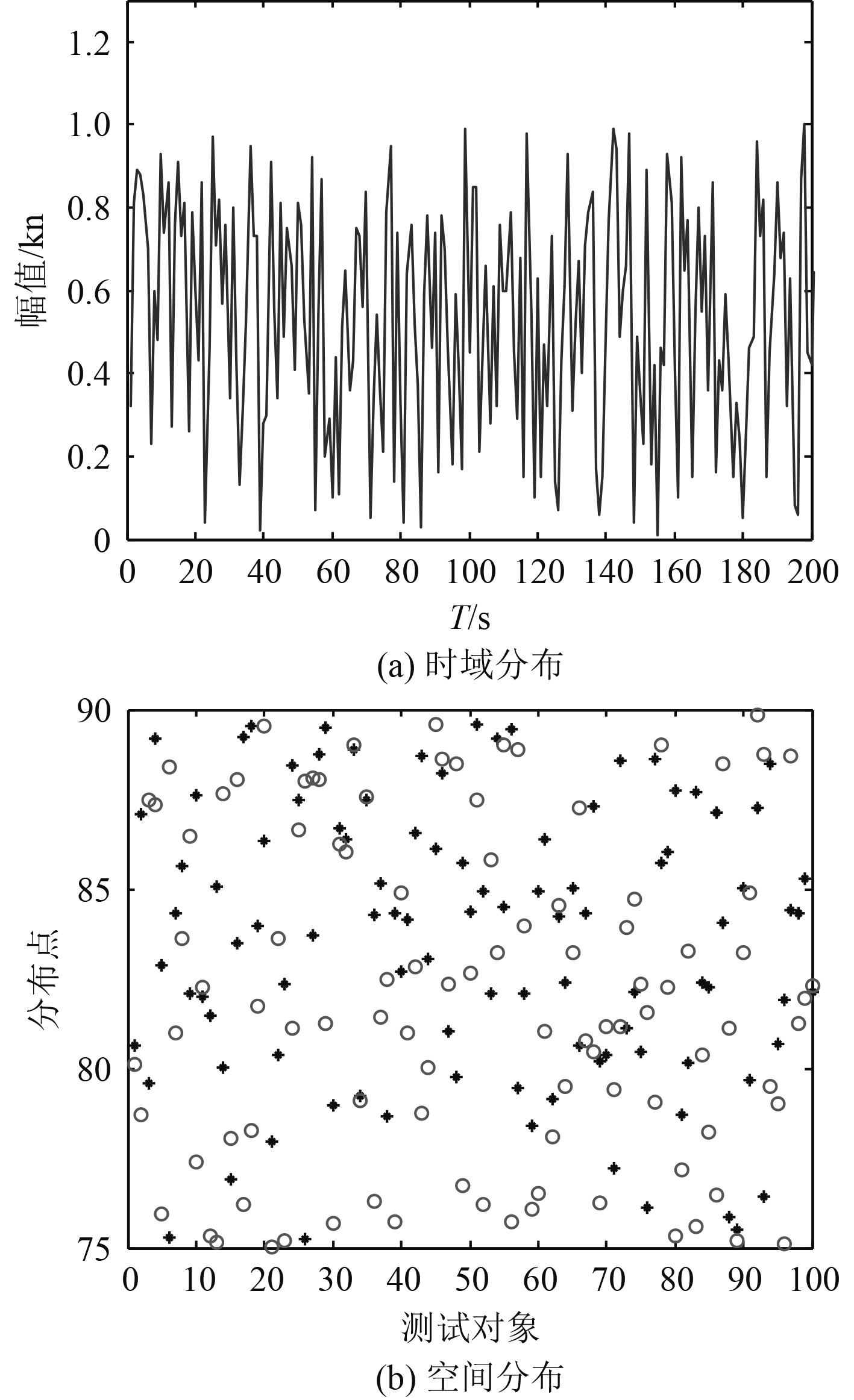
根据上述统计分析结果，进行船舶航线数据预测，得到初始数据采集结果如图2所示。

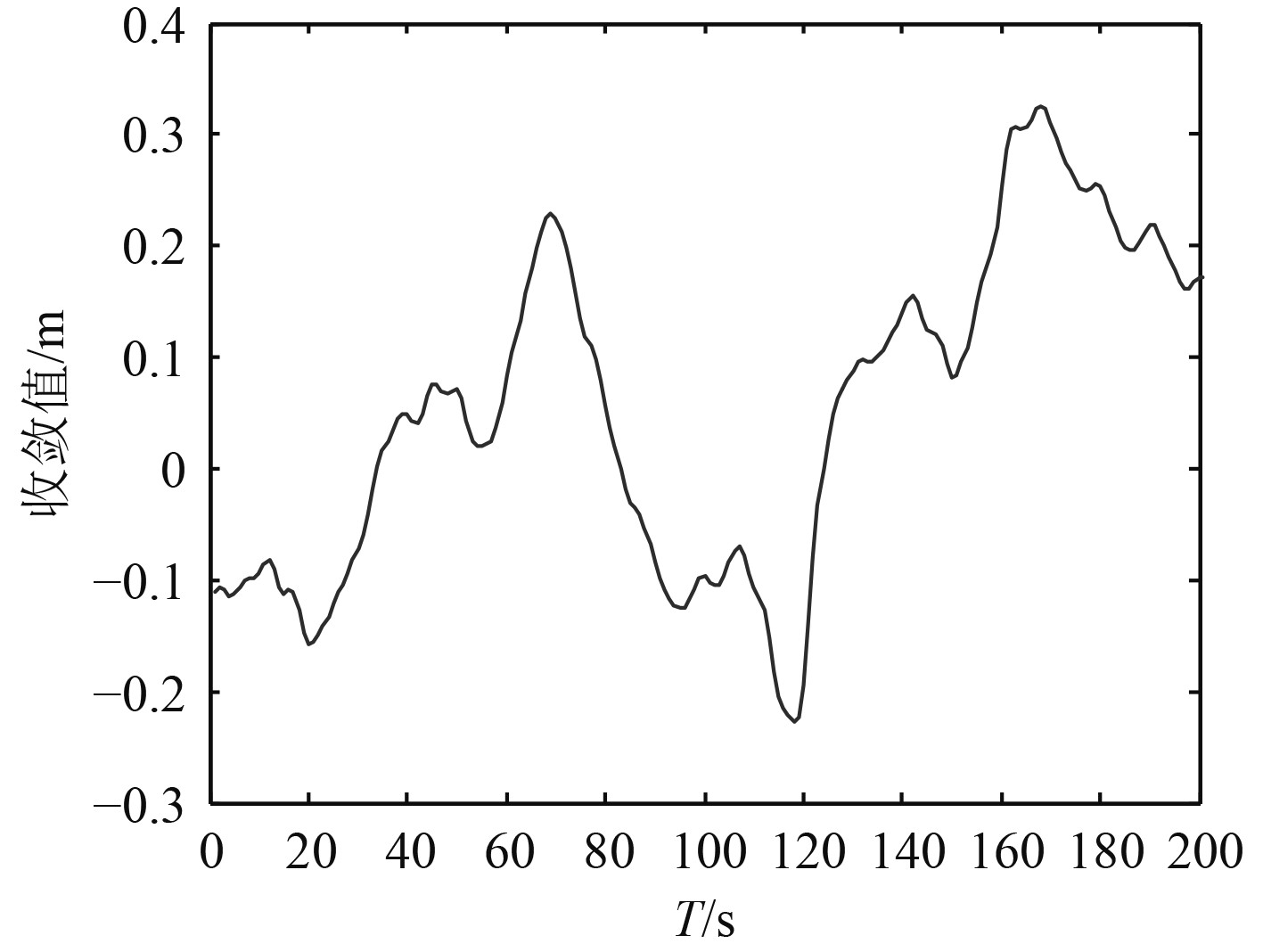
以图2采集的目标数据为测试对象，进行船舶航线数据趋势性预测，得到预测收敛曲线如图3所示。

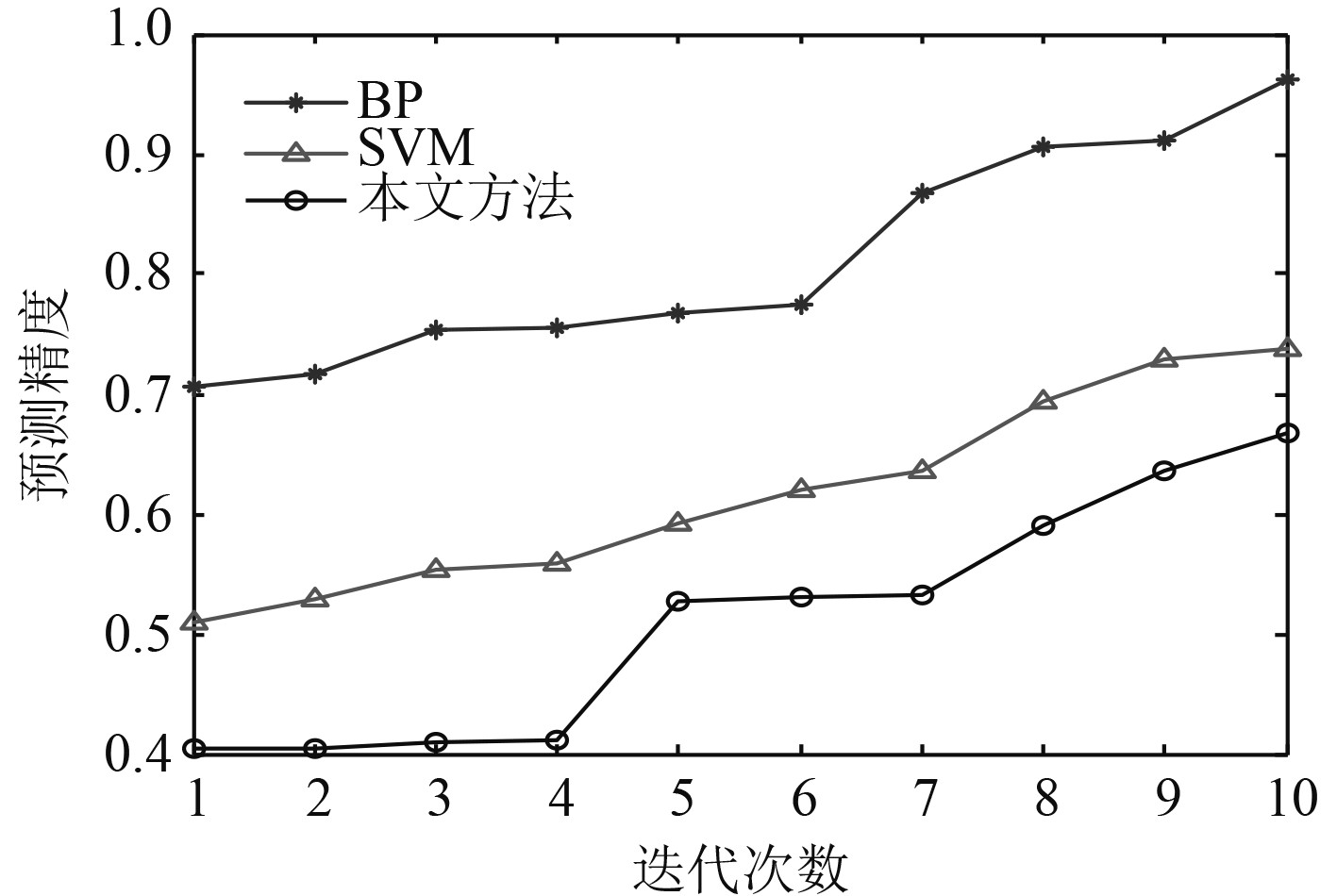
分析可知，本文方法对船舶航线数据趋势性预测的收敛性较好。测试预测精度，对比结果如图4所示。分析可知，本文方法对航线数据趋势性预测的聚类性较好，预测精度较高。

4 结　语

构建船舶航线数据融合和适应度评价模型，实现对船舶航线数据统计特征分析，本文提出基于深度学习的船舶航线数据趋势性预测方法。采用信道均衡控制技术，构建船舶航线数据趋势性预测模型特征量，采用相空间重构和特征压缩方法，建立船舶航线数据趋势性的特征聚类模型，得出船舶航线数据趋势性的概念图结构参数特征值，结合特征辨识结果和聚类结果实现对船舶航线数据预测。分析可知，本文方法对船舶航线数据趋势性预测的精度较高，收敛性较好。