0 引　言

全球经济一体化概念的提出令国家之间贸易联系更为密切^[1]，而集装箱海路运输是当前普遍采用的贸易运输方式^[2]，因此集装箱海运网络的脆弱性风险控制研究对于国际贸易的顺利实现发挥关键作用^[3]。

董利华等^[4]在研究海运网络脆弱性问题过程中，采用显著流分析法确定海运网络格局，并通过赫芬达尔-赫希曼指数描述海运网络脆弱性。该方法在实际应用过程中鲁棒性较差。张欣等^[5]在分析集装箱海运网络脆弱性问题过程中，基于复杂网络理论描述网络拓扑特征，通过海运网络平均度等指标计算网络脆弱性等级。但该方法研究过程中的指标较为片面，无法获取准确的脆弱性等级。针对上述问题，研究集装箱海运网络的脆弱性风险控制方法，针对脆弱性风险等级划分结果提出对应的策略与建议，提升集装箱海运网络的稳定运行。

1 集装箱海运网络脆弱性风险控制方法 1.1 集装箱海运网络脆弱性风险控制指标

集装箱海运网络脆弱性所描述的是集装箱海运网络结构因海啸、恐怖袭击或军事封锁等突发事件产生变化的条件(部分或全部无法正常运行)下，自身连通性受影响的水平。基于集装箱海运网络脆弱性的定义，可通过集装箱海运网络受攻击后不同指标值的波动衡量其脆弱性风险。脆弱性风险控制指标可概括为：

1)集装箱海运网络平均度

该指标所描述的是网络内全部同节点(即港口)相连接边数量的均值。在集装箱海运网络受到攻击的条件下，网络节点同边的数量波动令集装箱海运网络平均度也产生波动，波动水平越显著表示集装箱海运网络越敏感^[4]，也就是集装箱海运网络的脆弱性更高。 $ P $ 和 $ S $ 分别为集装箱海运网络平均度和节点数量，则

$ P = \frac{{\displaystyle\sum\limits_{i = 1}^S {{p_i}} }}{S} 。$

(1)

式中，p_i为同节点 $ i $ 相连接边数量的均值。

2)集装箱海运网络孤立节点比例

该指标所描述的是不存在连接边的节点在全部节点中所占比例。在集装箱海运网络内的某节点在受攻击不能有效运营的条件下，相邻节点的连接将受到影响，由此令该节点周边的支线港与喂给港成为孤立节点，这对于集装箱海运网络的规模与连通性产生直接影响。 $ \Delta S $ 和 $ {S^ * } $ 分别为孤立节点比例与集装箱海运网络受攻击后的节点总数，则

$ \Delta S = \left( {1 - \frac{{{S^ * }}}{S}} \right) \times 100\% 。$

(2)

3)集装箱海运网络聚集系数

该指标用于此体现集装箱海运网络的聚集程度。通常，集装箱海运网络受攻击后将造成聚集系数下降。 $ {\partial _i} $ 和 $ {M_i} $ 分别为节点 $ i $ 的簇系数和节点 $ i $ 的相邻节点间存在的边数，则装箱海运网络的聚集系数为

$ \partial = \frac{{\displaystyle\sum\limits_{i = 1}^S {\frac{{2{M_i}}}{{{p_i}\left( {{p_i} - 1} \right)}}} }}{S},i = 1,2,3, \cdots ,S 。$

(3)

4)平均路径长度

该指标所描述的是集装箱海运网络内全部节点对间路径最短条件下所经过边数的均值。通常，在集装箱海运网络受攻击但没有产生破碎的条件下，利用平均路径长度可体现不同节点间的分离程度均值。 $ L $ 和d_ij分别为集装箱海运网络平均路径长度和节点i，j间最短路径经过的边数，则

$ L = \frac{{2\displaystyle\sum\limits_{i = 1}^S {\sum\limits_{j = i + 1}^S {{d_{ij}}} } }}{{S\left( {S - 1} \right)}} 。$

(4)

5)集装箱海运网络效率

该指标所描述的是集装箱海运网络内全部节点效率的总和，其中节点效率可通过两节点间路径长度的倒数所描述，通过该指标可体现集装箱海运网络内运输的难易度，其值越高表示集装箱海运网络连通性越好。 $ \phi $ 和 $ {h_{ij}} $ 分别为集装箱海运网络效率和距离d_ij的倒数，则

$ \phi = \frac{{\displaystyle\sum\limits_{i = 1}^S {\sum\limits_{j = 1\left( {j \ne 1} \right)}^S {{h_{ij}}} } }}{{S\left( {S - 1} \right)}} 。$

(5)

6)最大连通子图相对大小

该指标所描述的是最大连通子图内全部节点总数占集装箱海运网络节点总数的比例。利用确定此指标值在集装箱海运网络受攻击前后波动性的过程，可直观体现集装箱海运网络受破坏的程度，该指标计算公式为

$ T = \frac{{S'}}{S} 。$

(6)

式中， $ T $ 和 $ S' $ 分别为最大连通子图相对大小和集装箱海运网络受攻击后最大连通子图中节点的数量。

7)集装箱海运网络节点强度

该指标所描述的是同任意节点相连全部边的权重之和，由此体现节点的关键度。

$ {\delta _i} = \sum\limits_{j = 1}^S {{q_{ij}}} 。$

(7)

式中： $ {\delta _i} $ 和q_ij分别为节点i的强度和节点i，j间边的权重。

1.2 基于熵权法的指标权重计算

基于信息熵确定不同指标权重，以此为指标分析与衡量提供依据的计算方式即为熵权法^[5]。该方法的主要优势为精度高，客观性更强，可更好地解释所获取的结果。基于熵权法的集装箱海运网络脆弱性风险控制指标权重计算过程中，熵权法按照不同指标的波动程度，通过信息熵确定不同指标的熵权，在此基础上修正不同指标的权重，由此获取较为客观的集装箱海运网络脆弱性风险控制指标权重。熵权法被普遍应用在多对象与多指标的权重计算过程中，针对任意集装箱海运网络脆弱性风险控制指标，通过熵权法确定其离散水平，指标信息熵同离散水平和权重间呈反比例相关。基于熵权法的集装箱海运网络脆弱性风险控制指标权重计算过程：

1)构建m个集装箱海运网络n个集装箱海运网络脆弱性风险控制指标的判断矩阵：

$ R = \left( {{x_{ij}}} \right)i = 1,2, \cdots ,n;j = 1,2, \cdots ,m 。$

(8)

式中， $ x $ 为集装箱海运网络脆弱性风险控制指标。

2)归一化处理 $ R $ ，获取归一化判断矩阵：

$ {\boldsymbol{B}} = \left( {{b_{ij}}} \right) = \frac{{{x_{ij}} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} ，$

(9)

式中：x_max和x_min分别为相同集装箱海运网络脆弱性风险控制指标条件下不同集装箱海运网络脆弱性的上限与下限。

3)依照熵的概念，基于m个集装箱海运网络n个集装箱海运网络脆弱性风险控制指标能够确定指标熵为：

$ \left\{ \begin{gathered} {A_i} = - \frac{1}{{\ln m}}\left[ {\sum\limits_{j = 1}^m {{f_{ij}}\ln {f_{ij}}} } \right] ，\\ {f_{ij}} = {b_{ij}}/\sum\limits_{j = 1}^m {{b_{ij}}} 。\\ \end{gathered} \right. $

(10)

4)确定集装箱海运网络脆弱性风险控制指标的熵权：

$ \left\{ \begin{gathered} W{\text{ = }}{\left( {{w_i}} \right)_{1 \times n}}，\\ {w_i} = (1 - {A_i})/n - \sum\limits_{i = 1}^n {{A_i}} \;\;。\\ \end{gathered} \right. $

(11)

1.3 脆弱性风险划分模型

1)构建因素集

依照已确定的集装箱海运网络脆弱性风险控制指标构建脆弱性风险等级划分因素集 $ x $ ，不同因素根据对集装箱海运网络脆弱性风险的影响程度可划分成m个等级，由此得到：

$ {x_i} = \left\{ {{x_{i1}},{x_{i2}}, \cdots ,{x_{im}}} \right\} 。$

(12)

2)脆弱性风险等级划分

集装箱海运网络脆弱性等级 $ K $ 共划分为5个等级，表1为集装箱海运网络脆弱性指数等级的划分结果。

3)构建模糊划分矩阵

依照表1内集装箱海运网络脆弱性风险等级划分标准，获取不同指标的模糊评价矩阵。

4)模糊综合划分

由于所构建的集装箱海运网络的脆弱性风险控制指标为单层次指标，因此构建单级模糊综合划分模型。利用式(13)求脆弱性风险等级矩阵 ${\boldsymbol{ D }}$ ，并对其实施归一化处理，计算脆弱性风险指数。

$ {\boldsymbol{D}}{\text{ = W}} {R_1} 。$

(13)

根据集装箱海运网络脆弱性风险等级以及集装箱海运网络中最薄弱的区域，提出对应的策略与建议，实现集装箱海运网络脆弱性风险控制。

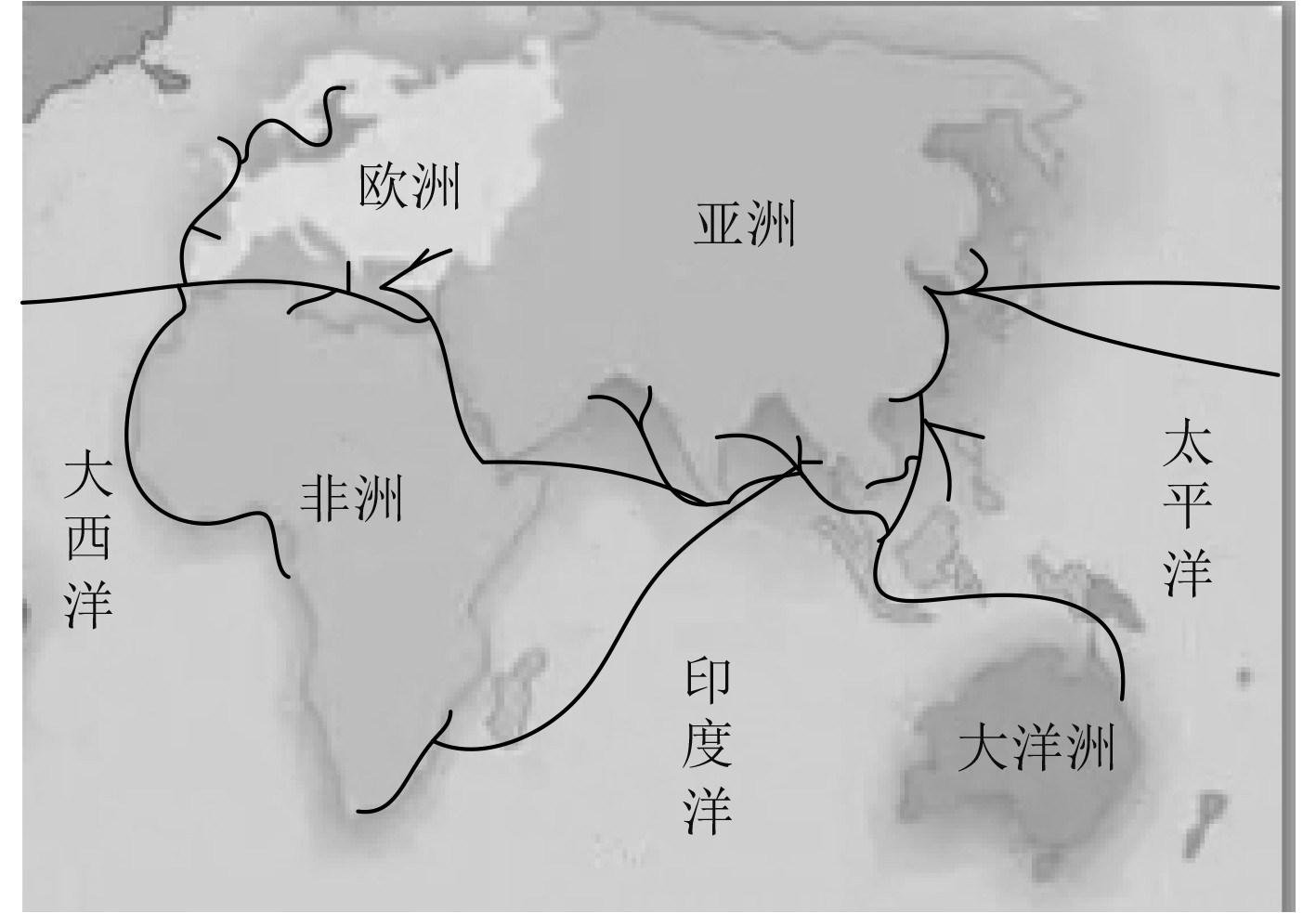
2 性能测试与结果分析

研究对象中包含由东亚经东南亚、南亚、西亚、东非和地中海，西至欧洲的海运走廊，其结构概况如图1所示。采集2021年相关网络上公示的全部海运集装箱班轮公司(约为世界范围内全部集装箱海运整体运力的95%左右)中的航运数据(其中包含港口与航线等数据)，其中包含航线约3000条，集装箱港口约850个。在清除重复航线与港口后得到，研究对象中包含航线约2400条，港口约450个，这说明研究对象覆盖面较为广泛，能够代表当前世界范围内集装箱海运的基本状况，具有重要研究意义。

2.1 指标权重计算

采用本文方法对集装箱海运网络的脆弱性风险控制指标的权重进行计算，结果如表2所示。分析表2可知，集装箱海运网络孤立节点比例、平均路径长度与集装箱海运网络节点强度3个指标的熵权较高，达到0.15以上，由此说明这3个指标对于集装箱海运网络脆弱性风险控制的影响关键。

2.2 脆弱性风险等级划分结果

表3为研究对象内主要区域在不同攻击模式下的脆弱性风险等级。分析表3可知，西亚和东非的脆弱性风险等级较低，在不同攻击模式下的调整能力较强。而东南亚、南亚与地中海的脆弱性风险等级相对较高，在不同攻击模式下的调整能力较差。同时能够得到研究对象的薄弱区域主要为东南亚，如果此区域的航线不能有效运行，那么研究对象的连通性最为薄弱。

2.3 风险控制效果分析

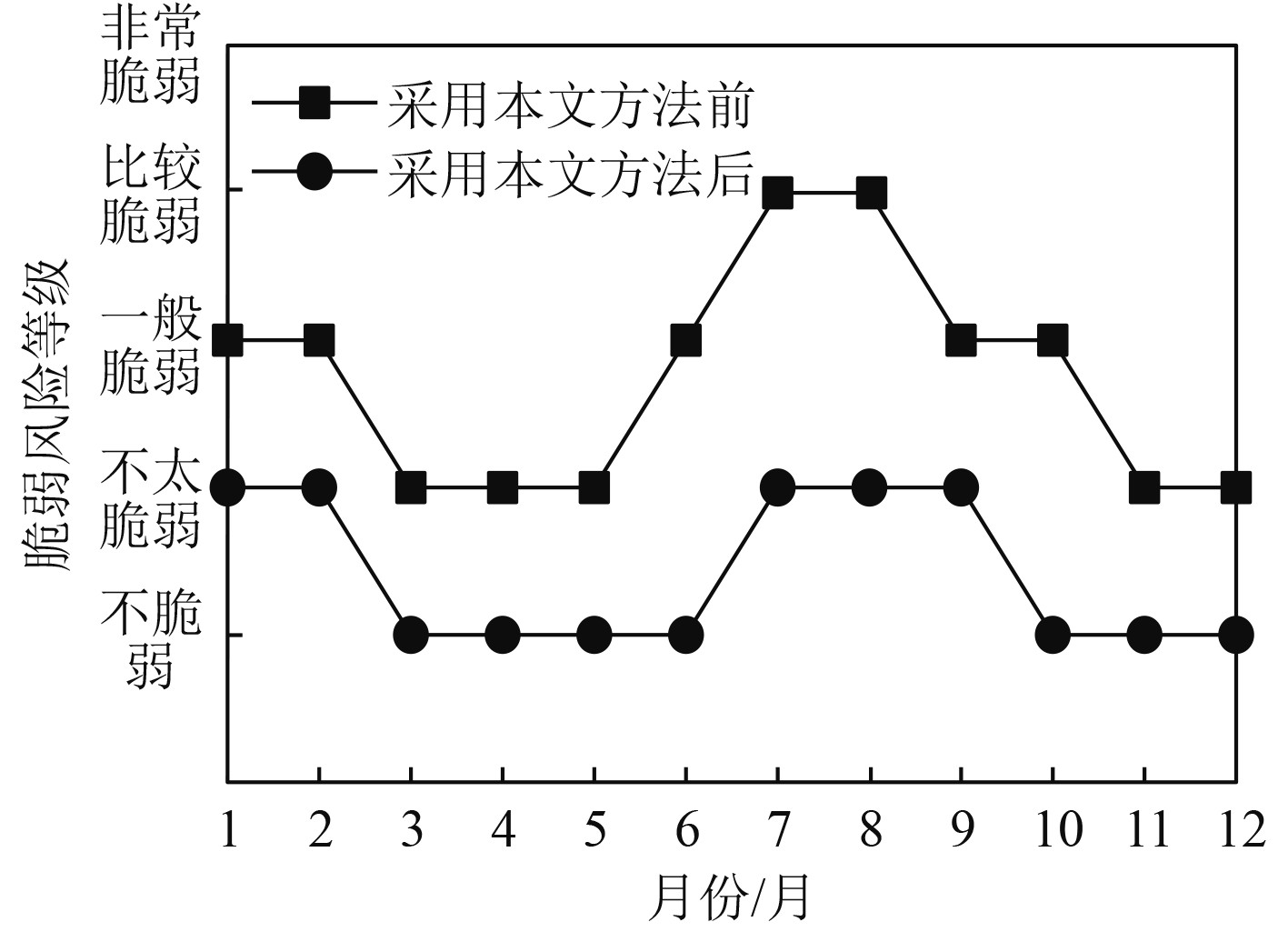
为验证本文方法的实际风险控制效果，分析采用本文方法前后，研究对象的风险等级变化情况，所得结果如图2所示。分析图2可知，采用本文方法对研究对象脆弱性风险等级进行划分并采用针对性的策略进行控制后，研究对象全年的脆弱性风险呈现显著下降趋势，由此说明本文方法具有较好的实际应用效果。

3 结　语

本文研究集装箱海运网络脆弱性风险控制方法，通过划分集装箱海运网络的脆弱性风险等级，针对不同风险等级提出对应的策略与建议，实现集装箱海运网络脆弱性风险控制。随着海路网络建设的完善，将持续有新的航线与港口产生，因此这些新航线与港口对于集装箱海运网络的影响是后续需研究的主要内容。