2. 长春理工大学 电子信息工程学院,吉林 长春 130022
2. School of Electronic Information Engineering, Changchun University of Science and Technology, Changchun 130022, China
相控阵雷达作为舰船智能感知家族中的重要一员,近年来在军事应用领域得到了长足发展。光束控制技术[1-4]作为相控阵雷达的核心关键,其指向精度越高,光束的偏转角度误差越小,对于光学动态捕获、跟踪、指向技术,指向精度的高低直接影响系统的性能和稳定性,是最关键的参量之一。
液晶相控阵[5]属于光学相控阵的一类,拥有高分辨率、高精准度、可以编程操控等特性,但在光束调制过程中难免受边缘效应、电极占空比、电压量化等因素对波阵面产生影响,从而导致波阵面发生畸变,最终降低指向精度。
自20世纪末以来,许多学者针对液晶相控阵的光束指向精度优化问题进行研究。1997年Mikhail A. Vorontsov等提出SPGD算法可以快速优化波阵面,但是由于算法极易困于局部最优值,性能稳定性不恒定。P.F.McManamon等通过单纯型法,以直线型作为优化方法,对波阵面校正。这样做能改进性能,但不能达到最好的效果。2009年,孔令讲等[6]分析了电压量化对光束指向精度的影响,但没有对其进行优化实验。2018年,黄志伟等[7]使用蝙蝠优化算法优化光束指向精度,仿真结果与粒子群算法比较收敛速度快,但优化精度没有显著提升。2021年,王承邈等[8]首先将预设子光斑尺寸约束至衍射极限,以统一实际光斑形貌,然后采用变步长反馈矫正过程,实现对指向位置的优化。在优化过程中,通过变化情况,动态调整步长大小矫正误差,以实现更加精确的优化,但准备阶段工作量巨大。
本文通过引入limit阈值观察解的停滞次数、柯西分布函数优化全局策略,及自适应余弦加权因子,从多方面增强HHO的性能,从而摆脱局部最优的困境。显著提高了光束指向精度,并具有收敛精度高、收敛速度快、鲁棒性强等优点,有效提高了舰载相控阵雷达的检测精度。
1 光束偏转模型与影响因素分析 1.1 光束偏转模型液晶相控阵的光束偏转模型实为连续角度偏转模型,主要用于描述光束在非周期闪耀光栅中的传输和偏转过程,而液晶相控阵是一种基于液晶技术的相位调制器。液晶单元通过改变其相位来控制光束的传播和偏转,其波控原理如图1所示。
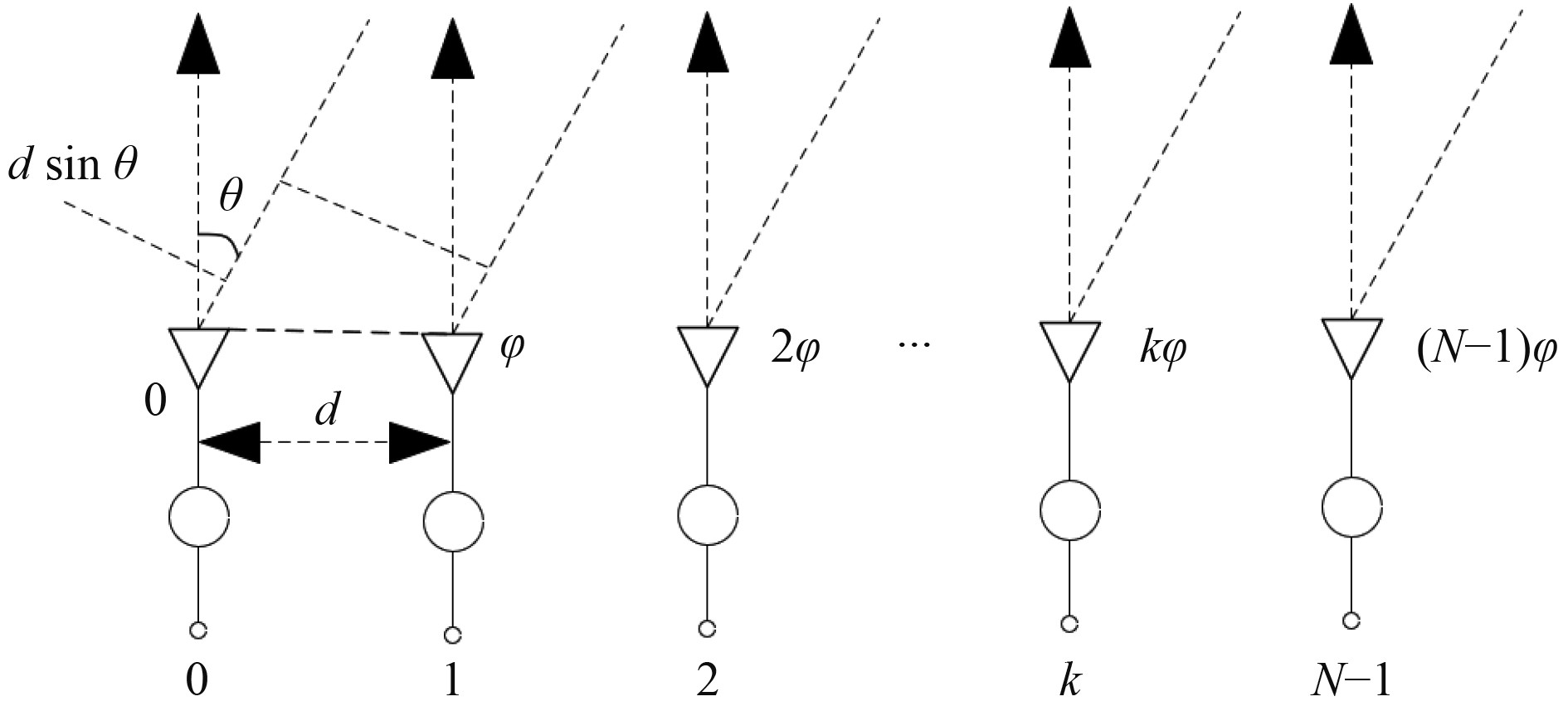
|
图 1 相控阵雷达波控原理 Fig. 1 Beam control principle of phased array radar |
其中,d为2个独立相控单元之间的间距,0,
| $ \theta = \arcsin \left( {\frac{{\lambda \Delta \varphi }}{{2\pi d}}} \right) 。$ | (1) |
式中:
在调整光束偏转时,光束传播会受到两方面的影响,分为器件的自身影响与外部环境干扰,外部环境因素无法定性,但可以通过数学模型对器件自身影响进行模拟。定义归一化精度误差
| $ {\varepsilon _{{\text{norm}}}} = \left| {\frac{{{\theta _{{\text{actual}}}} - {\theta _{{\text{ideal}}}}}}{{{\theta _{{\text{spot}}}}}}} \right| 。$ | (2) |
式中:
液晶相控阵的边缘效应是指,由于光束偏转角度受到相位调制量
| $ \phi (x) = \varphi (x) \otimes k(x) ,$ | (3) |
| $ k(x) = \left\{ {\begin{array}{*{20}{cc}} (1/\sigma )\exp (2x/\sigma ),& x < 0,\\ (1/\sigma )\exp ( - 2x/\sigma ),& x > 0 。\end{array}} \right. $ | (4) |
式中,
| $ \sigma (h) = \sqrt {\frac{{{\varepsilon _{//}}}}{{3{\varepsilon _ \bot }}}} \left[ {h - \frac{{\lambda \left( {\varepsilon _{//}^2 - \varepsilon _ \bot ^2} \right)n_o^2}}{{2{\varepsilon _{//}}{\varepsilon _ \bot }\left( {n_e^2 - n_o^2} \right){n_e}}}} \right] 。$ | (5) |
式中,
除了回程区之外,相位凹陷也是影响衍射效率的另一重要因素。因液晶分子的排列状态在电场强度控制下,往往很难得到理想的倾斜角度,导致相位低于两侧,进而形成相位凹陷,严重制约了电极占空比
| $ \gamma = \frac{a}{d} 。$ | (6) |
式中,
| $ {\varphi }^{\prime }(x)={\int }_{-\infty }^{\infty }[g(x)\phi (x)]k(x){\rm{d}}x 。$ | (7) |
| $ g(x)=\left\{\begin{array}{cc} \text{1}\text{,}& \mathrm{mod}(x,d) < a,\\ 0,& \text{others}。\end{array}\right. $ | (8) |
式中:
除了上述2项液晶分子固有影响因素之外,在液晶盒的制备过程中,其表面的平整度也往往受限于液晶注入玻璃基板中的实际过程状态。为此,可通过下式模拟表示液晶盒不平整度与相位误差之间的关系:
| $ {\varphi _{{\text{error }}}}(x) = 2\pi A\lambda \cos \left[ {2\pi \left( {\frac{{x - \bar x}}{D}} \right) - \frac{1}{2}} \right] 。$ | (9) |
式中:
在实际工作中,为电极供电的驱动芯片输出电压往往达不到理想电压,而因此形成的误差即可导致移相阵元的相位延迟分布出现量化误差,不同台阶相位出现高低错落,致使整个出射波阵面偏离了理想波阵面。为此,只有保证电压量化位数足够高,才可有效降低由此产生的精度误差。出于工程考虑,一般量化位数取 8 位较为适宜。
2 基于分数阶耦合复值神经网络的光束指向控制策略 2.1 分数阶复值神经网络的投影同步分数阶复值神经网络在同步方法的分析与控制研究主要包括状态同步、输出同步和FTS三个方面。状态同步主要使用基于Lyapunov的方法去解决问题,主要创新在于:
1)使用一种具有混合耦合和随时间变化的CNN同步方法;
2)处理具有随机耦合强度的耦合神经网络同步方法;
3)通过利用平均冲动间隔和平均冲动增益讨论耦合神经网络与混合冲动的指数同步问题。
由于神经网络无法自动实现同步,因此开发在神经网络节点中的控制策略,如间歇控制、脉冲控制、采样数据控制、自适应控制等。其中,通过利用自适应控制器和状态反馈控制器,获得一些充分条件来保证具有不连续激活函数的神经网络完全同步和指数同步的方法应用较多。
本文在探究分数阶复值神经网络的同步问题同时,结合多耦合神经网络的特点,提出基于自适应同步方法的具有耦合时延的多混合控制投影同步问题解决方案。
| $ \begin{split} &{}_{{t_0}}^CD_t^\alpha {y_r}(t) = - {c_r}{y_r}(t) + \sum\limits_{t = 1}^m {\sum\limits_{a = 1}^n {eA{a_{rq{l} }}{g_q}{f_{ij}}({y_q}(t))} } +\\[-7pt] &\qquad\qquad\quad \sum\limits_{t = 1}^m {\sum\limits_{a = 1}^n {\dot eB\dot O{a_{rq{l} }}{g_q}{{\dot f}_{ij}}({y_q}(t - \tau ))} } {\text{ + }}{I_r} ,\\ & r \in (1,2,\cdots ,n) 。\end{split} $ | (10) |
其中
哈里斯鹰算法搜索处理步骤可能经常出现局部最优、收敛精度低等缺陷。本文设计兼顾全局与局部并优策略的哈里斯鹰算法,对传统哈里斯算法进行改进。
2.2.1 limit阈值机制在HHO算法中,当猎物逃逸能量
在全局搜索阶段,引入柯西(Cauchy)分布函数使哈里斯鹰位置数据发生变异,Cauchy函数的峰值相对较小,尾部下降相对平缓,算法更容易跳出局部最优解。由于哈里斯鹰算法的多样性和随机性,能够抵抗局部最优解的约束力。因此,Cauchy函数和哈里斯鹰算法的结合,可以有效地优化搜索算法的性能,提高搜索效率。
| $ X_{{\text{best }}}^\prime = {X_{{\text{best }}}} + {X_{{\text{best }}}} \times {\text{ Cauchy }}(0,1) 。$ | (11) |
为了提高算法的局部开采能力,有必要对猎物位置的邻域进行再更新,以找出更优解。在局部搜索阶段,采用自适应余弦加权因子更新局部位置,在哈里斯鹰算法中表现为当哈里斯鹰针对兔子逃跑行为采取4种捕猎策略时,余弦加权因子会使兔子动态的更新位置信息,从而提高算法局部寻优能力。
| $ X_{{\text{rabbit }}}^\prime = \omega \times {X_{{\text{rabbit }}}} ,$ | (12) |
| $ \omega = - \cos \left(\frac{t}{T}\right) + 1 。$ | (13) |
式中:
在仿真实验中,通过对比选择适宜器件参数,使用多策略改进的多策略哈里斯鹰优化算法控制液晶的相位差,降低偏转误差,优化光束指向精度。仿真参数如表1所示。
|
|
表 1 多策略哈里斯鹰算法仿真参数 Tab.1 Multi strategy HHO simulation paramete |
由图2可知,通过不断增加t,可使归一化精度误差逐步跳出局部最优,最终达到全局最优。其优点明显表现出收敛速度快,精度较高。
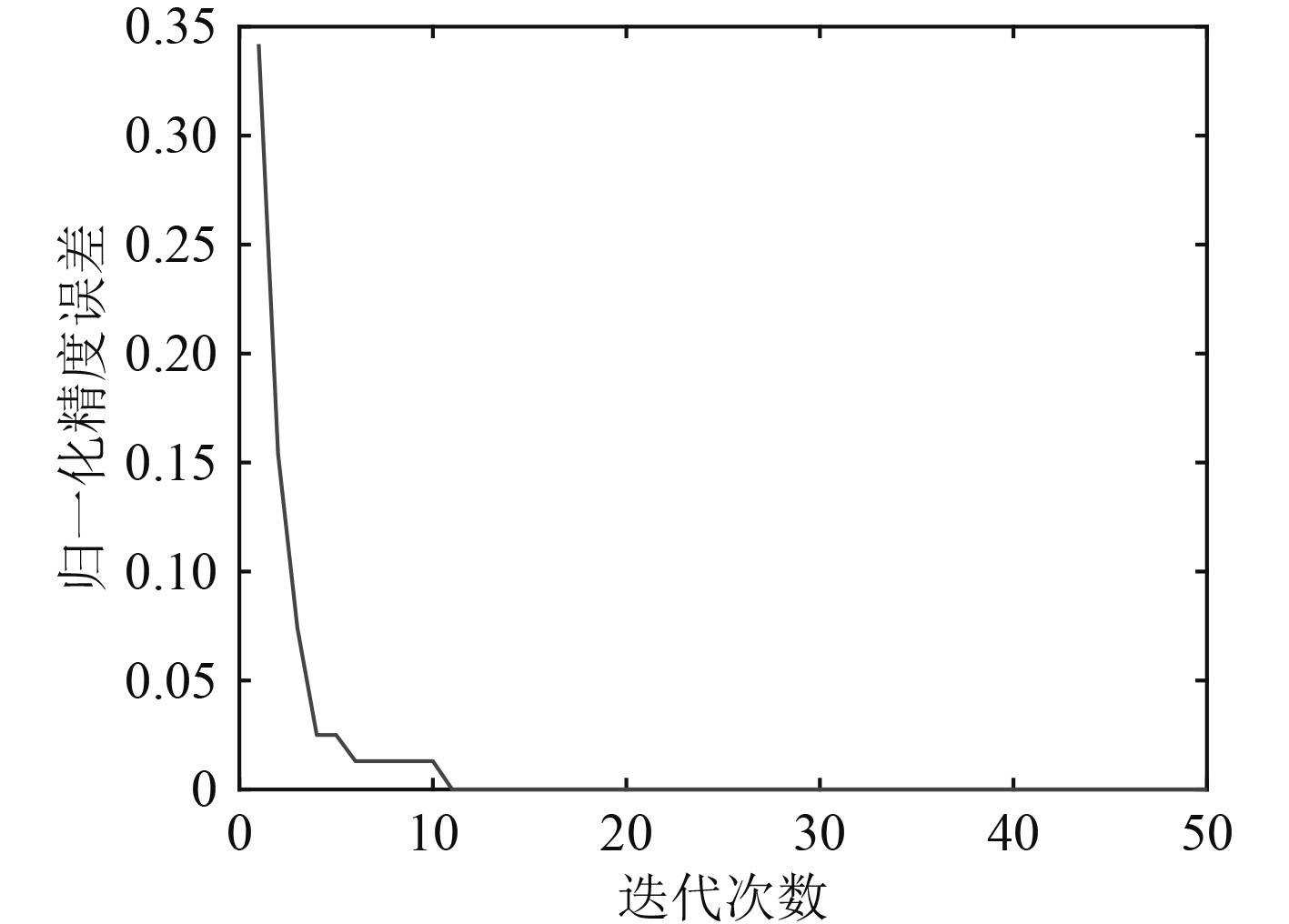
|
图 2 多策略哈里斯鹰优化算法的迭代曲线 Fig. 2 Iterative curve of multi strategy Harris Hawks optimization algorithm |
为验证算法的有效性,在最大偏转角度以内(0~0.106 6 rad)进行仿真实验,结果如图3所示。
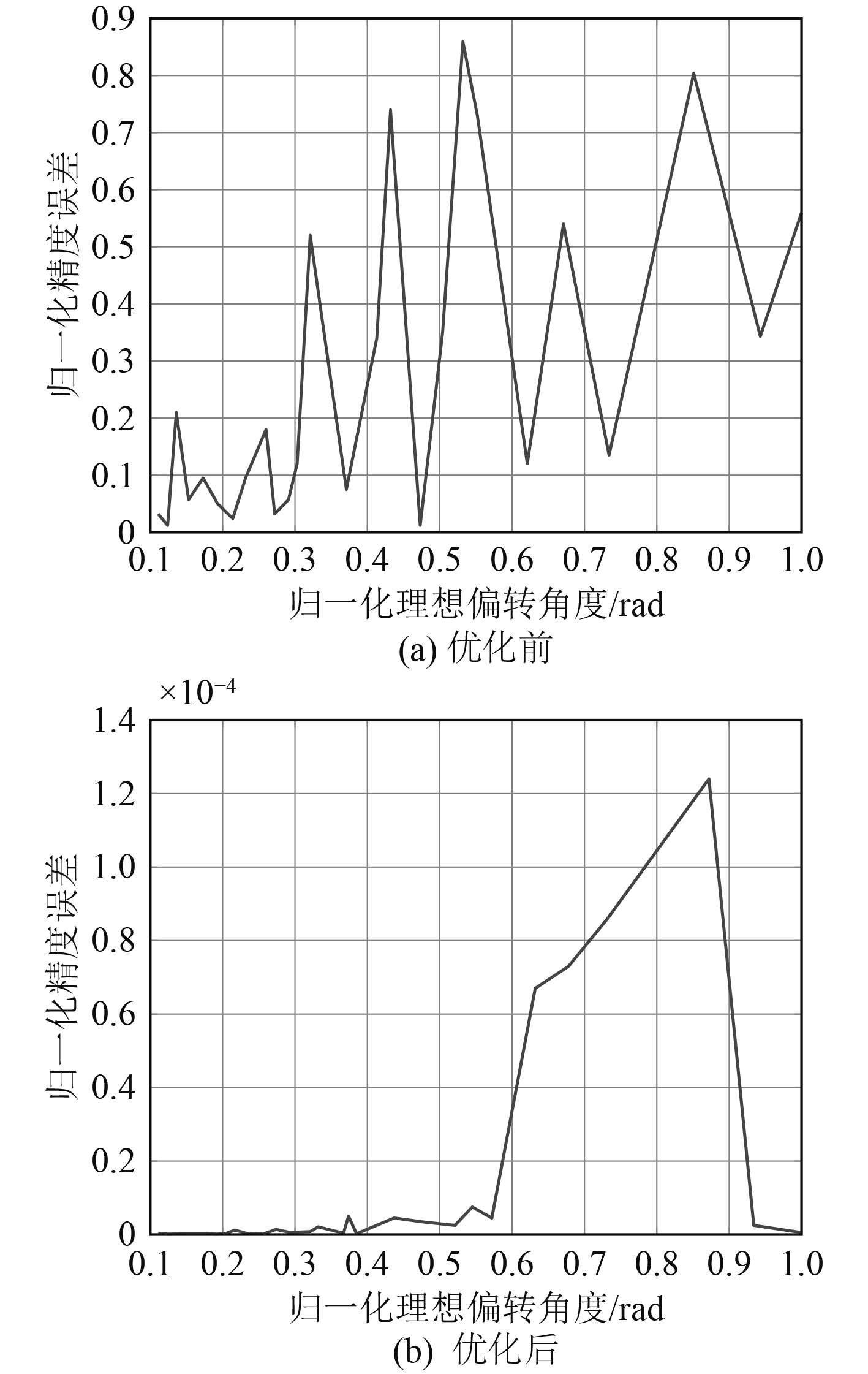
|
图 3 优化前后归一化精度误差 Fig. 3 Normalized accuracy error before and after optimization |
从图3(a)可以看出,优化之前误差波动和光束偏转误差均较大,而图3(b)中的
本文对舰载相控阵雷达光束偏转技术进行分析可知,液晶相控阵在光束调制调制过程中极易受到边缘效应、电极占空比、液晶盒面起伏、电压量化等因素影响,导致相控阵波面发生畸变,从而角度偏转产生误差,光束的指向精度降低。本文主要对影响液晶相控阵的因素进行分析,并对分数阶耦合复值神经网络的投影同步理论进行调参优化,从整个系统的角度证明该理论的有效性。最后本文设计了全局与局部并行优化策略的哈里斯鹰算法,增强哈里斯鹰算法的寻优性能。仿真实验结果表明:本文算法降低归一化精度误差波动幅值,并具有收敛精度高,收敛速度快,鲁棒性强等优点,有效提高了舰载相控阵雷达的检测精度。
| [1] |
王春阳, 李兰婷, 史红伟, 等. 基于液晶相控阵的光束偏转控制方法研究[J]. 液晶与显示, 2018, 33(10): 857-863. |
| [2] |
牛启凤, 王春阳, 张广平, 等. 液晶相控阵指向矢分布求解及其光束偏转[J]. 光学精密工程, 2018, 26(12): 2894-2901. |
| [3] |
WANG R X, WU L, XIONG C D, et al. Agile laser beam deflection with high steering precision and angular resolution using liquid crystal optical phased array[J]. IEEE Transactions on Nanotechnology, 2018, 17(1).
|
| [4] |
牛启凤. 液晶相控阵光束偏转关键技术研究[D]. 长春: 长春理工大学, 2020.
|
| [5] |
肖锋. 液晶光学相控阵关键技术研究[D]. 成都: 电子科技大学, 2018.
|
| [6] |
孔令讲, 易伟, 杨建宇, 等. 激光雷达液晶相控阵组件扫描精度分析[J]. 中国激光, 2009, 36(5): 1080-1085. |
| [7] |
黄志伟, 王春阳, 彭丽华, 等. 基于蝙蝠算法的液晶光学相控阵波束优化[J]. 激光与光电子学进展, 2018, 55(8): 438-442. |
| [8] |
王承邈. 基于液晶光学相控阵的高精度光束指向控制技术[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2021.
|
 2023, Vol. 45
2023, Vol. 45
