双转子结构能提高压气机的工作效率、增加燃气轮机的喘振裕度,使其在更佳的条件下工作,成为燃气轮机转子系统经常采用的结构形式之一[1],广泛应用于舰船、航空燃气轮机上。作为燃气轮机动力输出的核心部件,双转子系统中的多频不平衡激励力和非线性构件,中介轴承带来的振动耦合,使得双转子系统表现出复杂的动力学行为,给燃气轮机结构系统设计和故障诊断带来困难[2]。
关于双转子系统动力学研究主要集中在运动模型的分析上,通过建立系统的运动微分方程研究其运动规律。文献[3-4]基于拉格朗日方程、达朗伯原理推导给出了双转子系统的动力学方程,通过改变不平衡量、中介轴承非线性刚度等参数激励,分别得到其对系统振动特性的影响规律。文献[5-10]均采用传递矩阵法,分析研究了内外圈转速比、轴承支承刚度等参数对系统动力学响应的影响。随着计算机的发展,利用有限元软件对双转子系统进行仿真模拟成为新的研究方向。文献[11-16]就是利用梁单元法对双转子系统进行建模,通过计算系统的临界转速和振型,得到了双转子系统的稳态不平衡响应规律。但上述采用的低维方程、传递矩阵法以及梁单元法,都不能建立较为精确的双转子动力学模型,进而不能进行准确的定量分析。而有限元法中的实体单元建模法则具有精确建模、计算精度高、耦合分析能力强等优点,被广泛应用[17]。
本文以某型燃气轮机双转子系统为研究对象,将其简化为四盘四支承结构,利用有限元软件Workbench,建立中介轴承-双转子系统耦合的三维实体有限元模型。通过计算得到系统的固有频率及振型、临界转速,并将其与实验结果进行对比分析,验证仿真模型的可行性。通过计算双转子系统在不同转速下的振动响应,得到其不平衡振动耦合特性规律,为工程实际中转子系统的设计提供理论支撑。
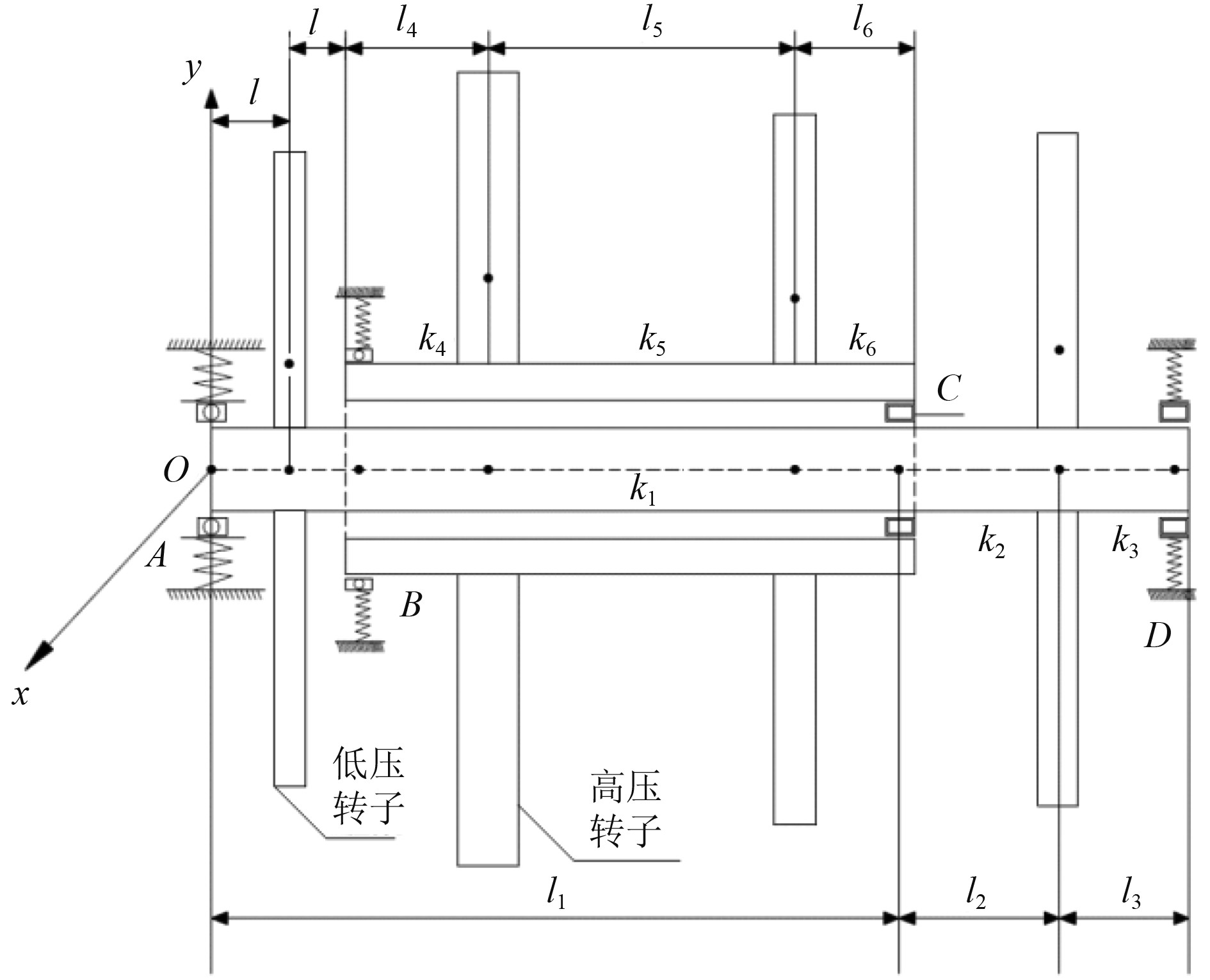
1 双转子系统有限元计算模型 1.1 几何模型结构某型燃气轮机转子系统采用双转子结构,其简化模型如图1所示。该系统由高压外转子和低压内转子组成,通过中介轴承(圆柱滚子轴承)耦合联接在一起。高、低压压气机轮盘和高、低压涡轮轮盘均简化集中为轮盘(图1中轮盘从左至右为盘1、盘2、盘3、盘4),整个双转子系统有4个轴承支承位置,其中A(轴承1)、D(轴承4)点为低压转子支点,B(轴承2)点为高压转子支点,C(轴承3)为中介轴承支点。
|
图 1 双转子系统结构示意图 Fig. 1 Schematic diagram of double rotor system structure |
基于有限元建模的双转子系统动力学方程可表示为:
| $ \begin{aligned} {\boldsymbol{M}}\ddot u + & ({\boldsymbol{C}} + {\varOmega _1}{{\boldsymbol{G}}_{\boldsymbol{1}}} + {\varOmega _2}{{\boldsymbol{G}}_{\boldsymbol{2}}})\dot u + ({{\boldsymbol{K}}_{\boldsymbol{d}}} + \varOmega _1^2{{\boldsymbol{K}}_{\boldsymbol{1}}} + \varOmega _1^2{{\boldsymbol{K}}_{\boldsymbol{2}}})u =\\ & \varOmega _1^2{f_1}{e^{j{\Omega _1}t}} + \varOmega _2^2{f_2}{e^{j{\Omega _2}t}}。\\ \end{aligned} $ |
式中:M,C,Kd分别为双转子系统的质量矩阵、阻尼矩阵、刚度矩阵;
| $ {K}_{rr}=0.237\times {10}^{5}{F}_{r}^{0.1}{n}^{0.9}{L}^{0.2}{\rm{cos}}^{1.9}{\beta }_{1}。$ |
式中:
在Workbench中,采用直接积分法中的中心差分法对系统动力学方程进行积分。在中心差分法中,加速度与速度可用位移
| $ \ddot{u}\left(t\right)=\frac{1}{\Delta {t}^{2}}({u}_{t-\Delta t}-2{u}_{t}+{u}_{t+\Delta t}) ,$ | (1) |
| $ \dot{u}\left(t\right)=\frac{1}{2\Delta t}(-{u}_{t-\Delta t}+{u}_{t+\Delta t})。$ | (2) |
将式(1)和式(2)代入系统动力方程中,可得到各个离散点解的递推公式:
| $ \begin{aligned} & \left( {M \cdot \frac{1}{{\Delta {t^2}}} + C \cdot \frac{1}{{2\Delta t}}} \right){u_{t + \Delta t}} =\\ & \quad \quad Q(t) - (K - M \cdot \frac{1}{{\Delta {t^2}}}){u_t} - (M \cdot \frac{1}{{\Delta {t^2}}} - C \cdot \frac{1}{{2\Delta t}}){u_{t - \Delta t}}。\end{aligned} $ | (3) |
通过给定边界条件和一定的起步计算方法后就可以利用上式求解各个离散时间点的位移,从而求出应力、应变、加速度等量。
2 双转子系统动力学建模 2.1 双转子系统尺寸参数根据对双转子分析,对实际结构进行简化处理。双转子系统的主要部件参数见如表1和表2所示。其中,
|
|
表 1 双转子主要部件参数 Tab.1 Parameters of main components of dual rotors |
|
|
表 2 中介轴承几何参数(NU304E) Tab.2 Geometric parameters of intermediate bearing |
根据双转子系统各部件的实际情况,定义各部件的材料参数,如表3所示。
|
|
表 3 双转子系统各部件材料参数 Tab.3 Material parameters of each component of the dual-rotor system |
首先在SolidWorks软件中建立四轴承支承的双转子-中介轴承系统三维模型,通过集中质量法,用刚性盘模拟压气机转子轮盘和涡轮转子轮盘,进行简化处理。然后将几何模型导入Ansys Workbench软件中。
在模型前处理时,在Geometry中设置各部件的材料参数,高低压转子与中介轴承均采用3D实体单元(Solid187)。该单元为三维10节点四面体固体结构单元,每个节点有3个方向的平动自由度,能够在做转动时考虑陀螺效应等影响。为避免初始穿透并且更加贴近实际结构,中介轴承中滚动体与轴承内、外圈以及保持架之间存在径向间隙。支承和其余轴承采用Connections中Bearing进行定义设置。假设轴承是各项同性的,
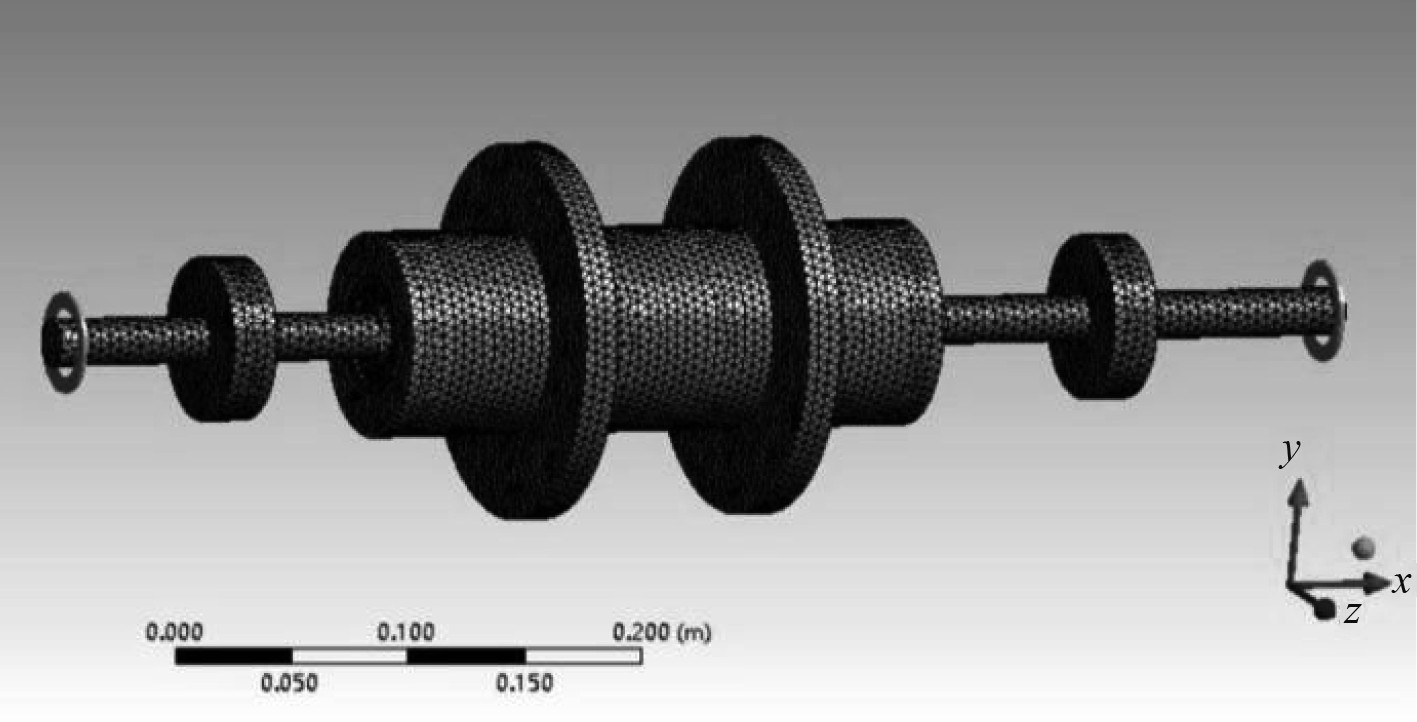
在Mesh中进行网格划分,由于系统中存在非线性结构,采用Quadratic二次单元来进行划分,通过定义实常数的形式来控制模型的网格密度。得到系统整体有限元模型以及中介轴承模型分别如图2和图3所示,其中系统整体模型一共有266355个节点、116056个单元。
|
图 2 双转子系统有限元模型 Fig. 2 Finite element model of dual rotor system |

|
图 3 中介轴承有限元模型 Fig. 3 Finite element model of intermediate bearing |
根据Ansys中各个接触类型的特点,中介轴承内圈与低压内转子、中介轴承外圈与高压外转子均采用Bonded接触行为。根据文献[15],在中介轴承中,滚动体分别与内圈、外圈之间均建立接触对,采用Frictional非线性接触行为,并设置滚动体与内圈、外圈之间的摩擦系数为0.2;滚动体与保持架之间建立接触对,并设置其摩擦系数为0.02。对于4个轴承,限制其沿轴向(X方向)的平动,以及沿Y,Z方向的转动,只考虑径向力作用的情况(即施加Standard Earth Gravity设置,方向为Y的负方向)。
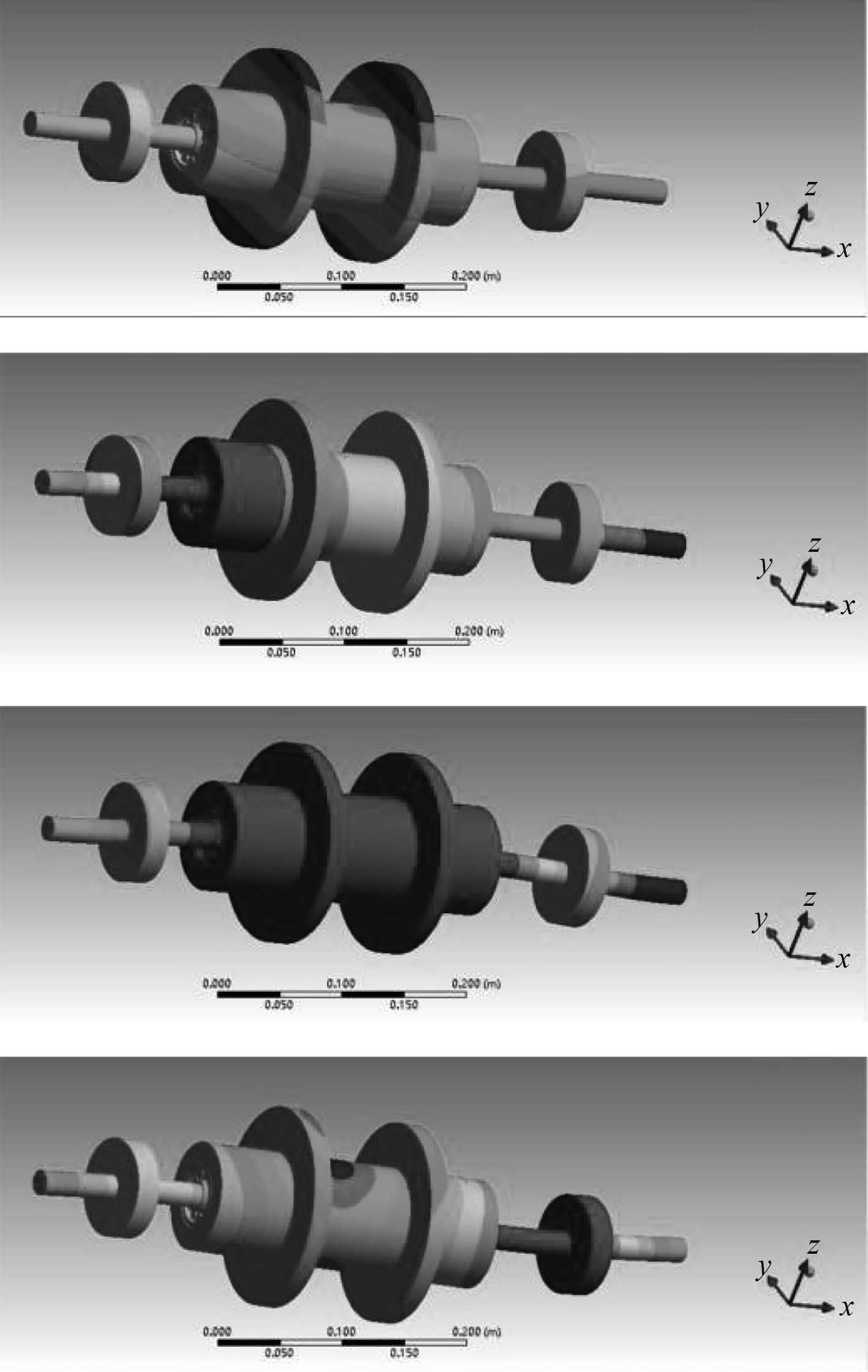
3 仿真过程与结果分析 3.1 转子系统临界转速特性根据建立的有限元模型和边界条件的设置,在分析时考虑陀螺效应。计算双转子系统同向旋转时,系统的前4阶固有频率及振型如图4所示(设定内外转速比为1∶1.28)。
|
图 4 双转子系统的前四阶振型 Fig. 4 The first four vibration modes of the dual-rotor system |
以整个系统为观测对象,得到其前4阶固有频率及振型图,可看出第1阶固有频率为51 Hz左右,其振型表现为内、外转子平动;第2阶固有频率为103 Hz左右,其振型表现为内转子弯曲、外转子平动振型;第3、4阶表现为内转子弯曲、外转子弯曲振型。
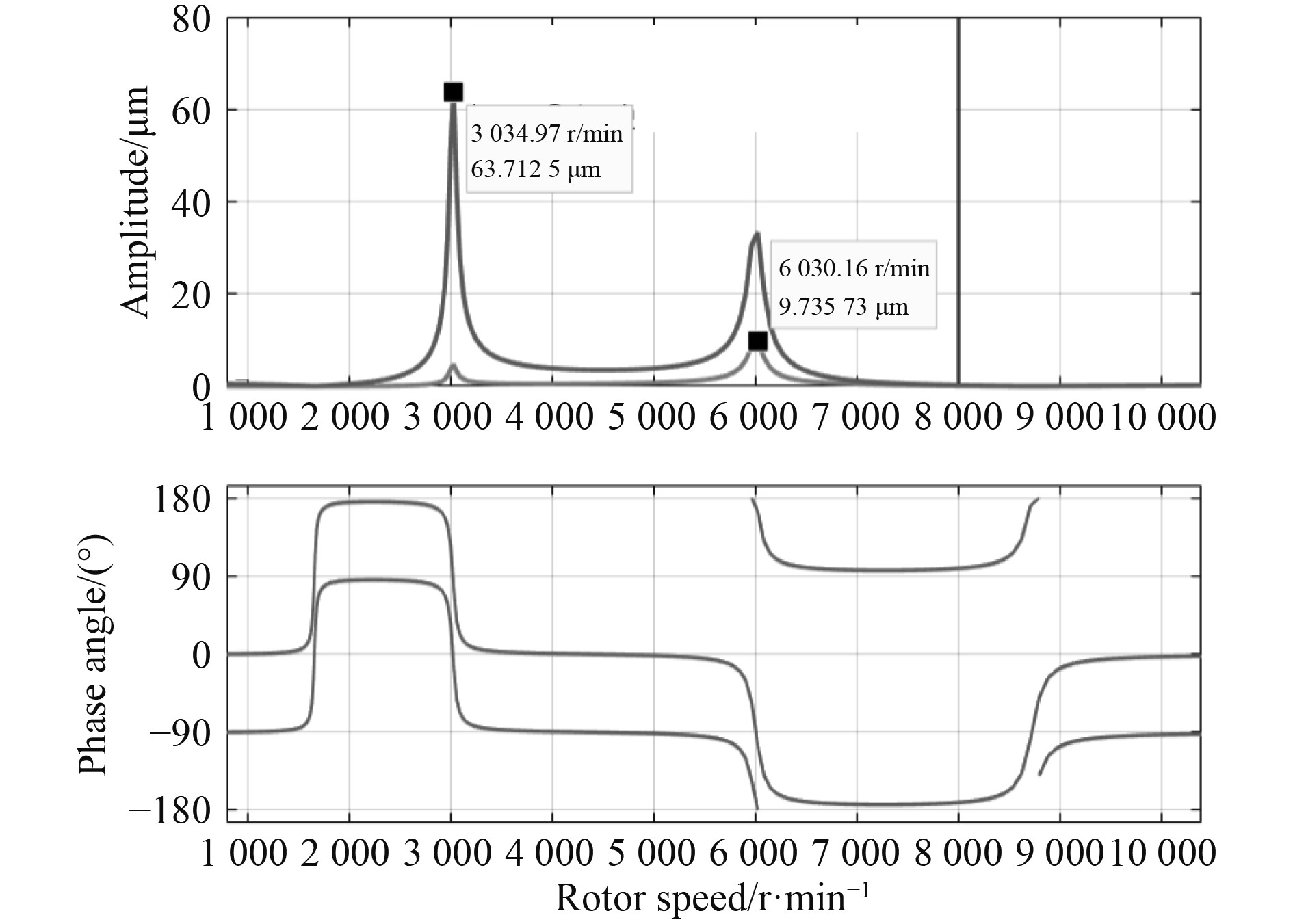
模型中低压转子盘1、高压转子盘3存在不平衡量(不平衡质量分别为2.5 kg和4 kg,偏心距均为1×E−5 m),高低压转速比一定。此时,2个转子都存在不平衡量,即当系统工作时内外转子都将受到不平衡力作用。通过模拟高压转子转速从0~10 000 r/min时振动测点的响应幅值,得到位移响应随转速变化的不平衡响应曲线,如图5所示。
|
图 5 双转子系统高、低压转子的不平衡响应 Fig. 5 Unbalanced response of high and low pressure rotors in a dual rotor system |
以高压转子盘3的Y向位移为观察对象,在后处理图中,上部分为转速与振幅的关系,下部分为相位与振幅的关系。由图5可以看出,测点处出现了2次幅值增大的现象,即出现2处振动突变,第一处振动突变在3 034 r/min左右,第二处振动突变在6 030 r/min左右,相位约为168°。
3.2 转子系统不平衡响应为研究不同转速下的双转子系统不平衡振动响应,选取2个振动突变处附近的转速以及1个非共振位置的转速。高压转子转速分别为320 rad/s,550 rad/s,640 rad/s,激振力为1 000 N时,以高压转子盘3作为观测对象,图6~图8分别为双转子系统在3种转速下,测点位置的振动响应。
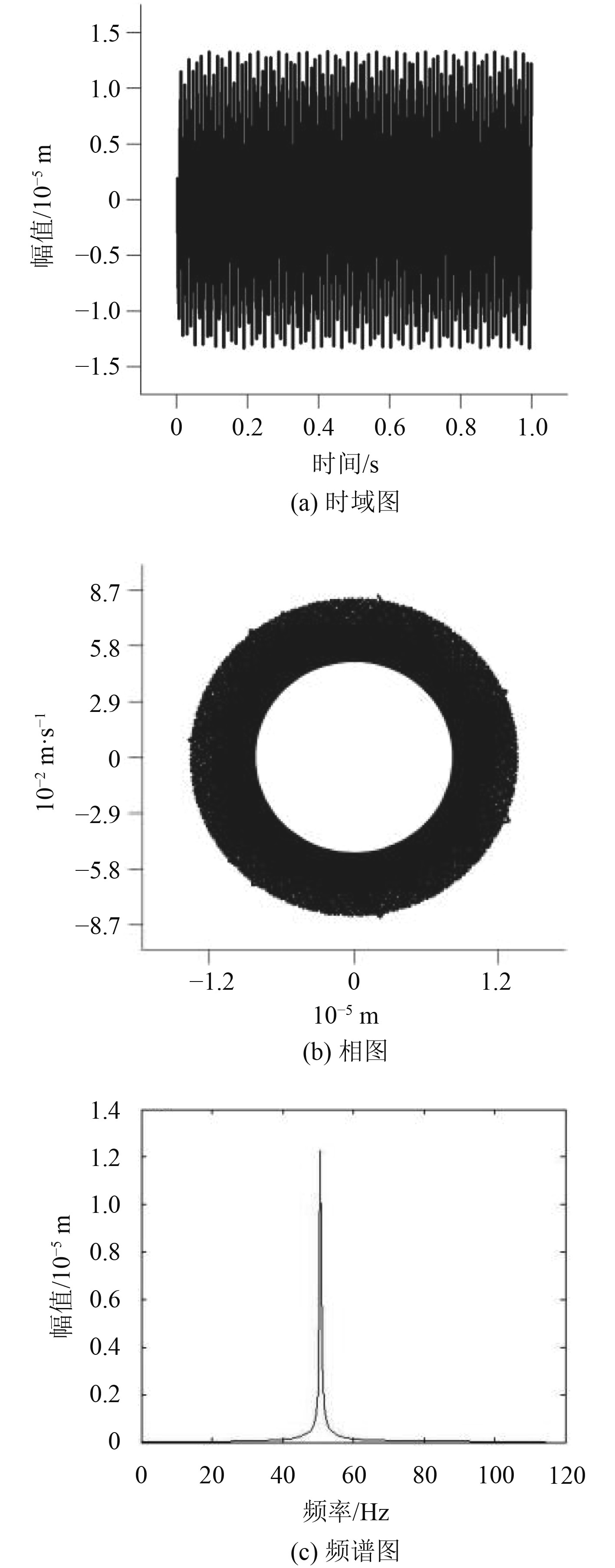
|
图 6 高压转子转速320 rad/s时,系统振动响应 Fig. 6 Vibration response of the system when the high voltage rotor speed is 320 rad/s |

|
图 8 高压转子转速640rad/s时,系统振动响应 Fig. 8 Vibration response of the system when the high voltage rotor speed is 640rad/s |
如图6和图8所示,双转子系统在2个幅值响应较大的转速附近,所得到的时域图均可看作近似的谐波信号;相图中的相轨迹均形成1个闭合圆轨道,表现为包络环形,但图6中相图的包络形状更接近实心,说明在第1个振动突变处的高低压转子间不平衡振动耦合更明显;对于频谱图,图6(c)只含高压转子转频,因此第1个振动突变是由高压转子偏心激励引起的。图8(c)中存在高、低压转子转频,以低压转子转频为主,可知第2个振动突变是由低压转子不平衡激励导致的。
由图7可知,选取双转子系统在振动响应不剧烈区域的转速下,其振动响应较小。相图中的相轨迹表现为椭圆形;频谱图中含高、低压转子的转频,系统的振动由高、低压转子的双频偏心激励引起。
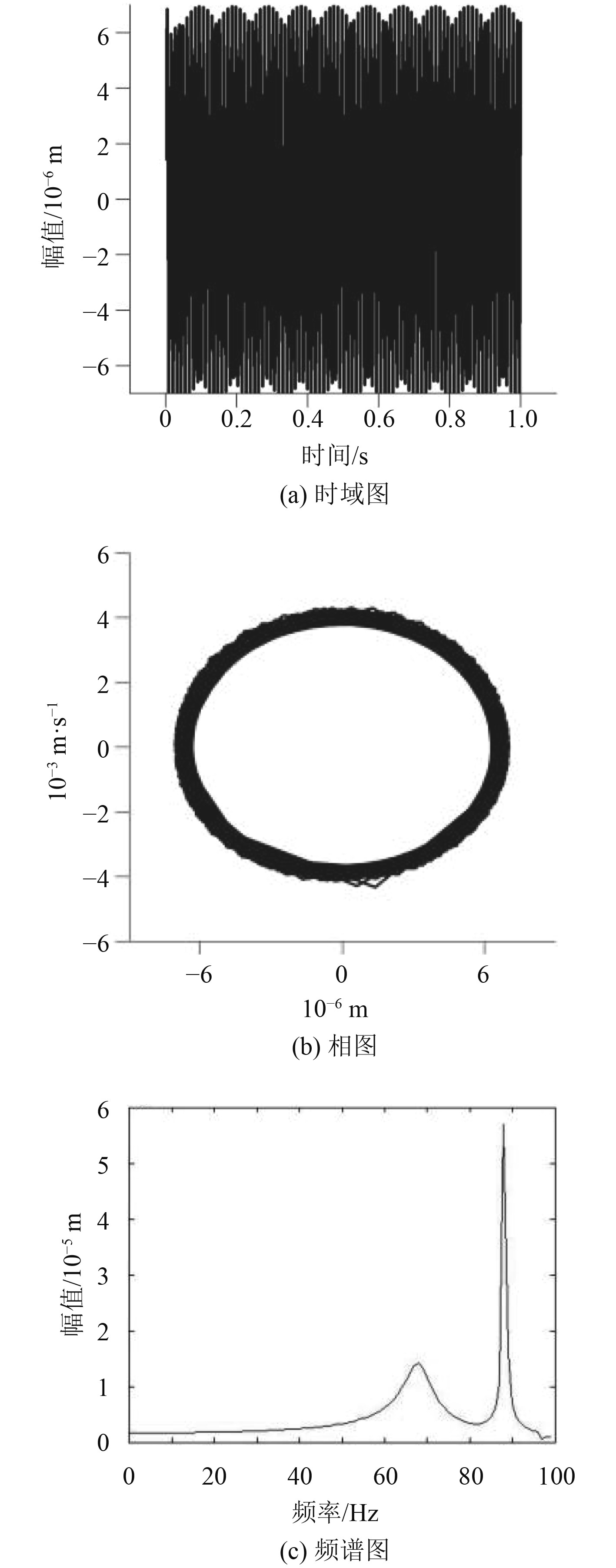
|
图 7 高压转子转速550 rad/s时,系统振动响应 Fig. 7 Vibration response of the system when the high voltage rotor speed is 550 rad/s |
采用双转子试验台,使用双电机驱动,以质量盘模拟压气机和涡轮结构,并且质量盘上可通过安装螺钉来设置不平衡量,增加不平衡激励。采用转速传感器来实时测量转子的转速,在高压转子位置处设置x和y两个方向的电涡流位移传感器,分别测量水平方向和竖直方向的位移,在轴承座上安装加速度传感器监测轴承振动情况。试验过程中,使用DASP智能采集系统进行数据采集,采样频率设为12.8 kHz。高压转子转速从0升至800 rad/s,设置高低压转速比为1.28。
高压转子的时域波形图如图9所示,横坐标为时间,纵坐标为位移幅值。可以看出,在150 s,275 s,300~360 s,380 s附近时,转子的振幅发生明显的变化,说明系统的运动状态发生了改变。高压转子的时间−转速曲线图和时间−振动幅值曲线如图10所示,250~310 s升速,350~400 s降速。可以看出在升速和降速过程中,转速在3 000 r/min,6 000 r/min附近时,高压转子的振幅出现突跳现象,振动明显增强,说明此时可能经过了临界转速,系统发生了共振。可得到高压转子的前2阶阶临界转速,将其与仿真结果相对比,相对误差均在1.2%以内,验证了仿真模型的准确性、可行性。
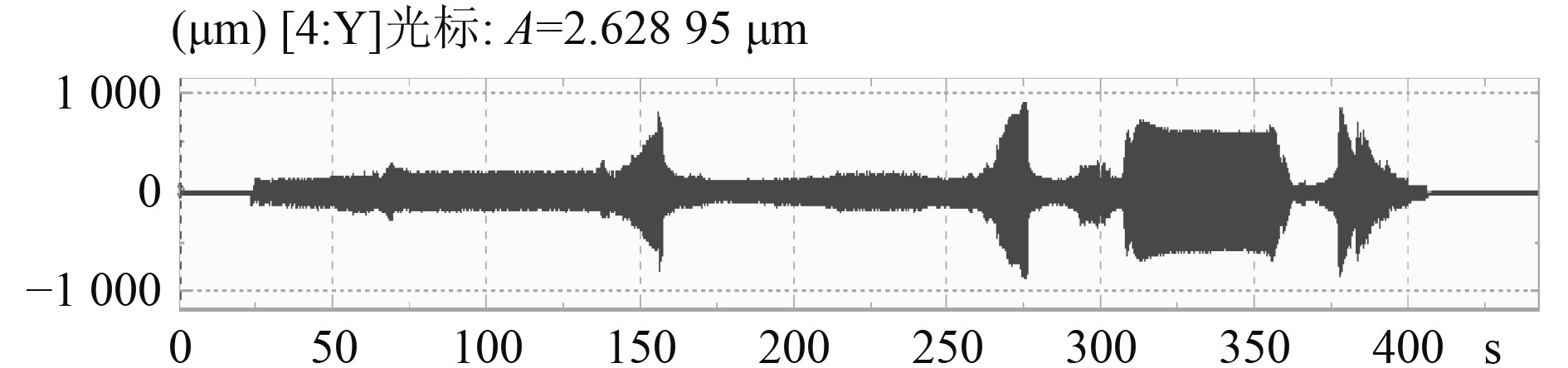
|
图 9 高压转子的时域波形图 Fig. 9 Time-domain waveform diagram of high-voltage rotor |
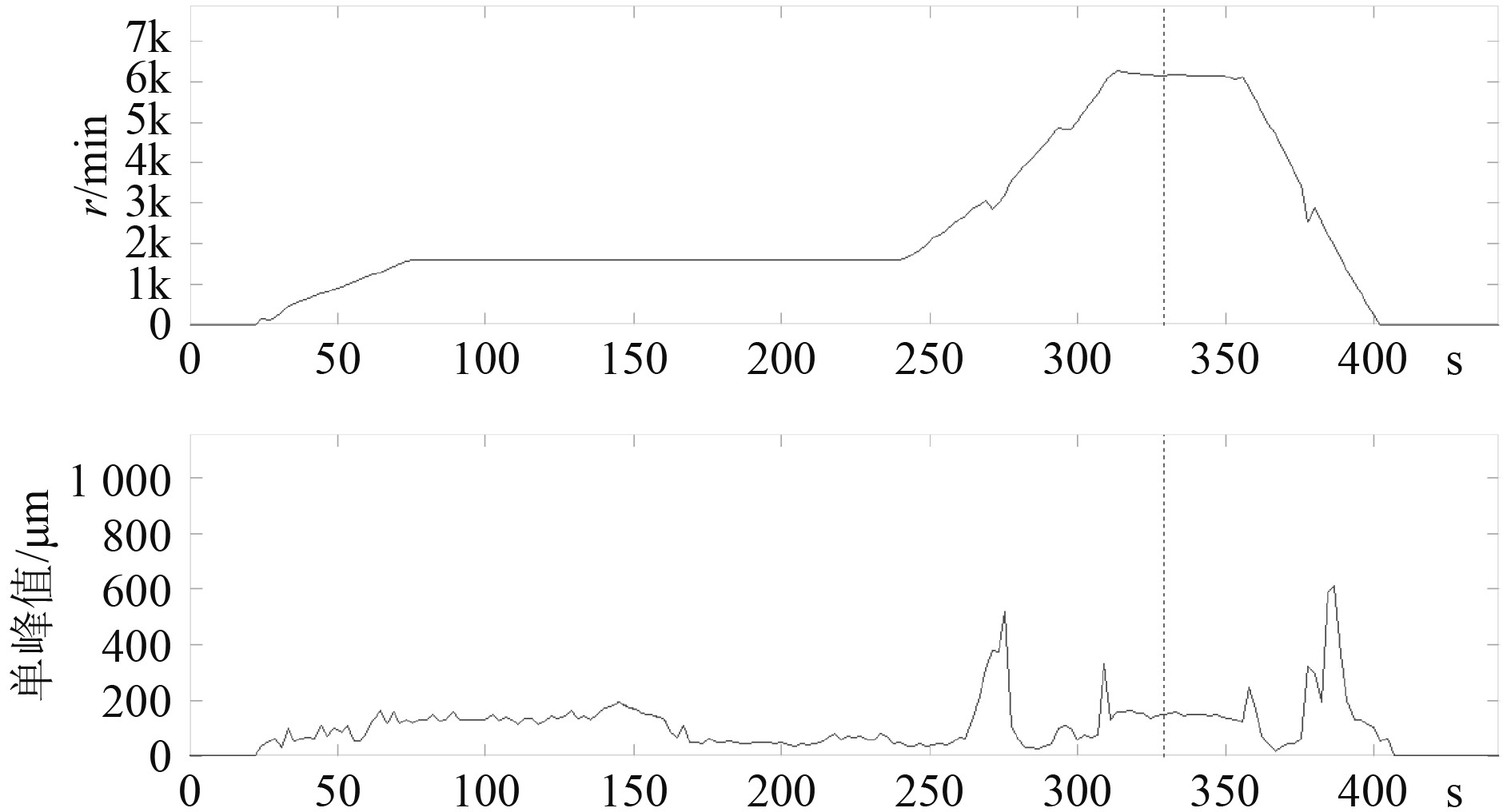
|
图 10 高压转子的转速幅值曲线 Fig. 10 Speed amplitude curve of high pressure rotor |
本文通过建立中介轴承-双转子系统的三维实体模型,基于显式算法,考虑内外转子转速、负载、偏心、接触及摩擦等因素,对双转子系统的动力学特性进行仿真研究,得到如下结论:
1)通过对系统的固有振动特性以及临界转速的计算,并与试验结果进行对比,证明仿真模型的可行性;
2)研究双转子系统存在偏心时的不平衡响应,并分别给出系统在振动平缓位置以及2个振动突变处的振动响应规律,为进一步研究双转子系统的故障特性提供基础。
| [1] |
孙传宗, 陈予恕, 侯磊. 复杂结构双转子系统的建模及模型缩减[J]. 航空动力学报, 2017, 32(7): 1747-1753. |
| [2] |
王杰, 左彦飞, 江志农. 带中介轴承的双转子系统振动耦合作用评估[J]. 航空学报, 2020.
|
| [3] |
罗真, 王艾伦. 组合转子动力学集中参数建模研究[J]. 机械科学与技术, 2017, 36(5): 717-721. |
| [4] |
周海仑, 陈果. 航空发动机双转子-滚动轴承-机匣耦合系统动力学分析[]. 航空动力学报, 2009, 24(6): 1284-1291.
|
| [5] |
杨喜关, 罗贵火. 支承非线性特性对双转子系统的响应特性影响研究[J]. 振动工程学报, 2014, 27(4): 572-581. DOI:10.3969/j.issn.1004-4523.2014.04.013 |
| [6] |
高朋, 侯磊, 陈予恕. 双转子-中介轴承系统非线性振动特性. 振动与冲击, 2019, 38(15): 1-10.
|
| [7] |
符毅强. 双转子系统非线性动力学响应分析[D]. 哈尔滨: 哈尔滨工业大学, 2015: 48-68.
|
| [8] |
李默. 轴承故障条件下某转子系统的非线性动力学研究[D]. 武汉: 海军工程大学, 2018.
|
| [9] |
于平超, 马艳红, 张大义, 等. 具有局部非线性刚度的复杂转子系统动力学模型及振动特性分析[J]. 推进技术, 2016, 37(12): 2343-2351. |
| [10] |
王海飞, 陈果. 含滚动轴承径向游隙的航空发动机整机振动响应特征分析[J]. 推进技术, 2016, 37(5): 945-959. |
| [11] |
向伟, 王华庆, 唐刚. 基于显示动力学的发动机转子中介轴承的仿真分析[J]. 北京化工大学学报(自然科学版), 2016, 43(3): 91-96. |
| [12] |
孙传宗, 杨瑞, 陈予恕. 机匣-双转子高维系统建模与实验验证[J]. 振动与冲击, 2018, 37(18): 152-157. DOI:10.13465/j.cnki.jvs.2018.18.022 |
| [13] |
缪辉, 王克明. 双转子系统临界转速的有限元分析[J]. 沈阳航空航天大学学报, 2011, 28(5): 27-31. DOI:10.3969/j.issn.2095-1248.2011.05.007 |
| [14] |
陶海亮, 潘波, 高庆, 等. 滚动轴承-转子系统非线性动力响应分析[J]. 燃气轮机技术, 2013, 26(1): 15-20. DOI:10.3969/j.issn.1009-2889.2013.01.004 |
| [15] |
吕运, 童大鹏, 田野, 等. 滚动轴承-转子系统动力学建模与仿真分析[J]. 机械强度, 2015, 37(6): 1178-1185. DOI:10.16579/j.issn.1001.9669.2015.06.023 |
| [16] |
廖明夫, 刘永泉, 王四季, 等. 中介轴承对双转子振动的影响[J]. 机械科学与技术, 2013, 32(5): 641-646. DOI:10.13433/j.cnki.1003-8728.2013.05.021 |
| [17] |
马辉, 李鸿飞, 俞昆等. 含局部故障的滚动轴承动力学建模及振动分析[J]. 东北大学学报, 2020, 41(3): 343-348. |
 2023, Vol. 45
2023, Vol. 45
