2. 江苏大学 土木工程与力学学院,江苏 镇江 212013;
3. 上海大学 力学与工程科学学院,上海200444
2. Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China;
3. School of Mechanics and Engineering Science, Shanghai University, Shanghai 200444, China
目前俘能器的主要研究方向包括线性多模态[1]、自调谐频率[2]、三次非线性[3]、双稳态[4]、三稳态[5]、多稳态[6]、相干共振[7]和非线性相互作用[8]。
流致振动俘能作为一种新型的清洁可再生能源,成为一个研究热点。流致振动俘能技术主要有风致振动能量和水致振动能量,其中风致振动俘能主要有涡激振动[9-10]、颤振[11-13]、驰振[13-14]、抖振[9, 15]。而水流致振动俘取得了许多有意义的成果[16-18]。脉动流诱发的振动在海洋工程中广泛存在,具有重要的研究价值。因此,本文设计一个脉动流致振动双稳态俘能器,考察该俘能器在水下脉动流致振动时的性能。
1 采集器模型如图1所示,该俘能器结构系统由2个倾斜的弹簧、阻尼器和圆柱体组成。电路系统由铜线圈、电阻和磁铁组成。
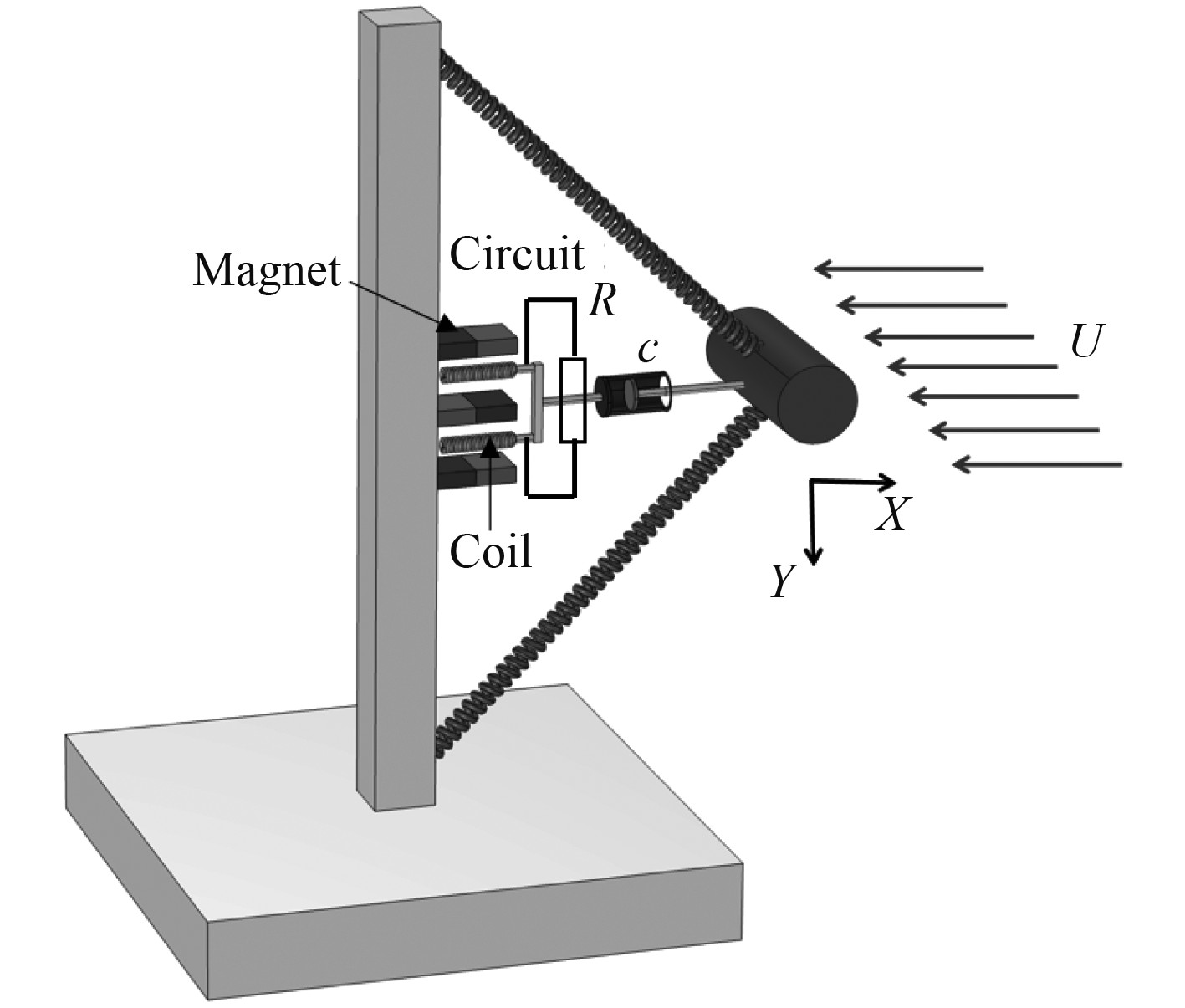
|
图 1 脉动流致振动双稳态俘能器 Fig. 1 Bistable energy harvesting induced by oscillating flow |
利用法拉第电磁感应定律,可以推导系统的机电耦合运动方程为:
| $\begin{split} & \left( {m + \rho A{C_l}} \right)\ddot X + c\dot X + kX\left( {1 - \frac{L}{{\sqrt {{X^2} + {l^2}} }}} \right) + BI{L_{coil}} = \\ &\rho A{C_m}\dot U + 0.5\rho \left( {U - \dot X} \right)\left| {U - \dot X} \right|D{C_D},\end{split} $ | (1) |
| $ {L_{ind}}\dot{ \bar I} + R\bar I - B{L_{coil}}\dot X = 0。$ | (2) |
其中:X为系统的位移;
为了简化计算,式(1)和式(2)可以无量纲化为
| $ \begin{split} \ddot x +& \varsigma \dot x + x\left( {1 - \frac{1}{{\sqrt {{x^2} + {\alpha ^2}} }}} \right) + \lambda I = \beta {u_m}\sin \omega t +\\ & \gamma \left( {{u_0} + {u_m}\sin \omega t - \dot x} \right)\left| {{u_0} + {u_m}\sin \omega t - \dot x} \right| ,\end{split} $ | (3) |
| $ \dot I + \chi I - \kappa \dot x = 0 。$ | (4) |
其中:
| $\begin{split} & x = \frac{X}{L},I = \frac{{\tilde I}}{L},t = T{\omega _0},\zeta = \frac{c}{{\sqrt {k\left( {m + \rho A{C_l}} \right)} }},{\omega _0} =\\ & \sqrt {\frac{k}{{m + \rho A{C_l}}}} ,u = \frac{U}{{{\omega _0}L}},\alpha = \frac{l}{L},\beta = - \frac{{\rho A{C_m}}}{m},\\&\gamma = \frac{{\rho D{C_D}L}}{{2m}},\lambda = \frac{{B{L_{coil}}}}{k},\chi = \frac{R}{{{\omega _0}{L_{ind}}}},\kappa = \frac{{B{L_{coil}}}}{{{\omega _0}{L_{ind}}}}。\end{split} $ |
系统的势能为:
| $ V\left( x \right) = \frac{1}{2}k{\left( {\sqrt {{x^2} + {l^2}} - L} \right)^2},$ | (5) |
对应的恢复力为:
| $ F\left( x \right) = kx\left( {1 - \frac{L}{{\sqrt {{x^2} + {l^2}} }}} \right)。$ | (6) |
系统势能和恢复力变化的曲线图如图2所示。由图2(a)可知,系统的势能在3组不同参数下,具有双势阱特征,且双势阱在势垒的左右两侧对称的分布。由图2(b)可知,系统的恢复力有3个解,即1个零解,2个关于零对称的解,相应的静平衡解见表1。因此,该系统(1)和(2),具有双稳态的特性。
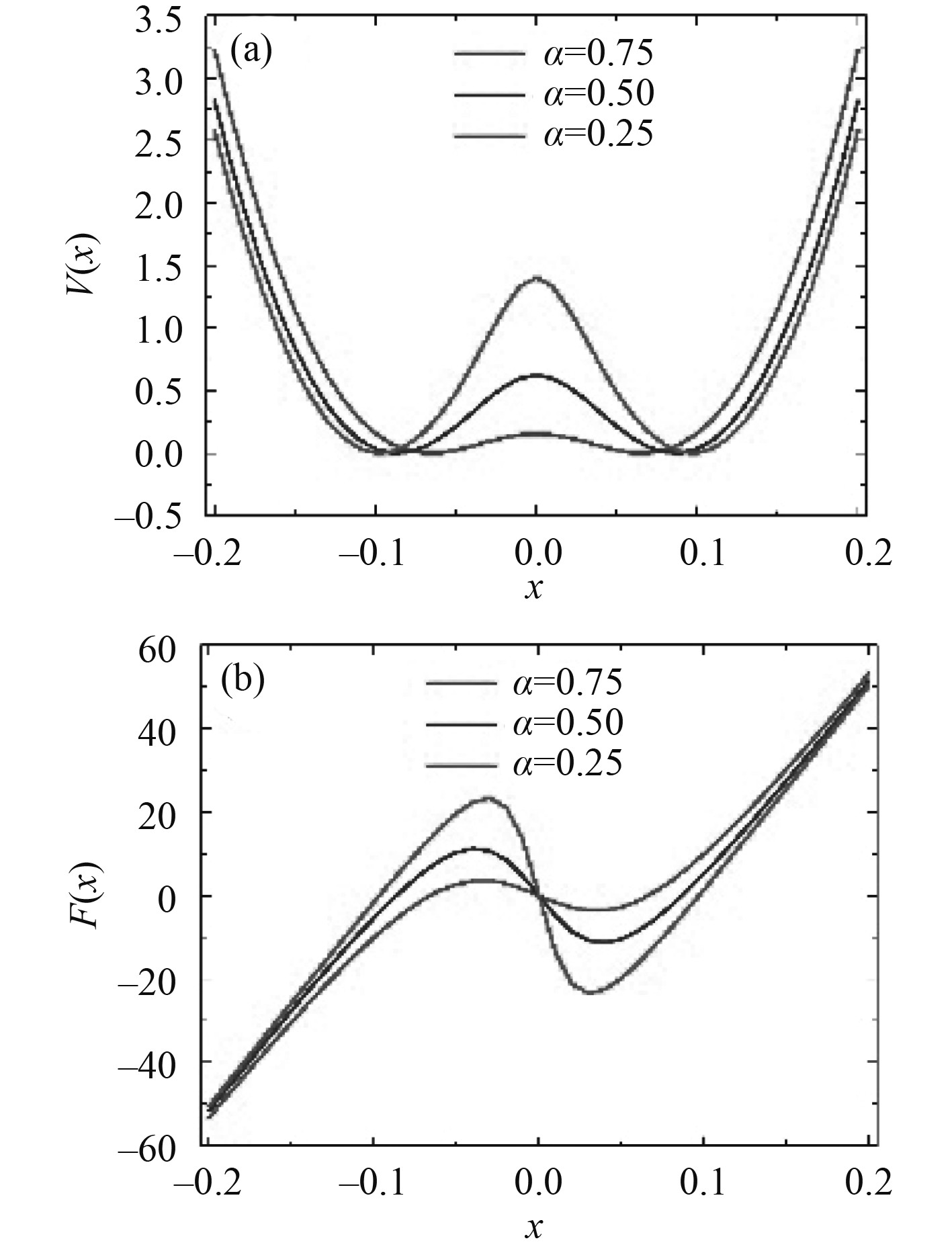
|
图 2 系统的势能和恢复力曲线 Fig. 2 Potential energy and restoring force curves of the system |
|
|
表 1 系统的静平衡值及泰勒系数 Tab.1 The static equilibrium value and Taylor coefficient of the system |
式(3)为非线性微分方程,没有精确解析解。若波浪流速的幅值远大于系统最大速度[19],则
| $ 0.5\rho \left( {U - \dot X} \right)\left| {U - \dot X} \right|D{C_D} \approx 0.5\rho {U^2}D{C_D} 。$ | (7) |
同时,当系统做小幅振动时,无理非线性刚度可以在静平衡点展开为多项式非线性形式,忽略三次以上高阶非线性和二次以上激励项,则系统的机电耦合方程可以重新简化为:
| $ \ddot x + \varsigma \dot x + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + \lambda I = \beta {u_m}\sin \omega t ,$ | (8) |
| $ \dot I + \chi I - \kappa \dot x = 0 。$ | (9) |
其中:
| $ \begin{split} &{a_1} = 1 + \frac{{{x^2}}}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^3}} }} - \frac{1}{{\sqrt {{x^2} + {\alpha ^2}} }},\\ & {a_2} = \frac{{2x}}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^3}} }} + x\left( { - \frac{{3{x^2}}}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^5}} }} + \frac{1}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^3}} }}} \right) ,\\& {a_3} = x\left( {\frac{{15{x^3}}}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^7}} }} - \frac{{9x}}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^5}} }}} \right) +\\ &\qquad 3\left( { - \frac{{3{x^2}}}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^5}} }} + \frac{1}{{\sqrt {{{\left( {{x^2} + {\alpha ^2}} \right)}^3}} }}} \right)。\\ \end{split} $ |
假设系统的一阶谐波解为:
| $ x = {x_1}\cos \omega t + {x_2}\sin \omega t,$ | (10) |
代入电路方程,可得解耦后的电流为:
| $ I = \frac{{\omega \kappa \left( {\left( {\omega {x_1} + {x_2}\chi } \right)\cos \omega t + \left( {\omega {x_2} - {x_1}\chi } \right)\sin \omega t} \right)}}{{{\omega ^2} + {\chi ^2}}}。$ | (11) |
把式(8)和式(9)代入式6),可得一阶谐波解满足如下关系:
| $\begin{split} &\frac{1}{4}\left( {4{a_1}{x_1} - 4{\omega ^2}{x_1} + 3{a_3}x_1^3 + 4c\omega y + 3{a_3}{x_1}x_2^2 - 4{u_1}\omega \beta } \right) +\\ & \frac{{\omega \kappa \lambda \left( {\omega {x_1} + {x_2}\chi } \right)}}{{{\omega ^2} + {\chi ^2}}} = 0,\\[-20pt] \end{split}$ | (12) |
| $\begin{aligned} & \frac{1}{4}\left( { - 4c\omega {x_1} + 4{a_1}{x_2} - 4{\omega ^2}{x_2} + 3{a_3}x_1^2{x_2} + 3{a_3}x_2^3} \right) + \\ & \frac{{\omega \kappa \lambda \left( {\omega {x_2} - {x_1}\chi } \right)}}{{{\omega ^2} + {\chi ^2}}} = 0 。\end{aligned}$ | (13) |
式(10)和式(11)是非线性的代数方程组,没有解析解,可以利用数值方法进行求解计算。
进一步根据式(9),可以得到输出电流幅值与位移响应幅值的关系为:
| $ \left| I \right|{\text{ = }}\frac{{\omega \kappa }}{{\sqrt {{\omega ^2} + {\chi ^2}} }}\left| x \right|\cos \left( {\omega t + \varphi } \right) ,$ | (14) |
功率方程:
| $ P = {\tilde I^2}R = \frac{{{I^2}}}{{{L^2}}}R{\text{ = }}\frac{{{\omega ^2}{\kappa ^2}{x^2}R}}{{{L^2}\left( {{\omega ^2} + {\chi ^2}} \right)}} 。$ | (15) |
基于式(10)~式(12),图3给出为不同激励下系统的幅频响应曲线。其中ζ=0.02,χ=0.016,κ=0.16,λ=0.002,β=-0.209。可知,系统的幅频响应曲线具有向左弯曲的软特性,且随着激励幅值的增加,响应的频率带宽增加,具有宽频的采集特性。
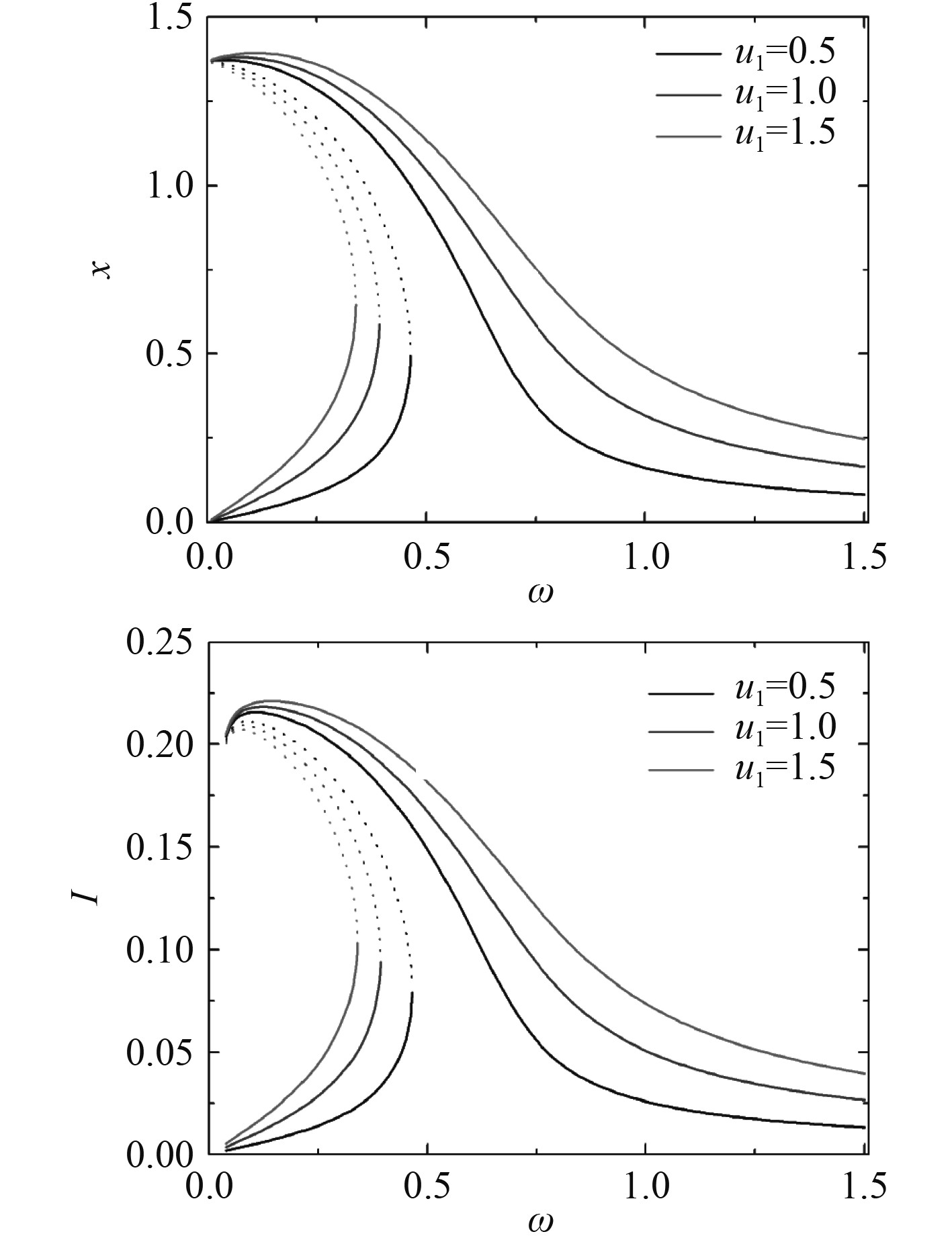
|
图 3 不同激励幅值下的幅频响应曲线 Fig. 3 Amplitude-frequency response curves under different excitation amplitudes |
图4为3组不同倾斜角余弦时的响应曲线随着外激励频率的变化趋势。可以看出,随着倾斜角余弦的减小,系统的位移和电量响应增加,且采集频率的带宽也增大。因此,小的倾斜角余弦能同时采集更多的电量和拥有宽频的带宽。
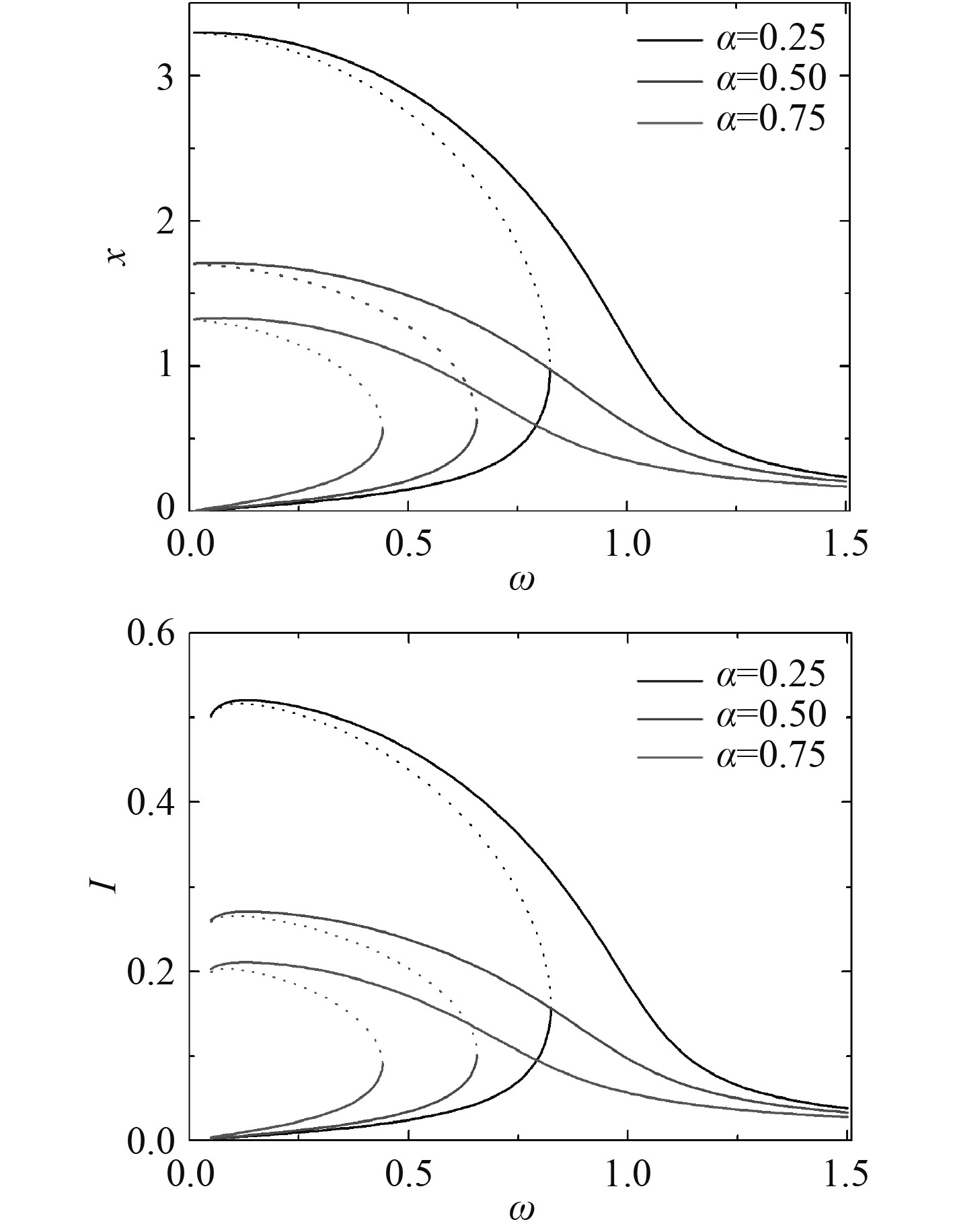
|
图 4 不同倾斜角下的幅频响应曲线 Fig. 4 Amplitude-frequency response curves at different inclination angles |
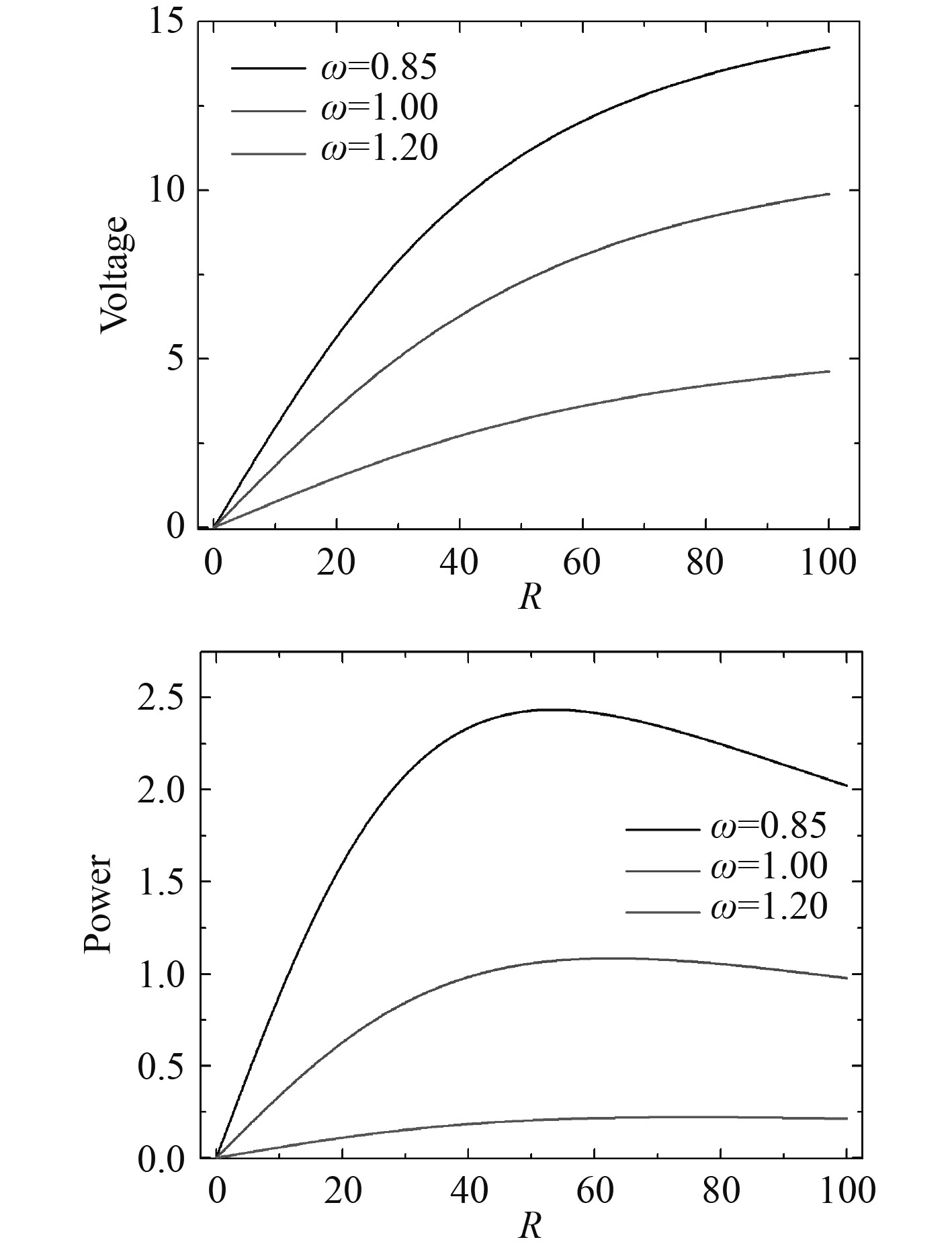
图5给出3组不同频率时,电压和功率s随电阻变化的规律。可以看出,在不同激励频率下,随着电压的增加电阻先极速增加再缓慢增加,功率随着电阻先极速增加再慢慢减小,存在一个最优电阻使得输出的功率最大。
|
图 5 不同频率下的输出电量随电阻的变化 Fig. 5 The output power at different frequencies varies with the resistance |
|
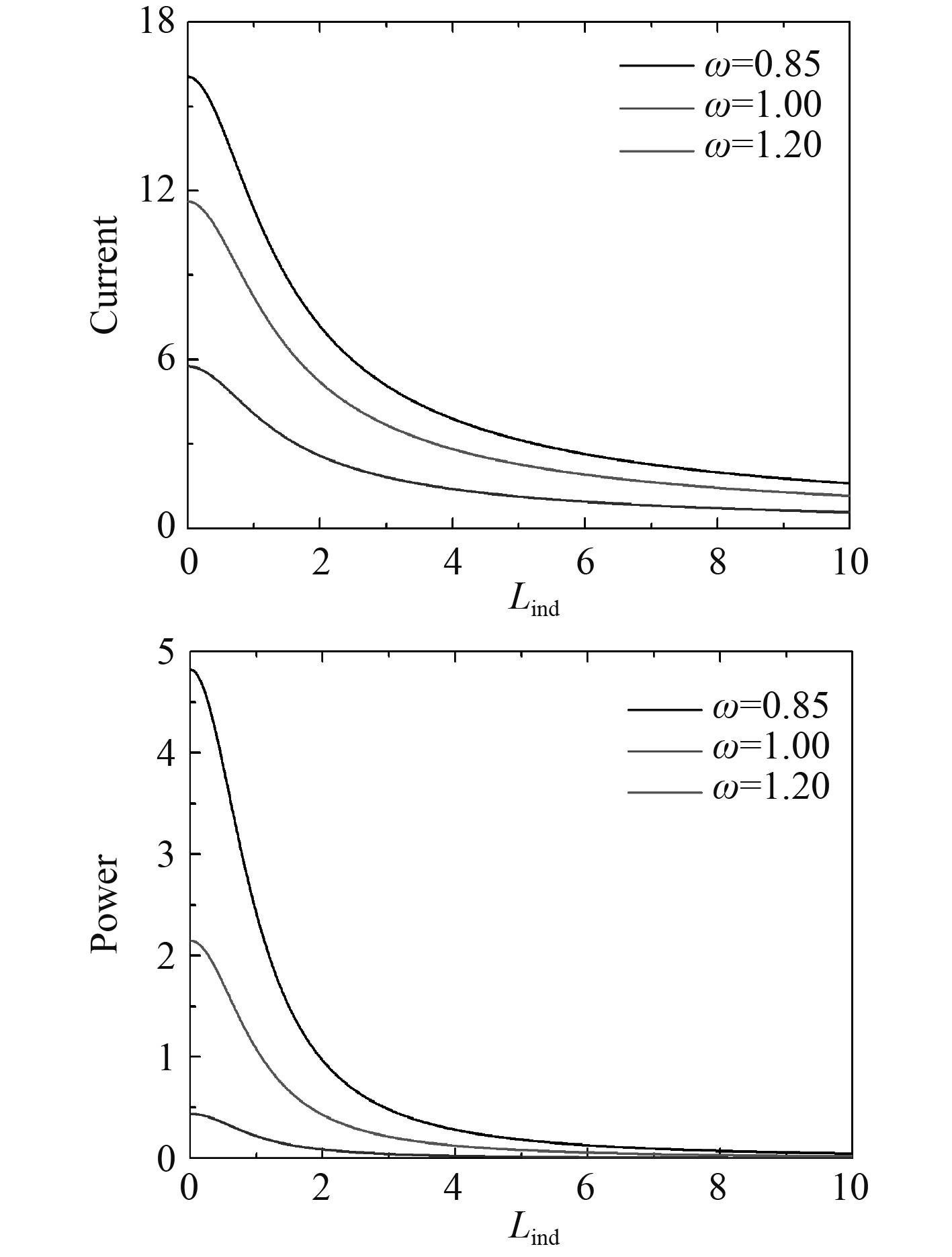
图 7 不同频率下的输出电量随电感的变化 Fig. 7 The variation of output power with inductance at different frequencies |
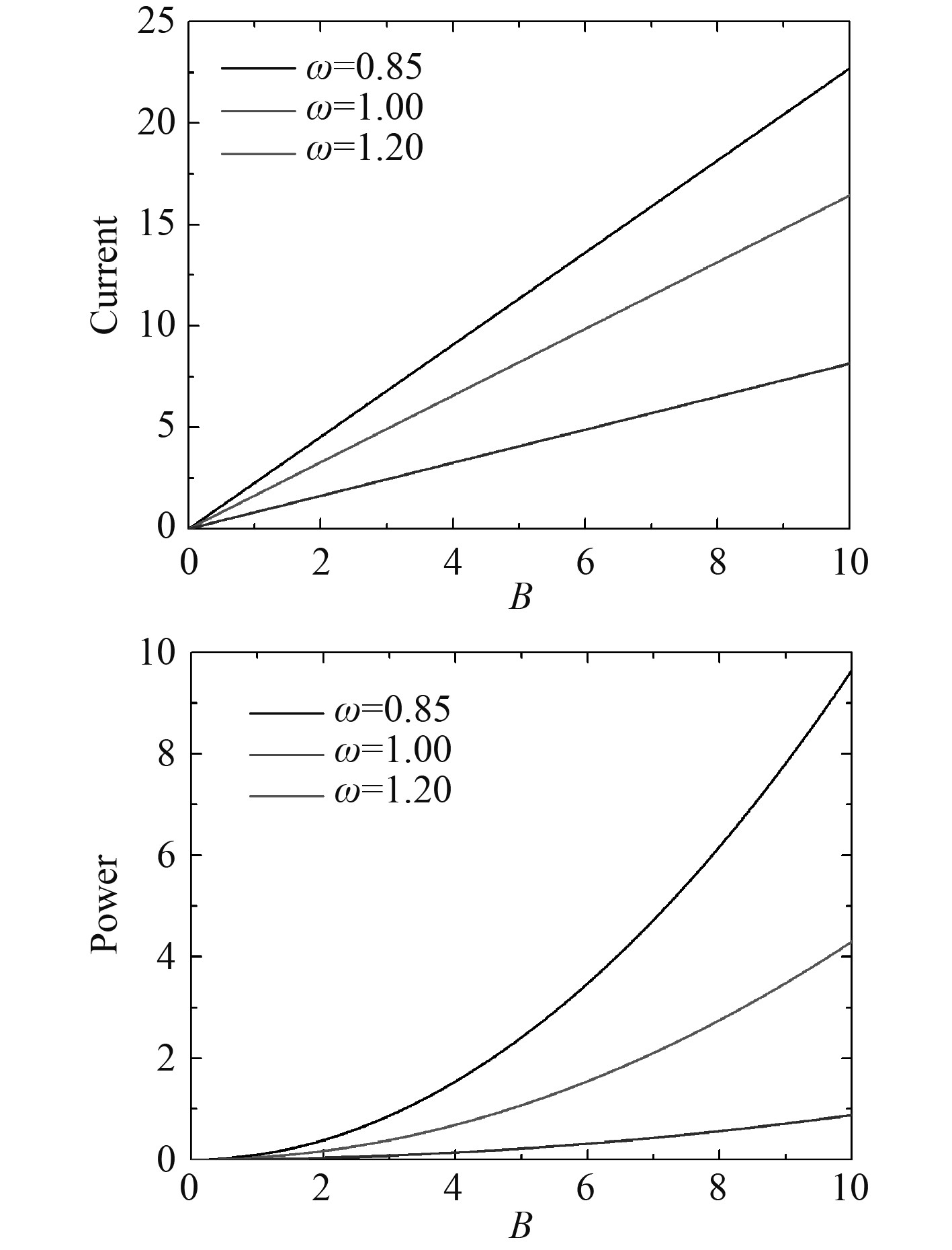
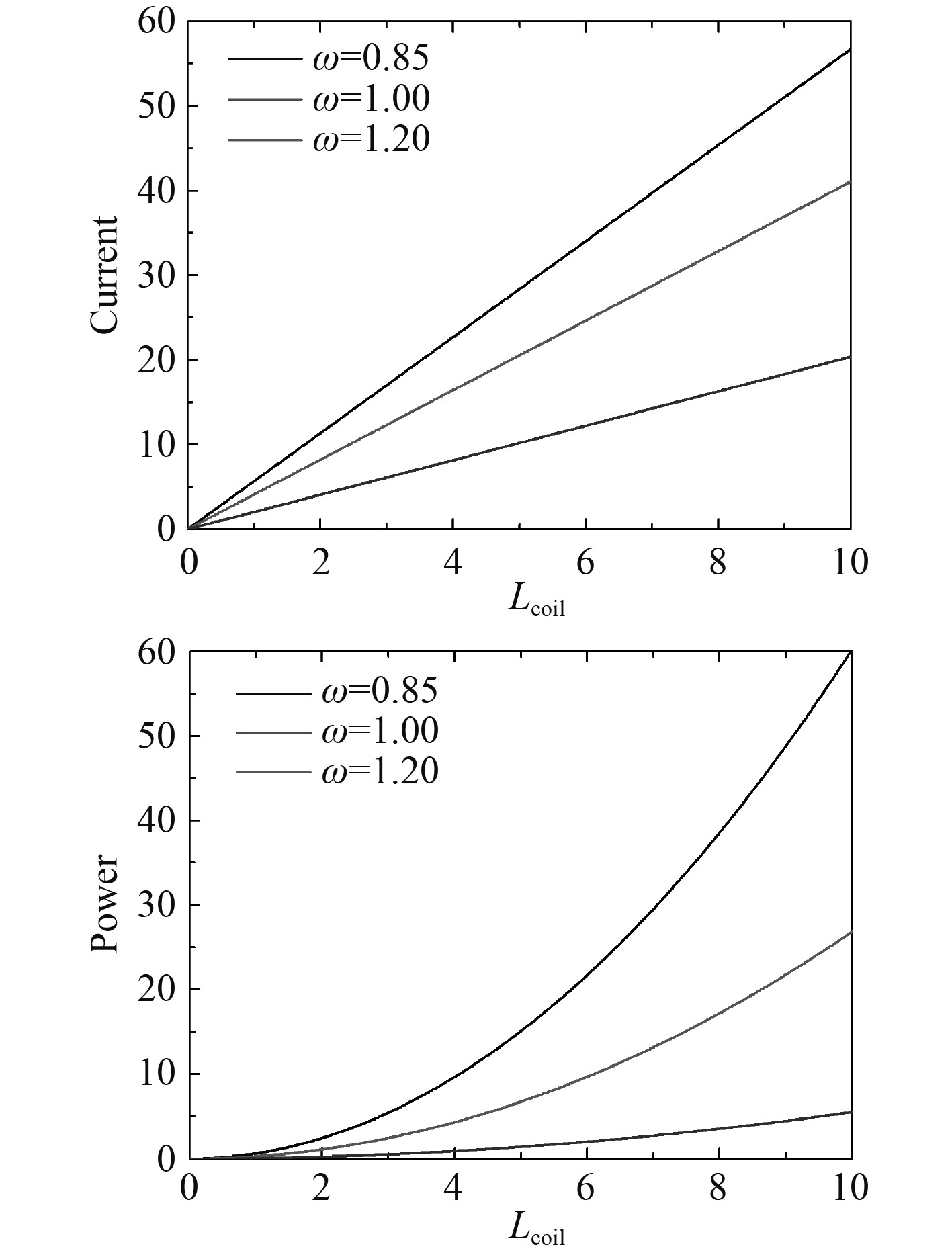
图6~图8为电量参数对输出响应的影响。可知,随着磁感线强度和线圈长度的增加,输出电流响应近似线性的增加,功率呈非线性增加。随着电感的增加,输出电流和功率呈非线性递减。
|
图 6 不同频率下的输出电量随磁感应强度的变化 Fig. 6 The variation of output power with magnetic induction intensity at different frequencies |
|
图 8 不同频率下的输出电量随线圈长度的变化 Fig. 8 The output power at different frequencies varies with coil length |
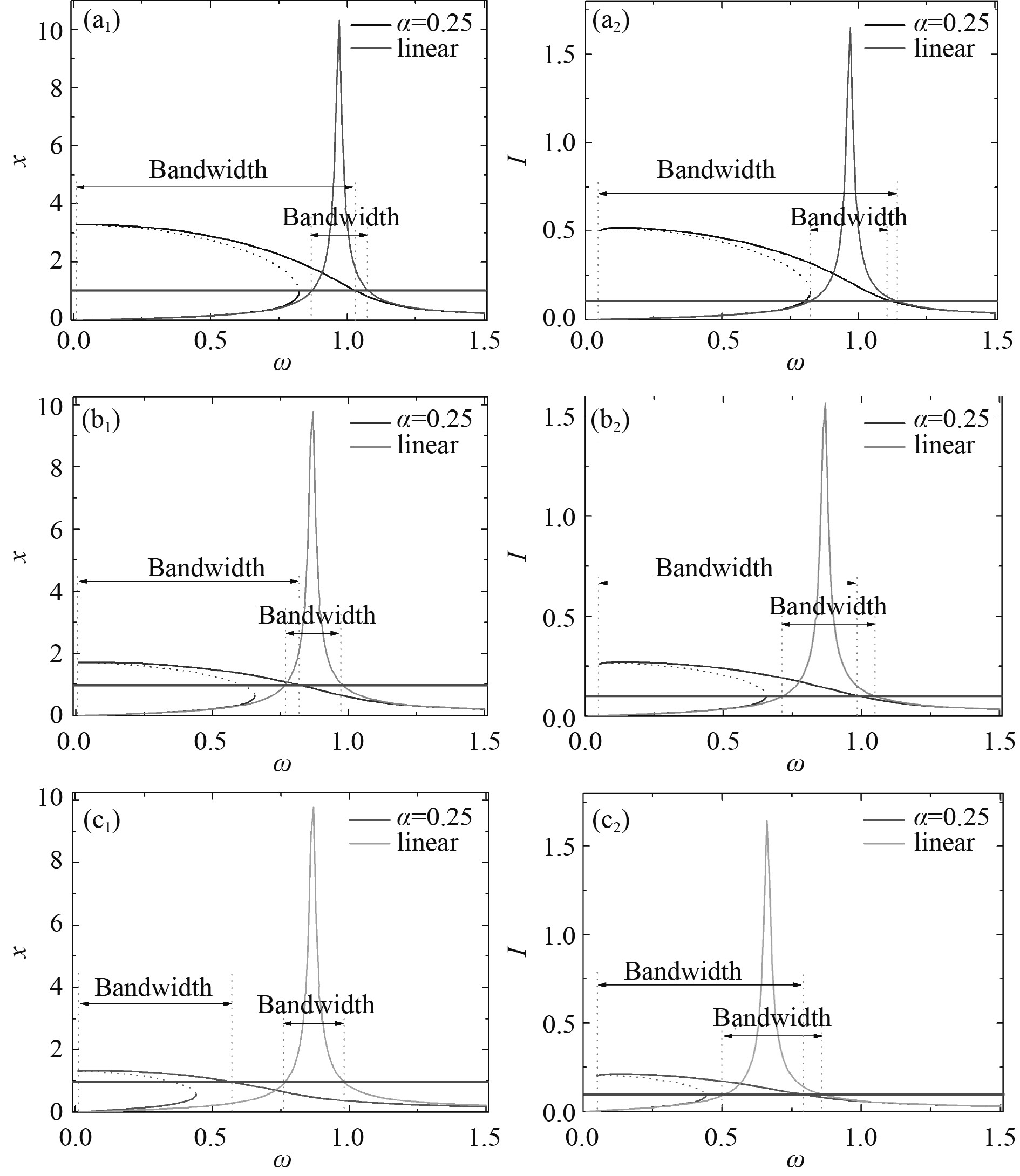
图9为3组不同倾斜角余弦(α=0.25, 0.5, 0.75)时的幅频响应曲线。其中比较的基准选取位移响应为1,电流响应为0.1。可知,线性系统在共振频率附近有比较大的幅值,但是采集的频率带宽只集中在共振频率附近,而非线性系统具有更宽的采集频率带宽。
|
图 9 与线性采集器幅频性能对比 Fig. 9 Compared with the amplitude and frequency performance of linear collector |
当波浪流速的幅值与系统速度之间的大小关系不确定时,式(3)和式(4)是含有绝对值的无理非线性微分方程组,系统的近似响应求解困难。采用四阶龙格库塔数值方法,对系统的响应进行求解。
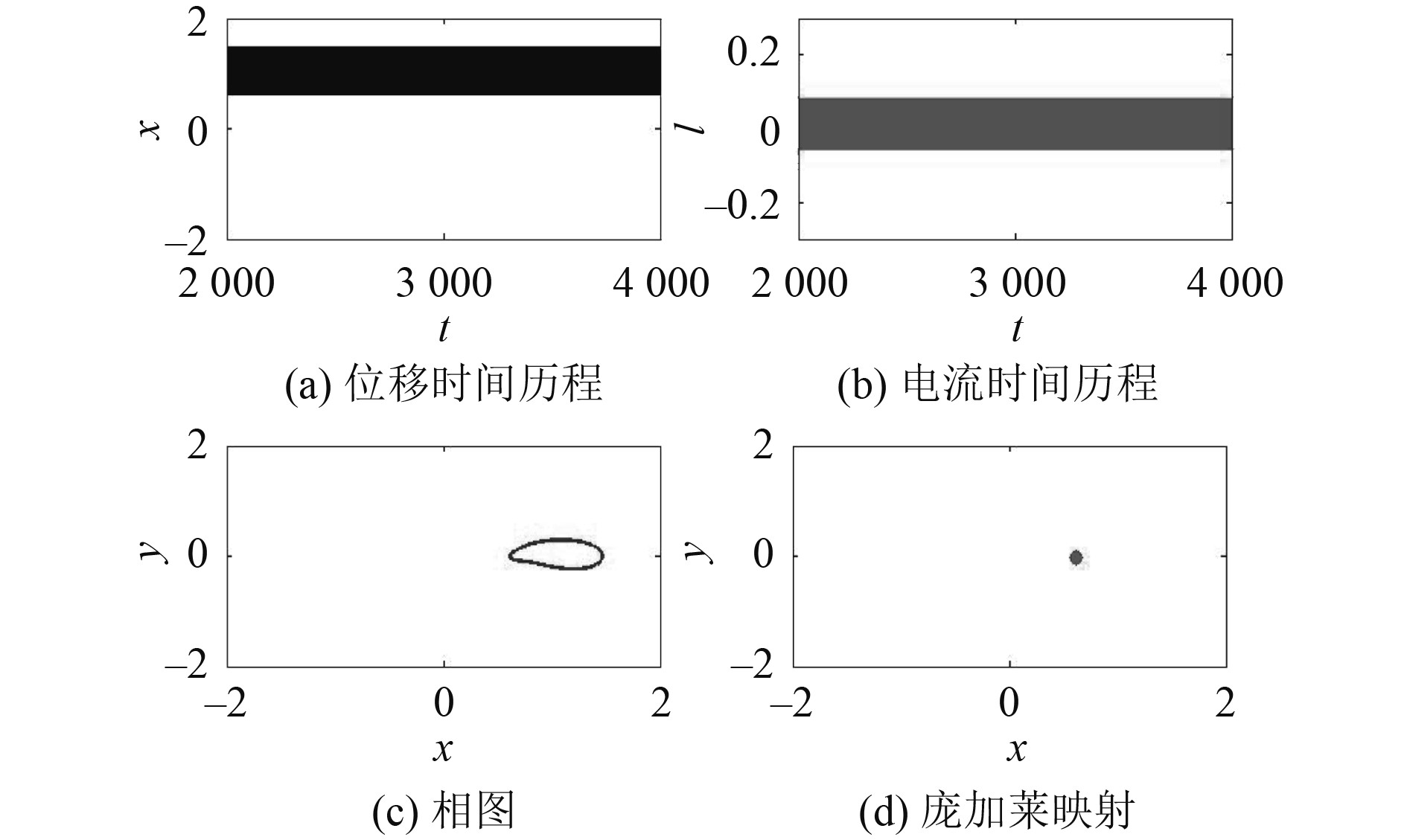
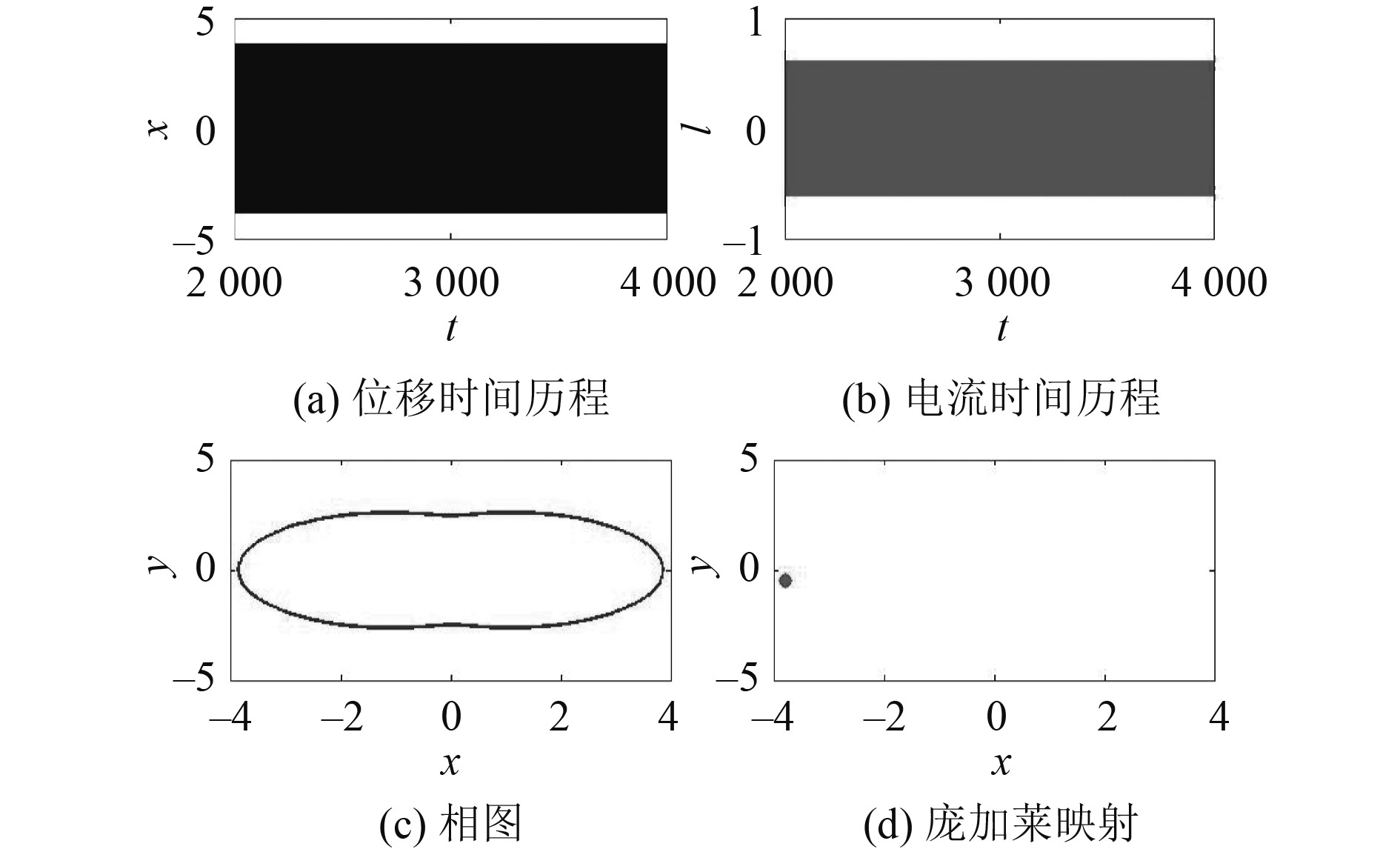
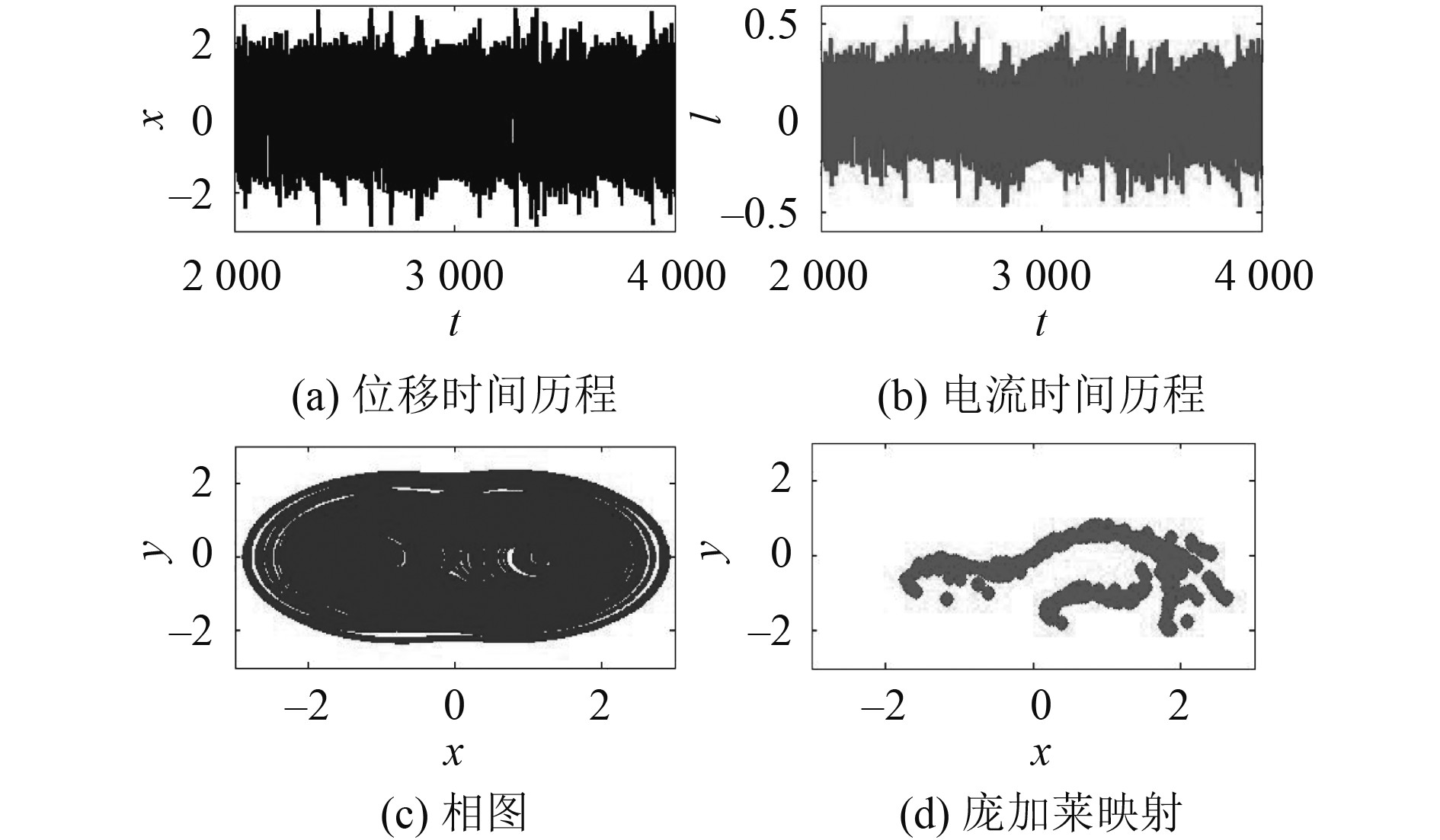
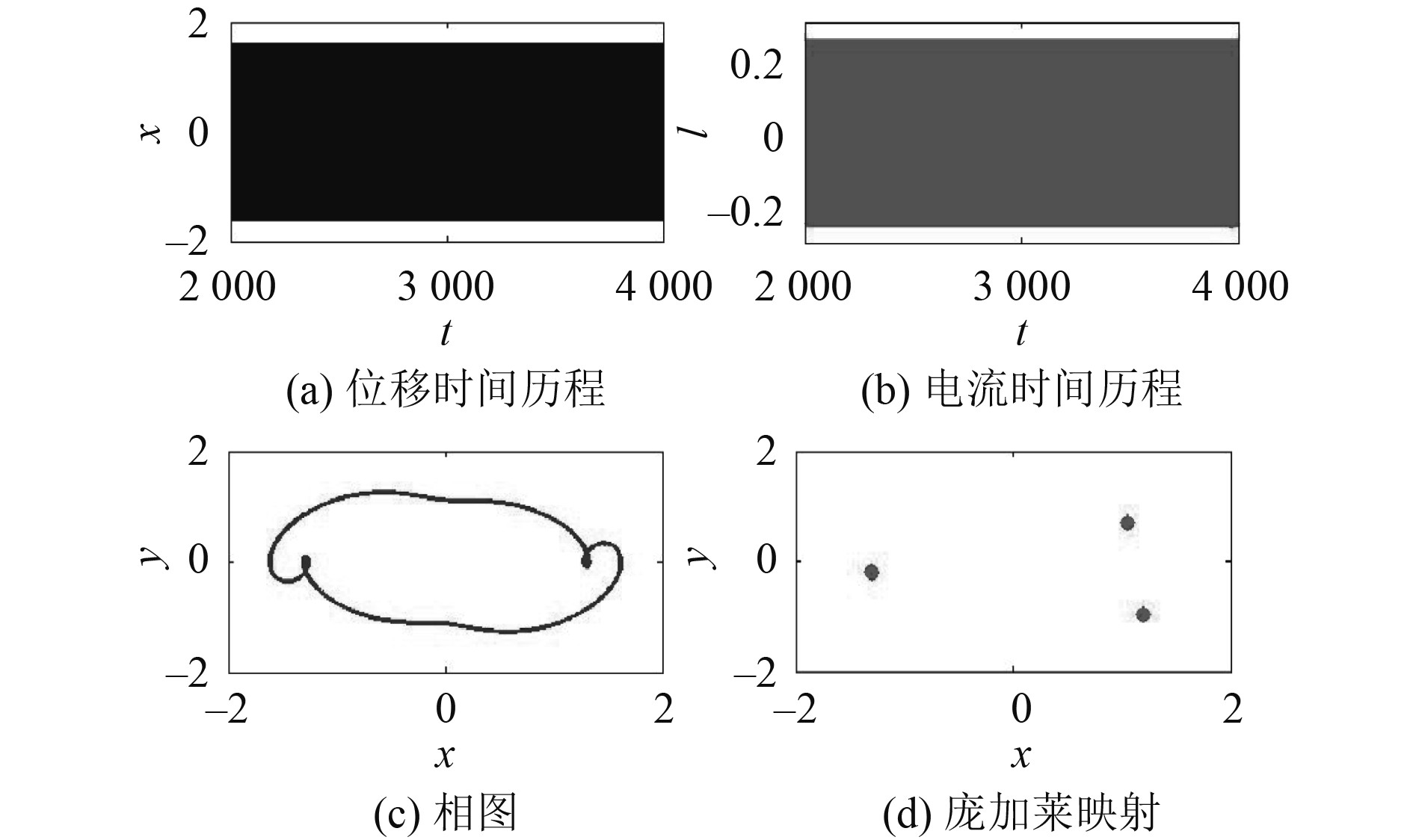
3.1 不同类型的运动响应图10~图13给出系统在不同频率时的动力学行为(ω= 0. 5, 0.75, 1.0,1.5)。可知,当ω=0.5时,系统存在小幅的周期运动;当ω=0.75时,系统做大幅的周期运动;当ω=1.0时,系统做混沌运动;当ω=1.5时,系统做3倍周期运动。
|
图 10 ω=0.5时的小幅周期响应 Fig. 10 Small periodic response at ω=0.5 |
|
图 11 ω=0.75时的大幅周期响应 Fig. 11 Small periodic response at ω=0.75 |
|
图 12 ω=1.0时的混沌响应 Fig. 12 Small periodic response at ω=1.0 |
|
图 13 ω=1.5时的倍周期响应 Fig. 13 Small periodic response at ω=1.5 |
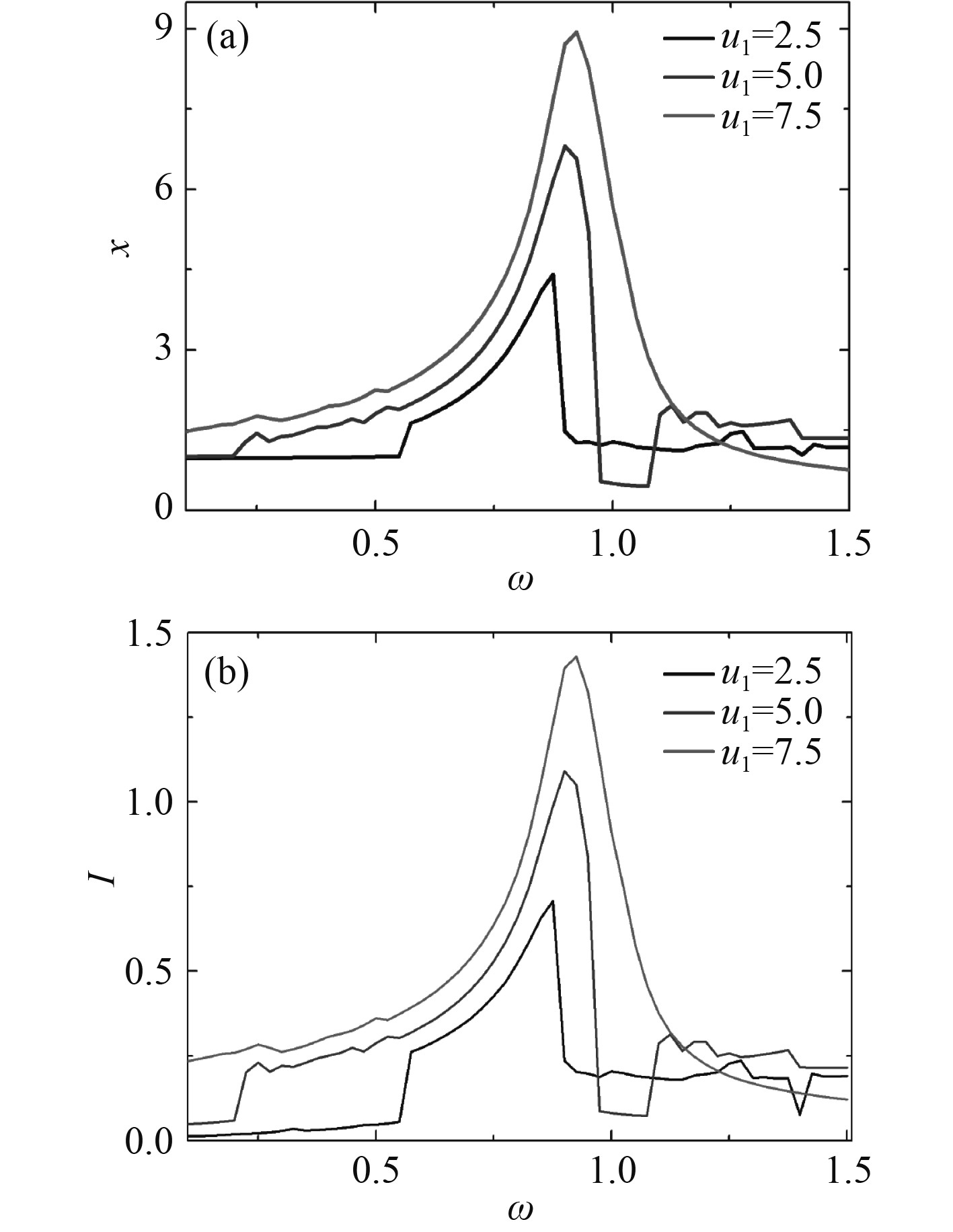
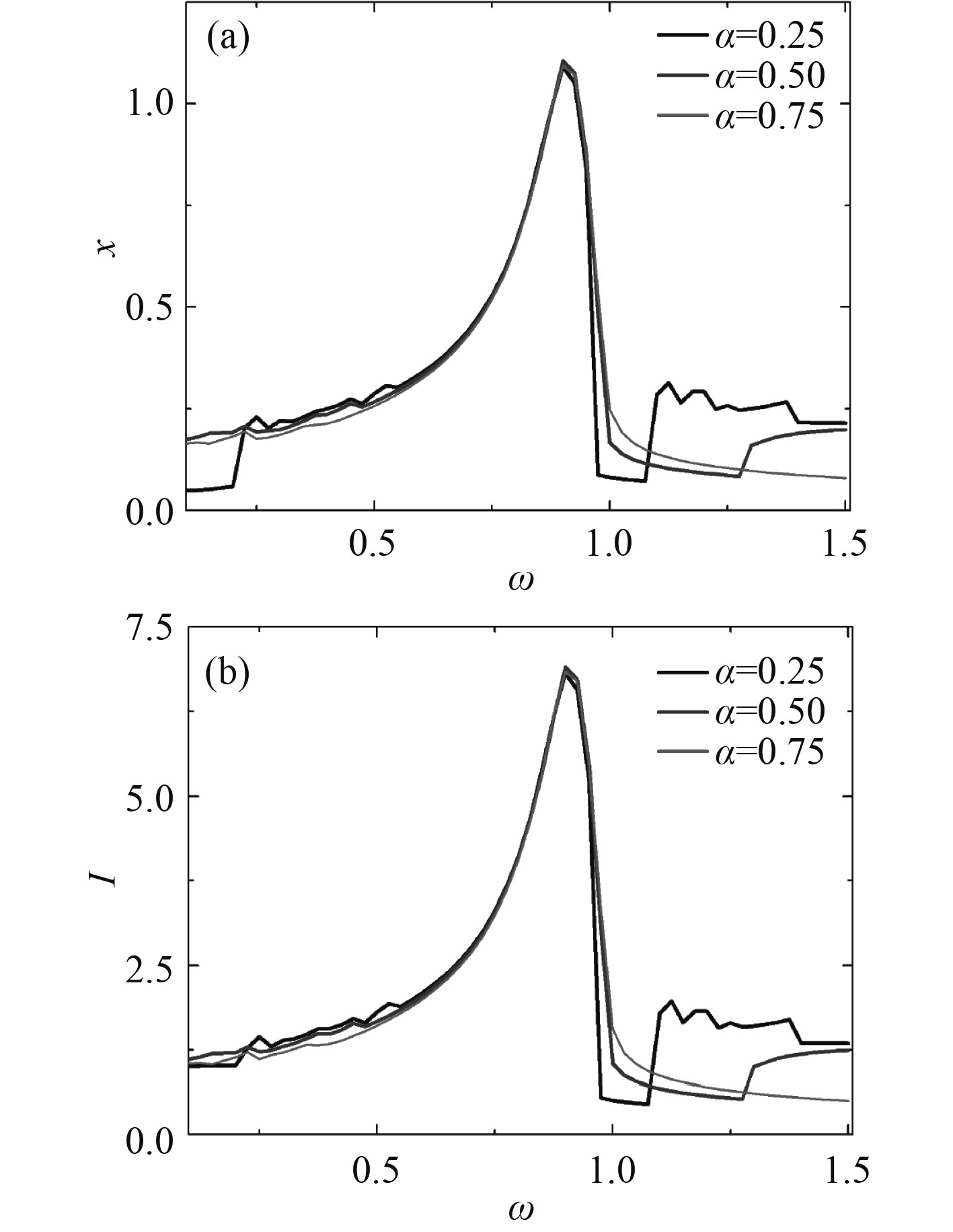
采用均方根的统计方法,计算系统的输出响应。图14为3组激励幅值下的幅频响应曲线。图15为3组不同倾斜角余弦时的响应曲线随着外激励频率的变化趋势。可以看出,随着激励幅值的增加,除个别频率外,系统的位移和电量响应增加,而倾斜角余弦对系统响应的影响差别不大。
|
图 14 波速与速度不确定时激励幅值变化的幅频响应曲线 Fig. 14 Amplitude-frequency response curve of excitation amplitude variation with uncertain wave velocity and velocity |
|
图 15 波速与速度不确定时不同倾斜角下的幅频响应曲线 Fig. 15 Amplitude-frequency response curves at different inclination angles when wave velocity and velocity are uncertain |
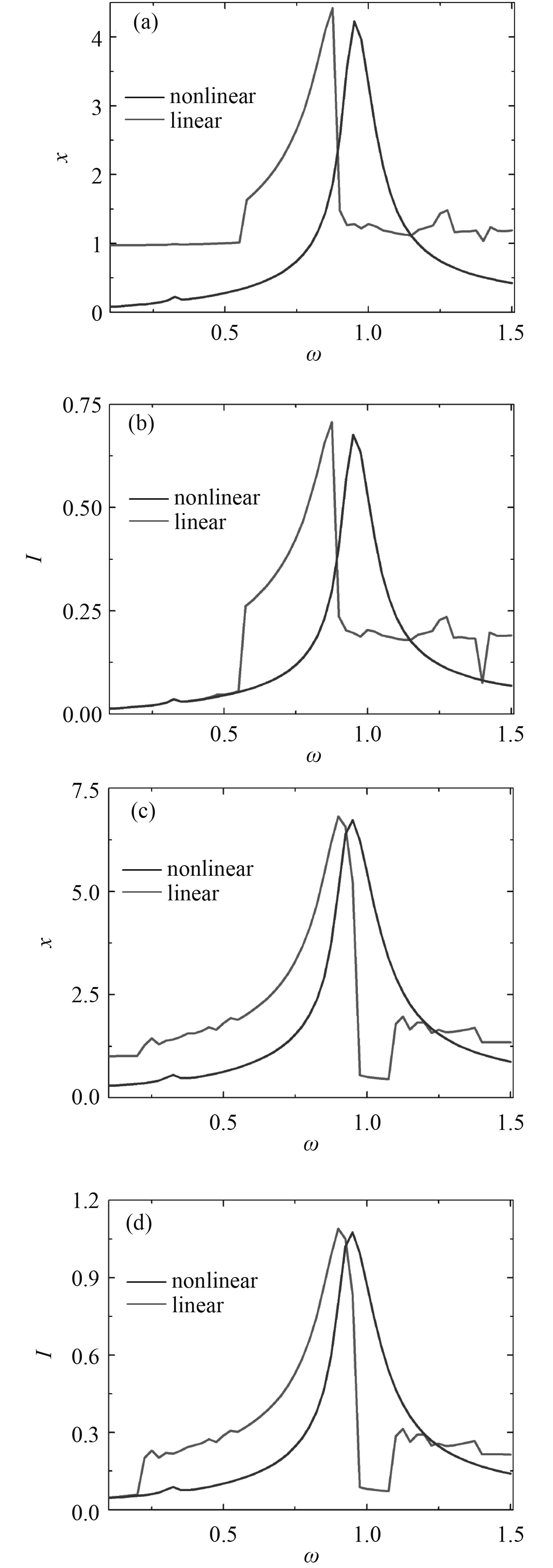
图16 为2组不同幅值(u1=2.5和u1=5)时非线性系统和相应线性系统幅频相应曲线的对比。可知,非线性线性系统比相应线性系统在多个频率有更大的响应幅值,具有宽频的采集特性。
|
图 16 波速与速度不确定时与线性采集器幅频性能对比 Fig. 16 Amplitude and frequency performance comparison with linear collector with uncertain wave velocity and velocity |
本文设计一个水下双稳态俘能器,研究系统在脉动流致振动下的采集性能,进行解析分析和数值计算,得出如下主要结论:
1)在波速远大于速度的小幅振动运动中,通过谐波分析,发现系统的幅频响应曲线具有向左弯曲的软特性。通过与线性系统对比,得到系统具有宽频的采集特性。随着系统电阻的变化,存在一个最优的电阻,使得输出电量的功率最大。
2)在波速与速度不确定的振动中,基于数值计算,发现系统存在小幅周期、大幅周期、混沌和倍周期等复杂的非线性动力学行为,且系统比线性系统有更宽的采集频带。
3)计算和分析结果可以为波浪能宽频发电技术提供一定的理论支撑。
| [1] |
SHAHRUZ SM. Design of mechanical band-pass filters for energy scavenging[J]. Journal of Sound and Vibration, 2006, 292(3): 987-998. |
| [2] |
CHALLA V, PRASAD M, SHI Y, et al. A vibration energy harvesting device with bidirectional resonance frequency tunability[J]. Smart Materials and Structures, 2008, 17(1): 015035. DOI:10.1088/0964-1726/17/01/015035 |
| [3] |
CAO D X, GAO Y H, HU W H. Modeling and power performance improvement of a piezoelectric energy harvester for low-frequency vibration environments[J]. Acta Mechanica Sinica, 2019, 35(4): 894-911. DOI:10.1007/s10409-019-00852-3 |
| [4] |
COTTOEN F, VOCCA H, GAMMAITONI L. Nonlinear energy harvesting[J]. Physical Review Letters, 2009, 102(8): 080601. DOI:10.1103/PhysRevLett.102.080601 |
| [5] |
CAO J Y, ZHOU S X, WEI W, et al. Influence of potential well depth on nonlinear tristable energy harvesting[J]. Applied Physics Letters, 2015, 106(17): 515-530. |
| [6] |
YANG T, CAO Q. Novel multi-stable energy harvester by exploring the benefits of geometric nonlinearity[J]. Journal of Statistical Mechanics Theory and Experiment, 2019, 2019(3): 033405. DOI:10.1088/1742-5468/ab0c15 |
| [7] |
LI H T, QIN W Y. Dynamics and coherence resonance of a laminated piezoelectric beam for energy harvesting[J]. Nonlinear Dynamics, 2015, 81(4): 1751-1757. DOI:10.1007/s11071-015-2104-3 |
| [8] |
CHEN L Q, PANYAM, et al. A broadband internally resonant vibratory energy harvester[J]. Journal of Vibration & Acoustics, 2016, 138: 061007. |
| [9] |
DAI H L, ABDELKEFI A, YANG Y, et al. Orientation of bluff body for designing efficient energy harvesters from vortex-induced vibrations[J]. Applied Physics Letters, 2016, 108(5): 053902-5. DOI:10.1063/1.4941546 |
| [10] |
ROSTAMI A B, ARMANDEI M. Renewable energy harvesting by vortex-induced motions: review and benchmarking of technologies[J]. Renewable and Sustainable Energy Reviews, 2017, 70: 193-214. DOI:10.1016/j.rser.2016.11.202 |
| [11] |
SUN W P, ZHAO D L, TAN T, et al. Low velocity water flow energy harvesting using vortex induced vibration and galloping[J]. Applied Energy, 2019, 251: 113392. DOI:10.1016/j.apenergy.2019.113392 |
| [12] |
YAN Z M, ABDELKEFI A. Nonlinear characterization of concurrent energy harvesting from galloping and base excitations[J]. Nonlinear Dynamics, 2014, 77: 1171-1189. DOI:10.1007/s11071-014-1369-2 |
| [13] |
YANG Y, ZHAO L, TANG L. Comparative study of tip cross-sections for efficient galloping energy harvesting[J]. Applied Physics Letters, 2013, 102(6): 064105. DOI:10.1063/1.4792737 |
| [14] |
ZHOU S, WANG J. Dual serial vortex-induced energy harvesting system for enhanced energy harvesting[J]. AIP Advances, 2018, 8(7): 075221. DOI:10.1063/1.5038884 |
| [15] |
HU Y L, YANG B, CHEN X, et al. Modeling and experimental study of a piezoelectric energy harvester from vortex shedding-induced vibration[J]. Energy Conversion and Management, 2018, 162: 145-58. DOI:10.1016/j.enconman.2018.02.026 |
| [16] |
ZHANG HC, XI R, XU D L, et al. Efficiency enhancement of a point wave energy converter with a magnetic bistable mechanism[J]. Energy, 2019, 181: 1152–1165.
|
| [17] |
SHAN X B, LI H L, YANG Y C, et al. Enhancing the performance of an underwater piezoelectric energy harvester based on flow-induced vibration[J]. Energy, 2019, 172: 134-140.
|
| [18] |
SONG Y, GUO X, WANG H, et al. Performance analysis of an adaptive bistable point absorber wave energy converter under white noise wave excitation[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 1090–1099.
|
| [19] |
BLEVINS R D. Flow-induced vibration[M]. Krieger Publishing Company, 2001.
|
 2023, Vol. 45
2023, Vol. 45

