2. 国电电力浙江舟山海上风电开发有限公司,浙江 舟山 316100;
3. 自然资源部第二海洋研究所,浙江 杭州 310012
2. Guodian Electric Power Zhejiang Zhoushan Offshore Wind Power Development Co., Ltd., Zhoushan 316100, China;
3. Second Institute of Oceanography, Hangzhou 310012, China
不同的观测任务需要携带不同的传感器,而现有的AUV设计对于更换传感器困难,因此模块化[1]是AUV必然的发展趋势。设计能够携带多种传感器的舱段能够减少制造成本,可以根据观测任务的需要自由更换或增加舱段。
一般情况下,实现AUV搭载更多探测设备的方法有增加附体、改变AUV外壳外形和增加舱段等。在增加附体方面,赵金鑫[2]根据某些任务为AUV设计了大尺度挂载,并根据操纵性分析对比,得出大尺度挂载对AUV的操纵性运动的性能影响量,对于大型的附加载体采用该方法较好。在通过改变AUV自身外形方面,许锦宇[3]设计出采取上下双半椭圆组合的橫截面结构,能让搭载的机械手收缩并贴合在AUV的耐压舱外表面,并分析了AUV在不同运动状态下机械手展开时与收起时受到力和力矩的变化,但在优化AUV外形阻力时没有把舵和推进器加入考虑。在通过模块化设计方面,王鑫[4]根据模块化思想,设计出自定义舱段的机械结构,安装自定义舱段可以自行搭载更多传感或探测装置,同时对外形进行算法优化,有了兼具一定要求的容积和较小的直航阻力,但是在操纵性方面没有过多涉及。
考虑能源量、观测任务所需要的传感器体积尺寸以及制造成本等综合因素,本文研究的AUV采用模块化设计,增加舱段搭载更多观测设备。良好的操纵性决定AUV的稳定性、机动性,一定程度上影响着可携带能源量和使用成本,而增加舱段会对原来AUV的操纵性产生影响,因此研究模块化AUV的操纵性非常重要。
在借鉴上述研究结果的基础上,首先建立AUV与加舱段AUV的三维模型,通过Fluent分别计算加装舱段的AUV和未加装舱段AUV的水动力系数,通过受力分析,建立数学模型进行仿真,给出水平回转运动仿真、水平面Z形操舵仿真及空间定常螺旋下潜3个方面的仿真结果,并分析加装舱段AUV和未加装舱段AUV操纵性发生的变化。
1 AUV的模块化舱段设计模块化设计的AUV不同舱段之间采取螺纹连接方式,舱段可以设计为密封舱段或者透水舱段,这里设计采用透水舱段,舱段安装有传感器和浮力材料等,与密封舱段之间通过水密接插件进行数据传输与能源供给,在原AUV上安装附加舱段后,会改变物理属性如质量、重心、排水体积等,并且也会改变计算的水动力系数数值,最终在操纵性上表现出来。

|
图 1 模块化AUV与附加舱段 Fig. 1 Modular AUV with additional compartments |
模块化AUV与安装附加舱段的模块化AUV设计参数如表1所示。
|
|
表 1 AUV设计参数 Tab.1 AUV design attributes |
建立坐标系,对AUV的水动力、复原力、控制面作用力和推进器推理4个方面的受力进行分析,建立完整的六自由度运动方程。
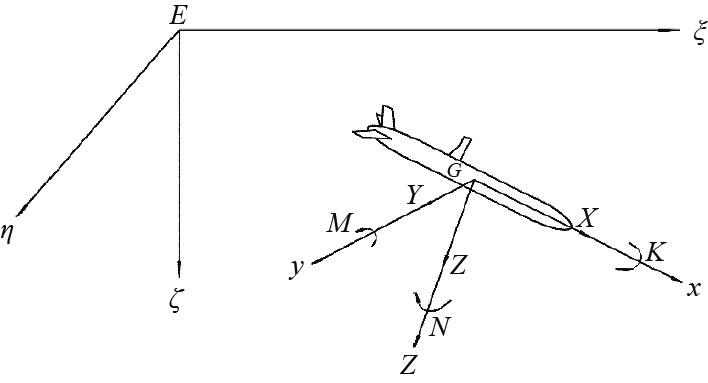
2.1 坐标系的建立建立空间运动坐标系描述AUV的空间运动,如图2所示。采用国际水池会议(ITTC)推荐的和造船与轮机工程学会(SNAME)术语公报的体系分别建立惯性(定系)坐标系和动系坐标系。
|
图 2 惯性坐标系和动坐标系 Fig. 2 Inertial and moving coordinates |
由刚体动力学理论可得水下航行体在空间六自由度运动方程[5]的一般形式如下:
| $ \left\{\begin{array}{l}X=m\cdot \left[(\dot{u}-vr+wq)-{x}_{G}\cdot \left({q}^{2}+{r}^{2}\right)+\right.\\ \left.\qquad {y}_{G}(pq-\dot{r})+{z}_{G}(pr+\dot{q})\right],\\ Y=m\cdot \left[(\dot{v}-wp+ur)-{y}_{G}\cdot \left({r}^{2}+{p}^{2}\right)+\right.\\ \left.\qquad{z}_{G}(qr-\dot{p})+{x}_{G}(qp+\dot{r})\right],\\ Z=m\cdot \left[(\dot{w}-uq+vp)-{z}_{G}\cdot \left({p}^{2}+{q}^{2}\right)+\right.\\ \left.\qquad{x}_{G}(rp-\dot{q})+{y}_{G}(rq+\dot{p})\right],\\ K={I}_{xx}\dot{p}+\left({I}_{zz}-{I}_{yy}\right)qr+m\left[{y}_{G}(\dot{w}+pv-qu)-\right.\\ \left.\qquad {z}_{G}(\dot{v}+ru-pw)\right],\\ M={I}_{yy}\dot{q}+\left({I}_{xx}-{I}_{zz}\right)rp+m\left[{z}_{G}(\dot{u}+qw-rv)-\right.\\ \left.\qquad{x}_{G}(\dot{w}+pv-qu)\right],\\ N={I}_{zz}\dot{r}+\left({I}_{yy}-{I}_{xx}\right)pq+m\left[{x}_{G}(\dot{v}+ru-pw)-\right.\\ \left.\qquad{y}_{G}(\dot{u}+qw-rv)\right]。\end{array}\right. $ | (1) |
其中:
| $ \left\{\begin{array}{c}X={X}_{Fluid}+{X}_{Proppeller}+{X}_{Rudder}+{X}_{Static},\\ Y={Y}_{Fluid}+{Y}_{Proppeller}+{Y}_{Rudder}+{Y}_{Static},\\ Z={Z}_{Fluid}+{Z}_{Proppeller}+{Z}_{Rudder}+{Z}_{Static},\\ K={K}_{Fluid}+{K}_{Proppeller}+{K}_{Rudder}+{K}_{Static},\\ M={M}_{Fluid}+{M}_{Proppeller}+{M}_{Rudder}+{M}_{Static},\\ N={N}_{Fluid}+{N}_{Proppeller}+{N}_{Rudder}+{N}_{Static}。\end{array}\right. $ | (2) |
式中:
公式中的作用力与力矩
AUV所受到的水动力一般分为粘性水动力和惯性水动力两类。取等速直航状态(u0=V且u0≠0)作为泰勒级数展开点,将力和力矩泰勒展开并水动力只取到二阶项,考虑到AUV几何模型的水平面非对称,得出下式[6]:
| $ \begin{aligned} {X}_{\rm{fluid}}=&\left[{X}_{qq}{q}^{2}+{X}_{rr}{r}^{2}+{X}_{rp}rp\right]+\left[{X}_{\dot{u}}\dot{u}+{X}_{vr}vr+{X}_{wq}wq\right]+\\& \left[{X}_{uu}{u}^{2}+{X}_{vv}{v}^{2}+{X}_{ww}{w}^{2}\right],\\{{Y}_{\text{fluid}}}=&\left[{Y}_{\dot{r}}\dot{r}+{Y}_{\dot{p}}\dot{p}+{Y}_{p\left|p\right|}p\left|p\right|+{Y}_{pq}pq+{Y}_{qr}qr\right]+\\&\left[{Y}_{\dot{v}}\dot{v}+{Y}_{vq}vq+{Y}_{wp}wp+{Y}_{wr}wr\right]+ \\&\left[{Y}_{r}ur+{Y}_{P}up+{Y}_{v\left|r\right|}\frac{v}{\left|v\right|}\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\left|r\right|\right]+\\&\left[{Y}_{0}{u}^{2}+{Y}_{v}uv+{Y}_{v\mid v}v\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right] +{Y}_{vw}vw,\\{{Z}_{\text{fluid}}}=&\left[{Z}_{\dot{q}}\dot{q}+{Z}_{pp}{p}^{2}+{Z}_{rr}{r}^{2}+{Z}_{rp}rp\right]+\\&\left[{Z}_{\dot{w}}\dot{w}+{Z}_{v}vr+{Z}_{vp}vp\right]+{Z}_{w}{v}^{2}+\\ &\left[{Z}_{0}{u}^{2}+{Z}_{w}uw+{Z}_{w\left|w\right|}w\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+\\&\left[{Z}_{\left|w\right|}u\left|w\right|+{Z}_{ww}\left|w{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+\\&\left[{Z}_{q}uq+{Z}_{w\left|q\right|}\frac{w}{\left|w\right|}\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\left|q\right|\right],\\ {K}_{\text{fluid}}=&\left[{K}_{p}\dot{p}+{K}_{r}\dot{r}+{K}_{qr}qr+{K}_{pq}pq+{K}_{p\left|p\right|}p\left|p\right|\right]+\\&\left[{K}_{p}up+{K}_{r}ur+{K}_{v}\dot{v}\right] +\\ &\left[{K}_{vq}vq+{K}_{wp}wp+{K}_{wr}wr\right]+\\&\left[{K}_{0}{u}^{2}+{K}_{v}uv+{K}_{v\mid v}v\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right] +{K}_{vw}vw,\\ {{M}_{\text{fluid}}}=&\left[{M}_{q}\dot{q}+{M}_{pp}{p}^{2}+{M}_{rr}{r}^{2}+{M}_{rp}rp+{M}_{q\left|q\right|}q\left|q\right|\right]+\\&\left[{M}_{w}\dot{w}+{M}_{vr}vr+{M}_{vp}vp\right]+\\ &\left[{M}_{q}uq+{M}_{\left|w\right|q}\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|q\right]+\\&\left[{M}_{0}{u}^{2}+{M}_{w}uw+{M}_{w\left|w\right|}w\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+\\ &\left[{M}_{\left|w\right|}u\left|w\right|+{M}_{ww}\left|w{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+{M}_{w}{v}^{2},\\ {{N}_{\text{fluid}}N}=&\left[{N}_{r}\dot{r}+{N}_{p}\dot{p}+{N}_{pq}pq+{N}_{qr}qr+{N}_{r\left|r\right|}r\left|r\right|\right]+\\&\left[{N}_{v}\dot{v}+{N}_{wr}wr+{N}_{wp}wp+{N}_{vq}vq\right]+\\ &\left[{N}_{p}up+{N}_{r}ur+{N}_{\left|v\right|r}\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|r\right]+\\&\left[{N}_{0}{u}^{2}+{N}_{v}uv+{N}_{v\left|v\right|}v\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+{N}_{vw}vw。\\[-300pt]\end{aligned} $ | (3) |
式中:
复原力(矩)描述艇身在横摇和纵摇自由度具备的横稳性和纵稳性,作用于AUV上的静力包括重力B、浮力P及力矩M。由于重力和浮力的方向一般铅锤向下,所以在定系中的分量为(0,0,P-B)。在动坐标系表示[7]为:
| $ \left\{\begin{array}{l}{X}_{Static}=-(P-B)\sin\theta ,\\ {Y}_{Static}=(P-B)\cos\theta \sin\phi ,\\ {Z}_{Static}=(P-B)\cos\theta \cos\phi 。\end{array}\right. $ | (4) |
重力P、浮力B对于随体坐标系原点的力矩为:
| $ \left\{ \begin{array}{l}{K}_{Static}=\left({-y}_{G}\mathrm{P}-{y}_{B}B\right)\cos\theta \cos\phi -\left({z}_{G}P-{z}_{B}B\right)\cos\theta \sin\phi ,\\ {M}_{Static}=-\left({z}_{G}P-{z}_{B}B\right)\sin\theta -\left({x}_{G}P-{x}_{B}B\right)\cos\theta \cos\phi,\\ {N}_{Static}=-\left({x}_{G}P-{x}_{B}B\right)\cos\theta \sin\phi +\left({y}_{G}P-{y}_{B}B\right)\sin\theta 。\end{array}\right. $ | (5) |
式中:(
AUV重心和浮心满足
舵和桨布局方式为桨前舵,舵型为NACA0012型。舵的外形参数[8]如表2所示。
|
|
表 2 NACA0012外形参数 Tab.2 NACA0012 Shape attribute |
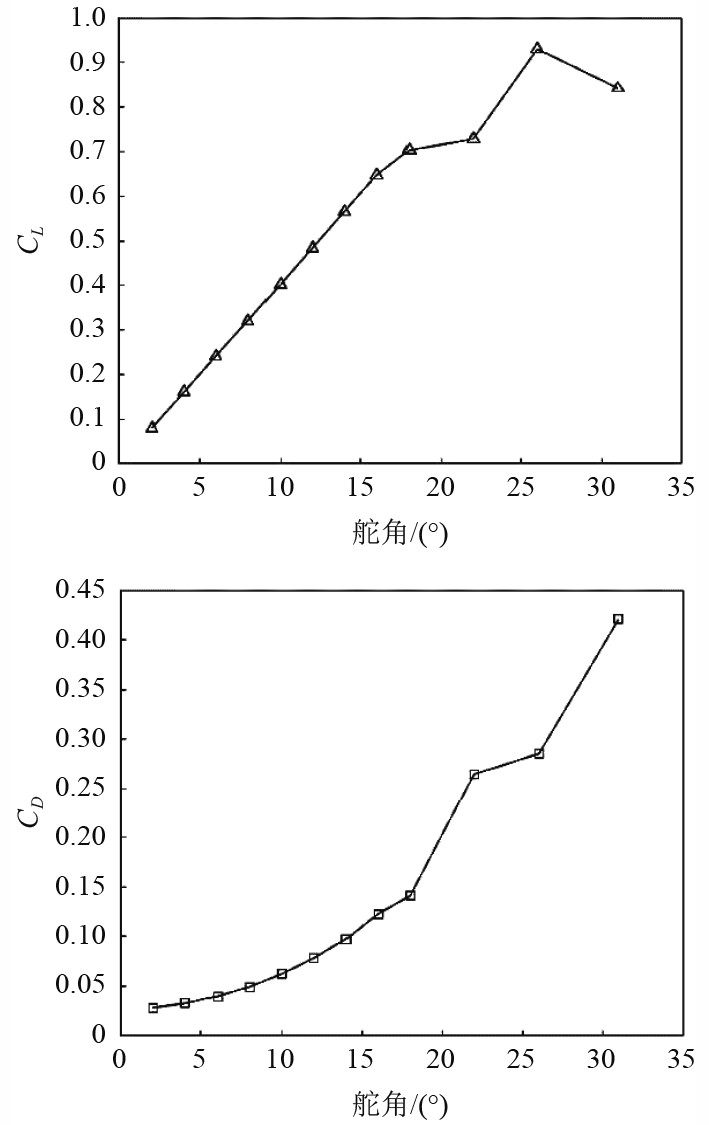
当攻角为α,速度为V时,舵受到力R的作用,可以分解为水平方向上的阻力D和与来流方向垂直的升力L,用升力系数CL和阻力系数CD来表征。本文研究的AUV舵的升力系数与攻角关系、阻力系数与攻角关系如图3所示。
|
图 3 NACA0012舵的升力系数、阻力系数与攻角关系 Fig. 3 The relation between lift coefficient, drag coefficient and Angle of attack of NACA0012 rudder |
使用Aitken插值法最终得到的升力系数、阻力系数与舵角的函数关系式,并通过下式和舵翼安装位置得到对AUV的力和力矩。
| $ \left\{\begin{split} L=\dfrac{1}{2}{C}_{L}\rho {A}_{R}{V}^{2},\\ D=\dfrac{1}{2}{C}_{D}\rho {A}_{R}{V}^{2}。\end{split}\right. $ | (6) |
式中:
只在尾部安装有一个单螺旋桨作为推进器,通过试验和查询资料从而获取螺旋桨直径D、进速系数
螺旋桨主要参数如表3所示。
|
|
表 3 Ka-4-70螺旋桨主要参数 Tab.3 Ka-4-70Main parameters of propeller |
推力和转矩的表达式如下:
| $ \left\{\begin{array}{c}T={K}_{T}\rho {n}^{2}{D}^{4},\\ Q={K}_{Q}\rho {n}^{2}{D}^{5}。\end{array}\right. $ | (7) |
速度为0~2 m/s,令AUV与加舱段AUV以2 m/s直行,此时AUV与加舱段AUV的航行阻力分别为32.62 N与37.38 N。螺旋桨推力系数
| $ T={K}_{T}\rho {n}^{2}{D}^{4}=35\;{\rm{N}},$ | (8) |
| $ Q={K}_{Q}\rho {n}^{2}{D}^{5}=1.138\;{\rm{N}}\cdot {\rm{m}} 。$ | (9) |
在765 r/min的转速下,加舱段AUV此时的螺旋桨推力与转矩为:
| $ T={K}_{T}\rho {n}^{2}{D}^{4}=39\;{\rm{N}} ,$ | (10) |
| $ Q={K}_{Q}\rho {n}^{2}{D}^{5}=1.269\;{\rm{N}}\cdot {\rm{m}} 。$ | (11) |
可知,在不同转速下旋转的螺旋桨推力能够满足AUV与加舱段AUV在2 m/s的直航阻力,该类型的螺旋桨能够满足要求。
3 AUV水动力系数的仿真获取计算AUV六自由度运动方程所需要的水动力系数,通过分别划分AUV和加舱段AUV的重叠网格后导入Ansys Fluent[9]计算获得。模拟AUV在
将得到的水动力系数进行无因次化处理[13],仿真试验所得部分水动力系数如表4所示。
|
|
表 4 PMM仿真所得水动力系数 Tab.4 hydrodynamic coefficients obtained by PMM simulation |
水动力系数中含有大部分的耦合系数,为非线性系数,这些系数测定比较困难,博尔曼[14]于1989年提出一种关于一些耦合水动力系数的近似关系式,由此可以推算出其他耦合系数。
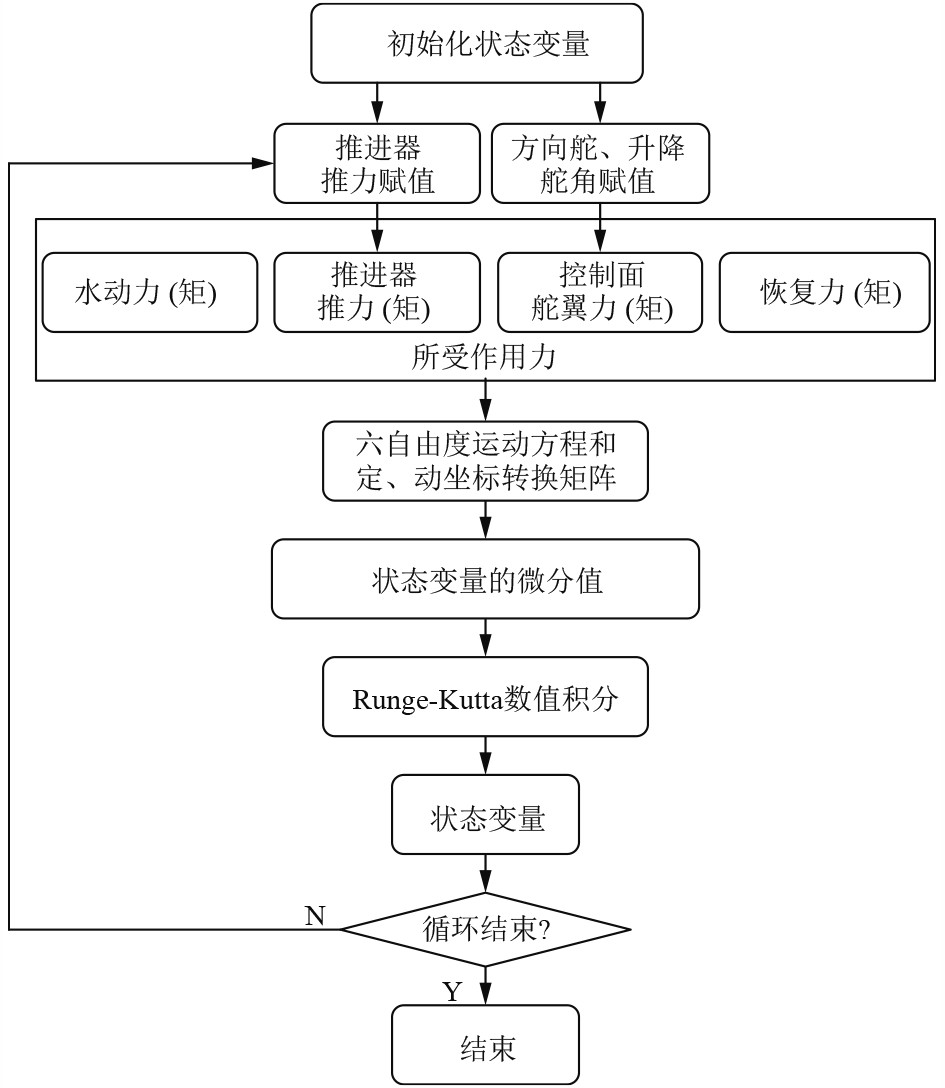
4 建立AUV六自由度运动仿真系统通过Matlab建立运动仿真程序,仿真流程如图4所示。首先初始化所有的运动状态变量,然后给输入变量赋值(推进器推力、垂直舵和方向舵的力矩),通过六自由度运动方程得到不同坐标系的加速度,根据四阶龙格库塔法[15]求解六自由度运动方程求出AUV的状态变量(速度、位置和姿态),从而得到运动仿真的重心轨迹。
|
图 4 AUV运动仿真流程 Fig. 4 AUV motion simulation flow |
研究水平面回转运动、水平面Z形操舵运动和空间定常螺旋下潜运动,并对AUV和加装舱段的AUV的仿真数据进行对比,分析加装舱段后对原AUV操纵性的影响和变化。
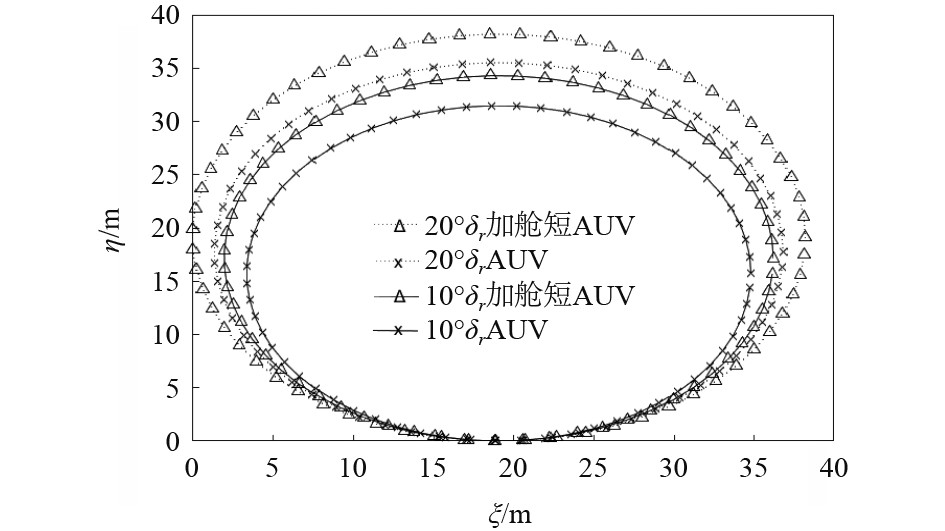
5.1 水平回转运动仿真试验仿真试验为评价AUV在水平面运动时的回转性能。设定直航速度为2 m/s,仿真总时长500 s ,输入控制量的方向舵舵角
|
图 5 10°与20°方向舵舵角下的AUV与加舱段AUV水平回转运动曲线对比 Fig. 5 Comparison of AUV and cabin added AUV horizontal rotation motion curves under different rudder angles |
仿真结果如表5所示。
|
|
表 5 回转运动仿真结果 Tab.5 Simulation results of rotary motion |
定常回转直径
该仿真试验是为了评价AUV的航向改变性能。水平面Z形操舵仿真时,设定直航速度为2 m/s,垂直方向舵舵角

|
图 6 水平面Z形操舵仿真 Fig. 6 Simulation of horizontal Z steering |
|
|
表 6 水平面Z形操舵仿真结果 Tab.6 Simulation results of horizontal Z steering |
初转期
该仿真试验是为了测定AUV空间定常螺旋潜浮机动时的升矩和回转半径。仿真时使AUV在适当深度以一个预定航速定深直航时,设定水平升降舵和垂直方向舵在预定舵角把定,此时AUV就会同时进行回转和潜浮运动。空间定常螺旋运动的表征参数有水平面投影直径
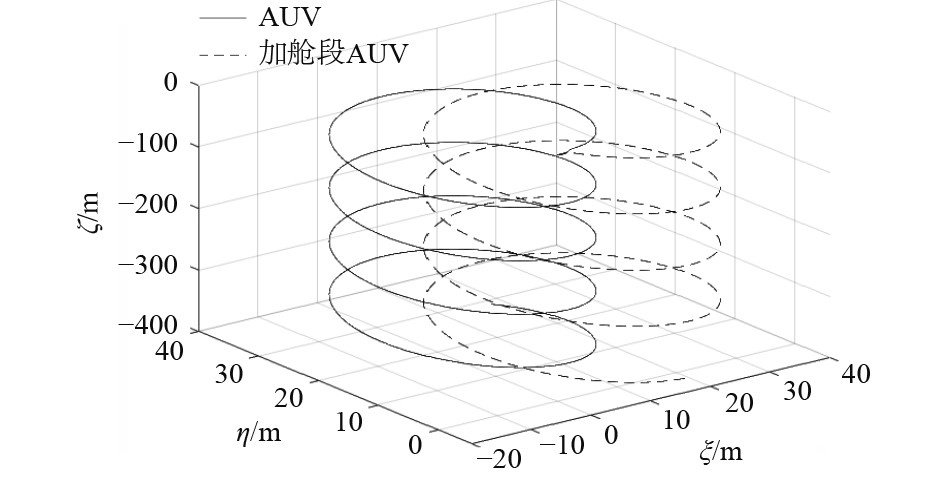
|
图 7 u=2 m/s,δr=20°,δs=20°的AUV/加舱段AUV重心轨迹 Fig. 7 u=2 m/s, δr=20°, δs= 20°AUV/ cabin added AUV center of gravity trajectory |
|
|
表 7 空间定常螺旋下潜运动仿真结果 Tab.7 Simulation results of space steady spiral diving motion |
水平投影直径
在水平面回转试验中,在设定条件下,加舱段AUV相比原AUV的定常回转直径分别大了8.42%,11.37%,10.79%,12.83%,定常回转直径越大,表明加舱段AUV相比原AUV水平面内机动性降低。加舱段AUV相比原AUV的回转周期时间分别长了11.22%,9.07%,5.56%和6.14%,表明加舱段AUV相比原AUV在大幅度转向的程度上减慢。因此在水平面回转实验中,加舱段AUV与原AUV相比,在同一舵角下回转直径
在水平面Z形操舵试验中,在设定条件下,加舱段AUV相比AUV初转期时间长了8.49%,加舱段AUV相比原AUV周期时间长了9.61%,表明加舱段AUV相比AUV首向改变减慢。加舱段AUV相比AUV的超越时间
在空间定常螺旋下潜试验中,在设定条件下,加舱段AUV要比原AUV的水平投影直径大10.83%,加舱段AUV要比原AUV的回转360°所需时间长6.8%,表明加舱段AUV回转360°比原AUV回转速度减慢。原AUV要比加舱段AUV的升矩大0.29%,表明加舱段AUV比原AUV下潜速度减慢。上述2个特征量表明在三维空间的运动下,附加舱段的AUV要相对于AUV下潜减慢,空间运动性能下降。
6 结 语运用Solidworks分别建立AUV与安装附加舱段的AUV的几何模型,并通过Ansys Fluent分别计算AUV与安装附加舱段AUV水动力系数以及舵翼的水动力性能。建立AUV操纵运动数学模型,通过进行AUV与加舱段AUV分别为水平回转运动、水平面Z形操舵、空间定常螺旋运动操纵性仿真试验,对AUV的操纵性能进行预报。最后对比AUV与加舱段AUV的操纵性试验所得试验数据,表明安装了附加舱段的AUV相比原AUV的运动性、应舵性均下降。
| [1] |
曹少华, 张春晓, 王广洲, 等. 智能水下机器人的发展现状及在军事上的应用[J]. 船舶工程, 2019, 41(2): 79-84+89. CAO S H, ZHANG C X, WANG G Z, et al. The current state of development of intelligent underwater robots and their application in the military[J]. Ship Engineering, 2019, 41(2): 79-84+89. |
| [2] |
赵金鑫. 大挂载水下航行器操纵性能分析及双体干扰研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 52–61.
|
| [3] |
许锦宇. 作业型AUV总体设计与水动力性能分析[D]. 哈尔滨: 哈尔滨工程大学, 2017: 9–12+31–37
|
| [4] |
王鑫. 小型自治水下机器人外形优化设计及水动力特性数值模拟[D]. 青岛: 中国海洋大学, 2012: 6–39
|
| [5] |
施生达. 潜艇操纵性[M]. 北京: 第1版国防工业出版社, 2021: 69
|
| [6] |
程健. 水下机器人水动力性能及其运动控制研究[D]. 大连: 大连理工大学, 2018.2: 18–19
|
| [7] |
戴君锐, 向先波, 于曹阳, 等. 六自由度水下航行器操纵性仿真及性能评估[J]. 华中科技大学学报(自然科学版), 2015, 43(S1): 452-456. DAI J R, XIANG X B, YU C Y, et al. Maneuverability simulation and performance evaluation of a six-degree-of-freedom underwater vehicle[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2015, 43(S1): 452-456. |
| [8] |
TIMOTHY C, ENG B. The Design, Conatruction, Outfitting, and Preliminary Testing of the C-SCOUT Autonomous Underwater Vehicle (AUV)[D]. Canada, Faculty of Engineering and Applied Science Memorial University of Newfoundland, 2001.
|
| [9] |
高婷, 庞永杰, 王亚兴, 等. 水下航行器水动力系数计算方法[J]. 哈尔滨工程大学学报, 2019, 40(1): 174-180. GAO T, PANG Y J, WANG Y X, et al. Underwater vehicle hydrodynamic coefficient calculation method[J]. Journal of Harbin Engineering University, 2019, 40(1): 174-180. |
| [10] |
胡坤, 李振北. Ansys ICEM CFD工程实例详解[M]. 北京: 人民邮电出版社, 2014: 214–215.
|
| [11] |
CHEN C W, JIANG Y, HUANG H C, et al. Computational fluid dynamics study of the motion stability of an autonomous underwater helicopter[J]. Ocean Engineering, 2017, 143: 227-239. DOI:10.1016/j.oceaneng.2017.07.020 |
| [12] |
张晓频. 多功能潜水器操纵性能与运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2008: 26–27+30–32.
|
| [13] |
于浩然. 碟型水下机器人水动力分析及操纵性能研究[D]. 沈阳: 沈阳工业大学, 2021: 36–41.
|
| [14] |
方人杰. 便携式AUV水动力数值计算方法应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2021: 52.
|
| [15] |
段斐. 微小型水下机器人运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 11–25.
|
 2023, Vol. 45
2023, Vol. 45
