水面智能高速无人艇研究涉及范围较广的跨领域学科,在对其进行设计的过程中,需要将多种技术融合在一起,因为在高速行驶时,无人艇的静浮力很小,与其他类型船舶相比,在低速时其浸湿面积大幅降低,这就造成阻力参数发生了很大的变化[1-3]。无人艇高速运动,所以数学模型相对不是特别精确,在设计中需要有准确的数学模型和恒定的参数。然而一般的控制器无法做到这点,所以需要结合鲁棒控制器来进行分析,将鲁棒控制器运用到水面智能高速无人艇中,使无人艇不管处于任何状态都能提供快速的响应和良好的控制精度[4-6]。
1 水面智能高速无人艇概述水面智能高速无人艇(USV)是一种集传感器、控制、通信与决策于一体的新型无人船,其在实际应用的过程中,可以在繁乱的场景中顺利完成指定的目标安排。由于水面智能高速无人艇具有自主航行、避障、执行任务等特点,在军事领域、海洋工程和环境保护等方面具有广泛的应用前景。
2 水面智能高速无人艇鲁棒控制 2.1 无人水面艇鲁棒控制系统方法论分析无人艇鲁棒控制一直是水面艇研究的难点和热点,主要分为无系统约束和存在系统约束2个方面。
许多学者针对无人艇在不受控制的条件下,提出了H∞型控制、滑模控制、自适应控制、神经网络等多种控制方法。然而,H∞控制器与Sliding模式下的H∞控制器通常在艇体模型上存在一定的不确定性,这限制了H∞控制器的实用化。同时,Sliding模式下的H∞控制器本身具有的颤振特性也将对其稳定性造成一定的影响。自适应控制器能够解决系统的结构不确定性,但无法解决系统的非结构不确定性,而艇体模型的不确定性既含有结构不确定性,又含有非结构不确定性。虽然基于神经网络与模糊的非线性模型可以增强控制器的鲁棒性能,但是对于时变性的非线性模型,神经网络与模糊学习方法的应用还有待进一步完善。干扰观测器因其运算复杂度低、易于实施等特点,也经常用于干扰的消除。在诸如自抗扰控制等一系列的非线性控制中具有非常关键的应用价值。
针对无人艇的特点,提出一种适用于无人艇的控制器设计方法。因为无人艇的航行范围受限于海洋面积,并且需要躲避海洋上的障碍,其本身也有最小回转半径,因此对无人艇的位置有制约。而对于无人艇来说,要确保其航行的安全性,就必须将无人艇的航速限制在某一特定的区间之内。为此,国外许多学者也开始致力于无人艇的鲁棒控制问题研究。
随着研究的深入,Li Z和Sun J针对无人艇的航迹维持问题,提出一种基于稳健的鲁棒预测控制方法。在已有研究中,将泰勒线性化模型应用于预报控制中,并在假定不确定因素是很慢的情况下,使用k-1时间的干扰估算来前馈补偿 k时间的干扰。然而,现有的基于Taylor的建模方法仍有如下不足之处:1)增加了建模的不确定性,使得鲁棒预测控制器的设计变得更加复杂;2)对于干扰的假定太严格,而且干扰对控制系统的作用随时间的延长而迅速增大;3)用一次预报法来构建预报控制,而没有给出闭环稳定的理论解析。
在控制系统的设计和分析中,1927年Black针对摄动的精确系统提出构思,但是这一设计因为动态的不稳定而无法成立。1932年Nyquist提出Nyquist曲线使得反馈增益和动态稳定的关系有所改善。
2.2 鲁棒控制器在水面智能高速无人艇中的模型分析鲁棒性是指通过标称模型对船舶的扰动行为进行调控,或是以其他的表现标准来刻画质量,则称为系统具有鲁棒性能准则。
控制系统的鲁棒性分析主要包括稳定性和性能分析两大类。鲁棒控制通常表示为∆max。设p(s)为数学模型,表示精确系统,p0(s)为不精确,误差为:
| $ \Delta P\left( s \right) = P\left( s \right) - {P_0}\left( s \right) \text{,} $ | (1) |
假设∆p(s)上界是确定的,则可得:
| $ \left| {\Delta P\left( {j\varpi } \right)} \right| < \left| {W\left( {j\varpi } \right)} \right|,\forall \varpi \in \left[ {0,\infty } \right) \text{。} $ | (2) |
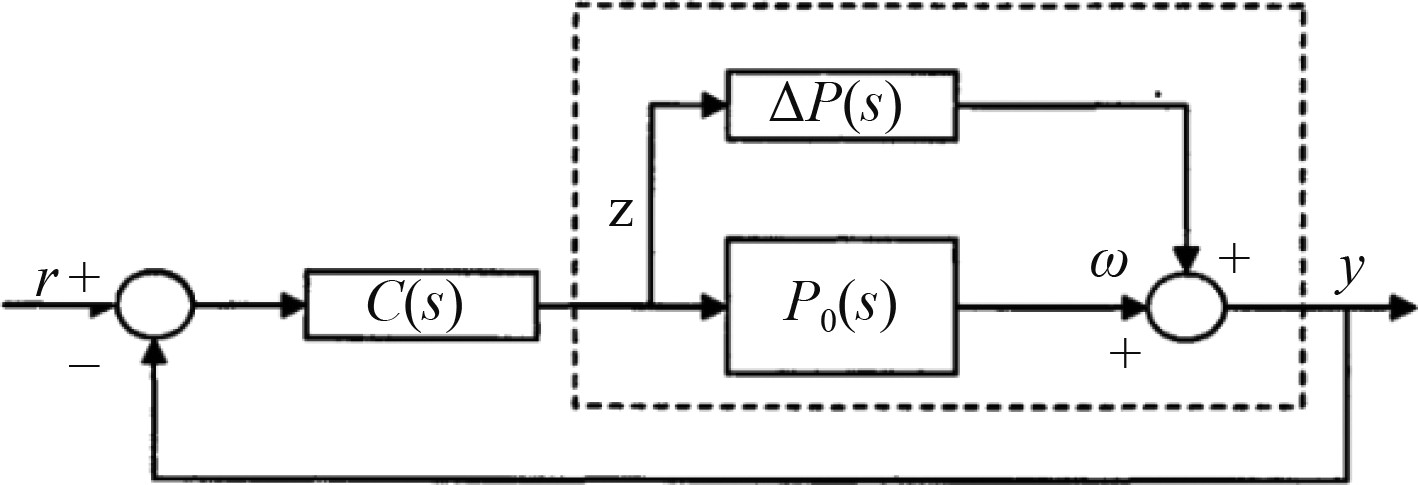
具有加法不确定性的控制系统如图1所示。控制系统的设计主要是设计一个控制器来保证每个被控对象的稳定性,通过反馈进行各项参数的调节,由此可得,模型误差越大,鲁棒性越强,反之则相反。
|
图 1 具有加法不确定性的控制系统 Fig. 1 Control system with additive uncertainty |
针对如上稳定性条件,可以得出不确定性系统的传递函数为:
| $ Tz\omega \left( s \right) = - \frac{{C\left( s \right)}}{{1 + {P_0}\left( s \right)C\left( s \right)}} \text{。} $ | (3) |
因为p0(s)与C(s)所表示的反馈系统具有稳定性,因此Tzω(s)也稳定,若∆p(s)也稳定,根据Nyquist的判断依据,∆p(s)的轨迹线对于所有的ω都不应该处于(−1,J0)范围内,此时系统稳定,但是对于∆p(s)的频率半径在|∆p(jω)|<|W(jω)|时,需要该点的各个运动参数都处于圆外。因此可以得知,鲁棒稳定性条件为:
| $ \left| {\Delta P\left( {j\varpi } \right)} \right| < \left| {W\left( {j\varpi } \right)} \right| < 1,\forall \varpi \in R \text{。} $ | (4) |
也可以将其简化归纳为:
| $ \left|\frac{C\left(j\varpi \right)}{1+{P}_{0}\left(j\varpi \right)C\left(j\varpi \right)}W\left(j\varpi \right)\right| < 1,\forall \varpi \in R \text{。} $ | (5) |
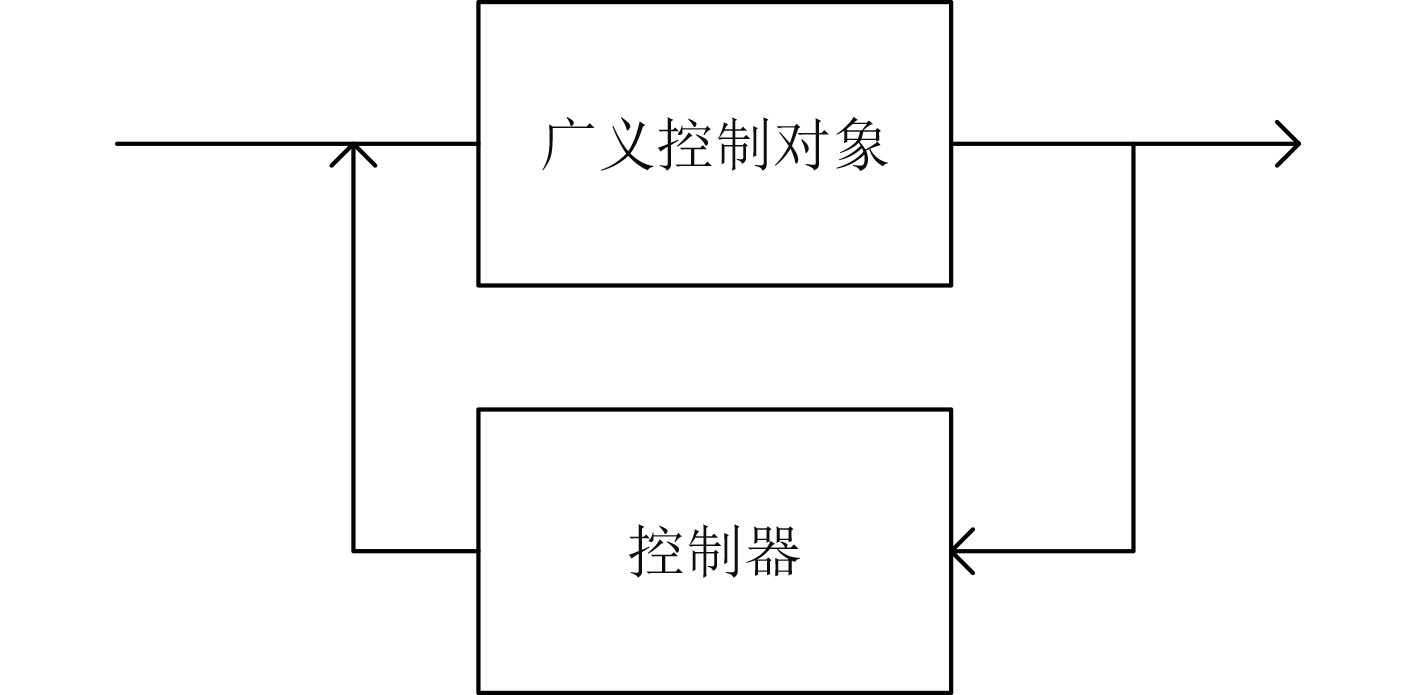
可知,若控制系统具有鲁棒性则可以对其特性进行较为全面的保证。基于这一特征,本文针对所有的控制问题均用图2表示。
|
图 2 基础控制系统 Fig. 2 Basic control system |
将传统的频率分析法和新的状态空间分析法有机地融合在一起,使其实现一次跨越式的发展,并最终步入了鲁棒控制的发展时期。自20世纪80年代开始,有关鲁棒的问题开始受到广泛关注,并被认为是一种成熟的控制方法。该项目既延续了已有的以利用状态空间建模为核心的鲁棒性理论,又从本质上解决了被控目标的建模与外部干扰的不确定问题,既可以进行SIMS的分析与设计,又可以将其推广至多个SIMS的情况,从而进一步提高SIMS的性能与鲁棒性。
目前关于提升鲁棒性的研究不断完善,随着研究成果的进一步发展,鲁棒控制的研究逐渐形成了较为完备的理论体系。其中的H∞控制和μ方法是鲁棒控制器研究中最重要的代表。加拿大的Zames于1981年在对干扰和不确定因素进行分析研究后,给出了H∞型最优化敏感性设计的新算法,为特定传递函数矩阵的H∞范数奠定了一定的研究理论基础。
假设鲁棒控制去的核心表达式为:
| $ {a_{mn}}\left( \theta \right) = {c_m}\exp \left\{ {j2{\text{π}} \frac{{\left( {m{d_t} + n{d_r}} \right)\sin \theta }}{{{\lambda _m}}}} \right\} \text{。} $ | (6) |
在考虑到外部的干扰因素后可以简化模型,假设存在外部的干扰模型为:
| $ \frac{{{f_m}n{d_r}\sin \theta }}{c} = \frac{{n{d_r}\sin \theta }}{{{\lambda _0}}} \cdot \frac{{{\lambda _0}}}{{{\lambda _m}}} = \frac{{{\varepsilon _m}n{d_r}\sin \theta }}{{{\lambda _0}}} \text{。} $ | (7) |
设
| $ a = {\left[ {{a_{11}} \cdots {a_{1N}} \cdots {a_{MN}}} \right]^{\rm{T}}}。$ |
| $ {a_{mn}}\left( \theta \right) = {c_m}\exp \left\{ {j2{\text{π}} \frac{{{\varepsilon _m}n{d_r}\sin \theta }}{{{\lambda _0}}}} \right\} \text{。} $ | (8) |
当系统存在如下噪声时:
| $ {\kern 1pt} X\left( t \right) = a\left( \theta \right)s\left( t \right) + {N_{mn}}\left( {{f_m}} \right) 。$ |
式中:
为了便于求解到最优的鲁棒控制器参数,对上述模型进行简化,可以分别对分子和分母进行矢量归一化,得到:
| $ G = \frac{{{{|{W^H}V{|^2}} \mathord{\left/ {\vphantom {{|{W^H}V{|^2}} {{W^H}W}}} \right. } {{W^H}W}}}}{{{{{W^H}QW} \mathord{\left/ {\vphantom {{{W^H}QW} {{W^H}W}}} \right. } {{W^H}W}}}} \text{,} $ | (9) |
设控制器的最优输出结果为:
| $ {\cos ^2}\varphi = \frac{{|{W^H}V{|^2}}}{{\left( {{W^H}W} \right)\left( {{V^H}V} \right)}} \text{,} $ | (10) |
其中,
| $ G = M{\cos ^2}\varphi \left\{ {\frac{{{W^H}W}}{{{W^H}QW}}} \right\} \text{,} $ | (11) |
式中,
无人船的航迹主要通过航迹计划器或远程操作员进行人工设定,而机器人则负责追踪所规划的航迹。一条路径是一条直线,而一艘无人船将在一条直线上移动。所以,一个无人船必须有2个控制装置:一个是航线控制装置,另一个是位置偏移装置。
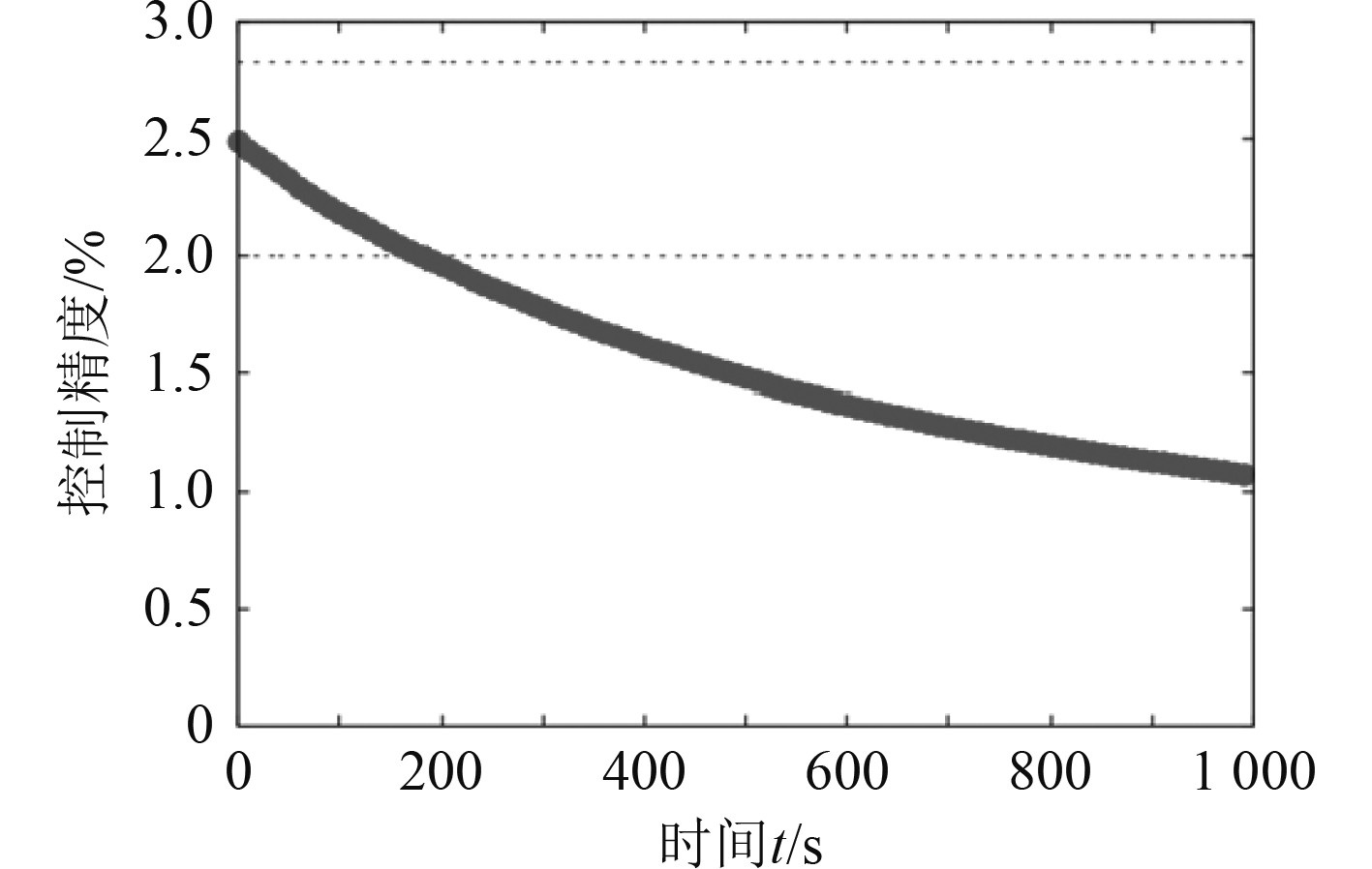
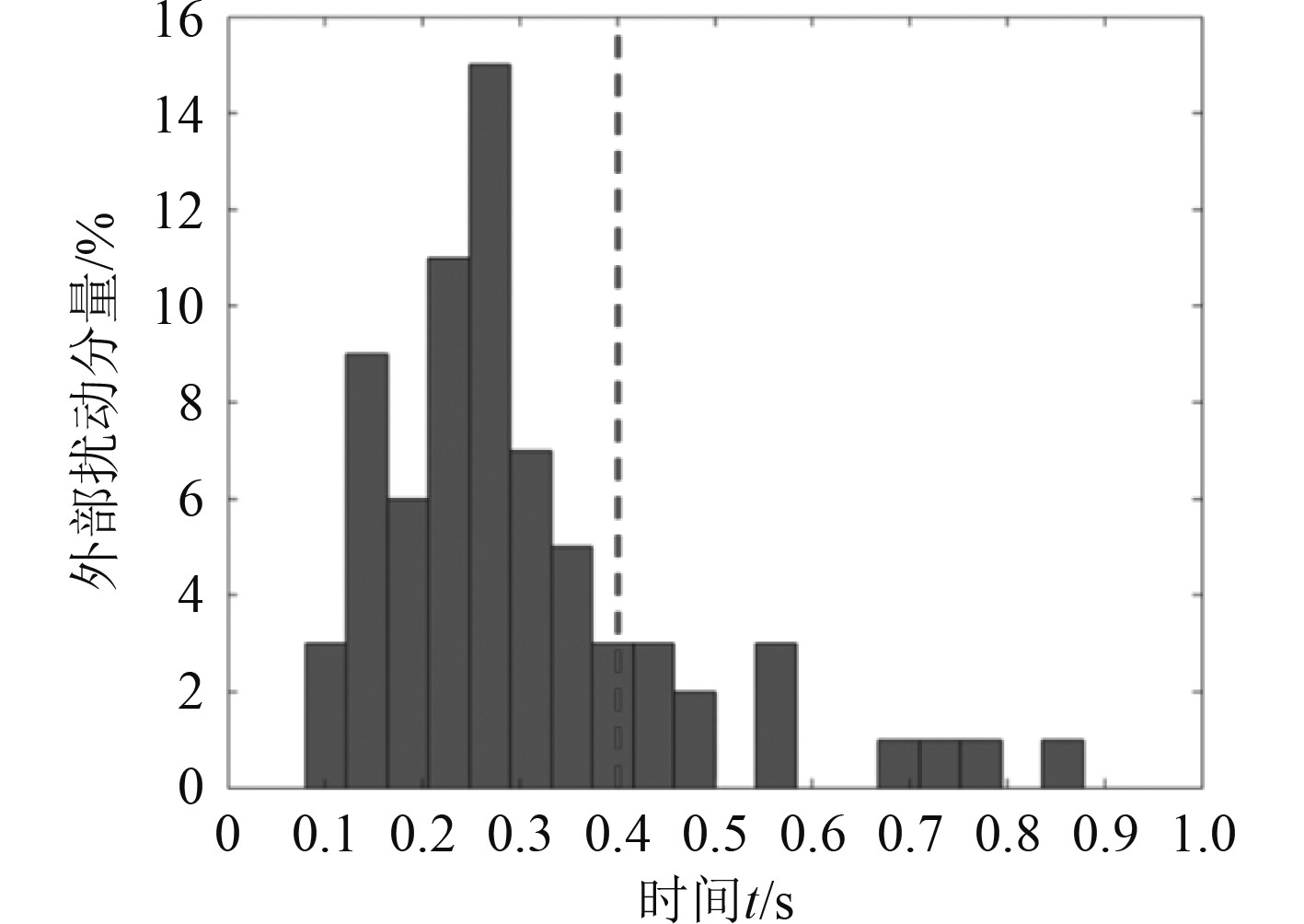
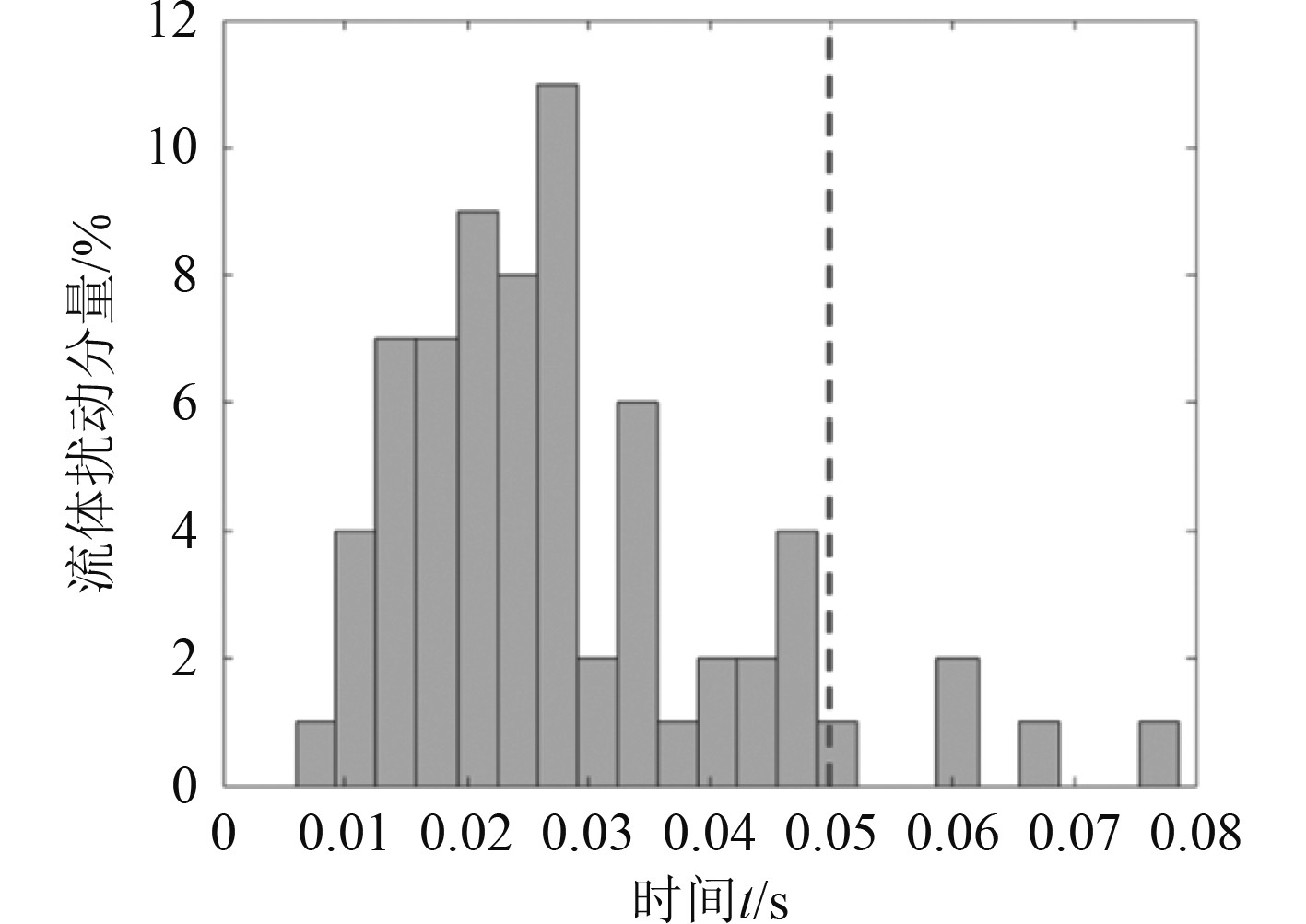
在有外界干扰的情况下,PID控制曲线较为粗糙,不能准确追踪位置,而鲁棒控制器追踪更为精确,外界的干扰也较轻。鲁棒控制器精度随时间变化曲线如图3所示,外部扰动分量随时间的变化曲线如图4所示。所以相比传统的PID控制,鲁棒控制在无人艇航线追踪时更为优良。流体扰动分量随时间的变化曲线如图5所示。
|
图 3 鲁棒控制器精度随时间变化曲线 Fig. 3 Robust controller accuracy vs. time variation curve |
|
图 4 外部扰动分量随时间的变化曲线 Fig. 4 Variation curve of external disturbance component with time |
|
图 5 流体扰动分量随时间的变化曲线 Fig. 5 Variation curve of fluid disturbance component with time |
PID控制器的模拟曲线没有鲁棒控制器那么平滑,因此,PID控制器对波浪干扰的鲁棒性小,但鲁棒控制器对波浪的扰动有很强的抑制作用。其主要原因在于:在鲁棒控制中,既要考虑外部扰动的不确定性,又要考虑外部扰动和流体力学参数的不确定性,同时要兼顾暂态特性、抗扰动性能以及鲁棒性,以增强鲁棒控制的有效性。
鲁棒跟踪算法的性能优于PID算法,尤其是在大拐角情况下,PID算法能使目标轨迹偏离。结果表明:鲁棒控制器能有效地抑制系统受到的外部扰动,因此在追踪无人艇位置的时候更加实用,系统的鲁棒性也更强。
4 结 语无人艇因其具有重量轻、模块化、自主、智能等显著优势而备受青睐。无人艇是一种非常复杂的艇航行体,它的数学建模具有很高的非线性特征。
当无人艇在海面上艇行时,由于其本身的质量、速度等动力因素的持续改变,会造成模型中的参数摄动,外部环境也会对模型形成干扰。同时,在建立的过程中,模型本身也会产生建模的误差,这几方面的因素共同作用,会造成无人艇模型中的不确定性。然而,由于其驱动力受限于其所处的驱动系统,而其航行距离又受限于其所处海域面积、海面障碍物及本身最小转向半径等,使得其航行速度、方位及所需驱动力都受到一定的制约。因此,当系统中含有不确定性或某些参数受限时,如何将其应用于工程实践,仍然是亟待解决的问题。
| [1] |
张海胜, 董早鹏, 杨莲, 等. 基于加权遗忘多新息RLS的无人艇响应模型在线参数辨识[J/OL]. 大连海事大学学报: 1–7[2023-03-06]. ZHANG Hai-sheng, DONG Zao-peng, YANG Lian, et al. On-line parameter identification of unmanned vessel response model based on weighted forgetting multi-innovation RLS[J/OL]. Journal of Dalian Maritime University: 1–7[2023-03-06]. |
| [2] |
谢志刚, 王建华, 郑翔, 等. 在排水箱涵中基于激光雷达的无人艇自主导航[J/OL]. 信息与控制: 1–12[2023-02-21]. XIE Zhi-gang, WANG Jian-hua, ZHENG Xiang, et al. Autonomous navigation of unmanned boat based on laser radar in drainage box culvert[J/OL]. Information and Control: 1–12[2023-02-21]. |
| [3] |
鲁兴益, 张丽珍, 孙鹏飞, 等. 基于CFD的半潜式无人艇水平面运动稳定性分析[J]. 制造业自动化, 2023, 45(1): 201-206. LU Xing-yi, ZHANG Li-zhen, SUN Peng-fei, et al. Stability analysis of semi-submersible unmanned boat horizontal plane based on CFD[J]. Manufacturing Automation, 2023, 45(1): 201-206. DOI:10.3969/j.issn.1009-0134.2023.01.042 |
| [4] |
姜兆祯, 王文龙, 孙文祺. 基于改进快速扩展随机树法的无人艇路径规划快速求解算法[J/OL]. 系统仿真学报: 1–14[2023-02-28]. JIANG Zhao-zhen, WANG Wen-long, SUN Wen-qi. A fast solution algorithm for unmanned vehicle path planning based on the improved rapid extended random tree method[J/OL]. Journal of System Simulation: 1–14[2023-02-28]. |
| [5] |
郭文轩, 唐国元, 赵帆, 等. 面向回收任务的无人艇自适应级联跟踪控制[J/OL]. 中国舰船研究: 1–11[2023-03-12]. GUO Wen-xuan, TANG Guo-yuan, ZHAO Fan, et al. Adaptive Cascade Tracking Control for Unmanned Vehicles for Recovery Tasks[J/OL]. Chinese Journal of Ship Research: 1–11[2023-03-12]. |
| [6] |
窦强, 阴启玉, 梁立. 基于吊放声呐的无人艇搜潜任务规划算法[J]. 指挥控制与仿真, 2023, 45(2): 9-16. DOU Qiang, YIN Qi-yu, LIANG Li. Unmanned submarine search mission planning algorithm based on dropping sonar[J]. Command Control and Simulation, 2023, 45(2): 9-16. |
 2023, Vol. 45
2023, Vol. 45
