2. 海军工程大学 振动与噪声研究所,湖北 武汉 430033;
3. 船舶振动噪声重点实验室,湖北 武汉 430033;
4. 中原工学院 机电学院,河南 郑州 450007
2. Institute of Noise and Vibration, Naval University of Engineering, Wuhan 430033, China;
3. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China;
4. School of Mechatronics Engneering, Zhongyuan University of Technology, Zhengzhou 450007, China
螺旋桨在船舶尾部不均匀流场中运转产生的交变分力,引发推进轴系、推力轴承及壳体纵向振动,进而在水中产生辐射噪声。该噪声主要分布在低频段,容易成为船舶声纹特征的贡献分量,已成为特种船舶减振降噪领域急需突破的问题之一[1-2]。近年来,国内外学者针对该问题先后提出了轴系纵向共振转换器[3-5]、减振推力轴承[6-7]、具有补偿功能推力轴承[8]、轴系纵振主动控制[9]等,部分研究搭建了试验台架进行验证,取得了较好的轴系纵振衰减效果。但也存在一定的不足,主要体现在推进轴系纵向刚度数值受船舶航行安全要求不允许过低,船舶航行生命力与纵向振动衰减效果难以兼顾,这也是工程应用阶段进展缓慢的原因之一。
基于大型智能气囊减振装置的研究成果[10],提出将推力轴承与尾部动力设备安装在同一大型公共筏体进行集成减振的设计构想。公共筏体与船体之间安装有高性能元器件气囊减振器,改变了原推进轴系、推力轴承振动的传递路径,借用中间大型筏体大阻抗特性和高性能元器件能够有效衰减螺旋桨交变分量引起的低频振动,同时对尾部动力设备进行高效集成减振,解决尾部复杂耦合振动。
在此背景下,本文运用传递矩阵法建立考虑集成减振系统的轴系纵振模型,利用该模型结合试验台架参数,开展推力轴承低频动态传递特性仿真分析。同时,开展船舶实尺度环境推力轴承纵向动刚度测试,运用测试结果讨论对传递特性的影响,研究结果可指导工程实际设计,完善推力轴承集成减振系统的参数化设计方法。
1 系统纵振模型应用传递矩阵法建立轴系纵振模型时,可将轴系分为质量元件、轴段元件和弹性元件,其传递矩阵的表达式如下:
质量元件
| $ T_{M}=\left[\begin{array}{cc} 1 & 0 \\ -m \omega^{2} & 1 \end{array}\right]。$ | (1) |
其中:m为参振质量,ω为振动圆频率。
轴段元件
| $ T_{s}=\left[\begin{array}{cc} \cos k L & \displaystyle\frac{\sin k L}{E S k} \\ -E S k \sin k L & \cos k L \end{array}\right]。$ | (2) |
其中:S为横截面积,L为长度,E为弹性模量,k为波数。
弹性元件
| $ T_{K}=\left[\begin{array}{cc} 1 & \displaystyle\frac{1}{K} \\ 0 & 1 \end{array}\right] 。$ | (3) |
其中:K为刚度,考虑阻尼时K=K*(1+jη),η为阻尼比。
对采用直接传动形式的船舶而言,对轴系纵向振动建模时,限定在螺旋桨至联轴器从动端之间的连续轴段,依照轴系截面突变处划分单元,将螺旋桨与联轴器从动端简化为集中质量单元,作为两端自由边界条件,不考虑径向支撑轴承,各元件之间通过传递矩阵表达传递关系。
推力轴承依靠推力盘与推力瓦块之间的流体动压油膜传递力学关系,可将推力轴承简化为固结于轴系上的质量单元,和联接于集成减振系统的等效弹簧单元,集成减振系统简化为质量弹簧单元,末端与船体相连,如图1所示。

|
图 1 耦合纵振模型示意图 Fig. 1 The schematic diagram of coupling longitudinal vibration model |
将集成减振系统与推力轴承弹性元件进行耦合,建立传递关系,如下式:
| $ \left[\begin{array}{l} x \\ F \end{array}\right]^{R}=\left[\begin{array}{cc} 1 & \displaystyle\frac{1}{K_{\rm{ni}}} \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} 1 & 0 \\ -M_{\rm{ni}} \omega^{2} & 1 \end{array}\right]\left[\begin{array}{cc} 1 & \displaystyle\frac{1}{K_{\rm{th}}} \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ F \end{array}\right]^{L} 。$ | (4) |
其中:Mivi和Kivi分别为集成减振系统纵向参振质量、刚度,Kth为推力轴承弹簧单元刚度用。利用集成减振系统末端与船体相连位移为0,可得:
| $ x^{R}=\frac{K_{\rm{ivi}}-M_{\rm{iiz}} \omega^{2}}{K_{\rm{ivi}}} x^{L}+\frac{K_{\rm{iji}}+K_{\rm{th}}-M_{\rm{ii}} \omega^{2}}{K_{\rm{ivi}} K_{\rm{th}}} F^{L}=0 ,$ | (5) |
推导可得:
| $ K_{e}=-\frac{K_{\rm{th}}\left(K_{\rm{ivi}}-M_{\rm{iv}} \omega^{2}\right)}{K_{\rm{th}}+K_{\rm{ivi}}-M_{\rm{ivi}} \omega^{2}},$ | (6) |
修正后的推力轴承元件传递矩阵为:
| $ T_{\rm{th}}=\left[\begin{array}{cc} 1 & 0 \\ -M_{\rm{th}} \omega^{2}+K_{e} & 1 \end{array}\right] 。$ | (7) |
最后,可依轴系物理中心线由尾至首将各元件传递矩阵串联起来:
| $ Z^{R}=T_{c} \cdot T_{\rm{si}} \cdots T_{\rm{th}} \cdots T_{s i} \cdots T_{p} Z^{L} 。$ | (8) |
利用该模型重点分析推力轴承经集成减振系统的纵向力传递特性,设传递至推力轴承处的螺旋桨分力为Fth=Fth0ejωt,集成减振系统与推力轴承满足达朗贝尔原理:
| $ \left[ \begin{array}{cc} M_{\rm{t h}} & 0 \\ 0 & M_{\rm{ivi}} \end{array}\right]\left[\begin{array}{l} \ddot{x}_{\rm{t h}} \\ \ddot{x}_{\rm{ivi}} \end{array} \right]+\left[ \begin{array}{cc} K_{\rm{t h}} & -K_{\rm{t h}} \\ -K_{\rm{t h}} & K_{\rm{ni}} \end{array} \right]\left[ \begin{array}{c} x_{\rm{t h}} \\ x_{\rm{ivi}} \end{array} \right]=\left[\begin{array}{c} F_{\rm{t h}} \\ 0 \end{array}\right] ,$ | (9) |
上述矩阵考虑阻尼时为复刚度矩阵,利用复矢量代入可得:
| $ x_{\rm{ivi}}=\frac{K_{\rm{th}}}{K_{\rm{th}}+K_{\rm{ivi}}-M_{\rm{iv}} \omega^{2}} x_{\rm{th}},$ | (10) |
最后用集成减振系统刚度乘以位移可得传递力,处以螺旋桨初始激励力,可得力传递率:
| $ T f=\frac{K_{\rm{ivi}} K_{\rm{th}}}{K_{\rm{th}}+K_{\rm{iii}}-M_{\rm{iin}} \omega^{2}} x_{\rm{th}} / F_{p} 。$ | (11) |
如图2所示,试验室台架配套轴系采用两型推力轴承串联的配置方案,其中推力轴承Ⅰ为常用米歇尔式推力轴承,采用传统安装方式刚性支撑于船体;推力轴承Ⅱ为自主研发的小载荷自调心推力轴承,安装于集成减振系统的公共筏体上。轴系参数如表1所示。

|
图 2 试验室台架配套轴系 Fig. 2 Schematic diagram of test mating shafting |
|
|
表 1 轴系主要参数 Tab.1 Main parameters of shafting |
推力轴承纵向刚度,主要包括推力盘与推力瓦块之间的动压油膜刚度,以及推力瓦块支撑钢结构的刚度,二者为串联关系,通常前者数值小于后者,采用文献[11]中提及的经验数值暂定为1E9 N/m。简化的集成减振系统质量、刚度单元参数由文献[12]中提及的设计方案读取,并结合试验室台架进行等效缩比,其中质量单元约40 T,弹簧单元的刚度由三向气囊减振器刚度并联组成,其中纵向减振器为垂向刚度,垂向、横向减振器为横向刚度,横向刚度与垂向刚度的比值横垂刚度比为气囊减振器主要设计参数。
对以上轴系参数应用传递矩阵法建模,并在尾端螺旋桨处施加单位激励力(Fp=1ejωt),进行扫频。
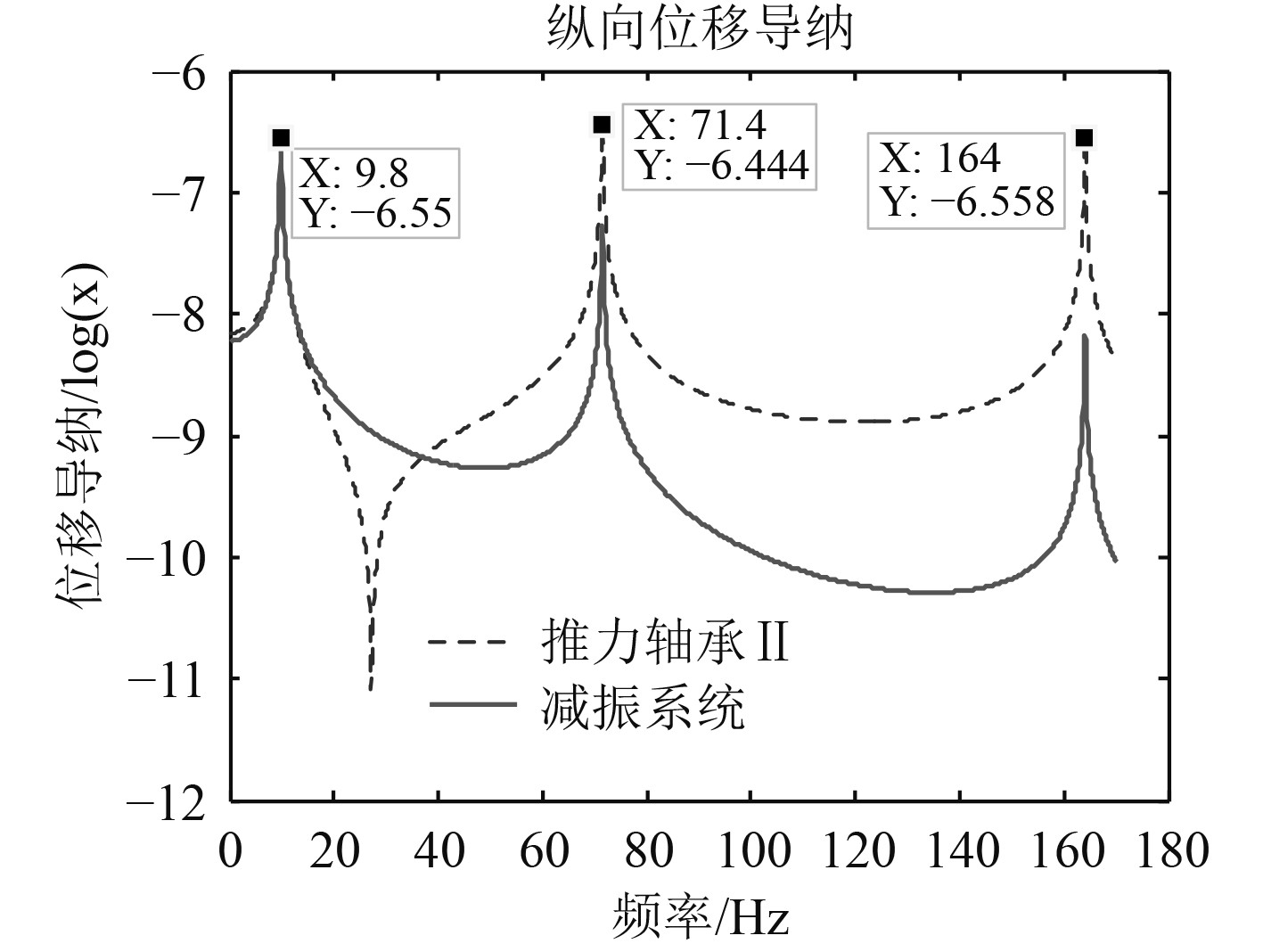
图3为推力轴承Ⅱ和集成减振系统处的位移导纳。可以看出,在0~170 Hz范围内出现了3个波峰,分别是一阶9.8 Hz、二阶71.4 Hz、三阶164.1 Hz。其中一阶时减振系统与推力轴承Ⅱ导纳幅值接近,表明轴系与减振系统呈现出一致的纵振特性;二阶及三阶时推力轴承Ⅱ代表的轴系纵振导纳幅值大于减振系统幅值,体现轴系纵向振动为主;推力轴承Ⅱ约在27 Hz出现反共振频率。
|
图 3 推力轴承Ⅱ与减振系统纵向位移导纳 Fig. 3 Longitudinal displacement admittance of thrust bearingⅡand isolation vibration system |
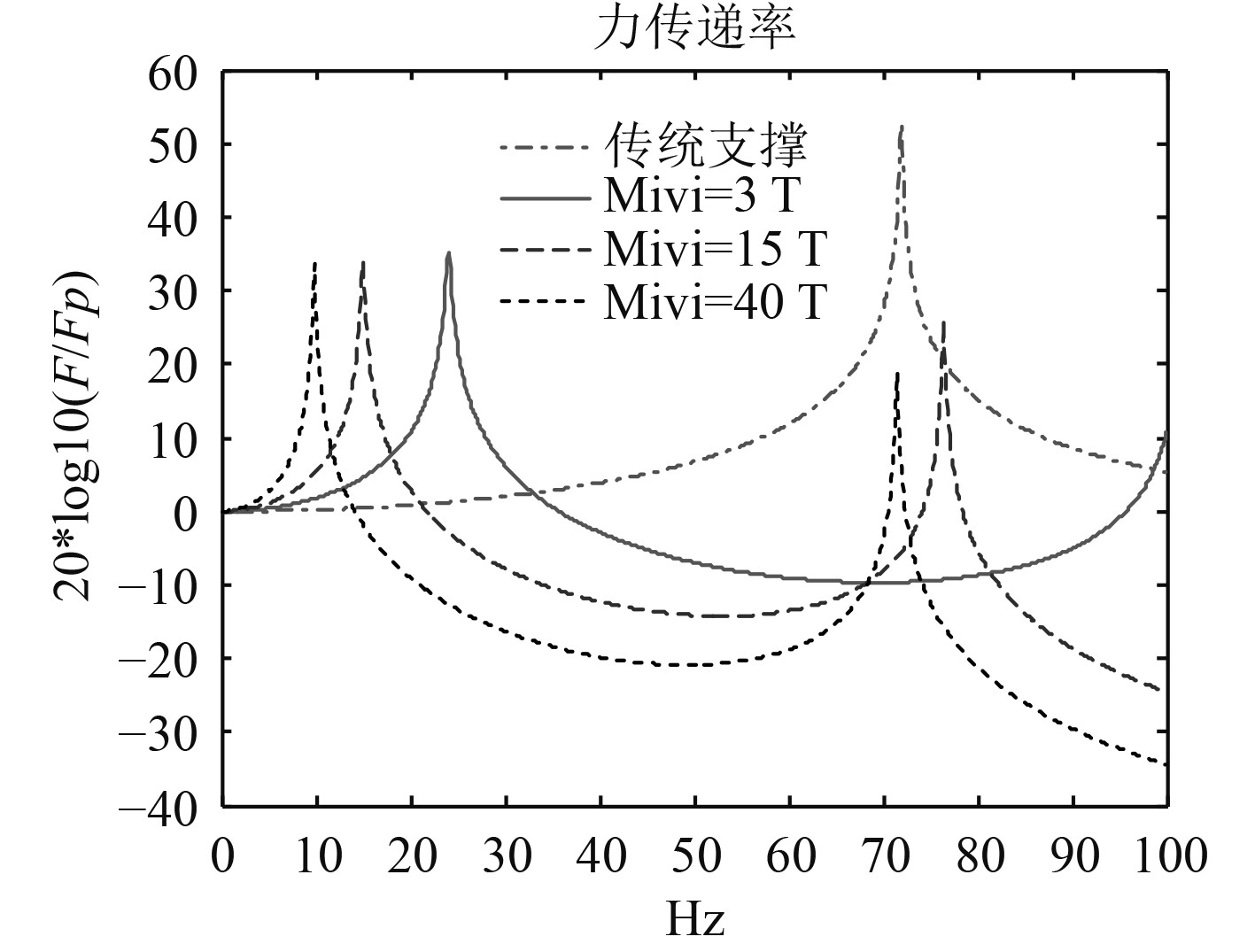
应用式(11)可求解集成减振系统纵向力传递率,讨论不同设计方案参数对减振效果的影响。选取减振系统质量参数分别为3 T,15 T,40 T,其中3 T为接近轴系质量参数,15 T为常规动力船舶等效缩比参数,40 T为核动力船舶缩比参数。
从图4可以看出,增大集成减振系统设计方案质量能够显著降低系统纵向振动一阶及二阶固有频率。质量参数为3 T时系统一阶纵振固有频率约24 Hz,质量参数为15 T时系统一阶纵振固有频率约15 Hz,质量参数为40 T时系统一阶纵振固有频率约9.8 Hz,且二阶固有频率与传统支撑下的固有频率一致。考虑低转速船舶螺旋桨叶频及1倍频通常分布在50 Hz以下,为有效实现20~50 Hz的低频减振,集成减振系统质量设计参数应大于15 T。
|
图 4 不同减振系统质量参数下纵向力传递率曲线 Fig. 4 Curves of longitudinal force transmissibility with different quality parameters of IVIS |
文献[13]分析了螺旋桨推力作用下系统位移特性,并就减振系统中气囊减振器的设计参数固有频率和横垂刚度比进行了讨论,本文在此基础上,进一步讨论气囊减振器设计参数对纵向力传递率的影响趋势,分别选取气囊隔振器常用工作参数:固有频率4 Hz,5 Hz,6 Hz;横垂刚度比2,2.5,3进行讨论。
从图5可以看出:气囊常用工作参数下,轴系一阶纵振频率变化量较小,能够实现20~70 Hz频段内推力轴承低频减振,固有频率设计参数对减振效果大于横垂刚度比设计参数;集成减振系统在设计阶段时可优先考虑增大气囊刚度特性或增加横向、纵向气囊减振器个数,以实现系统受推力作用下位移较小,保证推进系统运行安全。

|
图 5 不同气囊减振器工作参数下纵向力传递率曲线 Fig. 5 Curves of longitudinal force transmissibility with different working parameters of air spring |
鉴于推力轴承刚度数值在集成减振系统设计时具有较大的参考作用,本文依托试验室2型推力轴承试验台架对船用推力轴承纵向刚度数值开展参数范围识别,主要由轴系纵向激振系统、实船安装环境的推力轴承Ⅰ、电涡流位移传感器及BK测试软件等组成。
3.2 试验过程通过外置手摇泵切换两型推力轴承台架至推力轴承Ⅰ承载,即实船安装环境,记录此时电涡流位移传感器显示的轴系纵向初始位置。采用轴系纵振加载装置激振,分别测试不同推力及转速下轴系纵向变化量,将激振系统采集的纵向力与电涡流位移传感器测试的轴系纵向位移变化量FFT后,可得实船尺度与安装环境的推力轴承纵向动刚度:
| $ K_{\rm{th1}}(\omega)=\frac{F_{p}(\omega)}{{X}_{{\rm{S}}}(\omega)}。$ | (12) |
试验工况如表2所示。
|
|
表 2 测试工况 Tab.2 Test conditons |
部分试验结果如图6和图7所示。可以看出,推力轴承纵向刚度数值随外加载荷增大而增大,随转速提升而减小,且均表现出一定程度的非线性特征。载荷增大时动压油膜比压迅速提升,导致纵向刚度数值增大;转速提升时,推力盘单位时间内带走的流量增大,会降低油膜比压数值,致使纵向刚度数值下降。对比图6和图7可以发现,推力轴承纵向刚度数值受载荷的影响权重大于转速。

|
图 6 推力轴承纵向刚度随载荷变化曲线 Fig. 6 Curve of longitudinal stiffness of thrust bearing with varying load |

|
图 7 推力轴承纵向刚度随转速变化曲线 Fig. 7 Curve of longitudinal stiffness of thrust bearing with varying rpm |
将以上测试结果与文献[8]仿真计算结果进行对比,如图8所示。相较于理论仿真结果,实船推力轴承纵向刚度在主机工作转速下数值变化相对较小,基本保持在8E8~3E9 N/m之间。集成减振系统仅在部分况下(<90 r/min)对推力轴承非刚性支撑,此时推力轴承纵向刚度大致在(7E8~1.2E9 N/m)。选取静态测试时推力轴承刚度数值9.6 E9 N/m进行对比,分析该数值范围对减振效果的影响。

|
图 8 推力轴承纵向刚度数值对比 Fig. 8 Comparison of the longitudinal stiffness of thruste bearing |
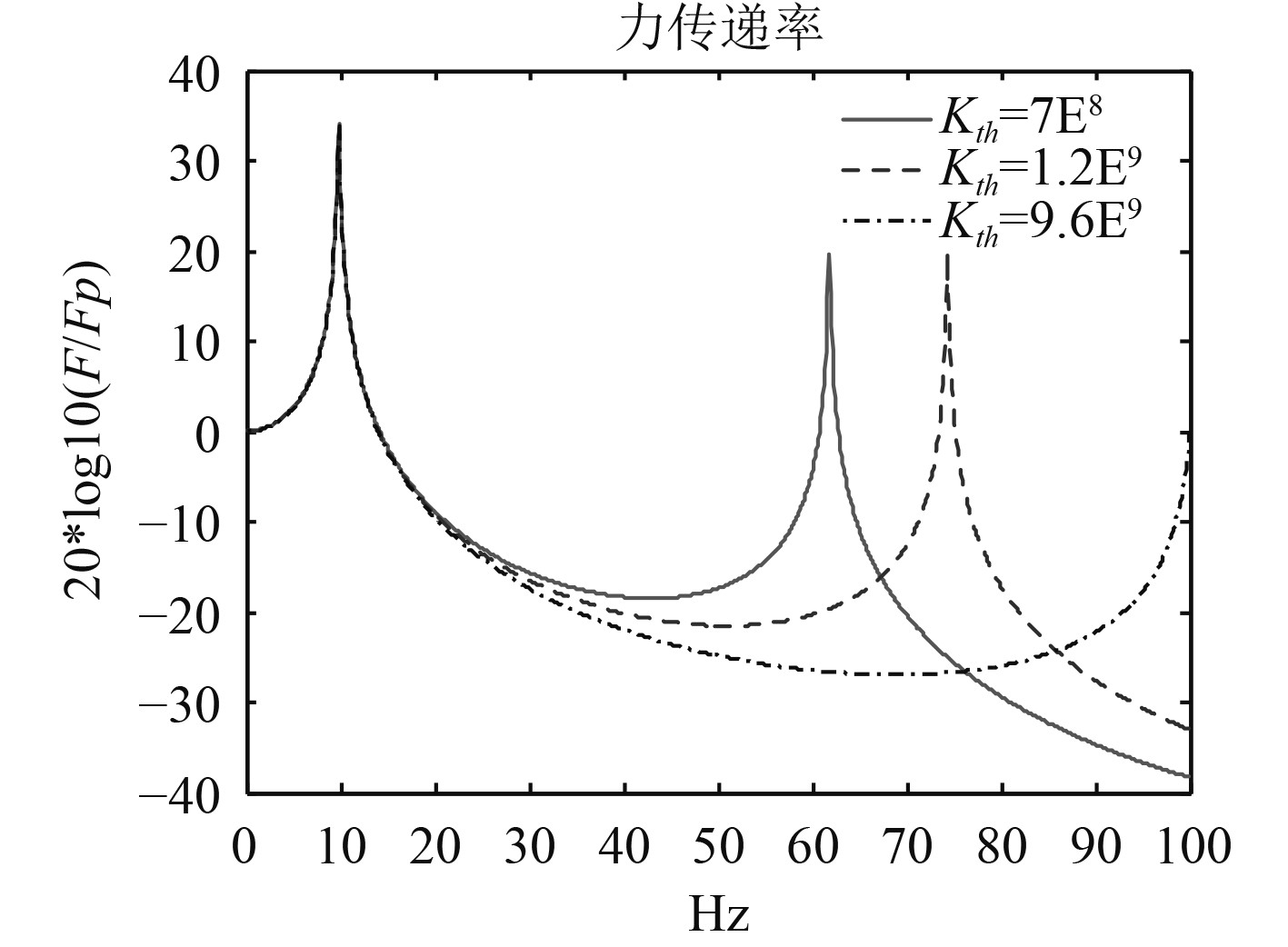
由图9可知,推力轴承动态情况下与静态情况下对轴系纵振特性的影响较大,表明推力轴承动压油膜特性不容忽略。不同工况下,不同推力轴承纵向刚度数值仅影响轴系二阶固有频率在低频段数值分布,对减振效果的影响较小。
|
图 9 推力轴承不同纵向刚度时,力传递率曲线 Fig. 9 Curves of longtidunal force transmissibility with different stiffness of thrust bearing |
本文运用传递矩阵法建立考虑集成减振系统的轴系纵振模型,以试验室台架参数为算例,对推力轴承集成减振系统低频纵向传递特性开展仿真分析,讨论了气囊减振器不同设计参数对纵向力传递率的影响。同时对推力轴承动刚度开展实船试验测试,得到推力轴承纵向刚度数值范围,讨论了不同推力轴承刚度数值对传递特性的影响,结论如下:
1)作为螺旋桨交变分量的主要传递路径,对推力轴承采用集成减振系统支撑后,能够有效衰减螺旋桨叶频及1倍叶频的低频振动;
2)集成减振系统设计参数中质量参数应至少大于轴系质量5倍以上,气囊减振器固有频率及横垂刚度比常用参数下,均能有效衰减20~70 Hz范围内推力轴承振动,且固有频率影响权重大于横垂刚度比,工程设计时还需结合螺旋桨推力作用下位移特性进行综合设计;
3)推力轴承实船纵向动刚度数值范围约在8E8~3E9 N/m之间,随着螺旋桨推力载荷增加而变大,随转速增大而减小,且均表现出非线性的特征。考虑不同推力轴承纵向刚度数值时,仅影响系统二阶纵振固有频率,对低频段减振效果影响较小。
| [1] |
何琳, 帅长庚. 振动理论与工程应用[M]. 北京: 科学出版社, 2015.
|
| [2] |
MERZ S, KINNS R, KESSISSOGLOU N J. Structural and acoustic response of a submarine hull due to propeller forces[J]. Journal of sound and vibration, 2009, b,325: 266-286. |
| [3] |
GOODWIN A J H. The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J]. Institute of Marine Engineers—Transactions, 1960, 72: 37-63. |
| [4] |
张维, 李天匀, 赵耀, 等. 基于液压阻尼减振器的轴系纵振控制研究[J]. 中国造船, 2012, 53(1): 18-27. |
| [5] |
胡泽超, 何琳, 徐伟, 等. 船舶推进轴系纵向振动共振转换器的优化设计[J]. 中国舰船研究, 2019, 14(1): 107-113. DOI:10.19693/j.issn.1673-3185.01077 |
| [6] |
杨志荣, 秦春云, 饶柱石, 等. 船舶推进轴系纵振动力吸振器设计及参数影响规律研究[J]. 振动与冲击, 2012, 31(16): 48-61. DOI:10.3969/j.issn.1000-3835.2012.16.010 |
| [7] |
秦春云, 杨志荣, 饶柱石, 等. 船舶推进轴系纵向振动抑制研究[J]. 噪声与振动控制, 2013, 33(3): 147-152. |
| [8] |
李正民. 用于潜艇艉部整体减振系统的推力轴承技术研究[D]. 武汉: 海军工程大学, 2016.
|
| [9] |
MERZ S, KESSISSOGLOU N, KINNS R, et al. Reduction of the sound power radiated by a submarine using passive and active vibration control[C]//Proceedings ofAcoustics 2009, Adelaide, Australia: Australian Acoustical Society, 2009.
|
| [10] |
HE Lin, XU Wei, BU Wenjun, et, al. Dynamic analysis and design of air spring mounting system for marine propulsion system[J]. Journal of Sound and Vibration, 2014, 333: 4912-4929. DOI:10.1016/j.jsv.2014.05.045 |
| [11] |
陈之炎. 船舶推进轴系振动[M]. 上海: 上海交通大学出版社, 1987.
|
| [12] |
何江洋, 何琳, 徐伟. 船舶推力轴承弹性支撑下减振系统与轴系耦合振动研究[J]. 舰船科学技术. 2018, 40(6): 52-56.
|
| [13] |
何江洋, 何琳, 帅长庚, 等. 船舶动力设备及推力轴承集成隔振系统设计研究[J]. 舰船科学技术. 2013(1): 126-131.
|
 2023, Vol. 45
2023, Vol. 45
