2. 渤海造船厂集团有限公司, 辽宁 葫芦岛 125000
2. Bohai Shipyard Group Co., Ltd., Huludao 125000, China
推力轴承是舰船推进轴系的重要组成部分,其性能的好坏直接决定舰船动力系统的运行效率。单支点可倾瓦推力轴承只有一个径向支撑点承载推力轴,因此在工作时允许轴系产生一定的倾斜。随着对舰船动力系统机动性和稳定性等要求的不断提高,对单支点可倾瓦推力轴承的静动特性进行分析具有现实意义。推力轴承工作时,在推力环与推力瓦块之间充满了润滑油,根据流体动压润滑原理,润滑油所形成的油膜会产生稳定的动力学特性,所以分析推力轴承的静动特性,其本质就是分析润滑油膜的静动特性。
邱家俊[1]采用指数膜假设,得到了油膜刚度与阻尼的解析解。李创业[2]在对可倾瓦推力轴承润滑机理研究分析的基础上,使用Fluent对推力轴承的润滑油膜进行仿真分析,采用位移扰动法对润滑油膜的刚度系数进行了计算。肖建海[3]采用有限差分法开展了止推轴承等温润滑特性研究,数值分析了润滑膜厚、轴瓦倾角和转速对平面瓦面止推轴承承载力和摩擦扭矩的影响规律。赵鸿博[4]通过对油膜瞬态数学模型的建立,在不考虑温度变化和轴瓦变形的情况下,仿真得到了瞬态载荷作用下的油膜刚度系数和阻尼系数。李贤燚[5]提出了“嵌套式二分法”的数值算法求解润滑油膜静特性,利用泰勒级数展开法将压力展开式代入瞬态雷诺方程进行求解得到推力轴承的轴向动特性系数。张文涛[6]建立了包含空穴模型的三维Navier-Stokes方程,采用数值分析方法对固定斜面瓦推力轴承的承载特性展开分析,研究了结构参数对轴承承载性能的影响规律。王报龙[7]提出以倾斜角和轴线投影角2个参数表征轴系的倾斜状态,建立了轴线倾斜下可倾瓦推力轴承热弹流体动压润滑计算模型,通过Matlab编写程序分析了轴线倾斜对可倾瓦推力轴承静动特性的影响。张松林[8]对推力轴承的热流体动力润滑性能进行研究,分析了温度对润滑性能的影响。姚亮[9]以斜平面推力轴承为基础,通过对推力瓦块形状的优化,得出了油膜间隙比和斜面平面角度比对推力轴承性能的影响规律。
目前,学者们采用计算流体力学的方法对推力轴承油膜的静动特性进行了研究,但是对轴系倾斜状态下油膜静动特性的研究较少。本文以流体动压润滑理论基本方程为基础,建立推力轴承油膜的几何模型,采用计算流体力学的方法分析轴系非倾斜和轴系倾斜2种状态下推力轴承油膜的静动特性。
1 理论基础 1.1 流体动压润滑原理流体动压润滑原理是动压轴承使用的基本原理,如图1所示。在A板与B板之间充满了具有一定粘度的润滑介质,B板静止不动且保持倾斜状态,A板相对于B板以速度v由两板间开口大的一边朝着开口小的一边移动,即δ1>δ2,于是润滑介质在两板之间形成了一个楔形的流体膜。润滑介质在粘性力的作用下随A板运动,并从开口大的一边运动到开口小的一边。润滑介质在流动过程中遵循质量守恒原理,且为不可压缩流动,其密度ρ保持不变。因此,在单位时间内从开口大的一边流入的流体质量等于从开口小的一边流出的流体质量。若液膜外部流体的压强和流速恒定,设流体流入和流出液膜的速度分别为v1和v2,根据上述条件,则有ρδ1v1=ρδ2v2,易得v1<v2,即流入速度小于流出速度。只有当两板之间液膜的压强大于外部压强时,才能使流体流入的速度减小,流出的速度增大,而A板也会受到液膜的压强作用在其表面的压力,且该压力与A板所受的工作载荷F的大小相等。因此,将液膜作用在A板上的压力称为动压力。
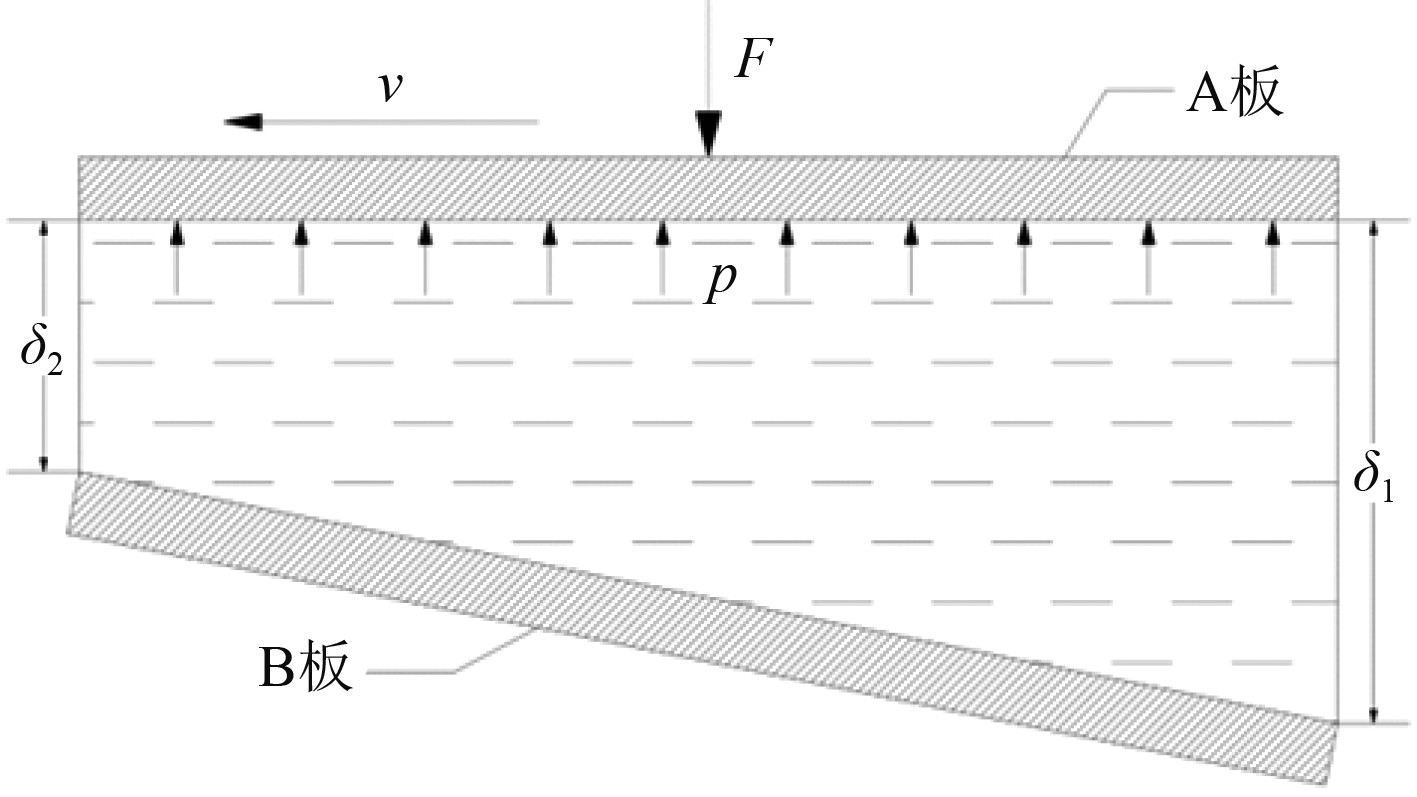
|
图 1 流体动压润滑原理图 Fig. 1 Schematic diagram of hydrodynamic lubrication |
流体动压润滑理论在数学角度上分析,实质上是对N-S方程在一种特别的形式下求解。通过联立连续方程和运动方程导出了流体动压润滑理论最基本的方程—雷诺方程,雷诺方程的求解过程相当于使用数学方法分析流体润滑的特性。
求解雷诺方程,润滑介质需满足等温条件,润滑介质的粘度和密度保持不变。此外,在运用雷诺方程时,还需要引入以下假设:
1)润滑介质不考虑体积力的作用,即不受外力场的作用;
2)沿液膜的厚度方向,其压强保持不变;
3)润滑介质为牛顿流体,即剪切应力与剪应变率成正比;
4)与刚性表面相接触的润滑介质在界面上无滑动;
5)润滑介质在间隙中的流动为层流,即不考虑惯性力的作用;
6)刚性运动副表面的曲率半径比液膜厚度要大得多,表面切向速度远大于径向速度,因此不必考虑曲率引起的速度方向的改变,可用平动速度代替转动速度。
根据上述条件和假设,经过推导可得雷诺方程的表达式:
| $ \frac{\partial }{\partial x}\left(\frac{{h}^{3}}{\mu }\frac{{\rm{d}}p}{{\rm{d}}x}\right)+\frac{\partial }{\partial z}\left(\frac{{h}^{3}}{\mu }\frac{\partial p}{\partial z}\right)=6U\frac{\partial h}{\partial x} 。$ | (1) |
式中:μ为流体的动力粘度,U为转子的运动速度,p为流体形成薄膜所提供的压强,h为流体形成薄膜的厚度。
2 计算模型及前处理 2.1 计算模型如图2所示,本文使用的单支点可倾瓦推力轴承的主要参数为:推力瓦块的外径DO为1240 mm,内径Di为620 mm;推力瓦块的宽度B为310 mm,在瓦块中径处的长度L为310 mm;推力瓦块的数量为8块,瓦块的径向偏支参数(Rz-Ri)/B的值为0.6,支承点位置Rz=496,支承点偏向瓦块的外侧;瓦块的周向偏支参数为0.5,支承点的位置位于瓦块的中点;轴承采用的润滑油密度为876 kg/m3,动力粘度为0.0187 Pa·s,油膜的标准厚度为0.5 mm,各个扇形瓦块之间间隙处轴向油膜厚度为15 mm,进出口油压为1.75 MPa;轴系最大倾斜角θ为0.0245°。
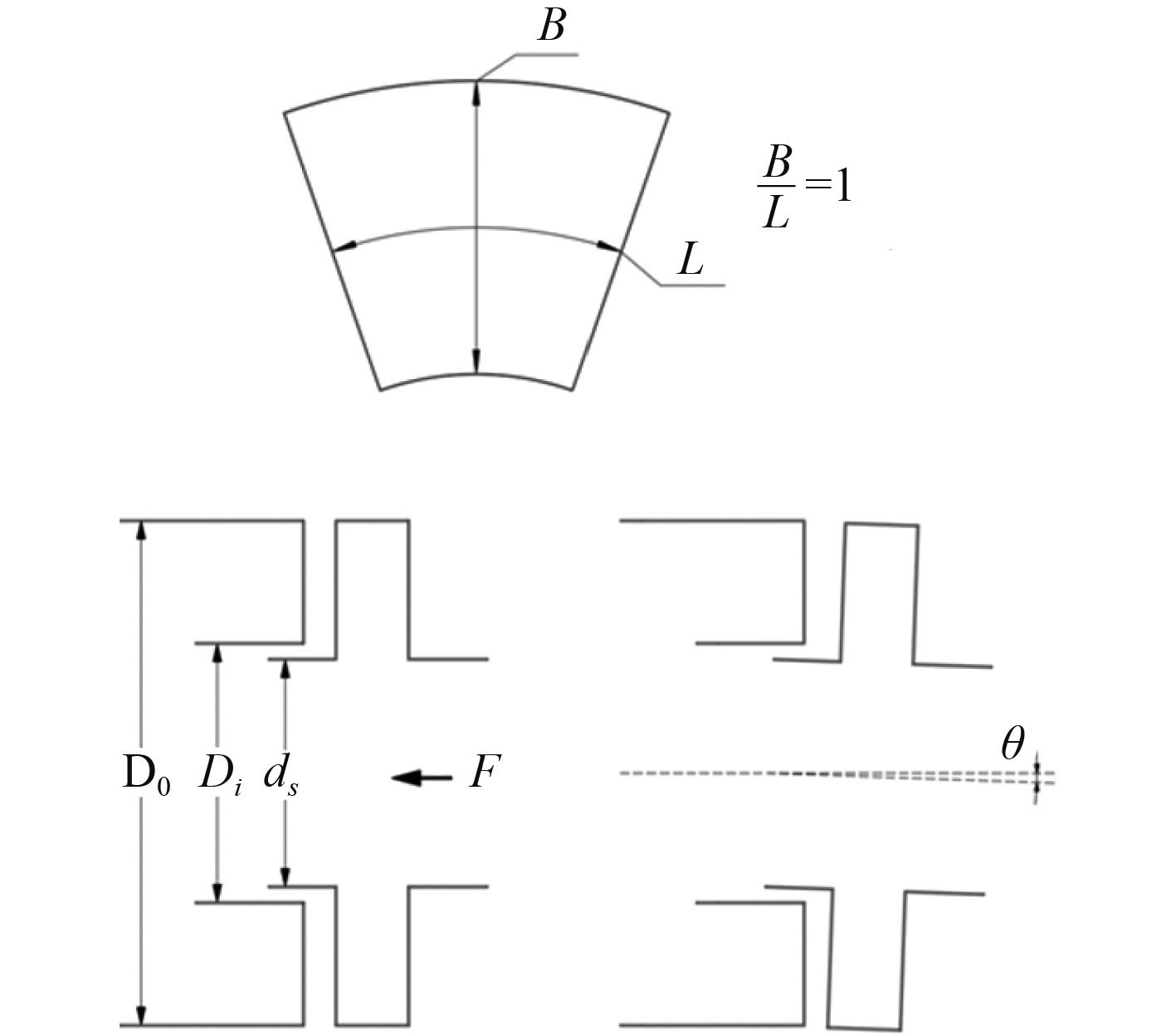
|
图 2 推力轴承参数图 Fig. 2 Thrust bearing parameter diagram |
对可倾瓦推力轴承的油膜进行建模时,采用SolidWorks三维软件。油膜几何模型的部分参数,通过扇形可倾瓦推力轴承的间隙比k得出。
间隙比k的定义如下:可倾瓦推力轴承工作时,推力环随轴转动,推力瓦块产生倾斜,在推力瓦块与推力环之间形成了稳定的楔形润滑油膜,润滑油从楔形油膜的大口流入,小口流出。设楔形油膜的大口高度为δ1,小口高度为δ2,(δ1-δ2)/δ2即为间隙比。
基于可倾瓦推力轴承的结构特性,工作时,间隙比不变化,由此可以计算不同油膜厚度情况下,其生成楔形油膜的大口高度和小口高度。根据这个特性,能够确定油膜的几何参数。
间隙比k计算公式如下:
| $ \frac{\left({R}_{z}-{R}_{i}\right)}{B}=\frac{k\left(k+2\right){\ln}k-\left(k-1\right)\left(2.5k+0.5\right)}{\left({k}^{2}-1\right){\ln}k-2{\left(k-1\right)}^{2}}。$ | (2) |
式中,(Rz-Ri)/B为瓦块的径向偏支参数。衡量支点在瓦块上的相对位置,依据上述推力轴承的参数,可知(Rz-Ri)/B=0.6,计算得到间隙比k=3。
建立完整的油膜几何模型,如图3所示。模型的简化方法如下:已知轴系倾斜的角度,且轴系倾斜角度与推力环倾斜角度相同,因此可以确定各个瓦块的瓦面与推力环之间的平均间隙,从而根据推力轴承的间隙比计算出不同位置的瓦块与推力环所形成的扇形油膜的几何参数。

|
图 3 完整的油膜模型 Fig. 3 Complete oil film model |
将建立好的油膜几何模型导入Ansys的DM中进行设置:油膜下端的弧形表面定义为“inlet”;上端的弧形表面定义为“outlet”;与推力环接触的平面定义为“rotation”;几何模型左侧与右侧的表面定义为“interface1”和“interface2”,便于后续通过周期性边界条件的设置将扇形油膜单元扩展为完整的油膜模型;其他的几个表面都定义为“wall”。
创建一个能够完整攘括扇形油膜单元的块,结合油膜模型的特点,对块进行处理,将块切割成由3个部分组成的“槽”形状的几何体,分别对应2个间隙实体和1个扇形油膜,将块上面的点和线与几何模型的点和线一一对应进行关联,对块上各条线的网格尺寸进行合理的定义,采用六面体网格对几何模型进行网格划分。
如图4所示,通过上述步骤所划分出来的网格数量可达到3×105,且网格质量较好。在这个基础上,就把预处理结果导入到Fluent模块,根据实际情况,设置好相应的条件进行分析运算。

|
图 4 油膜网格划分 Fig. 4 Meshing of oil film |
不同的油膜厚度和不同的转速条件会影响润滑介质的流动状态,因此需要通过雷诺数对润滑介质的流动状态进行判定。雷诺数的计算公式如下:
| $ Re=\frac{\rho vL}{\mu }。$ | (3) |
式中:ρ为流体的密度,kg/m3;v为流体的特征速度,m/s,使用轴承转速的角速度与瓦块中径处的半径相乘所得的线速度表示特征速度;L为特征长度,m,取未产生倾斜的瓦块面与推力环之间的距离表示特征长度;μ为流体的动力粘度,Pa·s。
一般认为,在内流域中,当Re<2100时,流场中粘滞力的影响超过了惯性力,这使得流场处在较小的扰动之下,在宏观来看,此时流体处于层流状态;当Re>4000时,粘滞力的影响弱于惯性力,流体处于湍流状态。
本文使用的推力轴承,其最大的特征速度为12.17 m/s,最大的特征长度为8×10−4 m,通过计算得到Re=456.1<2100,油膜的流动状态为层流状态。
4 静动特性分析将预处理结果接入到Fluent模块,根据对油膜流动状态的判断,采用Laminar模型进行计算,仿真计算所得到的结果为油膜表面的压强分布以及油膜提供给推力环的承载力,这2个结果体现的是推力轴承的静特性。
当推力轴转速和油膜厚度为某一定值时,可以得到该状态下润滑油膜的压强分布云图。为了更加清晰地查看某一工况下可倾瓦推力轴承的油膜压强分布云图,分别取转速为200 r/min,油膜厚度为0.5 mm时的工况,得到了压强分布云图,如图5所示。

|
图 5 油膜表面压强分布云图 Fig. 5 Nephogram of pressure distribution on oil film surface |
颜色越深,表示润滑油膜在该处的压强越大。可以看出,2块扇形瓦块之间的润滑油表面压力最小,没有为推力环提供主要的承载力。对单块扇形瓦块而言,其右上角受到的压强最大,所以是最容易产生磨损的部位。
在上述转速和油膜厚度不变的情况下,当轴系产生倾斜时,也能得到润滑油膜的压强分布云图。取轴系的最大倾斜角0.0245°,如图6所示。

|
图 6 轴系倾斜状态下油膜表面压强分布云图 Fig. 6 Nephogram of pressure distribution on oil film surface under shafting inclination |
可以看到,由于轴系产生了倾斜,推力环也产生了相同的倾斜,使各个瓦块与推力环之间油膜的厚度发生了改变,作用在推力环表面的压力从上到下逐渐增大,说明在轴系倾斜的情况下,主要靠下面与推力环之间油膜厚度小的瓦块来承载轴向的推力。
推力轴承的动特性主要指油膜的刚度系数和阻尼系数。刚度系数可以理解为改变单位油膜厚度所需的承载力变化量,阻尼系数可以理解为改变单位速度所需的承载力变化量。
计算刚度系数所使用的方法为位移扰动法,即在轴承稳定工作时有一个标准油膜厚度,此时推力环与瓦块在轴向不发生相对运动,油膜的几何形状保持不变,然后让推力环在轴向有一个小的位移,使油膜的几何形状发生改变,导致油膜表面的压强分布和承载力产生变化,之后选取多个位移点,计算得到不同油膜厚度在转速不变的情况下所对应的承载力。以油膜厚度为横坐标,承载力为纵坐标,采用多项式拟合的方法拟合出一条光滑的曲线,然后导出该曲线的解析式,对解析式在标准油膜厚度处求导数,得到油膜的刚度系数。
本文使用的推力轴承标准油膜厚度为0.5 mm,因此在计算中油膜厚度选取0.4~0.6 mm的一系列数值。推力轴的转速最大可达250 r/min,因此在计算中转速选取50~250 r/min的一系列数值。经过Fluent仿真计算,可以得到承载力-油膜厚度-转速关系表,计算结果如表1和表2所示。
|
|
表 1 轴系非倾斜状态下承载力-油膜厚度-转速关系表 Tab.1 The relationship table of bearing capacity-oil film thickness-speed in the non-inclined state of the shafting |
|
|
表 2 轴系倾斜状态下承载力-油膜厚度-转速关系表 Tab.2 The relationship table of bearing capacity-oil film thickness-speed in the inclined state of the shafting |
将5个转速下的计算结果在坐标系中进行拟合,得到承载力-油膜厚度关系图,如图7和图8所示。
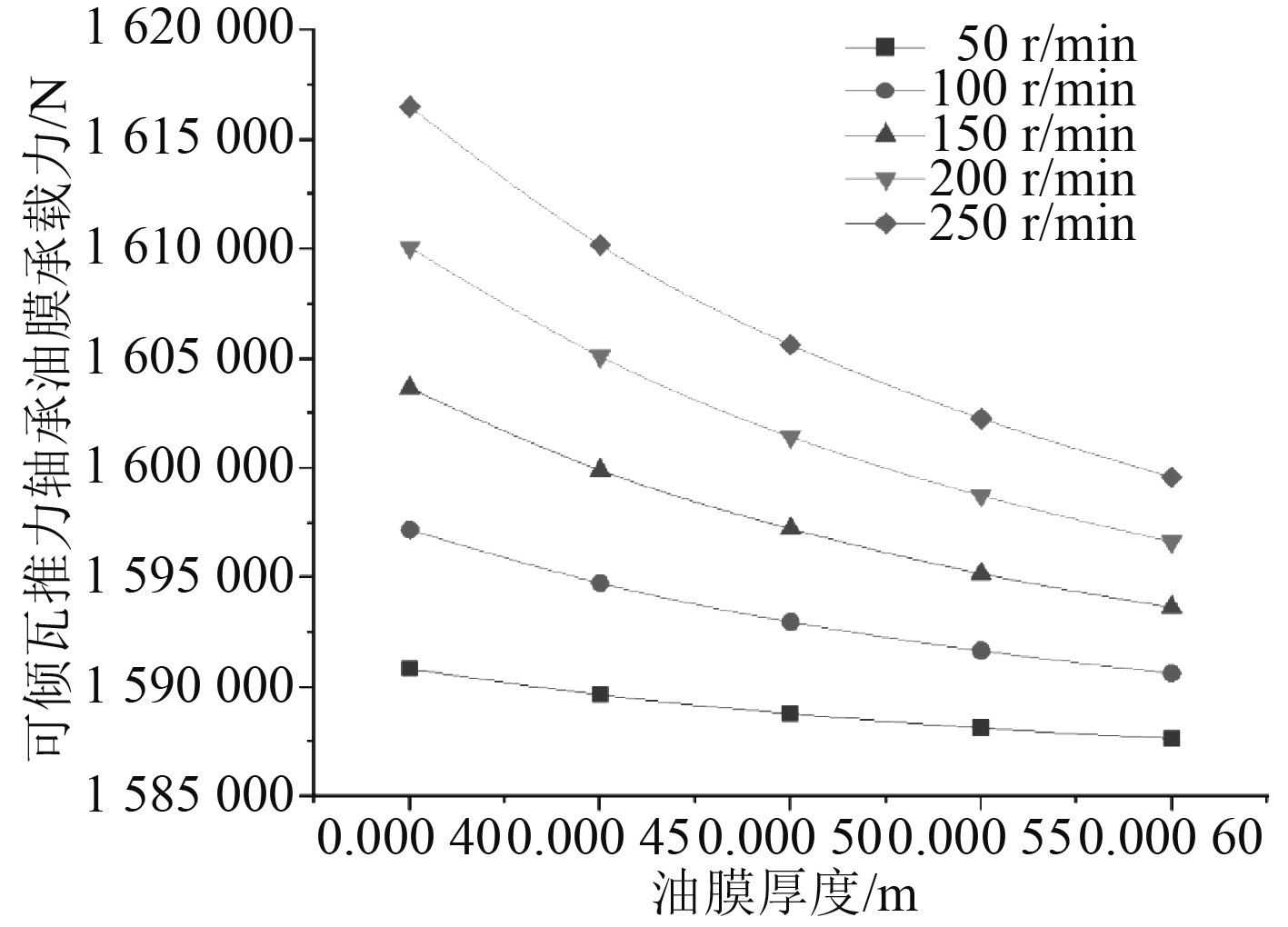
|
图 7 轴系非倾斜状态下承载力-油膜厚度关系 Fig. 7 The relationship diagram of bearing capacity-oil film thickness in the non-inclined state of the shafting |
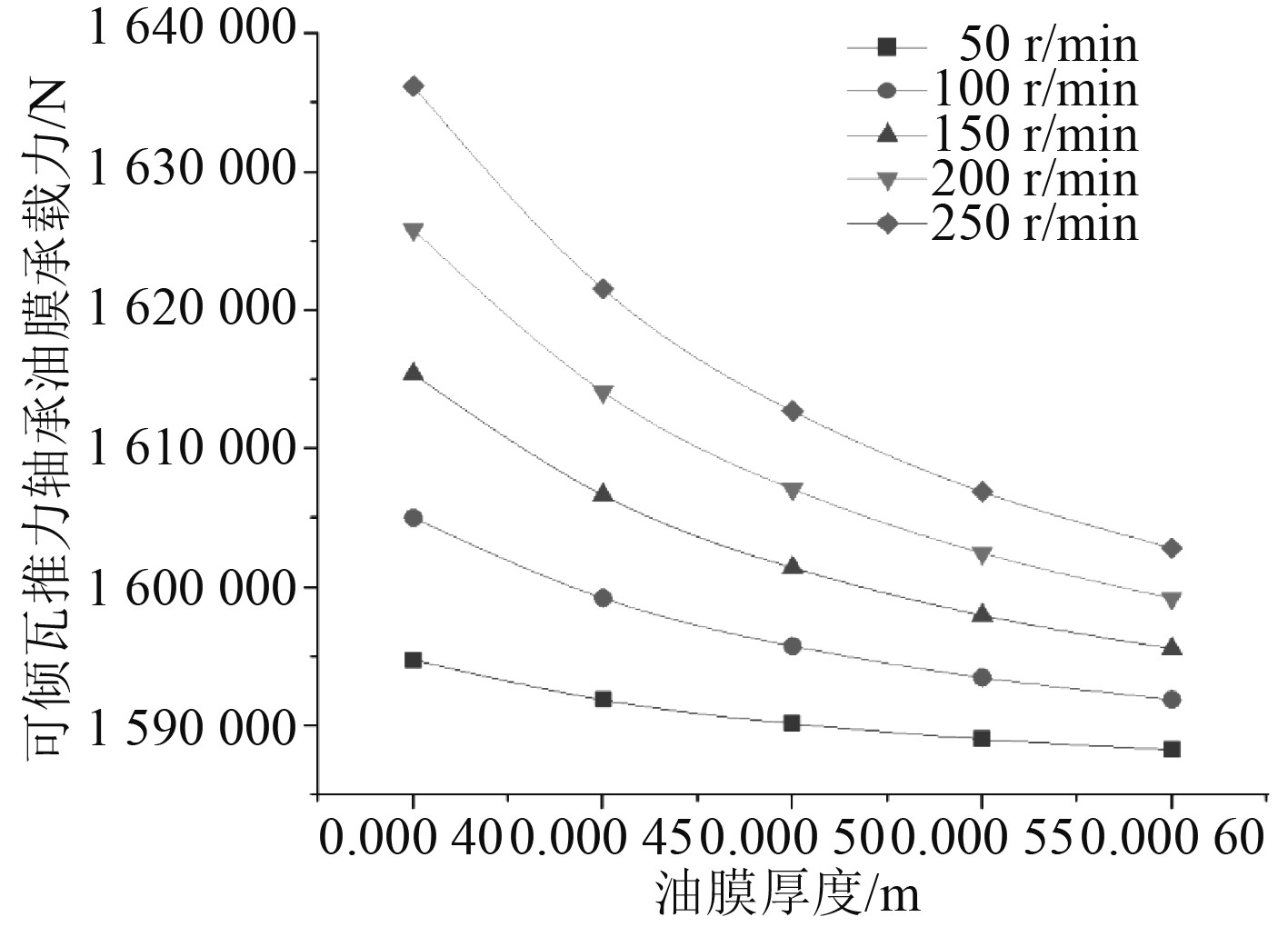
|
图 8 轴系倾斜状态下承载力-油膜厚度关系 Fig. 8 The relationship diagram of bearing capacity-oil film thickness in the inclined state of the shafting |
导出每一条曲线的函数解析式,对解析式在0.5 mm处求导数,得到不同转速所对应的油膜的刚度系数,结果如表3和表4所示。
|
|
表 3 轴系非倾斜状态下转速-油膜刚度表 Tab.3 Speed-oil film stiffness table in the non-inclined state of the shafting |
|
|
表 4 轴系倾斜状态下转速-油膜刚度表 Tab.4 Speed-oil film stiffness table in the inclined state of the shafting |
阻尼系数的求解方法与刚度系数的类似,其方法为速度扰动法,即轴承在标准油膜厚度的情况下工作,让推力轴使用不同的转速旋转,导致油膜表面的压强分布和承载力产生变化,计算得到不同转速在油膜厚度不变的情况下所对应的承载力,以转速为横坐标,承载力为纵坐标拟合曲线。对曲线的解析式在不同转速处分别求导数,得到油膜的阻尼系数。
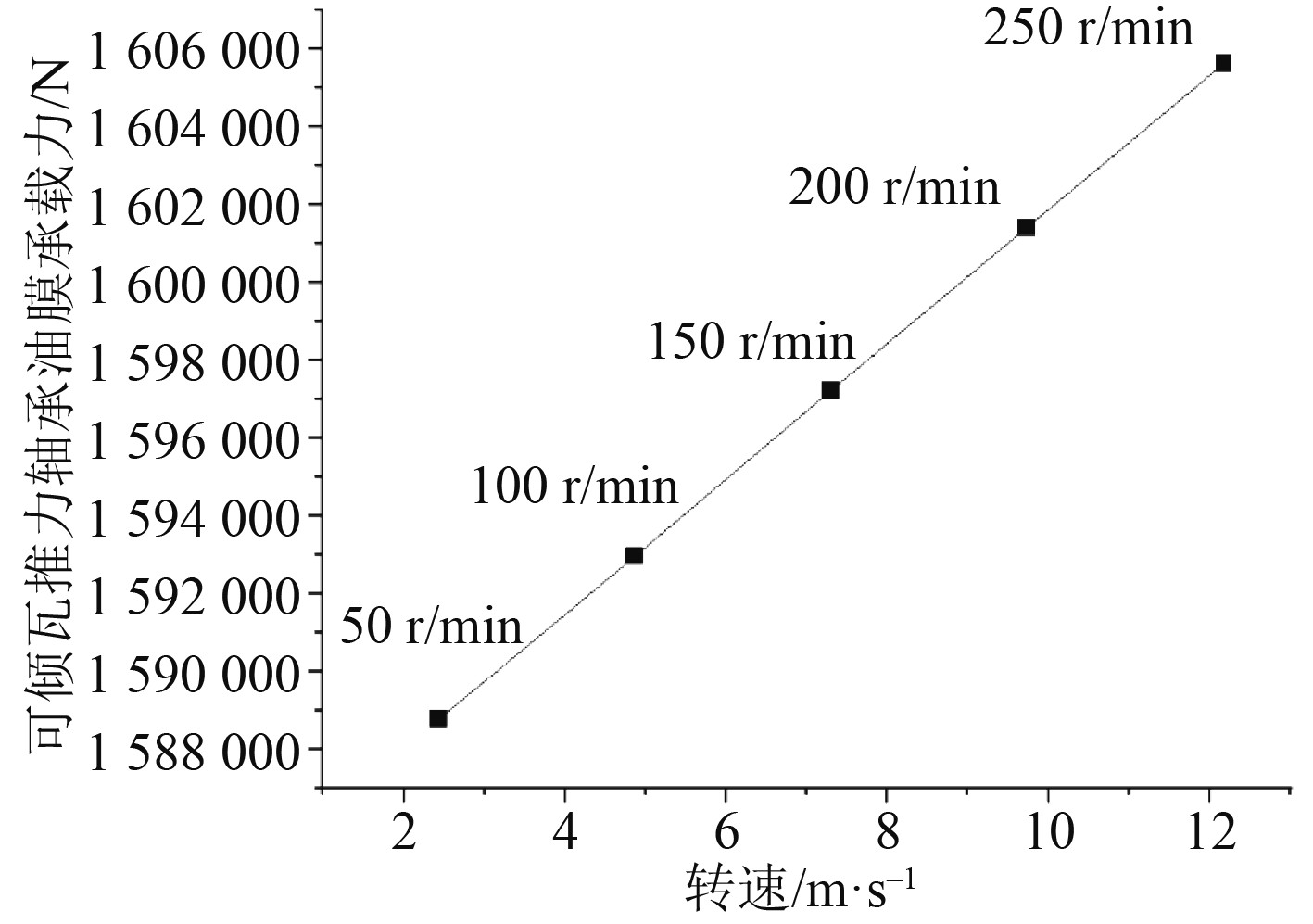
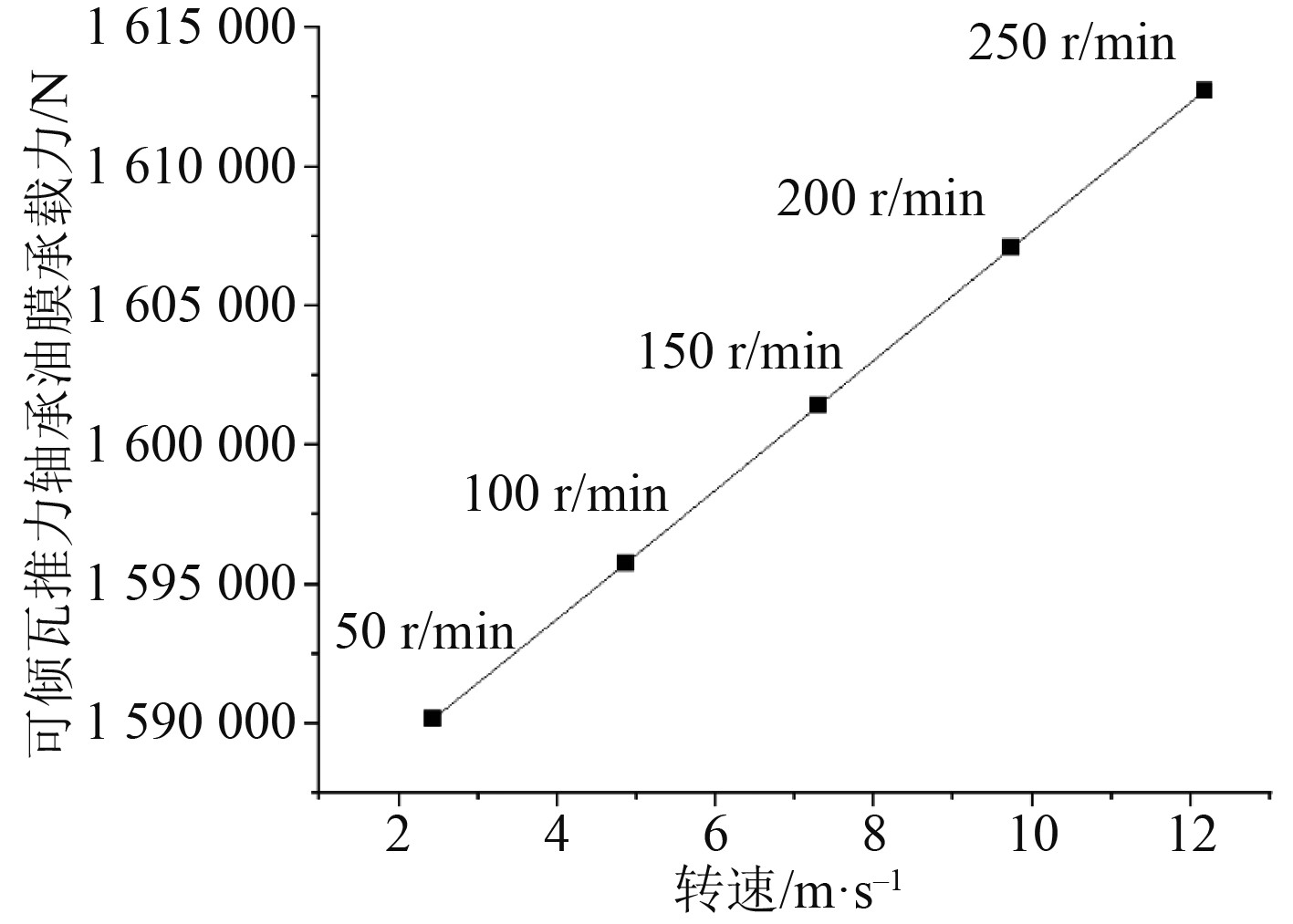
将表2中0.5 mm的计算结果在坐标系中进行拟合,可以得到承载力-转速关系图,如图9和图10所示。
|
图 9 轴系非倾斜状态下承载力-转速关系 Fig. 9 The relationship diagram of bearing capacity-speed in the non-inclined state of the shafting |
|
图 10 轴系倾斜状态下承载力-转速关系 Fig. 10 The relationship diagram of bearing capacity-speed in the inclined state of the shafting |
导出曲线的函数解析式,对解析式在5个转速处求导数,得到不同转速所对应的油膜的阻尼系数,结果如表5和表6所示。
|
|
表 5 轴系非倾斜状态下转速-油膜阻尼表 Tab.5 Speed-oil film damping table in the non-inclined state of the shafting |
|
|
表 6 轴系倾斜状态下转速-油膜阻尼表 Tab.6 Speed-oil film damping table in the inclined state of the shafting |
基于动压润滑理论,利用计算流体力学的方法分析轴系非倾斜状态与倾斜状态下单支点可倾瓦推力轴承油膜的静动特性,主要结论如下:
1)静特性方面,在转速不变的情况下,轴系倾斜时油膜所产生的承载力要略大于轴系非倾斜时油膜所产生的承载力,说明轴系倾斜对承载力的影响较小。但轴系倾斜时,不同瓦块所受的载荷大小不一,会导致部分所受载荷过大的瓦块产生烧瓦现象。
2)动特性方面,推力轴转速的变化对油膜刚度系数的影响较大,对油膜阻尼系数的影响较小。在转速不变的情况下,轴系倾斜时的刚度系数和阻尼系数大于轴系非倾斜时的刚度系数和阻尼系数,说明轴系倾斜对轴的纵振影响较大,会影响振动的频率和振幅。
本文未考虑润滑油工作时温度变化对油膜静动特性的影响,即求解时没有使用能量方程的模型,需要进一步研究。
| [1] |
邱家俊, 段文会. 推力轴承油膜刚度和阻尼的解析解[J]. 大电机技术, 2002(2): 5-8. QIU J J, DUAN W H. The analytical solution to oil film stiffness and damping of thrust bearing[J]. Large Electric Machine and Hydraulic Turbine, 2002(2): 5-8. DOI:10.3969/j.issn.1000-3983.2002.02.002 |
| [2] |
李创业. 滑动轴承液膜刚度特性对推进轴系耦合振动影响研究[D]. 济南: 山东大学, 2019.
|
| [3] |
肖建海. 船用止推轴承热流动力润滑特性研究[D]. 杭州: 浙江工业大学, 2012.
|
| [4] |
赵鸿博. 破冰船冰载荷对推力轴承润滑性能影响研究[D]. 哈尔滨: 哈尔滨理工大学, 2018.
|
| [5] |
李贤燚. 船用推力轴承润滑油膜静动特性分析方法及其应用研究[D]. 武汉: 华中科技大学, 2017.
|
| [6] |
张文涛, 马腾. 基于CFD的新型斜面推力滑动轴承承载性能分析[J]. 润滑与密封, 2017, 42(9): 70-75. ZHANG W T, MA T. Load capacity analysis of the new type tapered-land thrust bearing based on CFD[J]. Lubrication Engineering, 2017, 42(9): 70-75. DOI:10.3969/j.issn.0254-0150.2017.09.015 |
| [7] |
王报龙, 王亚兵, 刘洋洋, 等. 轴系倾斜下可倾瓦推力轴承静动特性分析[J]. 西安交通大学学报, 2020, 54(7): 129-138. WANG B L, WANG Y B, LIU Y Y, et al. Static and dynamic characteristics of tilting-pad thrust bearing on inclined shaft[J]. Journal of Xi′an Jiaotong University, 2020, 54(7): 129-138. DOI:10.7652/xjtuxb202007016 |
| [8] |
张松林. 基于CFD的曲面瓦推力滑动轴承承载特性分析及实验研究[D]. 长春: 长春理工大学, 2018.
|
| [9] |
姚亮. 基于CFD方法的推力轴承动力学特性分析[D]. 长春: 长春理工大学, 2016.
|
 2023, Vol. 45
2023, Vol. 45
