2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
舰船及舰载设备除要承受导弹、鱼雷等武器直接作用产生的接触式爆炸破坏外,还会受到因爆炸产生的冲击波等非接触式爆炸的破坏。对于舰船推进轴系用液压联轴器而言,受到非接触式水下爆炸冲击破坏的概率和破坏性更大[1-2]。作为舰船推进系统关键设备,联轴器安全可靠是保证舰船机动性的必要条件。因此,开展液压联轴器抗冲击性能及影响因素的分析对提高舰船战斗力和生命力具有重要意义。
实船爆炸等试验的开展需要耗费大量资源,且试验条件有限、操作不便。因此,模拟仿真研究在现代舰船设备抗冲击性能分析中发挥着越来越重要的作用。目前,国际上最常用的3种抗冲击分析方法分别是等效静力法、动态设计分析方法(dynamic design analysis method,DDAM)和时域模拟法。冯麟涵[3]基于DDAM法对舰用增压锅炉开展了抗冲击特性的研究。同时,也采用时域分析法进行抗冲击分析,为舰用设备抗冲击分析提供参考。张影[4]以船用齿轮箱为研究对象,对这3种主流的抗冲击方法进行对比研究。研究表明,DDAM法在保证结果具有较高准确性的情况下有较高的计算效率,且计算所需要的资源较少。因此,大量学者采用DDAM法对不同舰载设备进行抗冲击性能的研究和优化。计晨等[5-6]在采用模态试验验证船用柴油机有限元模型正确性的基础上,通过DDAM法计算其抗冲击性能,分析了动态运行条件对其抗冲击性能的影响。蒲军等[7]采用DDAM法对某舰用升降装置进行抗冲击分析,为舰用升降装置抗冲击设计和评估提供了参考。曹贻鹏等[8]采用DDAM法对船用柴油机的排气消声器进行了抗冲击优化研究,提出多种优化方案。而在液压联轴器抗冲击性能方面也有学者进行了研究。吴晖等[9]分别采用频域法和时域法对法兰式液压联轴器进行了抗冲击特性的分析,分析了冲击载荷作用下的应力分布情况。上述研究表明,模拟仿真的研究方法是在试验条件有限的情况下对舰载设备抗冲击性能评估和设计的最佳方案,有效推动舰载设备抗冲击性能研究的进展。
目前,舰载设备抗冲击性能评估主要是对其开展抗冲击性能的仿真分析。而在抗冲击性能影响因素方面国内外相关研究较少。因此,本文以某型套筒式液压联轴器为例,采用DDAM法对其进行抗冲击性能分析。进一步,对比分析液压联轴器抗冲击性能影响因素及影响规律,为液压联轴器的设计与优化提供参考。
1 抗冲击性能基础理论DDAM法是一种具有代表性且应用广泛的频域分析方法,基本思想是对模型进行模态分析得到模态频率和质量,再将计算得到的冲击载荷谱加载到各模态上得到模态响应。通过模态合成得到整个设备的冲击响应,适用于分析线性和弱非线性系统的动态响应,具有很高的计算效率[2,4]。根据GJB对舰载设备的分类,液压联轴器属于水面舰船船体部位安装的设备,其抗冲击等级为A级,需对其进行弹性分析[10]。初始加速度、速度设计值采用式(1)和式(2)进行计算,之后按GJB1060.1-1991规定得到设计加速度和速度。
| $ {A_0} = 196.2 \times \frac{{\left( {17.01 + {m_a}} \right)\left( {5.44 + {m_a}} \right)}}{{{{\left( {2.72 + {m_a}} \right)}^2}}},$ | (1) |
| $ {V_0} = 1.52 \times \frac{{5.44 + {m_a}}}{{2.72 + {m_a}}}。$ | (2) |
式中:A0为初始加速度;V0为初始速度;ma为模态质量。
采用美国海军研究实验室求和NRL方法进行模态合成,如下式:
| $ {\left\{ x \right\}_{{\text{NRL}}}} = \left\{ {{x_b}} \right\} + \sqrt {\sum\limits_a {\left\{ {{x_a}^2} \right\} - \left\{ {{x_b}^2} \right\}} } 。$ | (3) |
式中:
根据GJB1060.1-1991规定,在得到频域冲击应力后还需与工作应力进行合成得到综合应力,如下式:
| $ {\sigma _{total}} = \left| {{\sigma _{shock}}} \right| + \left| {{\sigma _{work}}} \right|。$ | (4) |
式中:
最后,将综合应力与许用应力值比较,判断其是否满足抗冲击性能要求。
2 数值建模 2.1 几何模型以某型船用套筒式液压联轴器为研究对象,其结构组成主要包括外套、内套、活塞共3个部件。分别建立其三维几何模型,并根据装配关系建立套筒式液压联轴器装配体模型,如图1所示。
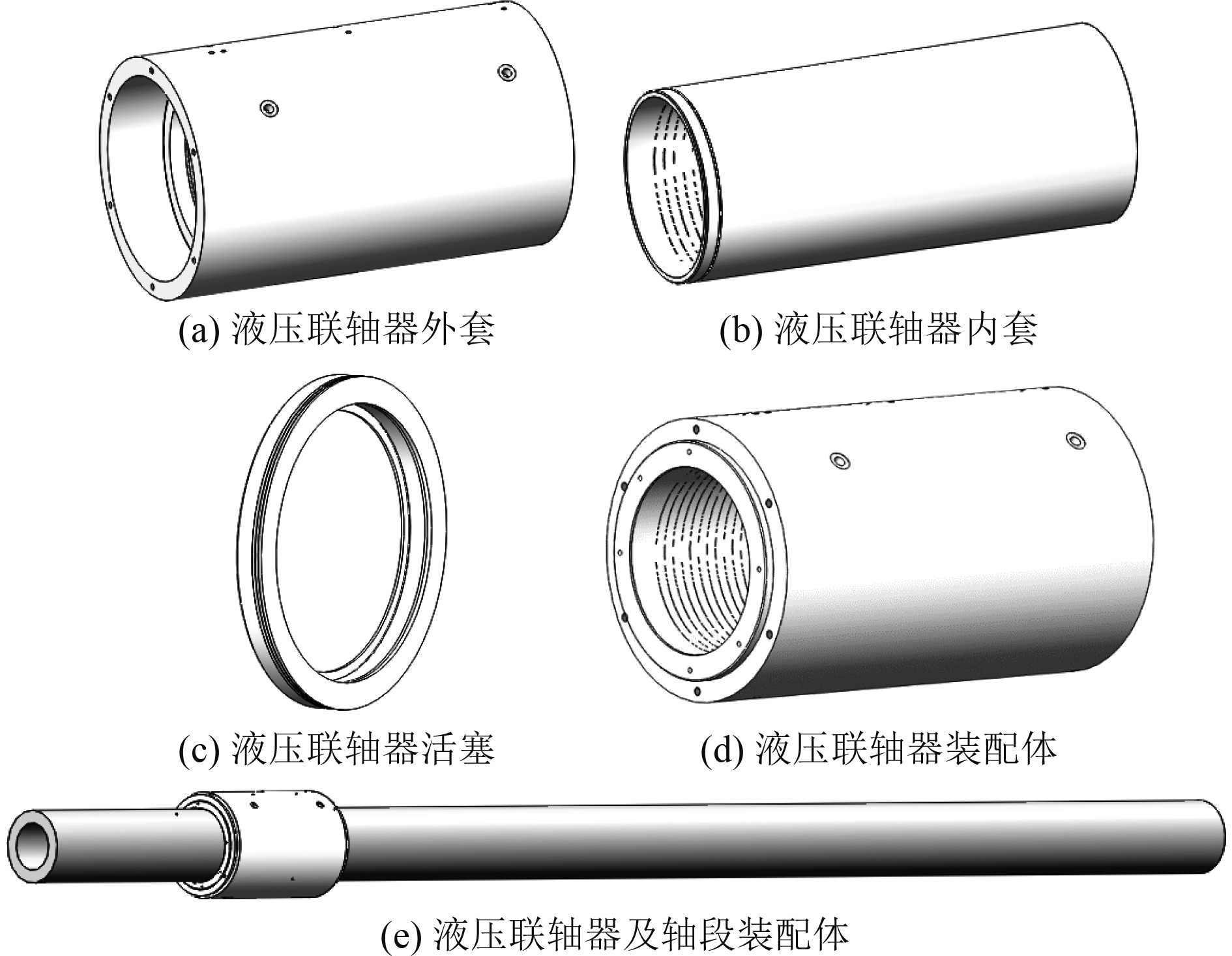
|
图 1 套筒式液压联轴器及轴段装配体几何模型 Fig. 1 Geometric model of sleeve hydraulic coupling and shaft assembly |
在进行计算网格划分前,首先进行几何模型的简化处理。在此基础上,对套筒式液压联轴器各部件进行网格划分采用六面体单元C3D8R进行网格划分并对内、外套和活塞等部件相互接触的关键部位网格进行合理加密。套筒式液压联轴器装配体网格信息如表1所示,网格模型如图2所示。
|
|
表 1 套筒式液压联轴器网格信息 Tab.1 Grid information of sleeve hydraulic coupling |

|
图 2 套筒式液压联轴器及轴段装配体三维网格模型 Fig. 2 Three dimensional mesh model of sleeve hydraulic coupling and shaft assembly |
套筒式液压联轴器各部件和轴段的材料属性参数如表2所示。
|
|
表 2 液压联轴器各部件材料属性 Tab.2 Material properties of components of hydraulic coupling |
基于DDAM法建立其抗冲击数值模型,边界条件设置如下:
1)由于DDAM抗冲击模型中不能考虑非线性因素,故将轴段、内套、外套及活塞等部件之间的接触面设置为接触绑定约束。
2)当考虑轴段固定时,将连接轴段的2个外端面设置为固定约束。完成模态分析后提取模态质量大于1%的频率,并按式(1)和式(2)计算得到相应的载荷谱,并以加速度形式输入计算模型。
3)当考虑轴段支撑位置油膜刚度影响时,将连接轴段两外端面的固定约束改为弹簧连接,并将连接弹簧的外部连接点固定,设置相应的弹簧刚度值。模态分析后计算载荷谱并施加到计算模型,载荷的提取与加载方法同上。
3 抗冲击性能根据GJB1060.1-1991规范要求,分别从垂向、横向、纵向对液压联轴器抗冲击性能进行校核。垂向冲击时,套筒式液压联轴器各部件应力分布如图3所示。
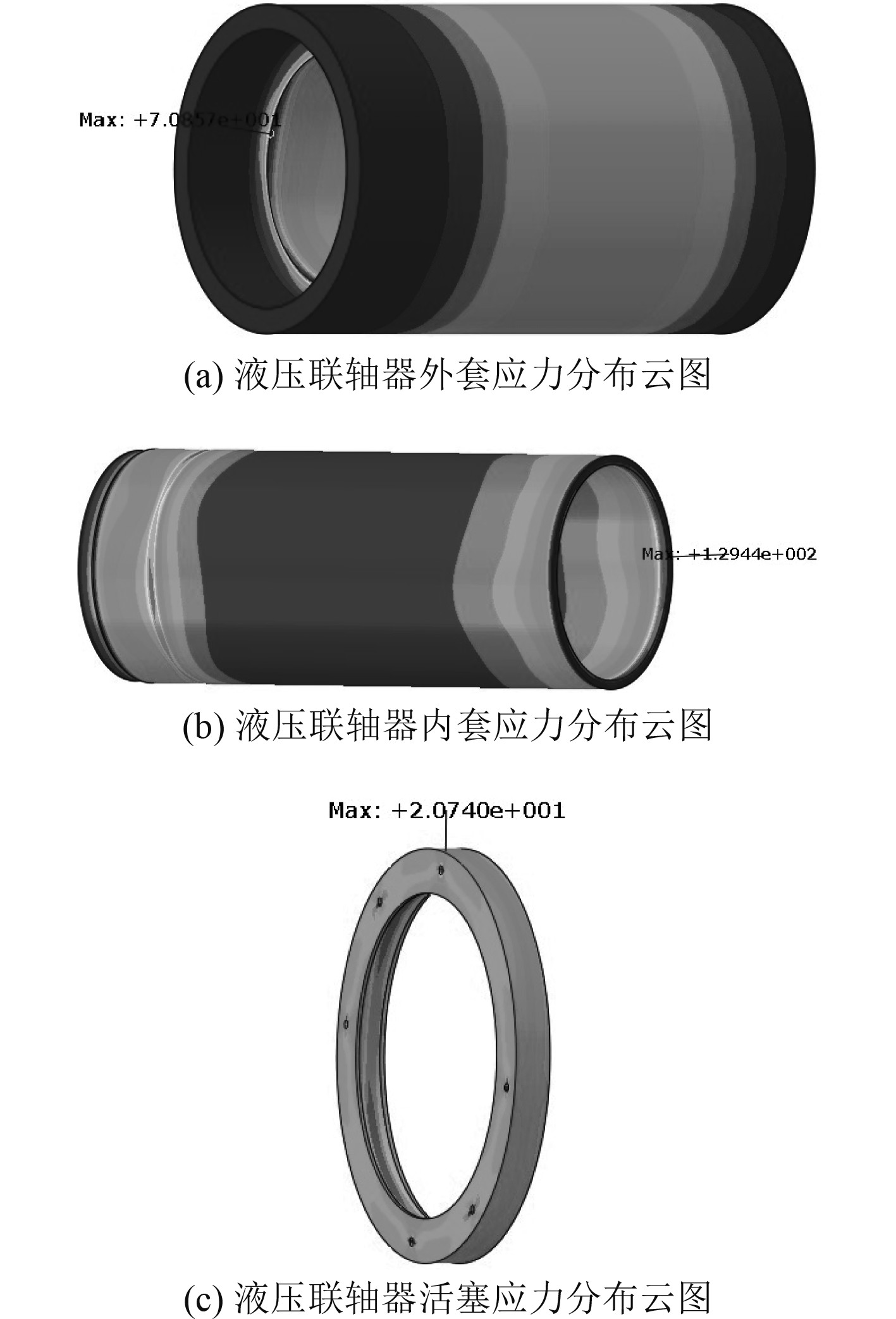
|
图 3 垂向冲击载荷作用下液压联轴器各部件应力分布云图 Fig. 3 Stress distribution of various components of hydraulic coupling under vertical impact load |
分别提取液压联轴器各部件在不同方向冲击载荷作用下的最大应力值,如图4所示。按GJB1060.1-1991规定,计算得到各方向的冲击应力后还需与最大负载工况时的应力按式(4)进行合成。不同方向冲击载荷作用下,套筒式液压联轴器各部件综合应力值如图5所示。
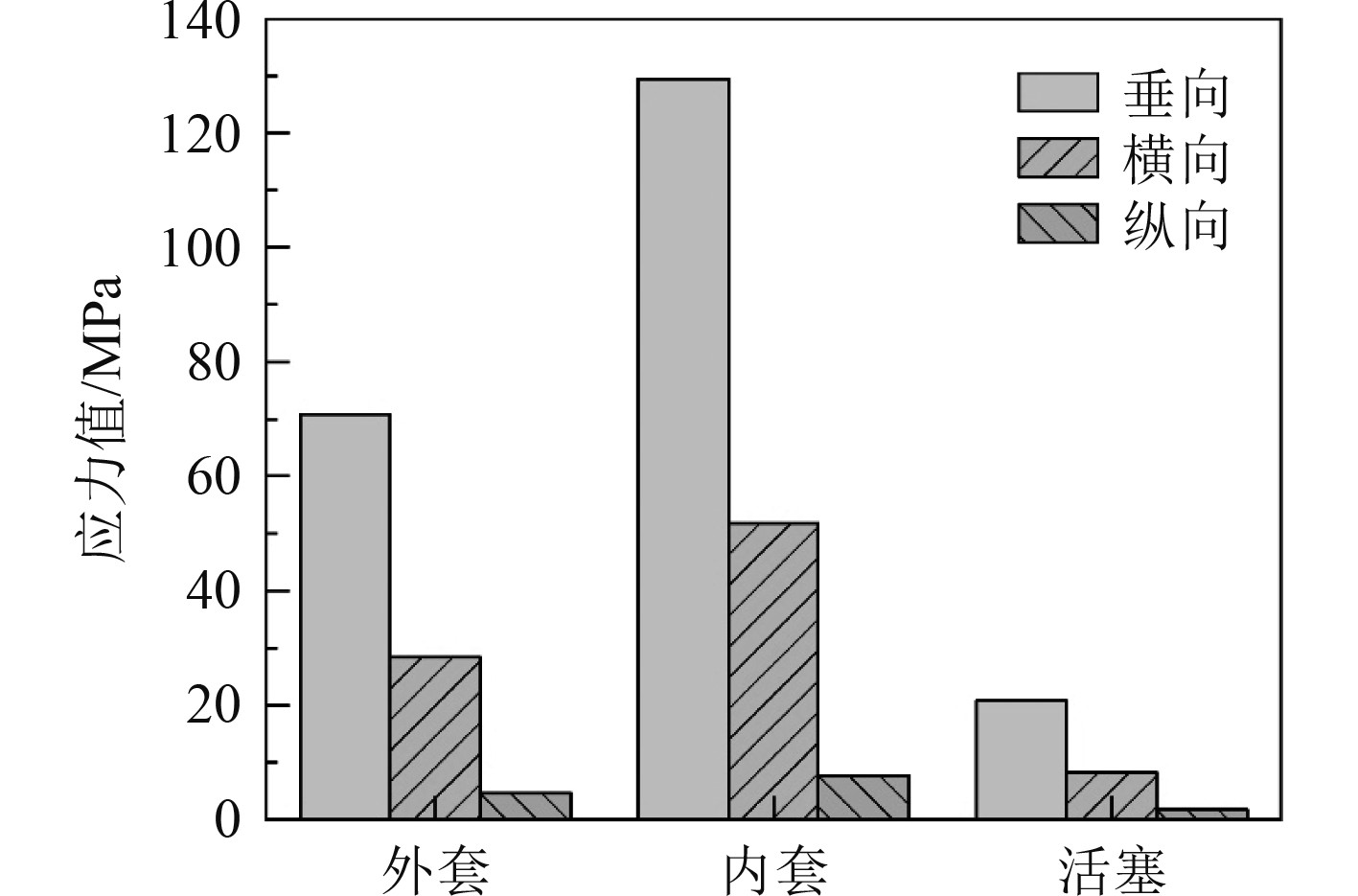
|
图 4 不同方向冲击载荷作用下液压联轴器各部件应力值 Fig. 4 Stress values of components of hydraulic coupling under different impact loads |
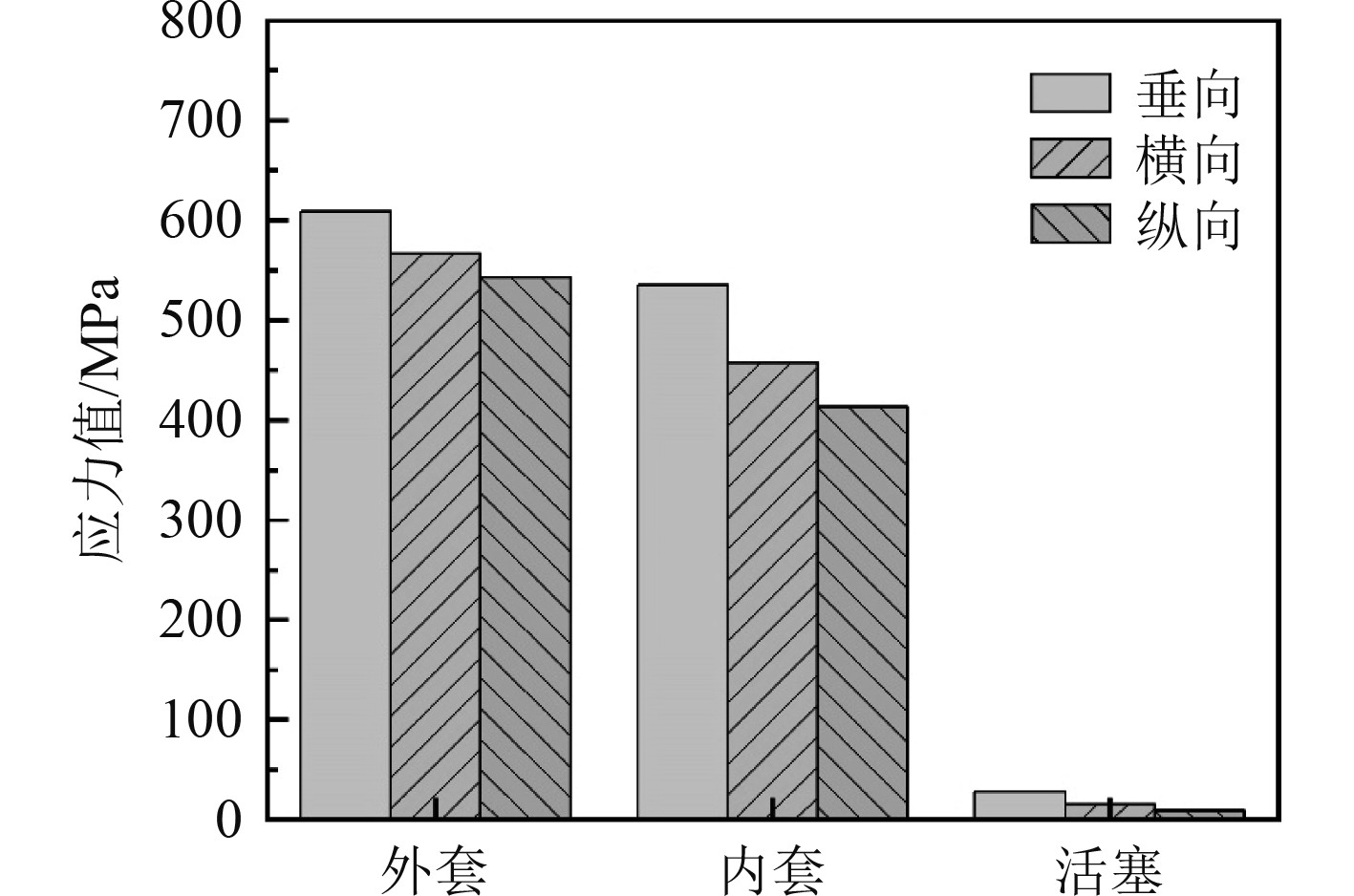
|
图 5 不同方向冲击载荷作用下液压联轴器各部件合成应力值 Fig. 5 Synthetic stress values of various components of hydraulic coupling under different impact loads |
通过对上述计算结果分析可知:
1)在不同方向冲击载荷作用下,液压联轴器各部件综合应力值均小于材料的屈服强度,满足抗冲击性能规定要求。
2)不同方向冲击载荷作用下,套筒式液压联轴器内套产生的冲击应力值均为最大。因此,内套是液压联轴器中对冲击载荷作用最敏感的部件,需重点关注。
3)在垂向冲击载荷作用下,套筒式液压联轴器各部件的最大应力值均大于另外2个方向的最大冲击应力。因此,与其余方向冲击载荷相比,垂向冲击载荷的影响最为恶劣。
4)液压联轴器外套最大应力出现在与内套接触面的后端;内套最大应力出现在与轴接触面的前端;活塞响应最小,最大应力出现在与内套连接的螺纹处。
4 抗冲击性能影响因素 4.1 影响因素设置根据液压联轴器安装特点,选取联轴器在轴段的相对布置位置D、连接轴段长径比L、轴段与联轴器重量比G及连接轴段端面约束方式M共4种影响因素。
1)相对布置位置D是一无量纲参数,以连接轴段左端面为基准,用于分析液压联轴器在两连接轴段相对布置位置对其抗冲击性能的影响。
2)轴段长径比L是一无量纲参数,表示液压联轴器两连接轴段总长度与轴段外径的比值。在保证轴段外径及总重量不变的前提下,通过改变轴段长度和密度,实现相同重量下不同的轴段长径比。
3)轴段与联轴器重量比G是一无量纲参数,表示液压联轴器两连接轴段总重量与联轴器总重量的比值。在不改变轴段结构参数的前提下,通过修改轴段材料的密度值实现重量比G的调节。
4)端面约束方式M,表示连接轴段两外端面的约束方式。当M为固支时,表示连接轴段两外端面施加固支边界条件。当M=1.00E+9时,表示连接轴段两外端面在垂向和横向方向上施加了弹簧约束,刚度为1.00E+9 N/m,弹簧外部端点自由度均被约束。因素M用于考虑支撑轴承刚度对液压联轴器抗冲击性能的影响。
上述影响因素分别选取了5种不同的取值,如表3所示。表中带有上标*的数据表示各影响因素用于对比的标准值。
|
|
表 3 影响因素取值表 Tab.3 Value table of influencing factors |
根据表3中各影响因素的取值,进行单因素影响分析,即以标准值为基础,每次只改变其中一个影响参数值进行垂向抗冲击校核,计算结果如表4所示。基于表中数据,可获得上述4种影响因素对套筒式液压联轴器抗冲击性能的影响变化规律,分别如图6~图9所示。
|
|
表 4 单因素对液压联轴器各部件在垂向冲击载荷下最大应力的影响 Tab.4 Influence of single factor on the maximum stress of each component of hydraulic coupling under vertical impact load |
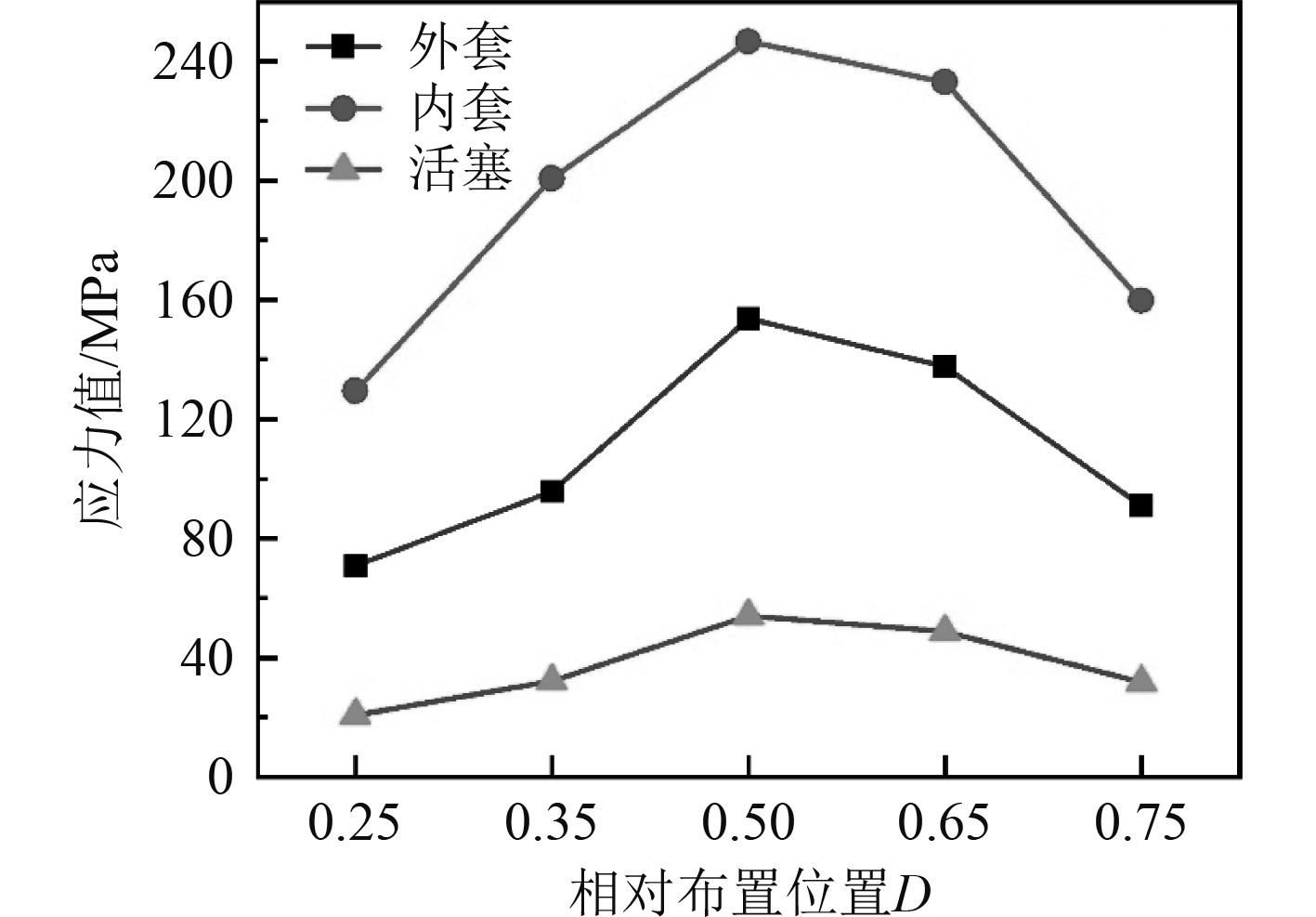
|
图 6 相对布置位置D对套筒式液压联轴器抗冲击性能的影响 Fig. 6 Influence of relative arrangement position D on impact resistance of sleeve hydraulic coupling |

|
图 7 轴段长径比L对套筒式液压联轴器抗冲击性能的影响 Fig. 7 Effect of shaft length diameter ratio L on impact resistance of sleeve hydraulic coupling |
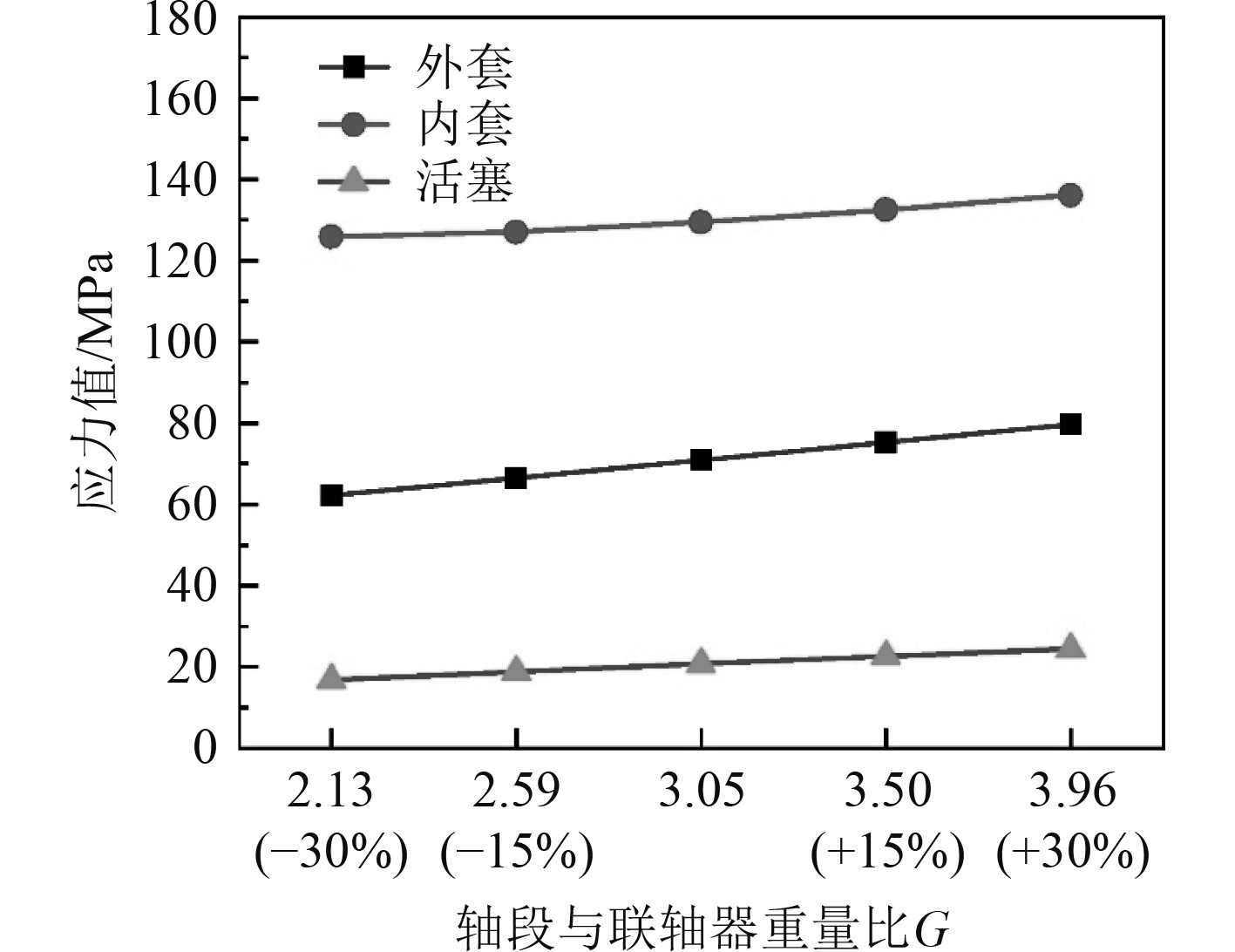
|
图 8 轴段与联轴器重量比G对套筒式液压联轴器抗冲击性能的影响 Fig. 8 Effect of weight ratio G of shaft to coupling on impact resistance of sleeve hydraulic coupling |
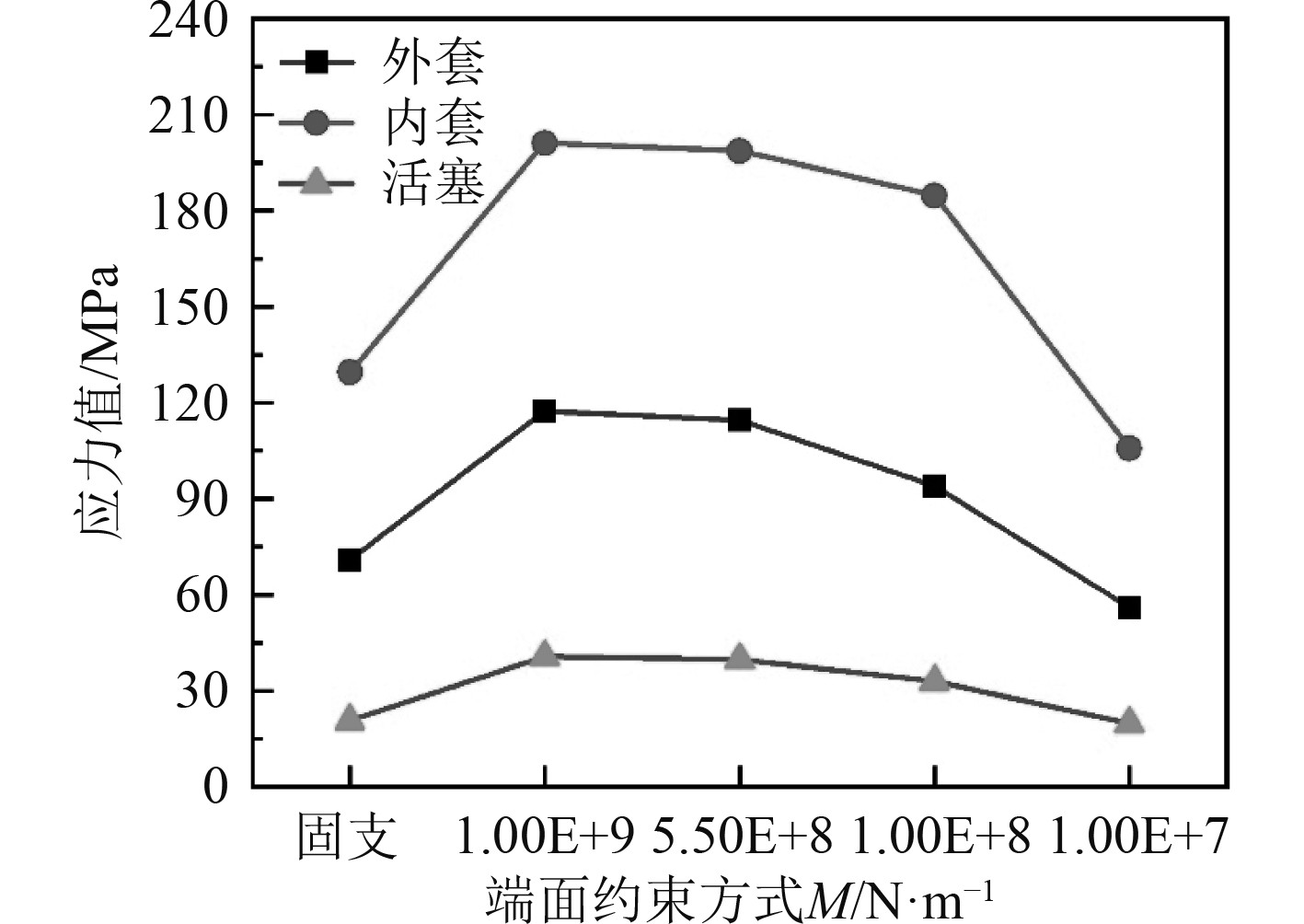
|
图 9 端面约束方式M对套筒式液压联轴器抗冲击性能的影响 Fig. 9 Influence of end face restraint mode M on impact resistance of sleeve hydraulic coupling |
通过对上述计算结果的对比分析,得到结论如下:
1)相对布置位置D对液压联轴器抗冲击性能影响较大。通过对应力分布对比可知,由于计算模型为长轴型,且两端固定,在冲击载荷作用下轴段中间位置处的变形量最大。受轴段变形影响,液压联轴器布置位置越靠近轴段中间位置,产生的冲击应力值越大。
2)在保持轴段总重量不变时,液压联轴器各部件最大冲击应力值在不同长径比L下存在一个最小值。其中,外套最大应力最小值出现在轴段长径比为18.60,内套最大应力最小值出现在长径比为21.40。
3)在不改变轴段几何结构参数的前提下,随轴段总重量增加,液压联轴器各部件最大冲击应力值也随之增大,且呈线性变化趋势。
4)考虑轴段端面约束条件M的影响时,当轴段两外端面采用弹簧约束时,液压联轴器各部件最大冲击应力值比采用固支约束的要大,且随着弹簧刚度减小,最大冲击应力值也随之下降。如图10所示,相对于固支约束边界,在施加弹簧约束边界条件后轴段最大应力出现的位置由轴段两外端面变为两轴段的中间位置。最大应力值由345.45 MPa减少到278.92 MPa,说明弹簧约束边界条件起到一定的缓冲吸能作用。与此同时,在轴段两外端面弹簧约束下轴段中间位置的变形量增大,导致液压联轴器各部件的应力值增加。随着弹簧刚度的减小,液压联轴器各部件的最大应力值也随之下降。

|
图 10 边界条件设置对模型冲击应力分布和大小的影响 Fig. 10 Influence of boundary conditions on the distribution and magnitude of impact stress in the model |
为探究上述影响因素对套筒式液压联轴器抗冲击性能的影响程度,采用正交试验法分析各影响因素对冲击应力值的贡献大小。设置的四因素三水平正交试验L9(34)如表5所示,为避免由于因素水平排序产生的极端情况,已将端面约束条件经过抽签随机化。
|
|
表 5 四因素三水平正交试验表 Tab.5 Four factors and three levels orthogonal test table |
由计算结果可知,液压联轴器各部件受到垂向冲击时响应最大,且所有部件中内套应力值最大,即破坏可能性最大,故以垂向冲击下内套的计算结果为例进行分析更具代表性。根据正交试验表计算得到的液压联轴器内套在垂向冲击载荷作用下的最大应力值如表6所示。其中,K1,K2,K3分别为各因素在各水平的结果累加值;U1,U2,U3分别为各因素各水平的结果均值;T为单因素在三水平均值间的结果极差,极差越大表明影响越大。
|
|
表 6 垂向冲击载荷作用下内套正交试验最大应力表 Tab.6 Maximum stress table of inner sleeve orthogonal test under vertical impact load |
通过正交试验分析可知,轴段端面约束方式M极差最大,即端面约束方式M对结果产生的影响最大,不仅由于固支与弹簧支撑2种约束形式差异大,弹簧刚度大小对联轴器冲击应力也会造成较大影响。轴段与联轴器重量比G影响次之,物体所受冲击力与物体的惯性联系紧密,说明模型质量是影响应力的主要原因之一。轴段长径比L的影响相对较小。同时,从上述分析结果可知,当处于D1,L2,G2,M3时液压联轴器内套的最大应力值最小。
5 结 语本文以某型套筒式液压联轴器为研究对象,基于DDAM法对其进行抗冲击性能分析。在此基础上,针对轴段布置位置D、轴段长径比L、轴段与联轴器重量比G以及轴段端面约束条件M开展了单因素影响分析,获得上述影响因素对联轴器抗冲击性能的影响规律。通过正交试验研究了上述因素的影响显著程度,得到结论如下:
1)在垂向冲击载荷作用下,液压联轴器各部件的冲击应力值最大。同时,在不同方向冲击载荷作用下,液压联轴器内套响应均最为剧烈。由于内套厚度较薄且开设环槽,设计时需特别注意其厚度控制。
2)液压联轴器在轴段相对布置位置对其抗冲击性能有较大影响。受轴段变形的影响,液压联轴器越靠近轴段中间位置,产生的冲击应力值越大。故在设计时应考虑其在轴段上的布置位置,尽量靠近轴承布置,减少其受到冲击时产生的应力。
3)轴段重量对液压联轴器的冲击应力结果有较大的影响。轴段重量越大,受冲击时联轴器各部件的冲击应力值越大,两者之间呈线性关系。
4)考虑轴段端面油膜刚度影响时,由于轴段中间位置变形量增加,液压联轴器各部件冲击应力值将增大。随着弹簧刚度减小,冲击应力随之降低。
5)轴段长度对液压联轴器的计算结果会产生一定的影响。轴段长度在一定范围内可使液压联轴器各部件应力值减小,但其影响不如前3种因素显著。
| [1] |
汪玉, 王官祥. 舰船系统和设备的抗冲击性能动力学仿真[J]. 计算机仿真, 1999, 16(1): 27-29. WANG Yu, WANG Guan-xiang. The dynamic simulation to the shock resistance proverty of ship system and equipment[J]. Computer Simulation, 1999, 16(1): 27-29. |
| [2] |
汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京: 科学出版社, 2005.
|
| [3] |
冯麟涵. 舰用增压锅炉抗冲击特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
| [4] |
张影. 船用齿轮箱抗冲击计算方法分析[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [5] |
计晨, 汪玉, 赵建华, 等. 舰用柴油机抗冲击性能频域分析[J]. 振动与冲击, 2010, 29(11): 171-176. JI Chen, WANG Yu, ZHAO Jian-hua, et al. Frequency domain analysis of marine diesel anti-shock capability[J]. Journal of Vibration and Shock, 2010, 29(11): 171-176. DOI:10.3969/j.issn.1000-3835.2010.11.037 |
| [6] |
计晨, 汪玉, 敖晨阳, 等. 舰用柴油机动态运行冲击响应分析[J]. 船舶工程, 2010, 32(4): 13-16. JI Chen, WANG Yu, AO Chen-yang, et al. Shock response analysis of marine diesel engine on dynamic operation[J] Ship Engineering, 2010, 32(4): 13-16. |
| [7] |
浦军, 石邦凯. 基于DDAM的某舰用升降装置抗冲击分析[J]. 舰船科学技术, 2017, 39(8): 128-132. PU Jun, SHI Bang-kai. Shock resistance analysis on certain ship lift based on DDAM[J]. Ship Science and Technology, 2017, 39(8): 128-132. DOI:10.3404/j.issn.1672-7649.2017.08.027 |
| [8] |
曹贻鹏, 费景州, 闫力奇, 等. 基于DDAM方法的船舶柴油机排气消声器抗冲击优化研究[J]. 舰船科学技术, 2018, 40(6): 67-72. CAO Yi-peng, FEI Jing-zhou, YAN Li-qi, et al. Shock resistance design of marine diesel silencer based on DDAM[J]. Ship Science and Technology, 2018, 40(6): 67-72. DOI:10.3404/j.issn.1672-7649.2018.06.014 |
| [9] |
吴晖, 周少伟. 法兰式液压联轴器抗冲击性能分析[J]. 舰船科学技术, 2015, 37(7): 38-42. WU Hui, ZHOU Shao-wei. Analysis of the anti-shock performance for flanged hydraulic coupling[J]. Ship Science and Technology, 2015, 37(7): 38-42. DOI:10.3404/j.issn.1672-7649.2015.07.009 |
| [10] |
GJB1060.1-91舰船环境条件要求-机械环境[S].
|
 2023, Vol. 45
2023, Vol. 45
