2. 上海船舶电子设备研究所,上海 201108
2. Shanghai Marine Electronic Equipment Research Institute, Shanghai 201108, China
螺旋桨辐射噪声是水面舰船和水下运动目标辐射噪声的重要组成部分。调制效应是螺旋桨辐射噪声重要的特性,通常被用于水声目标的被动检测和识别[1]。然而,通过水声设备获得的螺旋桨噪声信号通常包含干扰和噪声信号,且干扰和噪声信号在螺旋桨噪声信号各个频段的分布不同,使得螺旋桨噪声在不同频段具有不同的调制特性。因此开展螺旋桨分频段调制特性的提取研究,对于基于调制特征的水声目标被动检测和识别具有重要的意义。
针对螺旋桨噪声信号调制特征的有效提取问题,国内外学者展开了大量的研究。Lourens[2]和Lennartsson等[3]将噪声包络调制检测(detection of envelope modulation on noise, DEMON)算法用于舰船辐射噪声的检测与识别,提取得到了螺旋桨宽带噪声中的调制线谱,并反演得到了螺旋桨的几何参数。Kirsteins等[4]针对检测辐射噪声分频段调制的特点,提出了改进的DEMON算法,其基本思想是将各频段提取的调制线谱累加得到高信噪比DEMON谱。殷敬伟等[5]提出了基于DEMON线谱的轴频提取方法;程玉胜等[6]提出了船舶噪声DEMON谱质量评估方法;陈敬军等[7]分析了影响宽带幅度调制信号的检测因素。针对船舶螺旋桨噪声信号的循环平稳性质,Nikolaidis等[8]研究了船舶螺旋桨噪声信号的循环平稳随机振动特征;饶柏斌[9]利用循环谱理论研究了舰船辐射噪声弱调制特征提取方法。
目前针对船舶螺旋桨辐射噪声调制线谱提取尚存在以下问题:首先,基于高信噪比假设,忽略了舰船螺旋桨噪声存在分频段调制的特点。其次,针对分频段调制的问题,将各频段调制线谱直接累加,忽略了分频段调制能力存在强弱的问题。不同频段的调制线谱加权系数需进一步研究。
针对上述问题,提出基于循环调制谱分析(cyclic modulation spectrum,CMS)的船舶螺旋桨分频段调制特征提取方法,该方法使用循环平稳调制算法得到船舶螺旋桨噪声信号全频带调制谱。通过全频带调制谱判断调制线谱在各频带上的分布情况,基于循环调制谱熵得到分频段调制谱加权系数,提高信干比较强频带的加权系数,抑制噪声较多的频带。提升得到的DEMON谱信噪比,最终融合得到螺旋桨辐射噪声的调制谱。仿真和实测噪声信号验证了算法的有效性。
1 循环谱理论 1.1 循环功率谱与循环调制谱若二阶非平稳随机连续信号
| $ \left\{ \begin{gathered} {g_s}(t) = E[s(t)] = {g_s}(t + T),\\ {R_{ss}}(t,\tau ) = E[s(t){s^ * }(\tau )] = {R_{ss}}(t + T,\tau + T) ,\\ \end{gathered} \right. $ | (1) |
则称其为广义周期平稳信号。非平稳随机连续信号
| $ {R_{ss}}(t,\tau ) = E[s(t + \tau /2){s^ * }(t - \tau /2)] 。$ | (2) |
自相关函数
| $ {R_{ss}}(t + \tau /2,t - \tau /2) = \sum\limits_\alpha {R_{ss}^\alpha (\tau ){e^{i2{\text{π}} \alpha t}}}。$ | (3) |
其中,傅里叶系数
| $ R_{ss}^\alpha (\tau ) = \frac{1}{T}{\int\limits}_{ - T/2}^{T/2} {{R_{ss}}(t + \tau /2,t - \tau /2){e^{ - i2{\text{π}} \alpha t}}} {\rm{d}}t。$ | (4) |
其中,
| $ R_{ff}^\alpha (\tau ) = R_{ss}^\alpha (\tau ){e^{i2{\text{π}} \alpha {t_0}}}。$ | (5) |
式中,
| $ R_{ss}^\alpha (f) = {\int\limits}_{ - \infty }^\infty {R_{ss}^\alpha (\tau ){e^{ - i2{\text{π}} f{\text{ }}t}}} {\rm{d}}\tau。$ | (6) |
在实际信号处理过程中,循环功率谱估计计算成本较高。为了提高循环谱估计效率,Antoni等[10]基于傅里叶变换跟踪频带中的周期能量思想提出了循环调制谱理论,通过对信号做2次DFT即可得到循环调制谱。循环调制谱(cyclic modulation spectrum,CMS)典型的处理过程为:首先对离散信号
| $ {Spec} (n,f) = {\left| {{\rm{STFT}}(n,f)} \right|^2} = {\left| {\sum\limits_{m = 0}^{N - 1} {\omega (m)x(n + m){e^{ - i2{\text{π}} fm/N}}} } \right|^2} 。$ | (7) |
其中:
| $ \begin{aligned} CMS(\alpha ,f,{X_{0,L}}) = & {\rm{DFT}}(Spec(n,f)) =\\ & \sum\limits_0^{K - 1} {Spec(n,f){e^{ - i2{\text{π}} n\alpha /K}}} 。\end{aligned}$ | (8) |
式中,
螺旋桨噪声是船舶辐射噪声的组成部分,也是船舶辐射噪声具有循环平稳特性的重要原因。船舶辐射噪声的一般模型记为:
| $ p(t)=[1+h(t)]\cdot s(t)+n(t) 。$ | (9) |
其中,
| $ {g_p}(t) = E[p(t)] = {g_s}(t)[1 + h(t)] + {g_n}(t),$ | (10) |
| $ \begin{aligned} {R_p}(t,\tau ) = & E[p(t)p(t + t)] = \\&p(t)p(t + t){R_p}(t) + p(t)({R_s}(t) + {g_s}(t){g_n}(t)) +\\ & p(t + t)({R_s}(t) + {g_s}(t){g_n}(t)) + 2{g_s}(t){g_n}(t) + {R_n}(t) 。\end{aligned} $ | (11) |
其中:
船舶螺旋桨辐射噪声是典型的宽带噪声,调制线谱对不同频段信号的调制能力不同,需分频段解调融合处理得到全频段调制谱。循环调制谱分析方法可以得到船舶螺旋桨噪声不同频段上的调制线谱分布,为此提出基于循环调制谱熵的分频段调制线谱融合方法。对于接收的螺旋桨辐射噪声信号
| $ {g_\alpha }[f] = \frac{{R_s^\alpha [f]}}{{\sum\limits_{\alpha = 1}^W {R_s^\alpha [f]} }} 。$ | (12) |
定义循环调制谱熵为:
| $ F[f] = - \sum\limits_{\alpha = 1}^W {{g_\alpha }[f]} \cdot \log ({g_\alpha }[f]) 。$ | (13) |
循环调制谱熵能够表征调制线谱对分频段信号的调制能力。当循环调制谱熵值较大时,说明该频段噪声信号强,调制线谱的调制能力弱;当循环调制谱熵值较小时,说明调制线谱在该频段调制能力强。基于循环调制谱熵值给出分频段调制谱融合加权值,具体步骤如下:
1)循环调制谱熵
2)对循环调制谱熵值取倒数,得到循环调制谱质量系数
3)计算得到高斯噪声循环调制谱熵值
4)对步骤3得到的分频段调制谱加权系数归一化处理,得到分频段调制谱归一化加权系数:
| $ \overline \chi [f] = \frac{{\chi [f] - \min (\chi [f])}}{{\max (\chi [f]) - \min (\chi [f])}} 。$ | (14) |
通过仿真试验,验证基于循环谱的分频段调制谱融合算法提取信号调制谱的能力。仿真参数如表1所示。
|
|
表 1 仿真试验参数 Tab.1 Simulation test parameters |
对仿真信号添加高斯白噪声使其信噪比为0 dB,仿真得到的时域信号波形如图1(a)所示,仿真信号的循环调制谱如图1(b)所示。其中横轴为循环调制频率,即对螺旋桨辐射噪声起调制作用的调制线谱,纵轴为螺旋桨噪声信号的谱频率,表示螺旋桨噪声信号频段分布。可以看出,设置的调制线谱均出现在循环调制谱中。全频段调制处理得到的调制谱如图1(c)所示,为了方便显示,调制频率显示区间设置为[0,100 Hz]。可以看出,设置的调制线谱除10 Hz以外,均被淹没在噪声频率中。采用循环调制谱熵的分频段调制谱融合算法,得到的分频段融合调制谱如图1(d)所示,可以看出,设置的调制线谱均被清晰地提取出来,验证了本文算法的有效性。

|
图 1 仿真信号循环谱处理结果 Fig. 1 Simulation signal cycle spectrum processing results |
利用空泡水筒中测试得到的螺旋桨噪声,验证本文算法的有效性。空泡水筒试验段的体积为3.2 m×0.8 m×0.8 m, 侧壁安置有体积为1 m×0.6 m×0.6 m的水声测量消声舱。
由于空泡水筒噪声测试空间狭小,混响严重,导致测试螺旋桨噪声信噪比较低。因螺旋桨低频调制线谱对全频带噪声存在调制效应,可通过对空泡水筒截止频率外的信号处理得到其调制谱。对螺旋桨转速为600 r/min时测量的噪声信号进行循环调制分析,如图2所示空泡水筒螺旋桨辐射噪声循环谱处理结果。
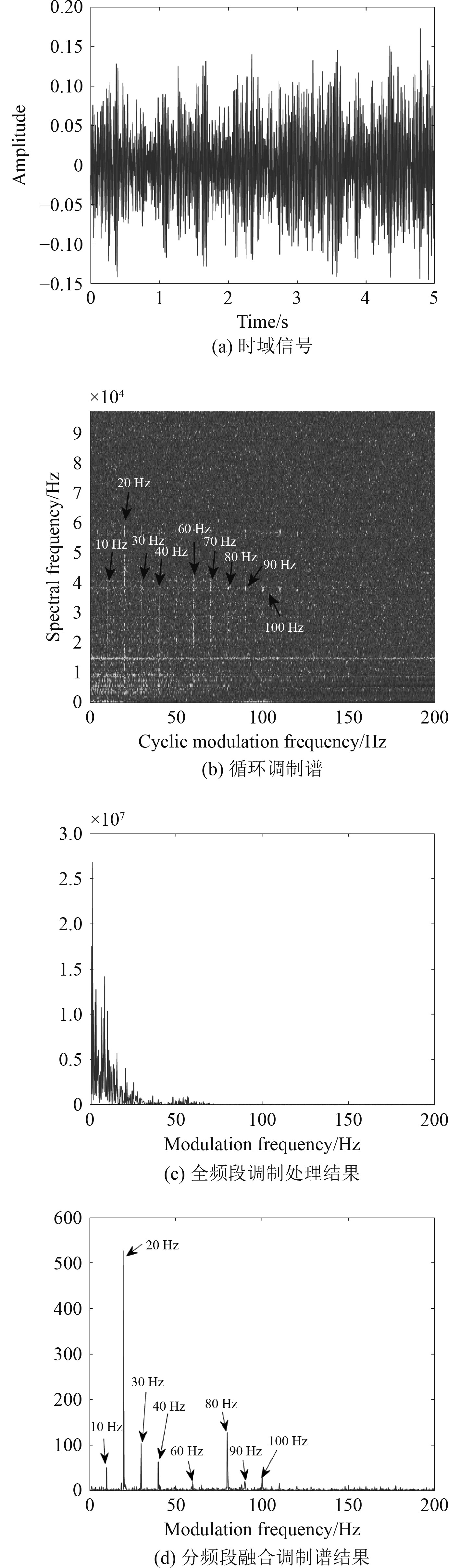
|
图 2 空泡水筒螺旋桨辐射噪声循环谱处理结果 Fig. 2 Results of cyclic spectrum of cavitation tunnel propeller radiated noise |
其中,螺旋桨噪声时域信号如图2(a)所示。螺旋桨噪声时,域信号通过循环谱方法处理得到的循环调制谱如图2(b)所示,可以看出,10 Hz轴频及其谐波和40 Hz叶频及其谐波均对螺旋桨噪声具有调制效应。但不同的调制线谱对螺旋桨噪声调制效应的作用频段不一样,10 Hz调制线谱对20~80 kHz的噪声均具备较强调制能力,而40 Hz调制线谱作用频段为5~40 kHz。利用常规DEMON处理方法进行全频段调制处理得到的结果如图2(c)所示,可以看出,图2(b)中的典型调制线谱均没有被检测出来。基于循环调制谱熵的分频段融合调制谱结果如图2(d)所示,可以看出本文算法的有效性。
3.2 实测舰船辐射噪声该辐射噪声为公开数据集[11],测试目标为marDeCangas船舶。数据采样率为52734 Hz,处理数据长度为60 s,循环谱分辨率为0.05 Hz,频谱分辨率为50 Hz。处理结果如图3所示。
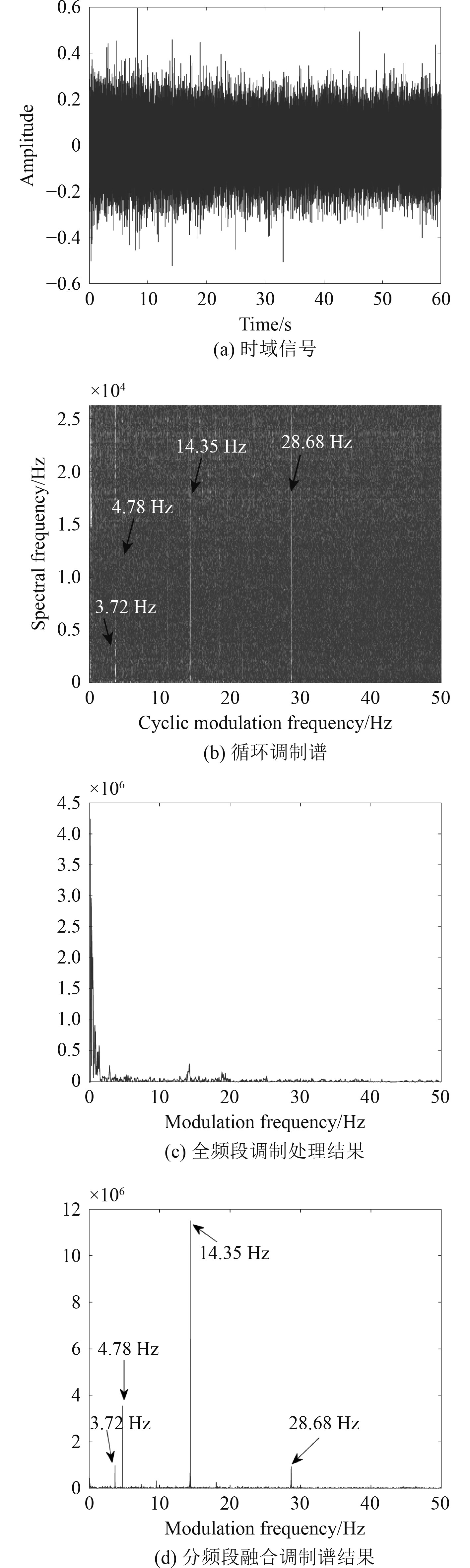
|
图 3 实测船舶辐射噪声循环谱处理结果 Fig. 3 Experimental results of cyclic spectrum processing of ship radiated noise |
实测船舶辐射噪声循环谱处理结果如图3所示。其中图3(a)为实测船舶噪声时域信号,图3(b)为通过循环谱方法处理得到的实测船舶辐射噪声循环调制谱,可以看出,3.72 Hz,4.78 Hz,14.35 Hz及28.68 Hz线谱对螺旋桨噪声具有调制效应,且不同的调制线谱对螺旋桨噪声调制效应的作用频段不一样。3.72 Hz调制线谱对0~2 kHz的信号均具备较强调制能力,4.78 Hz调制线谱作用频段为0~13 kHz,14.35 Hz调制线谱对0~18 kHz的信号均具备较强调制能力,28.68 Hz调制线谱对全频段具有调制效应。利用常规DEMON处理方法进行全频段调制处理得到的结果,如图3(c)所示。可以看出,图3(b)中的典型调制线谱均没有被检测出来。基于循环调制谱熵的分频段融合调制谱结果,如图3(d)所示,可以看出,典型调制线谱被提取出来,验证了本文算法的有效性。
4 结 语1)船舶螺旋桨辐射噪声具有循环平稳特性,调制线谱对不同频段内的噪声信号具有不同的调制能力,不同频段内调制谱融合处理有利于调制谱提取。
2)基于循环调制谱熵建立分频段调制谱融合加权系数,避免人工设置加权系数带来的影响,提升调制谱提取质量。
3)通过仿真试验、空泡水筒试验及海试试验数据,对所提出的基于调制谱熵分频段加权融合调制谱提取方法进行了验证。结果表明,船舶螺旋桨不同频段内的调制线谱均被有效提取,分频段加权融合处理的结果优于全频段调制处理结果。
| [1] |
孙焱. 被动目标分频段调制特征提取方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
| [2] |
LOURENS J G. Classification of ships using underwater radiated noise[C]// Southern African Conference on Communications and Signal Processing. Proceedings(IEEE COMSIG 88) Pretoria, South Africa. 1988: 130–134.
|
| [3] |
LENNARTSSON R K, ROBINSON J W C, PERSSON L, et al. Passive sonar signature estimation using bispectral techniques[C]//Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing (Cat. No. 00TH8496). IEEE, 2000: 281–285.
|
| [4] |
CLARK P, KIRSTEINS I, ATLAS L. Multiband analysis for colored amplitude-modulated ship noise[C]//2010 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2010: 3970–3973.
|
| [5] |
殷敬伟, 惠俊英, 姚直象, 等. 基于DEMON 线谱的轴频提取方法研究[J]. 应用声学, 2005, (6): 369-374. |
| [6] |
邱家兴, 程玉胜, 张惊丞. 船舶噪声DEMON 谱质量评估方法[J]. 舰船科学技术, 2014, 36(9): 46-49. |
| [7] |
陈敬军, 陆佶人, 孟昭文. 影响宽带幅度调制信号检测的因素分析[J]. 声学学报, 2005, (4): 373-378. |
| [8] |
JHA A, NIKOLAIDIS E, GANGADHARAN S. Cyclostationary random vibration of a ship propeller[J]. Journal of Ship Research, 2003, 47(4): 299-312. DOI:10.5957/jsr.2003.47.4.299 |
| [9] |
饶柏斌. 舰船辐射噪声弱调制特征提取方法[D]. 南京: 东南大学. 2019.
|
| [10] |
ANTONI J, HANSON D. Detection of surface ships from interception of cyclostationary signature with the cyclic modulation coherence[J]. IEEE Journal of Oceanic Engineering, 2012, 37(3): 478-493. DOI:10.1109/JOE.2012.2195852 |
| [11] |
SANTOS-DOMÍNGUEZ D, TORRES-GUIJARRO S, CARDENAL-LÓPEZ A, et al. Ships Ear: An underwater vessel noise database[J]. Applied Acoustics, 2016, 113: 64-69. DOI:10.1016/j.apacoust.2016.06.008 |
 2023, Vol. 45
2023, Vol. 45
