2. 浙江工业大学 土木工程学院,浙江 杭州 310023
2. School of Civil Engineering, Zhejiang University of Technology, Hangzhou 310023, China
近年来,单调载荷作用下加筋板、船体梁的试验已有较多的研究成果[1-5] ,但对于交变的加载形式即循环载荷作用下的试验却很少。船体梁在波浪中承受中拱与中垂交变弯矩的作用,如果超过弹性范围,会产生塑性应变,最终影响船舶的极限承载力大小[6],导致加筋板承受平面内交变的轴向压缩与拉伸。Fujita等[7]对“尾道丸”号船的海损事故进行分析,提出了递增塑性破坏的船体梁破坏新型式。
对于循环载荷作用下加筋板的极限强度研究,主要集中在理论解析法、有限元法等方面。崔虎威等[8]通过4个扶强材疏密程度不同和材质不同的箱型梁在循环载荷作用下的试验,对其极限承载力进行研究。黄震球等[9]对一系列纵向加强筋的箱型薄壁梁模型进行循环加载下的极限强度试验,观察加强筋在循环加载下的递增塑性破坏。
加筋板是船体结构的基本形式,扶强材(含带板)常作为加筋板分析和船体梁极限承载力的逐步迭代法基本单元。对于扶强材在循环载荷作用下的理论分析和有限元分析已有涉及,许俊等[10]通过有限元分析软件对加筋板在循环载荷混合作用下的极限强度进行研究,分析循环应变幅混合作用对极限承载性能的影响。孟志光等[11]提出了一种考虑扶强材在轴向循环荷载作用下的损伤累积力学模型,通过Visual Basic程序编制计算程序,程序计算结果能与有限元计算结果较好吻合。但扶强材在循环载荷作用下的试验几乎是空白。
为了验证扶强材在循环载荷作用下的极限强度计算方法和结果,本文设计了7个扶强材(含带板)试件,进行循环载荷作用下的扶强材(含带板)极限承载能力试验,初步获得了扶强材在循环载荷作用下的屈曲特性,可为循环载荷作用下船体梁极限承载力的逐步迭代法奠定基础。
1 循环载荷作用下扶墙材极限承载力试验 1.1 试验材料及试件试验材料为Q235B,所用钢材的性能参数取自同批钢材所加工的拉伸试件共6个,通过材料拉伸试验获得,材料拉伸试件尺寸及性能参数如表1所示。
|
|
表 1 材料性能参数 Tab.1 Material performance parameters |
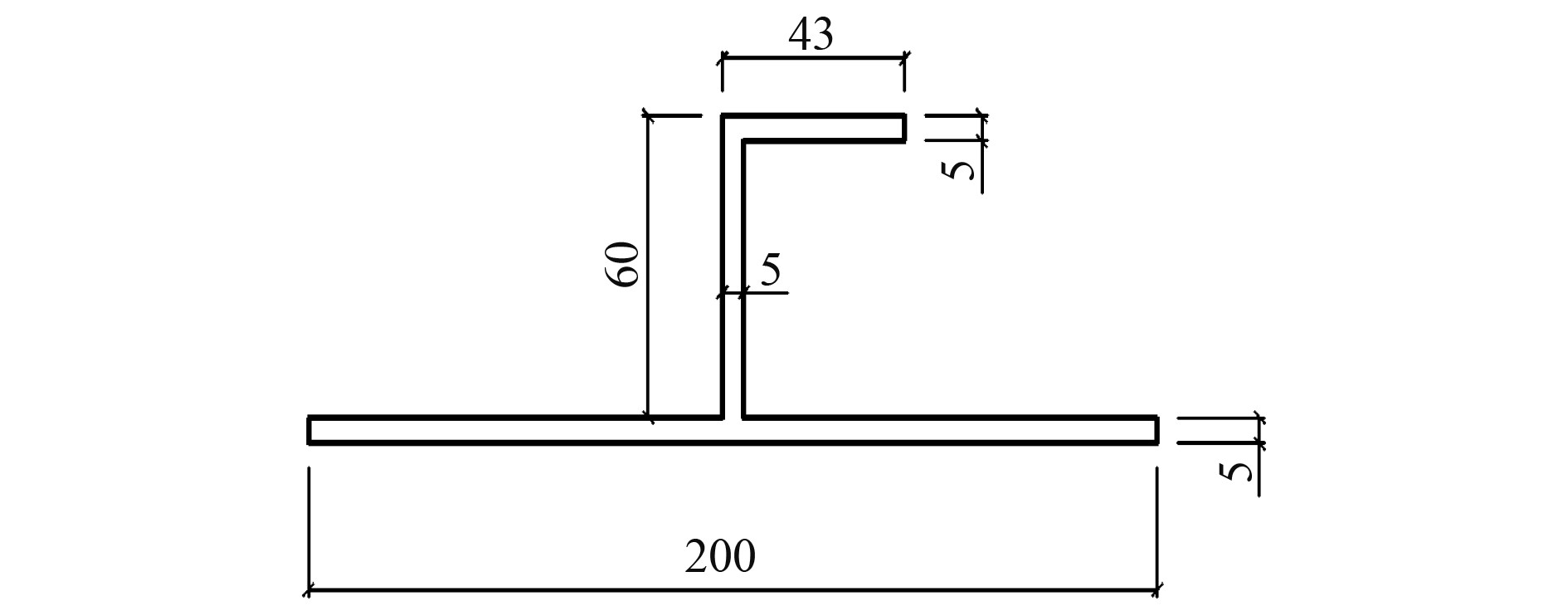
考虑到循环载荷模式对扶墙材极限承载性能的影响,本次试验共包含7个试件。试件横截面示意图如图1所示,各试件的具体尺寸、材料属性参数等如表2所示。
|
图 1 试件横截面示意图 Fig. 1 Schematic diagram of specimen cross section |
|
|
表 2 模型实际尺寸 Tab.2 Actual size of model |
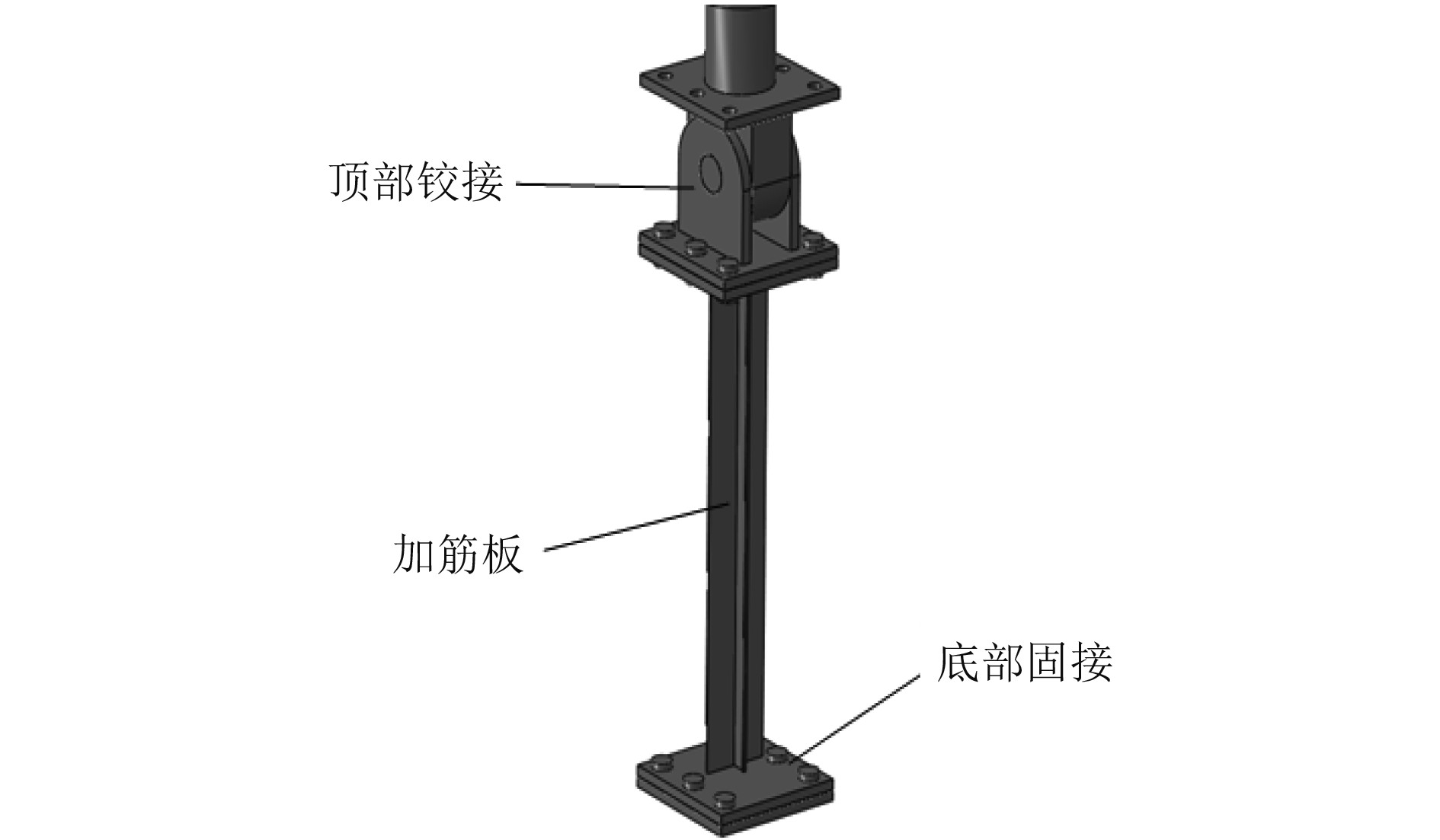
加载装置及分析系统采用静力电液伺服加载系统。扶强材试件两端分别焊接在两块端板上,端板与扶强材试件形心重合,形成整体试件。作动器加载头外力由端板平均作用于加筋板截面上,整体试件两端由螺栓固定于反力钢架与作动器之间。试件顶部作动器加载头为铰接,试件底部与反力钢架形成固接。扶强材试件试验装配形式如图2所示。
|
图 2 扶强材试件试验装配图 Fig. 2 Assembly drawing of stiffener specimen test |
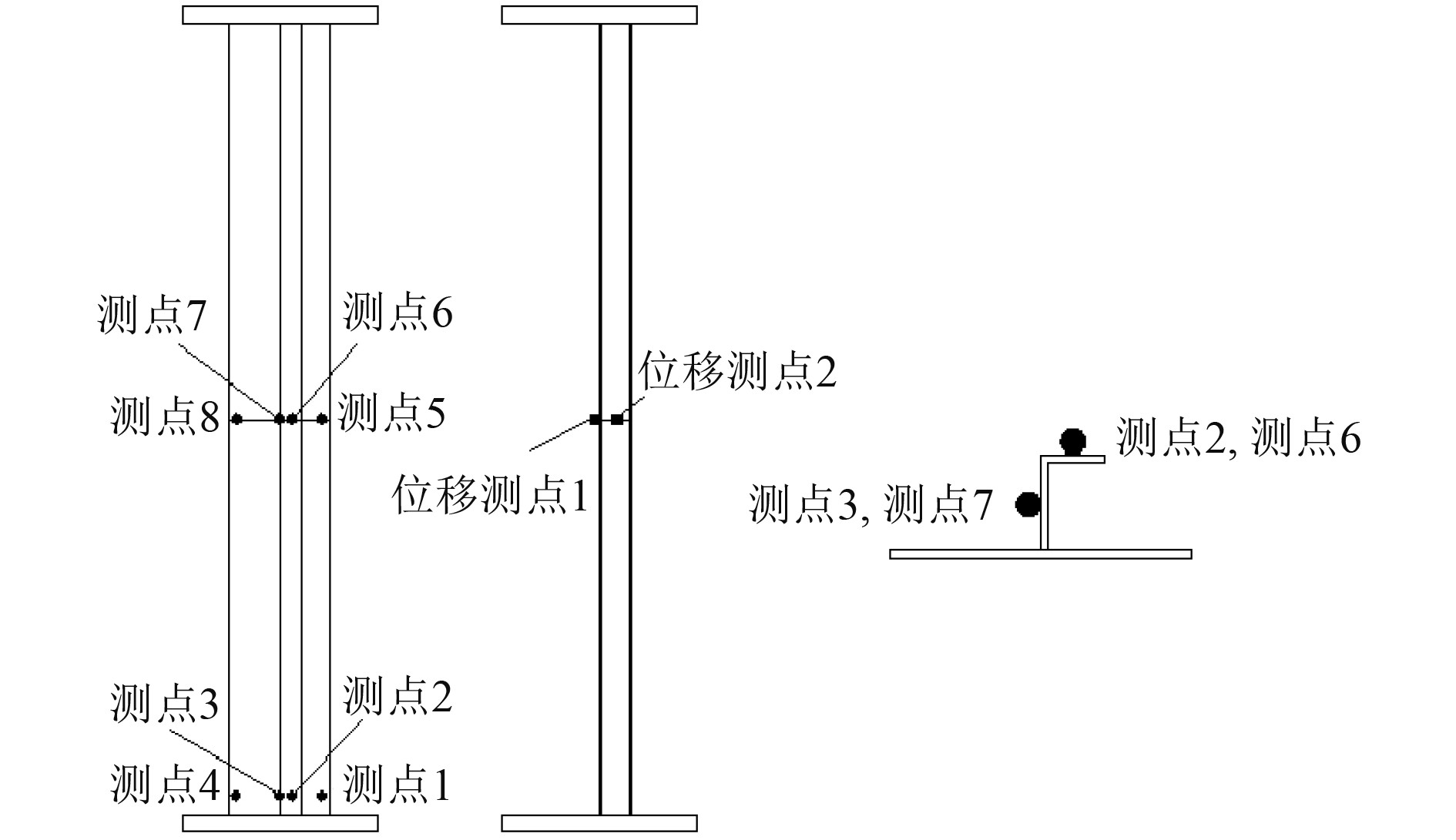
采用2台位移计与1台16通道应变仪进行数据测量。加筋板共8个应变测点和2个位移测点,测点位置图如图3所示。其中应变测点以测点1~测点8表示,位移测点以位移测点1、测点2表示。2个位移测点中,位移测点1监测试件中间位置的侧向位移,位移测点2监测加强筋角钢的侧向位移
|
图 3 试验测点布置图 Fig. 3 Layout of test measuring points |
为了得到试件的极限承载力,加载系统选取位移控制形式进行试验。为保证试件在多次轴向加载与卸载过程中不发生过度变形与整体失稳,采用如下加载步骤:
步骤1 预加载,施加2 kN的初始轴向压力,进行应变仪、位移计的调整,检查测量电脑的数据采集是否正常。
步骤2 正式加载,作动器先下压至目标位移,到达目标位移后,保持作动器位移固定不变,记录当前的载荷与位移数据。通过力控制将载荷卸载至“0”,进行下一步反向拉伸,作动器拉伸至目标位移后保持作动器位移固定不变,记录当前的载荷与位移数据。再次将载荷卸载至“0”,即完成一个循环加载。试验包含3种加载机制:
1)加载机制Ⅰ采用单调加压的形式,直至试件破坏。
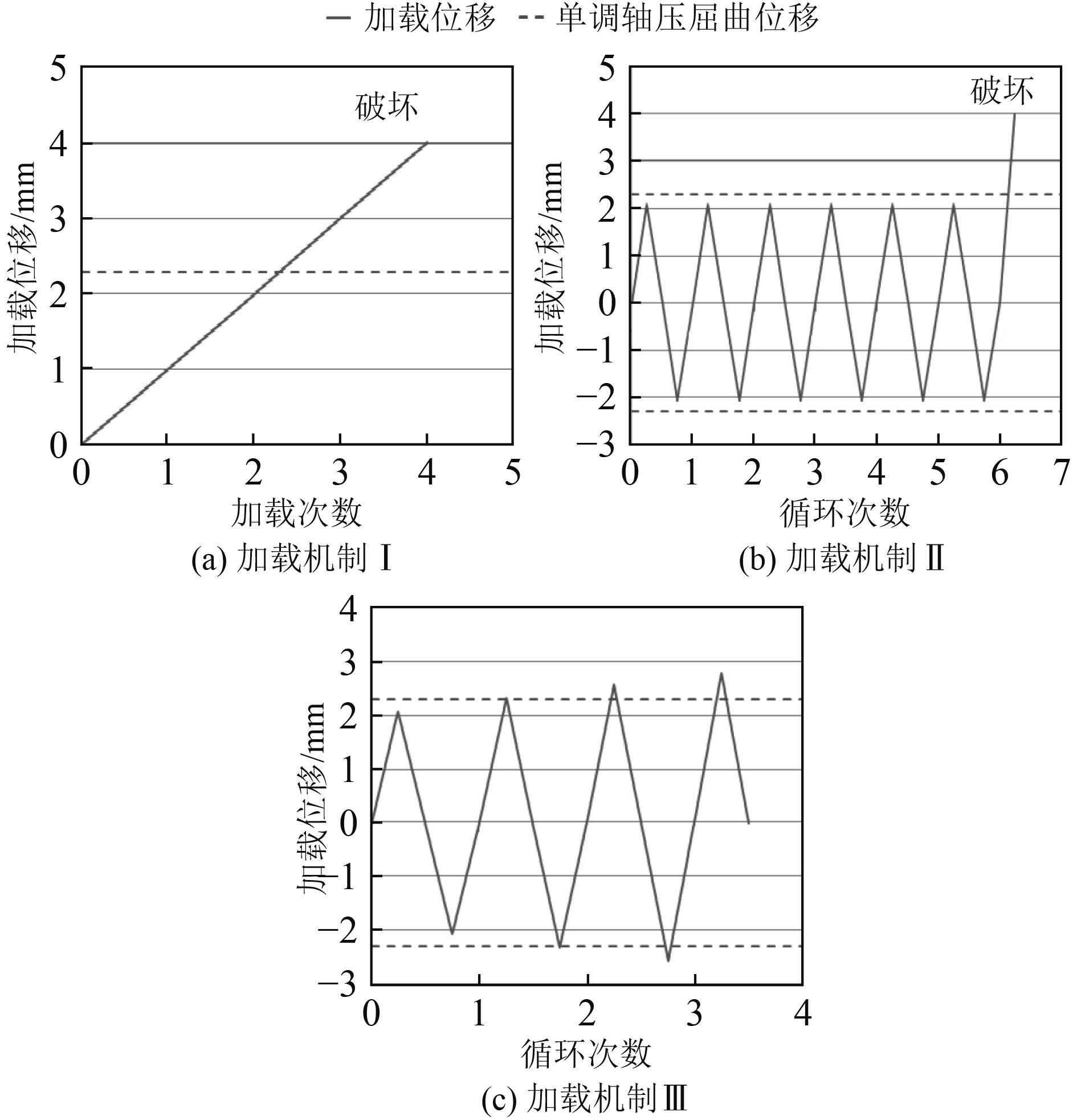
2)加载机制Ⅱ采用屈曲前等幅循环加载。在接近单调轴压屈曲位移前,在0.9倍单调轴压屈曲位移处循环6次,单调压载至试件破坏。
3)加载机制Ⅲ采用屈曲后循环加载。在单调轴压屈曲位移前,按0.9倍单调轴压屈曲位移循环1次加载至单调轴压屈曲循环1次。然后按0.1倍单调轴压屈曲位移分两级递增,每级循环1次,加载至1.2倍单调轴压屈曲位移后卸载,结束循环。
具体加载机制如图4所示,其中规定试件受压为正,受拉为负。
|
图 4 加载机制示意图 Fig. 4 Schematic diagram of loading mechanism |
本次试验共有7个试件,系列扶强材试件的加载形式按照3种加载机制进行。
3.1 变形及失效形式在加载机制Ⅰ作用下,各试件带板先出现局部屈曲,随压力增加,试件出现失稳趋势,直至整体失稳产生面外弯曲。
在加载机制Ⅱ加载过程中,随压力逐步增加,各试件底部或顶部带板出现局部屈曲,在接近试件屈曲位移处多次循环后,局部屈曲处位移随循环次数增加而增加,即使反向拉伸能抵消上一次循环产生的部分局部屈曲,但局部屈曲处位移总体仍为上升趋势。
在加载机制Ⅲ加载时,由于已超过试件屈曲位移,每次循环承载力较上一次循环结果下降明显,各试件失效模式基本为整体失稳,同时角钢两端部出现侧向位移。
3.2 应力应变曲线采用相对应力应变,根据试验结果,各试件相对应力应变曲线如图5所示。图中横坐标为相对应变
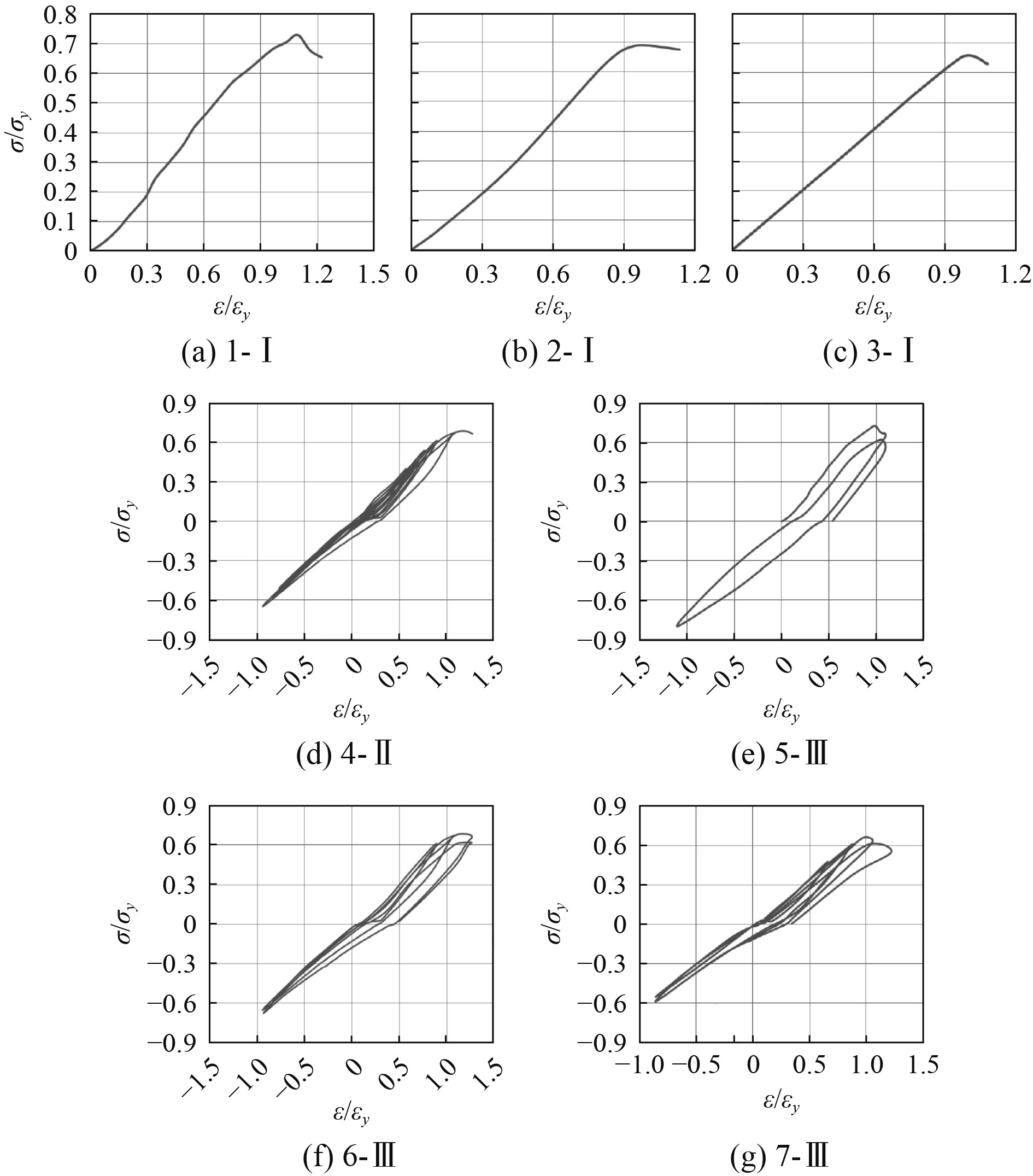
|
图 5 试验试件相对应力应变曲线图 Fig. 5 Relative stress-strain curve of test specimen |
| $ \varepsilon = {l_1}/{l_2} ,$ | (1) |
| $ \sigma = F/A 。$ | (2) |
其中:
由于3种加载机制的变形及破坏模式基本一致,且加载机制Ⅰ仅作为循环载荷试验的对照组,因此挑选4-Ⅱ试件为例进行分析。根据试验试件应变仪及位移计所采集的数据,在加载机制Ⅱ作用下试件4-Ⅱ局部屈曲处存在位移累计,位移值随循环压加载次数增加呈上升趋势,反向拉伸能抵消部分屈曲位移,但不影响屈曲处位移的上升趋势。应变测点中,带板同一垂直方向测点1与测点5对比,角钢同一垂直方向测点3与测点7对比可知,测点处应变随循环压载次数增加,在负方向即拉伸应变方向呈上升趋势。试件底部测点数值较试件中部测点数值变化大,原因是测点处已经产生局部屈曲,试件底部局部屈曲变形量大于试件中部,屈曲处存在位移累积。4-Ⅱ试件局部屈曲位移及应变如图6所示,各试件的最大承载力汇总如表3所示。
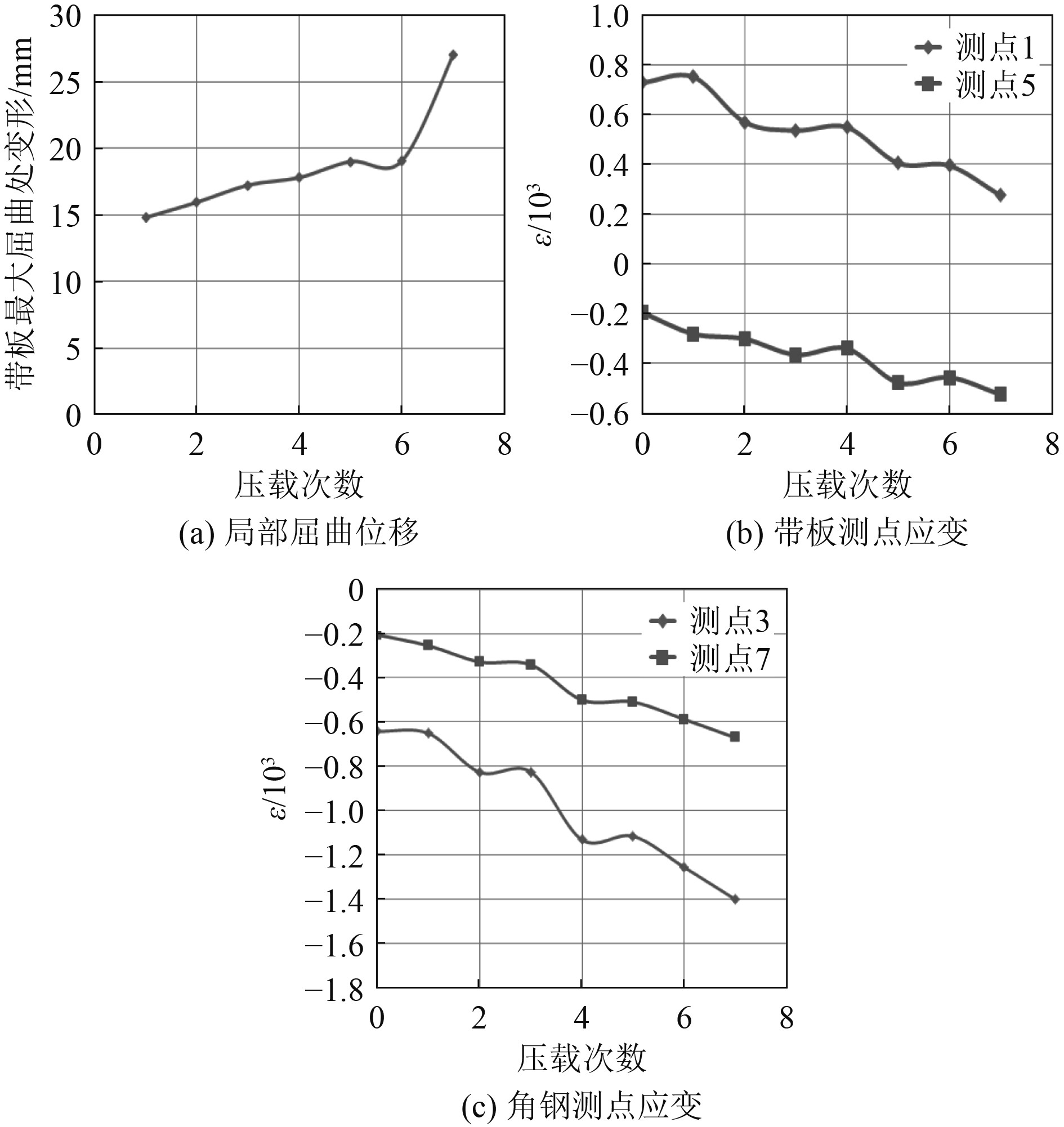
|
图 6 4-Ⅱ试件局部屈曲处位移与应变曲线图 Fig. 6 Plot of displacement and strain at local buckling of specimen 4-II |
|
|
表 3 各试件最大承载力 Tab.3 Summary of maximum bearing capacity of each specimen |
本文进行7个扶强材(含带板)试件的单调与循环载荷下的极限承载力试验。通过试验得到了扶强材(含带板)试件在3种加载机制下的变形和失效模式以及应力应变曲线。根据对试验结果的分析,可得以下结论:
1)7组试验中,试件失稳形式基本为整体失稳。试件出现整体面外弯曲,在加载过程中普遍出现带板的局部屈曲。
2)循环加载下试件应力应变曲线基本呈梭形,同一个应变处,循环曲线接近,表明扶强材试件轴向吸能能力差。
3)循环载荷下应力应变曲线与单调载荷下应力应变曲线相比,在循环机制Ⅱ作用下,经多次循环后,试件最大承载力出现下降。循环机制Ⅲ作用下,经多次循环后,试件承载力下降明显,且曲线较加载机制Ⅱ曲线与单调曲线更饱满。
4)在加载机制Ⅱ作用下,试件产生局部屈曲,且局部屈曲处位移随循环次数增加而增加。反向拉伸虽然能抵消部分屈曲变形,但不能完全消除屈曲变形,局部屈曲处位移随循环次数增加呈上升趋势。
5)同类型试件之间极限承载力存在一定偏差,与试件加工及试验过程中加载器具产生偏心加载有关。本试验试件相对较少,后续可增加试验试件数量,获得更稳定的试验数据。
| [1] |
XU M C, SOARES C G. Experimental study on the collapse strength of wide stiffened panels[J]. Marine Structures, 2013, 30(JAN.): 33-62. |
| [2] |
SHANMUGAM N E, DONGQI Z, CHOO Y S, et al. Experimental studies on stiffened plates under in-plane load and lateral pressure[J]. Thin-Walled Structures, 2014, 80: 22-31. DOI:10.1016/j.tws.2014.02.026 |
| [3] |
XKA D, YI YA, JIN G B, et al. Experimental and numerical investigation on the detailed buckling process of similar stiffened panels subjected to in-plane compressive load[J]. Thin-Walled Structures, 148.
|
| [4] |
GORDO J M, SOARES C G. Compressive tests on short continuous panels[J]. Marine Structures, 2008, 21(2-3): 113-137. DOI:10.1016/j.marstruc.2007.12.005 |
| [5] |
YUAN T, YANG Y, KONG X, et al. Similarity criteria for the buckling process of stiffened plates subjected to compressive load[J]. Thin-Walled Structures, 158.
|
| [6] |
喻霁, 杨平. 船体梁在循环载荷下的极限强度研究[J]. 舰船科学技术, 2019, 41(4): 44-48. DOI:10.3404/j.issn.1672-7649.2019.04.009 |
| [7] |
FUJITA Y, NOMOTO T, YUGE K. Behavior of deformation of structural members under compressive and tensile loads(1St report)-on the buckling of a column subjected to repeatedloading[J]. Journal of The Society of Nasal Architects of Japan, 1984, 156: 346-354. |
| [8] |
崔虎威, 杨平, 周杨, 等. 循环载荷下箱型梁极限强度性能试验研究[J]. 船舶力学, 2018, 022(5): 595-602. |
| [9] |
黄震球, 陈齐树, 骆子夜. 循环弯曲载荷下船体梁的极限纵强度[J]. 中国造船, 1996(3): 87-95. |
| [10] |
许俊, 吴剑国, 叶帆, 等. 循环载荷混合作用下加筋板格极限强度的研究[J]. 船舶, 2018, 29(2): 31-38. DOI:10.19423/j.cnki.31-1561/u.2018.02.031 |
| [11] |
孟志光, 王凡超, 叶帆, 等. 循环荷载作用下加筋板格单元的损伤累积及力学模型研究[J]. 船舶工程, 2018, 40(5): 94-98. DOI:10.13788/j.cnki.cbgc.2018.05.094 |
 2023, Vol. 45
2023, Vol. 45
