2. 广西质量工程职业技术学院,广西 南宁 530009;
3. 北部湾大学,广西 钦州 535011
2. Guangxi Vocational and Technical College of Quality and Engineering, Nanning 530009, China;
3. Beibu Gulf University, Qinzhou 535011, China
船舶在海上航行过程中,常会因周围环境里各种力的作用变化而产生剧烈的摇荡运动。从三维轴向研究,大致可以将其归纳为横摇、纵摇和首摇3个方向。若船舶在以上3个方向上进行激烈的摇晃,不仅会让作业人员在工作中容易失去重心造成安全隐患,同时还会缩短船舶的使用寿命。因此加强船舶的减摇鳍设计,完善相关功能性,显得尤为重要[1-3]。
目前,无论是军用还是在民用船舶,在减缓横摇的措施上,普遍采取的是减摇鳍减摇装置,在原理上通过其上升力而对横摇进行抵消。伴随着仿生学的兴起,以及人工智能技术的不断提升,不少研究人员在围绕减摇鳍的装置改进上,也进行了跨学科的设计,并最终在满足系统减摇的前提下,设计出了仿驼背鲸改进减摇鳍。这种前缘变形的特殊减摇鳍在实际应用的过程中,可以借助其前缘凸凹节结构,从而在减摇鳍前缘构建出正弦形,由此提升减摇鳍的升力,使其在复杂障碍场中保持正常工作[4-5]。
此外,也有不少学者将船舶的横摇非线性升力模型作为设计参考,利用仿驼背鲸改进减摇鳍存在的非线性、不确定性等特点,借助轴承形变求解升力,在试验中不仅有效削弱了外界干扰并降低了系统抖振,同时也有效提高了系统鲁棒性能,达到误差收敛的目的。为此,基于前人的理论研究成果,结合仿驼背鲸改进减摇鳍的升力系数进行相关的数值计算,并分析该仿真控制器的可操作性和有效性。
1 仿驼背鲸改进减摇鳍控制系统 1.1 仿驼背鲸改进减摇鳍工作原理仿驼背鲸改进减摇鳍在实际应用过程中,主要是依靠鳍体在流场中的运动,从而形成升力力矩,使其在力的相互作用下抵消海浪的扰动力矩,保障船舶的安全航行。
| $ {K_C} = \frac{1}{2}\rho {V^2}{A_f}C_L^\alpha \left( {{\alpha _m} + \frac{{\dot \phi {l_f}}}{V}} \right){l_f}。$ |
式中:ρ为海水密度,Af为仿驼背鲸改进减摇鳍的接触面积,CLα为仿驼背鲸改进减摇鳍的升力系数。
此外,还可以借助控制设备对鳍角进行调整,从而达到随时改变仿驼背鲸减摇鳍升力的目的。基于以上原理,分析仿驼背鲸改进减摇鳍的升力系数,并通过精确计算从而可以迅速抵消横摇的作用力。
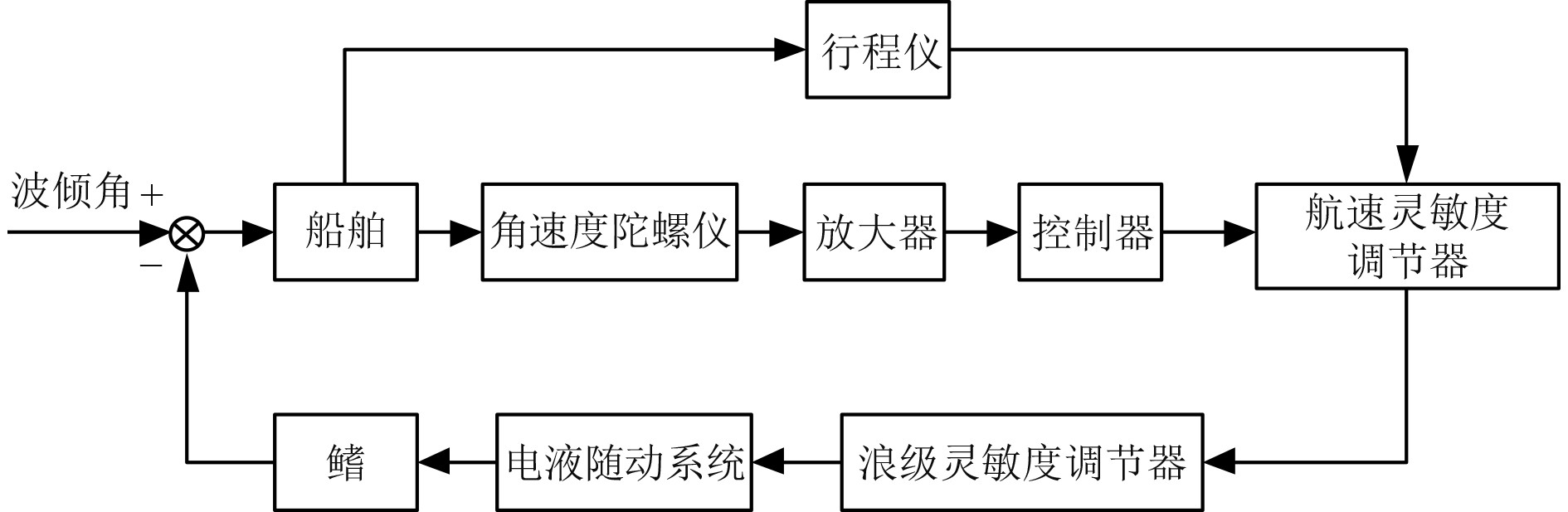
1.2 仿驼背鲸改进减摇鳍控制系统基本组成如图1所示,仿驼背鲸改进减摇鳍控制是一个系统且复杂的过程,每一个配件在实际应用的过程中,都会对升力系数的数值计算有一定的影响。通过连贯的操作指令驱使仿驼背鲸改进减摇鳍随时调整适宜角度,从而保障船舶的平稳航行。
|
图 1 仿驼背鲸改进减摇鳍系统控制框图 Fig. 1 Control block diagram of improved fin stabilizer system modeled after humpback whale |
角速度陀螺仪作为一个重要测量部件,对横摇角速度进行检测统计,是提供有效参数的关键。目前的仿驼背鲸改进减摇鳍可借助加速度传感器,在实际航行过程中通过对海洋环境的信息捕捉,从而获取横摇角加速度的相关参数,其传递函数为:
| $ {G_a}\left( s \right) = \frac{{400\;s}}{{{s^2} + 80\;{\rm{s}} + 4\;000}} \text{。} $ |
放大器将系统信号进行放大,对船舶的横摇角、横摇角速度和横摇角加速度信号等进行测算,信号通过操作室的计算机经处理后传入控制器。其中,当放大器作为比例放大的时候,仿驼背鲸改进减摇鳍的放大倍数与控制系统的选择相关,普遍按照大于1的常数代替。
作为仿驼背鲸改进减摇鳍的经典PID控制器,其在信息传递的函数为:
| $ {G_{PID}}\left( s \right) = {K_P} + \frac{{{K_I}}}{s} + {K_D}s \text{。} $ |
船舶航行过程中,为了保证仿驼背鲸改进减摇鳍提供的升力系数可以与周围环境的影响而相互抵消,对航速进行测算,并根据搜集到的相关信息对鳍角进行调整,航速与鳍角的关系如下:
| $ {\alpha _{m\_\max 0}} = \left\{ {\begin{array}{*{20}{l}} 0,& V < 6 ,\\ {\alpha _{m0}},&6 \leqslant V \leqslant {V_0},\\ {\alpha _{m0}}V_0^2/{V^2},&V \geqslant {V_0} 。\end{array}} \right. $ |
由计算结果可知,船舶航行速度的平方与仿驼背鲸改进减摇鳍所提供的升力成正比,其中αm-max0为最大鳍角,V0为目标设计航速,αm0为V0下的最大鳍角。
在船舶航行过程中,浪级灵敏度调节器持续通过仿驼背鲸减摇鳍来控制船舶的平稳度,缩短减摇装置使用寿命,因此要最大程度缓和仿驼背鲸改进减摇鳍被外界干扰的灵敏度。
此外,电液随动系统也是一个有效提升升力系数运作功能的设计配件,其改进后的传递函数为:
| $ {G_s}\left( s \right) = \frac{{550}}{{{s^2} + 15s + 225}} \text{。} $ |
鳍在实际工作中,同样会对升力系数带来一定的影响。通过接收随动系统的驱动信号,实现鳍角的调整,其是一项可以人为操作的被动影响因素。
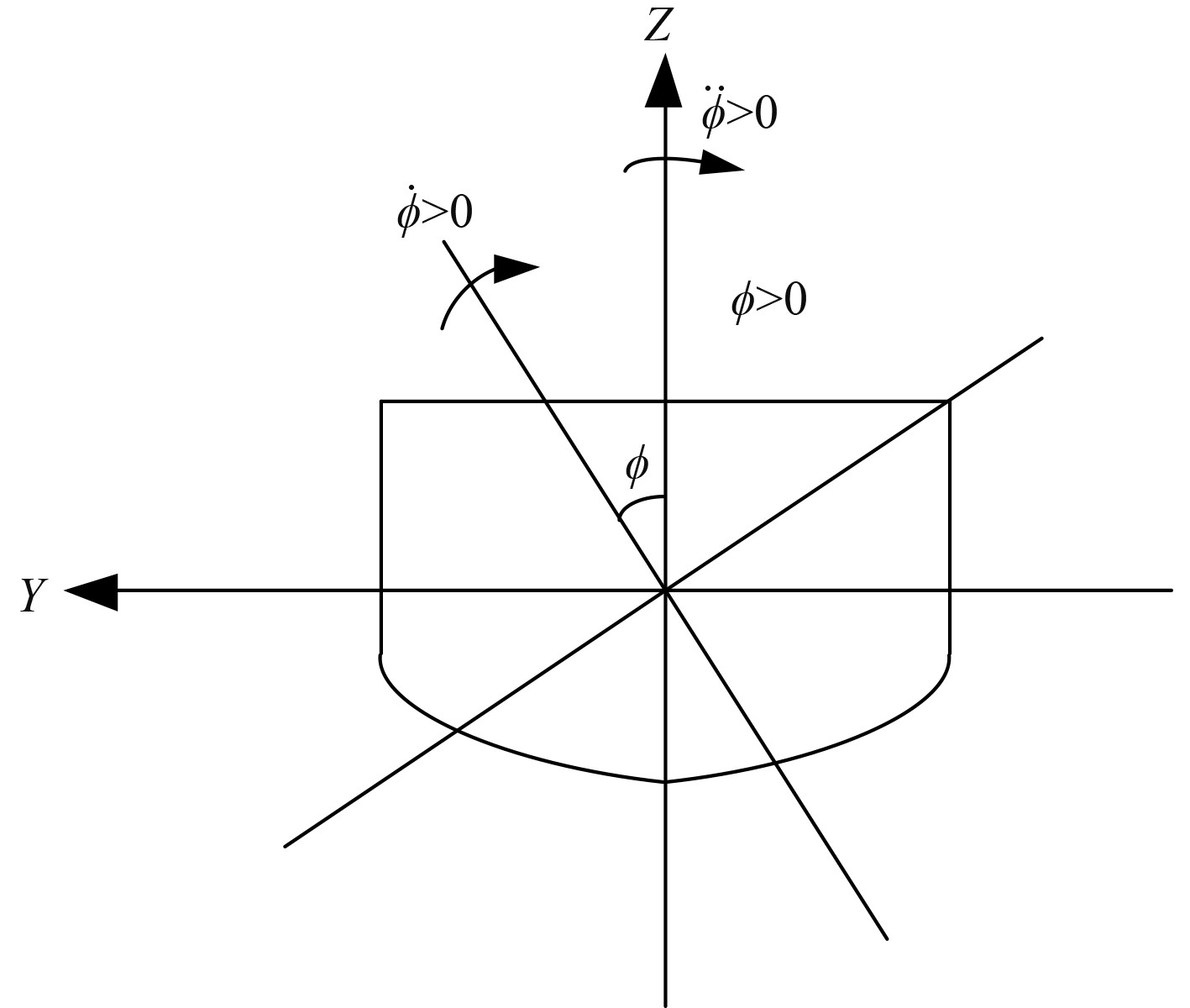
2 船舶横摇运动数学模型建立 2.1 船舶横摇升力系数受力分析当船舶在海上因受到外力影响而发生运动方向的转变时,仿驼背鲸改进减摇鳍所产生的升力会给船舶形成一个相反的力矩,并随着X轴进行顺时针的转动,如图2所示。
|
图 2 船舶横摇运动 Fig. 2 Ship rolling motion |
仿驼背鲸改进减摇鳍的抗扰动力矩,主要由以下几项构成:复原扰动力矩
| $ M\left( {{\alpha _f}} \right) = - Dh{\alpha _f} \text{,} $ |
| $ M\left( {\dot\alpha _f } \right) = - 2N\ddot\alpha _f \text{,} $ |
| $ M\left( {\ddot \alpha _f} \right) = - \Delta Ix\ddot\alpha _f \text{。} $ |
式中:D为排水量,h为初稳心高,N为仿驼背鲸改进减摇鳍阻尼力矩,ΔIx为转动惯量。
船舶在航行过程中,不仅会受到来自海风的影响,对于海浪的拍击,也会对其航向造成影响,甚至会促使其发生侧翻。而仿驼背鲸改进减摇鳍的出现,可以借助升力系数减摇力矩有效缓解这一困局,其表达式为:
| $ M\left( \phi \right) = - Dh\phi \text{。} $ |
船舶在发生横摇时,在仿驼背鲸改进减摇鳍的升力协助下会恢复到原位,但是随着惯性的发生,还是会出现一段时间惯性作用,并在仿驼背鲸改进减摇鳍的帮助下逐步减缓。减摇鳍阻尼力矩随时间的变化曲线如图3所示。而关于惯性力矩的表达式为:

|
图 3 减摇鳍阻尼力矩随时间的变化曲线 Fig. 3 Variation curve of fin stabilizer damping torque with time |
| $ M\left( {\ddot \phi } \right) = - \left( {{I_x} + \Delta {I_x}} \right)\ddot \phi \text{。} $ |
基于海浪、海风以及惯性的相关影响,对仿驼背鲸改进减摇鳍的阻尼力矩进行综合评估,经计算后得出如下表达式:
| $ M\left( {\dot \phi } \right) = - 2N\dot \phi \text{。} $ |
依据Conolly理论,结合计算的相关受力结果,得出仿驼背鲸改进减摇鳍的线性数学模型:
| $ \left( {{I_x} + \Delta {I_x}} \right){\ddot\varPhi} + 2N{\dot\varPhi } + Dh\varPhi = - \left( {\Delta {I_x}\ddot\alpha _{^{_f}} + 2N{\alpha _f} + Dh{\alpha _f}} \right) \text{。} $ |
结合相关研究数据分析计算可知,其作用于仿驼背鲸改进减摇鳍的复原力矩要比惯性扰动力矩以及阻尼扰动力矩的总和高出不少,继而上式可近似为:
| $ \left( {{I_x} + \Delta {I_x}} \right)\ddot \phi + 2N\dot \phi + Dh\phi = - Dh{\alpha _f} \text{。} $ |
基于上式计算对横摇角Φ进行推导,得出仿驼背鲸改进减摇鳍有效波倾角的传递函数:
| $ {G_\phi }\left( s \right) = \frac{{\phi \left( s \right)}}{{{\alpha _f}\left( s \right)}} = \frac{1}{{{K^2}{s^2} + 2\xi Ks + 1}} \text{。} $ |
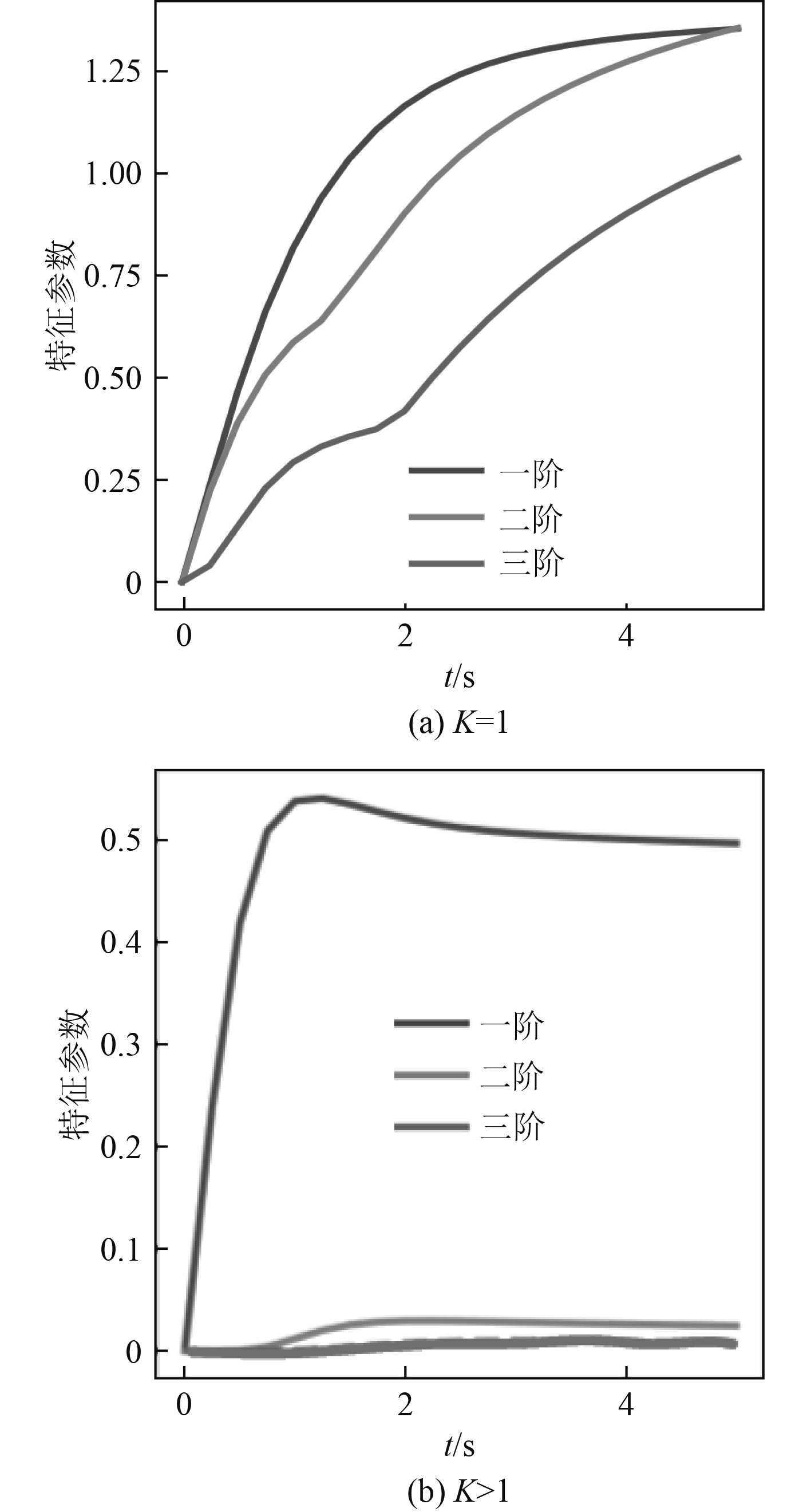
式中:1/K为仿驼背鲸改进减摇鳍的固有频率。不同K值下的三阶减摇鳍特征参数变化曲线如图4所示。
|
图 4 不同K值下的减摇鳍特征参数变化曲线 Fig. 4 Variation curves of fin stabilizer characteristic parameters under different K values |
由大连海事大学学报一项数据统计中可知,船舶在航行中受大风浪影响,其横摇角通常都会远远超出正常的摇晃范围(>10°)。此时前文分析的相关计算结果,就无法在仿驼背鲸改进减摇鳍的升力系数计算中具备普适性。结合2021年一项专利研究,从非线性升力系数入手进行丰富与微调,其表达如下:
| $ M\left( \phi \right) = - {C_1}\phi - {C_2}{\phi ^3} - {C_3}{\phi ^5} \text{。} $ |
式中:C1为仿驼背鲸改进减摇鳍排水量与初稳心高乘积,即满足常数要求。对其进一步优化得出:
| $ M\left( {\dot \phi } \right) = - {B_1}\dot \phi - {B_2}\left| {\dot \phi } \right|\dot \phi \text{。} $ |
式中:B1与B2皆为常数且与船型参数相关。基于以上结果,最终得出适用于风浪中的仿驼背鲸改进减摇鳍非线性升力系数:
| $ \left( {Ix + \Delta Ix} \right)\ddot \varphi + {B_2}\left| {\dot \varphi } \right|\dot \varphi + {C_1}\varphi + {C_2}{\varphi ^3} + {C_3}{\varphi ^5} = - Dh{\alpha _f} 。$ |
本次基于实验室相关参数指标以及前人的相关理论研究成果,借助Matlab对仿驼背鲸改进减摇鳍构建升力系数模型并对该仿真设计的可行性进行验证。通过本次结合高等流体力学理论的研究,系统整理了仿驼背鲸改进减摇鳍的升力系数数值计算的相关思路,并针对相关常数进行分析,为后续提升仿驼背鲸改进减摇鳍的实际操作能力奠定了一个较为完备的研究基础。
| [1] |
赵云瑞, 高海波, 林治国, 等. 基于组合赋权-TOPSIS法的极地邮轮减摇鳍选型评价[J]. 中国舰船研究, 2021, 16(5): 121–126+149. ZHAO Yun-rui, GAO Hai-bo, LIN Zhi-guo, et al. Selection and evaluation of fin stabilizers for polar cruise ships based on combined weighting-TOPSIS method[J]. Chinese Journal of Ship Research, 2021, 16(5): 121–126 +149. |
| [2] |
李乐宇, 吴建威, 万德成. 基于CFD的带附体KCS船在波浪中的阻力及纵摇优化[J]. 中国舰船研究, 2022, 17(2): 63-72. LI Le-yu, WU Jian-wei, WAN De-cheng. Resistance and pitch optimization of KCS ship with appendages in waves based on CFD[J]. China Ship Research, 2022, 17(2): 63-72. DOI:10.19693/j.issn.1673-3185.02169 |
| [3] |
高宇辉, 李晖, 张华健, 等. 基于NFTSM的吊舱推进器与减摇鳍联合减摇控制[J]. 船舶工程, 2022, 44(6): 100-108. GAO Yu-hui, LI Hui, ZHANG Hua-jian, et al. Combined anti-rolling control of pod propeller and fin stabilizer based on NFTSM[J]. Ship Engineering, 2022, 44(6): 100-108. DOI:10.13788/j.cnki.cbgc.2022.06.17 |
| [4] |
黄雪平, 王振强. 减摇鳍控制策略优化[J]. 船舶标准化工程师, 2021, 54(5): 71-76. HUANG Xue-ping, WANG Zhen-qiang. Optimization of fin stabilizer control strategy[J]. Ship Standardization Engineer, 2021, 54(5): 71-76. DOI:10.14141/j.31-1981.2021.05.012 |
| [5] |
孙云, 金方银, 曾启盛, 等. 大型减摇鳍液压机组隔振装置设计与试验[J]. 机电设备, 2022, 39(4): 1-6. SUN Yun, JIN Fang-yin, ZENG Qi-sheng, et al. Design and test of vibration isolation device for large fin stabilizer hydraulic unit[J]. Electromechanical Equipment, 2022, 39(4): 1-6. DOI:10.16443/j.cnki.31-1420.2022.04.001 |
 2023, Vol. 45
2023, Vol. 45
