2. 上海市公共建筑和基础设施数字化运维重点实验室,上海 200240
2. Shanghai Key Laboratory for Digital Maintenance of Buildings and Infrastructure, Shanghai 200240, China
传统规范采用许用应力法校核船体梁总纵强度,该方法具有计算简便、快捷的特点[1]。但许用应力法仅采用一个安全系数K确定结构的可靠程度,不能反映船体的实际承载能力。而建筑钢结构设计标准经历了许用应力法和以概率为基础的极限状态设计法阶段,进入以非线性分析计算极限强度为基础的高等分析法阶段[2]。高等分析法是考虑结构缺陷直接计算极限强度的设计方法,钟毅等[3-5]针对船体构件加筋板极限强度计算方法展开研究,但针对舱段或全船整体结构极限强度的计算方法研究较少。随着计算机计算能力的增强,基于舱段结构甚至全船结构的高等分析法进行船舶结构设计成为发展趋势。
相关研究[6-9]表明,高等分析法中所引入的初始缺陷形态至关重要,直接影响极限强度计算结果。船舶结构中存在凹陷、初始变形和残余应力等多种初始缺陷[10],现阶段一般通过施加结构整体位移缺陷来模拟结构中存在的各种缺陷形式。目前,常采用屈曲型初始挠度引入初始缺陷进行舱段极限强度计算。白宝强[11]应用Abaqus软件对一艘集装箱船舱段引入屈曲型初始缺陷的极限强度进行了研究;高本国等[12]应用Marc软件对船体梁引入屈曲型初始缺陷的极限强度进行了研究;刘明瑞[13]通过引入屈曲型初始缺陷研究了加筋板及箱型梁的极限强度。然而屈曲型初始缺陷往往只能体现结构的局部缺陷,尤其针对舱段结构而言,这种现象更加明显,难以体现舱段结构的整体缺陷分布,按这种初始缺陷引入方式不能准确获得舱段极限强度。
本文借鉴建筑钢结构中一致缺陷模态法[14],针对舱段极限强度计算,提出一种新的失稳模态型初始缺陷引入方法。失稳模态型初始缺陷能模拟舱段结构的整体位移缺陷,综合考虑结构中其他可能存在的缺陷,确定最大缺陷值,按此方法引入初始缺陷后,能较准确计算舱段结构极限强度。借助有限元软件Ansys,通过对比失稳模态型初始缺陷与同等最大缺陷值下屈曲型初始缺陷的舱段极限强度计算结果,论证失稳模态型初始缺陷引入方法的适用性。基于失稳模态型初始缺陷形态下船体舱段和局部加筋板达到极限强度的变形和应力分布结果,指出舱段结构模型优化时的关键部位,并给出相应的优化建议。该研究可完善船舶结构高等分析法中初始缺陷的计算方法,促进高等分析法在船舶结构设计中的推广应用。
1 船体舱段分析计算模型参考某挖泥船构造形式,提取关键构件建立舱段有限元模型。舱段沿船长方向为X轴,沿加强筋方向为Y轴,沿竖向为Z轴。甲板及舱壁均采用加筋板,为了与Tanaka系列加筋板[15]试验结果进行极限强度计算结果对比,加筋板几何参数均选自Tanaka系列加筋板试验。加筋板厚度
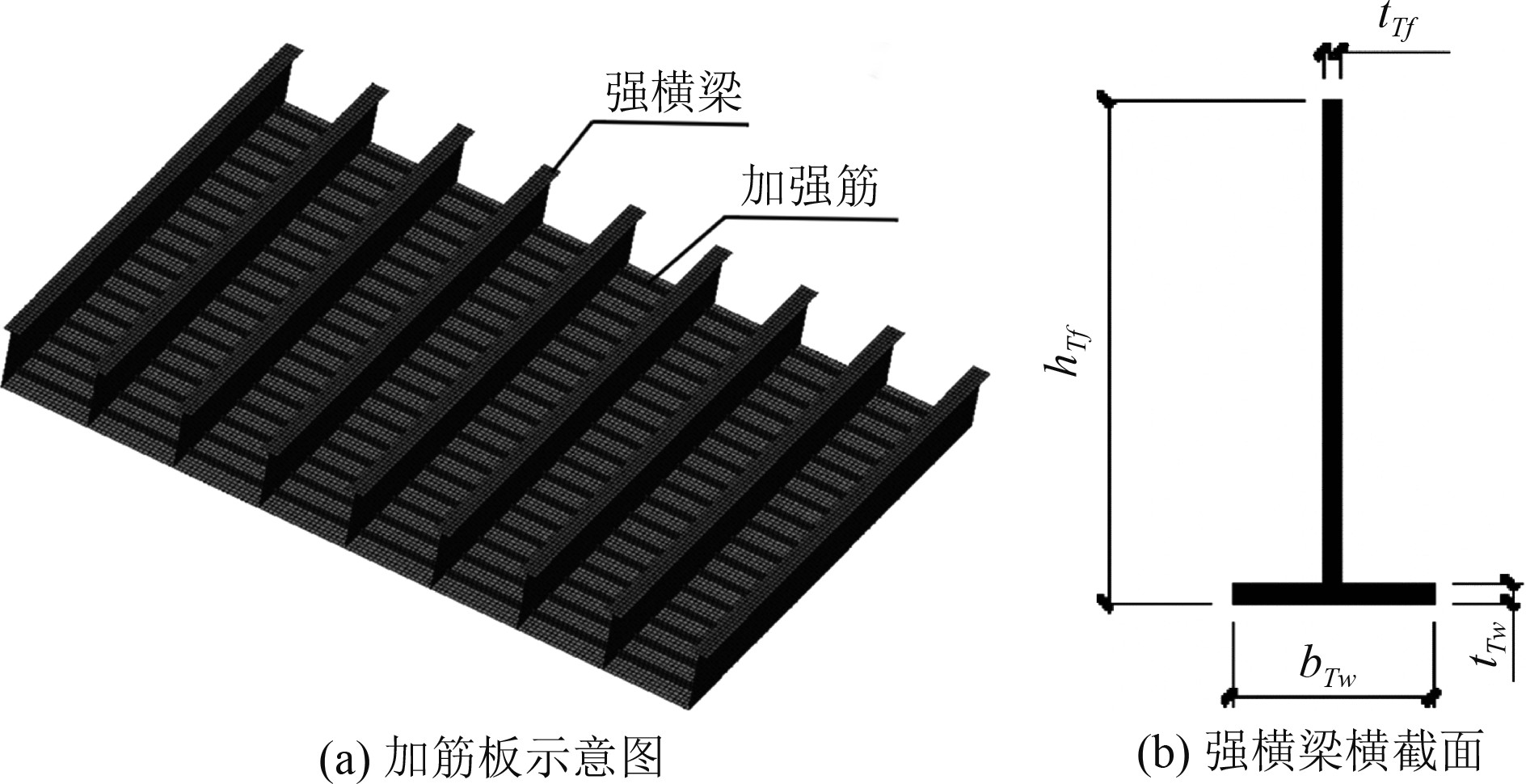
|
图 1 加筋板及强横梁示意图 Fig. 1 Schematic diagram of stiffened plate and strong beam |
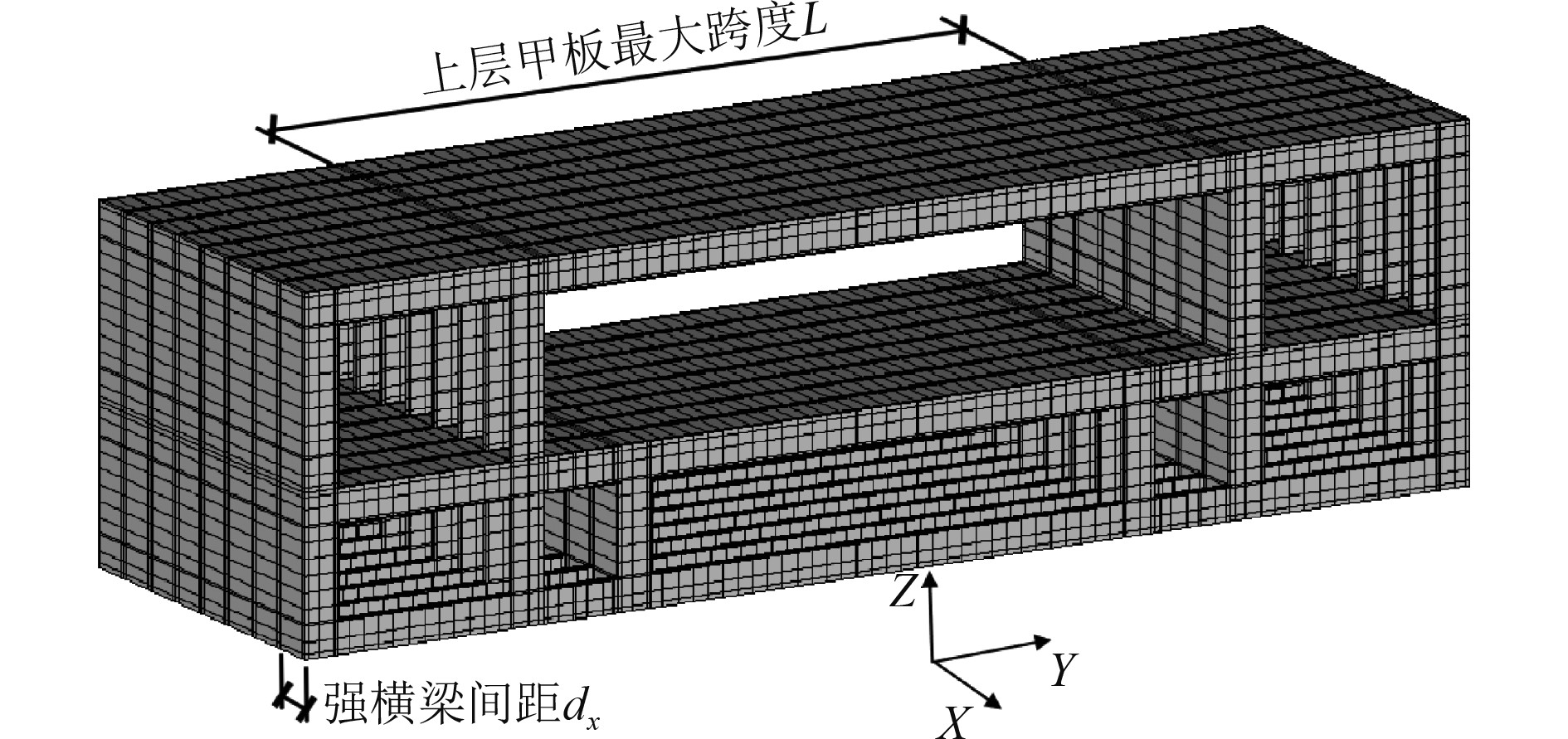
|
图 2 舱段整体结构模型 Fig. 2 Overall structure model of cabin section |
根据模型荷载和约束条件[11],荷载只考虑纯弯作用,在舱段两端截面施加弯矩;约束考虑舱段连续性条件并限制刚体位移。具体荷载及约束条件如下:
1)舱段两端截面(
2)舱段两端截面的甲板与底板约束Y向转动,考虑舱段连续性条件;
3)舱段中间截面(
采用屈曲型初始缺陷进行舱段极限强度计算,需要通过舱段结构的低阶屈曲模态或叠加后的屈曲模态建立初始挠度引入理想结构,再进行非线性分析。具体实现过程为:
1)对舱段理想模型进行线性特征值分析,得到理想结构的多阶屈曲模态;
2)选取合理的特征值屈曲模态作为初始缺陷形态,按最大缺陷值为
3)对该模型进行非线性分析,得到带屈曲型初始缺陷的舱段结构极限强度
屈曲型初始缺陷极限强度计算结果依赖于最大缺陷值
取图3所示的舱段结构第1阶模态作为初始缺陷模态,对比这2种
|
|
表 1 屈曲型初始缺陷极限强度结果 Tab.1 Ultimate strength results of buckling mode initial deflection |
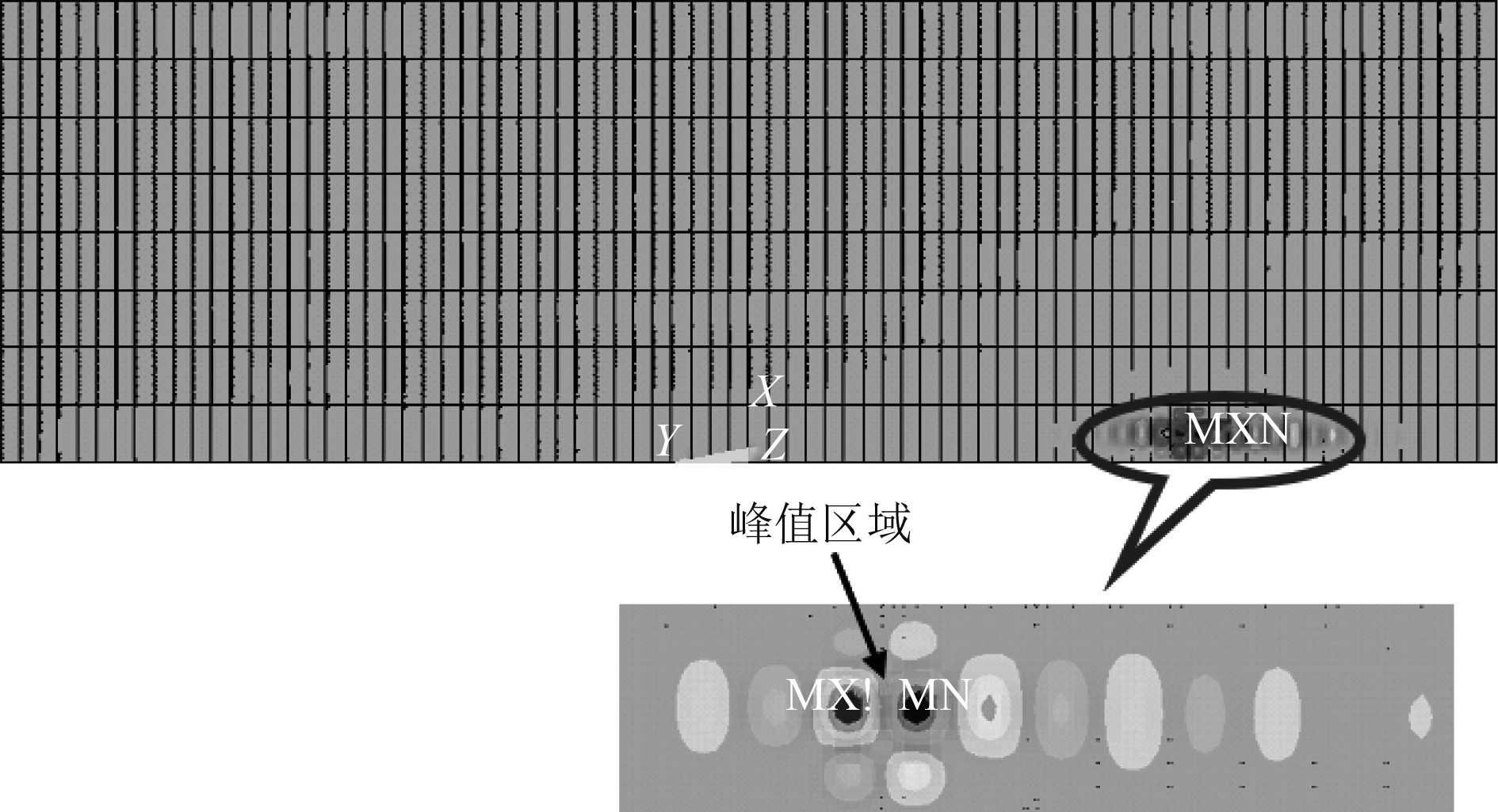
|
图 3 第1阶屈曲型初始缺陷形态 Fig. 3 Initial deflection form of first order buckling mode |
1)当
2)当
因此第1阶屈曲型初始缺陷无法反映舱段整体缺陷。为探讨能否选取到合适阶数的屈曲模态进行舱段结构极限强度计算,再次对舱段结构模型进行线性特征值分析,计算得到的前100阶屈曲模态均为局部屈曲,典型屈曲模态如图4所示。挑选屈曲区域范围较大的第90阶模态作为初始缺陷模态,

|
图 4 舱段典型屈曲模态(m为屈曲模态阶数) Fig. 4 Typical buckling mode of cabin section (m is the order of buckling mode) |
由于屈曲型初始缺陷引入方法对舱段结构并不适用,借鉴空间网壳结构中一致缺陷模态法,提出一种适用于舱段极限强度计算的初始缺陷引入方法。考虑失稳模态型初始缺陷极限强度计算具体过程为:
1)对舱段理想模型进行非线性分析;
2)选取理想模型在极限强度下的失稳模态作为初始缺陷形态,按最大缺陷值为
3)对该模型进行非线性分析,得到带失稳模态型初始缺陷的舱段结构极限强度
上述最大缺陷值
应用失稳模态型初始缺陷引入方法,取

|
图 5 失稳模态型初始缺陷形态 Fig. 5 Initial deflection form of instability mode |
采用失稳模态型初始缺陷计算所得舱段结构在极限强度下Z向变形及von Mises应力分布如图6所示。可知:
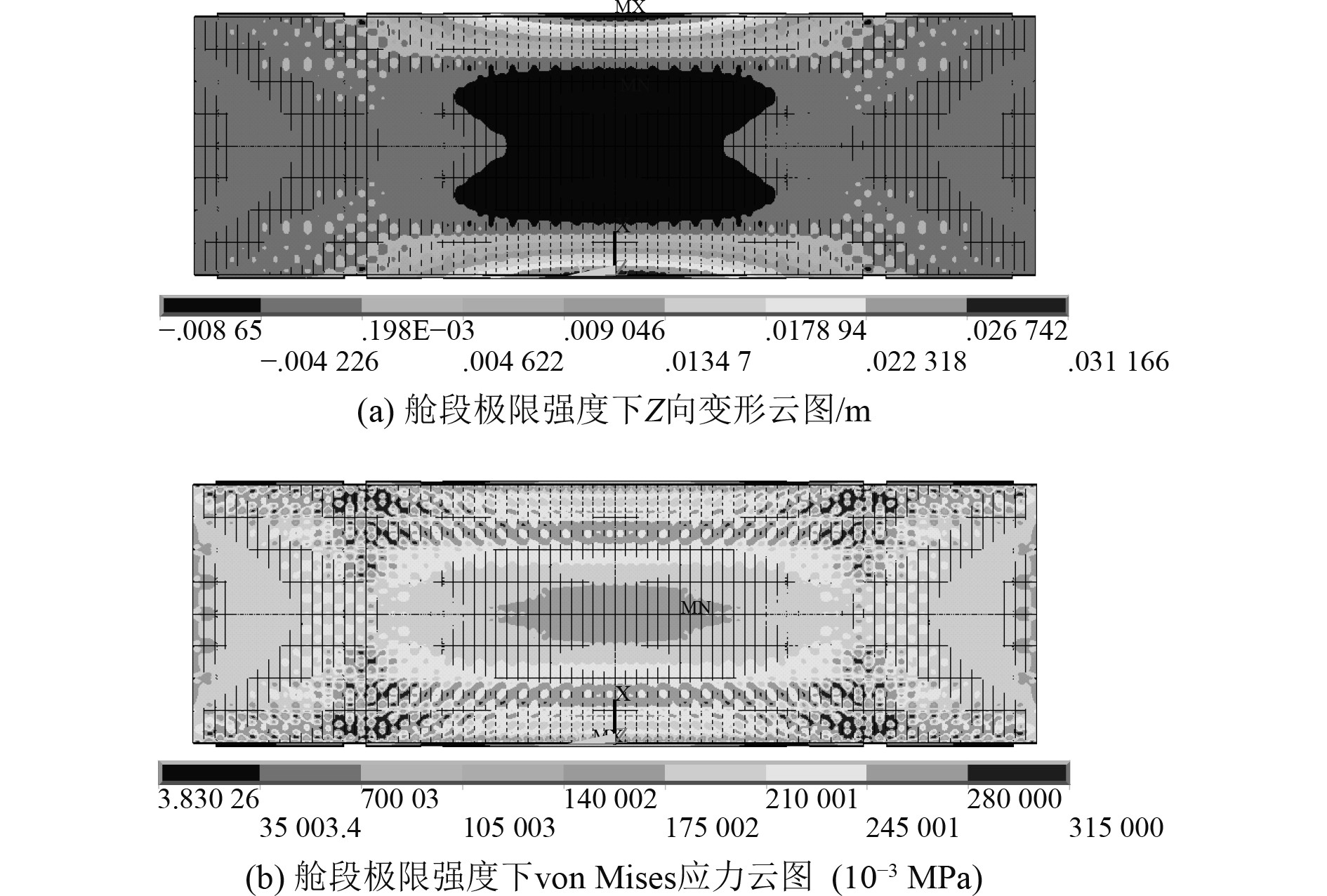
|
图 6 舱段极限强度下变形和应力分布 Fig. 6 Deformation and stress distribution under ultimate strength of cabin section |
1)舱段最大竖向变形为0.031 m,发生在上层甲板两端的跨中位置,上甲板两端发生翘曲,整体变形与失稳模态型初始缺陷形态基本一致;
2)舱段上甲板应力分布不均匀,与中间两舱壁交界处应力较大,而板中区域和靠近舷侧区域应力较小。
局部加筋板在极限强度下von Mises应力分布较为均匀,而舱段甲板应力分布明显不均匀。这是因为舱壁等其他船体构件对甲板应力分布存在影响,局部加筋板的分析结果不能反映整个甲板的应力状态。若仅依据局部加筋板极限强度结果进行甲板优化设计,会因无法准确考虑甲板受力不均匀的实际情况而导致材料浪费,优化空间有限。
4 结 语本文提出一种针对舱段极限强度计算的失稳模态型初始缺陷引入方法,通过对比采用失稳模态型初始缺陷与屈曲型初始缺陷的舱段极限强度计算结果,并结合试验结果,论证所提方法的适用性,分析了舱段达到极限强度时的变形和应力分布。主要研究结论如下:
1)舱段的屈曲失稳模态大多表现为局部屈曲,最大缺陷值难以选取,基于舱段跨度计算最大缺陷值时,所得舱段极限强度相对试验结果偏低8.36%;基于加筋板支撑(强横梁)间距计算最大缺陷值时,所得舱段极限强度相对试验结果偏高12.85%。因此,屈曲型初始缺陷引入方法不适用于舱段结构的极限强度计算。
2)理想舱段结构的失稳模态表现为结构整体变形形态,失稳模态型初始缺陷计算所得舱段极限强度与试验结果相差仅1.12%,能准确预测舱段结构极限承载能力。因此,失稳模态型初始缺陷引入方法更适用于舱段结构极限强度计算及船体结构高等分析法的初始缺陷取值。
3)舱段整体结构在极限强度下应力分布不均匀。建议考虑甲板受力不均匀的实际情况对舱段进行优化设计,对舱段甲板与舱壁交界区域应适当加强,对甲板板中区域和靠近舷侧区域部位适当削弱。
| [1] |
胡胜谦, 张延昌, 刘昆. 基于CSR共同规范的船体梁极限强度分析[J]. 船海工程, 2013, 42(1): 5-8+13. |
| [2] |
钢结构设计标准: GB50017—2017[S]. 北京: 中国建筑工业出版社, 2017.
|
| [3] |
钟毅, 吕岩松, 刘旭. 含初始变形船体加筋板有效宽度及剩余极限强度研究[J]. 舰船科学技术, 2022, 44(2): 43-47. |
| [4] |
CHONG Cui, PING Yang, CHUANG Li, et al. Ultimate strength characteristics of cracked stiffened plates subjected to uniaxial compression[J]. Thin-Walled Structures, 2017, 113. |
| [5] |
ZHANG Jing, SHI Xing-hua, GUEDES S C, et al. Ultimate strength of stiffened panels with a crack and pits under uni-axial longitudinal compression[J]. Ships and Offshore Structures, 2022, 17(2): 319-338. |
| [6] |
舒毅, 张莉. 随机初始缺陷对辐射式张弦梁结构非线性稳定的影响研究[J]. 结构工程师, 2022, 38(2): 16-24. DOI:10.15935/j.cnki.jggcs.2022.02.006 |
| [7] |
王秀丽, 王康, 张孝斌, 等. 考虑施工误差的大开孔悬挑网壳结构稳定性[J]. 空间结构, 2021, 27(4): 21-27. |
| [8] |
MORRIS N F. Effect of imperfection on lattice shells[J]. Journal of Structural Engineering, 1991, 117(6): 1796-1814. DOI:10.1061/(ASCE)0733-9445(1991)117:6(1796) |
| [9] |
田兆哲, 杨平, 胡康, 等. 组合初始缺陷对含裂纹加筋板极限强度的影响研究[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(6): 1091-1097. |
| [10] |
NOURI Z, KHEDMATI M R, SADEGHIFARD S. An Effective Thickness Proposal for Strength Evaluation of One-Side Pitted Steel Plates Under Uniaxial Compression[J]. Latin American Journal of Solids and Structures, 2012, 9(4): 475-496. DOI:10.1590/S1679-78252012000400004 |
| [11] |
白宝强. 船体梁极限强度的非线性有限元分析[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [12] |
高本国, 杨平. 破损船体的剩余极限强度评估[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(5): 1089-1092. |
| [13] |
刘明瑞. 典型船体结构的极限强度分析[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [14] |
范峰, 曹正罡, 马会环, 等. 网壳结构弹塑性稳定性[M]. 北京: 科学出版社, 2015.
|
| [15] |
TANAKA Y, ENDO H. Ultimate Strength of Stiffened Plates with Their Stiffeners Locally Buckled in Compression[J]. Journal of the Society of Naval Architects of Japan, 1988, 164: 456-467. |
| [16] |
张晓丹, 杨平. 加筋板在轴向压力下的极限强度研究[J]. 武汉理工大学学报(交通科学与工程版), 2011, 35(2): 305-308+312. |
 2023, Vol. 45
2023, Vol. 45
