潜艇在水下航行时,发出的噪声主要有3个方面的来源,分别是机械噪声、螺旋桨噪声和水动力噪声。其中,水动力噪声的典型特征是其噪声总级正比于流体速度的5~7次幂,在流体速度超过10 kn时,其噪声总级甚至与流体速度的10次幂成正比[1]。随着我国科研实力不断增强,潜艇航行时产生的机械噪声和螺旋桨噪声得到有效的控制,意味着水动力噪声成为潜艇的主要噪声源。已有的指挥台围壳设计时考虑的主要因素都是其对潜艇航行时产生的阻力以及操纵性能等方面的影响。随着潜艇航速的提升,指挥台围壳部位产生的水动力噪声问题逐渐引起关注。聚焦指挥台围壳产生的突出水动力噪声相关问题,美国专门研究潜艇水动力、噪声和结构的综合研究单位——水面战争研究中心卡得洛克分部,曾经专门提出有关先进围壳研发的项目(advanced sail project),此项目在水动力、复合材料技术、水动力噪声、结构设计等几个方面全面的对潜艇指挥台围壳进行详细研究[2]。马蹄涡是指挥台围壳主要噪声源,指挥台围壳线型对马蹄涡有显著影响。此外,指挥台围壳线型对围壳尾流也有显著影响,进而影响螺旋桨噪声。改变指挥台围壳的相对厚度就是优化指挥台围壳线型中的一种,相对厚度即最大宽度与弦长比值。相对厚度较小的指挥台围壳通常称之为“薄翼型”围壳。
Wang等[3]应用数值模拟技术研究了不同指挥台围壳形状对潜艇水动力噪声的影响。结果表明改变指挥台围壳前缘线型可以有效抑制潜艇水动力噪声,使声压级降低4.69 dB。张楠等[4]开展了潜艇指挥台围壳线型优化对抑制脉动压力与流激噪声的效果方面的数值模拟研究,对潜艇指挥台围壳进行了前缘加装填角以及三维座舱型围壳等优化,分别对原指挥台围壳和线型优化后的指挥台围壳进行了指挥台围壳部位涡量的分布特性和噪声分布特性数值计算,分析结果表明线型优化后的指挥台围壳可以减小脉动压力与流激噪声的产生,可以很好地改善流动品质,可以为潜艇流声耦合和未来潜艇的设计提供一定参考借鉴。刘龙举等[5]对SUBOFF标准模型进行沙丘化改进后,开展了指挥台围壳阻力和尾部伴流等方面的数值模拟研究,针对沙丘型指挥台围壳的优化方案对潜艇阻力和尾部伴流等方面的影响进行初步探索,为指挥台围壳的设计优化提供新思路。王志博等[6]将指挥台围壳分为两段,通过改变进流段的线型而不变去流段的线型的方法,设计出3种新指挥台围壳方案,然后分别对其数值模拟得出的桨盘面速度情况、桨盘面处涡量分布等结果进行分析,表明光顺过渡的前缘线型可以有效改善指挥台围壳的入流品质,优化指挥台围壳周围涡量分布,进而有助于尾流的均匀性。
通过上述国内外相关研究现状来看,虽说有大量学者利用数值模拟计算分析了潜艇指挥台围壳线型对潜艇流噪声的影响,但是却没有人对潜艇指挥台围壳相对厚度对潜艇绕流场和水动力噪声的影响进行研究分析。指挥台围壳相对厚度变化对潜艇绕流场和水动力噪声是否有影响尚不清楚;会有多大影响也不清楚,所以需要开展相关研究。
1 数值方法采用经过改良的延时分离涡模拟(IDDES)模型,对计算域内的流场进行数值模拟,计算得到潜艇指挥台围壳周围流场涡量、桨盘面速度分布情况以及指挥台围壳根部特征点处脉动压力分布特性。
1.1 改良的延迟分离涡模拟(IDDES)分离涡(detached-eddy simulation, DES)[7]方法是把雷诺平均方法(reynolds-averaged navier-stokes, RANS)与大涡模拟(large eddy simulation, LES)方法结合在一起的混合方法,经过很多学者的应用,已被证实是一种可靠、有效的仿真方法。DES方法会根据距离壁面的远近程度来应用不同的模型进行仿真计算,在距离壁面较近的位置使用RANS进行仿真计算,在远离壁面的分离区应用LES来进行仿真计算。
改良的延迟分离涡方法(IDDES)是在DES基础上提出的一种改进的方法。它把两类RANS/LES方法结合在一起来应用,一类是延迟的分离涡方法(DDES),另一类为使用壁面函数的大涡模拟方法(WMLES),将两类方法混合在一起,可以削弱DES方法对网格划分的依赖,同时还可以提高近壁面附近流场的求解精度[8]。
IDDES中长度尺度
| $ {l_{IDDES}} = {f_d}(1 + {f_e})d + (1 - \mathop {\tilde {f_d}})\psi {C_{des}}{\Delta _1} 。$ | (1) |
式中:下标d
IDDES提高了高雷诺数下大分离流动的数值求解精度,一定程度上解决了DES在应对大分离流动中所产生的模型应力耗散和对数层不匹配的问题[8]。
1.2 几何模型SUBOFF潜艇模型是美国大卫·泰勒研究中心(DTRC)用于检验潜艇流场计算方法准确性的标准模型,试验资料丰富。SUBOFF模型总长4.356 m;其首部长为1.016,平行中体长为2.229 m,尾部长为1.111 m,中部最大直径为0.508 m,指挥台围壳高0.206 m,长0.368 m,最大厚度0.066 m[10]。几何模型如图1所示。
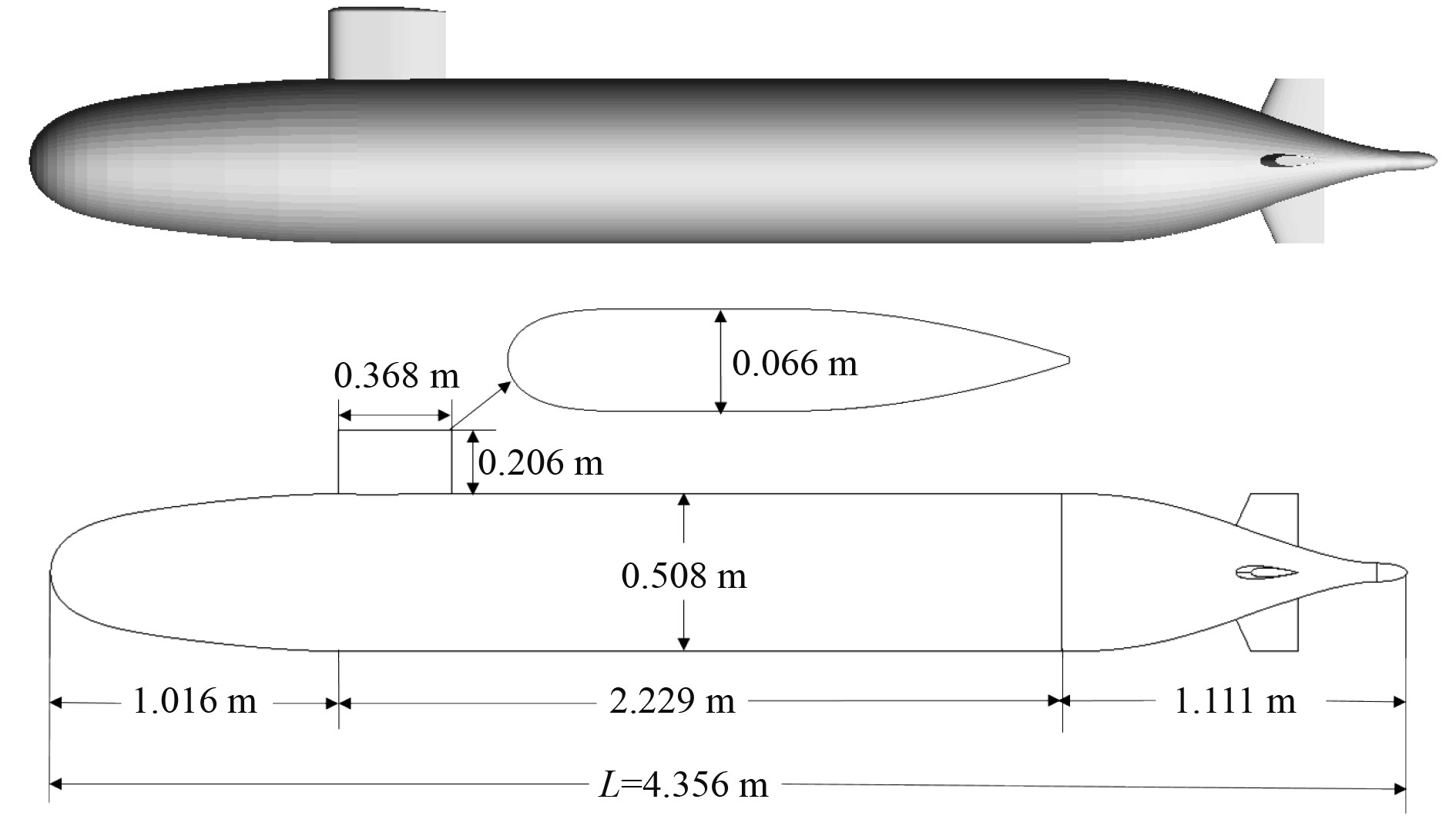
|
图 1 全附体SUBOFF几何模型 Fig. 1 Fully attached SUBOFF geometric model |
以SUBOFF标准模型的指挥台围壳为母型,改变指挥台围壳最大宽度,得到不同指挥台围壳相对厚度(最大宽度与弦长比值)的潜艇模型。因为指挥台围壳鼻艏的变化对水动力性能有很大影响,所以要在改变指挥台围壳相对厚度时尽量不变指挥台围壳鼻首的线型,以此为依据,不变指挥台围壳首部进流段线型,在增加指挥台围壳最大宽度同时减少指挥台围壳平行中体长度,直至平行中体长度减小至0。经过调研,指挥台围壳两侧都会存在自由空间,并且最大宽度的变化量都是微小的,所以指挥台围壳内部的空间基本保持不变,也就不用考虑因指挥台围壳相对厚度变化而导致的内部围封空间变化而引起的其他问题。
不同围壳的首部和尾部的长度按如下公式定义:
| $ {L_{fi}} = {L_{f0}}\left( {1 - {R_{Lp}}\frac{{{a_i} - {a_0}}}{{{a_2} - {a_0}}}} \right),\begin{array}{*{20}{c}} {}&{i = {\text{0}},1,2,3},\end{array} $ | (2) |
| $ {L_{ai}} = {L_{a0}}\left( {1 + {R_{Lp}}\frac{{{a_i} - {a_0}}}{{{a_2} - {a_0}}}} \right),\begin{array}{*{20}{c}} {}&{i = 0,1,2,3} ,\end{array} $ | (3) |
| $ {a_i} = \frac{{Lt \times R{w_i}}}{{{W_0}}}。$ | (4) |
根据由Grove et al 1989提供的DARPA SUBOFF指挥台围壳公式,修正后的指挥台围壳展向坐标和指挥台围壳盖坐标可以被定义为:
| $\begin{split} {y_{fi}} = &\pm {a_i} \times {y_{\text{0}}}[ 4.189518{C_i}{{\left( {{C_i} - 1} \right)}^4} +\\ &0.069059{C_i}^2{{\left( {{C_i} - 1} \right)}^3} - \left( {4{C_i} + 1} \right){{\left( {{C_i} - 1} \right)}^4}{\text{ + 1}} ]^{1/2},\\ i =& 0,1,2,3 。\end{split}$ | (5) |
| $ \begin{split}{y_{ai}} = & \pm {a_i} \times {y_{\text{0}}}[ 2.238361{D_i}{{\left( {{D_i} - 1} \right)}^4} +\\ &3.106529{D_i}^2{{\left( {{D_i} - 1} \right)}^3} - \left( {4{D_i} + 1} \right){{\left( {{D_i} - 1} \right)}^4}+ 1 ],\\ i =& 0,1,2,3 。\end{split}$ | (6) |
| $ {y_{ci}} = \pm {\left[ {{y_i}^2 - 4{{(z - 0.459581)}^2}} \right]^{1/2}},{i = 0,1,2,3} 。$ | (7) |
| $ {C_i} = \frac{x}{{{L_{fi}}}},\begin{array}{*{20}{c}} {}&{i = 0,1,2,3} 。\end{array} $ | (8) |
| $ {D_i} = \frac{{Lt - x}}{{{L_{ai}}}},\begin{array}{*{20}{c}} {}&{i = 0,1,2,3}。\end{array} $ | (9) |
可以观察到S4的线型不能用以上公式进行计算,因为其没有平行中体,S4的线型可以由S3的结果乘以参数
表1为所要研究5种不同相对厚度指挥台围壳具体参数。
|
|
表 1 模型相对厚度参数 Tab.1 Relative thickness parameters of model |
图2为5种不同相对厚度指挥台围壳示意图。
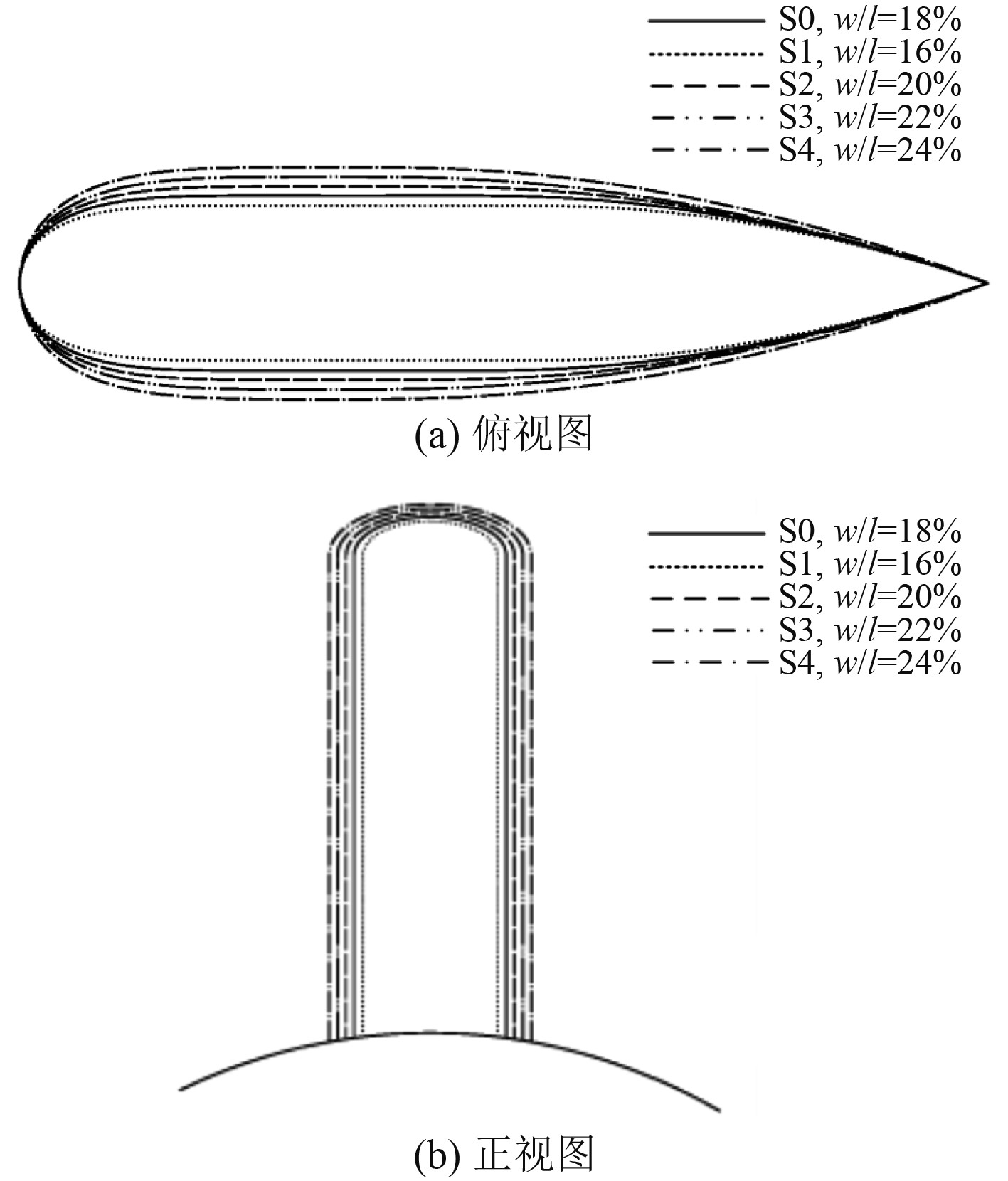
|
图 2 不同相对厚度指挥台围壳示意图 Fig. 2 Schematic diagram of sail with different relative thickness |
计算域为圆柱体,如图3所示。圆柱体长为4倍艇长,圆柱直径为10倍最大艇直径,进流段长度为1倍艇长,出流段长度为2倍艇长。边界条件定义为速度入口边界条件,压力出口边界条件,外流场取为对称面边界条件,艇体表面为壁面无滑移边界条件。利用商用软件Fluent进行数值计算。
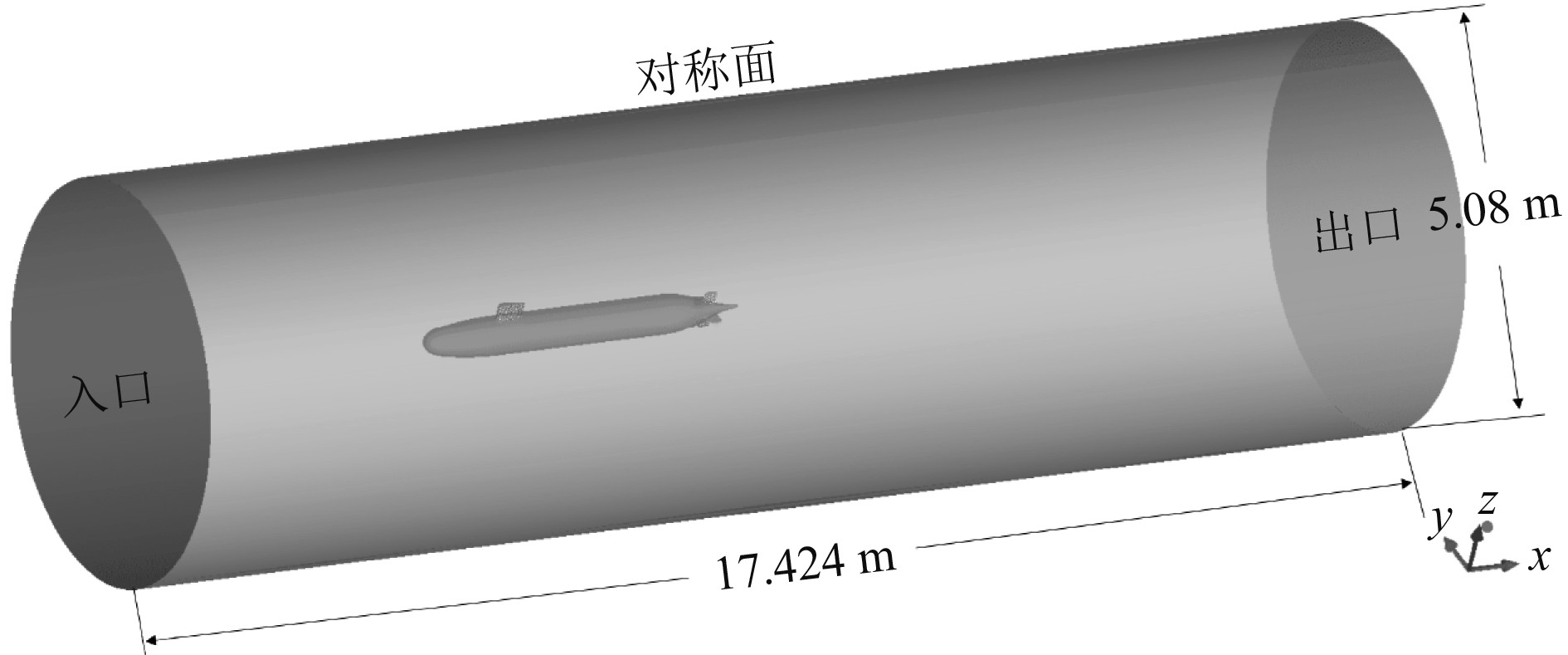
|
图 3 计算域及边界条件设置 Fig. 3 Calculation domain and boundary condition setting |
利用商用专业网格划分软件ICEM CFD进行整体的结构化网格划分,划分结果如图4所示。用在SUBOFF艇体表面生成边界层网格、在指挥台围壳部位进行网格加密等方式来提高计算精度。为很好捕捉艇体表面,特别是围壳周围流场特性,艇体表面Y+取为30。
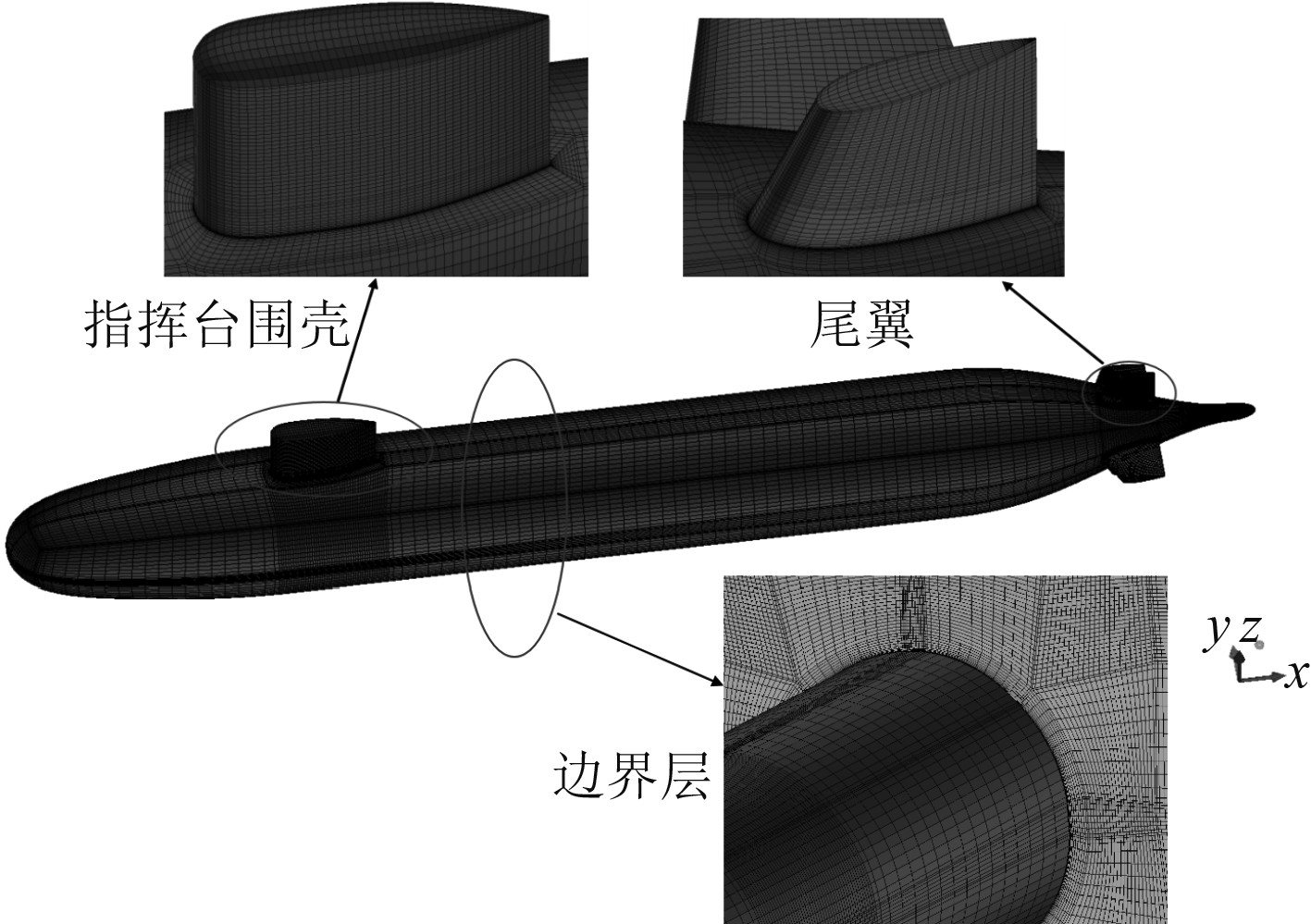
|
图 4 潜艇模型网格 Fig. 4 Submarine model grid |
为消除因网格划分不同而产生的对数值计算结果的影响,要进行网格无关性验证。本文设置4种不同单元数目的网格进行无关性验证,网格数目分别为637.8万、904.6万、1277.0万、1832.0万。数值模拟4种网格划分的潜艇航行阻力大小进行对比,表2为4种网格数值计算结果。根据结果可以看出4种网格仿真计算的结果几乎没什么变化,这说明四者都能够精准计算出阻力值,又考虑到计算机的计算负担,选择网格数量较少的进行数值计算比较理想,但是网格数量为637.8万的方案在进行仿真计算时收敛性没有其余3个网格方案理想,所以网格1方案不是最佳的仿真计算方案,故选择网格2方案作为本课题仿真计算的网格方案。
|
|
表 2 网格无关性验证 Tab.2 Grid independence verification |
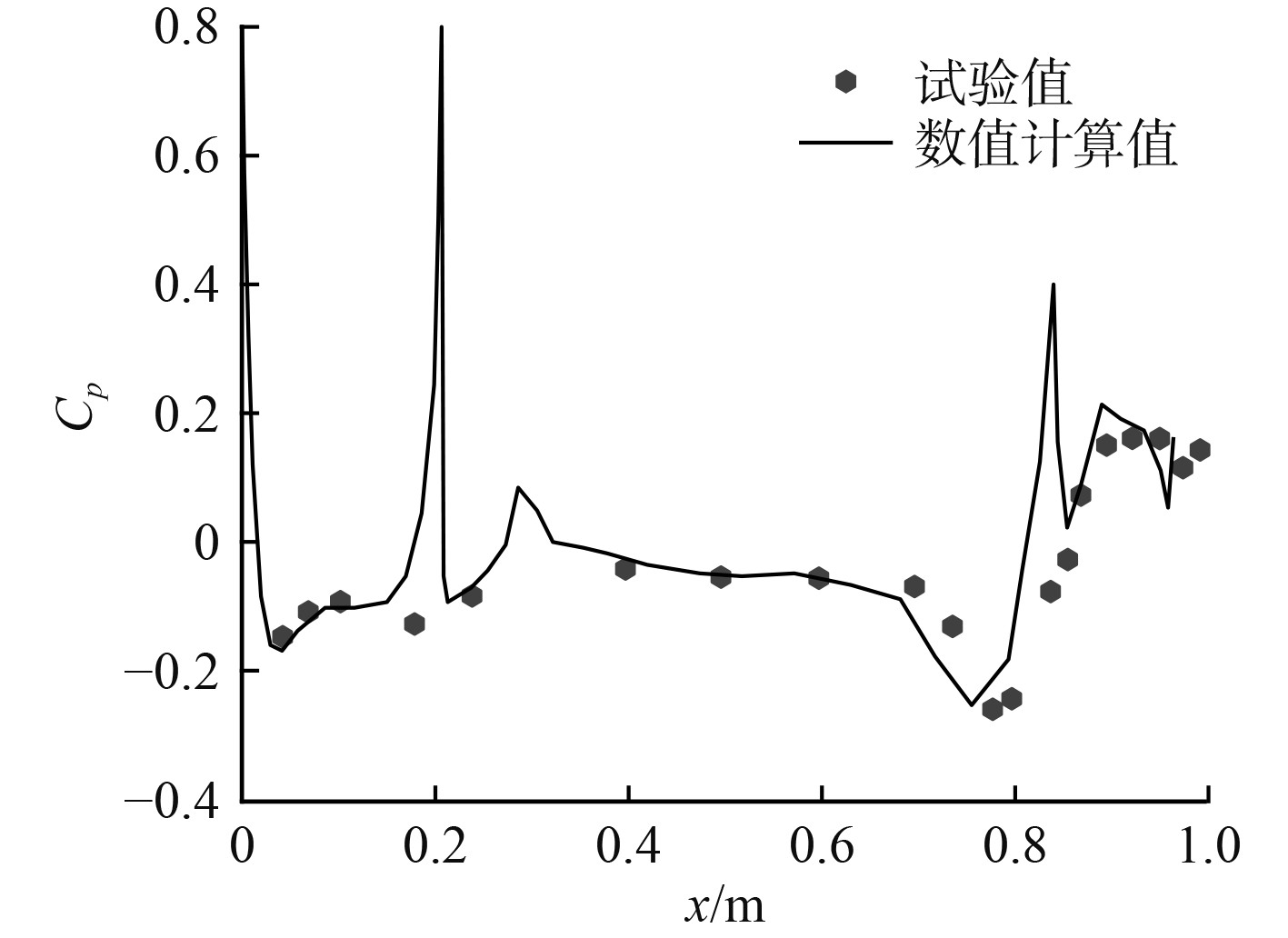
为验证本文中采用的数值模拟方法的可靠性,对SUBOFF标准模型进行数值模拟并与文献[11]试验值进行比较。总阻力数值计算值比试验值略大,误差为1.66%,如表3所示;摩擦阻力计算值与经验公式计算结果相比较,如表4所示,误差为1.71%;特征点(2.178,0,−2)处的总声压级为104 dB,与试验值101.3 dB接近,如表5所示,误差为2.67%。
|
|
表 3 总阻力数值计算值与试验值 Tab.3 Numerical calculation value and test value of total resistance |
|
|
表 4 摩擦阻力数值计算值与经验公式值 Tab.4 Numerical value of friction resistance and empirical formula value |
|
|
表 5 总声压级数值计算值与试验值 Tab.5 Numerical and experimental values of total sound pressure level |
压力系数
| $ {C_p} = \frac{{P - {P_0}}}{{0.5{\rho _0}\upsilon _0^2}}。$ | (10) |
其中:
图5为压力系数
|
图 5
潜艇表面压力系数
|
对5种不同相对厚度的指挥台围壳进行流场数值模拟研究,分析指挥台围壳相对厚度对潜艇绕流场和水动力噪声的影响。它们的计算条件相同,均为直航运动,航行速度均为3.05 m/s。
2.1 不同相对厚度指挥台围壳对流场涡量的影响指挥台围壳周围流场涡量包括马蹄涡、梢涡、尾涡和片状涡等[13]。其中马蹄涡是围壳绕流场中最为明显的流动结构,对噪声以及潜艇螺旋桨来流特性都有显著影响。后处理软件使用商用CFD-POST。图6为5种不同相对厚度指挥台围壳仿真结果,利用Q准则得到指挥台围壳周围的马蹄涡分布情况和指挥台围壳后方马蹄涡耗散情况,Q取为3.12×10−4。

|
图 6 指挥台围壳周围涡量分布 Fig. 6 Vorticity distribution around the sail |
可以看到,当流体经过指挥台围壳时,会出现明显的U型涡结构,这就是指挥台围壳周围的明显的马蹄涡,马蹄涡的形成是由于逆压梯度的存在。当边界层流体遇到障碍物时,障碍物会对流体产生阻碍作用,使流体速度减小,压力增大,进而产生下游压力大上游压力小的逆压梯度,在逆压梯度足够大时流体就会向上游反向运动,来流与逆流之间相互作用,就形成了马蹄涡。马蹄涡不仅会对结构本身产生侵蚀损坏的作用,还会产生噪声。通过观察可以看出,在指挥台围壳周围的马蹄涡“涡管”粗壮,在从指挥台围壳流向潜艇尾部时,“涡管”不断细化,马蹄涡强度逐渐减弱,“涡管”越粗壮,代表着马蹄涡强度越大,其产生的噪声也就越大。不同的指挥台围壳周围的马蹄涡强度不同,可以看出:图6(a)~6(c),随着指挥台围壳相对厚度的增加,指挥台围壳周围马蹄涡的“涡管”变得越来越粗壮,在围壳1周围,只有指挥台围壳前缘有“涡管”的形成,随着相对厚度的增加,“涡管”不断向后延伸,在围壳3周围,“涡管”几乎完整的包裹住了整个指挥台围壳,而6(d)指挥台围壳周围的马蹄涡与6(c)相比几乎没有什么变化。图6(a)~6(d)的 “涡管”消失的位置离指挥台围壳的距离也随着相对厚度的增加而不断增大,图6(e)中“涡管”消失的位置离指挥台围壳的距离有所减小,甚至比6(b)的距离还小。
通过观察指挥台围壳后方涡量的分布情况可以看出,围壳1后方的马蹄涡在潜艇尾翼前方的位置处就已经完全消失,恢复了正常的流场状态,随着指挥台围壳相对厚度的增加,指挥台围壳后方的马蹄涡向下游传播距离不断增大,在围壳4后方的潜艇尾翼前方,马蹄涡“涡管”依旧粗壮,马蹄涡的强度依然很大,同时还伴有梢涡等其他种类涡的存在。围壳5后方的潜艇尾翼前方马蹄涡强度有所减小。而艇体尾部指挥台围壳正后方的流体凹陷的部位代表着马蹄涡的冲击作用,在围壳1正后方的流体凹陷很微弱,在围壳1到围壳4对应的尾部流场中,随着相对厚度的增加,凹陷的程度不断加深,围壳5凹陷程度较围壳4有所缓和。
通过上述分析可以发现,指挥台围壳周围的马蹄涡强度不是随着指挥台围壳相对厚度的增加而单调增强。围壳1~围壳3的计算结果表明指挥台围壳相对厚度越大,指挥台围壳周围的马蹄涡强度也就越大,对潜艇表面的流场影响也就越大。继续增加指挥台围壳相对厚度,指挥台围壳周围的马蹄涡强度几乎不再变化,对潜艇表面的流场影响会随着指挥台围壳相对厚度的继续增加而减弱。故指挥台围壳相对厚度的增加对潜艇流场马蹄涡的影响不是单调的,而是在一定范围内随着指挥台围壳相对厚度的增加,马蹄涡会越来越强,超过这个范围,马蹄涡的强度会随着指挥台围壳相对厚度的增加而减弱。
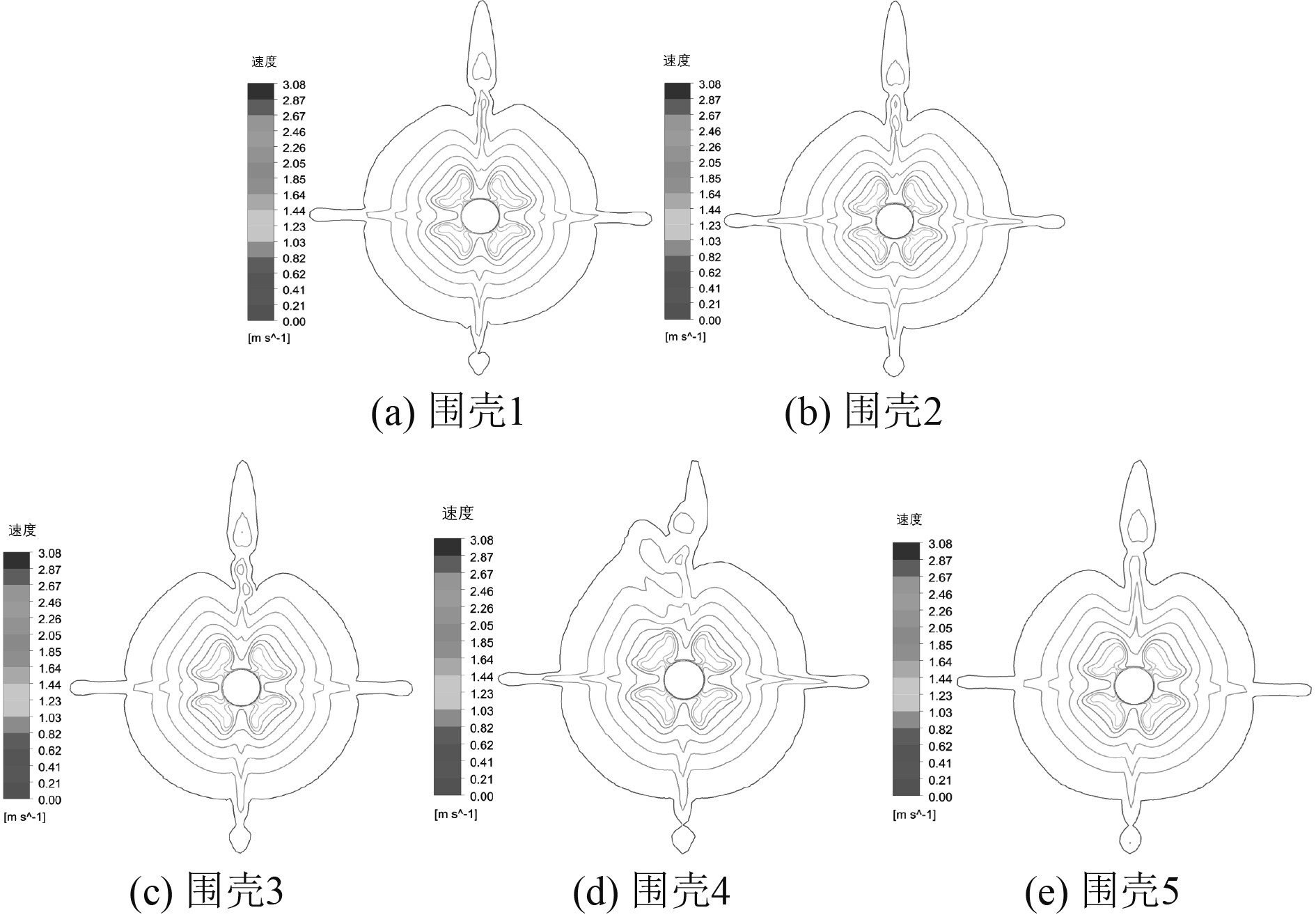
2.2 不同相对厚度指挥台围壳对桨盘面处速度场的影响螺旋桨噪声作为潜艇3大噪声源之一,桨盘面处的流动情况会直接影响螺旋桨噪声大小,桨盘面处的速度分布情况成为研究潜艇水动力噪声不可缺或缺的研究对象。桨盘面速度分布越均匀,代表着螺旋桨周围的流体流动越稳定,越有利于降低潜艇噪声。图7为5种不同指挥台围壳相对厚度潜艇的仿真结果桨盘面处速度分布情况。
|
图 7 桨盘面处速度分布 Fig. 7 Velocity distribution at the surface of the propeller |
通过对5种不同相对厚度指挥台围壳桨盘面处的速度分布情况可以看出,除了指挥台围壳正后方,即截面的正上方中央处的速度等值线分布情况随着指挥台围壳相对厚度的改变而改变外,其余位置的速度等值线分布情况几乎没有变化。在围壳1~围壳4的4个计算结果中,随着指挥台围壳相对厚度的增加,截面的正上方中央处的速度等值线分布均匀度逐渐降低,围壳1对应的速度等值线处是一条连续的等值线;围壳2相应位置出现2条速度等值线;围壳3相应位置出现3条速度等值线;围壳4相应位置的速度等值线分布情况更复杂,等值线的均匀度降低;围壳5相应位置的速度等值线分布比围壳1的还要均匀,表明围壳5桨盘面处的流场均匀度更好,更有利于降低潜艇的噪声。
通过以上分析可以看出,在一定范围内,随着指挥台围壳相对厚度的增加,桨盘面处的速度等值线均匀度逐渐降低,流场分布也就更加不稳定,当指挥台围壳相对厚度达到一定值后,桨盘面处的速度等值线均匀度随着指挥台围壳相对厚度的继续增加而提升。所以说指挥台围壳相对厚度对潜艇桨盘面处流场影响并不是单一的。在一定范围内,减小指挥台围壳的相对厚度可以改善桨盘面处的速度均匀程度,使流场更加稳定,有助于降低潜艇噪声。超出这个范围结论则相反。
2.3 不同相对厚度指挥台围壳对脉动压力的影响分别在5个潜艇计算模型的左侧指挥台围壳与艇体交接部位布置6个测点进行脉动压力大小结果的提取,测点位置如图8所示。
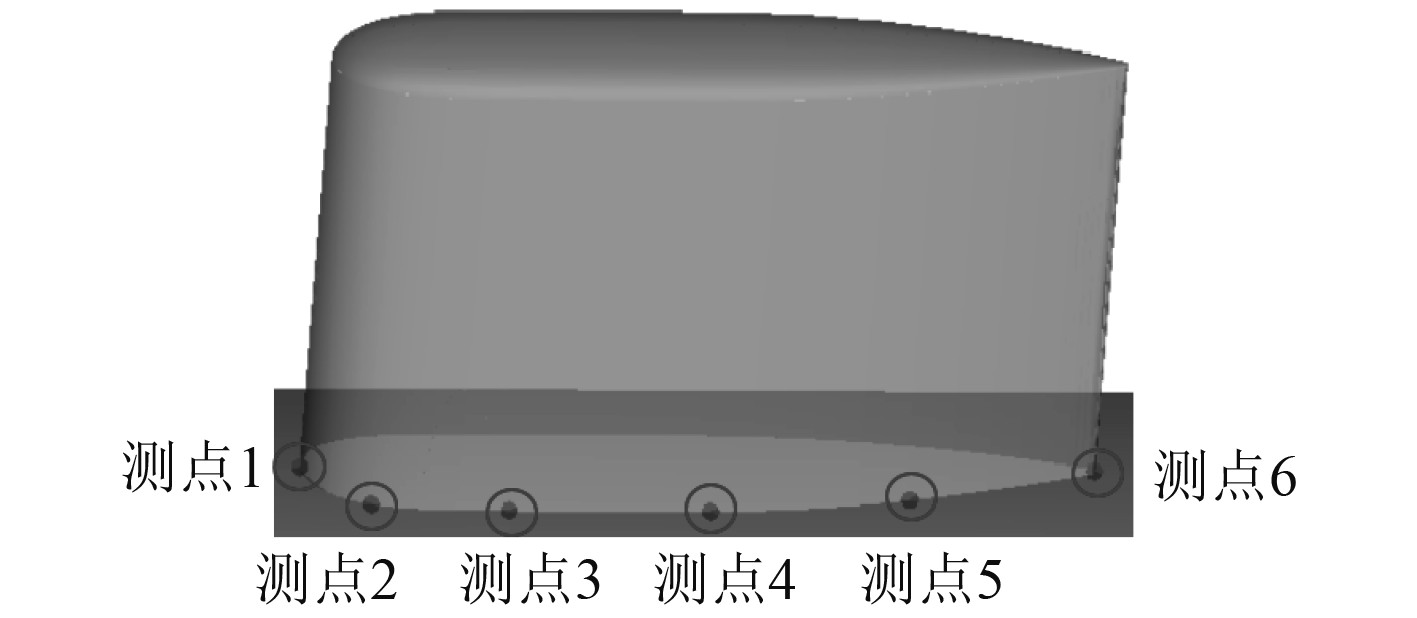
|
图 8 特征点分布 Fig. 8 Feature point distribution |
5个计算模型测点的x坐标不变,根据潜艇指挥台围壳相对厚度的改变,特征点的y坐标和z坐标会随之改变。将6个测点的脉动压力提取结果经过快速傅里叶变换得到频谱图,最终选择测点2与测点4进行分析总结。5种不同相对厚度的指挥台围壳测点2与测点4频谱图如图9所示。
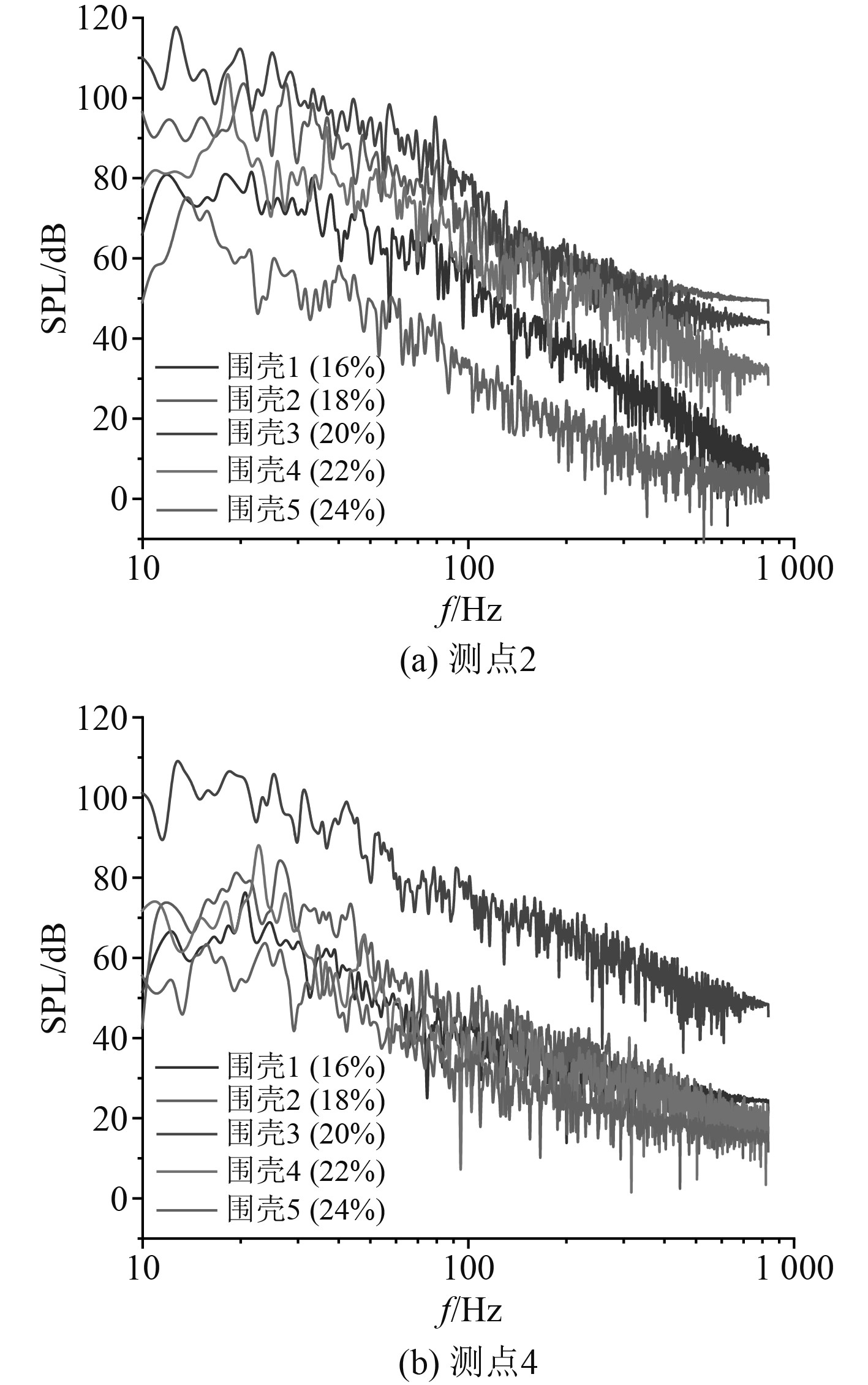
|
图 9 特征点脉动压力频谱图对比 Fig. 9 Comparison of sound pressure spectrum of feature points |
由于水动力噪声易与结构振动产生耦合,所以要重点关注水动力噪声的低频特性,脉动压力又是水动力噪声的主要来源,故需重点关注脉动压力的低频段特性。通过分析图9中测点2和测点4 的100 Hz以下的低频段脉动压力的频谱图可以发现,在围壳1、围壳2、围壳3中,随着指挥台围壳相对厚度的增加,低频段的脉动压力也越来越大;继续增大指挥台围壳相对厚度,即围壳4与围壳5的低频段的脉动压力越来越小,并且围壳5低频段脉动压力要小于围壳4。在一定指挥台围壳相对厚度范围内,随着指挥台围壳相对厚度的增加,低频段的脉动压力也对应跟着增大,但超出这个范围,低频段的脉动压力随着指挥台围壳相对厚度的增加而减小。
3 结 语本文采用延时分离涡模拟(IDDES)模型,研究分析了不同指挥台围壳相对厚度对潜艇绕流场和水动力噪声的影响,得出结论如下:
1)通过将仿真计算结果与标准SUBOFF模型试验值进行对比分析,发现仿真计算阻力值与试验阻力值误差仅为1.66%;摩擦阻力计算值与经验公式计算结果误差仅为1.71%;潜艇表面压力系数
2)指挥台围壳相对厚度的增加对潜艇绕流场马蹄涡的影响不是单调的。在一定范围内,减小指挥台围壳的相对厚度可以改善指挥台围壳周围的马蹄涡强度,可以减弱其对潜艇尾部流场的影响;超出这个范围,结论则相反。
3)指挥台围壳相对厚度的增加对潜艇桨盘面处流场影响并不是单一的。在一定范围内,减小指挥台围壳的相对厚度可以改善桨盘面处的速度分布,使螺旋桨周围流场分布更均匀,更稳定;超出这个范围,结论则相反。
4)在一定指挥台围壳相对厚度范围内,随着指挥台围壳相对厚度的增加,低频段的脉动压力也对应跟着增大,但超出这个范围,低频段的脉动压力随着指挥台围壳相对厚度的增加而减小。脉动压力是指挥台围壳部位水动力噪声的主要来源,即水动力噪声的变化规律与脉动压力的变化规律一致。
| [1] |
尚大晶, 李琪, 商德江, 等. 水下翼型结构流噪声实验研究[J]. 声学学报, 2012, 37(4): 416-423. DOI:10.15949/j.cnki.0371-0025.2012.04.010 |
| [2] |
DOZIER D, STOUT M, ZOCCOLA M. Advanced sail development wavelengths[J]. An Employee Digest of Events and Information, Carderock Division, Naval Surface Warfare Center, 2001: 15–17.
|
| [3] |
WANG X, HUANG Q, PAN G. Numerical research on the influence of sail leading edge shapes on the hydrodynamic noise of a submarine[J]. Applied Ocean Research, 2021, 117: 102935. DOI:10.1016/j.apor.2021.102935 |
| [4] |
张楠, 吕世金, 沈泓萃, 等. 潜艇围壳线型优化抑制脉动压力与流激噪声的数值模拟研究[J]. 船舶力学, 2014, 18(4): 448-458. DOI:10.3969/j.issn.1007-7294.2014.04.013 |
| [5] |
刘龙举, 许勇. 沙丘形围壳对潜艇流场影响的数值模拟[J]. 四川兵工学报, 2014, 35(11): 1-4. |
| [6] |
王志博, 姚惠之, 张楠. 指挥台围壳对潜艇尾流影响的计算研究[J]. 船舶力学, 2009, 13(02): 196-202. DOI:10.3969/j.issn.1007-7294.2009.02.006 |
| [7] |
SPALART P R, JOU W H, STRELETS M, et al. Comments on the feaslibility of LES for wings, and on a hybrid RANS/LES
|
| [8] |
胡晓峰, 张新曙, 李聪洲, 等. 深吃水半潜生产平台涡激运动特性研究及其参数化分析[J]. 船舶力学, 2021, 25(4): 435-442. DOI:10.3969/j.issn.1007-7294.2021.04.006 |
| [9] |
SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 |
| [10] |
GROVES N C, HUANG T T, CHANG M. Geometric characteristics of DARPA models (DTRC Model No. 5470 and 5471), DTRC/SHD-1298-01, 1989.3
|
| [11] |
LIU Hall-Lieh, THAMAS T H. Summary of DARPA SUBOFF experimental program data[R]. US: Naval Surface Warfare Center, Carderock Division (NSWCCD ), 1999.
|
| [12] |
BULL P. The validation of CFD predictions of nominal wake for the suboff fully appended geometry[C]// Twenty-First Symposium on Naval Hydrodynamics, 1997.
|
| [13] |
章文文, 徐荣武. 指挥台围壳水动力噪声及控制技术研究综述[J]. 中国舰船研究, 2020, 15(6): 72-89. ZHANG Wenwen, XU Rongwu. Summary of research on hydrodynamic noise and control technology of the sail[J]. Chinese warship Research, 2020, 15(6): 72-89. |
 2023, Vol. 45
2023, Vol. 45

