2. 宁波大学 海运学院,浙江 宁波 315211;
3. 宁波大学 东海战略研究院,浙江 宁波 315211
2. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China;
3. Donghai Academy, Ningbo University, Ningbo 315211, China
针对实尺度船舶的水动力性能研究,当前广泛采用的技术手段是利用模型尺度的水池试验或者数值模拟数据外推得到实船的水动力性能。然而,船模尺度与实船尺度之间往往不满足某些相似准则,其中最主要的是表征流体惯性力与粘性力比值的雷诺数。对于不同尺度下的船模试验或数值计算,不能同时满足傅汝德数与雷诺数相等,因此在水动力外推预报时存在“尺度效应”[1]。对于水下航行体而言,“尺度效应”问题是影响其水动力性能预报精度的重要因素,给实尺度船舶航行性能评估带来一定困扰。随着计算流体动力学(computational fluid dynamics, CFD)的发展,应用CFD方法对船舶及水下航行体水动力的尺度效应分析并预报实船水动力性能是当前船舶水动力学研究领域的热点之一。
操盛文等[2]对高雷诺数下SUBOFF潜艇的全附体模型绕流进行数值模拟,研究了网格数量及艇体尺度对高雷诺数条件下潜艇阻力计算结果的影响。吴方良等[3]对SUBOFF潜艇的主艇体模型和全附体模型在不同雷诺数条件下的流场进行了数值模拟,分析了潜艇粘压阻力系数随雷诺数变化的规律。司朝善等[4]以SUBOFF潜艇全附体模型为对象,通过改变潜艇尺度实现不同雷诺数下的潜艇直航绕流数值模拟,分析了模型尺度对潜艇阻力性能和绕流场的影响规律。王展智等[5]以DTMB5415裸船体和全附体模型为研究对象,计算了包含实尺度在内的多种缩尺模型的流场,详细分析了双桨水面舰船附体阻力的尺度效应。张恒等[6]以KCS船型作为研究对象,计算了不同雷诺数下的阻力并对船体尾部流场进行分析,探讨了改变介质的粘性系数以满足全相似在实尺度预报方面的可行性。蔡博奥等[7]针对不同缩尺比的三体船模型进行了各阻力成分的数值预报,探讨了三体船阻力成分关于水动力系数的变化规律并提出了三体船阻力换算的改进方法。师超等[8]开展了不同船体尺度下的裸船体斜航和定常回转数值计算,探讨了不同尺度下船体操纵运动水动力的变化规律,并结合船舶操纵运动数学模型分析了尺度效应对操纵性的影响。Dogrul等[9]对不同尺度下的KCS和KVLCC2船的阻力试验进行了数值模拟,探讨了不同阻力成分的尺度效应问题,并据此分析了不同外推方法在船舶实尺度阻力预报方面的有效性。宋科委等[10]以DTMB5415船型为研究对象,预报了多种尺度、多种工况及多种船体壁面条件下的阻力性能,对船体形状因子、兴波阻力及摩擦阻力的尺度效应问题进行了分析,探讨了多种实船阻力性能预报方法存在差异的原因。Sezen等[11]以SUBOFF潜艇模型为对象,研究了尺度效应对潜艇阻力等水动力性能参数的影响,通过对实尺度潜艇阻力试验的数值模拟,验证了基于傅汝德外推法的实尺度阻力预报方面的有效性。
从以上研究可以看出,针对船舶及水下航行体水动力性能尺度效应的研究大多集中在阻力性能方面,而针对船舶及水下航行体操纵性能尺度效应问题的研究还十分有限。本文针对水下航行体的操纵性能评估需求,开展水下航行体操舵水动力性能的尺度效应问题数值研究,应用CFD方法开展不同尺度的水下航行体直航操舵试验数值模拟,探讨艇体绕流场及水动力特性随雷诺数的变化规律,为构建实尺度水下航行体操舵水动力性能的外推预报方法提供参考。
1 数值方法考虑到水下航行体操舵工况下存在的大尺度流动分离现象,应用分离涡模拟(Detached Eddy Simulation, DES)求解器开展数值计算。求解器所采用的DES方法基于剪切应力输运(Shear Stress Transfer, SST)
| $ \left\{ \begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = P - {\beta ^*}\rho \omega k + \\ \qquad\qquad\qquad\qquad\frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}}\right],\\ \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\omega } \right)}}{{\partial {x_j}}} = \frac{{\rho \gamma }}{{{\mu _t}}}P - {\beta ^*}\rho {\omega ^2} + \\ \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] + 2\left( {1 - {F_1}} \right)\frac{{\rho {\sigma _{\omega 2}}}}{\omega } \cdot \frac{{\partial k}}{{\partial {x_j}}} \cdot \frac{{\partial \omega }}{{\partial {x_j}}} 。\\ \end{gathered} \right. $ | (1) |
式中:
将RANS湍流模型中的长度尺度采用DES的长度尺度代替,即可获得基于该湍流模型的DES方法,DES的长度尺度表示如下:
| $ {l_{DES}} = \min \left( {{l_{RANS}},{l_{LES}}} \right),$ | (2) |
其中,RANS长度尺度为最近壁面距离,表达如下:
| $ {l_{RANS}} = \frac{{{k^{1/2}}}}{{{\beta ^*}\omega }},$ | (3) |
此外,LES长度尺度仅与网格间距有关,表达如下:
| $ {l_{LES}} = {C_{DES}}\Delta 。$ | (4) |
式中,
由DES模型的构造可知,当RANS长度尺度激活时,以RANS湍流模型的方式计算;而当LES长度尺度激活时,湍流模型转换为经典的Smagorisnky亚格子模型,从而在求解流场时实现RANS方法与LES方法的耦合。
2 研究对象及工况本文以美国DARPA潜艇模型SUBOFF-8为研究对象,潜艇几何形状和主要尺度如图1和表1所示。针对不同缩尺比的潜艇模型,开展直航工况下的操舵试验数值模拟,工况见表1。数值模拟工况满足傅汝德数相似,对应傅汝德数Fr=0.512。

|
图 1 DARPA潜艇模型SUBOFF-8模型示意图 Fig. 1 Schematic diagram of DARPA submarine model SUBOFF-8 model |
|
|
表 1 研究对象及工况 Tab.1 Study object and working conditions |
主要关注对水下航行体操纵性能有显著影响的纵向力
| $ {X^{'}} = \frac{X}{{0.5\rho {V^2}{L^2}}} ,$ | (5) |
| $ {Y^{'}} = \frac{Y}{{0.5\rho {V^2}{L^2}}},$ | (6) |
| $ {N^{'}} = \frac{N}{{0.5\rho {V^2}{L^3}}} 。$ | (7) |
计算域为长方体,如图2所示。坐标系原点位于潜艇尾端,计算域入口(Inlet)边界距坐标系原点2.5倍艇长LOA,计算域出口(Outlet)边界距坐标系原点4.5倍艇长LOA,计算域左右边界(Left、Right)与上下边界(Top、Bottom)距坐标系原点2倍艇长LOA。边界条件方面,出口边界设为压力出口,其他边界均设置为速度入口,艇体表面设为无滑移壁面。
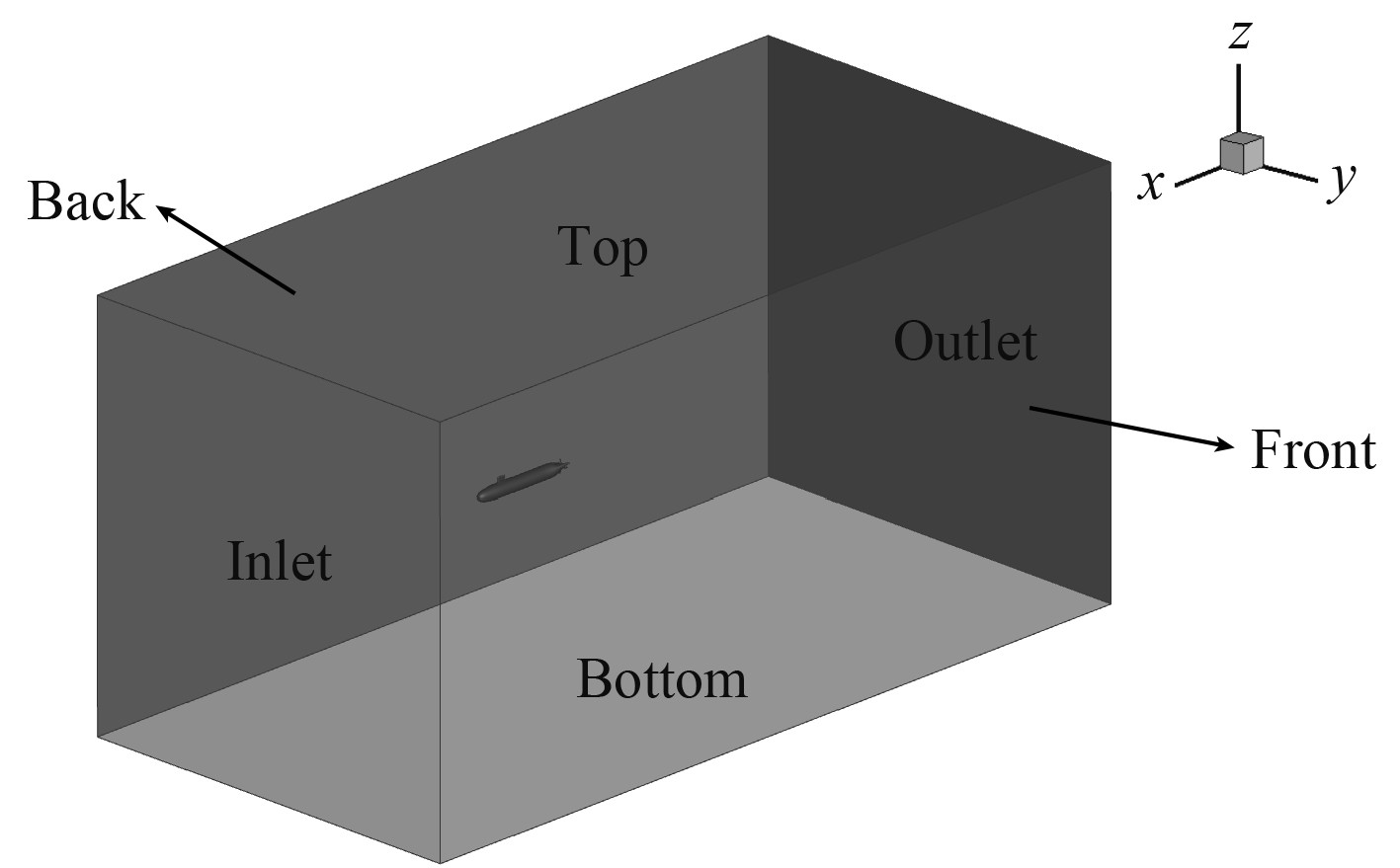
|
图 2 计算域划分及边界条件 Fig. 2 Division of the computational domain and boundary conditions |
计算域采用非结构六面体网格、棱柱层网格以及表面重构的方法进行网格划分。为了保证潜艇附近的网格质量,对其表面进行了加密。通过使用切割体网格单元,在艇体附近及其尾流进行网格密化,从而更好地捕捉流动细节,获得更准确的流场信息。通过调整棱柱网格层的厚度、层数及增长率来控制近壁面第一层网格高度,使无因次壁面距离y+值在30~300之间。图3和图4给出了潜艇表面和计算域的网格分布情况。
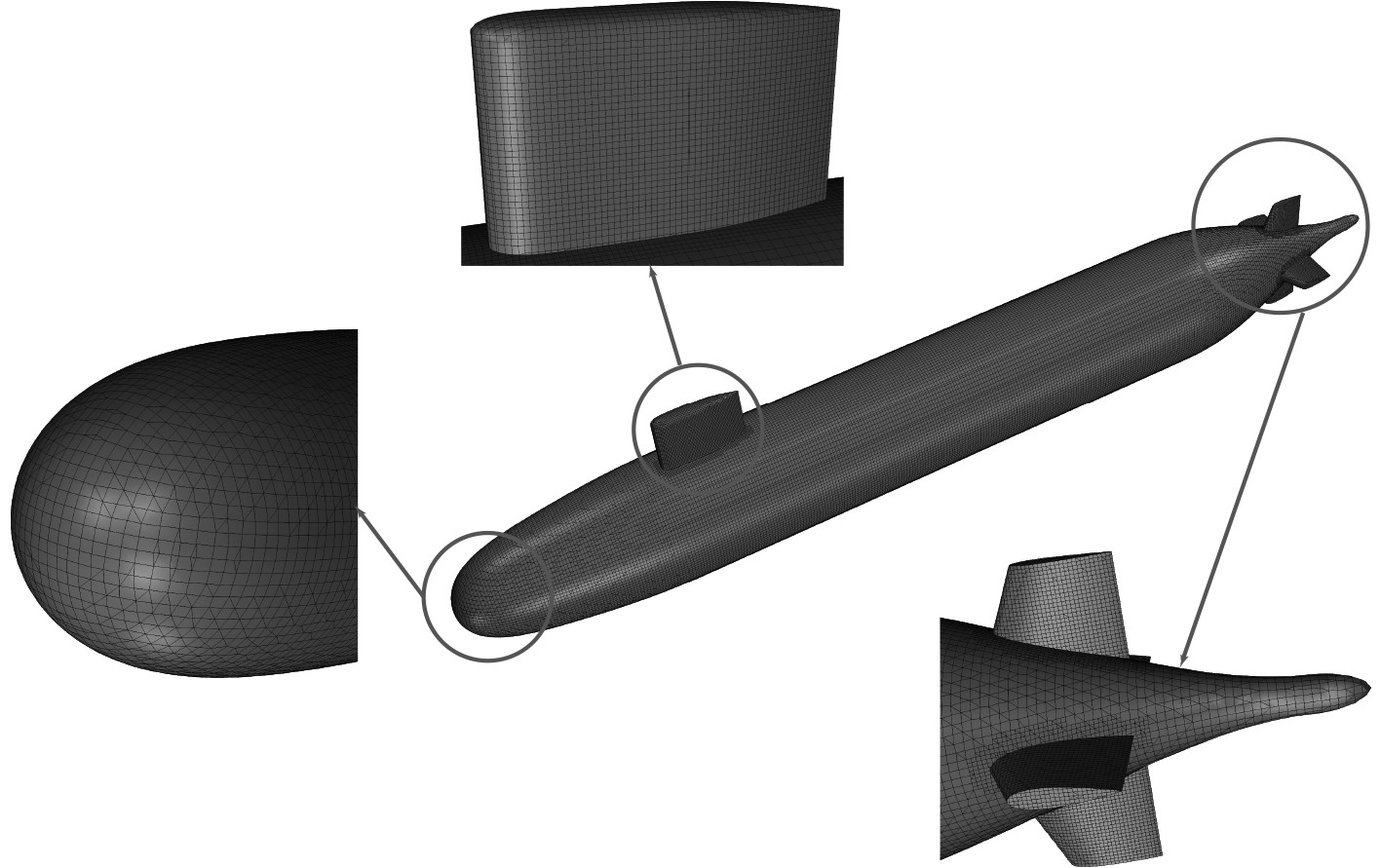
|
图 3 潜艇表面网格分布情况 Fig. 3 Grid distribution on the submarine surface |
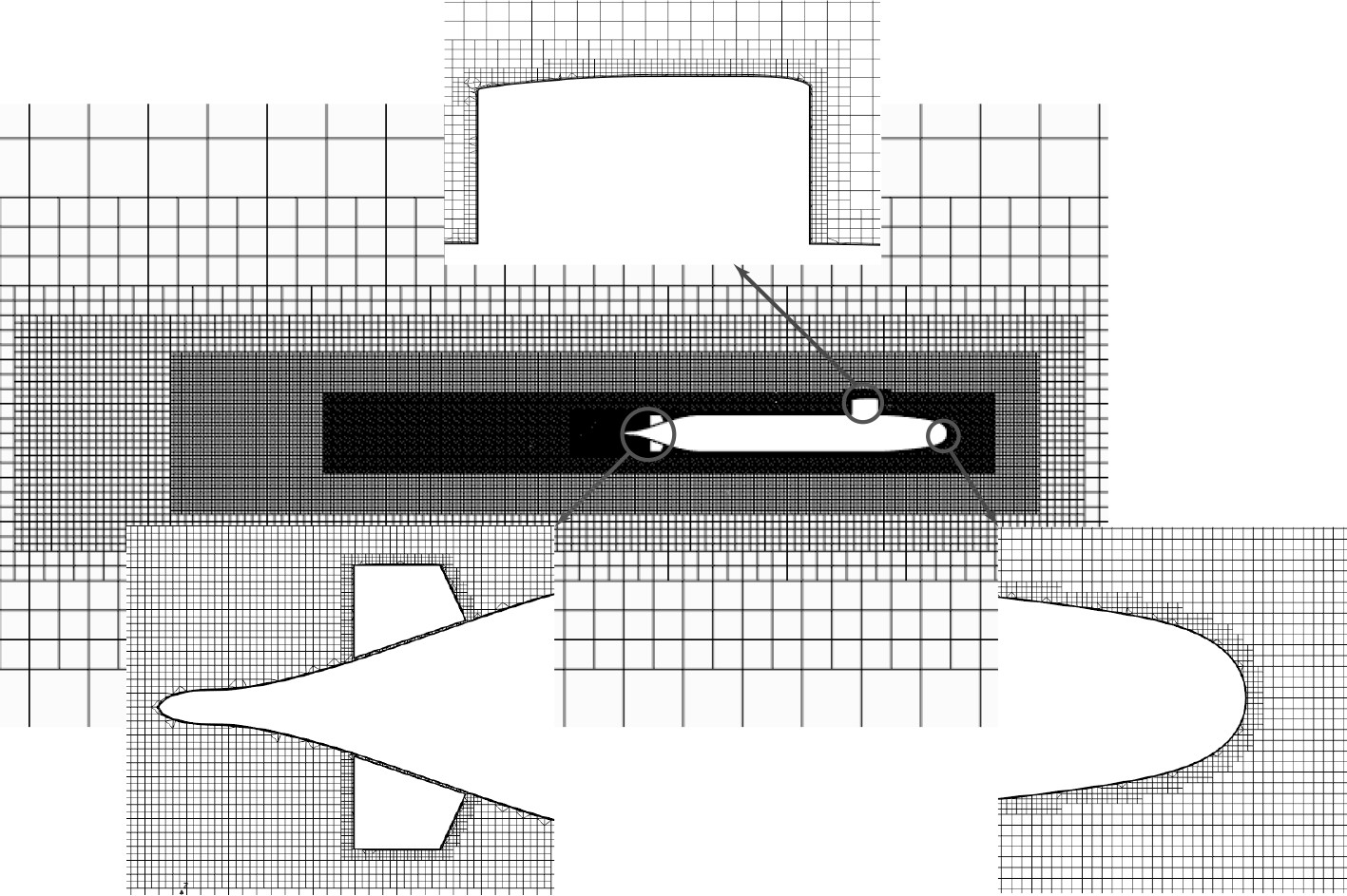
|
图 4 计算域网格分布 Fig. 4 Grid distribution in the computational domain |
采用Stern等[13]提出的方法开展网格收敛性分析:
| $ {\varepsilon _{G21}} = {S_{G2}} - {S_{G1}},$ | (8) |
| $ {\varepsilon _{G32}} = {S_{G3}} - {S_{G2}},$ | (9) |
| $ {R_G} = \frac{{{\varepsilon _{G21}}}}{{{\varepsilon _{G32}}}}。$ | (10) |
式中:
收敛性分析结果存在3种情况:1)0<
| $ {U_G} = \left| {\frac{1}{2}\left( {{S_U} - S{}_L} \right)} \right|。$ | (11) |
式中:
网格收敛时,采用广义理查森外推法计算误差的单项估算值和准确度阶数:
| $ \delta _{R{E_{G1}}}^{*\left( 1 \right)} = \frac{{{\varepsilon _{{G_{21}}}}}}{{r_G^{{p_G}} - 1}} ,$ | (12) |
| $ {p_G} = \dfrac{{\ln \left( {\dfrac{{{\varepsilon _{{G_{32}}}}}}{{{\varepsilon _{{G_{21}}}}}}} \right)}}{{\ln \left( {{r_G}} \right)}} 。$ | (13) |
式中,
若误差的单项估算值
| $ {C_G} = \frac{{r_G^{{p_G}} - 1}}{{r_G^{{p_{Gest}}} - 1}},$ | (14) |
式中,
如果修正因子远离1,缺少置信度,数值不确定度可以定义为:
| $ {U_G} = \left\{ {\begin{array}{*{20}{c}} {\left( {9.6{{\left( {1 - {C_G}} \right)}^2} + 1.1} \right)\left| {\delta _{R{E_{G1}}}^*} \right|,\left| {1 - {C_G}} \right| < 0.125},\\ {\left( {2\left| {1 - {C_G}} \right| + 1} \right)\left| {\delta _{R{E_{G1}}}^*} \right|,\left| {1 - {C_G}} \right| \geqslant 0.125} 。\end{array}} \right. $ | (15) |
在进行网格收敛性分析时,采用粗(S3)、中(S2)、细(S1)三套网格,网格细化比
|
|
表 2 网格收敛性研究网格数量 Tab.2 Grid number in the grid convergence study |
|
|
表 3 L/LOA=1时准确度阶数和网格不确定度分析 Tab.3 Estimated order of accuracy and grid uncertainty when L/LOA=1 |
|
|
表 4 L/LOA=2时准确度阶数和网格不确定度分析 Tab.4 Estimated order of accuracy and grid uncertainty when L/LOA=2 |
|
|
表 5 L/LOA=4时准确度阶数和网格不确定度分析 Tab.5 Estimated order of accuracy and grid uncertainty when L/LOA=4 |
|
|
表 6 L/LOA=8时准确度阶数和网格不确定度分析 Tab.6 Estimated order of accuracy and grid uncertainty when L/LOA=8 |
|
|
表 7 L/LOA=16时准确度阶数和网格不确定度分析 Tab.7 Estimated order of accuracy and grid uncertainty when L/LOA=16 |
对于网格收敛性研究中存在网格发散的情况,其原因是多方面的:潜艇大舵角操舵状态下舵附近流场往往存在大尺度流动分离现象,流场具有显著的非线性和非定常性;所采用的DES方法是一种混合算法,其湍流建模与网格尺度存在关联性,不同密度网格其流场内局部流动的湍流求解方式也有所差异,导致难以呈现出较好的网格收敛性。
5 计算结果 5.1 泄出涡系结构图5~图9给出了不同缩尺比潜艇的艇体及舵附近的无量纲Q准则瞬时等值面。等值面取Q=100s−2,并采用无因次纵向速度Ux/U0着色。可以看出,垂直舵附近产生了明显的泄出涡结构,这主要是由于舵背风面处由于舵角所产生的流动分离现象所致。通过观察不同缩尺比的等值面图可以发现,舵附近的泄出涡规模随着缩尺比的改变而逐渐变化。在缩尺比较小(L/LOA=1)时,舵背风面产生了大规模的流动分离现象,泄出涡脱落起始位置接近舵导缘位置。同时,舵叶梢部泄出涡与背风面泄出涡发生明显的相互作用,导致梢部泄出涡结构不明显。随着缩尺比增大(L/LOA=2,4,8,16),泄出涡脱落起始位置向尾缘移动,背风面泄出涡规模逐渐减小。同时,舵叶梢部泄出涡结构逐渐清晰,受背风面泄出涡的影响逐渐减小。总体而言,在舵角不变的条件下,舵背风面流动分离现象随着雷诺数的增大逐渐减弱。

|
图 5 L/LOA=1时艇体及舵附近的泄出涡结构 Fig. 5 Vortex structure around the submarine body and rudder with L/LOA=1 |
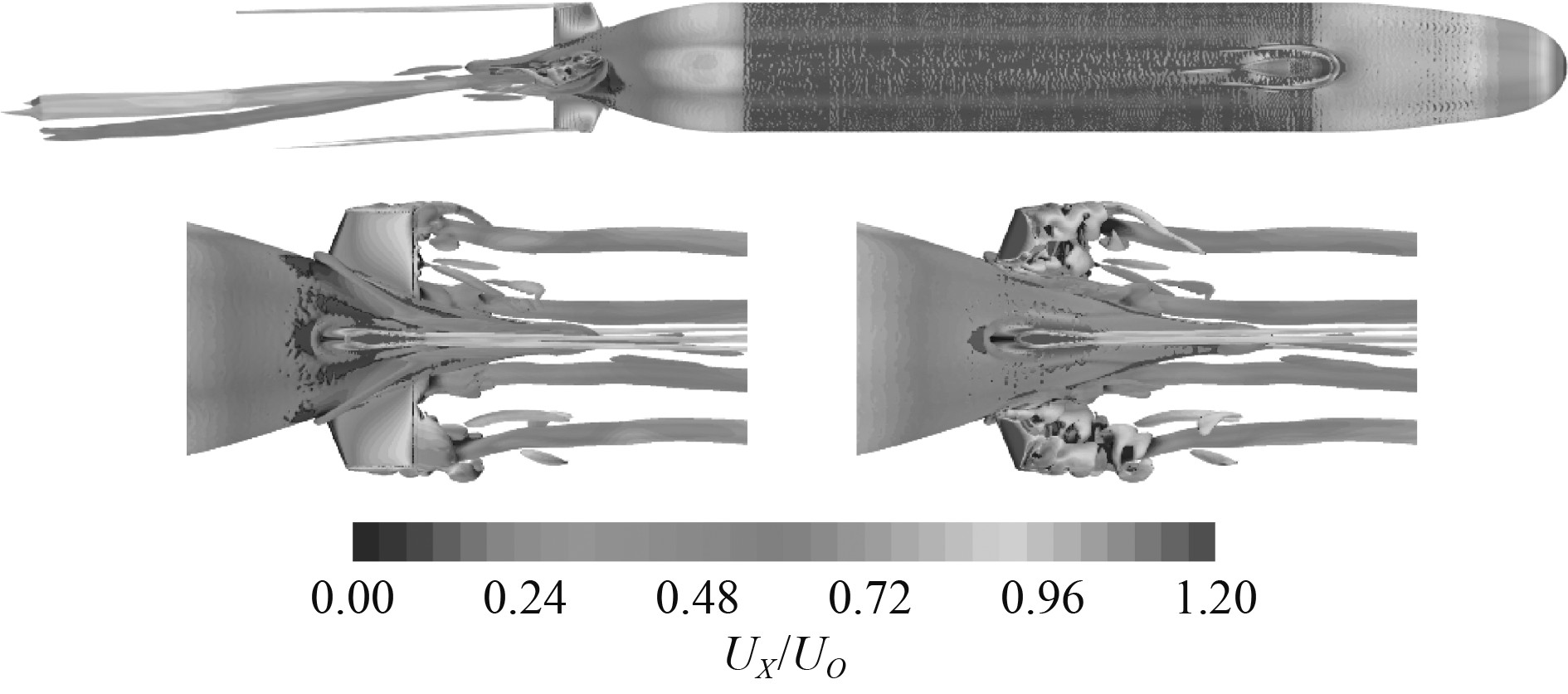
|
图 6 L/LOA=2时艇体及舵附近的泄出涡结构 Fig. 6 Vortex structure around the submarine body and rudder with L/LOA=2 |

|
图 7 L/LOA=4时艇体及舵附近的泄出涡结构 Fig. 7 Vortex structure around the submarine body and rudder with L/LOA=4 |

|
图 8 L/LOA=8时艇体及舵附近的泄出涡结构 Fig. 8 Vortex structure around the submarine body and rudder with L/LOA=8 |

|
图 9 L/LOA=16时艇体及舵附近的泄出涡结构 Fig. 9 Vortex structure around the submarine body and rudder with L/LOA=16 |
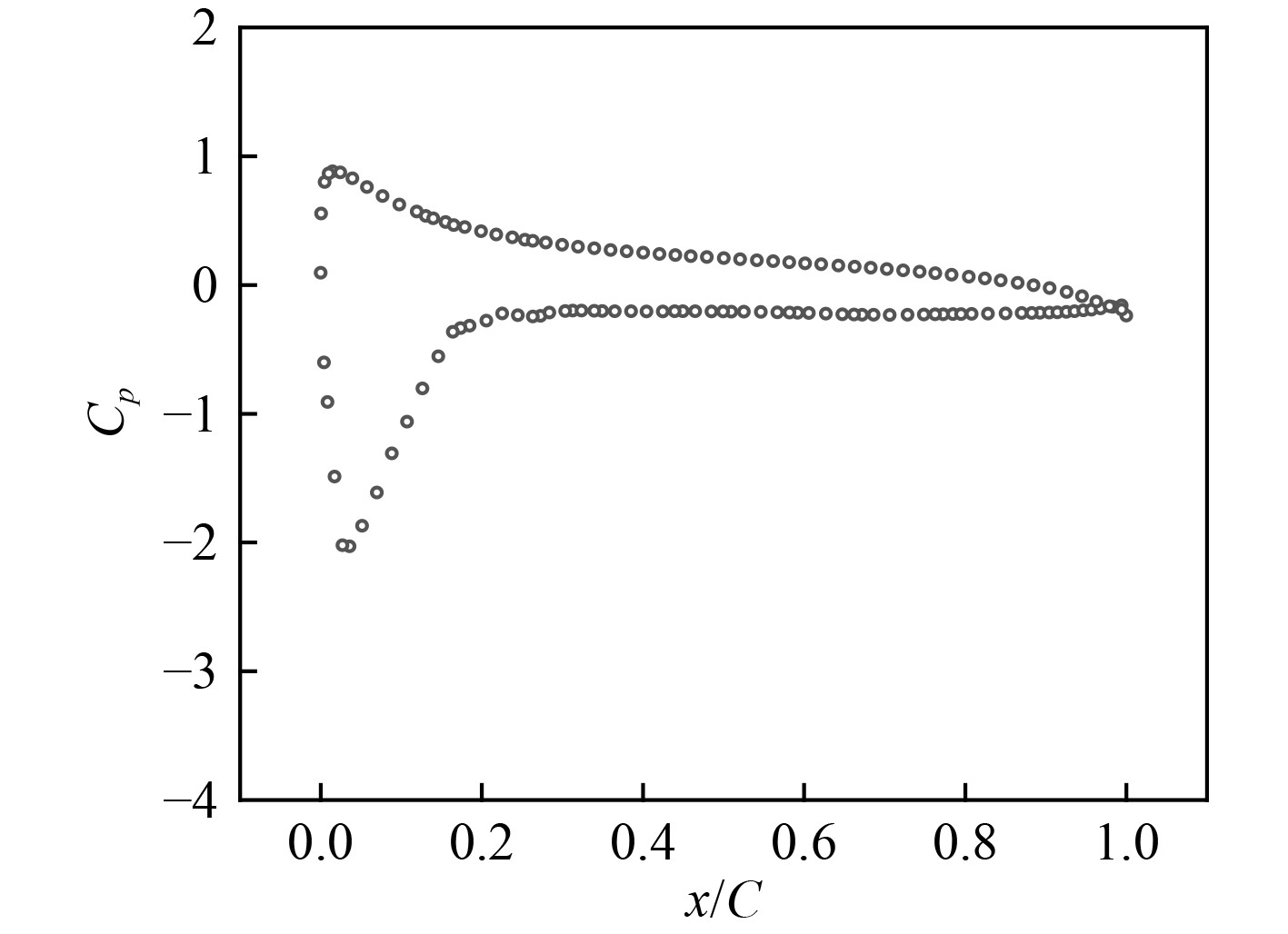
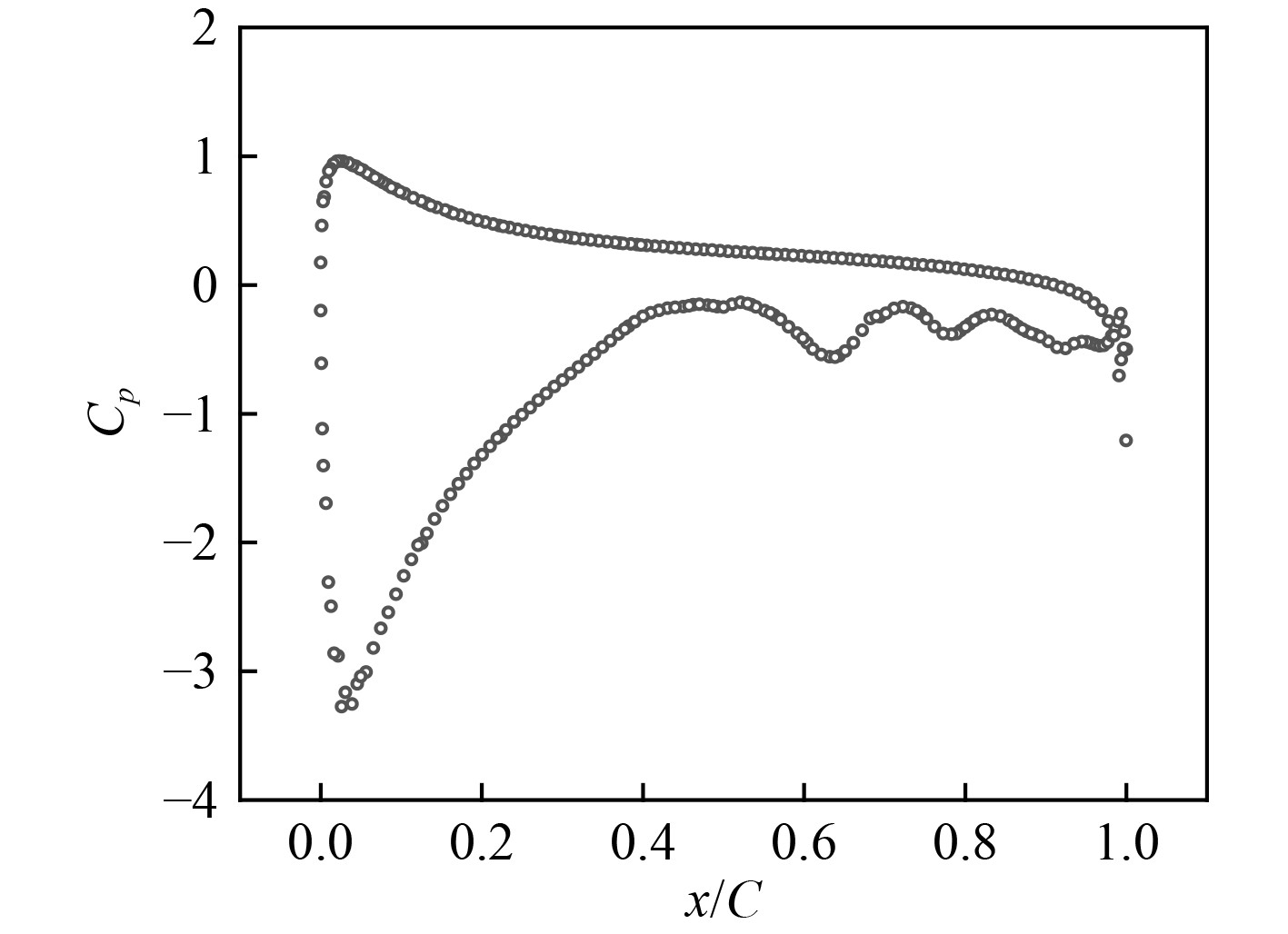
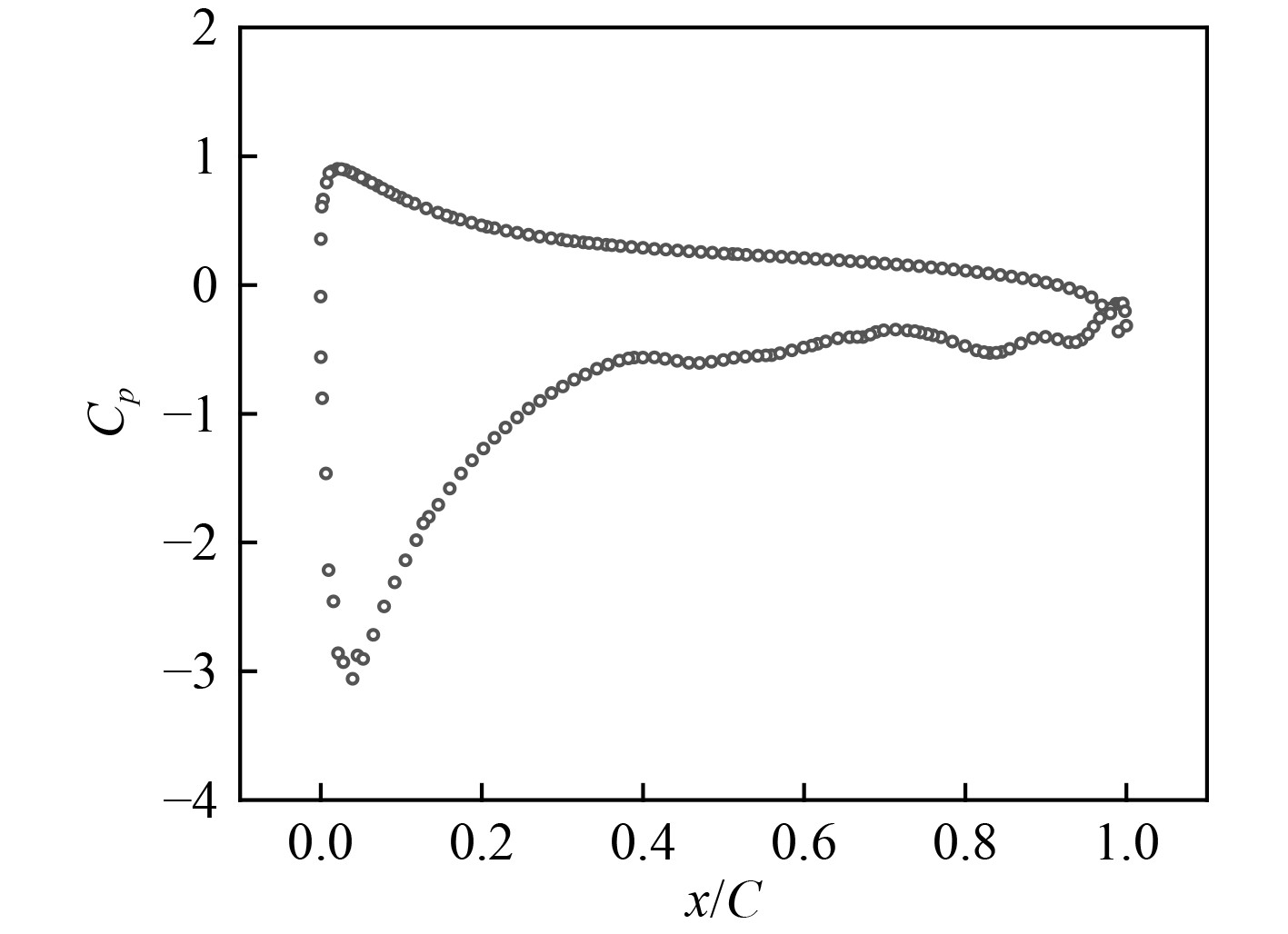
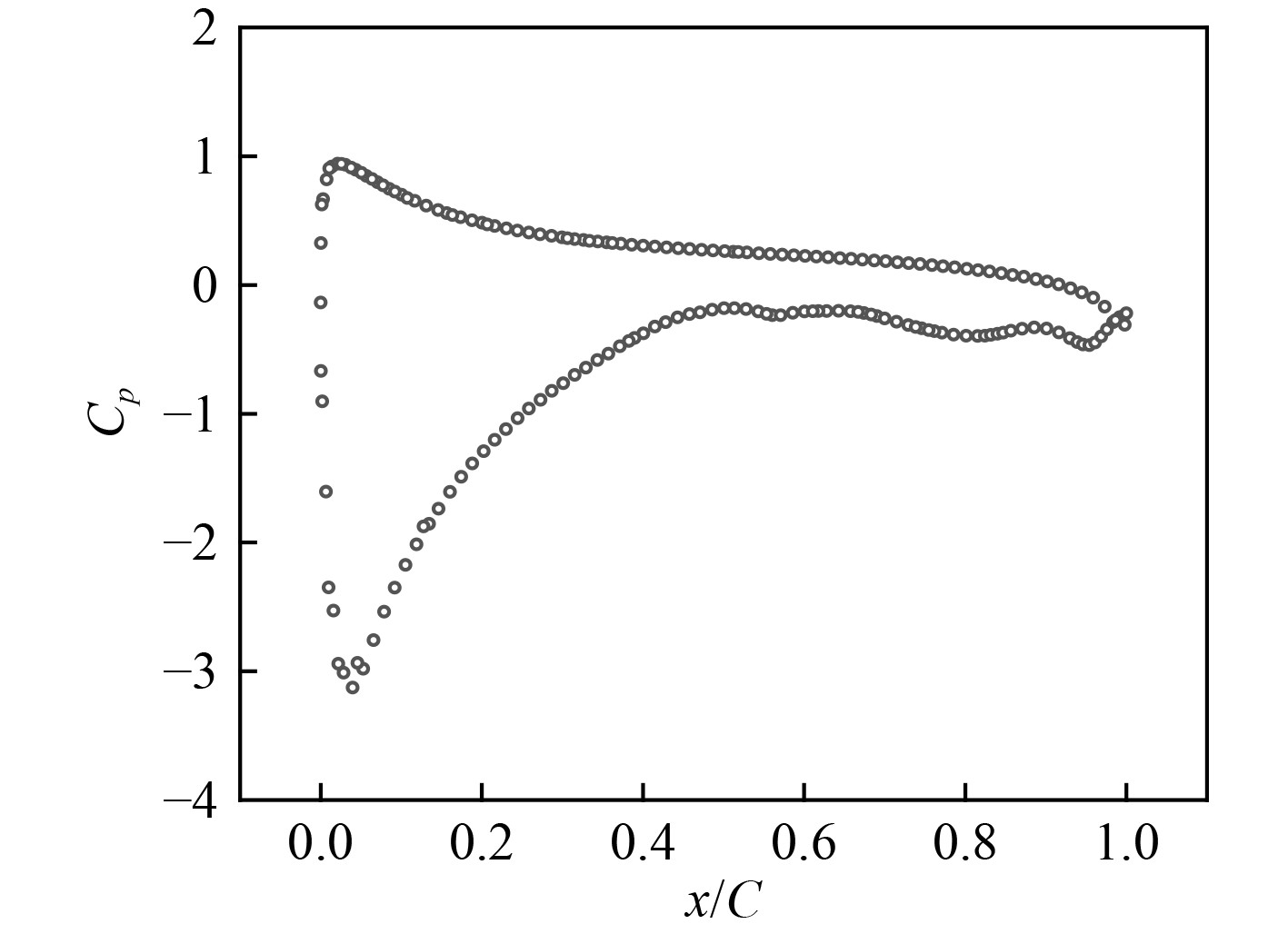
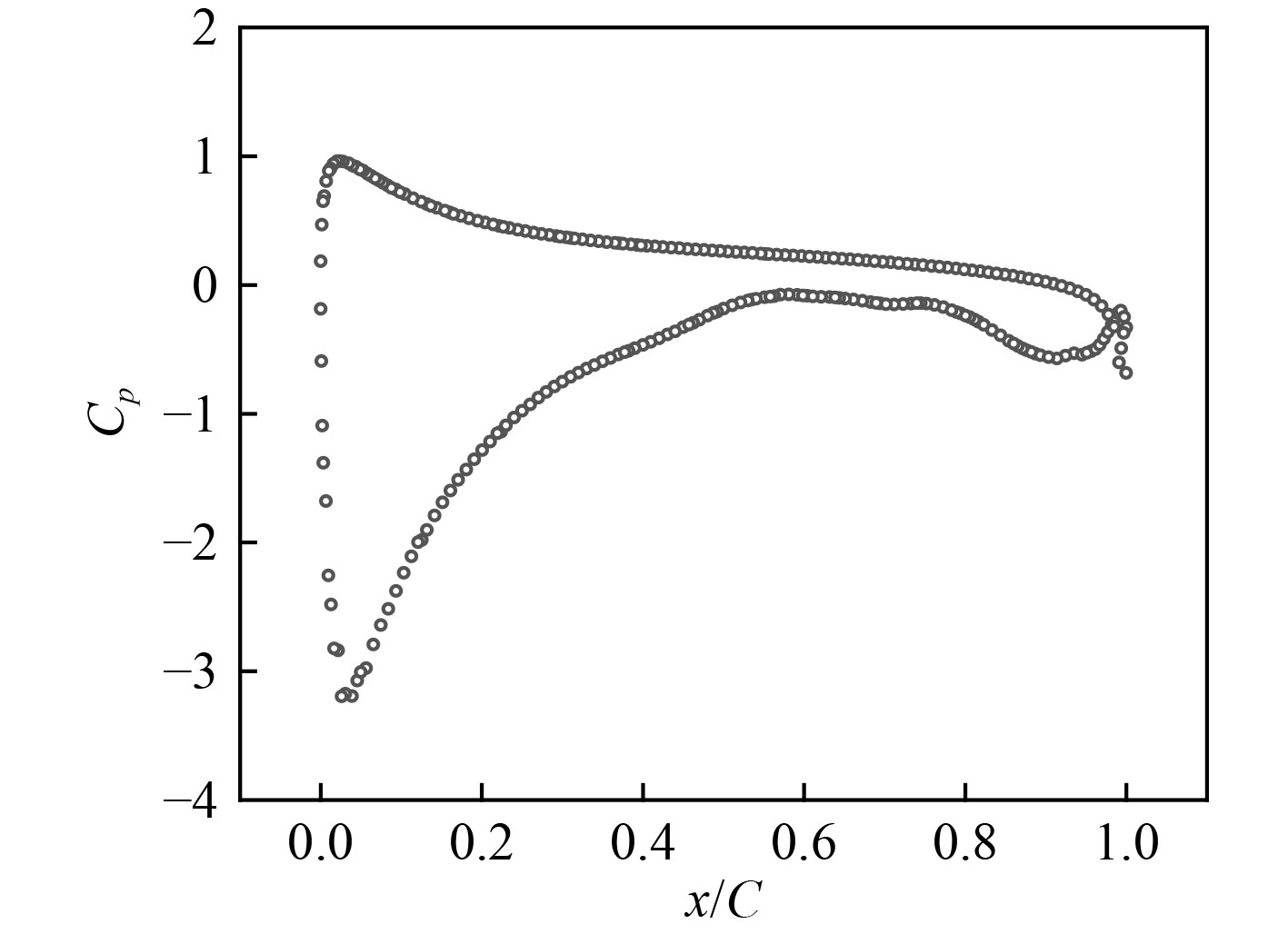
图10~图14给出了不同缩尺比潜艇的舵中剖面处的压力分布。压力采用无因次系数
|
图 10 L/LOA=1时舵中剖面处表面压力分布 Fig. 10 Pressure distribution on the midsection of the rudder with L/LOA=1 |
|
图 14 L/LOA=16时舵中剖面处表面压力分布 Fig. 14 Pressure distribution on the midsection of the rudder with L/LOA=16 |
|
图 11 L/LOA=2时舵中剖面处表面压力分布 Fig. 11 Pressure distribution on the midsection of the rudder with L/LOA=2 |
|
图 12 L/LOA=4时舵中剖面处表面压力分布 Fig. 12 Pressure distribution on the midsection of the rudder with L/LOA=4 |
|
图 13 L/LOA=8时舵中剖面处表面压力分布 Fig. 13 Pressure distribution on the midsection of the rudder with L/LOA=8 |
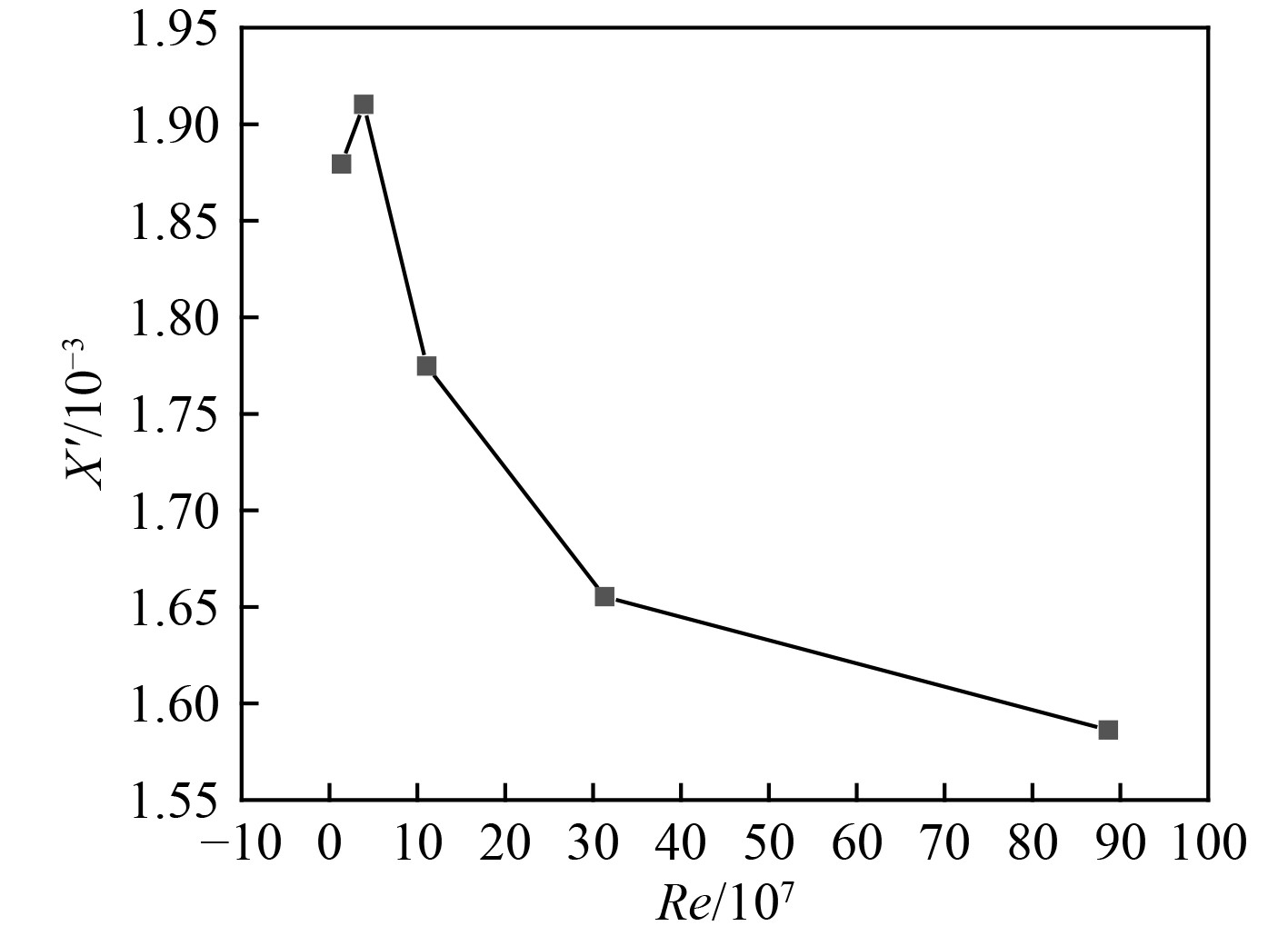
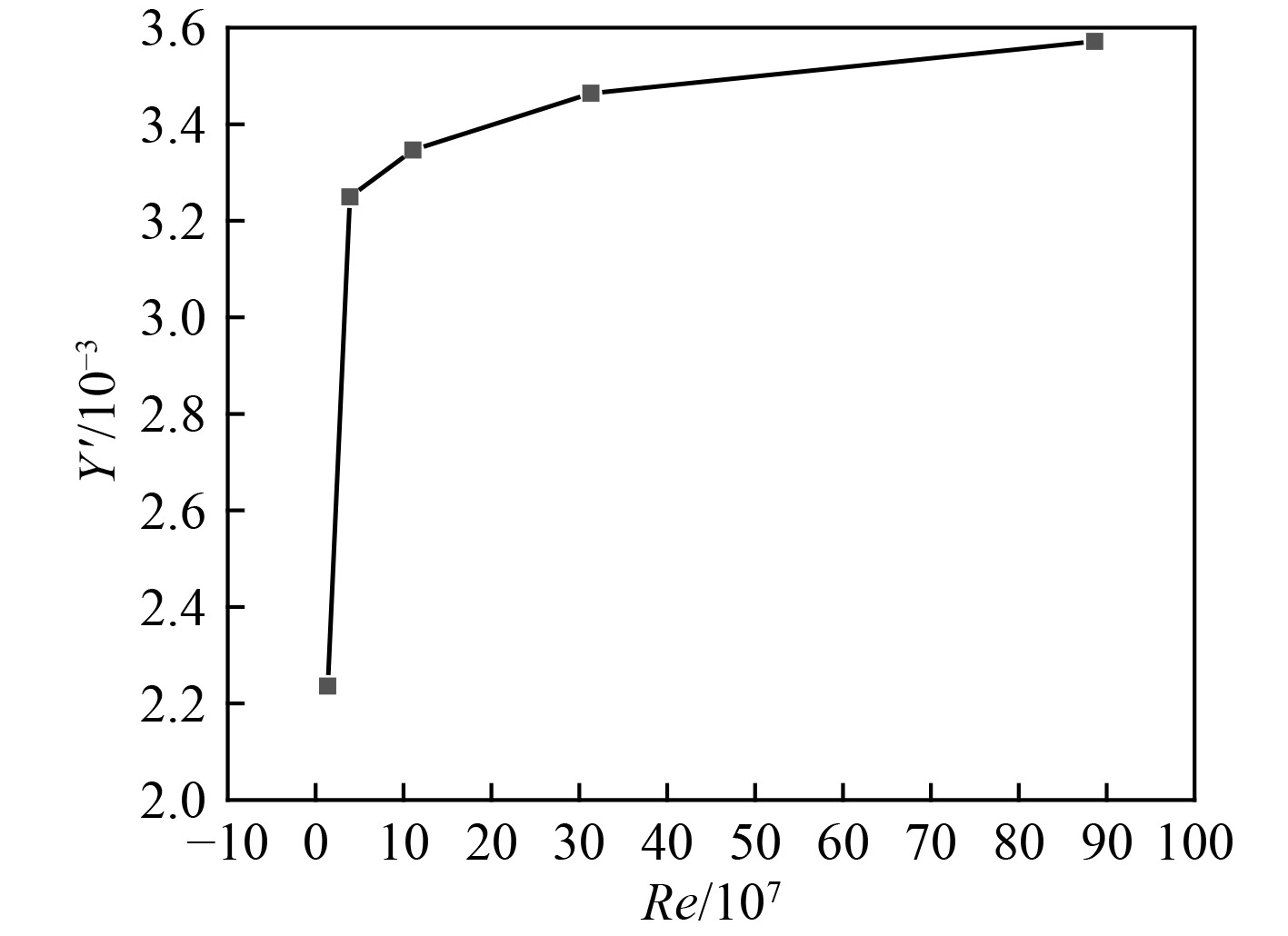
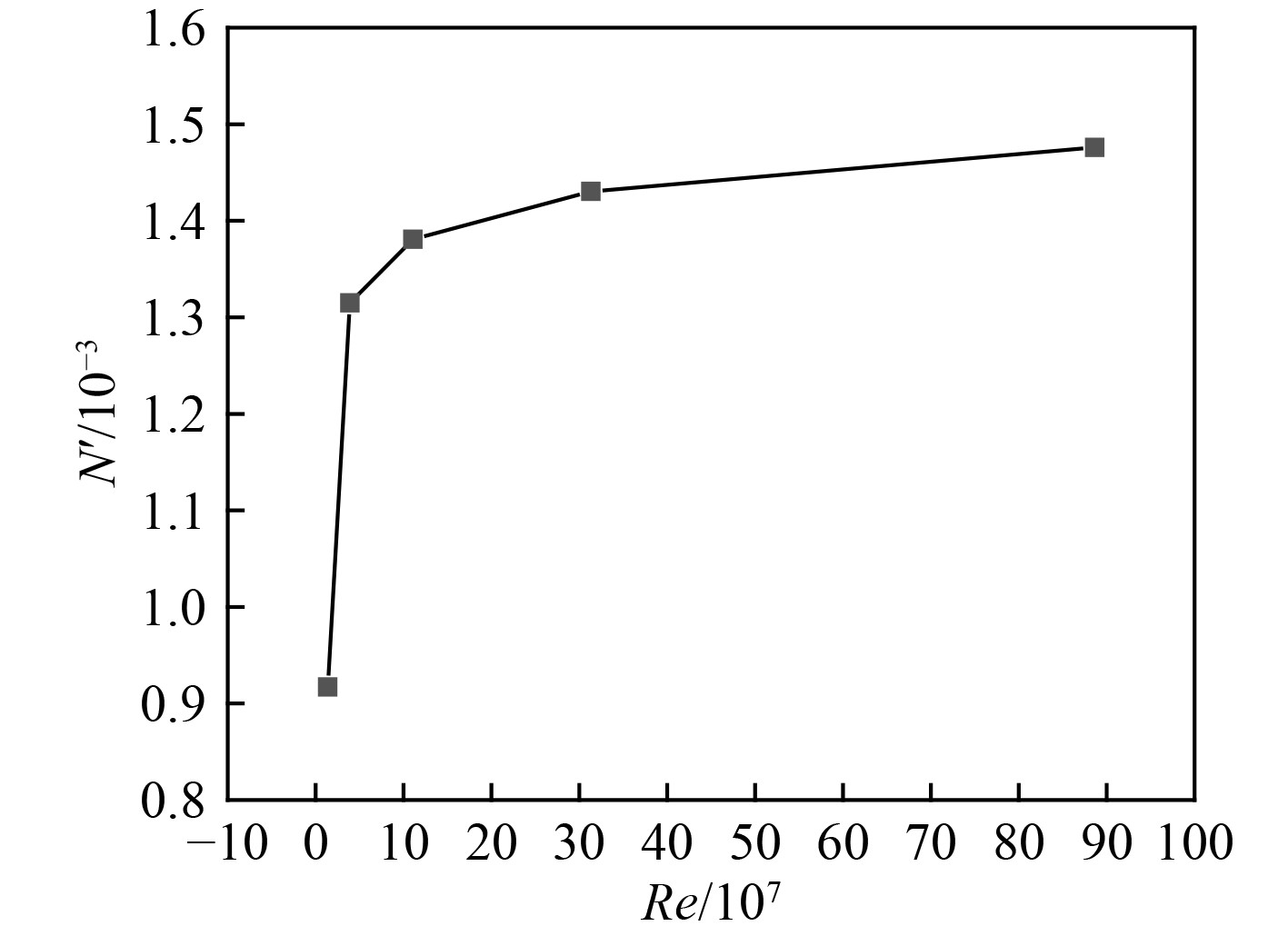
图15~图17给出了作用在不同缩尺比潜艇上的无因次纵向力、横向力及转首力矩的计算结果。对于纵向力,在雷诺数Re=1.4×107~31.3×107范围内变化最为明显,这意味着该雷诺数区间内尺度效应的影响十分显著。随着雷诺数进一步增加,纵向力系数的变化趋缓,尺度效应的影响有所下降,但仍然难以忽略。对于横向力,在雷诺数Re=1.4×107~3.9×107范围内变化较为明显,随着雷诺数进一步增加,横向力系数的变化显著减缓,意味着尺度效应的影响明显减弱。此外,转首力矩与横向力的变化规律基本一致。从以上分析可以看出,与潜艇阻力性能相关的纵向力系数其尺度效应较为明显,且随雷诺数的增加其影响变化较小。相较而言,与潜艇操纵性能相关的横向力及转首力矩系数其尺度效应在雷诺数高于某一值后影响显著减弱,横向力及转首力矩系数趋近于某一定值,这也意味着在研究潜艇操纵运动特性时,尺度效应的影响不可忽略。
|
图 15 不同雷诺数下的纵向力 Fig. 15 Longitudinal force under different Reynolds numbers |
|
图 16 不同雷诺数下的横向力 Fig. 16 Lateral force under different Reynolds numbers |
|
图 17 不同雷诺数下的转首力矩 Fig. 17 Yaw moment under different Reynolds numbers |
本文以SUBOFF潜艇模型为研究对象,按照1,2,4,8,16的缩尺比对潜艇进行等比例缩放,采用CFD方法对不同尺度的潜艇模型的直航操舵试验进行数值模拟,对获得的绕流场和水动力特性进行分析,可得到以下结论:
1)不同雷诺数下的艇体附近流场存在显著差异。舵面附近的流动分离现象随雷诺数的增大而减弱,流动分离发生位置逐步后移,导致泄出涡系结构也有所减弱,其中雷诺数较小时变化更为明显。舵面压力分布也随之发生改变,舵背风面的负压区逐渐扩大,导致舵剖面压差随雷诺数增大而增大。
2)潜艇纵向力、横向力及转首力矩系数随雷诺数的变化而发生显著变化。随雷诺数增大,尺度效应对潜艇纵向力的影响虽有所下降但依然显著,而对横向力和转首力矩的影响显著减弱。
| [1] |
苏玉民, 林健峰, 赵大刚, 等. 实尺度船舶快速性数值模拟方法综述[J]. 中国造船, 2020, 61(2): 229-239. SU Y M, LIN J F, ZHAO D G, et al. Review of numerical simulation methods for full-scale ship resistance and propulsion performance[J]. Shipbuilding of China, 2020, 61(2): 229-239. DOI:10.3969/j.issn.1000-4882.2020.02.022 |
| [2] |
操盛文, 吴方良. 尺度效应对全附体潜艇阻力数值计算结果的影响[J]. 中国舰船研究, 2009, 4(1): 33-37+42. CAO S W, WU F L. Investigation of scaling effects on numerical computation of submarine resistance[J]. Chinese Journal of Ship Research, 2009, 4(1): 33-37+42. DOI:10.3969/j.issn.1673-3185.2009.01.007 |
| [3] |
吴方良, 吴晓光, 马运义, 等. 潜艇实艇阻力预报方法研究[J]. 中国舰船研究, 2009, 4(3): 28-32. DOI:10.3969/j.issn.1673-3185.2009.03.006 |
| [4] |
司朝善, 姚惠之, 张楠. 大尺度高雷诺数下水下航行体的数值模拟分析研究[C]// 第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会文集(上册), 2012: 411-420.
|
| [5] |
王展智, 熊鹰, 孙海涛, 等. 双桨船附体阻力尺度效应[J]. 上海交通大学学报, 2015, 49(2): 255-261. DOI:10.16183/j.cnki.jsjtu.2015.02.020 |
| [6] |
张恒, 詹成胜. 基于CFD的船舶阻力尺度效应研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(2): 329-332. |
| [7] |
蔡博奥, 秦江涛, 毛筱菲, 等. 尺度效应对三体船各阻力成分的影响[J]. 武汉理工大学学报(交通科学与工程版), 2018, 42(3): 487-491+496. |
| [8] |
师超, 韩阳, 邱耿耀. 基于CFD技术船体尺度对操纵运动的影响研究[C]// 第三十一届全国水动力学研讨会论文集(下册), 2020: 648−655.
|
| [9] |
DOGRUL A, SONG S, DEMIREL Y K. Scale effect on ship resistance components and form factor[J]. Ocean Engineering, 2020, 209: 107428. DOI:10.1016/j.oceaneng.2020.107428 |
| [10] |
宋科委, 郭春雨, 孙聪, 等. 实尺度船舶阻力计算及尺度效应研究[J]. 华中科技大学学报(自然科学版), 2021, 49(6): 74-80. |
| [11] |
SEZEN S, DELEN C, DOGRUL A, et al. An investigation of scale effects on the self-propulsion characteristics of a submarine[J]. Applied Ocean Research, 2021, 113: 102728. DOI:10.1016/j.apor.2021.102728 |
| [12] |
MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, Heat and Mass Transfer, 2003, 4: 625-632. |
| [13] |
STERN F, WILSON R V, COLEMAN H W, et al. Verification and validation of CFD simulations[R]. IIHR Report No. 407, Iowa Institute of Hydraulic Research, The University of Iowa, 1999.
|
 2023, Vol. 45
2023, Vol. 45
