0 引　言

船体分段钢结构焊接是提高船舶结构的极限强度的关键，随着造船技术的发展，对船体的总体抗拉能力和断裂破坏响应控制能力提出更高的要求，船体在受到恶劣海洋和风浪环境下会导致断裂破坏，需要对船体分段钢结构进行优化的焊接工艺设计，提高船体分段钢结构的稳定性和可靠性的同时，提高整体强度。本文研究船体分段钢结构焊接变形控制方法，在提高船体分段钢结构焊接工艺的同时，提高船体的整体结构强度，相关的焊接变形控制方法研究受到人们的重视^[1]。

对船体分段钢结构焊接变形控制研究中，通过较大循环载荷作用下的累积应力特征分析，结合对累积塑性破坏与疲劳断裂破坏的交互特点，采用船体结构总体失效作为约束对象，进行变形控制，但当前方法对船体分段钢结构焊接变形控制中存在极限承载性能控制响应不好以及疲劳裂纹扩展较大等问题^[2]。

针对上述问题，本文提出一种新的船体分段钢结构焊接变形控制方法，并验证了本文方法的优越性能。

1 船体分段钢结构强度分析 1.1 船体分段钢结构加筋板试件的载荷分析

为了实现对船体分段钢结构焊接变形控制分析，构建船体分段钢结构船体板和加筋板试件的载荷分析模型，采用船舶中小组立自动化焊接技术，分析累积塑性损伤和疲劳裂纹损伤特性，采用Von Karman提出的矩形板件所能承受的临界应力分析船体分段钢结构的屈服像移，用b_e表示的临界应力^[3]，构建船体分段钢结构加筋板试件载荷分布的Von Karman方程：

$ {{{b_e}} \mathord{\left/ {\vphantom {{{b_e}} b}} \right. } b} = {{{\sigma _{ult}}} \mathord{\left/ {\vphantom {{{\sigma _{ult}}} {{\sigma _{Y} }}}} \right. } {{\sigma _{Y} }}} = {{1.9} \mathord{\left/ {\vphantom {{1.9} \beta }} \right. } \beta } 。$

(1)

式中：b_e为船体分段钢结构的有效板宽，b为实际船体分段钢结构的板宽， $ {\sigma _{ult}} $ 为焊接强度与焊后船体水密的最大平均应力（后称极限强度），σ_Y为材料的屈服强度，β为各种平直、弯曲的构件的柔度系数， $\ \beta = (b/t)\sqrt {{\sigma _{{Y}}}/E} $ 。

通过分析船舶建造过程中根据各部位的不同需求，结合柔度系数分析，将曲柄轴直接连接在直齿轮，进行焊接过程控制，得到弧线焊缝的焊接屈服像移为：

$ \dfrac{{{\sigma _m}}}{{{\sigma _{Y} }}} = \left\{ {\begin{array}{*{20}{c}} 1 ，& 0 \leqslant \beta < 1，\\ \dfrac{{{C_1}}}{\beta } - \dfrac{{{C_2}}}{{{\beta ^2}}}，& \beta \geqslant 1。\end{array}} \right. $

(2)

式中：C₁和C₂分别为弧点附近的应变特性， $ \beta $ 为初始挠度的船体板分量，取C₁=2，C₂=1；载荷都由板的有效板宽部分承担。

定义船体板中最容易启裂的位置分量

$ {\beta _e} = \frac{b}{t}\sqrt {\frac{{{\sigma _e}}}{E}} = \beta \sqrt {\frac{{{\sigma _e}}}{{{\sigma _{Y} }}}} 。$

(3)

式中，σ_e为板边应力，代入式(2)则裂纹局部应变能密度：

$ \dfrac{{{b_e}}}{b} = \dfrac{\sigma }{{{\sigma _e}}} = \left\{ {\begin{array}{*{20}{c}} 1，& 0 \leqslant {\beta _e} < 1 ，\\ \dfrac{{{C_1}}}{{{\beta _e}}} - \dfrac{{{C_2}}}{{\beta _e^2}}，& {\beta _e} \geqslant 1 。\end{array}} \right. $

(4)

式中： $ \sigma $ 为裂纹局部应变能密分布下的平均作用应力，b_e为到达后屈曲状态时板有效宽度。

由此建立船体分段钢结构加筋板试件的载荷分析模型，根据变形参数控制，进行应力特征分析^[4]。

1.2 循环载荷下船体板的极限强度解析

采用裂纹尖端应力场分析的方法，进行循环载荷下船体板的极限强度解析，得到裂尖附近的能量状态分量，采用船体板的平均应力-平均应变曲线进行变形控制特征分析^[5]，得到载荷分布关系：

$ {\beta _e} = \beta \sqrt {\overline \varepsilon }。$

(5)

式中， $ \bar \varepsilon = \varepsilon /{\varepsilon _{Y} } $ 为船体分段钢结构荷载无量纲化的平均应变， $ {\varepsilon _{Y} } = {\sigma _{Y} }/E $ 为船体分段钢结构板件的屈服应变。

设船体分段钢结构板件的有效宽度在板件到达崩溃的变形控制方向：

$ \dfrac{{{b_e}}}{b} = \dfrac{\sigma }{{{\sigma _e}}} = \left\{ {\begin{array}{*{20}{c}} 1，& 0 \leqslant \bar \varepsilon < \dfrac{1}{{{\beta ^2}}}，\\ \dfrac{{{C_1}}}{{\beta \sqrt {\bar \varepsilon } }} - \dfrac{{{C_2}}}{{{\beta ^2}\bar \varepsilon }}，& \bar \varepsilon \geqslant \dfrac{1}{{{\beta ^2}}} 。\end{array}} \right. $

(6)

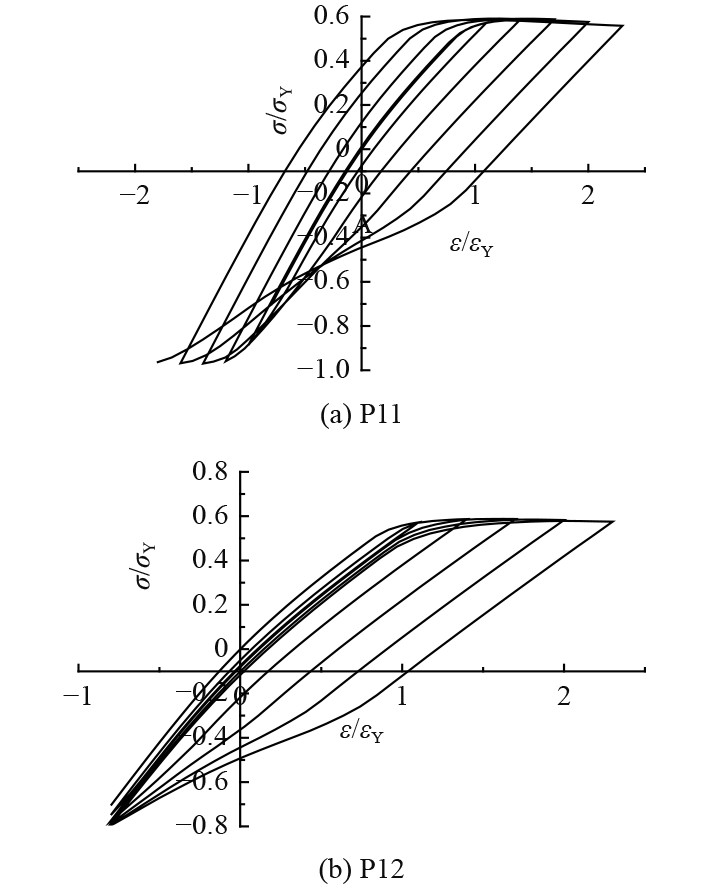
假定板边的应力-应变关系与材料应力-应变关系相同，分析应力-应变关系与材料应力-应变关系曲线，如图1所示。

基于应变能密度的动态分析，得到裂尖区域应变能密度场大小表示为：

$ {\bar \sigma _e} = \frac{{{\sigma _e}}}{{{\sigma _{Y} }}}\left\{ \begin{array}{cc} - 1，& \bar \varepsilon < - 1 ，\\ \bar \varepsilon，& - 1 \leqslant \bar \varepsilon < 1 ，\\ 1 ，& \bar \varepsilon \geqslant 1 。\end{array} \right. $

(7)

由式(6)和式(7)就能得到船体板船体分段钢结构焊接变形通知在单调压缩荷载下的无量纲化的平均应变 $ \bar \varepsilon $ 与无量纲化平均应力 $ \bar \sigma $ 关系的方程式：

$ \bar \sigma = \frac{\sigma }{{{\sigma _{Y} }}} = \frac{{{\sigma _e}}}{{{\sigma _{Y} }}}\frac{\sigma }{{{\sigma _e}}}\left\{ \begin{array}{llllllllll} \bar \varepsilon，& 0 \leqslant {\kern 1pt} \bar \varepsilon < \dfrac{1}{{{\beta ^2}}} ，\\ \bar \varepsilon \left(\dfrac{{{C_1}}}{{\beta \sqrt {\bar \varepsilon } }} - \dfrac{{{C_2}}}{{{\beta ^2}\bar \varepsilon }}\right)，& \dfrac{1}{{{\beta ^2}}} \leqslant \bar \varepsilon < 1，\\ \dfrac{{{C_1}}}{{\beta \sqrt {\bar \varepsilon } }} - \dfrac{{{C_2}}}{{{\beta ^2}\bar \varepsilon }}，& \bar \varepsilon {\kern 1pt} \geqslant 1。\end{array} \right. $

(8)

根据对船体分段钢结构焊接变形控制的强度解析结果，进行变形/应变的计算。

2 船体分段钢结构焊接变形控制优化实现

建立循环载荷幅值响应与裂纹分布的动态分布关系，根据单调载荷下船体板的极限强度的应变特征分析和动态反馈调整，计算得到开裂角 $ {\theta _{c} } $ (也称扩展角)，横裂纹的裂纹扩展计算模型为：

$ D = (1 - \lambda )\frac{{{\varepsilon _{i,\max }} - {\varepsilon _{Y} }}}{{{\varepsilon _u} - {\varepsilon _{Y} }}} + \lambda \sum\limits_{i = 1}^N {\frac{{{\varepsilon _i} - {\varepsilon _{Y} }}}{{{\varepsilon _u} - {\varepsilon _{Y} }}}} 。$

(9)

式中：ε_i,max为裂纹尖端附近的材料的屈服应变；ε_y为船体分段钢结构焊接的屈服应变；ε_i为船体分段钢结构焊接钢材在第i圈的累积塑性应变；ε_u取船体分段钢结构焊接变形的动态应变值； $ \lambda $ =0.0081；N为循环载荷的循环周数。

根据焊接裂纹的上、下表面发生接触的动态响应，得的变形退化公式为：

$ {\sigma _{{Y} ,i + 1}} = (1 - {\chi _1}{D_i}){\sigma _Y}_{,i}，$

(10)

$ {E_{i + 1}} = (1 - {\chi _2}{D_i}){E_i}。$

(11)

式中：σ_Y,i和σ_Y,i+1分别为第i次和i+1次的船体分段钢结构焊接变形的屈服强度；E_i和E_i+1分别为第i次和i+1次的弹性模量。

基于循环塑性区的动态响应分析，得到变形控制的动态卡门方程(Karman equation)如下：

$ \frac{D}{t}{\nabla ^4}\left( {w - {w_0}} \right) = \frac{{{\partial ^2}F}}{{\partial {y^2}}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}F}}{{\partial {x^2}}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} - 2\frac{{{\partial ^2}F}}{{\partial x\partial y}}\frac{{{\partial ^2}w}}{{\partial x\partial y}}, $

(12)

$ \frac{1}{E}{\nabla ^4}F = {\left( {\frac{{{\partial ^2}w}}{{\partial x\partial y}}} \right)^2} - \frac{{{\partial ^2}w}}{{\partial {x^2}}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} - \left[ {{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}}} \right)}^2} - \frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}} \right] 。$

(13)

式中： $ {\nabla ^4} = \dfrac{{{\partial ^4}}}{{\partial {x^4}}} + 2\dfrac{{{\partial ^4}}}{{\partial {x^2}\partial {y^2}}} + \dfrac{{{\partial ^4}}}{{\partial {y^4}}} $ ， $ D = \dfrac{{E{t^3}}}{{12(1 - {\nu ^2})}} $ 为船体分段钢结构焊接的裂纹结构变硬后的抗弯刚度，E和 $ \nu $ 分别表示船体分段钢结构焊材料的弹性模量与泊松比，F为应力函数，w₀和w表示船体分段钢结构板的初始挠度和总挠度。

在HRR应力-应变场分析基础上进行屈曲模态分析，根据弹性模量得到输出的弹性模量分析方法w₁=w−w₀，应力应变场表示为：

$ \left\{ \begin{gathered} {w_0}{\text{ = }}{W_0}\sin \frac{{m{\text{π}} x}}{a}\sin \frac{{{\text{π}} y}}{b} ，\\ w{\kern 1pt} {\text{ = }}W{\kern 1pt} \sin \frac{{m{\text{π}} x}}{a}\sin \frac{{{\text{π}} y}}{b} 。\end{gathered} \right. $

(14)

式中：W₀和W分别表示偏应力张量和总挠度幅值。

基于屈服面分析的方法，屈服准则用来描述材料的塑性变形，其屈服面方程为：

$ f({\mathbf{s - \alpha }},R) = \sqrt {\frac{3}{2}({\mathbf{s - \alpha }}):({\mathbf{s - \alpha }})} - \left( {{\sigma _0} + R} \right)。$

(15)

式中：f为船体分段钢结构的屈服面的函数， ${\boldsymbol{s}}$ 为船体分段钢结构偏应力张量， $ {\mathbf{\alpha }} $ 为背应力张量，σ₀为船体分段钢结构的初始屈服应力，(σ₀+R)为屈服面半径大小，R为非线性各向同性硬化特征，由此得到背应力表征材料的包辛格效应分布：

$ R = Q\left[ {1 - \exp ( - b \cdot p)} \right]。$

(16)

式中：Q为背应力演化的料参数， $ b $ 为屈第n+l次循环屈服面的演化变化率， $ p $ 为等效塑性应变累积值。

综上分析，根据单调载荷下船体板的极限强度的应变特征分析和动态反馈调整，在累积塑性应变达到材料断裂应变ε_f时，通过微小疲劳单元响应控制，实现对船体分段钢结构焊接变形控制。

3 仿真测试

实验中给出船体分段钢结构的承受轴压时裂纹弹性模量E=2.24×10⁵ MPa，压缩载荷的屈服应力σ_Y=124.6 MPa，泊松比 $ v{\text{ = 0}}{\text{.3}} $ ，几何尺寸如表1所示。

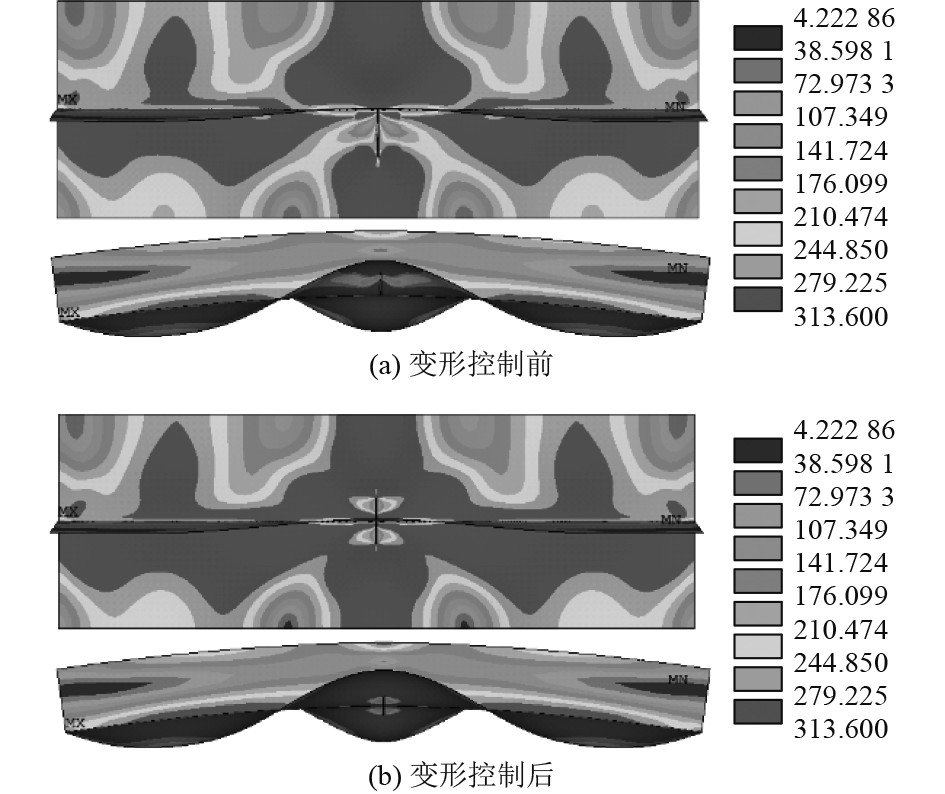
根据上述参数设定，得到船体分段钢结构焊接变形von Mises应力云图如图2所示。

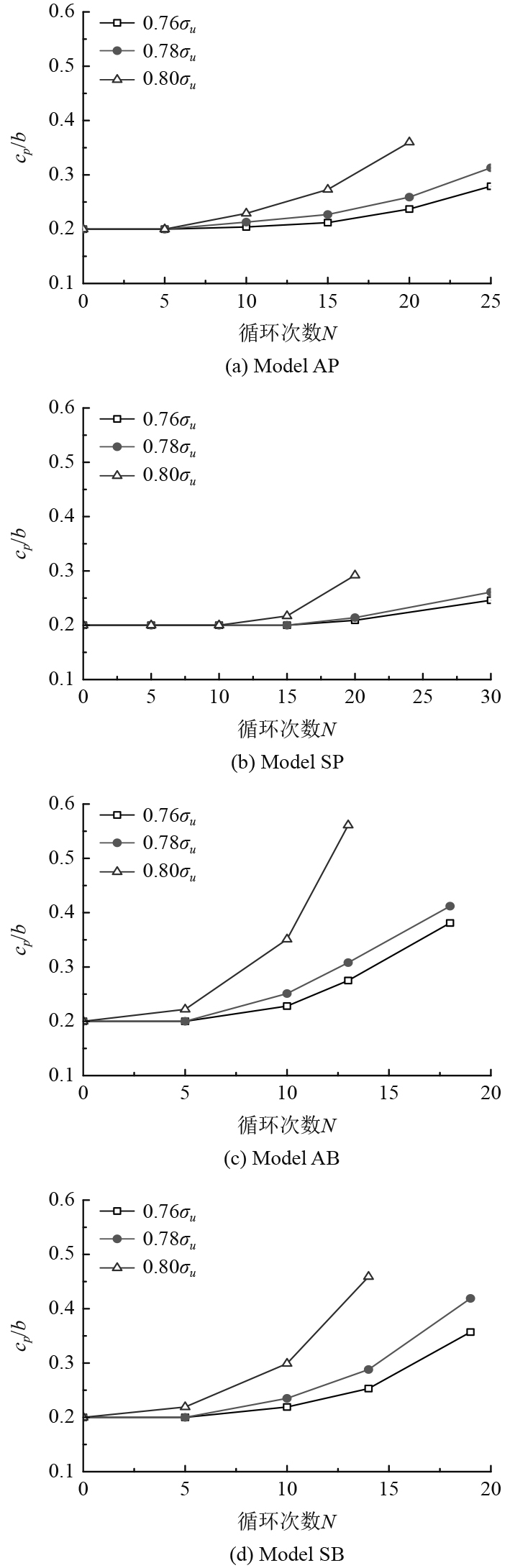
可知，本文方法能有效实现对船体分段钢结构焊接变形控制，单边裂纹控制能力较好，测试不同循环载荷幅值下4种裂纹分布模型板上裂纹长度-循环次数曲线，如图3所示。分析可知，本文方法对船体分段钢结构焊接变形控制能力较强，裂纹板极限强度值的误差很小, 降低变形屈服响应，提高极限承载性能。

4 结　语

本文研究了船体分段钢结构焊接变形控制方法，提高船体分段钢结构焊接工艺的同时，提高船体的整体结构强度。测试结果表明，本文方法对船体分段钢结构焊接变形控制能力较强，裂纹板极限强度值的误差很小, 降低变形屈服响应，提高船舶结构强度。