0 引　言

舰船在海上航行时，由于受到海浪等因素的影响，会发生横摇、纵摇、首摇、横荡、纵荡、垂荡6个自由度的运动，这些非期望运动会对各种舰载设备的正常作业造成干扰^[1]。舰载稳定平台可以抵消这些摇摆运动，由于应用在海洋背景下，所以舰载稳定平台控制系统是非线性和不确定性的，采用传统PID控制无法满足控制要求^[2]。若能实现PID参数在线自整定，不仅能方便控制系统的调试，还可提高控制系统的自适应能力。由于RBF神经网络可通过自学习自调整其权值和阈值找到最优的1组PID参数，从而逼近任意非线性函数，所以将RBF神经网络与PID控制相结合对液压驱动舰载稳定平台进行控制研究。针对液压系统突然启动、停止、变速或换向时产生的液压冲击问题，提出采用正弦加速度导数连续原则设计稳定平台理想速度曲线。

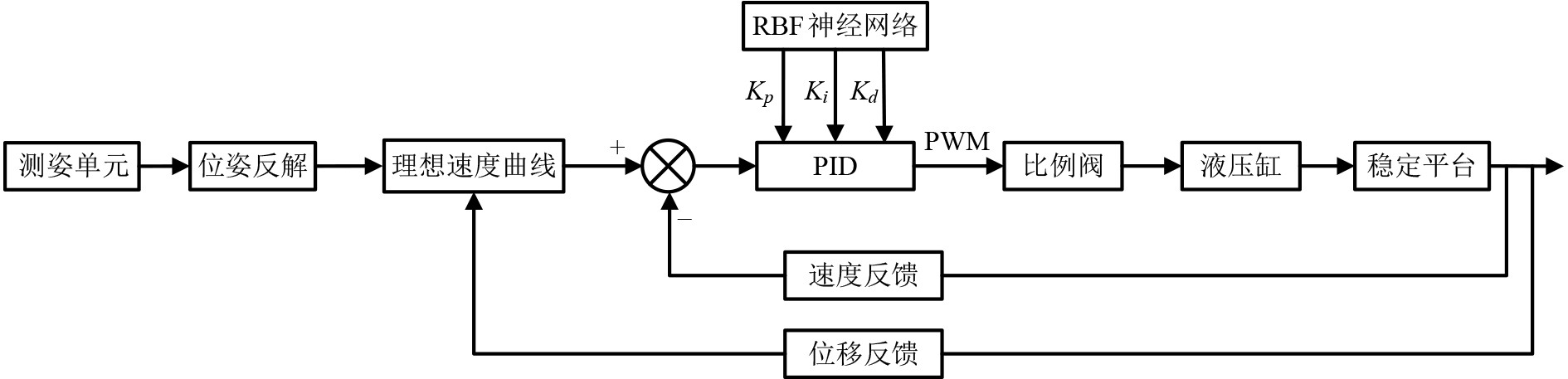
1 舰载稳定平台控制系统设计

舰载稳定平台主要由机械结构、执行机构、控制模块和反馈元件组成。控制系统采用以绝对剩余距离为原则的速度控制方式，控制系统原理如图1所示。该控制系统以STM32单片机为控制核心，当平台发生倾斜时，惯性传感器采集平台俯仰和横滚两轴的角度，通过位姿反解求出使平台稳定的活塞杆伸缩位移值，理想速度曲线根据活塞杆移动的剩余距离计算出相应的期望速度，期望速度与实时速度的偏差信号经过RBF神经网络PID控制器，输出PWM电压信号，控制比例阀阀芯产生一定大小的开口，从而控制流入液压缸工作腔的液压油流量，使液压缸按照理想速度伸缩指定位移，从而抵消船体的摇摆对上平台的影响，通过运动补偿使上平台始终保持水平稳定。

1.1 位姿反解

已知上平台在空间的位置和姿态，通过运动学逆解求出各伸缩杆的位移值，从而实现舰载稳定平台上台面始终保持水平。要抵消船体摇荡运动的干扰，首先需要解决稳定平台坐标系之间的相互转换问题^[3]。可将船体坐标系与惯性坐标系间的位置坐标变换描述为三次连续旋转的欧拉角变换，则船体坐标系与惯性坐标系间的位置旋转变换过程为：先绕Z轴旋转角度 $ \psi $ ，再绕Y轴旋转角度 $ \theta $ ，最后绕X轴旋转角度 $ \varphi $ ，可用如下旋转矩阵表示，即

$ \begin{split} R(\psi ,&\theta ,\varphi ) = R(z,\psi )R(y,\theta )R(x,\varphi ) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]\times\\ & \left[ {\begin{array}{*{20}{c}} {\cos \theta }&0&{\sin \theta } \\ 0&1&0 \\ { - \sin \theta }&0&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi }&{\cos \varphi } \end{array}} \right] =\\ & \left( \begin{array}{*{20}{c}} {\cos (\psi )\cos (\theta )}&{\cos (\psi )\sin (\theta )\sin (\varphi ) - \sin (\psi )\cos (\varphi )}\\ {\sin (\psi )\cos (\theta )}&{\sin (\varphi )\sin (\theta )\sin (\psi ) + \cos (\varphi )\cos (\psi )}\\ { - \sin (\theta )}&{\cos (\theta )\sin (\varphi )} \end{array}\right. \\ & \left. \begin{array}{*{20}{c}} {\cos (\varphi )\sin (\theta )\cos (\psi ) + \sin (\varphi )\sin (\psi )} \\ {\sin (\psi )\sin (\theta )\cos (\varphi ) - \cos (\psi )\sin (\varphi )} \\ {\cos (\theta )\cos (\varphi )} \end{array} \right)。\\[-30pt] \end{split} $

(1)

本文只研究横摇和纵摇，所以绕Z轴旋转的角度 $\psi = {0^ \circ }$ 。舰载稳定平台下平台随船体在做旋转运动时还会产生平移运动，设平移位移量分别为 $ {x_p} $ ， $ {y_p} $ ， $ {z_p} $ ，则位姿变换矩阵T定义为：

$ T = \left( {\begin{array}{*{20}{c}} {}&{}&{}&{{x_p}} \\ {}&{R(\psi ,\theta ,\varphi )}&{}&{{y_p}} \\ {}&{}&{}&{{z_p}} \\ 0&0&0&1 \end{array}} \right)，$

(2)

假设 $ {A_i}({A_{ix}},{A_{iy}},{A_{iz}}) $ (i=1,2)为惯性坐标系中上平台各铰链中心点， $ B'_i(B'_{ix},B'_{iy},B'_{iz}) $ (i=1,2)为船体坐标系中下平台各铰链中心点。齐次变换矩阵为T，则下平台中心点对应中的坐标 $ {B_i}({B_{ix}},{B_{iy}},{B_{iz}}) $ (i=1,2)为：

$ \left( {\begin{array}{*{20}{c}} {{B_i}} \\ 1 \end{array}} \right) = T\left( {\begin{array}{*{20}{c}} {B_i'} \\ 1 \end{array}} \right)，$

(3)

可得各连杆的长度 $ {L_i} $ 为：

$ {L_i} = \sqrt {{{({A_{ix}} - {B_{ix}})}^2} + {{({A_{iy}} - {B_{iy}})}^2} + {{({A_{iz}} - {B_{iz}})}^2}}，$

(4)

各连杆的初始长度设为 $ {L_{i0}} $ ，为隔离船体产生的摇荡运动，各连杆应协调伸缩位移 $ \Delta {L_i} $ ，使上平台相对惯性坐标系保持稳定，各连杆需要移动的位移为：

$ \Delta {L_i} = {L_i} - {L_{i0}} 。$

(5)

1.2 理想速度曲线设计

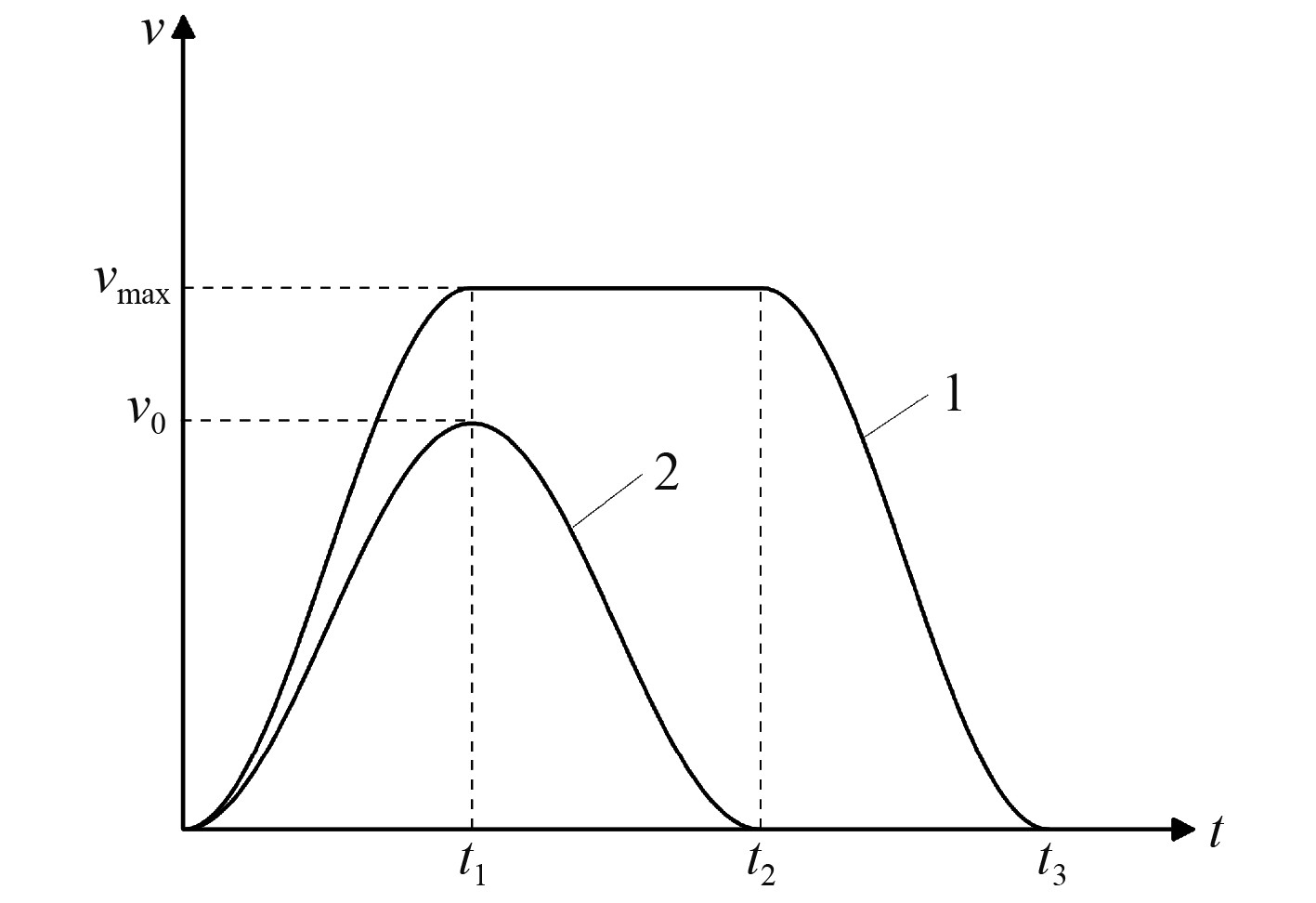
理想速度曲线的设计是实现速度控制的关键，液压缸突然起动和停止会产生液压冲击，而造成液压冲击的主要原因是液压缸的加速度存在突变，所以液压缸的控制曲线要满足以下基本条件：速度曲线连续；加速度曲线连续；加加速度曲线连续。由于正弦曲线加速度导数连续，所以采用正弦型曲线作为液压缸的期望运行曲线，控制活塞杆在全行程任意点缓冲定位^[4]。液压缸的运动行程决定了液压缸能否达到最大速度^[5]，所以控制曲线需要分成2种情况讨论，如图2所示。若液压缸无法达到最大速度，则采用理想速度曲线1，若液压缸能达到最大速度，则采用理想速度曲线2。其运动过程分为加速段、匀速直线段、减速段。

设计曲线时，假设加速段和减速段运行时间和运行距离均相等，则有 $ {t_1} = {t_3} $ ， $ {l_1} = {l_3} $ ，匀速段运行时间 $ {t_2} = 2{t_1} $ ，当液压缸流量、液压缸直径、活塞杆直径、缓冲距离确定时，缓冲时间则可确定。

1）加速段

$ v = \frac{{{v_0}}}{2}(1 - \cos (\omega t)){\text{ , }}0 \leqslant t < {t_1}。$

(6)

2）匀速段

由于采用的是单活塞杆液压缸，液压缸伸出和缩回两方向的推力和速度不相等，所以需要对液压缸的伸出和缩回过程中的匀速段分别进行分析。该阶段加速度为0，速度为v₀，v₀是液压缸运行过程中所能达到的最大速度。

活塞杆伸出时匀速段速度为：

$ {v_0} = \frac{q}{{{\text{π}} ({D^2} - {d^2})/4}}{\text{ }},{\text{ }}{t_1} \leqslant t < {t_2}，$

(7)

活塞杆缩回时匀速段速度为：

$ {v_0} = \frac{{4q}}{{{\text{π}} {D^2}}}{\text{ }},{\text{ }}{t_1} \leqslant t < {t_2} 。$

(8)

3）减速段

减速段初速度为v₀，速度v的曲线方程为：

$ v = \frac{{{v_0}}}{2}(1 - \cos (\omega (t - {t_2})){\text{ }},{\text{ }}{t_2} \leqslant t < {t_3}。$

(9)

由于上述公式中含有大量三角函数和浮点数的运算，计算过程会花费大量时间，降低了系统的实时性^[6]，且理想速度曲线是连续的，所以需要将速度曲线离散化，通过表格的形式存储在STM32的Flash中，以固定周期读表获取需要的速度指令。

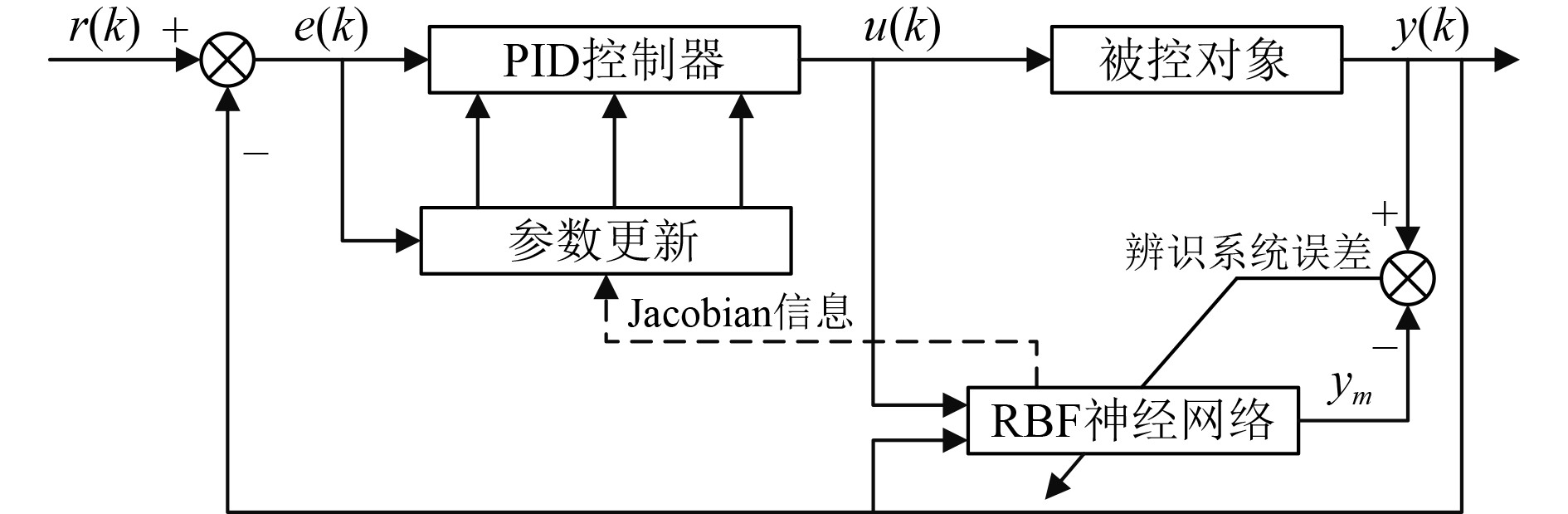
2 RBF神经网络PID控制器设计

RBF神经网络可根据稳定平台控制系统的性能要求和运行状态，对权值进行修正，从而对PID参数进行实时调整^[7]。本文使用RBF神经网络对舰载稳定平台位置控制系统进行在线辨识，根据得到的Jacobian信息对增量式PID参数进行在线整定。RBF神经网络PID控制器原理如图3所示，r(k)为活塞杆理想速度，y(k)为活塞杆实际速度，e(k)为活塞杆理想速度与实际速度的偏差，u(k)为PID控制器输出的控制量，y_m为RBF神经网络的输出。

2.1 增量式PID控制算法

采用增量式PID控制算法，公式为：

$ e(k) = r(k) - y(k)，$

(10)

$ \begin{split}\Delta u(k) =& {k_p}[e(k) - e(k - 1)] + {k_i}e(k) + {k_d}[e(k) - \\ &2e(k - 1) + e(k - 2)]，\end{split} $

(11)

$ u(k) = u(k - 1) + \Delta u(k) 。$

(12)

式中： $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ 为PID的3个调节参数； $ u(k) $ 为第k次采样时刻的控制量； $ e(k) $ 为第k次采样时刻期望输出与实际输出的差值。

2.2 RBF神经网络控制算法

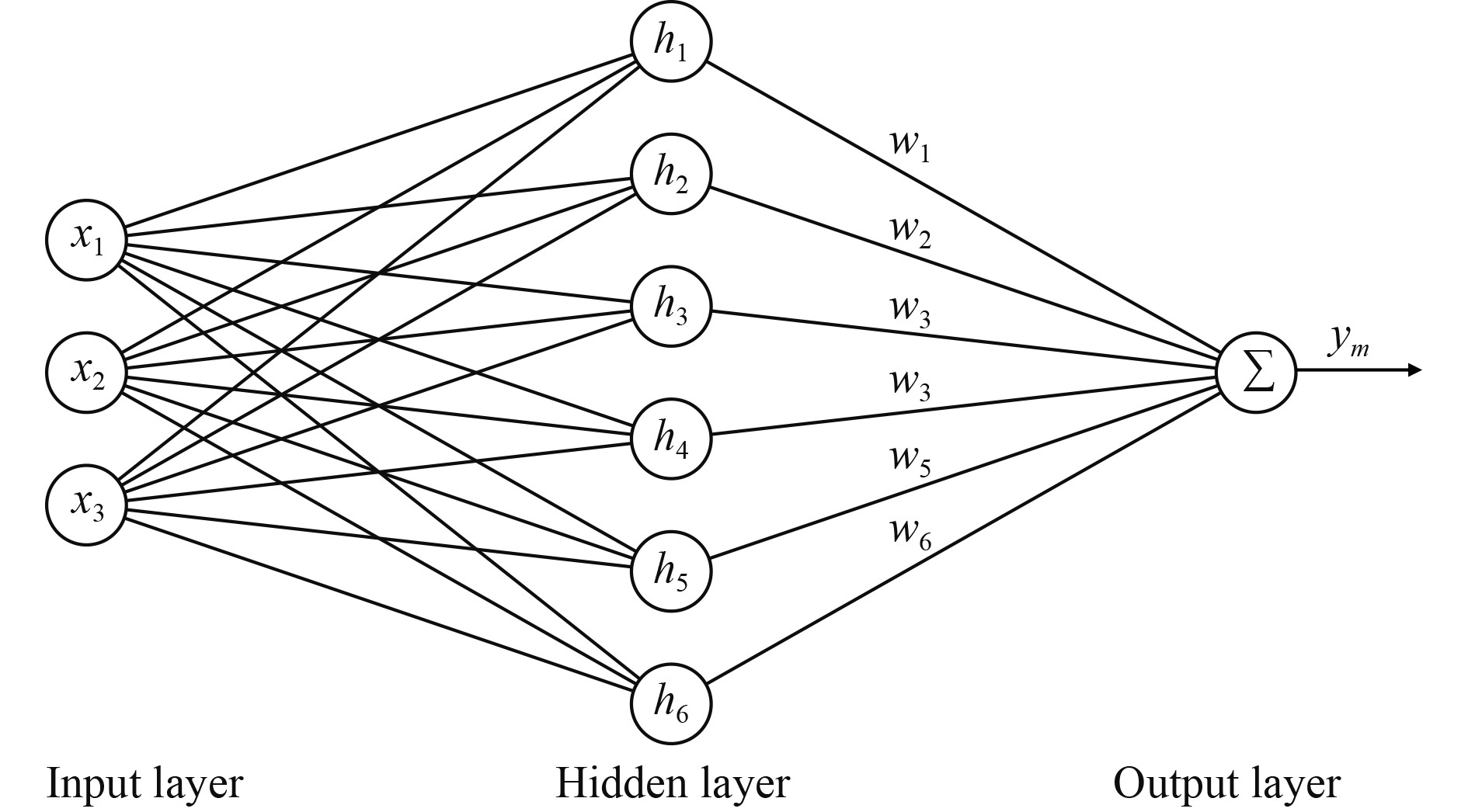
RBF神经网络包含输入层、单隐含层和输出层^[8]，输入到输出的映射是非线性的，隐含层到输出层的映射对可调参数而言是线性的，因此加快了学习速度且避免了局部极小的问题^[9]。本文采用3-6-1的神经网络结构，其结构如图4所示。

RBF神经网络通过输入层正向计算求解y_m，继而根据y与y_m的差值，逆向更新网络的输出权值、基宽参数、节点中心。

1）前向传播

$ X = {[{x_1},{x_2}, \cdot \cdot \cdot ,{x_n}]^{\rm{T}}} $ 为网络的输入，分别为PID输出控制量u(k)、系统当前实际输出值y(k)、系统上一次实际输出值y(k-1)； $ H = {[{h_1},{h_2}, \cdot \cdot \cdot ,{h_m}]^{\rm{T}}} $ 为隐含层的输出；隐含层到输出层的权值向量 $W = [{\omega _1},{\omega _2}, \cdots , {\omega _m}]^{\rm{T}}$ ；隐含层的激活函数为：

$ {h_j} = \exp \left( { - \frac{{{{\left\| {X - {C_j}} \right\|}^2}}}{{2b_j^2}}} \right)，j = 1,2, \cdot \cdot \cdot ,m。$

(13)

其中 $ {C_j} = {[{c_{j1}},{c_{j2}}, \cdot \cdot \cdot ,{c_{ji}}, \cdot \cdot \cdot {c_{jn}}]^{\rm{T}}} $ 为隐含层的第j个节点的中心矢量， $ {b_j} $ 为隐含层第j个节点的基宽度，基宽向量为：

$ B = [{b_1},{b_2}, \cdot \cdot \cdot ,{b_m}]{{\text{ }}^{\rm{T}}} ，$

(14)

辨识网络的输出为：

$ {y_m}(k) = {\omega _1}{h_1} + {\omega _2}{h_2} + \cdot \cdot \cdot + {\omega _m}{h_m}。$

(15)

2）反向传播

辨识器的性能指标函数为：

$ J = \frac{1}{2}{[y(k) - {y_m}(k)]^2}，$

(16)

为使 $ J $ 最小，采用梯度下降法调整网络的参数， $ \eta $ 为学习速率， $ \alpha $ 为动量因子，各参数的迭代算法为：

$ \Delta {\omega _j}(k) = \frac{{\partial J}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {\omega _j}}} = [y(k) - {y_m}(k))]{h_j} ，$

(17)

$ {\omega _j}(k) = {\omega _j}(k - 1) + \eta \Delta {\omega _j}(k) + \alpha [{\omega _j}(k - 1) - {\omega _j}(k - 2)]，$

(18)

$ \Delta {b_j}(k) = \frac{{\partial J}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {h_j}}}\frac{{\partial {h_j}}}{{\partial {b_j}}} = [y(k) - {y_m}(k)]{\omega _j}{h_j}\frac{{{{\left\| {X - {C_j}} \right\|}^2}}}{{b_j^3}}，$

(19)

$ {b_j}(k) = {b_j}(k - 1) + \eta \Delta {b_j} + \alpha [{b_j}(k - 1) - {b_j}(k - 2)] ，$

(20)

$ \Delta {c_{ji}} = \frac{{\partial J}}{{\partial {y_m}}}\frac{{\partial {y_m}}}{{\partial {h_j}}}\frac{{\partial {h_j}}}{{\partial {c_{ji}}}} = [y(k) - {y_m}(k)]{\omega _j}{h_j}\frac{{{x_j} - {c_{ji}}}}{{b_j^2}} ，$

(21)

$ {c_{ji}} = {c_{ji}}(k - 1) + \eta \Delta {c_{ji}} + \alpha [{c_{ji}}(k - 1) - {c_{ji}}(k - 2)] 。$

(22)

由RBF网络得到Jacobian信息，其算法为：

$ \frac{{\partial y(k)}}{{\partial \Delta u(k)}} \approx \frac{{\partial {y_m}(k)}}{{\partial \Delta u(k)}} = \sum\limits_{j = 1}^m {{\omega _j}} {h_j}\frac{{{c_{ji}} - {x_1}}}{{b_j^2}} ，$

(23)

RBF神经网络整定指标为：

$ E = \frac{1}{2}{[r(k) - y(k)]^2} ，$

(24)

通过梯度下降法调整 $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ ； $ {\eta _1} $ ， $ {\eta _2} $ ， $ {\eta _3} $ 为PID调节参数的学习率：

$ \begin{split}\Delta {k_p} = & - {\eta _1}\frac{{\partial E}}{{\partial {k_p}}} = - {\eta _1}\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial \Delta u}}\frac{{\partial \Delta u}}{{\partial {k_p}}} = \\ &{\eta _1}e(k)\frac{{\partial y}}{{\partial \Delta u}}[e(k) - e(k - 1)]，\end{split}$

(25)

$ \Delta {k_i} = - {\eta _2}\frac{{\partial E}}{{\partial {k_i}}} = - {\eta _2}\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial \Delta u}}\frac{{\partial \Delta u}}{{\partial {k_i}}} = {\eta _2}e(k)\frac{{\partial y}}{{\partial \Delta u}}e(k) ，$

(26)

$ \begin{split}\Delta {k_d} =& - {\eta _3}\frac{{\partial E}}{{\partial {k_d}}} = - {\eta _3}\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial \Delta u}}\frac{{\partial \Delta u}}{{\partial {k_d}}} =\\ &{\eta _3}e(k)\frac{{\partial y}}{{\partial \Delta u}}[e(k) - 2e(k - 1) + e(k - 2)]，\end{split}$

(27)

$ {K_p} = {k_p} + \Delta {k_p}，$

(28)

$ {K_i} = {k_i} + \Delta {k_i}，$

(29)

$ {K_d} = {k_d} + \Delta {k_d} 。$

(30)

3 舰载稳定平台控制系统数学模型的建立 3.1 液压缸的传递函数

选用油缸内径D=80 mm，活塞杆直径d=56 mm，行程L=200 mm(−100～100 mm)的液压缸，液压缸活塞杆的位移对指令输入的传递函数为：

$ {G_1}(s) = \dfrac{{{K_q}/{A_p}}}{{s\left(\dfrac{{{s^2}}}{{\omega _h^2}} + \dfrac{{2{\xi _h}s}}{{{\omega _h}}} + 1\right)}} ，$

(31)

故液压缸活塞杆的速度对指令输入的传递函数为：

$ {G_2}(s) = \dfrac{{{K_q}/{A_p}}}{{\dfrac{{{s^2}}}{{\omega _h^2}} + \dfrac{{2{\xi _h}s}}{{{\omega _h}}} + 1}}。$

(32)

式中：液压固有频率 $ {\omega _h} = \sqrt {\dfrac{{4{\beta _e}A_p^2}}{{{V_t}{m_t}}}} + \dfrac{{{B_P}}}{{4{A_p}}}\sqrt {\dfrac{{{V_t}}}{{{\beta _e}{m_t}}}} $ ，由于B_p较小可忽略；液压阻尼比 $ {\xi _h} = \dfrac{{{K_{ce}}}}{{{A_p}}}\sqrt {\dfrac{{{\beta _e}{m_t}}}{{{V_t}}}} $ ， $ {K_{ce}} $ 为流量压力系数， $ {A_p} $ 为活塞的有效面积。

3.2 比例放大器的传递函数

选用VT-MRPA1-1-1X型比例放大器，可近似为比例环节^[10]，传递函数为：

$ G(s) = \frac{{I(s)}}{{U(s)}} = {K_a} = \frac{{2.5}}{{10}} = 0.25{\text{ (}}A/V{\text{)}} 。$

(33)

式中： $ {K_a} $ 为比例放大增益； $ I(s) $ 为比例放大器输出电流， $ U(s) $ 为比例放大器的输入电压。

3.3 比例阀的传递函数

比例阀的输入信号是电压，输出信号是流量，其传递函数由液压动力元件的特性决定。采用4WRE1025-2X/G24K4/M型电液比例阀，其主要参数为：固有频率440 rad/s，阻尼比0.7。根据电液比例阀的自身固有频率与液压动力元件的固有频率的关系^[11]，可认为是二阶环节，传递函数为：

$ G(s) = \dfrac{{{Q_L}(s)}}{{I(s)}} = \dfrac{{{K_{sv}}}}{{\dfrac{{{s^2}}}{{{\omega _{sv}}^2}} + \dfrac{{2{\zeta _{sv}}}}{{{\omega _{sv}}}}s + 1}} = \dfrac{{0.0042}}{{\dfrac{{{s^2}}}{{{{440}^2}}} + \dfrac{{2 \times 0.7}}{{440}}s + 1}} ，$

(34)

$ {Q_L} = {K_q}{x_v}。$

(35)

式中： $ {K_{sv}} $ 为阀的流量增益； $ {\omega _{sv}} $ 为阀的固有频率； $ {\zeta _{sv}} $ 为阀的阻尼比。

3.4 系统的传递函数

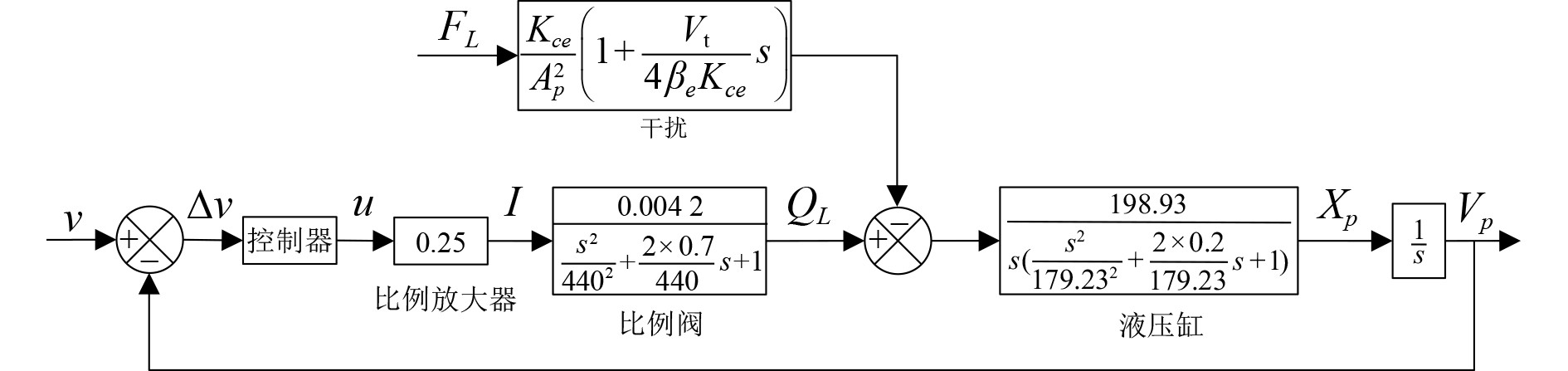
舰载稳定平台控制系统的传递函数方框图，如图5所示。此处选取的是活塞杆做伸出运动时的传递函数。

4 仿　真

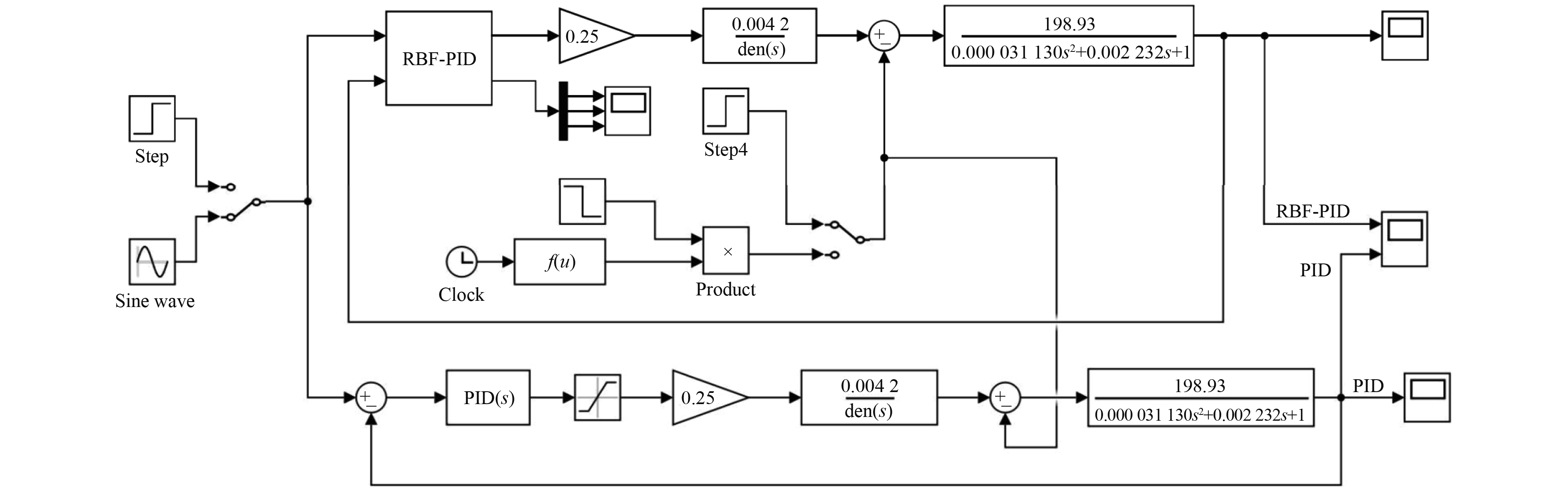
在Simulink中搭建仿真实验，由于选用的比例阀输入指令信号范围为−10～+10 V，需要加入饱和度模块，上下限分别取+10和−10。分别对液压缸阶跃信号、正弦信号、理想速度曲线的响应进行仿真，并对常规PID控制和基于RBF辨识网络的自适应PID控制的性能进行对比，系统模型的仿真框图如图6所示。

4.1 响应及调整性对比

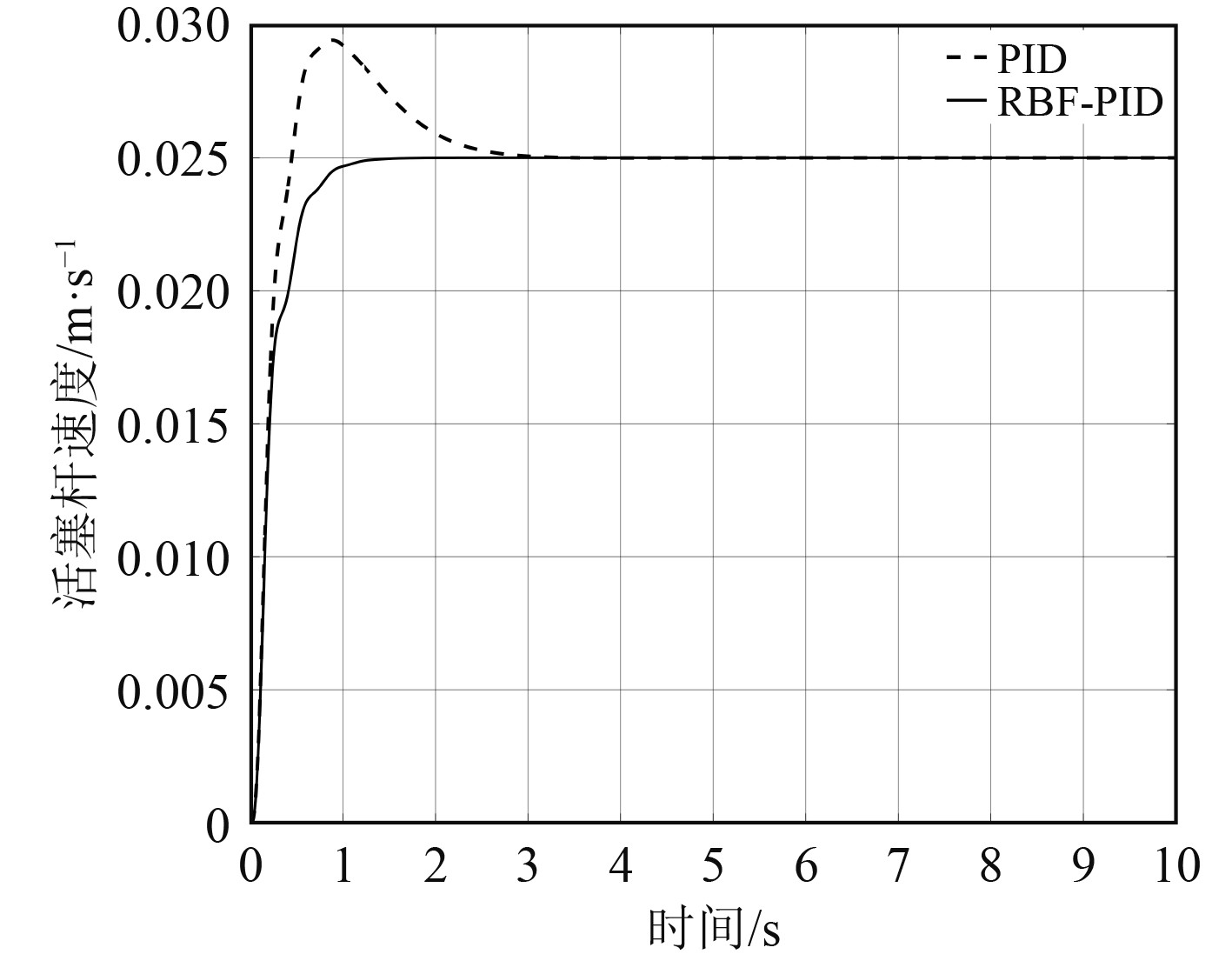
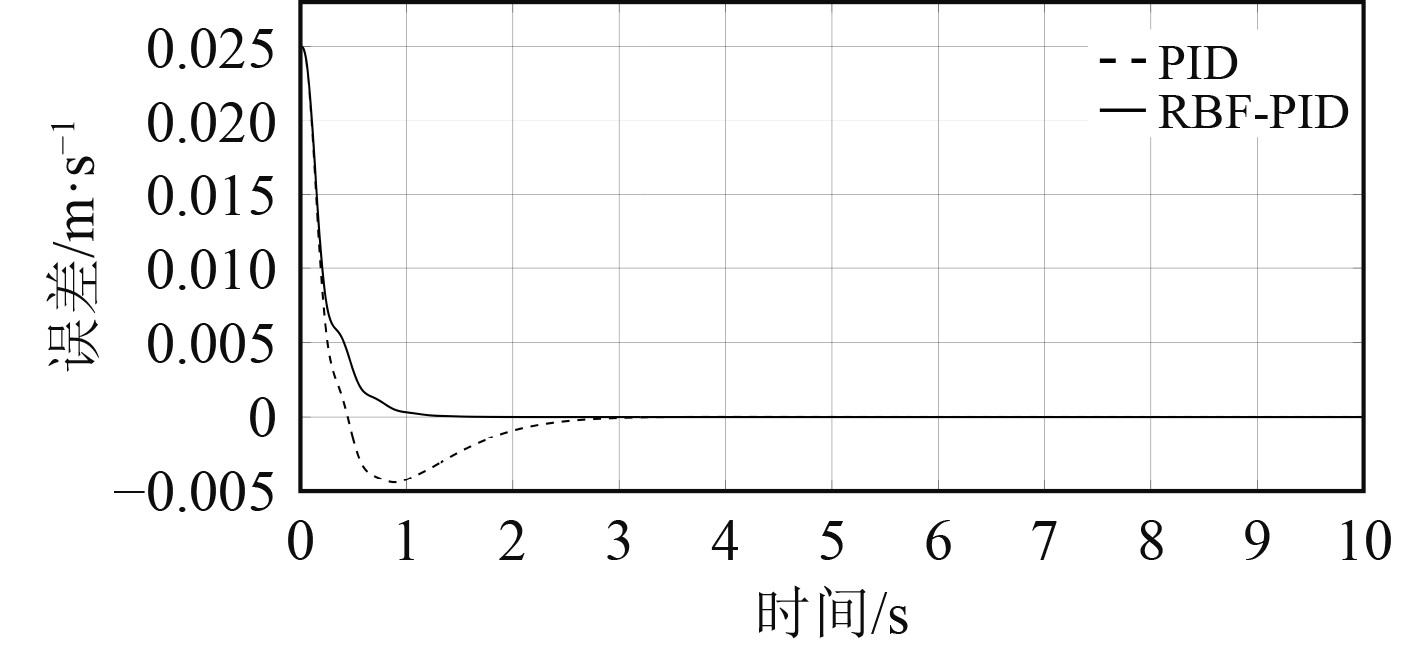
采样周期为0.001，RBF辨识器为3-6-1结构，其学习速率设为0.3，惯性因子设为0.05，PID参数的学习率设为0.2，仿真时间设为10 s，对RBF-PID控制器和常规PID控制器分别输入一个幅值为0.025 m/s的阶跃信号，并从5 s开始加入一个持续时间为0.05 s的干扰信号，阶跃信号响应结果如图7所示。2种控制方法的响应误差如图8所示。

由图7可知，PID控制的超调量为16%，RBF-PID控制器的响应时间较PID控制快1.6 s，且基本没有超调。在稳定状态受到干扰时，RBF-PID控制器的调整时间较传统PID控制器快1.2 s，回稳较快，且波动较小，因此与传统PID相比，RBF-PID具有更强的适应性和鲁棒性。在响应性能上，RBF-PID控制器优于常规PID控制器。

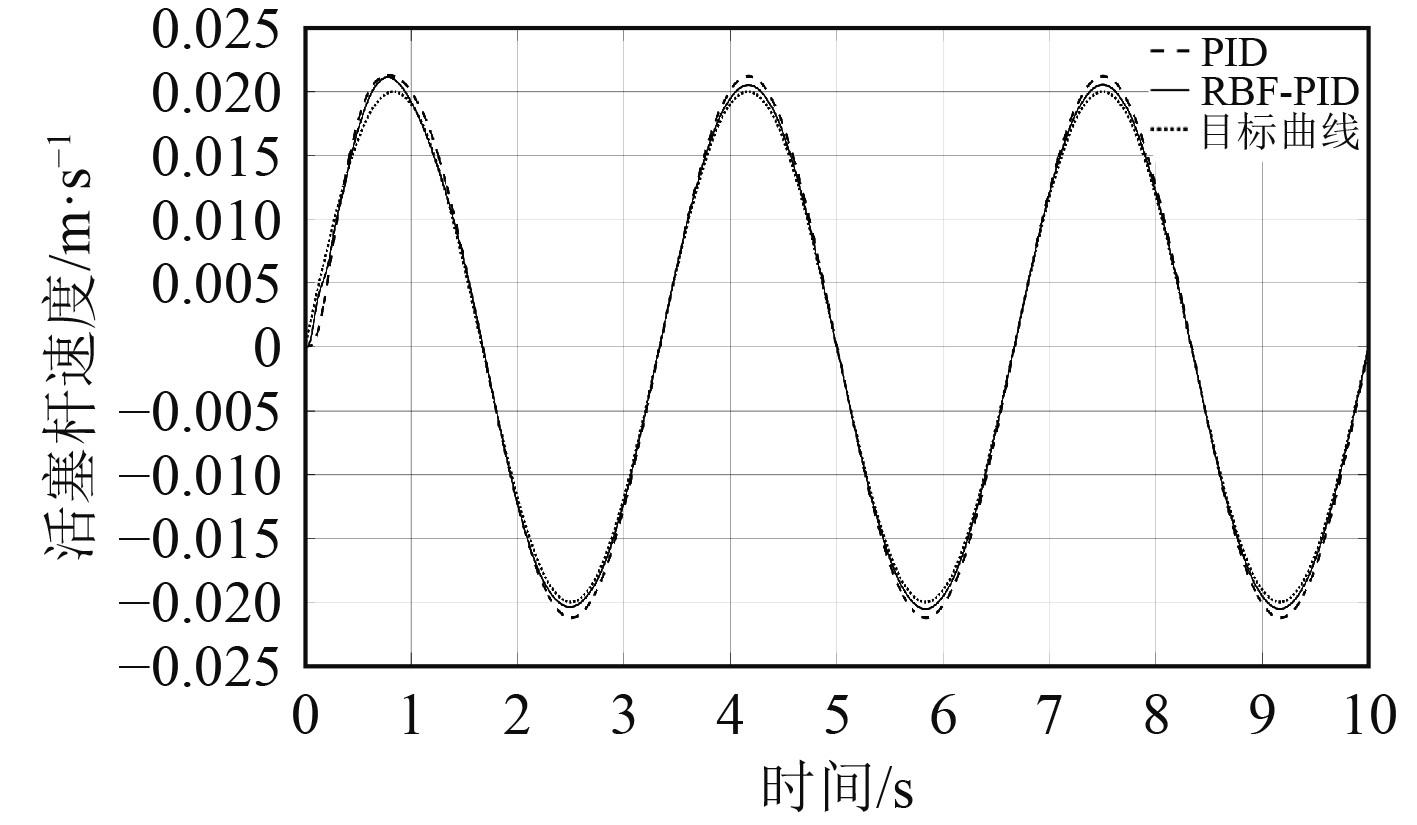
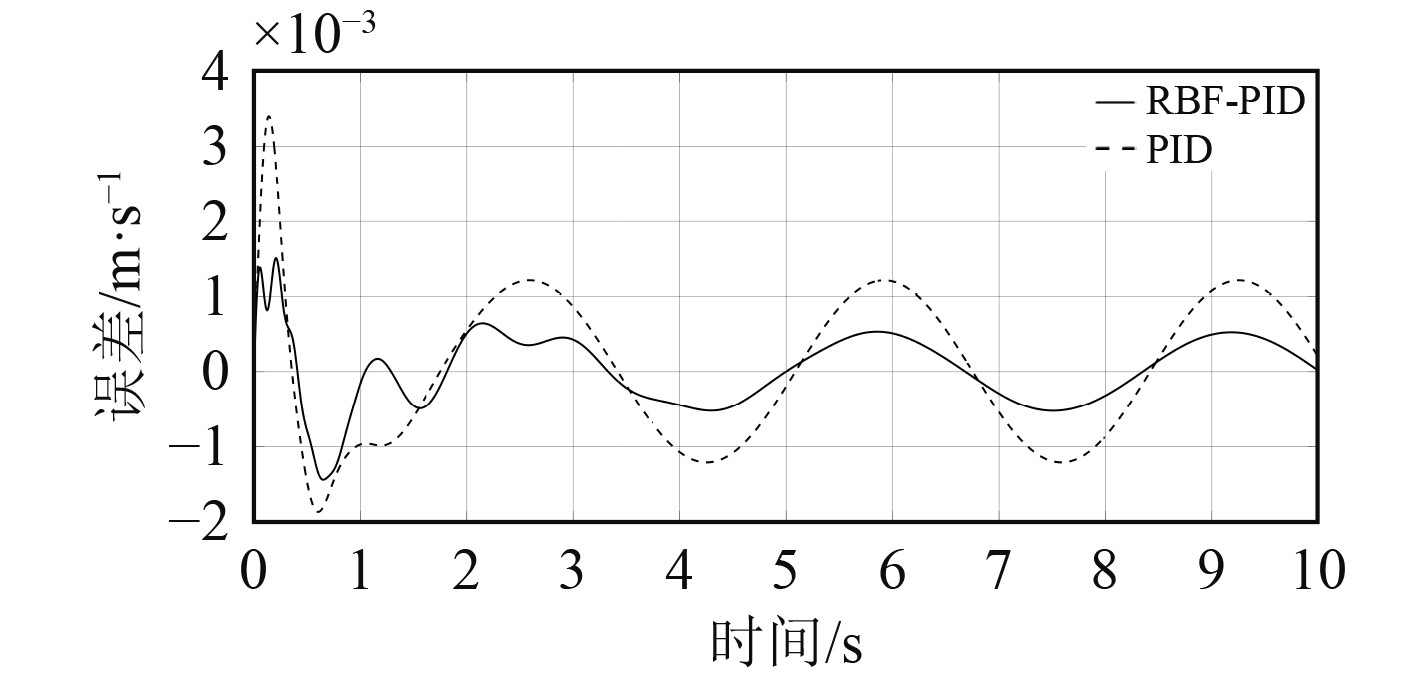
4.2 跟踪性能对比

将上述非线性系统的输入信号改为幅值为0.02 m/s，频率为0.3 Hz的正弦信号，跟踪结果如图9所示，跟踪误差曲线如图10所示。

可知，在速度跟随控制时存在滞后，但基于RBF辨识网络的自适应PID控制器在调整速度、跟踪精度时均优于传统PID控制器，调整时超调较小，控制精度和效率也较好，且会持续接近跟踪系统。

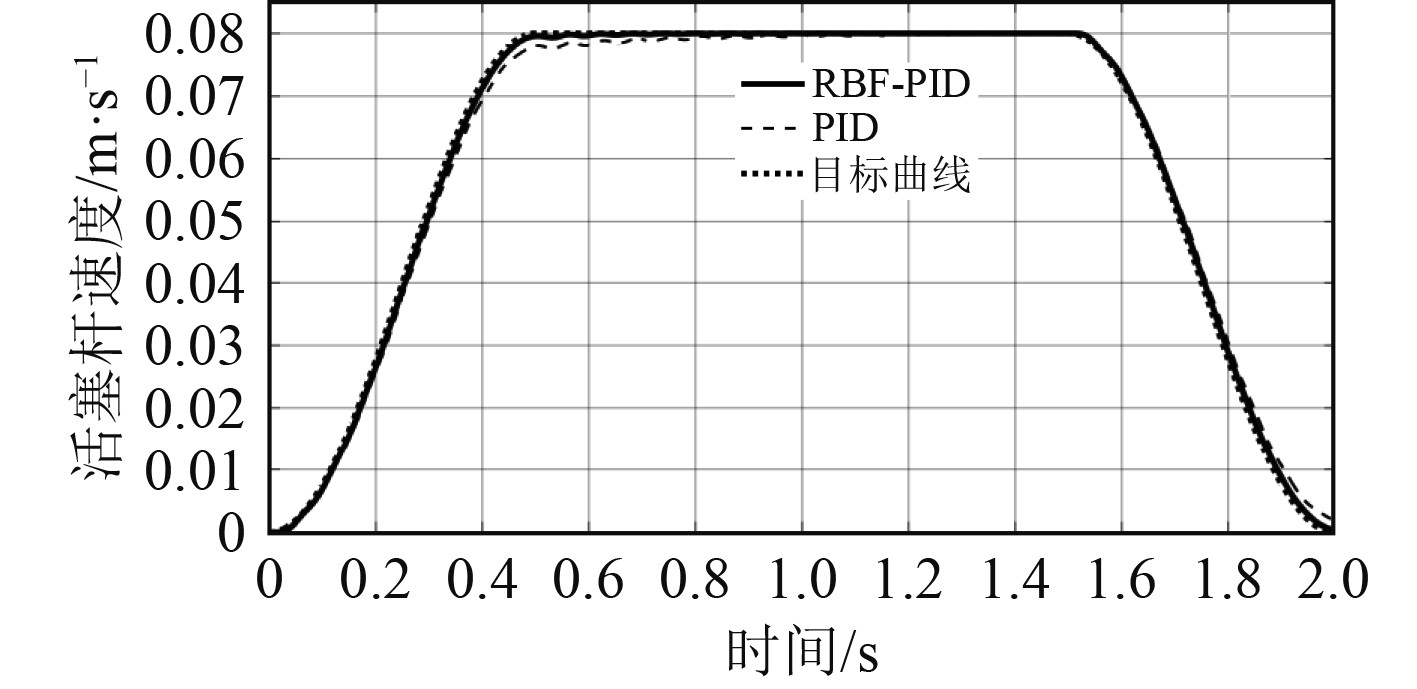
4.3 理想速度曲线仿真

q=24 L/min，由式（6）～式（9）计算活塞杆伸出0.12 m的理想速度曲线式（36），并在M文件中编写理想速度曲线，理想速度响应曲线如图11所示。

$ v = \left\{ \begin{array}{ll} 0.04(1 - \cos (2{\text{π}} t))&0 \leqslant t < 0.5，\\ 0.08 & 0.5 \leqslant t < 1.5，\\ 0.04(1 - \cos (2{\text{π}} (t - 1))&1{\text{.5}} \leqslant t < 2。\end{array} \right. $

(36)

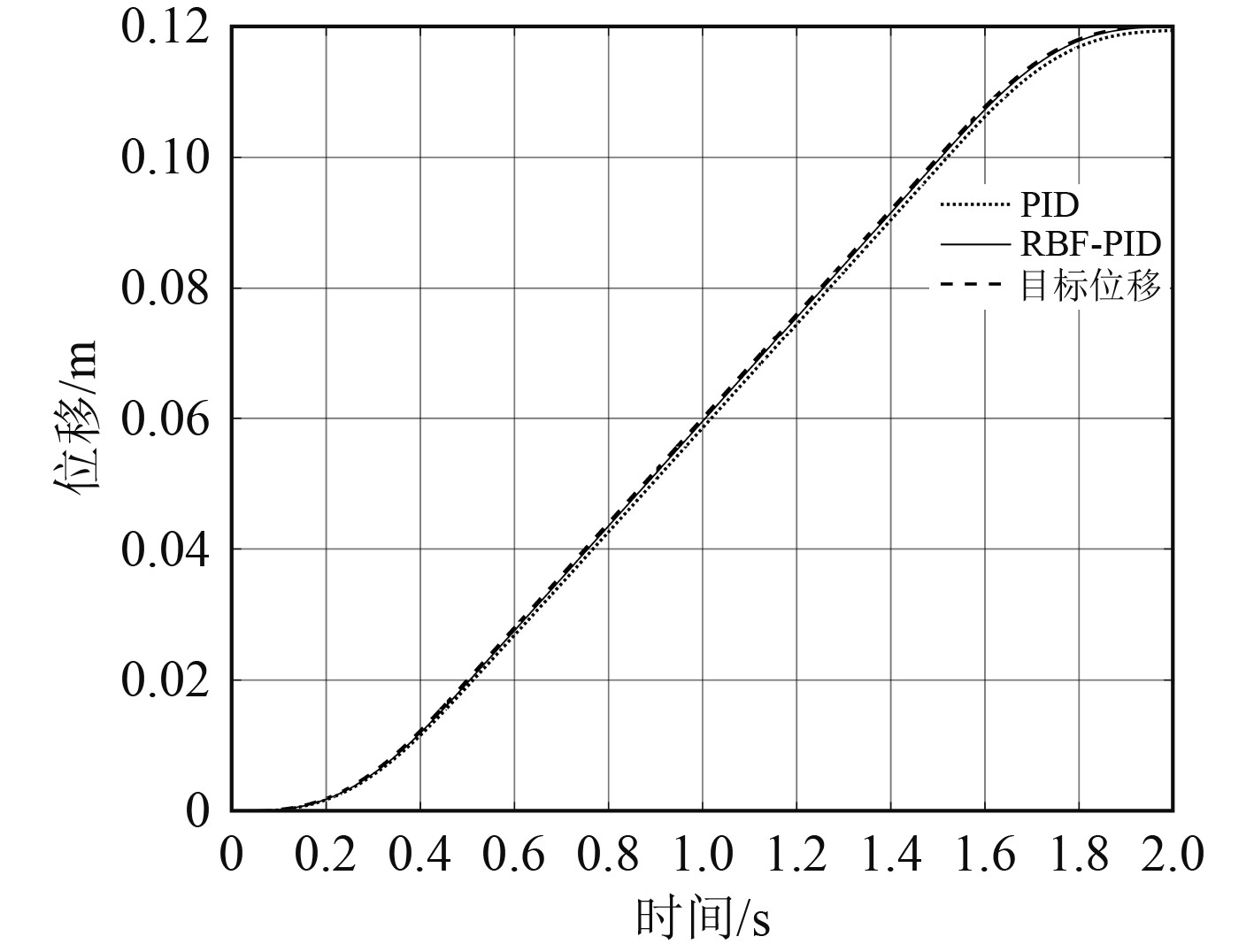
采用RBF-PID控制的仿真曲线与目标速度曲线基本重合，且在启动段和停止段基本没有出现加速度突变，验证了设计的理想速度曲线的可行性。图12为对应的位移响应曲线。

5 结　语

本文对舰载稳定平台的控制进行模型建立和仿真，并验证了设计的理想速度曲线有效性。仿真结果表明，RBF-PID控制器在响应、调整性能、跟踪性能方面均优于常规PID控制器，具有一定的自学习能力。采用RBF-PID控制算法可以在有效提高舰载稳定平台控制精度的同时增强其抗干扰能力，达到了良好的控制效果。