齿轮箱是船舶传动系统的重要组成部分,其工作环境恶劣,易受载荷、振动和冲击等多种因素的影响,从而产生各类故障。故障诊断根据设备运行状态和故障特征,采用合理的诊断策略,对设备进行状态监测和故障诊断[1-3]。基于模型的故障诊断方法存在依赖专家知识和经验、精度低等缺点,尤其在多类故障同时存在时,难以准确识别。深度学习是近年来才被提出的一种新型人工智能方法,其通过将图像处理领域中的深度神经网络(DNN)与深度置信网络(DBN)相结合的方式来进行特征提取与分类。
1 深度神经网络原理DNN是一种具有自组织、自适应、自动学习能力的人工神经网络。考虑到DNN在实际应用中具备多层前馈神经网络,在计算上和传统的线性层相比,能够更加快速地收敛。深度学习模型在本质上是一个多层感知器,即神经元每一个输出都包含了多个隐藏层的神经元的输出。DNN模型可以根据输入数据的不同来决定如何激活某个神经元,进而得到最终的输出。因此,深度神经网络可以通过不断地调整隐藏层来优化网络结构,最终使得模型获得较高的准确度[4-5]。
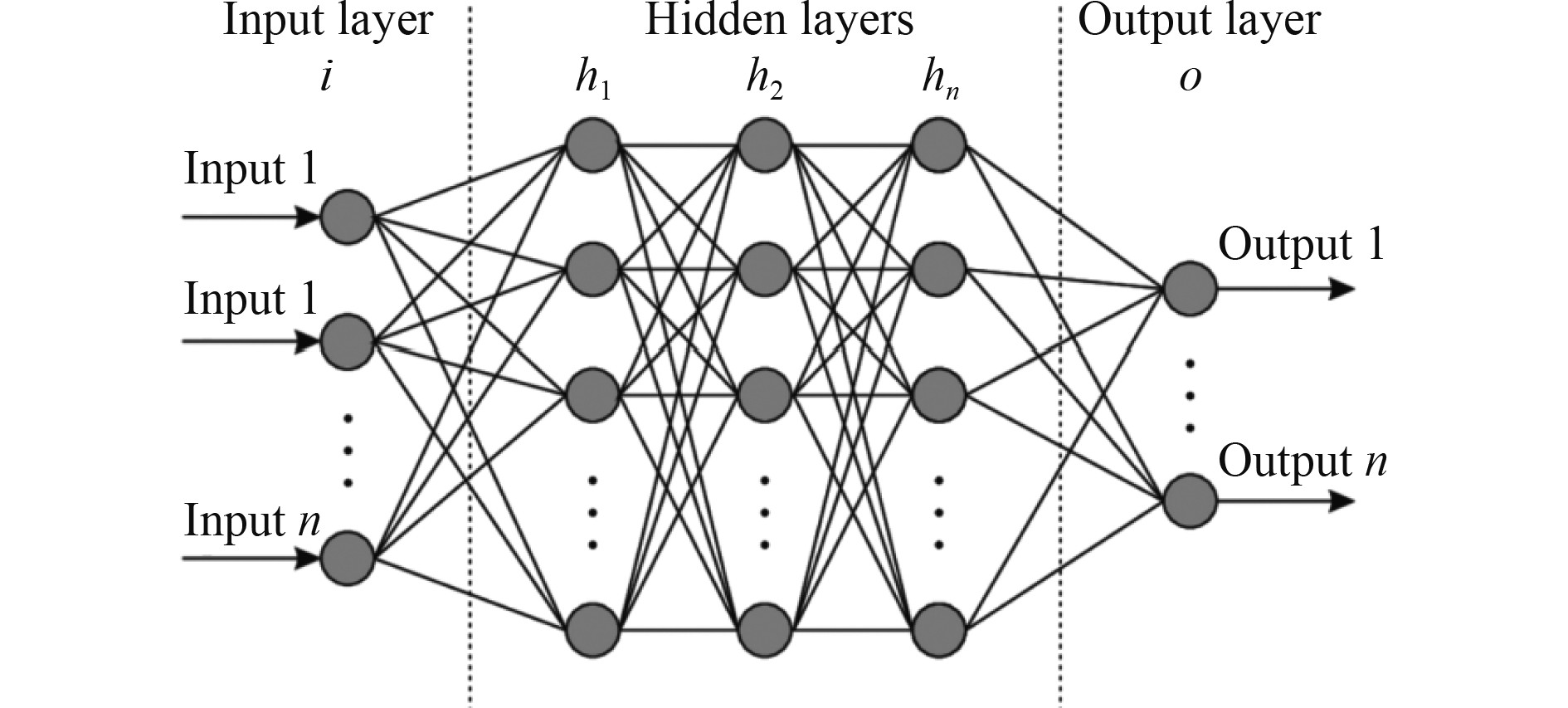
深度神经网络结构如图1所示,深度神经网络由多个隐藏层组成。隐藏层中包含输入层、中间层和输出层3个部分。输入层通过特征提取模块从输入数据中提取特征并作为输入参数输入到中间层中,包含多个神经元,其中每个神经元都包含多个输入参数,这些参数分别对应于不同的输出特征。经过前一步得到的输入数据和中间层维度共同构成了网络模型的输出。输出层将所有这些输出参数通过神经元连接起来,形成一个神经网络结构。最后,在输出层对新的数据进行预测,从而得到整个模型的分类结果。
|
图 1 深度神经网络结构 Fig. 1 Deep neural network structure |
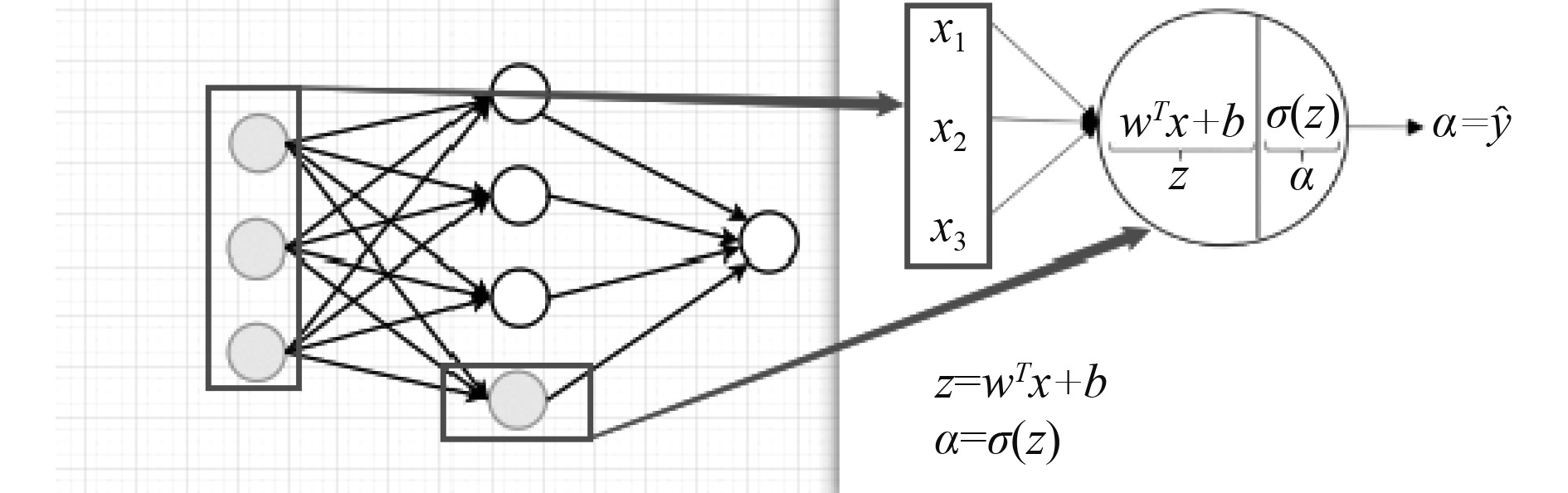
本文通过举例说明逻辑回归算法(LR)的思想,将其应用到DNN中,按照图1所示的结构思路,对某个隐藏层的神经元进行放大,进而得到了图2所示的DNN网络结构
|
图 2 DNN网络结构 Fig. 2 DNN network structure |
输入层的每一个样本特征与隐藏层的特征方程线性拟合得到一个z值,得出以下激活函数:
| $ {\rm{sig}}ma = z(\alpha )\text{。} $ | (1) |
基于以上函数,将z值映射到(0,1)之间的激活值α,得出逻辑回归的基本迭代公式。
其中前向迭代的算法思想是,通过前面一层得到的激活值,计算下一层的Z值,再通过Z值计算激活值A。将样本集如式(2)中样本的每一个特征权重和特征值按列堆叠,可以得到式(3):
| $ S=\left\{\begin{array}{c}{y}_{1}={w}_{11}^{(1)}{x}_{1}+{w}_{12}^{(l)}{x}_{1}+{w}_{13}^{(l)}{x}_{1}\\ {y}_{2}={w}_{21}^{(l)}{x}_{1}+{w}_{22}^{(l)}{x}_{1}+{w}_{23}^{(l)}{x}_{1}\\ \cdots\cdots \\ {y}_{m}={w}_{m1}^{(l)}{x}_{1}+{w}_{m2}^{(l)}{x}_{1}+{w}_{m3}^{(l)}{x}_{1}\end{array}\right\} \text{,} $ | (2) |
| $ {W}^{(l)}=\left[\begin{array}{c}{w}_{11}^{(l)}{w}_{21}^{(l)}\cdots \cdots {w}_{m1}^{(l)}\\ {w}_{12}^{(l)}{w}_{22}^{(l)}\cdots \cdots {w}_{m2}^{(l)}\\ {w}_{13}^{(l)}{w}_{23}^{(l)}\cdots \cdots {w}_{m3}^{(l)}\end{array}\right]\text{,} X=\left[\begin{array}{c}{x}_{1}\\ {x}_{2}\\ {x}_{3}\end{array}\right]\text{。} $ | (3) |
通过一些转换,根据矩阵乘法的计算方式,AB
| $ {Z^{(l)}} = {W^{(l)}}T{X^{(l - 1)}} + {b^{(l)}}\text{,} $ | (4) |
其中,用W(1)的转置矩阵为:
| $ {Z}^{(l)}=\left\{\begin{array}{c}{w}_{11}^{(l)}{w}_{12}^{(l)}{w}_{13}^{(l)}{x}_{1}\\ {w}_{21}^{(l)}{w}_{22}^{(l)}{w}_{23}^{(l)}\\ \cdots \cdots \\ {}_{m1}^{(l)}{w}_{m2}^{(l)}{w}_{m3}^{(l)}{x}_{1}\end{array}\right\}\times \left[\begin{array}{c}{x}_{1}\\ {x}_{2}\\ {x}_{3}\end{array}\right]+{b}^{(l)} \text{。} $ | (5) |
通过给Z(l)套上一个σ函数,由此计算最终的激活值。
2.2 DNN故障诊断模型计算流程DNN是一种可以自动进行特征提取和分类的神经网络模型,它将大量的特征提取操作转移到了网络中的底层,从而极大地降低了特征提取的复杂度。同时,由于其具有自动学习、非线性映射和并行计算等特性,在大数据处理方面具有其他算法所无法比拟的优势。因此,DNN被广泛应用于深度学习领域,主要包括分类、回归、聚类和预测等功能。
DNN模型的初始化:A(l)=X随机初始化一个服从正太分布Wl(=np.random.randn(0,1))但是不能为0,否则计算的结果都是0,没有意义。b可以为0,有了初始化的值,就可以通过公式一步一步迭代得到最后一层的输出结果,也就是需要的预测值A(1)。
在 DNN模型中,输入的数据通过第一个隐含层传递到输出层,经过前一层神经元得到的特征值作为该层的输入。当网络层数超过一定程度时,DNN将当前层数所得到的特征作为下一层输入。
计算第1个隐层如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{Z^{{\text{(1)}}}} = {W^{{\text{(1)}}}}^{\rm{T}}X + {b^{{\text{(1)}}}}},\\ {{A^{{\text{(1)}}}} = \sigma {\text{(}}{Z^{{\text{(1)}}}}{\text{)}}} 。\end{array}} \right. $ | (6) |
基于上式发现,除了第1层的X是X,之后的都是用A(1)来替代。前一层的A(1)就是计算下一层的X,因为A的值是通过Sigmoid激活函数计算出来的,所以A(l)也叫激活值,用来激活下一层的计算。
计算第2个隐层(输出层)得到下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{Z^{{\text{(2)}}}} = {W^{{\text{(2)}}}}^{\rm{T}} X + {b^{{\text{(2)}}}}},\\ {{A^{{\text{(2)}}}} = \sigma {\text{(}}{Z^{{\text{(2)}}}}{\text{)}}} ,\end{array}} \right. $ | (7) |
将计算推广到l层,在l-1层,可以得到下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{Z^{{{({\rm{l}} - 1)}}}} = {W^{{{({\rm{l}} - 1)}}}}^{\rm{T}}{A^{{{({\rm{l}} - 2)}}}} + {b^{{{({\rm{l}} - 1)}}}}},\\ {{A^{{{({\rm{l}} - 1)}}}} = \sigma {\text{(}}{Z^{{{({\rm{l}} - 1)}}}}{\text{)}}} ,\end{array}} \right. $ | (8) |
在l层,可以得到下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{Z^{{\text{(l)}}}} = {W^{{\text{(l)}}}}^{\rm{T}}{A^{{{({\rm{l}} - 1)}}}} + {b^{{\text{(1)}}}}}\text{,} \\ {\hat Y = {A^{{\text{(l)}}}} = \sigma {\text{(}}{Z^{{\text{(l)}}}}{\text{)}}} \text{。} \end{array}} \right. $ | (9) |
由于DNN模型是一种非线性映射模型,因此对输入数据进行特征提取时需要对其进行一定程度的降维处理,即将原始信号经过降噪、降维处理后得到的特征向量作为DNN模型输出特征向量。
在DNN模型中,每个隐含层包含多个神经元节点,其中一个节点通常对应一个输入层和一个隐含层,其余节点则对应多个输入层和隐含层。通常来说,DNN模型具有2种激活函数:Sigmoid函数和ReLU函数。因此在进行特征提取时需要对2种激活函数进行选取。为了方便计算用交叉熵损失函数如下式:
| $ L(\hat y,y) = - (y\ln \hat y + (1 - y)\ln (1 - \hat y)) \text{,} $ | (10) |
由此可以得到代价函数如下式:
| $ J(W,b,X,Y) = - \frac{1}{M}\sum {\left( {Y\ln Y + (1 - Y)\ln (1 - \hat Y)} \right)} 。$ | (11) |
将上述函数获得的结果写成矩阵的形式:
| $ {\boldsymbol{AF}}{{ = }}{\boldsymbol{G}} 。$ |
其中:
| $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1N}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2N}}} \\ \vdots & \vdots & \cdots & \vdots \\ {{r_{M1}}}&{{r_{M2}}}& \cdots &{{r_{MN}}} \end{array}} \right] ,{\boldsymbol{F}} = \left[ \begin{gathered} {f_1} \\ {f_2} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \\ {f_N} \\ \end{gathered} \right] ,{\boldsymbol{G}} = \left[ \begin{gathered} {g_1} \\ {g_2} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \\ {g_M} \\ \end{gathered} \right]。$ |
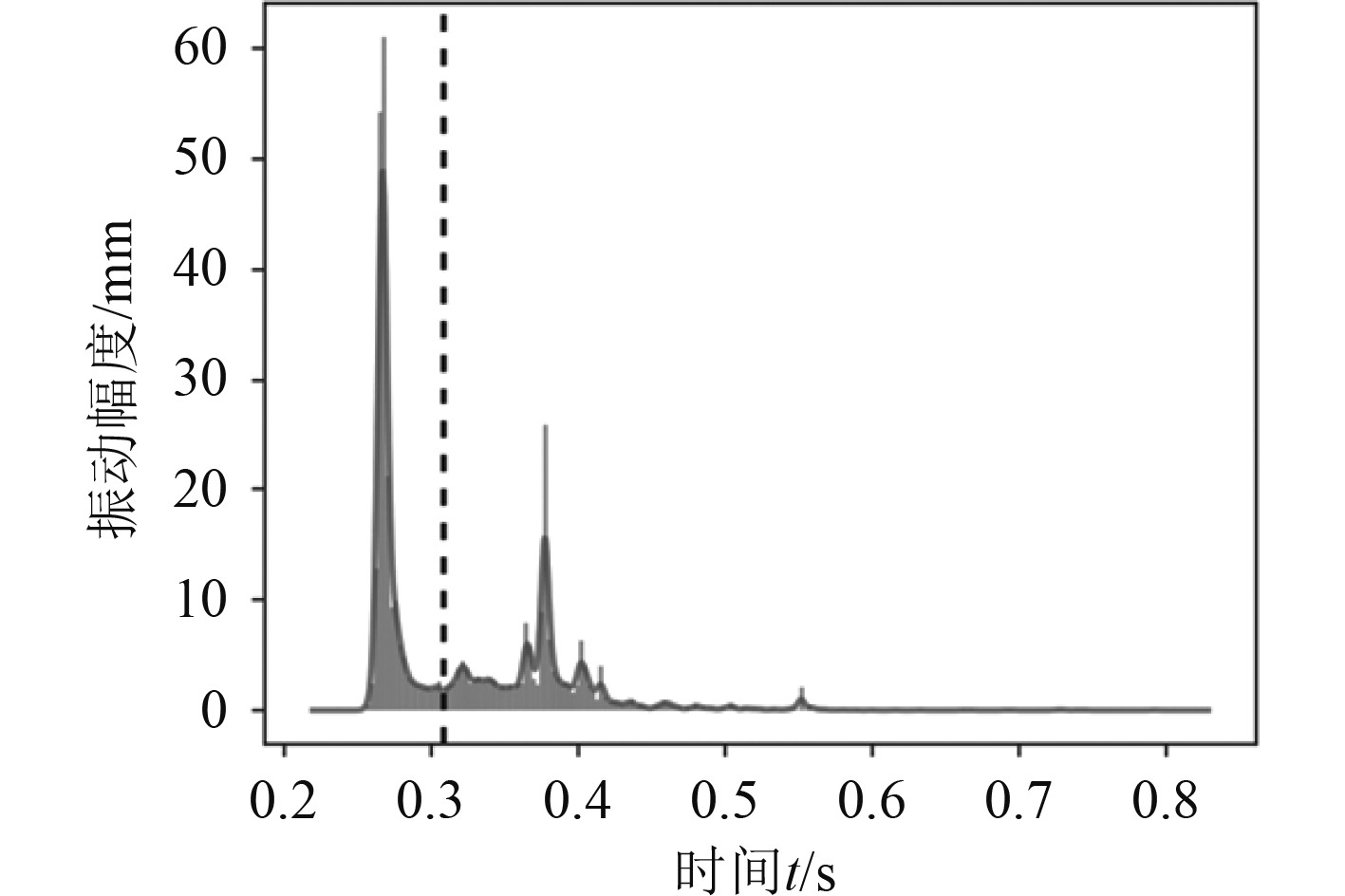
对某船用齿轮箱进行故障诊断,测试信号为齿轮表面振动信号。由于采集到的故障信号含有噪声,数据量较小,故采用小波包分解对原始数据进行处理。首先将原始信号通过小波包分解得到各个频带的分量,然后分别计算各个频带内各个分量的能量值,得到特征向量。该方法处理后的齿轮箱故障诊断数据如图3所示。
|
图 3 齿轮箱运行振动信号图 Fig. 3 Vibration signal diagram of gearbox operation |
将小波包分解后得到的各个频带内各个分量的能量值作为输入特征向量,并借助SVM对其进行故障诊断。在进行SVM故障诊断时需要考虑输入特征向量之间的相关性,然后对模型进行训练。为了避免特征向量之间存在相关性和相关性对模型训练造成不利影响,将故障特征向量进行标准化处理。
然后,根据Matlab软件提供的标准化函数实现对原始数据进行标准化处理。将经过预处理后得到的特征向量作为输入特征向量输入至SVM模型中进行训练与测试。为了保证模型训练过程不受噪声干扰,采用带有阈值和归一化处理的小波包分解方法对数据进行预处理。
3.2 实验验证实验装置是一种能模拟齿轮裂纹、点蚀、断齿、磨损、粘连及轴心错位等多种典型失效形式的实验装置。在测试过程中,采用的压电式加速度传感器经由Matlab软件进行PC端的数据分析。
首先,采用一个1024点的窗口,与深度置信网络(DBN)相结合,对收集到的振动信号进行傅里叶变换,得到一个1750×1024的诊断数据集,接着对各故障样本展开进一步训练,将最终剩余的25个样本视为一个测试数据集。然后,结合频率域信号的维数与故障的种类数目,将网络的层次(含输入层)设定为5个层次,节点数目是1024-500-300-100-5,学习速率是01,最多可以进行100次的迭代。
最后,提出一种基于softmax神经网络方法,输出矩阵形式为:[1,0,0,0,0]表示正常状态,[0,1,0,0,0]表示开裂故障,[0,0,1,0,0]代表断裂齿的缺陷,[0,0,0,1,0]代表点蚀缺陷,[0,0,0,0,1]表示磨损故障。
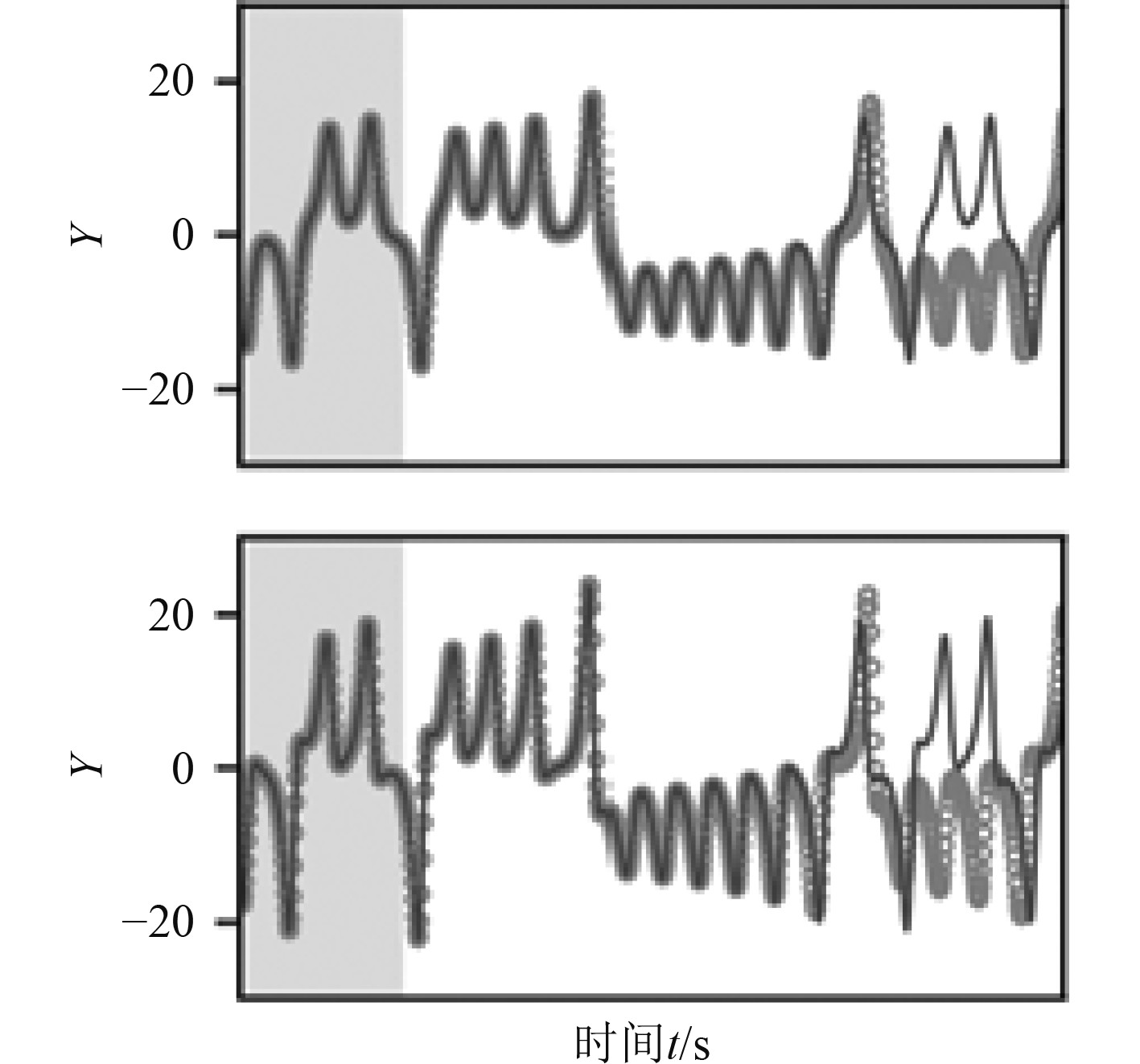
为了更好地体现DBN在图像中的应用,利用基于PC1,PC2和PC3的多维图像进行降维,实现图像的可视化。在此基础上,使用DBN算法从一组故障数据中抽取一组故障特征,并给出一个可视化的结果,如图4所示。
|
图 4 故障特征提取可视化 Fig. 4 Visualization of Fault Feature Extraction |
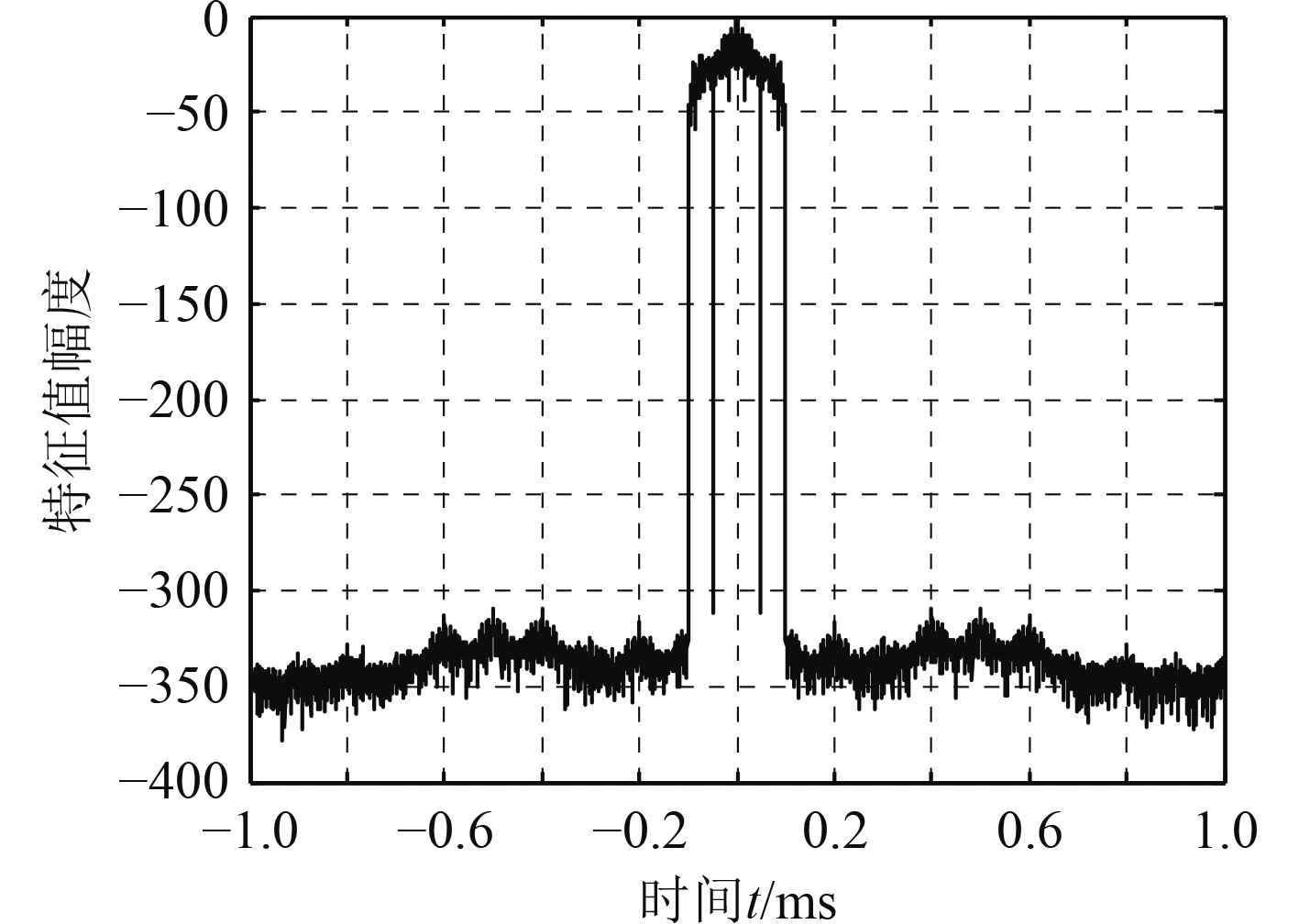
从图4可以看出,在凝聚状态下,原始数据的故障特征并不是很好分辨,误差始终在−20%~20%之间波动。特征值幅度曲线如图5所示。利用DNN算法对故障特征值进行优化,利用隐层进行调整,得出如图6所示的重构误差变化曲线。
|
图 5 特征值幅度曲线 Fig. 5 Eigenvalue magnitude curve |
|
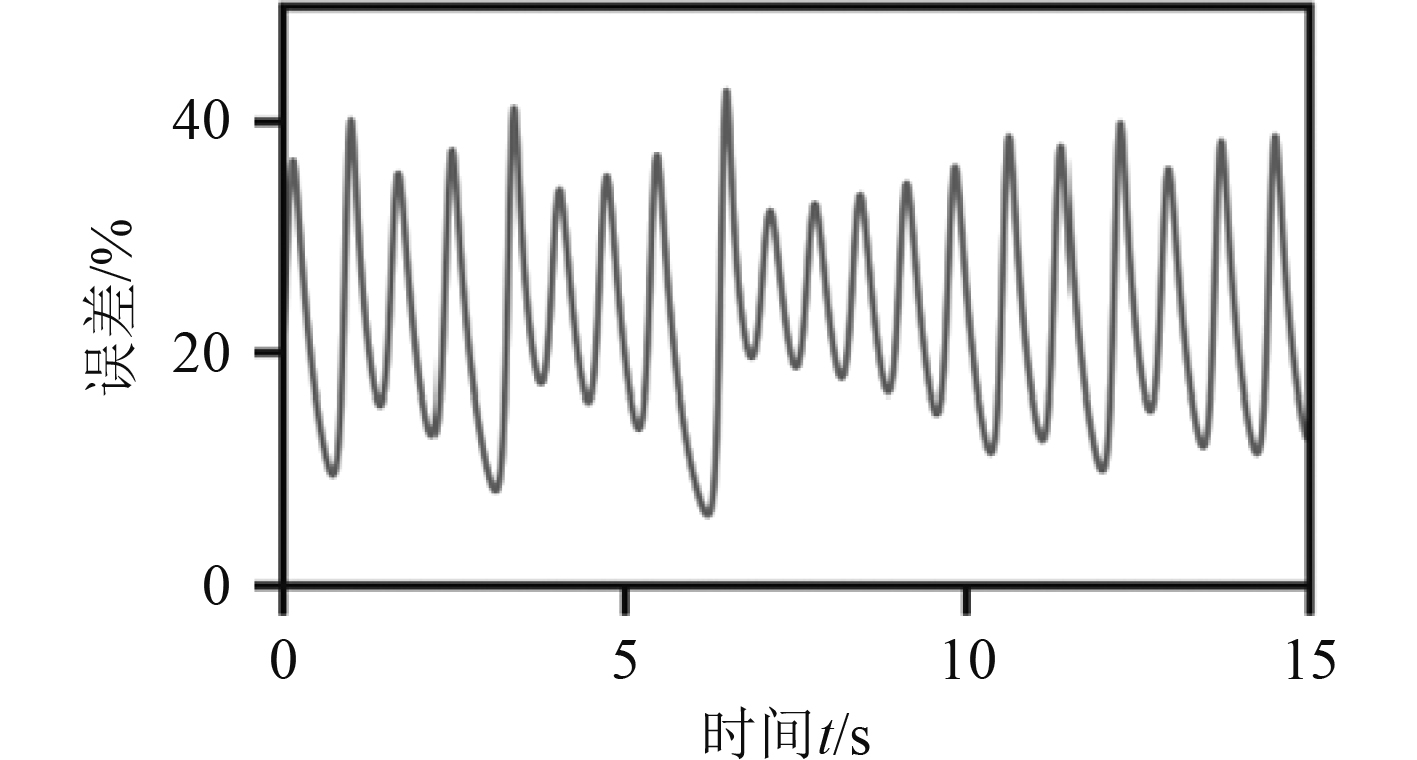
图 6 重构误差变化曲线 Fig. 6 Reconstruction error variation curve |
由图6可知,经过DNN算法一段时间的修正后,深度神经网络的重建精度稳定到20%~40%之间,在更多的数据更新后,重建误差出现了快速的收敛性,表明了该算法的优越性。
综上所述,经本次的最终实验验证后,得出深度神经网络在齿轮传动系统中的应用效果良好,对齿轮传动系统中出现的各种故障有很好的判别能力,其判别效果与实际状况一致,表明深度神经网络在齿轮传动系统中的应用是可行的。
4 结 语本文针对船用齿轮箱的振动信号特征提取和故障诊断,提出基于深度神经网络的故障诊断方法。采用基于模型的方法,先使用原始数据对模型进行训练,然后再将经过训练后的模型应用于新的数据,最后使用测试数据验证了该方法的有效性。实验结果表明,DNN在船用齿轮箱的相关故障诊断中,不仅精度高,而且收敛性好。主要结论如下:
1)虽然其收敛速度相对较慢,但对于具有一定数据量的系统,其收敛速度也能够满足使用要求。
2)由于船用齿轮箱振动信号特征复杂多变,本文通过大量实验研究,确定了DNN模型中最佳参数和超参数。
3)为了进一步提高故障诊断效果,可以通过增加DNN模型的层数、提高 DNN模型的隐含层节点数以及减小DNN模型中残差单元和随机单元等方式来进一步提高DNN模型的诊断性能。
基于深度神经网络的船用齿轮箱故障诊断方法具有一定的应用价值,今后将进一步研究模型优化、输入信号处理方式等。
| [1] |
骆江锋, 龙江启, 范进桢. 小波包和BP神经网络在齿轮箱故障诊断中的应用[J]. 机械传动, 2007(3): 84-90. DOI:10.3969/j.issn.1004-2539.2007.03.028 |
| [2] |
郑鹏飞, 周新聪, 方军强, 等. 基于深度信念网络在船用齿轮箱故障诊断中的应用研究[J]. 中国修船, 2018, 31(6): 32-36. DOI:10.13352/j.issn.1001-8328.2018.06.009 |
| [3] |
吕翔宙, 荆锴. 基于BP神经网络风机齿轮箱故障特征信号分析与诊断[C]. 天津市电子学会, 天津市仪器仪表学会. 第三十五届中国(天津)2021’IT、网络、信息技术、电子、仪器仪表创新学术会议论文集. 天津市电子会, 2021: 39–42.
|
| [4] |
许敬成, 陈长征. BP神经网络在齿轮箱故障诊断中的应用[J]. 噪声与振动控制, 2018, 38(2): 673-677. DOI:10.3969/j.issn.1006-1355.2018.Z1.146 |
| [5] |
赵天宇, 宿吉鹏, 邵钢, 等. 船用分扭人字齿轮传动系统振动能量与疲劳寿命研究[J]. 热能动力工程, 2021, 36(12): 111-117. DOI:10.16146/j.cnki.rndlgc.2021.12.017 |
 2023, Vol. 45
2023, Vol. 45
